Abstract
We suggest a new variant of a row layout problem: Find an ordering of n departments with given lengths such that the total weighted sum of their distances to a given checkpoint is minimized. The Checkpoint Ordering Problem (COP) is both of theoretical and practical interest. It has several applications and is conceptually related to some well-studied combinatorial optimization problems, namely the Single-Row Facility Layout Problem, the Linear Ordering Problem and a variant of parallel machine scheduling. In this paper we study the complexity of the (COP) and its special cases. The general version of the (COP) with an arbitrary but fixed number of checkpoints is NP-hard in the weak sense. We propose both a dynamic programming algorithm and an integer linear programming approach for the (COP) . Our computational experiments indicate that the (COP) is hard to solve in practice. While the run time of the dynamic programming algorithm strongly depends on the length of the departments, the integer linear programming approach is able to solve instances with up to 25 departments to optimality.
Keywords: Combinatorial optimization, dynamic programming, integer linear programming, global optimization, facilities planning and design
1. Introduction
In this paper we introduce and analyse a new variant of a row layout problem. An instance of the Checkpoint Ordering Problem (COP) consists of n one-dimensional departments, with given positive lengths 
and weights 
, and a checkpoint on a fixed position, e.g. left-aligned or at the center position. The optimization problem can be written down as
 |
(1) |
where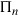 
is the set of permutations of the indices 
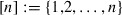and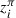 
is the distance between the center of department i and the checkpoint with respect to a particular permutation 
.
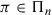Let us start with elaborating on the connections of the (COP) to the Linear Ordering Problem (LOP), the Single-Row Facility Layout Problem (SRFLP) and scheduling on identical parallel machines with the objective of minimizing the sum of weighted completion times.
1.1. The Single-Row Facility Layout Problem (SRFLP)
The simplest known layout type is single-row layout. It arises as the problem of ordering stations on a production line, where the material flow is handled by an automated guided vehicle (AGV) in both directions on a straight-line path [1]. An instance of the (SRFLP) consists of n one-dimensional departments, with given positive lengths 
, and pairwise weights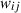 
. The optimization problem can be written down as
 |
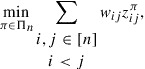(2) |
where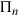 
is the set of permutations of the indices [n] and 
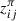is the center-to-center distance between departments i and j with respect to a particular permutation 
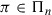. Note that the weights are assumed to be non-negative for all row layout problems to ensure boundedness of the objective value of the optimal layout. For the (SRFLP) 
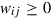further guarantees that all departments are placed next to each other without spacing. For the (COP) we do not need this restriction on the weights as space between the departments is not allowed.
Several practical applications of the (SRFLP) have been identified in the literature, such as the arrangement of rooms on a corridor in hospitals, supermarkets, or offices [2], the assignment of airplanes to gates in an airport terminal [3], the arrangement of machines in flexible manufacturing systems [1], the arrangement of books on a shelf and the assignment of disk cylinders to files [4].
Similar applications are conceivable for the (COP), e.g. the rooms on a corridor could be arranged such that the weighted sum of their distances with the office of the head is minimized or planes could be assigned to gates such that the weighted sum of their distances from the entrance of the airport terminal is minimized. When comparing the (SRFLP) with the (COP), we observe that the problems are quite similar. One difference is that an (SRFLP) instance has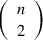 
weights while a (COP) instance has only n weights.
1.2. The Linear Ordering Problem (LOP)
Ordering problems associate to each ordering (or permutation) of the set [n] a profit and the goal is to find an ordering of maximum profit. In the simplest case of the Linear Ordering Problem (LOP) , this profit is determined by those pairs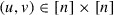 
, where u comes before v in the ordering. Thus in its matrix version the (LOP) can be defined as follows. Given an 
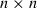matrix 
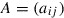of integers, find a simultaneous permutation 
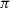of the rows and columns of A such that
 |
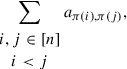is maximized. Equivalently, we can interpret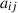 
as weights of a complete directed graph G with vertex set 
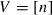. A tournament consists of a subset of the arcs of G containing for every pair of nodes i and j either arc (i, j) or arc (j, i), but not both. Then the (LOP) consists of finding an acyclic tournament, i.e. a tournament without directed cycles, of G of maximum total edge weight.
Although the (LOP) and the (COP) have apparently a similar structure, it is harder to directly relate these two problems. We will show in Section 2 that the (COP) with left-aligned or right-aligned checkpoint is in fact a (LOP) with some additional structure and can be solved efficiently by a greedy algorithm.
1.3. Scheduling on identical parallel machines
Furthermore we can relate the (COP) to the NP-hard [5] scheduling on identical parallel machines with the objective of minimizing the total weighted completion time that is defined as follows: We are given a set of jobs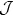 
that have to be scheduled on m identical parallel machines. Each job 
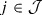is specified by its processing time 
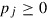and by its weight 
.
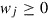Every machine can processat most one job at a time, and every job has to be processed on one machine in an uninterrupted fashion. The completion time of job j is denoted by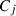 
. The goal is to minimize the total weighted completion time 
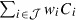. In the standard classification scheme of [6], this scheduling problem is denoted by 
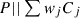for m part of the input, and by 
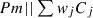for constant m.
For the special case of only one machine the problem can be solved in polynomial time by Smith’s Rule [7] that suggests to process the jobs in the order of non-increasing ratios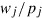 
. For a constant number 
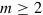of machines, the problem is weakly NP-hard as it can be solved in pseudopolynomial time by dynamic programming approaches [8–10]. For m part of the input, the problem is NP-hard in the strong sense by transformation from 3-PARTITION [11]. For further details on the complexity of various related variants of this scheduling problem we refer to problem SS13 in [11]. For a more general overview on machine scheduling we refer to the survey article by [12].
From a computational point of view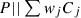 
has been tackled by various branch-and-bound methods [13–17], for which determining the optimal solution of instances with 30 or more jobs and two or more identical machines is typically difficult [18].
When comparing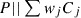 
and the (COP), we observe that there two important differences between the two problems:
-
(1)
The checkpoint must not lie exactly at a splitting point of two departments but it can also be covered by a department. I.e. the checkpoint does not necessarily define a partition of the departments. When considering a scheduling set-up the (COP) can be described as follows: It is allowed to split one arbitrary job into two parts at any point and then the two parts have to be scheduled first on the two machines.
-
(2)
For the (COP) the sum of the lengths of the departments that are placed to the left and to the right of the checkpoint are predetermined through the position of the checkpoint. E.g. for a centered checkpoint the sum of the lengths of the departments to the left and to the right of the checkpoint has to be equal. For
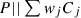the identical machines typically have no capacity restrictions.
Due to these differences it is not possible to directly carry over polyhedral results, dynamic programming algorithms and (mixed) integer linear programming (ILP) models and their corresponding approximation results [19] from scheduling on identical parallel machines to the (COP).
1.4. Toy examples
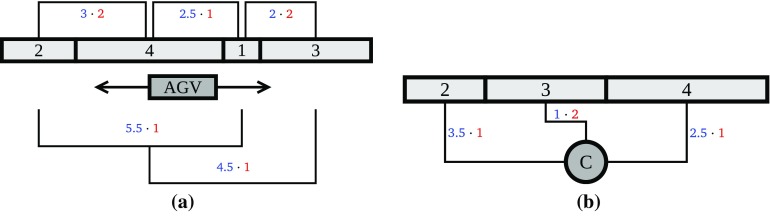
Now let us further clarify the similarities and differences of the (SRFLP) and the (COP) with the help of a toy example: We consider 4 departments with lengths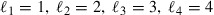 
. Additionally we are given the pairwise weights 
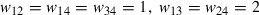. For the (COP) we assign department 1 to row 2 and all other departments to row 1 and hence disregard the weights 
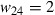and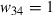 
. Figure 1 illustrates the optimal layouts and the associated costs for both problems.
Figure 1.
We are given the following data: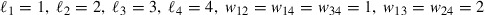 
. In (a) we display the optimal layout for the (SRFLP) with corresponding costs of 
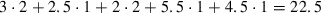. And in (b) we depict the optimal layout for the (COP) with department 1 assigned to row 2 and all other departments assigned to row 1, disregarding the weights 
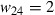and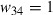 
. Further we assume that the checkpoint lies at the center. Then the costs of the optimal (COP) layout are 
.
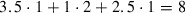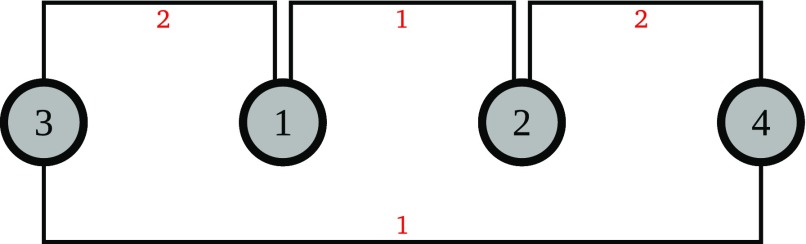
Finally we also want to clarify the workings of the (LOP) with the help of a toy example. We consider 4 objects and the weights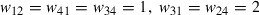 
. Figure 2 illustrates the optimal ordering of the objects and the corresponding benefit.
Figure 2.
We are given 4 objects and the weights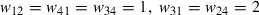 
. We display the optimal (LOP) solution with the corresponding benefit of 
.
1.5. Outline
The main contributions of this paper are the following:
We propose a new combinatorial optimization problem that is both of theoretical and practical interest.
We study the complexity of the (COP) and its special cases, pointing out several connections to related problems.
We propose two exact approaches for the (COP), namely a dynamic programming algorithm and an ILP approach.
We demonstrate the practical difficulty of the (COP) in a computational study. In this context let us also refer to our companion paper [20] for a comparison of the empirical difficulty of several row facility layout problems (including the (COP) ) on a variety of well-known benchmark instances.
The paper is structured as follows. In Section 2 we study the complexity of the (COP) and its special cases. In Sections 3 and 4 we suggest a dynamic programming algorithm and an ILP approach for the (COP) respectively. Finally in Section 5 we conduct computational experiments, indicating the practical applicability and limitations of the approaches suggested. Section 6 concludes the paper.
2. Complexity of the Checkpoint Ordering Problem
Consider the decision variant of the (COP) : given some value M we ask whether there exists a permutation of the departments such that the obtained costs are at most M:
Decision Checkpoint Ordering (DCO):
Instance: n departments with given lengths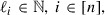 
and integer weights 
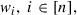and a checkpoint on a fixed position.
Question: Is there an ordering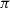 
of the departments such that the total costs 
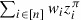are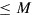 
?
In the following proof we assume w.l.o.g. that the checkpoint is located at the center in order to simplify the presentation.
Theorem 1:
DCO is NP-complete.
Proof 1It is clear that DCO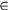 
NP since a nondeterministic algorithm needs only to guess an ordering 
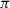and then can check in polynomial time if the corresponding costs are 
.
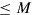To prove that DCO is NP-complete, we give an NP-complete problem and a polynomial-time transformation to DCO. The following problem is NP-complete (see Section 3.1.5 of [11], originally proven by [21]):
PARTITION:
Instance: A finite set A and a ‘size’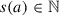 
for each 
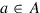such that 
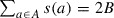is even.
Question: Is there a subset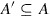 
such that 
?
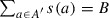Now we transform an instance of PARTITION to an instance of DCO as follows. We replace each element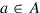 
with given size s(a) by a department a with length 
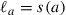and weight 
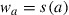. Additionally to this local replacement we use an enforcer by introducing a further department t with length 
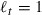and weight 
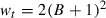. Clearly this DCO instance can be constructed from the PARTITION instance in polynomial time.
If the ordering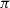 
is optimal then the center of department t is located exactly above the checkpoint because of the large weight of department t. Due to the definition of the weights of the departments 
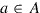, it does not change the objective value if we switch the positions of two departments both located left or right of t. Hence the only way to influence the objective value is to decide whether the departments should be located left or right of t. If we can find a subset 
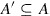of the departments such that 
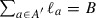and place them left of t and all other departments right of t, then the corresponding ordering 
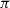is for sure optimal. If the sum of lengths of the departments left of t in the optimal ordering 
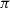does not give B, then there exists no subset 
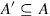such that 
.
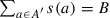In summary we have shown that there exists an ordering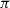 
of the departments such that the total costs are 
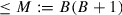if and only if there exists a subset 
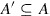of the corresponding PARTITION instance such that 
.
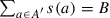In the layout context the above result can be interpreted as follows: The minimization of the inter-row costs that occur in all multi-row layout problems is NP-hard, even in its simplest version. This is not only an interesting theoretical insight on its own but also supports our definition of the Single-Row bound in our companion paper [20]. Next let us consider some more specialized versions of the (COP) that turn out to be solvable by a greedy algorithm and hence in particular in polynomial time.
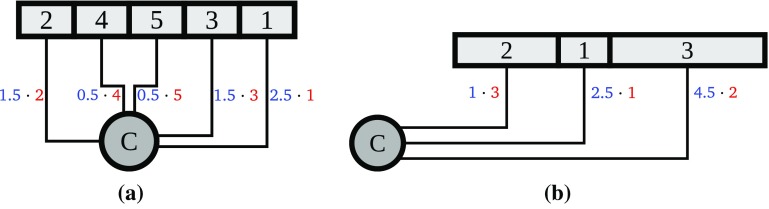
First we assume that all departments have the same length. In this case the optimal permutation of the departments can be obtained by a simple greedy selection. We choose the permutation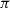 
with the following property: The higher the weight of a department the smaller is its distance from the checkpoint. Next we give a short formal argument for the above claim and refer to Figure 3 for a toy example of this variant of the (COP).
Figure 3.
In (a) we display the optimal layout for the (COP) with identical department lengths equal to 1 and weights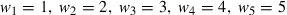 
. The corresponding layout costs are 
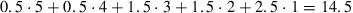. In (b) we show the optimal layout for the (COP) with left-aligned checkpoint on the following instance with 3 departments: 
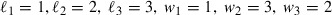. The associated layout costs are 
.
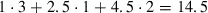Fact 2:
A permutation
is optimal for the (COP) with identical department lengths iff it ensures the inequalities
(3) where
denotes the distance of the center of department i from the checkpoint.
Proof 2The change of the objective function caused by swapping two departments i and j is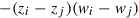 
. Hence in particular the change in the objective function caused by this swap is independent of the length and weights of all other departments 
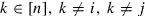. Now assume that there exists an optimal permutation that does not ensure one inequality in (3), i.e. 
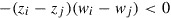for some departments i and j. Now swapping the two departments improves the objective value. As all other departments are not affected by pairwise swaps, it is not possible to improve the objective value by an arbitrary number of pairwise changes if (3) holds. Hence (3) is not only a necessary condition but also a sufficient one.
Note that the special case of the (SRFLP) where all department lengths are equal and the weights are binary is still NP-hard [22]. This problem is called Minimum Linear Arrangement (LA), belongs to the class of graph layout problems and is NP-hard even if the underlying graph G is bipartite [11]. (LA) was originally proposed by Harper [23,24] to develop error-correcting codes with minimal average absolute errors and was since then applied to VLSI design [25], single machine job scheduling [26,27] and computational biology [28,29]. There exist approximation algorithms for (LA) with performance guarantee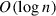 
[30,31] and 
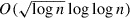[32,33]. For further details on graph layout problems we refer to the survey paper of Díaz et al. [34].
Next we assume that the checkpoint is left-aligned or right-aligned. Also in this case the optimal permutation of the departments can be obtained by a simple greedy selection. We choose the permutation 
with the following property: The higher the relative weight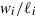 
of a department i, the smaller is its distance from the checkpoint. Next we give a short formal argument for the above claim and refer to Figure 3 for a toy example of this variant of the (COP) . To facilitate the presentation of the proof, we assume w.l.o.g. that
-
(1)
the checkpoint is left-aligned and
-
(2)
the relative weights
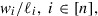are all distinct.
The following result is in fact known as Smith’s Rule [7] in the scheduling context, where it describes a greedy algorithm to solve single-machine scheduling with the objective of minimizing the sum of completion times. For convenience we restate the proof in our notation.
Fact 3:
[7] The permutation
is optimal for the (COP) with a left-aligned checkpoint iff it satisfies the conditions
(4)
Proof 3Assume that there exists an optimal permutation that does not satisfy condition (4) for two departments i and j: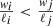 
and 
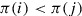. Then there are also two neighboring departments k and l (
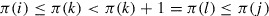) that do not satisfy condition (4): 
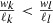and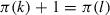 
. Now if we swap k and l, the value of the objective function changes by the term 
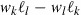. But this term is negative as 
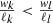holds which yields a contradiction to the assumption that the permutation was optimal. Finally note that condition (4) defines a unique permutation, hence it is not only necessary but also sufficient.
We can interpret the (COP) with left-aligned checkpoint also as a (LOP) with special structure. We collect the lengths of the departments in a column vector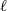 
and the weights of the departments in a column vector c. Now we aim to find a simultaneous permutation 
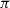of the rows and columns of 
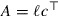such that
 |
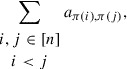is minimized. Contrary to the general (LOP), which is NP-hard [22], the matrix entries of W are not independent but determined by an outer product of two vectors. We have just seen in Fact 3 that the (COP) with left-aligned checkpoint can be solved by a simple greedy heuristic. Hence this special structure of the (LOP) cost matrix W as an outer product of two vectors is the reason why this (LOP) version can be solved in polynomial time.
We summarize the above results as follows: The (COP) is NP-hard and its ‘hard’ part is to determine where the centers of the departments are located with respect to the checkpoint in the optimal solution. In the following section we show that the (COP) with one checkpoint that is neither left- nor right-aligned can be solved by a dynamic programming algorithm and hence is NP-hard in the weak sense. If the number of checkpoints is not part of the input, then the (COP) is NP-hard in the strong sense.
3. A Dynamic Programming Algorithm for the (COP)
We exploit the following two simple properties of (COP) layouts for designing a dynamic programming algorithm:
In every (COP) layout there is at most one department covering the checkpoint. All other departments lie completely to the left or to the right of the checkpoint.
In an optimal (COP) layout all departments, except for the department covering the checkpoint, have to be arranged in non-increasing order from the checkpoint to the border of the layout with respect to their relative weights
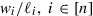. This structural characteristic is denoted as V-shaped property [35,36].
In order to simplify the description of our dynamic programming algorithm we assume w.l.o.g. that the checkpoint is centered and hence that the sum of the lengths of the departments to the left and to right of the checkpoints has to be equal. Now let us outline the workings of our dynamic programming algorithm in detail.
The input for our algorithm is a (COP) instance, where the list of departments is given in non-decreasing order with respect to their relative weights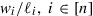 
. First we choose one of the given departments as center department that covers the checkpoint, where 
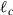is the length of the center department, 
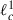is the length of the part of the center department left to the checkpoint and 
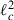is the length of the part of the center department right to the checkpoint. Hence 
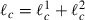and additionally due to symmetry we can always assume w.l.o.g. that 
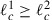holds.
Next we choose an alignment of the center department above the checkpoint: We start with the right end of the center department above the checkpoint and then shift the center department 0.5 to the right in each iteration until the center of the center department is placed directly above the checkpoint. Clearly it suffices to consider 0.5 shifts of the center department as the checkpoint is centered and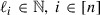 
. In the inner loops we determine with the help of the following recursive relation whether to place the remaining departments to the left or to the right of the checkpoint
 |
(5) |
where s indicates the remaining free space to the left of the checkpoint and M gives the overall remaining free space either to the left or to the right of the checkpoint, which is equal to the sum of the lengths of the departments not yet assigned. As we arrange the departments in non-increasing order with respect to their relative weights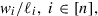 
from the checkpoint to the border, the V-shaped property of the resulting layout is ensured.
We refer to Algorithm 1 for a detailed description of our dynamic programming algorithm that we implemented in C. In Section 5 we computationally compare the dynamic programming algorithm to an ILP approach for the (COP) that we suggest in the following section. In summary our dynamic programming algorithm for solving the (COP) runs in pseudo-polynomial time, to be precise in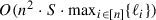 
with
 |
(6) |
Hence the (COP) with one checkpoint is NP-hard in the weak sense. If the number of checkpoints is not part of the input, then the (COP) is NP-hard in the strong sense, which can be proven by a deduction from 3-PARTITION.
To further clarify the workings of our dynamic programming algorithm let us consider a toy example with centered checkpoint and the following input data: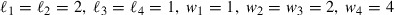 
. The optimal objective value is 9 and the optimal layouts are (1, 3, 4, 2), (1, 4, 3, 2), (2, 3, 4, 1) and (2, 4, 3, 1). All 
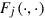-values for 
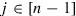that were determined by our algorithm for this example are stated in Figure 4.
Figure 4.
All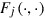 
-values for 
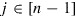that were determined by our dynamic programming algorithm for a toy example with centered checkpoint and input data 
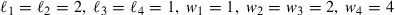. The optimal objective value is 9 and the optimal layouts are (1, 3, 4, 2), (1, 4, 3, 2), (2, 3, 4, 1) and (2, 4, 3, 1).
4. An ILP Formulation for the (COP)
In the section we propose an ILP approach for solving the (COP) . To simplify the notation, we consider the (COP) on 
departments. First we introduce binary ordering variables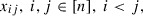 
with the interpretation
 |
(7) |
in order to relate the positions of the 
departments to each other and to the checkpoint n that is again w.l.o.g. assumed to be centered. To ensure transitivity on the ordering variables we use the 3-cycle inequalities
 |
(8) |
that rule out the existence of directed 3-cycles and are sufficient for guaranteeing that there is no directed cycle.
Now the distances of the departments from the checkpoint can be expressed as quadratic terms in ordering variables: For department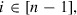 
we sum up the lengths of the departments left of i plus 
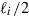and denote it by 
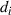. Furthermore we compute the position of the checkpoint 
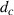as S / 2, i.e. the total length of the departments divided by 2. Then we subtract 
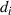from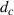 
. This difference gives the distance of the center of department i from the checkpoint, if department i is located to the left of the checkpoint. If department i is located to the right of the checkpoint, this difference is minus the distance of the center of department i from the checkpoint. Therefore we multiply this difference by the term 
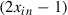that is 1, if the center of department i lies to the left of the checkpoint and 
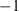if the center of department i lies to the right of the checkpoint:
 |
(9) |
with
 |
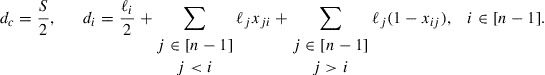The additional multiplication with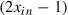 
ensures a correct calculation of all distances through the following constraints:
 |
(10) |
Expanding and simplifying (9) yields
 |
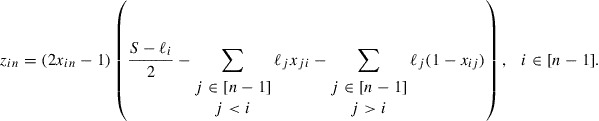(11) |
To model the (COP) as an ILP we apply standard linearization and introduce new variables for all products of ordering variables in (11):
 |
(12) |
Note that we have to introduce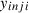 
for all 
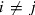as the variable i appears twice in the indices. Now (11) can be further rewritten as:
 |
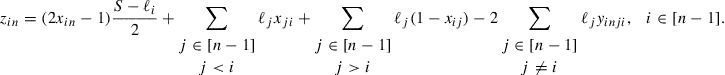(13) |
Moreover we use the following standard constraints to relate the orderings variables and their products:
 |
(14) |
In summary we obtain the following ILP model for the (COP) :
 |
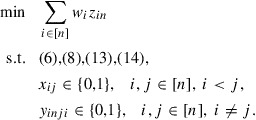In the following section we computationally compare an ILP approach based on this model with our dynamic programming algorithm introduced in the previous section.
5. Computational experiments
We report the results of computational experiments with our dynamic programming algorithm and ILP approach respectively. All computations were conducted on an Intel Xeon E5160 (Dual-Core) with 2 GB RAM, running Debian 5.0 in 64-bit mode. The algorithms were implemented in C (dynamic programming algorithm) and Gurobi 6.5 (ILP) respectively. To generate (COP) instances we use layout benchmark instances from the literature by simply choosing one department i as checkpoint and deducing the (COP) weights from the pairwise weights as follows: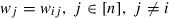 
. In order to test the effect of varying department lengths on our approaches, we generated additional instances using the same weights but substituting the original department lengths lying in the range of 1–20 with random department lengths between 1 and 10,000. We add an L to the instance name for indicating the instances with the new random department lengths. All instances considered can be downloaded from http://tinyurl.com/layoutlib.
In Tables 1 and 2 we state the results of our ILP approach. For instances with up to 25 departments the ILP succeeds in determining the optimal solution. For instances with a higher number of departments (except from ‘ste36.5’) we observe quite large gaps even after 24h. The performance of the ILP approach is hardly influenced by the department lengths as can be seen by comparing the results in Tables 1 and 2.
Table 1.
Results obtained by our ILP approach on instances with regular department lengths using Gurobi 6.5 [37] restricted to one thread on our machine with a time limit of 24 h. The running times are given in sec or in h:min:sec respectively.
| Instance | Lower bound | Upper bound | Gap in % | Time | B&B nodes |
|---|---|---|---|---|---|
| P15 | 189 | 189 | 0.0 | 30 | 15360 |
| P17 | 675.5 | 675.5 | 0.0 | 1:59:00 | 2368737 |
| P18 | 679.5 | 679.5 | 0.0 | 3:05:00 | 3241655 |
| H_20 | 710 | 710 | 0.0 | 5:30:00 | 4767725 |
| N25_05 | 368 | 368 | 0.0 | 17:00:00 | 3885648 |
| H_30 | 645 | 1441 | 55.2 | 24:00:00 | 1593134 |
| N30_05 | 973.5 | 3224.5 | 68.8 | 24:00:00 | 1514491 |
| Am33_03 | 600.5 | 1898.5 | 86.4 | 24:00:00 | 106547 |
| Am35_03 | 185.5 | 2132.5 | 91.3 | 24:00:00 | 210111 |
| ste36.5 | 1444 | 1444 | 0.0 | 1:24:00 | 38781 |
| N40_5 | 81 | 2772 | 97.1 | 24:00:00 | 42135 |
| sko42-5 | 84 | 4059 | 97.9 | 24:00:00 | 27352 |
Table 2.
Results obtained by our ILP approach on instances with large department lengths using Gurobi 6.5 [37] restricted to one thread on our machine with a time limit of 24 h. The running times are given in min:sec or in h:min:sec respectively.
| Instance | Lower bound | Upper bound | Gap in % | Time | B&B nodes |
|---|---|---|---|---|---|
| P15L | 148059.5 | 148059.5 | 0.0 | 1:08 | 24589 |
| P17L | 438935.5 | 438935.5 | 0.0 | 28:25 | 504935 |
| P18L | 589182.5 | 589182.5 | 0.0 | 24:51 | 225180 |
| H_20L | 245666 | 245666 | 0.0 | 2:43:41 | 1109189 |
| N25_05L | 401212.5 | 555504.5 | 27.7 | 24:00:00 | 3050435 |
| H_30L | 389374 | 754755 | 48.4 | 24:00:00 | 4860433 |
| N30_05L | 239436 | 935762.5 | 74.4 | 24:00:00 | 483913 |
| Am33_03L | 138929.5 | 1094984.5 | 87.3 | 24:00:00 | 322711 |
| Am35_03L | 24.5 | 1645539.5 | 100 | 24:00:00 | 44175 |
| ste36.5L | 813222.5 | 814001.5 | 0.1 | 24:00:00 | 662589 |
| N40_5L | 192379 | 2518555 | 92.4 | 24:00:00 | 535358 |
| sko42-5L | 67631 | 2363015 | 97.1 | 24:00:00 | 411416 |
In Tables 3 and 4 we state the results of our dynamic programming algorithm that determines the optimal solution for all benchmark instances with short department lengths within seconds. As our dynamic programming algorithm runs in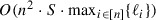 
, it is much slower on the benchmark instances with large department lengths, where it is able to solve instances with up to 33 departments. If the dynamic programming algorithm does not finish within the time limit, then it does not provide a lower bound and hence also no global gap for the optimal solution.
Table 3.
Results obtained by our dynamic programming algorithm on instances with regular department lenghts. The running times are given in sec.
| Instance | Optimum | Time |
|---|---|---|
| P15 | 189 | 0.01 |
| P17 | 675.5 | 0.02 |
| P18 | 679.5 | 0.02 |
| H_20 | 710 | 0.15 |
| N25_05 | 368 | 0.03 |
| H_30 | 1439 | 0.46 |
| N30_05 | 3191.5 | 3.70 |
| Am33_03 | 1879.5 | 0.55 |
| Am35_03 | 2116.5 | 0.32 |
| ste36.5 | 1444 | 1.73 |
| N40_5 | 2747 | 0.64 |
| sko42-5 | 3694 | 6.42 |
Table 4.
Results obtained by our dynamic programming algorithm on instances with large department lengths. The running times are given in min:sec or in h:min:sec respectively. The entries * indicate that the algorithm did not finish within the time limit of 24 h.
| Instance | Optimum | Time |
|---|---|---|
| P15L | 148059.5 | 47:45 |
| P17L | 438935.5 | 1:54:44 |
| P18L | 589182.5 | 3:58:42 |
| H_20L | 245666 | 1:32:45 |
| N25_05L | 554740.5 | 10:31:00 |
| H_30L | 752966 | 9:58:20 |
| N30_05L | 920622.5 | 16:10:33 |
| Am33_03L | 1078710.5 | 20:51:16 |
| Am35_03L | * | * |
| ste36.5L | * | * |
| N40_5L | * | * |
| sko42-5L | * | * |
Comparing our two approaches we observe that the dynamic programming algorithm is clearly superior for all benchmark instances from the facility layout literature that only contain departments with short lengths 
. For instances with department lengths up to 10000 the dynamic programming algorithm is still preferable although there already exist instances (see e.g. ‘ste36.5’) on which the ILP yields clearly better results. Finally for instances with even larger department lengths the ILP gradually outperforms the dynamic programming algorithm.
6. Conclusion
In this paper we proposed a new variant of a row facility layout problem and two exact algorithms for solving it. The Checkpoint Ordering Problem (COP) is weakly NP-hard. It is both of theoretical and practical interest and has several important relations to other well-studied combinatorial optimization problems. In our computational study we showed that the (COP) is hard to solve in practice for both dynamic programming and ILP approaches.
It would be interesting to examine if the models, results and algorithms for scheduling on two parallel machines, which is a very well-studied problem, can be used to obtain stronger approximation results and/or to design stronger exact approaches for the (COP) in particular and layout problems in general.
Acknowledgements
I gratefully acknowledge constructive comments by two anonymous referees that led to the current version of the paper.
Funding Statement
This work was partially supported by the Austrian Science Fund (FWF) [Project J3793-N95].
Disclosure statement
No potential conflict of interest was reported by the author.
References
- [1]. Heragu SS, Kusiak A. Machine layout problem in flexible manufacturing systems. Oper Res. 1988;36(2):258–268. [Google Scholar]
- [2]. Simmons DM. One-dimensional space allocation: an ordering algorithm. Oper Res. 1969;17:812–826. [Google Scholar]
- [3]. Suryanarayanan J, Golden B, Wang Q. A new heuristic for the linear placement problem. Comput Oper Res. 1991;18(3):255–262. [Google Scholar]
- [4]. Picard J-C, Queyranne M. On the one-dimensional space allocation problem. Oper Res. 1981;29(2):371–391. [Google Scholar]
- [5]. Lenstra JK, Rinnooy AH. Kan, and P. Brucker. Complexity of machine scheduling problems. Ann. Discrete Math. 1977;1:343–362. [Google Scholar]
- [6]. Graham RL, Lawler EL, Lenstra JK, et al. Optimization and approximation in deterministic sequencing and scheduling: a survey. In and , editors In: Hammer E LJPL, Korte BH, editors. Discrete optimization II. Elsevier; 1979. (Annals of discrete mathematics, Vol. 5, p. 287–326). [Google Scholar]
- [7]. Smith WE. Various optimizers for single-stage production. Naval Res Logistics Q. 1956;3(1–2):59–66. [Google Scholar]
- [8]. Rothkopf MH. Scheduling independent tasks on parallel processors. Manage Sci. 1966;12(5):437–447. [Google Scholar]
- [9]. Lawler EL, Moore JM. A functional equation and its application to resource allocation and sequencing problems. Manage Sci. 1969;16(1):77–84. [Google Scholar]
- [10]. Lee C-Y, Uzsoy R. A new dynamic programming algorithm for the parallel machines total weighted completion time problem. Oper Res Lett. 1992;11(2):73–75. [Google Scholar]
- [11]. Garey MR, Johnson DS. Computers and Intractability: A Guide to the Theory of NP-Completeness. New York (NY), USA: W. H. Freeman & Co.; 1979. [Google Scholar]
- [12]. Lawler EL, Lenstra JK, Kan HR, et al. Sequencing and scheduling: algorithms and complexity Logistics of production and inventory. Amsterdam: North-Holland; 1993. (Handbooks in operations research and management science; Vol. 4, p. 445–522). [Google Scholar]
- [13]. Elmaghraby SE, Park SH. Scheduling jobs on a number of identical machines. AIIE Trans. 1974;6(1):1–13. [Google Scholar]
- [14]. Sarin SC, Ahn S, Bishop AB. An improved branching scheme for the branch and bound procedure of scheduling n jobs on m parallel machines to minimize total weighted flowtime. Int J Prod Res. 1988;26(7):1183–1191. [Google Scholar]
- [15]. Belouadah H, Potts CN. Scheduling identical parallel machines to minimize total weighted completion time. Discrete Appl Math. 1994;48(3):201–218. [Google Scholar]
- [16]. Chen Z-L, Powell WB. Solving parallel machine scheduling problems by column generation. INFORMS J Comput. 1999;11(1):78–94. [Google Scholar]
- [17]. Azizoglu M, Kirca O. On the minimization of total weighted flow time with identical and uniform parallel machines. Eur J Oper Res. 1999;113(1):91–100. [Google Scholar]
- [18]. Xu J, Nagi R. Identical parallel machine scheduling to minimise makespan and total weighted completion time: a column generation approach. Int J Prod Res. 2013;51(23–24):7091–7104. [Google Scholar]
- [19]. Queyranne M, Schulz AS. 2004. Polyhedral approaches to machine scheduling. Technical report, Working paper, Berlin. [Google Scholar]
- [20]. Hungerländer P. A comparison of global optimization approaches for row facility layout problems Technical report. Klagenfurt: Alpen-Adria Universität Klagenfurt, Mathematics, Optimization Group, TR-AAUK-M-O-16-07b; 2017. [Google Scholar]
- [21]. Karp RM. Reducibility among combinatorial problems In: Miller RE, Thatcher JW, editors. Complexity of computer computations. New York (NY): Plenum Press; 1972. p. 85–103. [Google Scholar]
- [22]. Garey MR, Johnson DS, Stockmeyer L. Some simplified NP-complete problems STOC ’74: Proceedings of the sixth annual ACM symposium on Theory of computing. ACM; 1974. p. 47–63. [Google Scholar]
- [23]. Harper LH. Optimal assignments of numbers to vertices. SIAM J Appl Math. 1964;12:131–135. [Google Scholar]
- [24]. Harper LH. Optimal numberings and isoperimetric problems on graphs. J Comb Theory. 1966;1:385–393. [Google Scholar]
- [25]. Vanelli A, Rowan GS. An eigenvector based approach for multistack VLSI layout. Proceedings of the Midwest Symposium on Circuits and Systems. 1986;29:135–139. [Google Scholar]
- [26]. Ravi R, Agrawal A, Klein P. Ordering problems approximated: Single-processor scheduling and interval graphs connection In: Albert JL, Artalejo BR, Monien B, editors. 18th International Colloquium on Automata, Languages and Programming. New York (NY): Springer-Verlag; 1991. (Lecture notes in computer science, Vol. 150, p. 751-762). [Google Scholar]
- [27]. Adolphson D. Singlemachine job sequencing with precedence constraints. SIAM J Comput. 1977;6:40–54. [Google Scholar]
- [28]. Karp RM. Mapping the genome: some combinatorial problems arising in molecular biology Proceedings of the Twenty-Fifth Annual ACM Symposium on Theory of Computing, STOC ’93. New York (NY), USA: ACM; 1993. p. 278–285. [Google Scholar]
- [29]. Mitchison G, Durbin R. Optimal numberings of an N N array. SIAM J Algebraic Discrete Methods. 1986;7:571–582. [Google Scholar]
- [30]. Bornstein CF, Vempala S. Flow metrics. Theor Comput Sci. 2004;321:13–24. [Google Scholar]
- [31]. Rao S, Richa AW. New approximation techniques for some linear ordering problems. SIAM J Comput. 2005;34:388–404. [Google Scholar]
- [32]. Charikar M, Hajiaghayi MT, Karloff H, et al. l22 spreading metrics for vertex ordering problems Proceedings of the seventeenth annual ACM-SIAM symposium on Discrete algorithm, SODA ’06. New York (NY), USA: 2006. p. 1018–1027. [Google Scholar]
- [33]. Feige U, Lee JR. An improved approximation ratio for the minimum linear arrangement problem. Inf Process Lett. 2007;101:26–29. [Google Scholar]
- [34]. Díaz J, Petit J, Serna M. A survey of graph layout problems. ACM Comput Surv. 2002;34:313–356. [Google Scholar]
- [35]. Hall NG, Posner ME. Earliness-tardiness scheduling problems, I: Weighted deviation of completion times about a common due date. Oper Res. 1991;39(5):836–846. [Google Scholar]
- [36]. Samuel IGC. Eilon. Minimising waiting time variance in the single machine problem. Manage Sci. 1977;23(6):567–575. [Google Scholar]
- [37]. Gurobi Optimization Inc 2016. Gurobi optimizer reference manual. Available from: http://www.gurobi.com
- [38]. Szymanski TG. Assembling code for machines with span-dependent instructions. Commun ACM. 1978;21:300–308. [Google Scholar]