A temporal offset between movement and distorted visual feedback (e.g., visuomotor rotation) influences the subsequent motor recalibration, but the effects of this offset for altered movement dynamics are largely unknown. Here we examined the influence of 1) delayed and 2) removed visual feedback on the adaptation to novel movement dynamics. These results contribute to understanding of the control strategies that compensate for movement errors when there is a temporal separation between motion state and sensory information.
Keywords: motor adaptation, sensory feedback, acclimation, vision, prediction error
Abstract
Delays in transmitting and processing sensory information require correctly associating delayed feedback to issued motor commands for accurate error compensation. The flexibility of this alignment between motor signals and feedback has been demonstrated for movement recalibration to visual manipulations, but the alignment dependence for adapting movement dynamics is largely unknown. Here we examined the effect of visual feedback manipulations on force-field adaptation. Three subject groups used a manipulandum while experiencing a lag in the corresponding cursor motion (0, 75, or 150 ms). When the offset was applied at the start of the session (continuous condition), adaptation was not significantly different between groups. However, these similarities may be due to acclimation to the offset before motor adaptation. We tested additional subjects who experienced the same delays concurrent with the introduction of the perturbation (abrupt condition). In this case adaptation was statistically indistinguishable from the continuous condition, indicating that acclimation to feedback delay was not a factor. In addition, end-point errors were not significantly different across the delay or onset conditions, but end-point correction (e.g., deceleration duration) was influenced by the temporal offset. As an additional control, we tested a group of subjects who performed without visual feedback and found comparable movement adaptation results. These results suggest that visual feedback manipulation (absence or temporal misalignment) does not affect adaptation to novel dynamics, independent of both acclimation and perceptual awareness. These findings could have implications for modeling how the motor system adjusts to errors despite concurrent delays in sensory feedback information.
NEW & NOTEWORTHY A temporal offset between movement and distorted visual feedback (e.g., visuomotor rotation) influences the subsequent motor recalibration, but the effects of this offset for altered movement dynamics are largely unknown. Here we examined the influence of 1) delayed and 2) removed visual feedback on the adaptation to novel movement dynamics. These results contribute to understanding of the control strategies that compensate for movement errors when there is a temporal separation between motion state and sensory information.
voluntary movements are guided and modified by our sensory feedback, specifically through visual and proprioceptive signals (Sabes 2011; Sober and Sabes 2003, 2005; van Beers et al. 2002). Various studies have examined the specific role these two feedback modalities play during different stages of movement control and suggest a complex integration process (Bagesteiro et al. 2006; Crevecoeur et al. 2016; Fuentes and Bastian 2010; Gritsenko et al. 2007; Jones et al. 2010; Lateiner and Sainburg 2003; Proske and Gandevia 2009; Rothwell et al. 1982; Sainburg et al. 1993, 1995, 2003; Scheidt et al. 2005). For example, there is evidence that the information from the two sensory streams are combined but exert different influences over movement: visual feedback is largely utilized for forming the limb position estimate required for planning the movement trajectory, while proprioception is used to convert the movement plan into the necessary feedforward motor commands required for execution (Sabes 2011; Sarlegna and Sainburg 2009; Sober and Sabes 2003, 2005; van Beers et al. 2002). The latter is supported by the changes in motor commands in response to disruptions of movement dynamics; learning to account for these perturbations is generally unaffected when visual feedback is not available or is uninformative (DiZio and Lackner 2000; Franklin et al. 2007; Lackner and Dizio 1994; Scheidt et al. 2005; Shadmehr and Mussa-Ivaldi 1994). Additionally, the correct temporal motion patterns for motor coordination, planning, and feedforward control are significantly disrupted when proprioception is absent or impaired (Gordon et al. 1995; Pipereit et al. 2006; Sainburg et al. 1993, 1995). However, there is also evidence that these roles are flexible, with changes in the weighting of visual and proprioceptive feedback when different computations are required for task completion (Sober and Sabes 2005).
To compensate for delays in sensory feedback (Cordo et al. 1994; Gritsenko et al. 2009; Keele and Posner 1968), it is widely accepted that the brain forms a feedforward prediction of the movement-induced sensory outcomes based on a duplicate (an efference copy) of the executed motor commands (Ariff et al. 2002; Kawato 1999; Miall et al. 1993). When errors between the predicted and actual sensory consequences (based on vision and proprioception) are experienced, the motor system corrects for the error between the sensory feedback and the issued motor command by updating the feedforward prediction (Tseng et al. 2007; Wolpert et al. 1995). Additionally, it has been shown that humans adapt to novel dynamics (i.e., force-field perturbations) by associating the external change of the environment with the motion state of the arm (Conditt et al. 1997; Diedrichsen et al. 2007; Karniel and Mussa-Ivaldi 2003; Sing et al. 2009, 2013). That is, adaptation updates an internal model of the new physical environment dependent upon changes in motion state—the position, velocity, and acceleration signals that characterize the motion.
In the present study, we sought to determine the extent to which this updating of the feedforward prediction was dependent on the temporal synchrony between arm motion and visual feedback and, furthermore, whether the complete elimination of this feedback disrupts the formation of the required temporal patterns of force. In light of the aforementioned evidence that adaptation to disruptions of movement dynamics can occur when visual feedback is not available or is uninformative (DiZio and Lackner 2000; Franklin et al. 2007; Lackner and Dizio 1994; Scheidt et al. 2005; Shadmehr and Mussa-Ivaldi 1994), one might assume that delayed or withheld feedback would not influence this type of movement recalibration. However, there are several behavioral observations that challenge this null hypothesis: 1) even limited visual information has been shown to be integrated into an ongoing motor plan (Gritsenko et al. 2009; Körding and Wolpert 2004) and partially compensate for the loss of proprioception (Ghez et al. 1995), and 2) artificial delays of visual feedback influence the accuracy, speed, and smoothness of simple movements (Held et al. 1966; Held and Durlach 1989; Kalmus et al. 1960; Smith 1972; Smith et al. 1960; Smith and Bowen 1980). In addition, the temporal manipulation of visual feedback has been shown to influence the recalibration of movement in response to visual perturbations (visuomotor rotation and prism displacement, Honda et al. 2012a, 2012b; Kitazawa et al. 1995). However, movement recalibrations in response to altered movement dynamics and to distorted visual feedback involve at least partially distinct neural mechanisms, leaving the effects of delayed feedback on the adaptation of movement dynamics an unaddressed issue (Krakauer et al. 1999; Rabe et al. 2009; Tanaka et al. 2009).
We first hypothesized that the delay of visual feedback motion would impair the ability to accurately update the internal model dependent on the magnitude of the feedback lag (Foulkes and Miall 2000; Kitazawa et al. 1995; Smith 1972). We applied an artificial 75- or 150-ms delay to online visual feedback while subjects made point-to-point reaching movements perturbed by a velocity-dependent force field. Utilizing error-clamp trials, we quantified the temporal characteristics of the compensatory response for different magnitudes of temporal feedback offset throughout the initial baseline and training periods (Joiner et al. 2011, 2013; Joiner and Smith 2008; Sing et al. 2009; Wagner and Smith 2008). To test whether acclimation during the baseline period alleviated potential learning rate deficits due to the feedback delay, we examined performance under two onset conditions and a control group who performed with no visual feedback. (We use the term “acclimation” to describe the compensation to the visual feedback delay, distinct from the adaptation to the movement perturbation.) In one group of subjects, we introduced the feedback delay at the beginning of the experimental session (constant condition). In a second group, we applied the delay at the same time that the first movement perturbation was experienced (abrupt condition). The third group performed the adaptation experiment with no visual feedback of hand position during adaptation. We examined the rate of adaptation for the different delay, onset, and visual feedback conditions, the influence of the delay and acclimation on movement end-point errors and corrections, and whether perceptual awareness of the feedback dissociation differentially affected motor performance. Importantly, these results may provide insight into the control strategies used when there is a delay between activation of the limb and observation of the motion (Farshchiansadegh et al. 2015).
METHODS
Participants.
Eighty-four healthy, right-handed subjects (45 men and 39 women, 18–33 yr of age) were recruited for this study. All participants had no known neurological impairment and were naive to the purpose of this study, which consisted of making point-to-point reaching movements. Other than the familiarization baseline trials subjects did not receive any training before collection of experimental data, and each individual completed one 1-h session. The study protocol was approved by the George Mason University Institutional Review Board. All participants gave informed consent and were compensated for their participation.
Experimental setup.
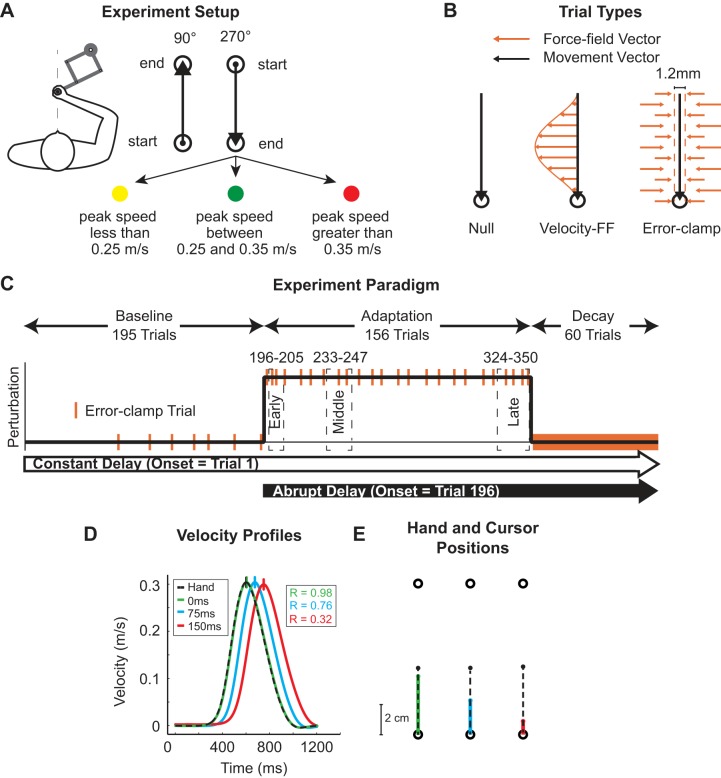
As in our previous studies (Joiner et al. 2011, 2013), the experiment was based on the standard force-field adaptation paradigm (Shadmehr and Mussa-Ivaldi 1994). While grasping the handle of a robotic manipulandum (KINARM End-Point Laboratory, BKIN), subjects moved a cursor (0.3 cm in diameter) between two targets (0.6 cm in diameter), 10 cm apart on the sagittal axis of the body (Fig. 1A). A semitransparent mirror was used to project the cursor and visual targets to the plane of movement while occluding the subject’s view of the hand (refresh rate of 60 Hz). The manipulandum measured hand position, velocity, and forces applied by subjects, all at a sampling rate of 1,000 Hz.
Fig. 1.
Force-field adaptation task with delayed visual feedback. A: experiment setup. Subjects grasped a robotic manipulandum while moving a cursor between 2 targets presented on a horizontal plane. Subjects made movements in both the 90° and 270° directions, but only movements in the 270° direction were used in data analysis. The location of the subject’s hand was represented by a white cursor, while the view of the arm was occluded. Subjects received performance feedback via a change in target color based on their peak speed. B: trial types. Subjects experienced 3 different trial types during the experiment. Null movements (black arrow) were made in the absence of any force from the robot. During force-field trials, the robot applied forces that were dependent on hand velocity (orange arrows). During error-clamp trials movements were constrained to the direction of the target (dashed lines) by implementation of a virtual spring damper that counteracted lateral motions. C: experiment paradigm. Subjects first experienced 160 null trials over 4 blocks during the baseline period. Error-clamp trials (orange bars) were presented pseudorandomly during the last 2 blocks of baseline trials. The adaptation period (156 trials) contained only force-field trials and error-clamp trials. During the decay period, every trial was an error-clamp trial (solid orange bar). Two subject groups experienced either a constant (from trial 1 of baseline period to end of experiment) or an abrupt (from beginning of adaptation period to end of experiment) onset of the feedback delay. In a third group, visual feedback of the cursor was withheld during the experiment (see methods). D: velocity profiles: average velocity profiles of the hand and the cursor (0, 75, and 150 ms). The vertical line on each velocity profile marks the time of peak velocity, and traces are respectively aligned to peak hand velocity at 600 ms. E: hand and cursor positions. Hand position (black dashed trace) and cursor position (colored traces) were plotted for the 0 (green)-, 75 (blue)-, and 150 (red)-ms delay conditions to show the decreasing correspondence between the cursor and the hand with increasing delay magnitude.
Three trial types were used during the experiment: null trials, velocity-dependent force-field (FF) trials, and error-clamp (EC) trials (Fig. 1B). Null trials were used for practice, during which the motors of the robotic manipulandum did not apply any force to the hand. During FF trials, the robot applied a force to the hand that was dependent upon movement velocity. The force that the robot applied was proportional in magnitude and orthogonal in direction to the velocity of the movement and had the general form of
| (1) |
where Fx and Fy are the force vectors and ẋ and ẏ are the velocity vectors, both determined by a 2 × 2 matrix B = [0 −b; b 0], as shown in Eq. 1. The resulting shape of B resulted in a curl force field where the force and velocity vectors were orthogonal to each other. The magnitude and orientation (clockwise or counterclockwise) of the force were determined by b, which was equal to 15 Ns/m. Note that the orientation of the force perturbations was constant for a given subject, counterbalanced between subjects, and only applied to movements in the 270° direction (trained direction).
During EC trials, the robot motors constrained movements in a straight line toward the reach target by counteracting any motion perpendicular to the target direction (Joiner et al. 2011; Joiner and Smith 2008; Scheidt et al. 2000). This was achieved by applying a stiff one-dimensional spring (6 kN/m) and a damper (150 Ns/m) in the axis perpendicular to the reach direction. In these trials, perpendicular displacement from a straight line to the reach target was held to <0.6 mm and averaged ~0.2 mm in magnitude. The inertial properties of the robot arm were the same on both active (FF and EC) and passive (null) trials.
Task.
On each trial, the subject used the robotic manipulandum to move the cursor, which represented his/her relative hand position, from one target to the next. At the end of each trial, subjects received visual and auditory feedback about the completed movement. If the peak movement velocity was between 0.25 and 0.35 m/s and the movement duration was shorter than 750 ms (from leaving the start target to reaching the end target) the reach target filled green (Fig. 1A), with an auditory reward indicating that the movement was within the required criteria. If the peak movement speed was <0.25 m/s (or >0.35 m/s), the reach target filled yellow (red) to indicate that the movement was too slow (fast). In both of these cases no auditory feedback was given. The end point of each movement was used as the start point for the following trial, and movements were made only in the 90° and 270° directions, as illustrated in Fig. 1A.
Subjects received a performance score at the end of each block of movements that indicated the percentage of correct trials (green-filled targets) for movements only in the trained 270° movement direction. Subjects were asked to keep their score above 50% throughout the experiment. Only 270° movements with a peak velocity between 0.2 and 0.4 m/s were used in the subsequent data analysis of error-clamp trials. (Note that the results were quantitatively and statistically consistent if this speed criterion was not applied.) In addition, subjects had to initiate their movement within 75–2,000 ms after the reach target appeared on the screen. Otherwise, all targets disappeared and the trial was immediately repeated.
Procedure.
Each subject experienced the same basic experimental paradigm shown in Fig. 1C. (There is a minor exception for the no-visual feedback experiment as described below.) Each experiment began with a baseline period, during which subjects completed 360 null movements (180 trials in the trained 270° direction). These null movements were divided into four blocks. The first two blocks had 80 movements each, and the last two blocks had 100 movements each. During the last two blocks of trials 12 EC trials were pseudorandomly interspersed in the 270° movement direction to measure the baseline levels of applied force for each subject. The average lateral forces during these trials were then subtracted from the forces applied on EC trials during the adaptation and decay periods.
After the baseline period, subjects completed the first adaptation block (124 total trials, 62 in the trained 270° direction), during which the FF environment was abruptly introduced after 30 null trials (15 in the trained 270° direction). We designed the first adaptation block to capture the immediate changes in the applied force due to initial exposure to the FF. Once the perturbation was introduced all 90° movements were EC trials, and the FF was only applied to the 270° direction. For the first 10 training trials, the ratio of FF to EC trials was 3 FF:2 EC, which was then reduced to 5 FF:1 EC for the last 84 trials (42 in the trained direction). The first adaptation block was followed by two additional blocks of training (96 total trials each) in which the subjects experienced FF and EC trials. Similar to the baseline period, we pseudorandomly inserted 16 EC trials in the 270° direction to measure the adaptation level at different points in training. The ratio 5 FF:1 EC was maintained throughout this training period. Only the 270° direction trials were used for the analysis of adaptation and decay.
To ensure that the block change did not serve as a cue, the adaptation period extended into the decay block. That is, we concatenated the end of the adaptation period with the decay period to remove the need for a break between the different blocks of trials and eliminate any possible signal that the trial structure was changing. This transition block began with 26 training movements (13 in the trained 270° direction), which started with the ratio 5 FF:1 EC and increased to 4 FF:3 EC for the last 14 training trials. The change in ratio of FF to EC trials was intended to increase the number of trials during which we measured the applied subject force and ensure an accurate measure of final adaptation levels. These 26 trials were then followed by 120 consecutive EC movements (60 in the trained 270° direction), referred to as the decay period, during which the adaptation decayed to baseline levels before experiencing the FF. The transition from FF to consecutive EC trials effectively occurred within the same block of trials, which avoided any possible context-dependent changes in the behavior of the subject due to the removal of the perturbation (Brennan and Smith 2015; Vaswani and Shadmehr 2013). This number of EC trials was sufficient to observe asymptotic levels of decay and allowed us to avoid breaks and possible cognitive influences during the decay period.
Delayed-visual feedback conditions.
An artificial delay between the actual hand location and the online visual feedback was introduced in one of two ways—a constant onset or an abrupt onset. To gain insight into the control strategies used when there is a delay between the activation and actuation of motion, we selected the delays of 75 and 150 ms in order to span the range of experienced delays when operating prosthetics or brain-machine interfaces (Carmena et al. 2003; Farrell and Weir 2007; Mussa-Ivaldi and Miller 2003; Velliste et al. 2008).
In the constant condition, the delay of the online cursor feedback occurred on the first movement of the first baseline block and continued throughout the entire experiment (Fig. 1C). In the abrupt condition, the delay occurred simultaneously with the onset of the FF perturbation and continued for the remainder of the experiment (Fig. 1C). Four experimental groups experienced four different delay conditions: constant 75-ms delay, constant 150-ms delay, abrupt 75-ms delay, and abrupt 150-ms delay (n = 14 for each). Subjects in each group were not informed of any manipulation in the temporal alignment of the visual feedback. A control group experienced a constant 0-ms delay (n = 14). The inherent delay of the BKIN KINARM End-Point Laboratory system is 48.4 ± 1.2 ms, and we considered this our 0-ms delay condition. The system attempts to reduce the perceived cursor delay by producing a feedforward estimate of hand position. The feedforward estimate utilizes the current instantaneous velocity vector to calculate where the hand/cursor will be in 50 ms. This predicted position of the hand results in the perceived delay of the cursor being less than the inherent delay of the system. This feedforward compensation of the system was present in all experimental conditions, ensuring that changes in motor behavior were in response to the added delays (75 and 150 ms) to the cursor feedback.
We examined the correlation between the hand motion and the cursor feedback for the three delay conditions during null trials. Figure 1D shows the average velocity profiles for the cursor and the hand for each delay condition; the vertical ticks along each trace represent the time of peak velocity and show the increase in the temporal separation between the hand and cursor velocity as delay increased. In each case the cursor lags behind the hand, as illustrated in Fig. 1E. To quantify the correspondence between the hand and cursor feedback, we determined the correlation coefficient between the two velocity profiles (the actual hand velocity and the cursor velocity) for each delay condition. Not surprisingly, the correlation between hand and cursor decreased with the increase in the feedback delay (R2 values of 0.98, 0.76, and 0.32 for 0-, 75-, and 150-ms delay, respectively). At the end of the experiment, subjects in the constant-delay conditions (75 and 150 ms) were asked to report whether they perceived a difference between the movement of the cursor and the movement of their hand. Each subject was asked the same question, “Did you notice any difference between the movement of your hand and the cursor?”, and had to give a written yes or no answer. If their answer was yes, they described the difference they experienced. Our main motivation for assessing awareness of the cursor feedback delay was to determine whether there was an effect on motor adaptation. That is, did the acclimation to the delay (in terms of perception or movement) assist the motor recalibration to the force field? To address this question, we only assessed perceptual awareness on the condition that allowed acclimation before training—the constant condition.
No-visual feedback condition.
Similar to the delay conditions above (Fig. 1C), the experiment began with a baseline period consisting of four blocks of trials. First, subjects (n = 14) completed two baseline blocks of 80 trials each. During these trials, subjects made null movements while visual feedback was provided. Subjects then completed two additional baseline blocks of 120 trials each. Here, 50% of trials in the 270° direction (randomly selected) had visual feedback (cursor on), while in the other 50% of trials visual feedback was withheld (cursor off). On trials where no visual feedback was provided, the cursor disappeared at movement onset and reappeared 200 ms after movement offset. Movement onset and offset were based on the velocity being above or below 0.05 m/s for 50 ms. This was also true for the movements in the delay condition. If the subjects did not stop the movement inside the target, they were allowed to move the cursor into the goal target after the cursor reappeared. The 90° movements immediately following no-visual feedback trials in the 270° direction were always passive movements in which the robot moved the hand back to the start position. These passive movements were also without visual feedback. During the final two blocks of the baseline period, 12 EC trials (6 with visual feedback, 6 without visual feedback) were pseudorandomly inserted in the 270° direction to measure baseline levels of the applied force. The adaptation period and decay periods were structured as described above (Fig. 1C). During the adaptation and decay periods, trials in the 270° direction were always no-visual feedback trials and trials in the 90° direction were always passive trials with no visual feedback.
Analysis and statistics.
The delayed-feedback experiments consisted of 822 total movements, with 411 trials in the trained 270° direction used for analysis. In the no-visual feedback experiment there were 862 total movements, with 431 trials in the trained direction. The difference comes from an additional 20 trials in each of the last two baseline blocks to familiarize the subjects to the lack of visual feedback. From this point forward, only trials in the trained direction are referenced as trial numbers. To capture the temporal changes in learning during the delayed-feedback experiments, we operationally defined three periods during the adaptation period: early (trials 196–205, a window of 10 trials), middle (trials 233–247, a window of 15 trials), and late (trials 324–350, a window of 27 trials) (Fig. 1C). Similarly, baseline performance was analyzed early (trials 1–14, a window of 14 trials) and late (trials 182–195, a window of 14 trials). It should be noted that, except for the early baseline, these windows were shifted by 10 trials in the no-visual feedback experiment because of the additional baseline trials.
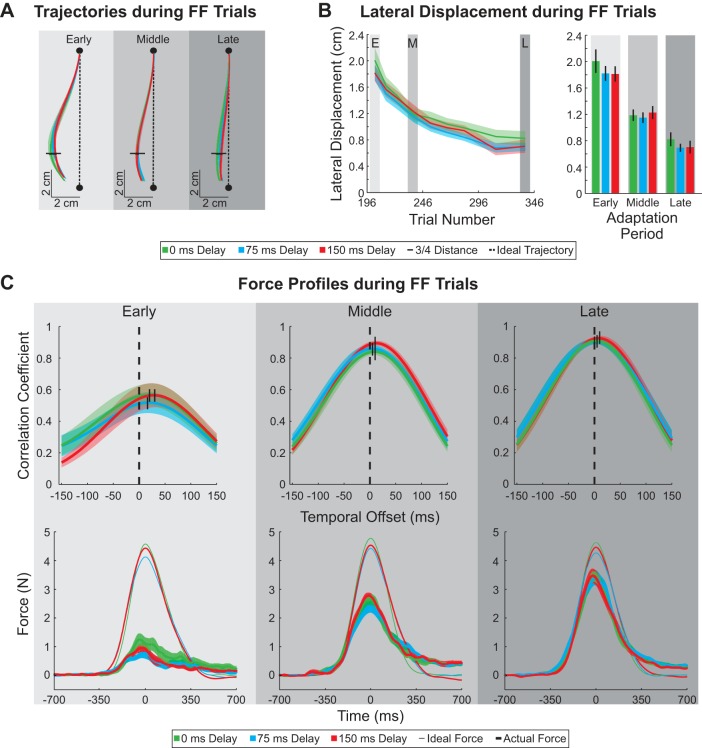
To determine whether movement trajectories varied across the delay conditions, we examined the lateral displacement for each subject during FF trials (see Fig. 2A and Fig. 6A). Similar to Franklin et al. (2007), to ensure that all movements were aligned on the same scale we first transformed the y-position data from movement onset to offset as a percentage from 0 to 100% of the total movement. We then determined the x- and y-position at each 1% increment. Within a given period, the horizontal and vertical positions of the hand were averaged across all FF trials for each subject and then averaged across subjects, with the respective intersubject variability represented by colored shadings. In the analysis, all trajectories were oriented so that the perturbation directions were aligned. The lateral deviation from a straight line trajectory was calculated for each trial when the hand traveled 75% of the required movement distance (when the hand moved 7.5 cm from the start target in the y-direction), averaged for each subject, and averaged across subjects. The lateral deviations were calculated throughout the adaptation period and compared across each delay condition during the different adaptation periods (see Fig. 2B and Fig. 6B).
Fig. 2.
Hand trajectories, lateral displacement, and force profiles during force-field trials. A: average hand trajectories during force-field trials are plotted for 3 constant delay conditions (0, 75, and 150 ms). Horizontal black dashes represent the point at which the hand is 75% into the movement. Black dashed lines represent the ideal straight line trajectory between the start and end targets (black circles). B: average lateral displacements at the point the hand was 75% into the movement (horizontal black lines in A) was plotted over the course of the adaptation period (left) for each of the constant delay conditions. Average lateral displacements during early, middle, and late periods of adaptation are shown on right. Vertical black dashes represent SE. C, top: correlation coefficient between the actual and ideal force profiles plotted as a function of temporal offset for each period during adaptation. For each subject, the average ideal force profile was shifted in 5-ms increments (between −150 and +150 ms) and a linear regression was performed against the actual force profile for the 3 constant delay conditions. Black dashed lines mark the correlation at 0-ms temporal offset. Correlations between the ideal and actual force profiles with the highest values are signified by black tick marks. C, bottom: applied and ideal force profiles. Force is plotted as a function of time for each period during adaptation (early, middle, and late). Average ideal force (thin trace) and average applied force (thick trace) are plotted for each constant delay condition.
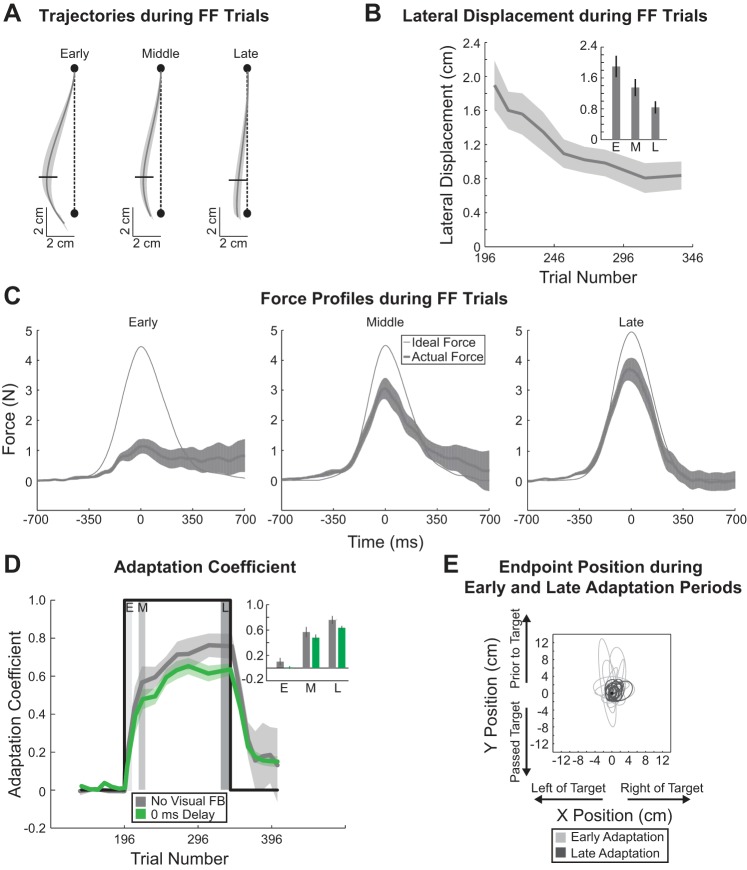
Fig. 6.
Movement trajectories, end-point positions, and adaptation with no visual feedback. A: average hand trajectories during force-field trials when no visual feedback of hand position was provided. Horizontal black dashes represent the point at which the hand is 75% into the movement. Black dashed lines represent the ideal straight line trajectory between the start and end targets (black circles). B: average lateral displacements at the point the hand was 75% into the movement (horizontal black lines in A) are plotted over the course of the adaptation period. Inset: average lateral displacement during early, middle, and late periods of adaptation. Vertical black dashes represent SE. C: applied and ideal force profiles. Force is plotted as a function of time for each period during adaptation (early, middle, and late). Average ideal force and average applied force are shown for each period. D: average adaptation coefficient for each feedback condition [green, with visual feedback (0 ms constant delay); gray, without visual feedback (FB)] during the end of baseline, adaptation, and decay periods. Perturbation onset and offset are represented by the thick black line. Gray shaded regions represent early, middle, and late windows during adaptation that were used for comparison of the average adaptation coefficient in inset. Trial 196 represents trial in which onset of the force-field perturbation occurred. E: error ellipses (2 SDs) for the movement end-point positions. The ellipse for each subject (n = 14) is presented for each period.
As described previously, we used EC trials to measure the change in feedforward motor output during the adaptation and decay periods (Joiner et al. 2011, 2013; Joiner and Smith 2008; Sing et al. 2009; Wagner and Smith 2008). The use of EC trials reduces the lateral errors made during the movement that elicit online feedback correction. Given that the lateral force during EC trials reflects the predictive feedforward adaptive response to the force fields, we limited our analysis to these force patterns. Based on Eq. 1, subjects fully compensated for the force field when they produced a countering force that is proportional to the movement velocity. We first computed the ideal force pattern by examining the longitudinal velocity during the EC trial movement. The movement and force signals were analyzed within a temporal window of 1,400 ms centered on the peak velocity (±700 ms) (Fig. 2C, bottom, and Fig. 6C). Once the ideal and actual force patterns were determined, we shifted the ideal force pattern in time by 5-ms increments between −150 and +150 ms. We then performed a linear regression between the actual and ideal force patterns at these points to quantify the extent to which the force pattern generated by subjects was temporally correlated to the velocity profile of the movement or the visual feedback of the movement and measured the temporal offset for each condition (Fig. 2C, top).
We quantified the extent of motor recalibration with the adaptation coefficient—the linear regression coefficient between the ideal force at 0 ms and the lateral force applied by the subject during the EC trials (Gonzalez Castro et al. 2014; Joiner et al. 2011, 2013; Joiner and Smith 2008; Sing et al. 2009). We computed the adaptation coefficient for each subject during both the adaptation and decay periods and averaged the values over all subjects within each delay and feedback condition.
Movement duration was the time between the first point at which the movement speed rose above 0.05 m/s and the point when the movement speed fell below 0.05 m/s for 50 ms. As described above, these crossings were the estimates of movement onset and offset. [Note that here we used a speed-only criterion to determine the duration of the point-to-point movement. To determine the additional time for end-point correction, we applied an additional spatial criterion (with respect to the movement goal) as described below.] Based on this speed criterion, the average durations (±SE) during baseline movements were 507 ± 12, 534 ± 10, and 579 ± 16 ms for the 0-, 75-, and 150-ms delay conditions, respectively. During adaptation the respective durations were 554 ± 14, 587 ± 14, and 610 ± 27 ms. During baseline, our longest delay (150 ms) was ~26% of the movement duration, comparable to previous studies (100 ms used in Honda et al. 2012b). A comparison to force-field movement durations is problematic because, unlike studies that solely utilized a visual manipulation, the movement duration in our study was directly affected by both the delay and the novel movement dynamics; even for the 0 ms condition there was a ~9 ± 3% increase in the movement duration when the force-field perturbation was applied. In other words, the applied force-field perturbation increased the time for the movements to terminate and thus artificially decreased the overall percentage of the delay with respect to the movement duration.
To initially quantify movement end-point performance, we examined two different measures: constant and variable error (Darling and Gilchrist 1991; Rossetti et al. 1994). We first defined the end point of the movement as the x- and y-positions of the subject’s hand at the first time when the movement speed was <0.05 m/s for at least 50 ms. Constant error is the displacement between the movement end point and the center of the target location. This measure takes into account the polarity of the error with respect to the target (right or left, undershoot or overshoot). Variable error was calculated as the standard deviation of these displacements. We determined the constant and variable errors for both the x- and y-directions (see Tables 2 and 4). In addition, we also determined the magnitude of the vector displacement between the movement end points and 1) the target location and 2) the mean end-point location (see Fig. 4A and Fig. 5B). Note that these measures represent the absolute value of the displacement with respect to these two locations.
Table 2.
Constant and variable error during early and late baseline
| CEx, mm | CEy, mm | VEx, mm | VEy, mm | |
|---|---|---|---|---|
| Early baseline | ||||
| 0-ms Delay | −0.3 ± 0.3 | −2.4 ± 0.7 | 2.5 ± 0.2 | 5.4 ± 0.9 |
| 75-ms Constant delay | 0.3 ± 0.2 | −0.7 ± 0.8 | 2.4 ± 0.1 | 5.2 ± 0.6 |
| 150-ms Constant delay | −0.3 ± 0.4 | −0.8 ± 0.7 | 3.1 ± 0.2 | 7.0 ± 0.5 |
| Late baseline | ||||
| 0-ms Delay | −0.9 ± 0.2 | −1.3 ± 0.2 | 1.9 ± 0.2 | 3.1 ± 0.2 |
| 75-ms Constant delay | 0.1 ± 0.1 | −1.1 ± 0.4 | 2.4 ± 0.2 | 4.3 ± 0.2 |
| 150-ms Constant delay | −0.3 ± 0.2 | −0.2 ± 0.5 | 2.5 ± 0.1 | 5.0 ± 0.3 |
Values represent means ± SE. CE, constant error; VE, variable error.
Table 4.
Constant and variable error during early and late adaptation
| CEx, mm | CEy, mm | VEx, mm | VEy, mm | |
|---|---|---|---|---|
| Early adaptation | ||||
| 0-ms Delay | 11.7 ± 1.6 | −4.8 ± 1.2 | 15.5 ± 1.0 | 12.6 ± 1.7 |
| 75-ms Constant delay | 13.1 ± 1.0 | −8.2 ± 0.9 | 15.7 ± 0.9 | 15.7 ± 1.1 |
| 150-ms Constant delay | 13.5 ± 1.9 | −7.5 ± 1.5 | 15.5 ± 1.1 | 15.8 ± 1.7 |
| 75-ms Abrupt delay | 11.9 ± 1.1 | −6.3 ± 1.1 | 16.1 ± 1.2 | 14.8 ± 1.2 |
| 150-ms Abrupt delay | 10.9 ± 1.9 | −5.5 ± 2.1 | 12.1 ± 0.9 | 15.1 ± 1.6 |
| No visual feedback | 12.6 ± 2.4 | 12.9 ± 5.7 | 10.3 ± 1.5 | 16.5 ± 3.3 |
| Late adaptation | ||||
| 0-ms Delay | 4.7 ± 1.1 | −0.8 ± 0.4 | 4.6 ± 0.4 | 4.1 ± 0.3 |
| 75-ms Constant delay | 3.6 ± 0.7 | −0.8 ± 0.5 | 4.7 ± 0.4 | 4.5 ± 0.3 |
| 150-ms Constant delay | 4.0 ± 0.4 | −0.8 ± 0.5 | 5.3 ± 0.5 | 5.5 ± 0.3 |
| 75-ms Abrupt delay | 4.0 ± 0.7 | −0.8 ± 0.5 | 4.7 ± 0.4 | 4.5 ± 0.3 |
| 150-ms Abrupt delay | 3.8 ± 0.6 | 0.6 ± 0.5 | 5.0 ± 0.4 | 5.0 ± 0.3 |
| No visual feedback | 6.6 ± 1.9 | 4.2 ± 1.3 | 7.4 ± 0.5 | 9.1 ± 0.6 |
Values represent means ± SE. CE, constant error; VE, variable error.
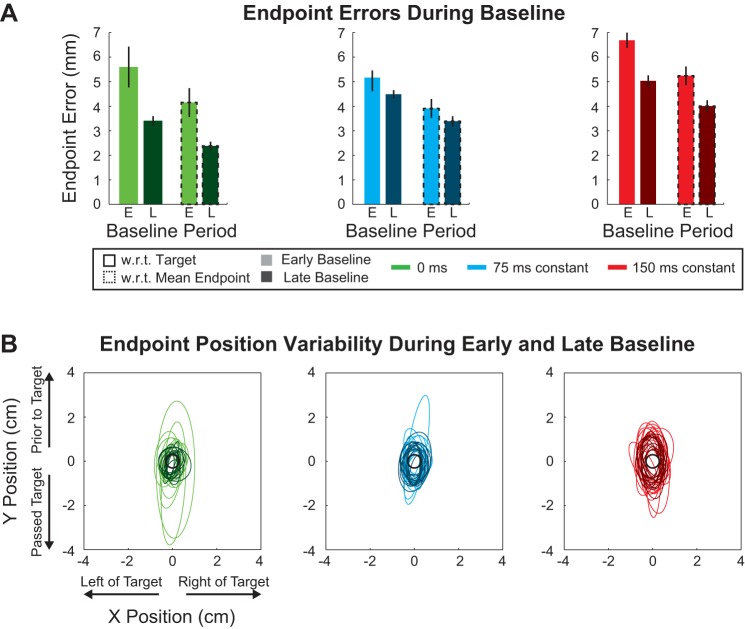
Fig. 4.
Movement end-point error during baseline trials. A: average movement end-point displacements with respect to (w.r.t.) the 1) target and 2) mean end-point location across subjects are represented by colored bars for each constant delay condition (0, 75, and 150 ms). Light colors represent early baseline (E) and dark colors late baseline (L). Bars with black dashed outline distinguish the average displacement from the mean end point from the average displacement from the target (no outline). Vertical black lines represent SE. B: each error ellipse represents the 2-SD extent of the movement end-point positions for a single subject. Each panel/color represents a delay condition (0, 75, and 150 ms). Early baseline is represented by ellipses with thin light lines. Late baseline is represented by ellipses with thick dark lines. Thus each panel displays 28 ellipses that represent the movements of 14 subjects: 14 ellipses for early baseline and 14 ellipses for late baseline.
Fig. 5.
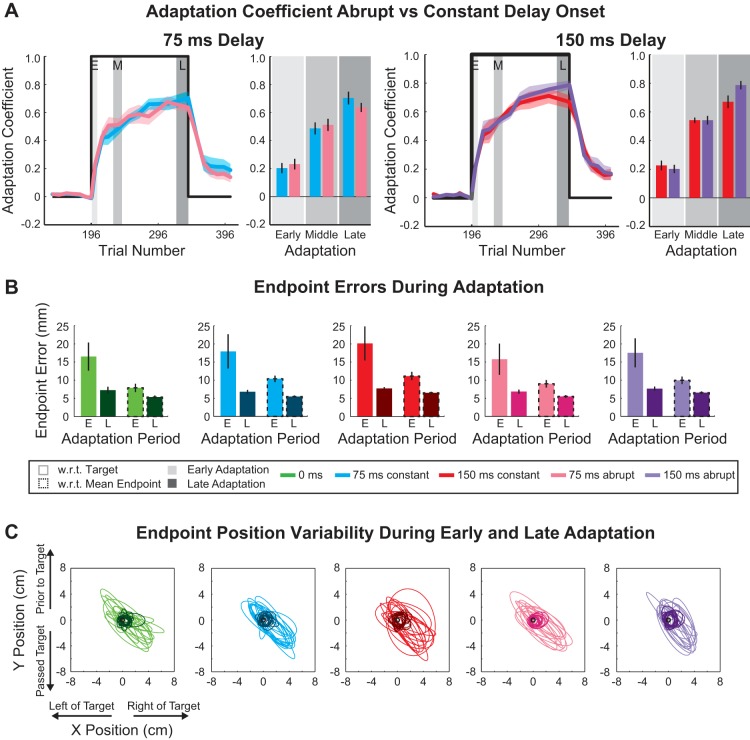
Abrupt and constant delay adaptation coefficients and movement end-point error during training. A: adaptation coefficient: constant vs. abrupt onset condition. Thick colored traces represent average adaptation coefficient for 75-ms (left) and 150-ms (right) abrupt and constant delay conditions (blue, 75 ms constant; black, 75 ms abrupt; red, 150 ms constant; gray, 150 ms abrupt) with SE shading. The coefficients were calculated for the end of baseline, adaptation, and decay periods. Perturbation onset and offset are represented by thick black line (trial 196 represents trial in which onset of the force-field perturbation occurred). Gray shaded boxes represent early, middle, and late windows during adaptation that were used for comparison of the average adaptation coefficients in bar graphs on right. B: movement end-point error during the adaptation period. Colored bars represent average movement end-point displacement for each delay and onset condition. Light colors represent early adaptation and dark colors late adaptation. Bars with black dashed outline distinguish mean displacement of movement end points from the average movement end point and mean displacement of movement end points from the target (no outline). Vertical black lines represent SE. Gray shaded boxes represent early and late windows during the adaptation period. C: error ellipses (2 SDs) for the movement end-point positions. The ellipse for each subject is presented for each period and delay condition (early adaptation: thin light lines; late adaptation: thick dark lines).
The end-point movement variabilities for each subject from which these measures were taken are represented as ellipses (2-standard deviation intervals) during the early and late periods of baseline (Fig. 4B) and adaptation (Figs. 5C and 6E). All errors were averaged across early and late baseline trials (constant delay condition), respectively, for each subject and averaged across subjects (Fig. 4A). To quantify the improvement of movement end-point error during the adaptation period, we also calculated the constant and variable errors, vector displacements for FF trials for the constant and abrupt delay conditions and no-visual feedback experiment during the early and late adaptation periods (Fig. 5B). It should be noted that, unlike the error-clamp analysis, we included all movements regardless of peak speed in our analysis of end-point errors because we were specifically interested in the trial-to-trial variability in motor performance.
To further assess the end movement correction strategies, we conducted three additional analyses: the number of velocity peaks before stopping (indicating discrete submovement corrections), the deceleration duration (the time to enter the target from peak velocity), and the number of changes in direction of the hand at the end of motion. The number of peaks in velocity was calculated as the number of maxima between two time points: when movement speed increased above and decreased below 0.05 m/s. The deceleration duration was calculated as the time from the peak velocity to when movement speed decreased below 0.05 m/s. The number of changes in the movement direction of the hand was calculated as the number of maxima and minima of the x velocity component between two time points—when velocity in the y-direction increased above and decreased below 0.05 m/s. All three analyses had to meet the above speed criteria for at least 50 ms and were determined until the cursor was within a 6-mm square centered on the movement target. (Note here that, unlike the movement duration estimation described above, we applied speed and spatial criteria to examine the correction behavior following the completion of the point-to-point movement portion of the trial.) For each subject, each calculation was averaged across early and late baseline trials (constant delay condition) and during the early, middle, and late adaptation periods for both the constant and abrupt delay conditions and no-visual feedback experiment.
Statistical significance of multiple effects such as delay amount, delay onset, adaption period (early, middle, and late), baseline period (early and late) on the movement trajectory, adaptation coefficient, and movement end-point displacements/errors was determined by ANOVA. Nonpaired, two-tailed t-tests were performed to examine the influence of the two delay onsets (abrupt vs. constant) on the adaptation level within each period. Where appropriate, the statistical values were corrected for multiple comparisons. All statistical analyses were performed with MATLAB, and for all tests the significance level was 0.05.
RESULTS
Subjects were asked to make point-to-point reaching movements using a robotic manipulandum. After a baseline period, subjects adapted to a velocity-dependent force field while a 0-, 75-, or 150-ms delay was applied to the online visual feedback of the cursor position or the feedback was completely removed. The first experiment (constant delay condition) examined the influence of this delayed visual feedback on movement recalibration. The feedback delay was applied at the beginning of the experiment during the baseline trials and remained throughout the training and decay periods. The second experiment (abrupt delay condition) examined whether acclimation to the delayed feedback during baseline trials played a role in movement recalibration. In this case the feedback was applied abruptly at the same time the force-field perturbation was introduced. The third experiment (no visual feedback) examined the influence of visual feedback on the movement recalibration. Here the cursor was extinguished from movement onset to 200 ms after movement offset (see methods) during the training session.
Adaptation of reaching movements (constant delay condition).
During training, subjects experienced a velocity-dependent force field applied orthogonal to their movement direction that resulted in a lateral displacement from the ideal straight trajectory. To ensure that subjects had similar movement patterns despite delayed visual feedback we examined the movement trajectories for each period during adaptation (early, middle, and late; see methods) and delay conditions (0, 75, and 150 ms). The average trajectories during force-field trials were similar among the three constant delay conditions (0, 75, and 150 ms) in early, middle, and late periods of adaptation (Fig. 2A). The lateral displacement at the point the hand reached 75% of the movement distance (7.5 cm from the start target; Fig. 2A) was analyzed over the adaptation period. The lateral displacement at this point decreased over the training period but was not significantly different between the three different delay conditions (2-way ANOVA, P < 0.01 for period during adaptation, P = 0.41 for delay amount) (Fig. 2B). The lateral deviation decreased on average by 11.9 ± 1.5, 11.3 ± 0.9, and 11.1 ± 1.4 mm from the early to late adaptation periods for the constant 0-, 75-, and 150-ms delay conditions, respectively. This suggests that despite the differences in delayed visual feedback subjects made similar movements during force-field perturbation trials and the lateral deviation due to the movement perturbation decreased at a similar rate for the different delays to feedback.
Subjects who experienced the constant condition applied increasing amounts of force to the manipulandum as the adaptation period progressed to compensate for the velocity-dependent force field. We examined the temporal pattern of applied force to determine whether this pattern was influenced by the amount of delayed visual feedback. We shifted the ideal force in time by 5-ms increments between −150 and +150 ms and correlated this with the applied force. The amount of maximum correlation (represented by the thick vertical black lines in Fig. 2C) was not significantly different across the delay conditions (0-ms, 75-ms, and 150-ms delay), but the correlation value significantly increased throughout the periods of adaptation (2-way ANOVA, P = 0.26 for delay amount, P < 0.01 for period during adaptation). Similarly, the timing of the maximum correlation was not significantly different across the delay conditions but significantly decreased (from a positive offset to zero) throughout the periods of adaptation (2-way ANOVA, P = 0.19 for delay amount, P < 0.01 for period during adaptation). As illustrated in Fig. 2C, bottom, the applied force increased over training toward the ideal force. The means of the maximum applied force measured for all three constant delay conditions were similar within each period during adaptation (2-way ANOVA, P < 0.01 for period during adaptation, P = 0.09 for delay amount).
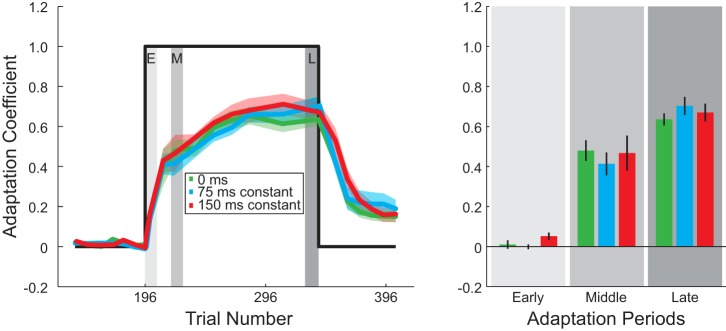
Next, to compare the rate of adaptation we calculated the adaptation coefficient, the linear regression between the ideal and actual force profile (see methods). We determined the adaptation coefficient for no shift (0 ms) in the ideal force profile. The adaptation coefficient as a function of trial number is plotted in Fig. 3 for the three constant delay conditions. The adaptation coefficient was not significantly different across the delay conditions (0-ms, 75-ms, and 150-ms delay) during the early, middle, and late periods of adaptation (2-way ANOVA, P < 0.01 for period during adaptation, P = 0.26 for delay amount). At the end of training subjects were able to compensate for 64 ± 3%, 70 ± 5%, and 70 ± 5% (mean ± SE across subjects) of the force field for the 0-ms, 75-ms, and 150-ms delays, respectively. This suggests that subjects adapted to the velocity-dependent force field at similar rates regardless of delayed visual feedback.
Fig. 3.
Adaptation coefficient for constant delay conditions: average adaptation coefficient for each delay condition (0, 75, and 150 ms) during the end of baseline, adaptation, and decay periods. Perturbation onset and offset are represented by the thick black line. Gray shaded regions in plot on left represent the early, middle, and late windows during adaptation that were used for comparison of the average adaptation coefficient for the 3 delay conditions in the bar graph on right. Trial 196 represents the trial in which onset of the force-field perturbation occurred.
After the adaptation period, subjects experienced consecutive EC trials to examine the decay of adaptation. Adaptation for all three groups of subjects decayed to ~20% over 60 trials, and no significant difference was observed at the end of the decay period (1-way ANOVA, P = 0.77).
We also examined whether perceptual awareness of the feedback delay played any role in the observed motor behavior. At the end of the experiment 1 of 14 subjects reported that there was an offset between hand motion and cursor movement for the constant 75-ms delay condition. This number increased to 4 of 14 subjects for the 150-ms delay condition. In the latter case, we found no significant difference in adaptation (the adaptation coefficients in the 3 periods depicted in Fig. 3) between subjects who reported that the cursor lagged the hand motion and those who did not (2-way ANOVA, P < 0.01 for period during adaptation, P = 0.97 for perceptual awareness).
Acclimation to delayed visual feedback and its effect on movement end-point displacements during baseline period.
In the constant condition, the imposed visual feedback delay was applied at the start of the experiment and continued through the training and decay periods. It is possible that subjects acclimated to the delay during the initial baseline trials, which may have influenced the motor performance when the force-field perturbation was applied. First, we examined the change in several performance measures reflecting movement correction strategies during the baseline period: 1) the number of velocity peaks before stopping and 2) deceleration duration (see methods). These measures are summarized in Table 1. Overall, the number of velocity peaks significantly increased with delay and decreased over the baseline period (2-way ANOVA, P = 0.02 for period during baseline, P < 0.01 for delay amount). Similarly, the deceleration duration significantly increased with delay and decreased over the baseline period (2-way ANOVA, P < 0.01 for period during baseline, P < 0.01 for delay amount). Together this suggests that some aspects of performance were influenced by the delay as early as the baseline period but improved over this initial familiarization with the task.
Table 1.
Motor correction values during baseline
| Early Baseline | Late Baseline | |
|---|---|---|
| Deceleration duration, ms | ||
| 0-ms Delay | 435.5 ± 28.0 | 376.1 ± 8.3 |
| 75-ms Constant delay | 472.0 ± 14.1 | 426.0 ± 9.1 |
| 150-ms Constant delay | 659.3 ± 36.3 | 529.7 ± 14.7 |
| No. of velocity peaks | ||
| 0-ms Delay | 1.4 ± 0.1 | 1.2 ± 0.0 |
| 75-ms Constant delay | 1.5 ± 0.1 | 1.4 ± 0.1 |
| 150-ms Constant delay | 2.0 ± 0.2 | 1.7 ± 0.1 |
Values represent means ± SE.
To further determine whether acclimation to the delay influenced motor recalibration, we examined the movement end-point errors. These measures were based on movement end-point variability, which is illustrated in Fig. 4B as ellipses for two standard deviations for the early and late periods during baseline for each subject and each delay condition (0, 75, and 150 ms). The constant and variable errors (see methods) of the movement end points for the baseline period are summarized in Table 2. The constant error in both the x- and y-directions was not significantly different across the delay conditions (0, 75, and 150 ms) or periods (early vs. late) (2-way ANOVA, P > 0.07 for delay amount, P > 0.37 for period during baseline). In contrast, the variable error in both the x- and y-directions significantly increased with the temporal delay of the cursor but decreased over the baseline period (2-way ANOVA, P < 0.01 for delay amount, P < 0.01 for period during baseline). Thus, unlike the average, the variability of these movement errors was sensitive to the cursor delay and experience with the temporal offset.
We also determined the absolute error with respect to the target and mean movement end point. As shown in Fig. 4A, we found that the absolute displacement of the movement end point with respect to the target was significantly different between the 0-, 75-, and 150-ms constant delay conditions and decreased over the course of the baseline period (2-way ANOVA, P < 0.01 for delay amount, P < 0.01 for period during baseline). Specifically, the absolute displacement with respect to the target was not significantly different between the different delay conditions in the early baseline (P > 0.05, adjusted for multiple comparisons). However, in late baseline this absolute displacement was significantly greater for both the 75- and 150-ms delay conditions compared with the 0-ms delay condition (P < 0.01 for both, adjusted for multiple comparisons).
Similarly, the displacement with respect to the mean end-point location was also significantly different between the 0-, 75-, and 150-ms constant delay conditions and decreased over the baseline period (2-way ANOVA, P < 0.01 for delay amount, P < 0.01 for period during baseline). As above, the absolute displacement with respect to the mean end-point location was not significantly different between the different delay conditions in the early baseline (P > 0.05, adjusted for multiple comparisons). In the late baseline, this absolute displacement was greater for both the 75- and 150-ms delay conditions compared with the 0-ms delay condition (P < 0.01 for both, adjusted for multiple comparisons). Thus, in the constant condition, the delay in feedback influenced the movement corrections and different aspects (variability and magnitude) of the end-point errors. Importantly, the extent of this influence decreased with experience, suggesting acclimation to the feedback perturbation before the training in the force-field perturbation. We therefore conducted a second experiment during which the feedback delay was introduced simultaneously with the force-field perturbation to determine the influence of this acclimation on adaptation on movement recalibration.
Adaptation of reaching movements (abrupt condition).
Because of the decrease in deceleration duration, velocity peaks, and end-point errors over the course of the baseline period for the longer feedback delays, it is possible that this acclimation had a direct influence on the adaptation to the force-field movement perturbation. In the second experiment, we tested two new groups of subjects with the abrupt introduction of the visual feedback delay (75 or 150 ms). In this case, the onset of the delayed visual feedback occurred simultaneously with the onset of the force field, thus removing potential acclimation to the visual feedback perturbation before the onset of the force-field perturbation.
First, as in the baseline period, we examined several measures of the movement correction strategy: the number of velocity peaks before stopping, deceleration duration, and changes in direction of the hand at the end of motion (see methods). These measures are summarized in Table 3 for the adaptation period. Both the number of velocity peaks and deceleration duration were significantly different between the delay conditions and decreased over the adaptation period (2-way ANOVA, P < 0.01 for both delay condition and period during adaptation). While the number of changes in the movement direction of the hand significantly decreased over the training period, there was not a significant difference between the delay conditions (2-way ANOVA, P < 0.01 for period during adaptation, P = 0.05 for delay amount).
Table 3.
Motor correction values during adaptation
| Early Adaptation | Middle Adaptation | Late Adaptation | |
|---|---|---|---|
| Change in directions | |||
| 0-ms Delay | 2.3 ± 0.1 | 1.4 ± 0.1 | 1.1 ± 0.1 |
| 75-ms Constant delay | 2.3 ± 0.1 | 1.5 ± 0.1 | 0.9 ± 0.1 |
| 75-ms Abrupt delay | 2.2 ± 0.1 | 1.5 ± 0.1 | 0.9 ± 0.1 |
| 150-ms Constant delay | 2.3 ± 0.1 | 1.6 ± 0.1 | 0.9 ± 0.1 |
| 150-ms Abrupt delay | 2.2 ± 0.2 | 1.2 ± 0.1 | 0.7 ± 0.1 |
| Deceleration duration, ms | |||
| 0-ms Delay | 674.2 ± 38.8 | 485.8 ± 13.6 | 461.1 ± 15.4 |
| 75-ms Constant delay | 846.5 ± 32.0 | 592.8 ± 30.2 | 528.4 ± 17.0 |
| 75 ms Abrupt delay | 831.9 ± 56.2 | 645.4 ± 26.5 | 526.6 ± 21.1 |
| 150-ms Constant delay | 986.1 ± 51.7 | 709.1 ± 45.6 | 599.6 ± 18.2 |
| 150-ms Abrupt delay | 1,099.2 ± 57.0 | 768.6 ± 36.7 | 670.3 ± 23.4 |
| No. of velocity peaks | |||
| 0-ms Delay | 2.4 ± 0.1 | 1.7 ± 0.1 | 1.5 ± 0.1 |
| 75-ms Constant delay | 3.1 ± 0.2 | 2.0 ± 0.2 | 1.6 ± 0.1 |
| 75-ms Abrupt delay | 3.1 ± 0.3 | 2.2 ± 0.1 | 1.7 ± 0.1 |
| 150-ms Constant delay | 3.6 ± 0.2 | 2.5 ± 0.3 | 1.9 ± 0.1 |
| 150-ms Abrupt delay | 4.2 ± 0.2 | 2.6 ± 0.2 | 2.1 ± 0.1 |
Values represent means ± SE.
Next, we report that the abrupt introduction of the 75-ms and 150-ms feedback delays did not significantly influence adaptation performance compared with when the delay was applied at the start of the experiment (constant) (Fig. 5A). The adaptation coefficients were not significantly different within the early, middle, or late period of adaptation (2-way ANOVA, P < 0.01 for period during adaptation, P = 0.45 for delay onset). At the end of training, subjects were able to compensate for 64 ± 3% and 78 ± 3% (mean ± SE across subjects) for the abrupt 75- and 150-ms delay conditions, respectively. Similar to the first experiment, we compared the decay period to determine whether the return to baseline performance was similar for the different conditions. The four groups decayed back to ~20% performance with no significant difference at the end of the decay period (1-way ANOVA, P = 0.82). These data suggest that acclimation did not influence the rate of motor adaptation or the decay.
Similar to the baseline period, we examined the constant and variable error during the adaptation period (Table 4). As shown in Fig. 2A, the movement end points tended to undershoot (fall short of the target) and fall on the same side as the perturbation direction. We found that the constant and variable errors in both the x- and y-directions were not significantly different across the delay conditions (0, 75, and 150 ms) or onsets (abrupt vs. constant) but did decrease over the course of training (early vs. late) (3-way ANOVA, P > 0.14 for delay amount, P > 0.08 for delay onset, P < 0.01 for period during adaptation, for all cases). Thus the average movement error and corresponding variability during training were not sensitive to the cursor delay or how the temporal offset was applied, but both types of errors were influenced by the prolonged experience with the temporal offset during training.
Finally, we examined the movement end-point displacements with respect to the target and average end-point location over the course of the adaptation period for the constant and abrupt delay conditions (Fig. 5B) measured from movement end-point variability (Fig. 5C). Ellipses (2 standard deviations) represent this variability for early and late periods during adaptation for each subject and each delay condition (0 ms, 75 ms constant, 150 ms constant, 75 ms abrupt, and 150 ms abrupt). During adaptation, we found that the displacement with respect to the target was not significantly different for delay onset or delay amount but was significantly different over the course of adaptation (3-way ANOVA, P = 0.11 for delay onset, P = 0.05 for delay amount, and P < 0.01 for period during adaptation). Similarly, we found that the displacement with respect to the average end-point location was not significantly different for delay onset or delay amount but was significant over the training period (3-way ANOVA, P = 0.26 for delay onset, P = 0.07 for delay amount, and P < 0.01 for period during adaptation). Collectively, these results suggest that any initial acclimation to the feedback delay did not play a significant role in the motor recalibration to the force-field perturbation. In addition, the respective similarities in end-point displacement across the different delay onset conditions and magnitudes suggest that the movement perturbation played a larger role in the amount of end-point error rather than a graded effect due to the delayed visual feedback.
Adaptation of reaching movements (no-visual feedback condition).
In this control experiment we tested a group of subjects (n = 14) who were provided no visual feedback during force-field adaptation. In this case, the cursor was occluded from movement onset to movement offset (see methods). Previous studies have shown that learning to account for perturbations to movement dynamics is generally unaffected when visual feedback is not available or is uninformative (DiZio and Lackner 2000; Franklin et al. 2007; Lackner and Dizio 1994; Scheidt et al. 2005; Shadmehr and Mussa-Ivaldi 1994). Here we extended this previous work to determine the extent to which the temporal pattern of the applied compensatory force (measured on EC trials) matched the ideal compensatory force.
To ensure that subjects had similar movement patterns despite not having visual feedback, we examined the movement trajectories for each period during adaptation (early, middle, and late; see methods). The average trajectories during FF trials were generally similar to the delay conditions in early, middle, and late periods of adaptation (Fig. 2A and Fig. 6A); the end points fell on the same side as the perturbation direction, similar to the delayed-feedback movements. However, unlike the delayed-feedback cases (Fig. 2A), the movement end points for the no-visual feedback condition (Fig. 6A) tended to overshoot (fall beyond the target). The lateral displacement at the point the hand reached 75% of the movement distance (7.5 cm from the start target; Fig. 6A) was analyzed over the adaptation period. The lateral displacement at this point decreased over the training period but was not significantly different from the 0-ms delay case (2-way ANOVA, P < 0.01 for period during adaptation, P = 0.88 for feedback type) (Fig. 6B). (Our main comparison for the no-visual feedback experiment is to the 0-ms delay condition because the only difference between the two is the visibility of the cursor throughout the reaching movement.) The lateral deviation decreased on average by 10.6 ± 2.8 mm from early to late adaptation periods for the no-visual feedback condition. This suggests that despite the differences in visual feedback subjects made similar movements during the force-field perturbation trials and the lateral deviation due to the movement perturbation decreased at a similar rate for the different feedback conditions.
Subjects who experienced the no-visual feedback condition applied increasing amounts of force to the manipulandum as the adaptation period progressed to compensate for the velocity-dependent force field. As illustrated in Fig. 6C, the applied force increased over training toward the ideal force. However, the mean of the maximum applied force measured for 0-ms delay and the no-visual feedback condition was not significantly different over the adaptation period (2-way ANOVA, P < 0.01 for period during training, P = 0.19 for feedback type).
Next, to compare the rate of adaptation we plotted the adaptation coefficient as a function of trial number (Fig. 6D) for the no-visual feedback condition and, as a comparison, the 0-ms delay condition. The adaptation coefficient was not significantly different across the two feedback conditions during the early, middle, and late periods of adaptation (2-way ANOVA, P < 0.01 for period during adaptation, P = 0.99 for feedback type). At the end of training subjects in the no-visual feedback condition were able to compensate for 76 ± 6% (mean ± SE across subjects). This suggests that subjects adapted to the velocity-dependent force field at similar rates regardless of a lack of visual feedback. As above, after the adaptation period subjects experienced consecutive EC trials to examine the decay of adaptation. Adaptation for the no-visual feedback condition decayed to ~20% over 60 trials. Additionally, the adaptation coefficient was not significantly different across the two feedback conditions (0-ms delay condition compared with no-visual feedback condition) at the end of the decay period (1-way ANOVA, P = 0.70).
Finally, we examined the end-point errors over the course of the adaptation period for the no-visual feedback condition and compared this to the 0-ms delay condition. Ellipses (2 standard deviations) in Fig. 6E represent the movement end-point variability for early and late periods during adaptation for each subject in the no-visual feedback condition. As above, we examined the constant and variable errors during the adaptation period (Table 4). Compared with the full-feedback condition (0-ms delay) we found that only the constant error in the y-direction was significantly different across the feedback conditions, with no significant difference across the training period (2-way ANOVA, P < 0.01 for feedback type and P = 0.43 for period during adaptation). In contrast, constant error in the x-direction was not significantly different across the feedback conditions or the training period (2-way ANOVA, P > 0.05 for feedback type and P = 0.42 for period during adaptation). The variable error decreased across the training period for both the x- and y-directions, but only the variable error in the y-direction was significantly different across the feedback conditions (x-direction: 2-way ANOVA, P = 0.24 for feedback type and P < 0.01 for period during adaptation; y-direction: 2-way ANOVA, P = 0.02 for feedback type and P < 0.01 for period during adaptation). Thus the absence of visual feedback mostly affected the end-point error and variability in the direction of movement (y-direction) during adaptation.
In addition to the constant and variable errors we also examined the absolute movement end-point displacements with respect to the target and average end-point location over the course of the adaptation period. During adaptation, we found that the average absolute displacement of the movement end points to the target was significantly different for feedback type (visual compared with no visual feedback) and was significantly different over the course of adaptation (2-way ANOVA, P < 0.01 for feedback type and P < 0.01 for period during adaptation). Similarly, we found that the average absolute displacement of the movement end points to the average movement end-point location was significantly different for feedback type; however, this displacement was not significant over the training period (2-way ANOVA, P < 0.01 for feedback type and P = 0.08 for period during adaptation). Collectively, these results show that the lack of visual feedback did not significantly influence the ability to adapt to the novel dynamics but did affect the variability in movement end points and end-point errors with respect to the target.
DISCUSSION
Examining motor performance in response to delayed visual feedback can provide insight into the mechanisms and strategies the motor system uses to integrate (and compensate for) delayed sensory feedback information. In this study, we utilized a standard force-field adaptation paradigm to examine the ability to adapt to a motion state-dependent perturbation while either delaying or completely removing the visual feedback of movement. In the former case, we quantified the level of motor adaptation and awareness and acclimation to the delayed visual feedback (75 and 150 ms). Overall our results show that delaying the visual feedback of movement did not influence adaptation to novel movement dynamics. When the respective feedback delays were introduced at the beginning of the experiment (constant condition), subjects were able to adapt to the same level and at similar rates as subjects who experienced no temporal manipulation of the visual feedback. However, acclimation to these delays was observed before introduction of the force-field perturbation. By examining a sudden introduction of the feedback delay (abrupt condition) in which the artificial delay was experienced at the same time as the force-field perturbation was applied, we eliminated the possible acclimation to the feedback delay before the motor adaptation. Similar to the constant condition, subjects were able to adapt at a comparable rate and level, suggesting that performance was not due to acclimation to the artificial delay. In addition, adaptive performance was not influenced by awareness of the feedback delay; the ability to recalibrate movement was similar between subjects who reported that the cursor lagged the hand motion and those who did not. In a control experiment (no visual feedback), we also show that adaptation performance was comparable when visual feedback was completely removed, strongly implying that proprioception is the main driver of adaptation in this task. However, the deceleration duration and the number of velocity peaks before entering the target were influenced by the temporal offset of visual feedback, suggesting that the ability to correct for movement end-point errors was disrupted by the feedback manipulation.
Relation to previous studies.
To accurately update future movements in response to experienced perturbations, the brain must correctly temporally associate the delayed sensory information to the previously issued motor commands. The flexibility of this temporal association has been examined for different motor tasks. For example, early studies of the effects of artificial delays of visual feedback reported a decrease in accuracy, speed, and smoothness in simple motor tasks, such as writing and tracing, but typically did not comprehensively quantify these relationships (Held et al. 1966; Held and Durlach 1989; Kalmus et al. 1960; Smith 1972; Smith et al. 1960; Smith and Bowen 1980). Levy and colleagues (Levy et al. 2010) and more recently Avraham et al. (2017b) examined the ability to adapt reaching movements to novel dynamics when there is a temporal offset (50, 70, or 100 ms) between the visual feedback of hand motion and the applied movement perturbation. In this case, the motion disturbance (a velocity-dependent force field) experienced by the subject either matched the current visually observed state of the hand (represented accurately by the visual feedback) or lagged this motion state by a set delay. In other words, when there was a temporal offset, the magnitude of the experienced perturbation at time t was based on the motion state (movement velocity) τ ms prior, t − τ ms. In both studies the authors showed that subjects were able to recalibrate movements based on this delayed motion state perturbation, largely independent of the visual feedback dissociation. However, unlike the present results, in Levy et al. (2010) this conclusion was based on an analysis of the movement trajectories (perpendicular displacement), making it difficult to examine the temporal properties (the applied force profile) of the feedforward adaptive response. In addition, there is the confounding issue that an increase in limb impedance accompanies motor learning, complicating the interpretation of changes in movement trajectories (Franklin et al. 2008; Joiner et al. 2013; Milner and Franklin 2005; Takahashi et al. 2001). In the subsequent study (Avraham et al. 2017b), the authors used error clamps to directly measure the temporal force patterns subjects exerted in response to the delayed forces. Interestingly, the authors showed that the compensatory force pattern was a combination of the delayed velocity information and the current position and velocity information—a pattern that transferred to novel, faster movement speeds. Consistent with the delayed visual feedback results, the compensation to the delayed forces suggests that the motor system has a robust temporal representation of limb state that can be utilized even when the visual feedback of the limb is temporally misaligned or absent.
Our results for motion-based adaptation are distinctly different from previous studies that have examined the influence of feedback delay on the adaptation to perturbations of movement visual feedback. For example, Kitazawa and colleagues (Kitazawa et al. 1995, 2002) examined the ability of human subjects and monkeys to compensate for visual shifts (prism displacements) to reaching movements. The authors showed that the rate and amount of motor adaptation in response to the prism manipulation are reduced when visualization of the shifted movement end point was delayed by as little as 50 ms. More recently, Honda and colleagues (Honda et al. 2012a, 2012b) demonstrated that a delay between hand motion and the corresponding cursor representation reduced the ability to adapt to visual feedback manipulations of the movement vector (visuomotor rotation). Compared with the present results, this difference in performance suggests that the alignment of visual feedback differentially affects movement recalibration in response to physical disturbances and remapping of movement based on visual information, consistent with the respective compensations involving at least partially distinct neural mechanisms (Krakauer et al. 1999; Rabe et al. 2009; Tanaka et al. 2009).
It is possible that the delay in visual feedback could be interpreted as a spatial perturbation to the cursor. That is, the delay induces spatial errors, similar to a difference in gain between the cursor and the actual position of the hand. Recently, Marko et al. (2012) applied a visual gain of the cursor trajectory that exaggerated the visual lateral errors (orthogonal to the movement direction) due to a force-field perturbation (smaller than, the same as, or larger than that experienced by the hand). In this study, the gain did influence the adaptation to the force-field perturbation, suggesting that perhaps the temporal offset used in the present study was too small to observe an effect. However, in contrast to the exaggeration of lateral errors in Marko et al. (2012), the possible spatial errors induced solely by the visual delays in the present study were mostly longitudinal (aligned with the movement direction)—an exaggeration along the y-axis. Even if the delay was increased in the present study, the temporal delay and any spatial displacement would still remain along the movement direction rather than in the direction of the perturbation, complicating the interpretation of the delay as a difference in movement gain and the direct comparison to the results of Marko et al. However, a recent study examining visuomotor delay (Avraham et al. 2017a) provides evidence that delayed visual information of movement dynamics is not represented as a visual spatial shift or modified gain but rather based on the state of the limb. Here, subjects performed a pong game in which there was a delay between the paddle and the hand movement. After prolonged training, the authors examined the transfer of the delay effects to reaching and tracking tasks without visual feedback. The movements in these tasks revealed a state-based representation of the delay. That is, the experienced dynamics in the paddle game were represented based on the state of the movements rather than a visual spatial shift or modified movement gain due to the delayed feedback. Similar to the compensatory force profiles presented in Fig. 2, the subjects utilized information about the current state of the limb rather than the time lag of the visual feedback.
The finding that adaptation to the force-field perturbation is largely unaffected by delayed or even absent visual feedback raises the question as to why subjects would rely heavily on proprioception in forming the compensatory temporal force patterns. A recent study by Crevecoeur et al. (2016) may provide a theoretical framework to understand this bias in sensory information utilization. The authors show that the feedback motions in response to mechanical perturbations (applied torques of different magnitudes) to the upper limb relied largely on limb proprioception despite the concurrent availability of visual information. Utilizing dynamic Bayesian estimation, the authors propose that when combining the two sensory modalities the respective temporal delays of the information flow is an important consideration in the neural integration. Thus the relatively shorter delays associated with limb afferent feedback may result in a stronger influence over the compensatory response. Such reasoning may also explain why delayed or even absent visual feedback had a minimal effect on the adaptation to the novel dynamics applied in the present study.
Differences between perception and motor response to temporal offset of visual feedback.
At the end of each experimental session we assessed subjects’ perceptual awareness of the lag between arm motion and the cursor feedback for the constant delay condition. The proportion of subjects who reported perceptual awareness of the temporal offset increased with the magnitude of the feedback delay (from 1 of 14 subjects for constant 75 ms to 4 of 14 subjects for constant 150 ms). As shown in Figs. 3 and 5, subjects adapted to the force perturbation in a similar manner for both delay amounts and onset conditions, suggesting that awareness of the temporal manipulation was not required to compensate for the movement disturbance. This further suggests that perceptual awareness of the offset was largely independent of changes in motor behavior even when utilizing the same sensory information.
This possible dissociation between the perceptual and motor systems is consistent with performance in other motor tasks. For example, Brayanov and Smith (2010) compared perceptual and motor behavior (through involuntary postural adjustments) when estimating the weight of a held object. The study demonstrated that the biases of the respective systems are opposite: the perceptual system estimates a small cube to be heavier than a comparable large cube, whereas the motor system estimates this small cube to be lighter. In addition, Tanaka et al. (2011) examined the extent to which adaptation to prism displacement was influenced by the modification of the subjective timing between sensory and motor events. The authors altered subjective simultaneity by delaying the feedback of a pointing movement by 100 ms. Although the perception of temporal order for the motor and sensory events was modified, the adaptation rate to prism displacement was not affected. This indicates that motor adaptation occurred independently of the adapted subjective timing. In light of these previous results, it would be informative to determine the extent to which the two systems work independently by comparing the threshold for perceptual awareness of the asynchrony between feedback and motion to the ability to compensate for these temporal manipulations, especially for visual manipulations to movement (i.e., visuomotor rotation or prism adaptation).
Implications for prosthetic control.
In all experimental conditions examined (delayed or absent visual feedback), proprioceptive feedback was aligned with the actual motion of the hand and therefore provided an accurate, albeit physiologically delayed, estimate of the motion state. Counter to our hypothesis, we found that motor adaptation was not significantly different among the three delay conditions or for the different methods by which the temporal manipulation was introduced. Furthermore, subjects were able to compensate for the perturbation when visual feedback was completely removed. Together, this suggests that continuous, accurate, proprioceptive feedback largely provides the motion state information necessary to determine the error-based feedback required for movement recalibration in response to the novel dynamics. This is consistent with previous reports that have shown that learning to account for disruptions of movement dynamics is largely unaffected when visual feedback is withheld or uninformative (DiZio and Lackner 2000; Franklin et al. 2007; Lackner and Dizio 1994; Scheidt et al. 2005; Shadmehr and Mussa-Ivaldi 1994).
These results could help improve the design requirements of prosthetics. For example, these systems are usually associated with a significant inherent delay of ~60–200 ms between initiation of the motion and the actuation of the device action (Carmena et al. 2003; Farrell and Weir 2007; Mussa-Ivaldi and Miller 2003; Velliste et al. 2008). This visual feedback delay, combined with the lack of proprioception, influences the operation strategy. For example, when using a prosthetic arm to complete simple motor tasks such as reaching and grasping, subjects typically fixate on the prosthesis rather than the object of interest, even when significant training is provided (Sobuh et al. 2014). This is in contrast to normal movement, during which eye movements are directed to the parts of the environment critical for action completion rather than the hand movement (Flanagan and Johansson 2003; Johansson et al. 2001). This variation suggests a difference in control strategy when using the prostheses: subjects rely more on visual feedback to guide movement because of the lack of proprioceptive feedback. Our present work shows that delays in visual feedback significantly influence the correction strategies (deceleration duration and number of corrective submovements) during both the baseline and training periods. This suggests that the inherent delays in current prosthetics may limit the ability to correct for fine end-point movement disturbances, even if patients are able to partially acclimate to the temporal offset. However, in line with recent studies (Dadarlat et al. 2015; Suminski et al. 2010), the minimal effect of the delayed or absent visual feedback on the overall motor learning in this paradigm strongly implies that the development of intuitive, feedforward control of prosthetics requires adequate proprioceptive feedback.
GRANTS
This work was supported by a grant from the National Eye Institute (EY-021252) to W. M. Joiner.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
AUTHOR CONTRIBUTIONS
E.M. and W.Z. performed experiments; E.M. and L.C.J.B. analyzed data; E.M., L.C.J.B., and W.M.J. interpreted results of experiments; E.M., L.C.J.B., W.Z., and W.M.J. prepared figures; E.M., L.C.J.B., and W.M.J. drafted manuscript; E.M., L.C.J.B., W.Z., and W.M.J. edited and revised manuscript; E.M., L.C.J.B., W.Z., and W.M.J. approved final version of manuscript; W.M.J. conceived and designed research.
REFERENCES
- Ariff G, Donchin O, Nanayakkara T, Shadmehr R. A real-time state predictor in motor control: study of saccadic eye movements during unseen reaching movements. J Neurosci 22: 7721–7729, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avraham G, Leib R, Pressman A, Simo L, Karniel A, Shmuelof L, Mussa-Ivaldi F, Nisky I. Representation of visuomotor delay with current state information. Annual Society for the Neural Control of Movement Conference, Dublin, Ireland, 2017a. [Google Scholar]
- Avraham G, Mawase F, Karniel A, Shmuelof L, Donchin O, Mussa-Ivaldi FA, Nisky I. Representing delayed force feedback as a combination of current and delayed states. J Neurophysiol 118: 2110–2131, 2017b. doi: 10.1152/jn.00347.2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bagesteiro LB, Sarlegna FR, Sainburg RL. Differential influence of vision and proprioception on control of movement distance. Exp Brain Res 171: 358–370, 2006. doi: 10.1007/s00221-005-0272-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brayanov JB, Smith MA. Bayesian and “anti-Bayesian” biases in sensory integration for action and perception in the size-weight illusion. J Neurophysiol 103: 1518–1531, 2010. doi: 10.1152/jn.00814.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brennan AE, Smith MA. The decay of motor memories is independent of context change detection. PLoS Comput Biol 11: e1004278, 2015. doi: 10.1371/journal.pcbi.1004278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carmena JM, Lebedev MA, Crist RE, O’Doherty JE, Santucci DM, Dimitrov DF, Patil PG, Henriquez CS, Nicolelis MA. Learning to control a brain-machine interface for reaching and grasping by primates. PLoS Biol 1: E42, 2003. doi: 10.1371/journal.pbio.0000042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Conditt MA, Gandolfo F, Mussa-Ivaldi FA. The motor system does not learn the dynamics of the arm by rote memorization of past experience. J Neurophysiol 78: 554–560, 1997. [DOI] [PubMed] [Google Scholar]
- Cordo P, Carlton L, Bevan L, Carlton M, Kerr GK. Proprioceptive coordination of movement sequences: role of velocity and position information. J Neurophysiol 71: 1848–1861, 1994. [DOI] [PubMed] [Google Scholar]
- Crevecoeur F, Munoz DP, Scott SH. Dynamic multisensory integration: somatosensory speed trumps visual accuracy during feedback control. J Neurosci 36: 8598–8611, 2016. doi: 10.1523/JNEUROSCI.0184-16.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dadarlat MC, O’Doherty JE, Sabes PN. A learning-based approach to artificial sensory feedback leads to optimal integration. Nat Neurosci 18: 138–144, 2015. doi: 10.1038/nn.3883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Darling WG, Gilchrist L. Is there a preferred coordinate system for perception of hand orientation in three-dimensional space? Exp Brain Res 85: 405–416, 1991. doi: 10.1007/BF00229417. [DOI] [PubMed] [Google Scholar]
- Diedrichsen J, Criscimagna-Hemminger SE, Shadmehr R. Dissociating timing and coordination as functions of the cerebellum. J Neurosci 27: 6291–6301, 2007. doi: 10.1523/JNEUROSCI.0061-07.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- DiZio P, Lackner JR. Congenitally blind individuals rapidly adapt to coriolis force perturbations of their reaching movements. J Neurophysiol 84: 2175–2180, 2000. [DOI] [PubMed] [Google Scholar]
- Farrell TR, Weir RF. The optimal controller delay for myoelectric prostheses. IEEE Trans Neural Syst Rehabil Eng 15: 111–118, 2007. doi: 10.1109/TNSRE.2007.891391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farshchiansadegh A, Ranganathan R, Casadio M, Mussa-Ivaldi FA. Adaptation to visual feedback delay in a redundant motor task. J Neurophysiol 113: 426–433, 2015. doi: 10.1152/jn.00249.2014. [DOI] [PubMed] [Google Scholar]
- Flanagan JR, Johansson RS. Action plans used in action observation. Nature 424: 769–771, 2003. doi: 10.1038/nature01861. [DOI] [PubMed] [Google Scholar]
- Foulkes AJ, Miall RC. Adaptation to visual feedback delays in a human manual tracking task. Exp Brain Res 131: 101–110, 2000. doi: 10.1007/s002219900286. [DOI] [PubMed] [Google Scholar]
- Franklin DW, Burdet E, Tee KP, Osu R, Chew CM, Milner TE, Kawato M. CNS learns stable, accurate, and efficient movements using a simple algorithm. J Neurosci 28: 11165–11173, 2008. doi: 10.1523/JNEUROSCI.3099-08.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Franklin DW, So U, Burdet E, Kawato M. Visual feedback is not necessary for the learning of novel dynamics. PLoS One 2: e1336, 2007. doi: 10.1371/journal.pone.0001336. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fuentes CT, Bastian AJ. Where is your arm? Variations in proprioception across space and tasks. J Neurophysiol 103: 164–171, 2010. doi: 10.1152/jn.00494.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghez C, Gordon J, Ghilardi MF. Impairments of reaching movements in patients without proprioception. II. Effects of visual information on accuracy. J Neurophysiol 73: 361–372, 1995. [DOI] [PubMed] [Google Scholar]
- Gonzalez Castro LN, Hadjiosif AM, Hemphill MA, Smith MA. Environmental consistency determines the rate of motor adaptation. Curr Biol 24: 1050–1061, 2014. doi: 10.1016/j.cub.2014.03.049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordon J, Ghilardi MF, Ghez C. Impairments of reaching movements in patients without proprioception. I. Spatial errors. J Neurophysiol 73: 347–360, 1995. [DOI] [PubMed] [Google Scholar]
- Gritsenko V, Krouchev NI, Kalaska JF. Afferent input, efference copy, signal noise, and biases in perception of joint angle during active versus passive elbow movements. J Neurophysiol 98: 1140–1154, 2007. doi: 10.1152/jn.00162.2007. [DOI] [PubMed] [Google Scholar]
- Gritsenko V, Yakovenko S, Kalaska JF. Integration of predictive feedforward and sensory feedback signals for online control of visually guided movement. J Neurophysiol 102: 914–930, 2009. doi: 10.1152/jn.91324.2008. [DOI] [PubMed] [Google Scholar]
- Held R, Durlach N. Telepresence, time delay and adaptation. In: Spatial Displays and Spatial Instruments, edited by Ellis SR, Kaiser MK, Grunwald A. Moffett Field, CA: NASA, 1989, p. 28-1–28-16. [Google Scholar]
- Held R, Efstathiou A, Greene M. Adaptation to displaced and delayed visual feedback from the hand. J Exp Psychol Gen 72: 887–891, 1966. doi: 10.1037/h0023868. [DOI] [Google Scholar]
- Honda T, Hirashima M, Nozaki D. Adaptation to visual feedback delay influences visuomotor learning. PLoS One 7: e37900, 2012a. doi: 10.1371/journal.pone.0037900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Honda T, Hirashima M, Nozaki D. Habituation to feedback delay restores degraded visuomotor adaptation by altering both sensory prediction error and the sensitivity of adaptation to the error. Front Psychol 3: 540, 2012b. doi: 10.3389/fpsyg.2012.00540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johansson RS, Westling G, Bäckström A, Flanagan JR. Eye-hand coordination in object manipulation. J Neurosci 21: 6917–6932, 2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joiner WM, Ajayi O, Sing GC, Smith MA. Linear hypergeneralization of learned dynamics across movement speeds reveals anisotropic, gain-encoding primitives for motor adaptation. J Neurophysiol 105: 45–59, 2011. doi: 10.1152/jn.00884.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joiner WM, Brayanov JB, Smith MA. The training schedule affects the stability, not the magnitude, of the interlimb transfer of learned dynamics. J Neurophysiol 110: 984–998, 2013. doi: 10.1152/jn.01072.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Joiner WM, Smith MA. Long-term retention explained by a model of short-term learning in the adaptive control of reaching. J Neurophysiol 100: 2948–2955, 2008. doi: 10.1152/jn.90706.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jones SA, Cressman EK, Henriques DY. Proprioceptive localization of the left and right hands. Exp Brain Res 204: 373–383, 2010. doi: 10.1007/s00221-009-2079-8. [DOI] [PubMed] [Google Scholar]
- Kalmus H, Fry DB, Denes P. Effects of delayed visual control on writing, drawing, and tracing. Lang Speech 3: 96–108, 1960. doi: 10.1177/002383096000300205. [DOI] [Google Scholar]
- Karniel A, Mussa-Ivaldi FA. Sequence, time, or state representation: how does the motor control system adapt to variable environments? Biol Cybern 89: 10–21, 2003. [DOI] [PubMed] [Google Scholar]
- Kawato M. Internal models for motor control and trajectory planning. Curr Opin Neurobiol 9: 718–727, 1999. doi: 10.1016/S0959-4388(99)00028-8. [DOI] [PubMed] [Google Scholar]
- Keele SW, Posner MI. Processing of visual feedback in rapid movements. J Exp Psychol 77: 155–158, 1968. doi: 10.1037/h0025754. [DOI] [PubMed] [Google Scholar]
- Kitazawa S, Kohno T, Uka T. Effects of delayed visual information on the rate and amount of prism adaptation in the human. J Neurosci 15: 7644–7652, 1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitazawa S, Yin PB. Prism adaptation with delayed visual error signals in the monkey. Exp Brain Res 144: 258–261, 2002. doi: 10.1007/s00221-002-1089-6. [DOI] [PubMed] [Google Scholar]
- Körding KP, Wolpert DM. Bayesian integration in sensorimotor learning. Nature 427: 244–247, 2004. doi: 10.1038/nature02169. [DOI] [PubMed] [Google Scholar]
- Krakauer JW, Ghilardi MF, Ghez C. Independent learning of internal models for kinematic and dynamic control of reaching. Nat Neurosci 2: 1026–1031, 1999. doi: 10.1038/14826. [DOI] [PubMed] [Google Scholar]
- Lackner JR, Dizio P. Rapid adaptation to Coriolis force perturbations of arm trajectory. J Neurophysiol 72: 299–313, 1994. [DOI] [PubMed] [Google Scholar]
- Lateiner JE, Sainburg RL. Differential contributions of vision and proprioception to movement accuracy. Exp Brain Res 151: 446–454, 2003. doi: 10.1007/s00221-003-1503-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Levy N, Pressman A, Mussa-Ivaldi FA, Karniel A. Adaptation to delayed force perturbations in reaching movements. PLoS One 5: e12128, 2010. doi: 10.1371/journal.pone.0012128. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marko MK, Haith AM, Harran MD, Shadmehr R. Sensitivity to prediction error in reach adaptation. J Neurophysiol 108: 1752–1763, 2012. doi: 10.1152/jn.00177.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miall RC, Weir DJ, Wolpert DM, Stein JF. Is the cerebellum a Smith predictor? J Mot Behav 25: 203–216, 1993. doi: 10.1080/00222895.1993.9942050. [DOI] [PubMed] [Google Scholar]
- Milner TE, Franklin DW. Impedance control and internal model use during the initial stage of adaptation to novel dynamics in humans. J Physiol 567: 651–664, 2005. doi: 10.1113/jphysiol.2005.090449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mussa-Ivaldi FA, Miller LE. Brain-machine interfaces: computational demands and clinical needs meet basic neuroscience. Trends Neurosci 26: 329–334, 2003. doi: 10.1016/S0166-2236(03)00121-8. [DOI] [PubMed] [Google Scholar]
- Pipereit K, Bock O, Vercher JL. The contribution of proprioceptive feedback to sensorimotor adaptation. Exp Brain Res 174: 45–52, 2006. doi: 10.1007/s00221-006-0417-7. [DOI] [PubMed] [Google Scholar]
- Proske U, Gandevia SC. The kinaesthetic senses. J Physiol 587: 4139–4146, 2009. doi: 10.1113/jphysiol.2009.175372. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabe K, Livne O, Gizewski ER, Aurich V, Beck A, Timmann D, Donchin O. Adaptation to visuomotor rotation and force field perturbation is correlated to different brain areas in patients with cerebellar degeneration. J Neurophysiol 101: 1961–1971, 2009. doi: 10.1152/jn.91069.2008. [DOI] [PubMed] [Google Scholar]
- Rossetti Y, Meckler C, Prablanc C. Is there an optimal arm posture? Deterioration of finger localization precision and comfort sensation in extreme arm-joint postures. Exp Brain Res 99: 131–136, 1994. doi: 10.1007/BF00241417. [DOI] [PubMed] [Google Scholar]
- Rothwell JC, Traub MM, Day BL, Obeso JA, Thomas PK, Marsden CD. Manual motor performance in a deafferented man. Brain 105: 515–542, 1982. doi: 10.1093/brain/105.3.515. [DOI] [PubMed] [Google Scholar]
- Sabes PN. Sensory integration for reaching: models of optimality in the context of behavior and the underlying neural circuits. Prog Brain Res 191: 195–209, 2011. doi: 10.1016/B978-0-444-53752-2.00004-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sainburg RL, Ghilardi MF, Poizner H, Ghez C. Control of limb dynamics in normal subjects and patients without proprioception. J Neurophysiol 73: 820–835, 1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sainburg RL, Lateiner JE, Latash ML, Bagesteiro LB. Effects of altering initial position on movement direction and extent. J Neurophysiol 89: 401–415, 2003. doi: 10.1152/jn.00243.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sainburg RL, Poizner H, Ghez C. Loss of proprioception produces deficits in interjoint coordination. J Neurophysiol 70: 2136–2147, 1993. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sarlegna FR, Sainburg RL. The roles of vision and proprioception in the planning of reaching movements. Adv Exp Med Biol 629: 317–335, 2009. doi: 10.1007/978-0-387-77064-216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheidt RA, Conditt MA, Secco EL, Mussa-Ivaldi FA. Interaction of visual and proprioceptive feedback during adaptation of human reaching movements. J Neurophysiol 93: 3200–3213, 2005. doi: 10.1152/jn.00947.2004. [DOI] [PubMed] [Google Scholar]
- Scheidt RA, Reinkensmeyer DJ, Conditt MA, Rymer WZ, Mussa-Ivaldi FA. Persistence of motor adaptation during constrained, multi-joint, arm movements. J Neurophysiol 84: 853–862, 2000. [DOI] [PubMed] [Google Scholar]
- Shadmehr R, Mussa-Ivaldi FA. Adaptive representation of dynamics during learning of a motor task. J Neurosci 14: 3208–3224, 1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sing GC, Joiner WM, Nanayakkara T, Brayanov JB, Smith MA. Primitives for motor adaptation reflect correlated neural tuning to position and velocity. Neuron 64: 575–589, 2009. doi: 10.1016/j.neuron.2009.10.001. [DOI] [PubMed] [Google Scholar]
- Sing GC, Orozco SP, Smith MA. Limb motion dictates how motor learning arises from arbitrary environmental dynamics. J Neurophysiol 109: 2466–2482, 2013. doi: 10.1152/jn.00497.2011. [DOI] [PubMed] [Google Scholar]
- Smith WM. Feedback: real-time delayed vision of one’s own tracking behavior. Science 176: 939–940, 1972. doi: 10.1126/science.176.4037.939. [DOI] [PubMed] [Google Scholar]
- Smith WM, Bowen KF. The effects of delayed and displaced visual feedback on motor control. J Mot Behav 12: 91–101, 1980. doi: 10.1080/00222895.1980.10735209. [DOI] [PubMed] [Google Scholar]
- Smith WM, McCrary JW, Smith KU. Delayed visual feedback and behavior. Science 132: 1013–1014, 1960. doi: 10.1126/science.132.3433.1013. [DOI] [PubMed] [Google Scholar]
- Sober SJ, Sabes PN. Multisensory integration during motor planning. J Neurosci 23: 6982–6992, 2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sober SJ, Sabes PN. Flexible strategies for sensory integration during motor planning. Nat Neurosci 8: 490–497, 2005. doi: 10.1038/nn1427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sobuh MM, Kenney LP, Galpin AJ, Thies SB, McLaughlin J, Kulkarni J, Kyberd P. Visuomotor behaviours when using a myoelectric prosthesis. J Neuroeng Rehabil 11: 72, 2014. doi: 10.1186/1743-0003-11-72. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suminski AJ, Tkach DC, Fagg AH, Hatsopoulos NG. Incorporating feedback from multiple sensory modalities enhances brain-machine interface control. J Neurosci 30: 16777–16787, 2010. doi: 10.1523/JNEUROSCI.3967-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takahashi CD, Scheidt RA, Reinkensmeyer DJ. Impedance control and internal model formation when reaching in a randomly varying dynamical environment. J Neurophysiol 86: 1047–1051, 2001. [DOI] [PubMed] [Google Scholar]
- Tanaka H, Homma K, Imamizu H. Physical delay but not subjective delay determines learning rate in prism adaptation. Exp Brain Res 208: 257–268, 2011. doi: 10.1007/s00221-010-2476-z. [DOI] [PubMed] [Google Scholar]
- Tanaka H, Sejnowski TJ, Krakauer JW. Adaptation to visuomotor rotation through interaction between posterior parietal and motor cortical areas. J Neurophysiol 102: 2921–2932, 2009. doi: 10.1152/jn.90834.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tseng YW, Diedrichsen J, Krakauer JW, Shadmehr R, Bastian AJ. Sensory prediction errors drive cerebellum-dependent adaptation of reaching. J Neurophysiol 98: 54–62, 2007. doi: 10.1152/jn.00266.2007. [DOI] [PubMed] [Google Scholar]
- van Beers RJ, Wolpert DM, Haggard P. When feeling is more important than seeing in sensorimotor adaptation. Curr Biol 12: 834–837, 2002. doi: 10.1016/S0960-9822(02)00836-9. [DOI] [PubMed] [Google Scholar]
- Vaswani PA, Shadmehr R. Decay of motor memories in the absence of error. J Neurosci 33: 7700–7709, 2013. doi: 10.1523/JNEUROSCI.0124-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Velliste M, Perel S, Spalding MC, Whitford AS, Schwartz AB. Cortical control of a prosthetic arm for self-feeding. Nature 453: 1098–1101, 2008. doi: 10.1038/nature06996. [DOI] [PubMed] [Google Scholar]
- Wagner MJ, Smith MA. Shared internal models for feedforward and feedback control. J Neurosci 28: 10663–10673, 2008. doi: 10.1523/JNEUROSCI.5479-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wolpert DM, Ghahramani Z, Jordan MI. An internal model for sensorimotor integration. Science 269: 1880–1882, 1995. doi: 10.1126/science.7569931. [DOI] [PubMed] [Google Scholar]