Intercepting virtual balls approaching under different gravity conditions: evidence for spatial prediction

Here we show that an internal model of gravity plays a key role in predicting where to intercept a fast-moving target. Participants also assumed an accelerated motion when intercepting balls approaching in a virtual environment at constant velocity. We also show that the role of visual information in guiding interceptive movement increases when more time is available.

Abstract

To accurately time motor responses when intercepting falling balls we rely on an internal model of gravity. However, whether and how such a model is also used to estimate the spatial location of interception is still an open question. Here we addressed this issue by asking 25 participants to intercept balls projected from a fixed location 6 m in front of them and approaching along trajectories with different arrival locations, flight durations, and gravity accelerations (0g and 1g). The trajectories were displayed in an immersive virtual reality system with a wide field of view. Participants intercepted approaching balls with a racket, and they were free to choose the time and place of interception. We found that participants often achieved a better performance with 1g than 0g balls. Moreover, the interception points were distributed along the direction of a 1g path for both 1g and 0g balls. In the latter case, interceptions tended to cluster on the upper half of the racket, indicating that participants aimed at a lower position than the actual 0g path. These results suggest that an internal model of gravity was probably used in predicting the interception locations. However, we found that the difference in performance between 1g and 0g balls was modulated by flight duration, the difference being larger for faster balls. In addition, the number of peaks in the hand speed profiles increased with flight duration, suggesting that visual information was used to adjust the motor response, correcting the prediction to some extent.

NEW & NOTEWORTHY Here we show that an internal model of gravity plays a key role in predicting where to intercept a fast-moving target. Participants also assumed an accelerated motion when intercepting balls approaching in a virtual environment at constant velocity. We also show that the role of visual information in guiding interceptive movement increases when more time is available.

interceptive actions require accurate visuo-motor coordination. How the central nervous system (CNS) achieves such accuracy is still a matter of debate (Brenner et al. 2016; Tresilian 2005; Zago et al. 2008, 2009; Zhao and Warren 2015). Because of the stringent spatiotemporal constraints, a small error in the position and/or in the timing of the end-effector leads to a failure in intercepting a moving object (Alderson et al. 1974; Cesqui et al. 2015, 2016). To generate an accurate motor plan, the CNS must rely on visual information acquired during target motion. However, since it takes ~100–200 ms to process visual information and to transmit the resulting motor commands to the muscles and limbs, anticipatory mechanisms are also required to bring the effector to the right time and place (Brenner et al. 2016; Tresilian 2005; Zago et al. 2008, 2009). Moreover, our visual system is poor at discriminating accelerations over short viewing periods (Brenner et al. 2016; Brouwer et al. 2002; Calderone and Kaiser 1989; Werkhoven et al. 1992). For targets normally accelerated by gravity, such as flying or falling objects, it has been hypothesized that prior knowledge of the effects of terrestrial gravity is internalized and integrated with sensory information to time the interceptive action (Lacquaniti et al. 1993; Tresilian 1993). Evidence that interceptive timing is guided by an internal model of gravity has been found in several behavioral studies in which participants intercepted a free-falling ball in either normal (Lacquaniti and Maioli 1989) or microgravity (McIntyre et al. 2001) conditions. Moreover, fMRI studies have identified specific brain regions encoding the effects of gravitational acceleration on visual motion (Ferri et al. 2016; Indovina et al. 2005; Maffei et al. 2015).

In one study, Zago and collaborators (Zago et al. 2004) investigated the role of gravity in interceptive actions by comparing the motor responses used to hit balls descending vertically under normal gravity (accelerated by 1g) or without gravity (not accelerated, 0g). Performance was worse for 0g targets, as participants timed their motor responses consistently with the assumption of the effect of gravity, anticipating the time of arrival of the ball (Zago et al. 2004; see also Senot et al. 2005). Thus support for predictive control relying on an internal model of gravity has come from studying the interception of balls descending along the vertical. A few studies have addressed similar issues in the case of projectile motion in the frontal plane. Bosco et al. (2012) found that interception of fully visible targets was based on combined servo-control and predictive strategies involving the internal model of gravity, while interception of occluded targets mainly involved the predictive strategy. Also, eye movements exhibited a similar reliance on the internal model of gravity during the same paradigm (Delle Monache et al. 2015). In another study (La Scaleia et al. 2015), the interception points were distributed along the parabolic trajectories of a ball falling from an incline even for occluded trajectories, indicating that participants were able to extrapolate an extended segment of the target trajectory based on a 1g internal model. A few other studies considered the role of internalized gravity for approaching projectile motions. In Diaz et al. (2013) it was found that prebounce eye saccades predicted time and location of the target after the bounce by taking into account gravity and elasticity effects. A modeling study indicated that prior knowledge of ball size and gravity combined with optic parameters may yield accurate estimates of time-to-contact (TTC) for approaching projectile motion (Gómez and López-Moliner 2013). This was confirmed experimentally by de la Malla and López-Moliner (2015) for a catching task involving early, late, or full vision of a parabolic path of approaching balls in a virtual environment.

Studies involving approaching projectile motion have mainly focused on the temporal aspects of interception. However, to date little work has been done to investigate the spatial characteristics of these movements. Here we tested the role of the internal model of gravity on predicting the spatial characteristics of targets approaching horizontally, i.e., with a large component of the velocity on the horizontal plane. Differently from a free-falling ball accelerated by gravity, moving along the same vertical path as a ball descending at constant downward velocity without gravity, a ball projected toward a participant will move along different paths depending on the gravity level, i.e., a parabolic path (neglecting air drag) at 1g and a linear path at 0g. Spatial information, then, is different in the two acceleration conditions. Balls falling vertically with a given initial velocity will arrive at the same spatial position at different times depending on the acceleration. Thus, with vertically descending balls, the arrival time at a given spatial position discriminates between an accelerated and a nonaccelerated ball. If participants relied on prior knowledge of gravity to time their motor responses, their estimate of the arrival time would be accurate only when the ball moves in accordance with Earth gravity. In contrast, approaching balls with the same initial horizontal velocity will arrive on a vertical plane at a given distance from launch at the same time with and without gravity. However, gravity will affect the arrival position along the vertical direction. Even if the vertical component of the initial velocity is adjusted according to gravity acceleration such that the ball will arrive at the same spatial location at a given distance from launch, the paths will intersect only at that point and the arrival locations will be different for any other distance. It follows that, when intercepting an horizontally approaching ball under different gravity conditions, it is critical to identify where to intercept the ball, because the temporal estimate, i.e., when to intercept the ball at a specific distance from launch, can be estimated by relying on first-order information in both 1g and 0g conditions [although according to Gómez and López-Moliner (2013) time estimates in 1g conditions are more accurate when gravity effects are taken into account].

Therefore, according to a strategy that relies on an internal estimate of gravity (1g model), we hypothesized that participants would achieve a better performance when they intercept 1g balls. Moreover, according to this hypothesis, participants should expect lower arrival positions than the actual ones for 0g balls, under the assumption that the ball would fall down anyway. To test these predictions, we asked participants to intercept 0g and 1g balls projected with different spatial and temporal characteristics from a fixed position toward them in an immersive virtual reality (VR) system in which it was possible to reproduce a zero-gravity environment on Earth. Participants were asked to intercept the targets with a racket, and they were free to choose the time and place of interception along the target trajectory.

MATERIALS AND METHODS

Participants

Twenty-nine individuals gave their written informed consent to participate in the study, which had been approved by the Ethical Review Board of the Santa Lucia Foundation. Only right-handed participants with a height between 1.67 and 1.83 m were included in the study. Handedness selection was motivated by the fact that participants were required to intercept with their right hand and was assessed by a questionnaire based on the Edinburgh Inventory (Oldfield 1971). Height selection ensured optimal view in the apparatus and reachability of all via points (see below). All participants had normal or corrected to normal vision, as assessed by two visual tests performed before the beginning of the experimental session, as described in Experimental Protocol. One participant did not pass both tests, and he was excluded from the experimental session. Because of accidental problems with the motion capture system and with the data acquisition software during the experimental session, data from three additional participants were excluded from the analysis. Overall, data from 25 individuals were used for the analyses (13 men and 12 women; 26 ± 8 yr, mean age ± SD; 1.73 ± 0.05 m, mean height ± SD).

Apparatus

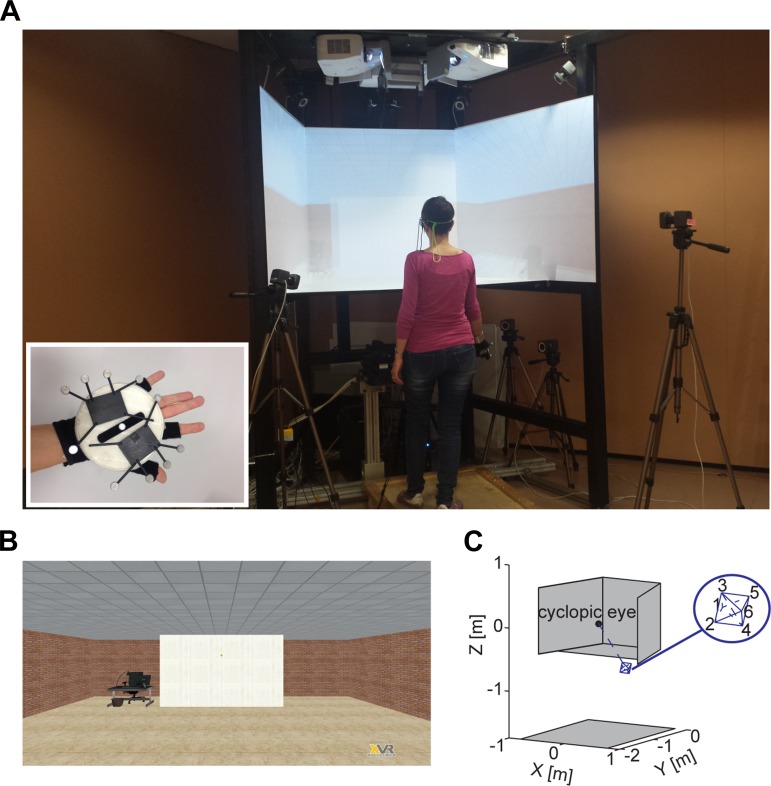
Experiments were carried out in an immersive virtual environment [mini-CAVE, VRMedia, Pisa, Italy; as in Cave Automatic Virtual Environment (Cruz-Neira et al. 1992)] system that consisted of four projectors (3 U300X, NEC Display Solutions of America, and 1 S5301WM, Acer; resolution 1,024 × 768 pixels) and four projection screens (Fig. 1). A horizontal screen (trapezoidal screen with bases 1.05 m and 1.58 m long and sides 1.00 m long) was located at 1.22 m from the ground and was in contact with the lower edges of three vertical screens (see Fig. 1C). Two lateral vertical screens (1.05 × 1.40 m) formed an angle of 15.75° with the frontal vertical screen (1.05 × 1.05 m). Participants stood in front of the mini-CAVE with the sternum near the edge of the horizontal screen at a horizontal distance of ~1 m from the frontal screen. As shown in Fig. 1C, the lateral screens extended beyond the edge of the horizontal screen closer to the participant, allowing a horizontal field of view of ~180°. The vertical field of view was ~55° and included the manual workspace of the participant (occluded by the horizontal screen).

Fig. 1.

Experimental setup. A: participants stood at a distance of 1 m from the frontal screen of the mini-CAVE watching a virtual environment stereoscopically through shutter glasses. Participants held a racket in their right hand (see inset, where retroreflective markers attached to the racket for motion capture are also visible). B: the virtual environment consisted of a room with a screen located 6 m in front of the participant and some objects (a desk and a chair) of familiar sizes. Balls were projected from a fixed position on the screen. C: the positions of 6 via points are shown with respect to the mini-CAVE and with respect to the estimated position of the cyclopic eye for a participant of average height. The via points (see inset) were arranged around a central position (see text) at 2 different distances along the line of sight (3 and 4), at different azimuth angles (1 and 6), and at different elevation angles (2 and 5).

Stereoscopic images were generated according to the position in space of the two eyes and were viewed as alternated monocular images through shutter glasses (frame rate 60 Hz for each eye; Optoma 3D-RF Glasses, Optoma Europe, Watford, UK). The position of the eyes was continuously updated by tracking the position and orientation of the glasses with an inertial-ultrasonic motion capture system (IS-900 System, InterSense, Bedford, MA). An emitter was fixed on the shutter glasses. The position of the eyes was computed with respect to the emitter and used to update the virtual scene coherently with head movements. The distance between the two eyes was considered as the difference between the center of the two lenses, i.e., 6.5 cm. The center position between the lens was 3 cm below the emitter and 2 cm backward.

The XVR software platform (Tecchia et al. 2010; eXtreme Virtual Reality, VRMedia) was used to generate an immersive virtual scene depicting a room with a large screen (4 m × 3 m, width × height) located at 6 m from the participant, that is, at 5 m behind the frontal screen, as shown in Fig. 1B. The scene roughly reproduced the experimental setup of our previous studies of catching in naturalistic conditions (Cesqui et al. 2012), in which a launching machine was hidden behind the screen. Objects of known size (a desk and a chair) were also displayed to facilitate spatial calibration of the scene.

Because the workspace of the inertial-ultrasonic motion capture system used to track eye position did not include the volume below the horizontal screen, hand position and orientation were tracked with a second optical motion capture system (120 Hz, 8 Flex13 cameras; Optitrack System, NaturalPoint), whose workspace included the volume under the horizontal screen. During the familiarization session (see Experimental Protocol) only the position of a marker on the right index tip was tracked, while during the experimental session the position and orientation of the center of a handheld plastic racket (a thin disk of radius 0.06 m and weight 29 g) were tracked. To this end, 11 retroreflective markers were attached to the surface of the racket, which was attached (without any handle) to the palm of participants’ right hand. Participants wore a glove, and the racket was attached to the glove with Velcro (Fig. 1A). The racket was represented in the virtual environment as a black disk.

The optical motion capture system (Optitrack) and the VR system (XVR) ran on two networked workstations and communicated via UDP protocol. Optitrack data were transmitted to the XVR software with custom code written by means of the NatNet SDK tools of the API provided by NaturalPoint. A custom graphical user interface, implemented in MATLAB (MathWorks, Natick, MA), was used to control the experiment.

The coordinate system of the inertial-ultrasound motion capture system (Intersense) used to track the shutter glasses was also used in the virtual environment. The origin of this coordinate system was located at the center of the frontal screen, and coordinate axes were oriented with the x-axis pointing to the right of the participant, the y-axis directed from the participant toward the frontal screen, and the z-axis vertical. A calibration was required to transform the position of the racket measured by the Optitrack motion capture system into the coordinate system used for the virtual scene. To this end, a marker tracked by Optitrack was attached on top of an Intersense emitter and they were tracked while they were moved together within their overlapping workspace. The data recorded by the two motion capture systems were submitted to a calibration algorithm to extract the rotation matrix and the translation vector representing the transformation matrix between the two coordinate systems (Arun et al. 1987). Once the Optitrack-Intersense transformation was calibrated, its accuracy was assessed with a second data acquisition. The error between the two motion capture systems was evaluated by computing the difference between the position of the center of the Optitrack marker and the position of the Intersense emitter. The mean value and standard deviation of this parameter computed across samples was 1.3 ± 0.8 mm.

The XVR software provided online feedback to the participant about the success of the interceptive movement (see below). The position of the virtual ball and the position and orientation of the racket were used at each iteration of the software loop, running at 1 kHz, to determine whether the racket hit the ball. Because of the latency between the software instruction to update the video output and the actual change of the image of the ball on the screens, the software compared the position of the racket with the position of the ball 50 ms earlier. Such latency was determined experimentally by recording the time of execution of the video output update and the time of change of the image on the screen with an analog-to-digital converter board (USB 6008, National Instruments Italy, Assago (MI), Italy; sampling at 2.5 kHz). The time of execution of the video output was indicated by a command sent by the XVR software on the TCP/IP network to a personal computer that generated a TTL pulse with its parallel port. The time of change of the image on the screen was measured by a photodiode (BPW21, Siemens, Munich, Germany).

Experimental Protocol

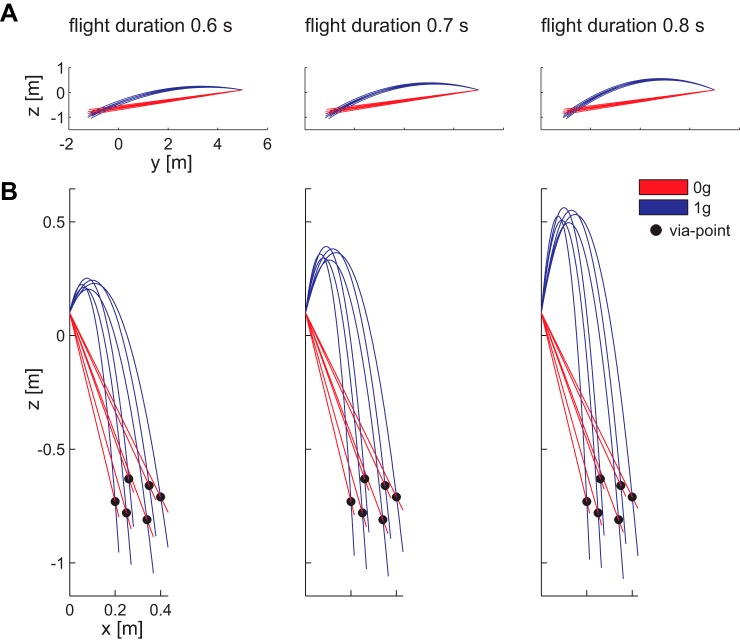
Participants were instructed to intercept a virtual ball (radius 0.035 m) projected from a fixed position and reaching one of six via points after flying for one of three time intervals with or without gravitational acceleration (Fig. 2). Thus 36 ball flight conditions were obtained by combining three gravity acceleration values (0g and 1g, where g = 9.81 m/s²), three flight durations (T: 0.6, 0.7, and 0.8 s) and six via points. In all trials, the ball was projected from a hole in the virtual screen at 1.66 m from the ground. Via-point positions (see Fig. 1 for further details) were used to define the lateral variability of ball trajectories and were not shown to participants. Participants performed 360 trials (10 repetitions for each condition) in a fully randomized sequence.

Fig. 2.

Ball paths for different flight conditions. Ball paths are illustrated in the lateral (y-z plane; A) and frontal (x-z plane; B) views for each flight duration, for all via-point positions (black dots) and for both acceleration conditions from the starting position to the point reached 50 ms after passing through the via-point position.

Before the beginning of the experimental session, visual acuity and correct vision in the environment were tested and participants were familiarized with the virtual environment. To assess visual acuity, participants were asked to read letters from a Snellen chart (Snellen 1862; Stevens 2007) at a distance of 6 m, one eye at a time. To assess whether participants could see the image projected on the screens, they were asked to wear shutter glasses and watched a scene in the mini-CAVE in which a red ball (radius 3.5 cm) was displayed in front of them at 50 cm from their point of view. They were thus required to confirm whether they saw the ball or if they saw two different images. Inclusion criteria were 1) a visual acuity of at least 6/7.5 and 2) a positive response to the test. To familiarize with the virtual environment and to assess via points’ reachability, a pointing task was performed. Participants had to reach a target with the tip of their right index. Targets positions were the same as the via points in the interception task.

Participants then performed the experimental session. They were instructed to intercept the ball with the handheld racket. The racket was attached to the palm of the open hand to perform an interception task. No specific instructions were provided about the position of the via points or where to intercept the ball along its trajectory.

The XVR routine computed the distance between the racket and the ball at each software iteration (1 kHz) to assess whether an interception had occurred. Time of interception was defined as the instant at which the ball surface contacted the planar surface of the racket. A ball was classified as “hit” when intercepted and “missed” otherwise. A hit ball was further classified as “center hit” if the orthogonal projection of the center of the ball on the racket surface was inside the racket at the time of contact. A hit ball was classified as “side hit” if the projection was outside the racket but at a distance lower than the ball radius, i.e., the ball surface touched the edge of the racket. The normal vector of the racket was pointing in the direction opposite to the hand palm; thus only projection on this side of the racket led to a successful trial. An example of how the impact occurred is shown in Fig. 3.

Fig. 3.

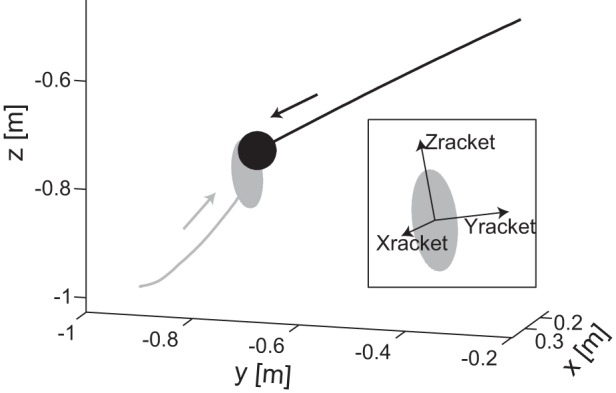
Example of racket and ball positions in space for a center hit trial. Hand trajectory (gray line) is shown together with ball trajectory (black line) for 1 trial in which the subject hit the ball (subject MD, 1g condition, 0.7-s ball flight duration, via point 5). Figure shows an example of an interception in a 3-dimensional view (e.g., an orthographic projection) in which the racket appears ellipse-shaped. The axes of the racket at impact are shown in inset.

Participants received both visual and auditory feedback about the interceptive outcome. In particular, hit balls remained attached to the virtual racket at the impact position for 2 s, changing color to red if the ball was side hit or to green if the ball was center hit. If the ball was missed, it continued its flight until it reached the ground. These events were also signaled by brief tones of different frequencies, the lowest frequency indicating a missed ball and the highest frequency a center hit ball.

To ensure that participants maintained the same initial head position throughout the experiment, a head reference position was recorded at the beginning of the experimental session and compared with the position recorded at the beginning of each trial. If subjects did not keep the head in the reference position (considering a tolerance region of 10 cm of radius) when each trial was starting, the trial did not start until the subject went back to the correct position. Once the ball appeared at the release point on the screen, it started to move after a random delay varying from 0.2 s to 1 s.

Data Analysis

Impact position on the racket.

To determine whether the racket hit the surface of the ball, we computed the projection of the center of the ball on the plane of the racket for the first sample in which the surface of the ball touched that plane, i.e., at impact time. The distance of this projection from the center of the racket determined whether a trial was labeled as “successful” or “unsuccessful.” In this analysis, both successful and unsuccessful trials were included. We considered the position of the ball at the impact time in the reference frame of the racket. The vector normal to the racket surface was Y_racket; thus the impact point on the racket was determined by X_racket and Z_racket coordinates (Fig. 3). The reference frame of the racket at impact was rotated around the Y_racket axis such that the X_racket axis was horizontal. In this fashion, Z_racket indicated the vertical direction on the racket.

Spatial distribution of impact positions.

Participants were free to intercept the ball along its trajectory; thus we computed the spatial distribution of hand positions, i.e., the center of the racket, at the impact time for both successful and unsuccessful trials. The impact time was defined as above. We determined an ellipse for each condition (gravity value, flight duration, and via point), pooling the impact positions on the sagittal plane (y-z) across subjects and repetitions. To characterize shape, size, and orientation of these distributions we computed the 95% tolerance ellipse and the relative eigenvalues and eigenvectors (La Scaleia et al. 2015; McIntyre et al. 1997). Then, we computed the angle between the first eigenvector of the ellipse and the direction of the ball trajectory at the point of minimum Euclidean distance from the center of the ellipse for each condition. We determined for both the 0g and 1g conditions the angle between the eigenvector and the direction of each trajectory (0g and 1g) in order to assess the orientation of the ellipse with respect to ball trajectories.

Hand movements.

The position and orientation data samples of the racket were digitally low-pass filtered (low-pass Butterworth filter; 10-Hz cutoff frequency; MATLAB filtfilt function) and differentiated (MATLAB diff, spline functions) to obtain first-, second-, and third-order derivatives. Six kinematic parameters were computed to characterize hand movements: 1) onset time, defined as the time at which the magnitude of hand tangential velocity (speed) exceeded 10% of its maximum value; 2) peak speed, defined as the maximum value of the hand speed; 3) time to peak, defined as the time interval between movement onset and the time of peak speed; 4) impact time, i.e., the time at which the interception occurred; 5) hand velocity and speed at onset and impact times; and 6) the number of peaks in the speed profile. We analyzed both speed and velocity of the hand because while ball speed differed depending on flight duration and gravity conditions, the horizontal component of ball velocity differed only depending on flight duration. The vertical component of ball velocity differed depending on gravity condition. Then, the number of peaks was computed to quantify the presence of submovements. For each trial, the speed profile was interpolated and then differentiated (MATLAB diff, spline, fnder functions) to find zero-crossings of the tangential acceleration, with negative jerk, and to find minima of the tangential acceleration close to zero, i.e., zero-crossings of the jerk profile.

All analyses were performed with custom software written in MATLAB (MathWorks).

Statistical Analysis

We wanted to assess whether participants achieved a better performance in intercepting 1g balls rather than 0g balls, as predicted by the prior assumption of our sensorimotor system of an accelerated ball motion. Moreover, this prior assumption would predict an error in the spatial prediction of interception for 0g balls. Thus we tested whether the impact position differed depending on gravity conditions. Finally, we investigated kinematic variables to examine whether participants adopted different strategies in response to different accelerations.

We assessed how the interceptive performance and the motor response depended on the experimental conditions by means of generalized linear mixed models (GLMMs). GLMMs account for a normally distributed variability between participants (random effects), the effects of the experimental variables (fixed effects), which are consistent across participants, and a residual variability, which in the analysis of the probability of “success” arises from a binomial distribution. Fixed-effect parameters estimate the effect of the experimental variables (i.e., gravity conditions G, flight durations T, and via points V) on participants’ responses. Random-effect parameters estimate the heterogeneity between different participants (Baayen et al. 2008; Bates et al. 2014; Moscatelli et al. 2012) (see appendix for further details on GLMM). Additionally, we applied Bartlett’s test to evaluate for a difference in a response’s variance between the two gravity conditions. Moreover, we performed a multivariate analysis of variance to examine whether the experimental conditions affected the spatial distribution of impact positions. To determine whether the eigenvalues of the 95% tolerance ellipse of the impact positions were statistically different, we performed a χ²-test at 95% confidence level (${\chi }^2>{\chi }_{{}^{0.05,2}}^2$).

Statistical analyses were performed in the R software environment (R Development Core team, 2011; R Foundation for Statistical Computing, Vienna; ISBN: 3-900051-07-0, https://www.r-project.org) with the lme4 and stats package.

RESULTS

Performance

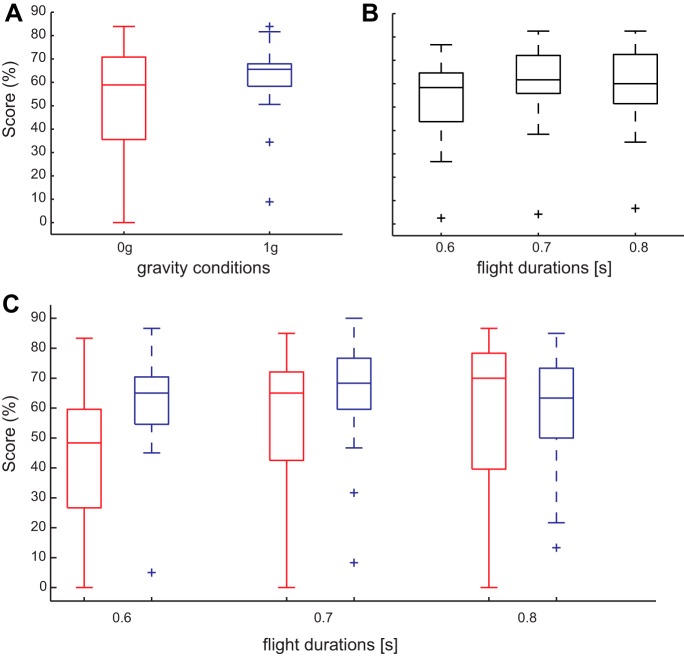
The interceptive performance of each participant was assessed by computing the proportion of successful trials (hit, i.e., either center or side hit) with respect to the total number of trials. Performance was broadly distributed across participants, ranging from 4.4% for the worst participant to 79.4% for the best participant. However, success rate was much more variable across participants for balls moving at constant speed (0g) than for balls accelerated by gravity (1g; see Fig. 4A). As shown in Fig. 4A, participants’ success rates were distributed mostly >50% in the 1g condition while in the 0g condition the success rates were much more broadly distributed, from 0% to 85%. To take into account such a variability across participants, we assessed how interceptive performance depended on the experimental conditions by means of a GLMM (see appendix), relating the probability of trial success to the linear combination of fixed-effect (i.e., G, T, and V) and random-effect (i.e., different participants) predictors.

Fig. 4.

Interception performance across experimental conditions. Box plots represent the score distributions achieved by participants in the 2 acceleration (0g and 1g) conditions (A), in the 3 ball flight durations (B), and in the 2 acceleration conditions for each ball flight duration (C). Medians of the distributions are indicated by horizontal lines inside each box. Edges of the box indicate the first and the third quartiles. The whiskers extend within 1.5 of the interquartile range below the lower quartile and above the upper quartile. Outliers are plotted individually as crosses. Red, 0g condition; blue, 1g condition.

GLMM analysis indicated a significant effect of gravity and T on performance (P_T < 0.001, P_G <0.001; see Table 1 for further details). Specifically, success rate was higher with 1g balls than with 0g balls, and success rate was higher with longer flight durations (0.7 and 0.8 s) than with the shortest duration (0.6 s). The significant interaction between the factors gravity and T (P_GT < 0.001) indicated that the difference between 0g and 1g success rates depended on T. Such difference decreased as T increased (Fig. 4C). It should be noted that although 0g performance improved with increasing flight duration, the overall variability remained significantly higher than that of 1g performance for all T (Bartlett’s k² = 184.37, P < 0.001). Success rate also depended significantly on the via point (see Table 1). GLMM analysis showed that success rates were similar between via points 1 and 2 but were lower for other via points. Moreover, gravity affected the slope of via-point factors, i.e., participants had different performances depending on both gravity and V. Indeed, the interaction term between gravity and each V was significant for all via points except for via point 6, which presented an interaction term similar to that obtained for via point 2. For via points 2, 3, and 5 participants intercepted more balls in the 1g condition, while for via point 1 the result obtained was similar both in 0g and in 1g and for via point 4 the score was higher in the 0g condition.

Table 1.

Effects on performance of ball flight conditions (fixed effects)

	G	T	V1	V3	V4	V5	V6	GT	GV1	GV3	GV4	GV5	GV6
β	2.64	2.62	0.05	−1.16	−0.12	−0.59	−0.40	−3.05	−0.50	0.39	−1.18	0.23	0.14
P	***	***	0.51	***	0.09	***	***	***	***	***	***	*	0.18

All β coefficients of the GLMM for the fixed factors (i.e., G, T, and V, where V goes from 1 to 6 as the number of via points and V2 is the baseline) in the model used to fit the score reached by participants and the relative P values are shown.

^*P < 0.05,

^***P < 0.001.

Kinematics

Hand trajectories started from the instructed initial position, i.e., with the arm beside the participant’s body and the racket facing the hip, and arrived at an interception position that varied across trials since participants could intercept the ball anywhere along the reachable portion of its path (Fig. 5A). We focused the analysis on the temporal features of hand movements and on their velocity profiles. See Table 2 for a complete listing of the results of the statistical analyses.

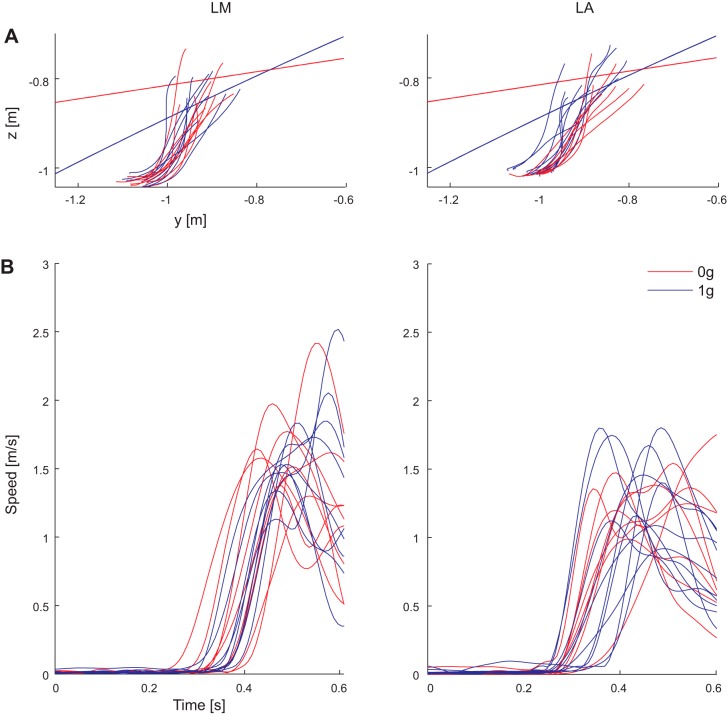
Fig. 5.

Examples of hand paths and speed profiles. Projection of the hand paths on the sagittal plane (A) and speed profiles (B) are plotted from the starting position to the impact for 2 subjects (LM and LA) for both gravity conditions for 1 flight duration (0.6 ms) and via point 2.

Table 2.

Fixed and random factors for all kinematic features

	G		T		GT		Random Slope G Factor		Random Slope T Factor
Analyzed Movement Features	βG	PG	βT	PT	βGT	PGT	corr	PSG	corr	PST
No. of peaks	−1.42	***	3.47	***	2.12	***	−0.48	***	−0.85	*
Z Vel at impact	0.32	*	−1.80	*	−0.26	***	−0.51	***	−0.96	***
Y Vel at impact	0.02	0.43	−1.26	***			−0.43	***	−0.96	***
Speed at impact	−0.09	0.053	−2.62	***	0.21	*	−0.35	***	−0.95	***
Z Vel at onset	0.02	***	−0.01	0.48	−0.01	0.17	0.11	***	−0.76	***
Y Vel at onset	0.02	**	−0.12	***	−0.03	*	−0.20	***	−0.95	***
Peak speed	0.21	*	−1.18	*	−0.25	***	−0.49	***	−0.87	***
Onset	0.04	0.58	0.07	**	−0.05	***	−0.51	***	−0.71	***
Time to peak	−0.002	0.49	0.29	***			−0.18	***	−0.95	***
Impact time	0.002	0.61	0.96	***			−0.42	***	−0.81	***

The first 3 columns show the regression coefficients (β) of G and T factors and their interaction (GT), if present in the model, with their relative P values. The fourth and fifth columns show the significance of the random effects with respect to both the T factor (P_ST) and the G factor (P_SG) and the correlation between the random intercept and the relative random effect. Vel, velocity.

^*P < 0.05,

^**P < 0.01,

^***P < 0.001.

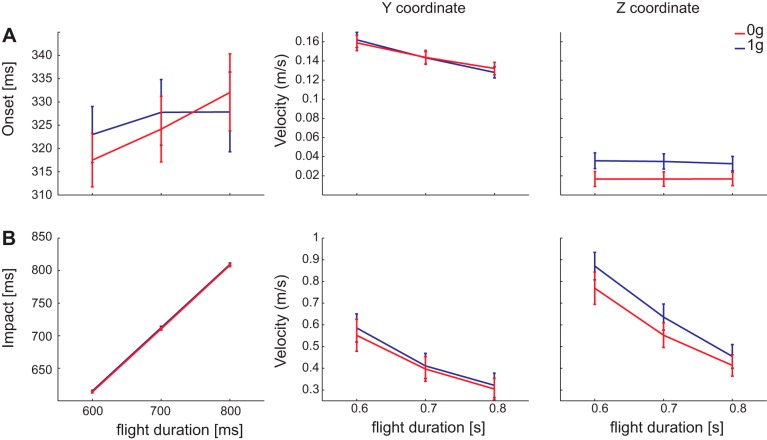
On average, participants waited 326 ± 7 ms (mean ± SE, n = 25) after ball launch before moving. The difference in movement onset between 0g and 1g was only 5 ± 7 ms (mean ± SE across participants, n = 25). Such difference, indeed, was not significant. However, onset time increased slightly with T, but for the shortest T onset was longer in 1g while for the longest T onset was longer in 0g, as assessed by a significant interaction (see Fig. 6A). Time to peak was significantly smaller for shorter ball flight durations, although the difference between gravity conditions was not significant (201 ± 8 ms, 229 ± 10 ms, and 259 ± 13 ms for 600-ms, 700-ms, and 800-ms flight durations, respectively, mean ± SE, n = 25). The interception occurred a few milliseconds after the ball reached the via-point location, i.e., after the specific flight duration (see Fig. 6B). Impact times were 615 ± 1 ms, 713 ± 2 ms, and 810 ± 2 ms (mean ± SE, n = 25) for 600-ms, 700-ms, and 800-ms ball flight durations, respectively, pooling the results across participants, repetitions, gravity, and via-point conditions. The impact time depended on ball flight duration but not on gravity condition.

Fig. 6.

Movement kinematics. A: onset time with respect to ball launch (mean ± SE across participants) and horizontal (approaching along the y-axis) and vertical (z-axis) components of hand velocity at onset for each ball flight duration and for 0g and 1g conditions. B: impact time with respect to ball launch (mean ± SE across participants) and horizontal and vertical components of hand velocity at impact time.

We then investigated hand velocity at onset and impact times, as well as the maximum hand speed and the number of its peaks. The horizontal velocity of the ball was the same for 0g and 1g conditions, as gravity affected only the vertical component of ball motion. At movement onset the horizontal (i.e., approaching, y-axis) component of hand velocity was similar between 0g and 1g trials (see Fig. 6A) but decreased with flight duration (0.16 ± 0.01 m/s, 0.14 ± 0.01 m/s, 0.13 ± 0.05 m/s for flight durations 0.6 s, 0.7 s, 0.8 s, respectively, mean ± SE, n = 25). On the other hand, the vertical (z-axis) component was smaller in 0g trials than in 1g trials but did not vary with flight duration (0.02 ± 0.01 m/s for 0g and 0.03 ± 0.01 m/s for 1g, mean ± SE, n = 25; see Fig. 6A). Such difference was consistent across ball flight durations as assessed by the absence of a significant interaction.

Because of gravity acceleration, the value of the ball vertical velocity at impact was higher for an accelerating ball than for a nonaccelerating ball and the difference increased with flight duration. Participants’ vertical hand velocity at impact time was affected by the ball’s vertical velocity, showing a coupling between the velocity of the hand and the velocity of the ball (Fig. 6B). Participants indeed moved faster for faster balls. They also arrived at accelerated balls with higher hand vertical velocity than on nonaccelerated balls (0.58 ± 0.06 m/s for 0g and 0.65 ± 0.06 m/s for 1g, mean ± SE, n = 25; see Fig. 6B). Moreover, there was a significant difference in hand vertical velocity with respect to the ball flight duration, and the difference between the two gravity conditions decreased with flight duration. It is noteworthy that the coupling was between the absolute values of the hand and ball vertical velocities, which have opposite signs. At impact the horizontal (y-axis) component of the hand velocity decreased with ball flight durations (0.57 ± 0.07 m/s, 0.40 ± 0.05 m/s, 0.31 ± 0.05 m/s for 0.6-s, 0.7-s, 0.8-s flight durations, respectively, mean ± SE, n = 25), as shown in Fig. 6B, but the effect of gravity was not significant.

Maximum hand speed was 1.45 ± 0.05 m/s (mean ± SE, n = 25) in the 0g condition and was lower than the maximum speed in the 1g condition (1.47 ± 0.05 m/s, mean ± SE, n = 25). The analysis carried out on the peak speed confirmed the fact that participants moved faster for faster balls, in agreement with previous studies (Brenner et al. 1998; La Scaleia et al. 2014). In addition, the significant interaction indicated that the difference in the peak speed between 0g and 1g decreased with ball flight duration.

Differently, impact speed varied depending on the acceleration condition (0.90 ± 0.05 m/s for 0g and 0.96 ± 0.05 m/s for 1g, mean ± SE, n = 25) but mostly for the longer flight durations. However, also at impact, hand speed was tuned according to the ball speed as indicated by the dependence on flight duration and confirming the presence of a ball-hand coupling.

Hand speed profiles displayed multiple peaks, as shown in the example profiles of two representative subjects in Fig. 5B. For all flight durations participants exhibited speed profiles with multiple peaks (which are shown on average in Fig. 7). However, the number of peaks increased significantly with ball flight duration and was significantly higher for 1g than for 0g trials for the longest flight duration.

Fig. 7.

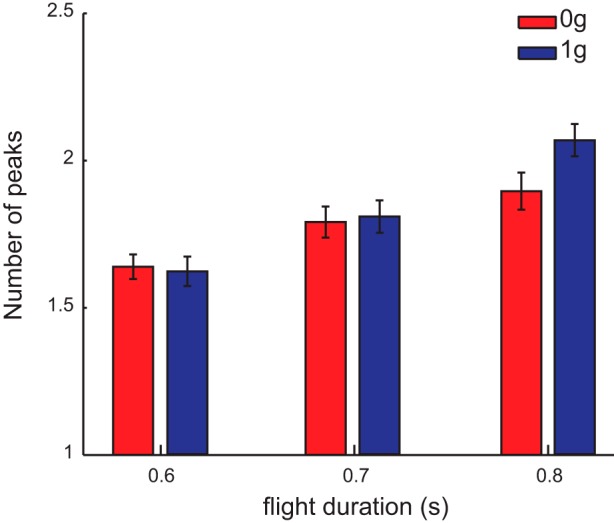
Number of speed peaks. Number of peaks in the speed profile (mean ± SE across participants) in 0g and 1g conditions for different ball flight durations.

Impact Positions

Positions of the center of the racket at impact time were significantly different between all experimental conditions (multivariate analysis of variance, 2 gravity conditions × 3 flight durations × 6 via-point positions, P < 0.001), indicating that the interception location was not the same across all conditions; in particular, it was not the same in the two acceleration conditions for each via point. From the analysis of the eigenvectors of the ellipses computed for each condition (pooling results across participants and repetitions), we found that the orientation of the ellipses in the 0g condition was much closer to the 1g trajectory than the 0g trajectory, just as the orientation of the ellipses in the 1g condition was close to the 1g trajectory (Fig. 8). Indeed, the angle between the first eigenvector of the ellipses for 0g trials and the 1g trajectory was not significantly different from the angle between the first eigenvector of the ellipses for 1g trials and the 1g trajectory (P = 0.1).

Fig. 8.

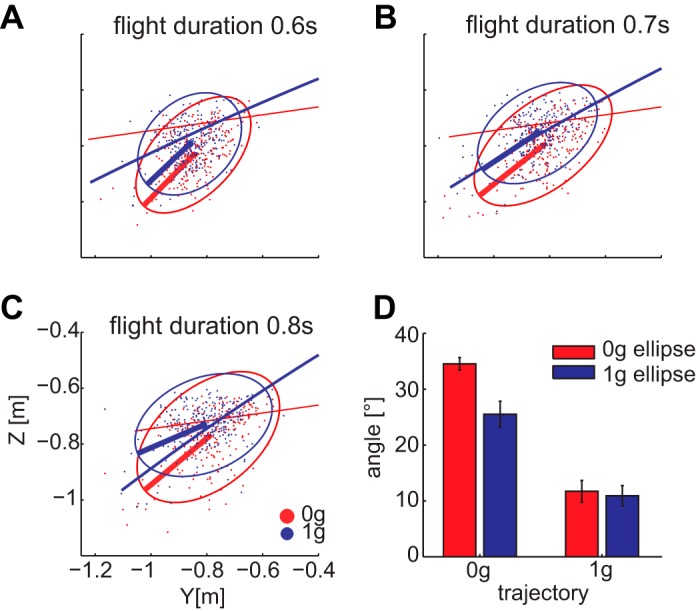
Distribution of impact positions in space. A–C: impact points for via point 6 projected on the sagittal plane (y-z) for each ball flight duration and the relative tolerance ellipse including 95% of the points. Color coding identifies different gravity conditions. Thick lines identify the major axis of the ellipse and thin lines the ball trajectory. D: means and SEs of the angles computed between the first eigenvector and the direction of the trajectory at the point of minimum distance from the center of the ellipse. Means are computed pooling results across all the via points and flight durations.

As shown in Fig. 9A, participants intercepted 0g balls mostly in the upper half of the racket’s plane. The difference in position between 0g and 1g conditions along the Z_racket axis of the racket was significant (β_G = −0.01, P_G < 0.001). The mean value of the Z_racket coordinate of the impact point on the racket’s plane was 0.079 ± 0.014 m (mean ± SE, n = 25) for 0g balls and −0.016 ± 0.007 m (mean ± SE, n = 25) for 1g balls. The difference between 0g and 1g impact points on the racket’s plane along the Z_racket axis was consistent across ball flight durations (Fig. 9B), although impact points on the racket were lower for longer ball flight durations, both for 0g and 1g balls (β_T = −0.24, P_T < 0.001; β_GT = −0.08, P_GT < 0.001).

Fig. 9.

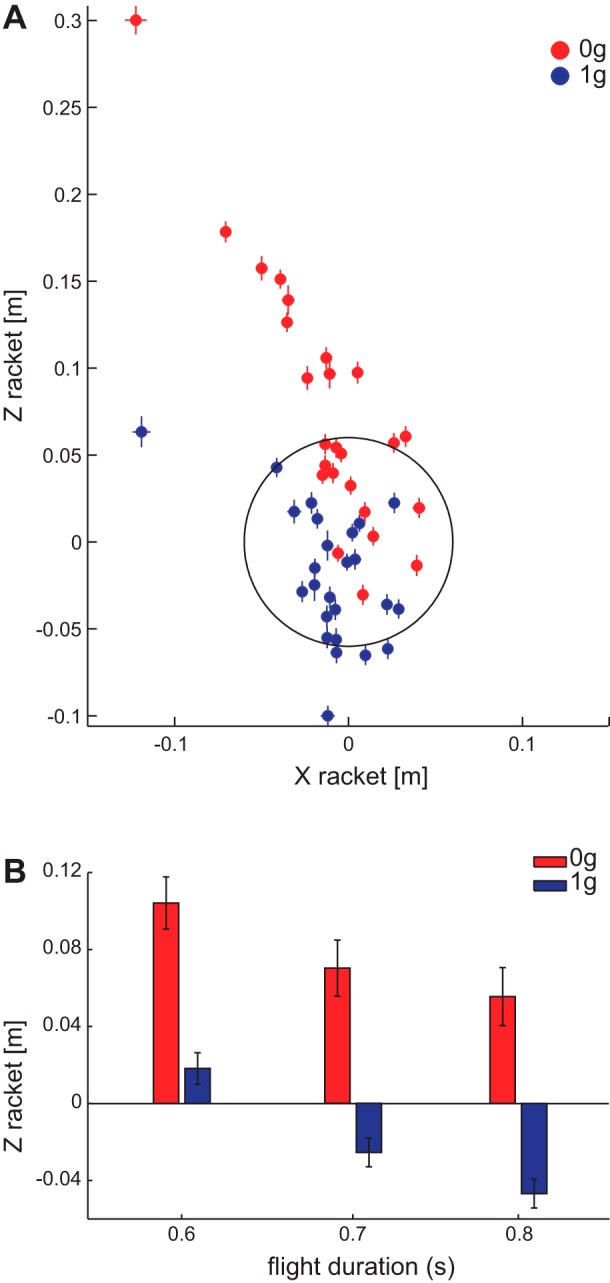
Impact positions on the racket plane. A: median ± SE of projection of the ball center on the racket at impact time is shown on the racket’s surface for 0g and 1g conditions for each participant. Medians are computed pooling together both successful and unsuccessful trials. B: means of Z_racket coordinate of the projection on the racket are shown for each ball flight duration. Only the Z_racket coordinate is shown because the Y_racket axis is perpendicular to the racket surface; thus the Y_racket coordinate of ball position was zero at impact with respect to the racket and there was not a significant effect of gravity on the X_racket coordinate.

DISCUSSION

We investigated motor responses to horizontally approaching balls, flying under normal (1g) or zero-gravity (0g) conditions. In contrast to balls falling along the vertical, for projectile balls the spatial path rather than the arrival time is affected by gravity, thus allowing us to test the role of an internal model of gravity in predicting the spatial location of interception. In line with similar findings for the case of interception of balls falling along the vertical (McIntyre et al. 2001; Zago et al. 2004), we found that participants were often able to intercept accelerated balls better than nonaccelerated ones. Moreover, interception of 0g balls occurred on the upper half of the racket, indicating a misprediction of the spatial location of the forthcoming interception and suggesting that such a prediction relied on the expectation that the ball was accelerated downward by gravity even under zero-gravity conditions. In addition, the impact positions tended to be better aligned with 1g trajectories than with 0g trajectories irrespective of whether ball kinematics complied with 1g or 0g conditions. However, the effect of gravity on performance and on spatial location was significantly modulated by ball flight duration. As flight duration increased, 0g performance improved, although it remained much more variable across trials than 1g performance. Moreover, participants tuned their movements according to the ball speed, and the number of peaks in the speed profile increased with ball flight duration. Overall, these findings suggest that for all tested flight durations the interception of approaching balls relies on an internal model of gravity but for longer flight durations, as more time is available for processing visual information and updating motor commands, inaccuracies in the spatial prediction estimates occurring when intercepting nonaccelerated balls are corrected to some extent.

Role of an Internal Model of Gravity in Predicting the Spatial Location of Interception

Zago and colleagues (Zago et al. 2004) reported that participants performed better when intercepting vertically descending balls under 1g than 0g conditions. We found a similar difference in performance when participants intercepted approaching balls, indicating that the expectation of gravitational acceleration also affected performance when an internal model of gravity predicted the spatial location rather than the timing of interception. In fact, for vertically descending balls the differences in performance between 1g and 0g conditions were due to errors in the timing of the interceptive actions, the time of arrival at a relatively constant interception point being estimated too early for 0g balls. Instead, here, for horizontally approaching balls the differences in performance were due to the spatial location of the interception, which was estimated too low for 0g balls. Indeed, we observed a difference in the impact location on the racket depending on the gravity condition (Fig. 9), and in particular participants intercepted 0g balls with the upper half of the racket (Fig. 9A).

One might wonder whether the observed distribution of impact positions on the racket in the 0g condition could be due to temporal errors or to spatial errors. To address this issue, we first need to define a temporal error. In a task in which the interception point is specified, the temporal error can be defined as the interval between the time at which the interception occurs and the time of arrival of the target at the specified location. However, as in the present task there was no specified interception point, it is not possible to fully disentangle spatial and temporal aspects of interception unless one introduces additional assumptions in the definition of temporal errors.

One way to define a temporal error is to assume that participants aimed at intercepting approaching balls on a given fronto-parallel vertical plane at a location on the plane defined when the ball was at a specific TTC from the plane. If so, the temporal error can be defined with respect to the time of arrival of the ball on the plane. Indeed, as the horizontal component of the ball velocity was constant for both acceleration conditions, a first-order visual variable such as the ratio of image size and its rate of change (τ variable, Lee et al. 1983) could provide a rough estimation of TTC in all conditions. Despite its known limitations (e.g., it does not account for acceleration and for 3-dimensional contextual information), as a first approximation we assumed that TTC could be estimated relying on a τ model (Gómez and López-Moliner 2013). Let a critical TTC value (λ) be the time left to the ball to arrive at the plane and the time at which the participant makes a final prediction about the position (along the vertical axis) at which the ball will arrive. Because of sensorimotor delays, after that time the prediction cannot be further adjusted. The outcome of such a prediction depends on the control strategy the participant uses. If the participant assumes an accelerated ball motion, i.e., a 1g model, both for an accelerated ball and for a nonaccelerated ball, he/she will make an exact prediction if the ball is accelerated and an incorrect prediction if the ball is moving at constant velocity.

On the other hand, if the participant assumes a uniform ball motion, i.e., a 0g model or a τ-based strategy, the prediction would be correct for a 0g ball and incorrect for a 1g ball. An error in the prediction would then lead to a systematic error along the vertical direction. Assuming that the mean vertical spatial error on the racket for the 0g condition is due to a misestimation of the spatial position of interception obtained by using a 1g model at a critical TTC value (λ), such value can be estimated by a simple fit ($\Delta z=\frac{1}{2}g{\lambda }^2$). The resulting λ of 110 ms is close to the value of the sensorimotor delay estimated in interceptive movements (Bootsma and van Wieringen 1990; Brenner et al. 1998; Senot et al. 2008). Furthermore, if subjects accurately estimated the time of arrival on the plane, temporal errors would be due to variability in movement execution. As the hand velocity had a vertical component, a temporal error would then give rise to a vertical spatial error, even if the subjects made an accurate estimate of the position of the arrival of the ball on the plane. However, assuming normally distributed execution errors with zero mean, a temporal error would affect the variance of the spatial error (i.e., the spatial precision of the interception) but not its mean. Any error in the mean interception position in the two acceleration conditions would be due to an error in the estimation of the position, and thus a variable timing error could not explain the mean vertical spatial error observed.

On the other hand, if participants aimed at intercepting the ball at the point of minimum distance between the ball path and the racket path but incorrectly timed their movements, we can define a temporal error as the interval between the time at which the ball reached that point and the time at which the racket was at the minimum distance from that point. If subjects predicted the location of interception correctly and the spatial error derived from the temporal error, the minimum distance between ball and racket paths should be zero. Figure 10 shows, instead, that even at the point of minimum distance between ball and hand paths the spatial error on the racket remains large, indicating that the observed spatial error was not due to incorrectly timed movements aiming at a correct interception point.

Fig. 10.

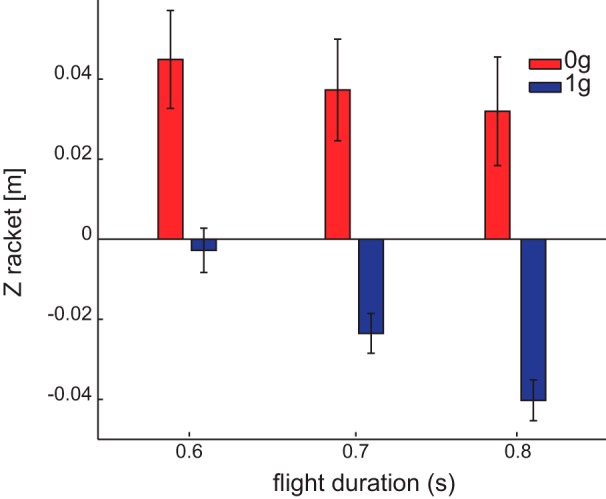
Z_racket coordinate at the point of minimum distance. Mean ± SE (across participants) of Z_racket coordinate of the projection on the racket is shown for each ball flight duration. Impact location is defined as the point of minimum distance between ball and hand paths.

In summary, our results with approaching balls indicate that participants rely on an internal model of gravity not only for timing their interceptive action but also for the spatial location of interception (Jörges and López-Moliner 2017).

Changes in Performance and in Number of Speed Peaks with Flight Duration

While the differences in performance and in the impact location on the racket for 1g and 0g balls support the role of an internal model of gravity in predicting the spatial location of interception for both accelerated and nonaccelerated trajectories, the increase in performance (Fig. 4C) and the decrease in the mean vertical error (Fig. 9B) for 0g balls with increasing flight duration remain to be explained.

Longer availability of visual information might reduce inaccuracies by dynamically updating the prediction (Zago et al. 2008, 2009). For short flight durations, when there is not enough time for detecting a discrepancy between the predicted trajectory and the actual trajectory through visual feedback (Tresilian 2005), the interceptive movement would be triggered according to the prediction of a 1g model. However, for longer flight durations, as visual feedback indicates that the prediction of a 1g model is not accurate for 0g trajectories, the prediction might be updated. According to a Bayesian approach, an adjustment of the prediction in response to 0g balls might result from updating the prior. In this approach, the contributions of sensory information and of priors in generating motor commands is typically weighted by the noise of the sensory information and the reliability of the prediction (Orban de Xivry et al. 2013). If updating the prediction, then, is a gradual process, the predicted interception location for 0g trajectories would be progressively closer to the actual trajectory and this would explain the progressive reduction of error and increase in performance observed for longer flight durations.

Moreover, the hand speed profiles often had more than one peak, and the number of peaks increased with ball flight durations (Fig. 7). The presence of several peaks is often related to movement corrections (Cirstea and Levin 2000; Rohrer et al. 2002). A single-peak bell-shaped speed profile, which corresponds to a minimum of the squared and integrated jerk profile (Flash and Hogan 1985), is considered as the kinematic pattern of a preplanned smooth movement, while speed profiles with multiple peaks may indicate corrective movements occurring because of poor motor planning, variation in motor execution, or task constraints. Thus the number of peaks in the speed profile can be used to quantify corrections made by participants during the interceptive movement in response to feedback-detected errors (Lee et al. 1997; Tresilian 2005). Thus corrective movements, for both 1g and 0g trajectories, might be generated when the prediction of ball position derived from the 1g model, compared with the actual position estimated from visual information, results in an error. This error can also be used to update the prediction (Maffei et al. 2016). With a control strategy that admits corrections, there would be overlap between movement planning and execution, allowing the participant to initiate an inaccurate movement early and to plan an accurate adjustment later on the basis of new incoming information (Orban de Xivry et al. 2017). If the motor plan is not entirely defined when the movement starts, there is more time to determine the final strategy and to account for the adjustments needed to achieve a successful interception (Tresilian 2005). Hence, in the present task the first phase of the movement could allow the participant to transport the hand toward the interception plane with the required temporal accuracy. Then, in the second (or last) phase, when TTC reaches a critical value, a ballistic movement could be triggered to adjust the movement and achieve the required spatial accuracy. Further investigations are needed to precisely formulate and test such hypotheses.

Hand-Ball Speed Coupling

As in many previous studies of interceptive movements (Bootsma and van Wieringen 1990; Savelsbergh et al. 1992; Smeets and Brenner 1995; Tresilian 2005; Tresilian et al. 2009), we found a coupling between the speed of the hand and the speed of the ball. The horizontal component (Y, Fig. 6A) of the onset velocity and both horizontal (Fig. 6A) and vertical (Z, Fig. 6A) components of the impact velocity of the hand decreased for longer flight duration, i.e., for slower ball velocities. Moreover, maximum and impact speed increased with ball speed, indicating that the hand-ball coupling affected the overall tangential velocity (Brouwer et al. 2000). Increasing the speed of the hand for faster balls may be a strategy for minimizing the effects of spatial prediction errors, as temporal precision increases for faster movements (Brenner and Smeets 2015; Brouwer et al. 2000; Tresilian 2005). Furthermore, the fact that gravity acceleration had no significant effect on the horizontal components of hand onset and impact velocities (Fig. 6B), a significant but small effect on onset time (Fig. 6A), and no significant effect on impact time (Fig. 6B) suggests that the timing of interception on a fronto-parallel plane was planned according to the horizontal approaching speed independently of gravity, and that faster movements were selected for faster balls to reduce the spatial vertical error associated with a timing error because of the ball vertical velocity. Adjustments associated with multiple speed peaks were then mostly affecting the spatial location of interception on the plane rather than the timing of interception, as also observed when participants intercepted targets moving on a screen in front of the subject (Brenner and Smeets 2015).

Interception of Real and Virtual Balls

In one-handed catching tasks with real balls, the success rate, evaluated as the number of caught balls over the total number of launches, has been shown to increase with flight duration (Cesqui et al. 2012, 2016; Mazyn et al. 2006; Tijtgat et al. 2010). In our experiment, in which participants were required to intercept a virtual ball with a racket, in the 1g condition no significant relation between the interceptive performance and the ball flight duration was observed. This discrepancy may be due to the fact that what affected the performance most when participants were catching real balls was the timing of the closing of the fingers on the ball (Cesqui et al. 2016), an action not required in the present interception task. However, the success rate remains lower for virtual balls even if we consider the number of real balls caught or only touched. One possibility is that the lower performance is an effect of the virtual environment, because of the absence of haptic feedback and the presence of lags in the rendering of the scene. Previous studies, showing that participants are able to intercept virtual targets (Dessing et al. 2004; Diaz et al. 2013; Zaal and Michaels 2003), have also reported some differences in the movement responses with respect to those observed with real balls. Dessing and collaborators (Dessing et al. 2004) found that the movement onset in VR was delayed with respect to the onset in a real catching task. We found a similar result: participants waited more in our virtual interception task (325 ± 63 ms, mean ± SE) than in a real catching task with similar experimental conditions (120 ± 40 ms, mean ± SE; Cesqui et al. 2012). We believe that in our task, because of the presence of the horizontal screen, participants were aware that they would have to intercept the ball below the screen and relatively close to their body, thus with a short movement time. Participants could then wait longer to gather more information on the ball trajectory before starting to move.

Conclusions

We found differences in performance and impact position on the racket between 0g and 1g conditions when participants intercepted approaching balls. These findings are in agreement with the 1g model proposed by Lacquaniti et al. (1993), McIntyre et al. (2001), and Zago et al. (2004) and confirm that participants rely on an internal model of gravity acceleration to determine the spatial location of interception and to predict ball motion in order to control their actions even when approaching balls move without gravity acceleration. However, performance in the 0g condition increased with flight duration, suggesting that when more time is available the contribution of visual information increases. Moreover, participants displayed multiple peaks in their hand speed profiles, suggesting the presence of corrections during movement. We therefore conclude that to successfully perform interceptive actions in different conditions, the CNS relies on priors about ball motion under gravity plus online visual information. Further investigations are needed to precisely address the role of movement adjustments in this control strategy. A computational implementation of a model combining second-order cues with online adjustments could be tested with new experimental data to clarify how the CNS determines where and when to intercept a moving target.

GRANTS

This work was supported by the Italian University Ministry (PRIN Grant 2015HFWRYY), the Italian Space Agency (Grant no. I/006/06/0 and ARIANNA Grant 2014-008-R.0), and the Horizon 2020 Robotics Program (ICT-23-2014 under Grant Agreement 644727-CogIMon).

DISCLOSURES

The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript. No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

M.R., B.C., F.L., and A.d'A. conceived and designed research; M.R., B.C., and F.C. performed experiments; M.R., B.C., and A. Moscatelli analyzed data; M.R., B.C., B.L.S., A. Maselli, A. Moscatelli, M.Z., F.L., and A.d'A. interpreted results of experiments; M.R. prepared figures; M.R., B.C., and A.d'A. drafted manuscript; M.R., B.C., B.L.S., F.C., A. Maselli, A. Moscatelli, M.Z., F.L., and A.d'A. edited and revised manuscript; M.R., B.C., B.L.S., F.C., A. Maselli, A. Moscatelli, M.Z., F.L., and A.d'A. approved final version of manuscript.

APPENDIX

We assessed how interceptive performance and movement response depended on the experimental conditions by the means of generalized linear mixed models (GLMMs). The GLMM is an extension of the general linear model (GLM) to clustered data, which in our case is the collection of repeated responses in 25 participants. The GLMM is a hierarchical model, including fixed- and random-effect parameters. Fixed-effect parameters estimate the effect of the experimental variables (G, T, and V) on participants’ responses. Random-effect parameters estimate the heterogeneity between different participants. GLMM assumes that the random-effect parameters are normally distributed (Bates et al. 2014; Cesqui et al. 2015; Moscatelli et al. 2012). Here we include three random effects, the random intercept (i.e., by-subject random intercept S_0i) and two random regression slopes (S_Ti, S_gi, by-subject random slopes).

In this way, the expected value of a dependent response variable R is

$${\Phi }^{-1}[E(R)]=\beta X$$

where Φ⁻¹ is the link function that relates the response variable to the linear predictor βX.

To relate a binomial response variable, as the interceptive outcome, to a linear predictor we used the probit link function, which is the inverse of a standard normal cumulative distribution function. The probit model can be motivated by means of a latent variable Y*, i.e., a continuous variable that is a linear function of the predictors:

$$Y_{ij}^{*}={\beta }_{0i}+{\beta }_{1i}{X}_{ij}+S_i+{\epsilon }_{ij}$$

where S_i and ε_ij are the between-participant and residual error terms, respectively. The score response variable Y could have only two possible outcomes, indicating hit (Y = 1) or missed (Y = 0) balls; thus we introduce the latent response variable Y* according to which the dichotomous response variable Y can be viewed as

$$Y_{ij}=\{\begin{array}{l}\text{1 if\hspace{0.17em}}{Y}_{ij}^{*}>0\\ \text{0\hspace{0.17em}}if\hspace{0.17em}{Y}_{ij}^{*}\le 0\end{array}$$

To determine the relation between the number of peaks and experimental conditions, the relation was instead

$$Y_{ij}=\{\begin{array}{l}\text{1 if\hspace{0.17em}}{Y}_{ij}^{*}>2\\ \text{0 if\hspace{0.17em}}{Y}_{ij}^{*}\le 2\end{array}$$

because the response variable of the number of peaks assumed discrete but not dichotomous values and 2 was its median computed across trials and subjects (Rossi et al. 2013; Sombekke et al. 2010).

In contrast, all kinematic parameters were modeled with a linear mixed model (LMM), which is a special case of the GLMM assuming an identity link function. In LMM, the response variable is assumed to have a conditional Gaussian distribution. The response variable is modeled as a linear combination of the fixed-effect and random-effect parameters.

To identify the model that best fitted the experimental data, we adopted an iterative procedure described by Cesqui et al. (2015, 2016). Briefly, first we assessed whether the use of a GLMM, i.e., the inclusion of random effects in the model, was justified. To this end, we compared the Akaike information criterion between the GLM and the GLMM fit and we chose the model with the lowest Akaike information criterion (Cesqui et al. 2015, 2016).

Then, according to the confirmatory hypothesis testing method (Baayen et al. 2008; Barr 2013), we iteratively compared models to assess whether it was necessary to include interaction terms or random-effects slopes. At each iteration we compared a simpler model and a more complex one (nested models), using the likelihood ratio test. If in the comparison of two models we saw that the additional parameter is highly significant, we preferred the more complex model. We had to establish a threshold (5%) above which the results are regarded as representing an “insignificant” improvement in the fitting of the experimental data.

The model that we considered to fit all the analyzed parameters, including all the possible factors, is the following:

$$Y_{ij}^{*}={\beta }_0+\left({\beta }_T+S_{Ti}\right)T_j+\left({\beta }_G+S_{Gi}\right)g_j+S_{0i}+{\beta }_P{V}_j+{\beta }_{GT}{G}_j{T}_j+{\beta }_{GV}{G}_j{V}_j+{\epsilon }_{ij}$$

where Y* is the latent response variable for each subject i for each trial j, T is the duration of the ball flight (continuous variable T: 0.6 s, 0.7 s, and 0.8 s), G is the dummy variable for the acceleration condition (G: 0 and 1 for 0g and 1g, respectively), GT represents the interaction between the ball flight duration and the acceleration condition, V is the categorical variable (V: from 1 to 6) describing the different via points, and GV represents the interaction between the via-point positions and the acceleration conditions. β are the fixed-effects coefficients, S are the random-effects coefficients. Interaction terms (GT and GV) test whether the slope related to a factor (T or V) is significantly different in the two experimental conditions (0g and 1g).

Arrival positions of the hand on ball trajectories are all in a specific region, which has via point 2 in its center. Thus via point 2 has been considered as the reference level of factor V in the models, i.e., each model assesses the difference in the response variable assuming as a reference the value that the response variable assumes for via point 2.

For each parameter a different model has been chosen according to the confirmatory hypothesis testing method, and the factors included in the fit are specified in Tables 1 and 2.