Object comparison in the lateral intraparietal area

Studies in object recognition have focused on the ventral stream, in which neurons respond as a function of how similar a stimulus is to their preferred stimulus, and on prefrontal cortex, where neurons indicate which stimulus is being looked for. We found that parietal area LIP uses its known mechanistic properties to form an intermediary representation in this process. This creates a perceptual similarity map that can be used to guide decisions in prefrontal areas.

Abstract

We can search for and locate specific objects in our environment by looking for objects with similar features. Object recognition involves stimulus similarity responses in ventral visual areas and task-related responses in prefrontal cortex. We tested whether neurons in the lateral intraparietal area (LIP) of posterior parietal cortex could form an intermediary representation, collating information from object-specific similarity map representations to allow general decisions about whether a stimulus matches the object being looked for. We hypothesized that responses to stimuli would correlate with how similar they are to a sample stimulus. When animals compared two peripheral stimuli to a sample at their fovea, the response to the matching stimulus was similar, independent of the sample identity, but the response to the nonmatch depended on how similar it was to the sample: the more similar, the greater the response to the nonmatch stimulus. These results could not be explained by task difficulty or confidence. We propose that LIP uses its known mechanistic properties to integrate incoming visual information, including that from the ventral stream about object identity, to create a dynamic representation that is concise, low dimensional, and task relevant and that signifies the choice priorities in mental matching behavior.

NEW & NOTEWORTHY Studies in object recognition have focused on the ventral stream, in which neurons respond as a function of how similar a stimulus is to their preferred stimulus, and on prefrontal cortex, where neurons indicate which stimulus is being looked for. We found that parietal area LIP uses its known mechanistic properties to form an intermediary representation in this process. This creates a perceptual similarity map that can be used to guide decisions in prefrontal areas.

visual object recognition in primates is a reliable cognitive ability that has its foundation in the perception of shape similarity (Cortese and Dyre 1996), and neurons in inferotemporal cortex (IT) respond to a stimulus as a function of how similar it is to their preferred stimulus (Allred et al. 2005). It is thought that similar shapes are represented in adjacent columns in IT (Tanaka 2003), and computational methods and machine learning algorithms have shown that IT encodes similarity at the level of low-level visual properties (Kiani et al. 2007; Op de Beeck et al. 2001; Ratan Murty and Arun 2015). It has also been shown that perceptual learning forms the representation of shapes in IT such that the neuronal representations of the relevant features are enhanced (Sigala and Logothetis 2002; Woloszyn and Sheinberg 2012). However, the representation of object images in IT is formed during long-term exposure, and, while responses can be modulated by task conditions (Chelazzi et al. 1993), the overall representations of objects remain stable in the short term (McKee et al. 2014; Suzuki et al. 2006).

Neurons in prefrontal cortex (PFC), on the other hand, encode abstract cognitive variables, such as rules and categories, on a trial-by-trial basis (Freedman et al. 2001; Wallis et al. 2001). The representation in PFC tends to relate to the outcomes of their computations rather than the actual stimulus (Lara and Wallis 2014; Riggall and Postle 2012; but see Kobak et al. 2016). The benefit of these high-level low-dimensional categorical representations is that they can perform fast, stable decision making in complex, changing environments (Edelman and Intrator 1997). However, it is thought that these representations cannot be formed directly from self-organizing sensory maps (Grossberg 1998), such as those represented in IT. Computational and theoretical studies have suggested that this level of abstraction needs cognitive control and learned top-down expectations integrated with bottom-up sensory data (Dayan et al. 1995; Grossberg 1980) to form a perceptual similarity map, which can provide a dynamic task-relevant representation.

The dynamic short-term representation of task-relevant priority in the lateral intraparietal area (LIP) makes it a good candidate for such an intermediate representation. Here, priority represents the fusion of bottom-up salience and top-down goal-directed guidance used to guide covert attention (Bisley and Goldberg 2003; Herrington and Assad 2010) and eye movements (Ipata et al. 2006a; Mazzoni et al. 1996; Steenrod et al. 2013). In this way, the LIP activity in visual search can be thought of as filtering channels of visual information so that stimuli that share features with the goal of the search are represented by greater activity (Bisley and Goldberg 2010; Zelinsky and Bisley 2015). This principle can also be seen in previous studies looking at relative value (Louie and Glimcher 2010; Sugrue et al. 2004), the integration of sensory signals (Shadlen and Newsome 2001), or conjoint disparate task-relevant visual features in LIP (Ibos and Freedman 2014). Even in overtrained stimulus recognition tasks, LIP responses represent the fusion of the top-down task relevance signal and some degree of low-level feature integration (Sarma et al. 2016; Swaminathan and Freedman 2012). Given that this activity is likely used to guide eye movements (Ipata et al. 2006a; Snyder et al. 1997) and eye movements are the way we identify where particular objects are in visual space, we propose that the processing machinery in LIP would enable it to act as a perceptual similarity map, one that reflects the perceptual distance, or similarity, between the object present in the response field and the object being looked for.

We hypothesize that LIP should identify stimuli that are similar to the object being looked for, even with complex shapes that cannot be categorized by simple low-level stimulus properties. Specifically, we predict that the responses of LIP neurons should represent the relative similarity of each stimulus to the sample in our match-to-sample task and this should not depend on stimulus identity. Thus we expect that the response to the matching stimulus (the match) should always be the same because it is identical to the sample and the response to the nonmatch should be lower depending on how similar it is to the sample: similar nonmatching stimuli should elicit higher responses than dissimilar nonmatching stimuli.

MATERIALS AND METHODS

Subjects.

All experiments were approved by the Chancellor’s Animal Research Committee at UCLA as complying with the guidelines established in the US Public Health Service Guide for the Care and Use of Laboratory Animals. Two male rhesus monkeys (~11 and ~16 kg) were implanted with head posts, scleral coils, and recording cylinders during sterile surgery under general anesthesia (Bisley and Goldberg 2006; Mirpour et al. 2009). The animals were initially anesthetized with ketamine and xylazine and maintained with isoflurane. They were trained on a standard memory-guided saccade task and a match-to-sample task (Fig. 1). Experiments were run with REX (Hays et al. 1982), and all data were recorded with the Plexon system (Plexon). Visual stimuli were presented on a CRT (running at 100 Hz, 57 cm in front of the animal) with the associated VEX software. Eye position signals were sampled with a magnetic search coil system (DNI) at 2 kHz and recorded for analysis at 1 kHz.

Fig. 1.

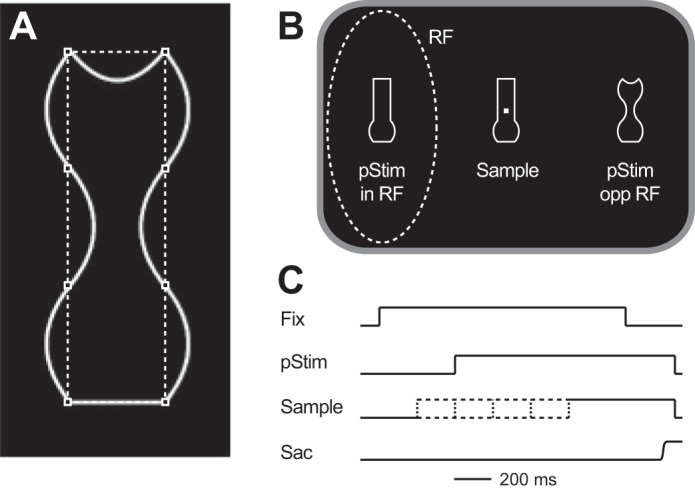
Behavioral task. A: each object was made up of 8 solid white lines that connected 8 imaginary points (squares). Each line could be straight, concave, or convex, and each object was vertically symmetrical. B: stimulus arrangement. On each trial a sample stimulus was presented around a fixation point and 2 stimuli were presented in the visual periphery (pStim), with 1 placed in the neuron’s response field (RF) and the other diametrically opposite. One of the peripheral stimuli matched the sample (match); the other did not (nonmatch). Stimuli were chosen from a set of 5 that were new in each session. C: time course of a trial. Each trial began (Fix) after the animal had fixated a central fixation point for 500–1,000 ms. After this the peripheral stimuli (pStim) appeared 400 ms later and remained on until the end of the trial. The sample could appear 200 ms before the peripheral stimuli, at the same time as the peripheral stimuli, or 200, 400, or 600 ms after the peripheral stimuli (indicated by dashed lines). We refer to these as having stimulus onset asynchronies (SOAs) of −200, 0, 200, 400, or 600 ms respectively. The animal had to make a saccade (Sac) to the match to obtain a reward.

Neuronal recording and behavioral tasks.

Single-unit activity was recorded from the right hemispheres of two monkeys with tungsten microelectrodes (Alpha Omega). The location of LIP was determined with MRI images, and neurons were only included if they or their immediate neighbors showed typical visual, delay, and/or perisaccadic activity in a memory-guided saccade task (Barash et al. 1991). The size and position of the response field of each neuron were estimated with the visual responses from an automated memory-guided saccade task (for details see Mirpour and Bisley 2016). Response field centers ranged from 5° to 17° eccentricity and did not overlap with the sample stimulus placed centrally on the screen.

Stimuli were white line objects presented on a black background. Each stimulus was made up of eight lines that joined eight points around an imaginary rectangle (Fig. 1A; squares and dashed lines were not present on the stimulus presented to the animal), which was a multiple of 1.19° wide × 3.64° tall, depending on eccentricity. Each line could be straight, concave, or convex. The image was vertically symmetrical, so only five of the lines varied independently: the top line, the bottom line, and three pairs of lines on the sides. This resulted in 243 (3⁵) different shapes. The objects were drawn in MATLAB (MathWorks) and saved as TIFF files for presentation. For the first animal, five shapes were randomly selected for each session. The same sets of five shapes were used for the second animal. Fewer sessions were performed in the second animal, so some sets tested on the first animal were not tested in the second.

Neuronal data were collected while the animals performed a match-to-sample task using white stimuli on a black background. To begin the task, the animal had to fixate a central fixation square for 500–1,000 ms (Fig. 1B). Four hundred milliseconds after the trial began (Fig. 1C), two stimuli appeared in the periphery: one appeared in the center of the neuron’s response field; the other appeared diametrically opposite the center of the neuron’s response field. The animal’s task was to find which of the two peripheral stimuli matched the sample stimulus placed centrally and make a saccade to it within 600 ms after the fixation point was extinguished. We define the stimuli in terms of whether they match the sample or they are a nonmatch. The fixation point was always extinguished 1,000 ms after the peripheral stimuli appeared; however, the sample stimulus could appear at one of five times (Fig. 1C): 200 ms before the peripheral stimuli were presented [stimulus onset asynchrony (SOA): −200 ms]; at the same time that the peripheral stimuli were presented (SOA: 0 ms); or 200, 400, or 600 ms after the peripheral stimuli were presented (SOAs: 200 ms, 400 ms, and 600 ms, respectively). When the animal was presented the sample stimulus before the peripheral stimuli (negative SOA) it already knew what stimulus it was looking for, and when the animal was presented the sample stimulus after the peripheral stimuli (positive SOAs) it already knew what the choices were before it would know what it was looking for. In this report, we primarily examine the latter condition to see how the LIP activity evolves after the animal is presented with the stimulus it must find a match to, removing any influence of the on-response in the response field; however, we show that our results remain similar with 0 and negative SOAs. Trials in which the animal broke fixation before the fixation point was extinguished were not rewarded, even if the animal looked at the matching stimulus. Error trials were defined as trials in which the animal made a saccade to the nonmatch within 600 ms of the fixation point being extinguished.

Experimental design and statistical analysis.

Data were recorded from 200 LIP neurons (110 from animal H and 90 from animal I) in 49 days of recording (28 from animal H and 21 from animal I). Action potentials were roughly sorted online and then accurately sorted off-line with SortClient software (Plexon). Data were analyzed with custom code written in MATLAB (MathWorks). Population spike density functions were created with a σ of 10 ms, and differences between the traces were calculated each millisecond with t-tests at the single-neuron level and paired t-tests at the population level. It should be noted that when comparing significance over time it is important to remember that isolated significant events may be due to chance; however, the probability of having many consecutive significant bins in a row becomes very low, particularly given a 10-ms smoothing kernel. When calculating spike rates for the correlation analyses, the number of action potentials within a set window was used.

Calculating stimulus similarity.

We calculated stimulus similarity using the similarity concept introduced by Tversky (1977), in which similarity was defined as a linear combination between the vector of the common features of a pair of stimuli and the distinct features of that pair. In a simple form it can be written as a concept formula:

$$sim\left(A,B\right)=\overrightarrow{a}\times \overrightarrow{com(A,B)}-\overrightarrow{b}\times \overrightarrow{dist\left(A\right)}-\overrightarrow{c}\times \overrightarrow{dist\left(B\right)}$$ (1)

where A and B are the two shapes, sim(A,B) defines the similarity function, $\overrightarrow{com\left(A,\hspace{0.17em}B\right)}$ calculates the common features between two shapes, and $\overrightarrow{a}\times \overrightarrow{com\left(A,\hspace{0.17em}B\right)}$ is the weighted sum of common features; $\overrightarrow{dist\left(x\right)}$ defines the features that exist in one but not the other stimulus. $\overrightarrow{b}\times \overrightarrow{dist\left(A\right)}$ and $\overrightarrow{c}\times \overrightarrow{dist\left(B\right)}$ are the weighted sum of distinct features, and $\overrightarrow{a}$, $\overrightarrow{b}$, and $\overrightarrow{c}$ are vectors of coefficients.

For simplicity, we assume the similarity as being symmetrical [i.e., sim(A, B) = sim(B, A)] and instead of two terms for distinct features we use only the differences between the two shapes. In this process, each individual shape was defined into a 15-dimensional shape space based on the five lines that could vary and the three ways they could vary, as a concave, flat, or convex edge. In this shape space each shape was defined as a unique vector. Because we use only the differences between the two shapes, the similarity can be simplified as

$$sim\left(A,B\right)=\overrightarrow{a}\times \overrightarrow{com(A,B)}-b\times diff(A,B)$$ (2)

where $\overrightarrow{com\left(A,\hspace{0.17em}B\right)}$ calculates a 15-dimensional vector that represents all common features of A and B as 1 and all other distinct or absent features as 0. $\overrightarrow{a}$ is a 15-dimensional vector of common features coefficients. $\overrightarrow{a}\times \overrightarrow{com\left(A,\hspace{0.17em}B\right)}$ is the weighted sum of common features, which results in a scalar number. diff(A, B) is calculated by finding the Euclidean distance between the feature vectors of the two shapes and b is the scalar coefficient of Euclidean distance, so the output of sim(A,B) is a scalar value for each pair of shapes.

We assumed that shape similarity should be correlated with the behavioral matching performance: similar shapes should be harder to tell apart. Therefore, to find coefficients a and b, we created a generalized linear model (GLM). The behavioral performances of the two monkeys from all posttraining sessions (including those in which neuronal data were not recorded; n = 97 in total) were used as the response variable. The behavioral performance was fed into the model as the average proportion correct of all instances of a pair, independent of which stimulus was the sample. The GLM was fit to common the feature vector com(A,B) and the Euclidean distance value diff(A,B) as the predictor variables, such that

$$\text{log}\left(\text{PC}\right)={\beta }_0+\overrightarrow{{\beta }_1}\overrightarrow{X}+e$$ (3)

where PC is the proportion correct across all trials in which stimuli A and B were compared and β₀ and e are the intercept and error of the model, respectively. Shape features and Euclidean distances were used as categorical and continuous variables, respectively. X is the input data matrix of 16 main terms including all the shape features (x1 to x15), the Euclidian distance (x16) and 120 interaction terms (x1x2, x1x3,… x2x3, x2x4,… x15x16). β₁ is the vector of all 136 coefficients of input matrix X. $\overrightarrow{{\beta }_1}\overrightarrow{X}$ is the weighted sum of the input matrix.

Because the distribution of the behavioral data was considered as an inverse Gaussian, we used a log link function in the model. The GLM was fit with maximum likelihood estimates using an iterative least squares method in MATLAB. To avoid overfitting the GLM, a jackknife method was used. An individual GLM for each pair of shapes was made, in which all instances of behavior utilizing either shape were excluded from the training pool. Thus the similarity model was created by using all the data from both monkeys except for behavior from the stimuli of interest. After the model for the pair of interest was built, the similarity of the pair was predicted solely on the basis of feature structure since the GLM had never been exposed to any behavioral data related to the pair or the individual stimuli before. For predicting the similarity of the pair of interest we used the coefficients of GLM and inverse link function in the form of

$$sim\left(A,B\right)=\text{exp}({\beta }_0+\overrightarrow{{\beta }_1}\overrightarrow{X})$$ (4)

where β₀ and β₁ were the calculated coefficients from the GLM. The procedure was repeated for all the stimulus pairs used in the neuronal recording sessions. In predicting the similarity, any predictor with a P value of >0.05 or a coefficient of <10⁻⁵ was excluded from the prediction formula. On average 81.63 ± 0.10 (mean ± SE) of 136 coefficients were included in the prediction model. The predicted similarity values correlated well with the behavioral performance, with a mean ± SE Pearson correlation coefficient of 0.73 ± 0.01.

In addition to the similarity measures obtained by the GLM, we calculated two parametric measures of shape difference. For the first, we used the 15-dimensional shape space that was the input for the GLM. For each stimulus pair, we looked at the distance between the vectors in that space. For the second, we calculated a simple distance between pairs of shapes based on number of shared or different edges. To do this, we numerically scored the difference between each of the edges of the two stimuli with a value of 0, 1, or 2, where 0 meant the edge was the same on both stimuli, 1 meant the edge changed from concave or convex to straight, and 2 meant the edge changed from concave to convex (or vice versa). We then added the scores from all eight edges to give a summed difference. Thus if the only difference between a pair of stimuli was an edge that went from straight to concave, then the summed difference would be 1, and if two stimuli differed completely (e.g., all edges went from concave to convex), then the summed difference would be 16. In our data, the summed differences ranged from 1 to 15, with a mean ± SE of 7.43 ± 0.0635. For the analyses presented below we flipped the sign of these two metrics so that higher values (i.e., less negative values) would represent more similar stimuli.

RESULTS

Two male rhesus monkeys were trained to perform a match-to-sample task using unique line stimuli (Fig. 1). Each day, 5 new line objects, which varied parametrically from each other, were randomly chosen from a set of 243 (Fig. 1A); any given object could be presented as the match or the nonmatch stimulus. On each trial, one stimulus (the sample) was presented centrally and two stimuli, the match, which was identical to the sample, and the nonmatch, were presented in the visual periphery: one in the neuron’s response field and the other diametrically opposite (Fig. 1B). The sample could appear 200 ms before the peripheral stimuli, at the same time as the peripheral stimuli, or 200, 400, or 600 ms after the peripheral stimuli (Fig. 1C). We refer to these by their SOAs of −200, 0, 200, 400, and 600 ms. To get the reward, the animal had to make a saccade to the matching stimulus after the fixation point was extinguished. For most of the following results, except where noted, we restrict our analyses of the neuronal data to the trials with SOAs of 200 ms and 400 ms. In these trials, the neuronal response following sample onset is unaffected by the transient on-response of the peripheral stimuli. However, as we show below, our general findings are consistent across all stimulus timings.

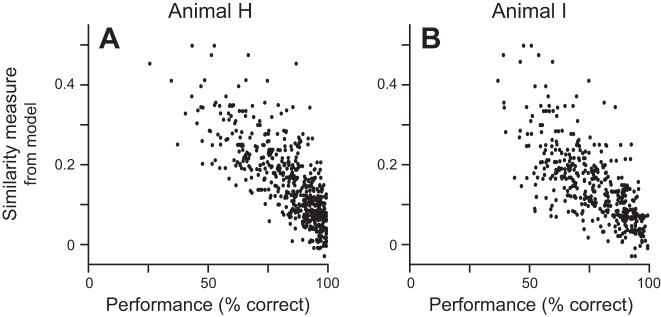
The two animals were proficient at the task. Across the 28 days in which neuronal data were recorded animal H had a mean ± SE performance of 84.7 ± 1.3% correct, and across the 21 days in which neuronal data were recorded animal I’s mean performance was 77.0 ± 1.2% correct. Within a session, performance for different stimulus pairs ranged widely, showing that the animals were better at identifying a match for some pairs than for other pairs and confirming that they were not overtrained in the overall feature space. We hypothesized that performance was greater when the two stimuli were more dissimilar and was worse when the two stimuli were similar. We initially compared performance for each pair of stimuli to our objective measures of stimulus difference, but the correlations, while significant, were relatively poor: r² = 0.090 and 0.048 (n = 560, P = 3.57 × 10⁻¹³ and n = 420, P = 5.41 × 10⁻⁶ for animals H and I, respectively) when using the 15-dimensional shape space and r² = 0.115 and 0.105 (P = 1.48 × 10⁻¹⁶ and P = 1.06 × 10⁻¹¹, for animals H and I, respectively) when using the summed difference. However, when we used the similarity measure for each stimulus pair from the GLM, which was not based on the animal’s actual behavior with either of those stimuli, we found much stronger correlations for both animals (r² = 0.593 and 0.496, P = 3.8 × 10⁻¹¹¹ and P = 5.24 × 10⁻⁶⁴, for animals H and I, respectively), with greater performance correlating with lower measures of similarity (Fig. 2). Because the model only compares the shapes of the two stimuli, it does not differentiate which is the sample/match and which is the nonmatch; however, the animals’ performance did vary depending on which stimulus was the sample. Figure 2 shows the performance measures for comparisons of the same two stimuli separately based on which stimulus was the sample. Pooling the performance for the pairs of stimuli only improved the correlation statistics to r² = 0.745 (P = 1.65 × 10⁻¹⁶⁷, n = 280) for animal H and r² = 0.632 (P = 6.36 × 10⁻⁹³, n = 210) for animal I. Given that the modeled similarity values were a better predictor of performance, we use these measures in the remaining analyses, except where noted.

Fig. 2.

Comparison of the similarity measure from the GLM to performance. For each match-nonmatch pair, the similarity measure from the model is plotted against animal H’s (A) or animal I’s (B) performance for the same match-nonmatch pair. Performance comes only from sessions in which neuronal activity was recorded, independent of which stimulus was in the neuron’s response field.

Although the task was not a reaction time task, we asked whether our similarity metric related to reaction time. For each recording session, we used our similarity measure to identify the most similar pair of stimuli and the least similar pair of stimuli. We found that, on average, the animals’ reaction times to the pair that were least similar were significantly shorter than their reaction times to the pair that were the most similar [means ± SE: 193 ± 4.5 ms compared with 205.8 ± 4.9 ms; t(48) = 3.65, P = 0.00064, paired t-test]. This was also true for each animal independently [t(27) = 2.49, P = 0.019 and t(20) = 3.05, P = 0.0063, animals H and I, respectively]. In addition, we plotted the reaction time for each comparison in a session against the similarity measure and looked to see whether there was a correlation. The correlation was significant in only six sessions, but in five of these the reaction times correlated positively with similarity, meaning that when stimuli were similar and hard to tell apart the reaction times were longer. In each animal, there was also a trend for positive correlation coefficients. In animal H the mean correlation coefficient was 0.175 ± 0.050, and in animal I the mean was 0.154 ± 0.051. In both animals these distributions were significantly shifted to the right of 0 (P = 0.0016 and P = 0.0070 for animals H and I, respectively, t-tests).

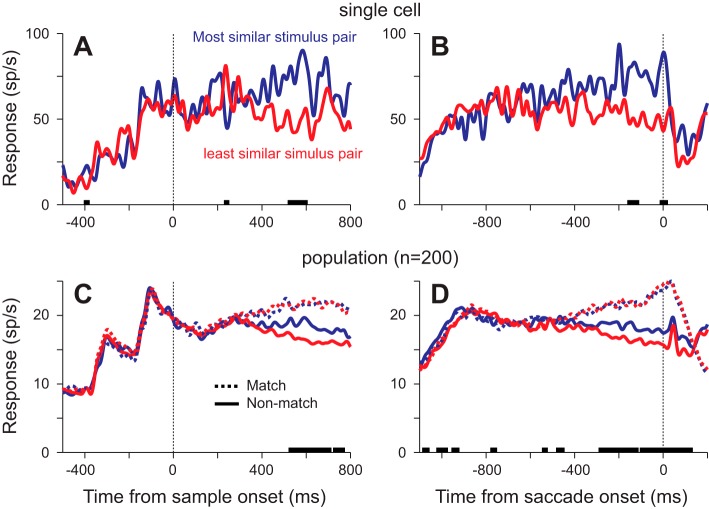
Our hypothesis stated that the response to a stimulus should correlate with the relative similarity of that stimulus to the sample. This would predict that the response to nonmatches should vary as a function of how similar they are to the sample, with higher responses for more similar stimuli. As a first pass, we examined the responses to the nonmatch from the pair in which it was most similar to the sample based on our similarity measure and the nonmatch from the pair with the least similarity (Fig. 3, A and B). We present the data from correct trials only: these are trials in which a saccade was made to the matching stimulus diametrically opposite to the response field, so the responses do not include any motor component. In this neuron, the mean response to the nonmatch in the most similar stimulus pair was greater than the mean response to the nonmatch in the least similar stimulus pair whether aligned by sample onset (Fig. 3A) or by saccade onset (Fig. 3B). Because these data come from a small subset of the trials (n = 22 and n = 33), this difference was only significant briefly (P < 0.01, t-test at every millisecond). However, the bias was seen in many neurons, so we see the same result when we look at the population of 200 neurons (Fig. 3, C and D): the response to the nonmatch in the most similar pair is greater than the response to the nonmatch in the least similar pair. This difference was consistently significant starting ~520 ms after sample onset and ~280 ms before saccade onset (P < 0.01, n = 200, paired t-tests).

Fig. 3.

Neuronal responses from correct trials to the most similar and least similar stimulus pairs. A and B: mean neuronal responses to a nonmatch stimulus from an example neuron from trials with 200-ms or 400-ms SOAs, aligned by sample onset (A) or saccade onset (B). Using the similarity model, we identified the match-nonmatch pair that were most similar and the pair that were least similar. Thick lines on the x-axis indicate times at which the responses to the nonmatches (solid lines) were significantly different (P < 0.01, t-tests at each millisecond). C and D: mean population responses under the same conditions, aligned by sample onset (C) or saccade onset (D). Solid lines show the response to the nonmatch, and dotted lines show the response to the match in the most (blue) and least (red) similar match-nonmatch pairs. Thick lines on the x-axis indicate times at which the responses to the nonmatches (solid lines) were significantly different (P < 0.01, paired t-tests at each millisecond).

If the response to a stimulus is related to how similar it is to the sample, then we would predict that the responses to match stimuli should be the same, independent of similarity. Consistent with this hypothesis, we found that the responses to the matches (Fig. 3, C and D) were similar at all times after sample onset and before saccade onset and at no point during these critical periods were the responses significantly different (P > 0.05, n = 200, paired t-tests).

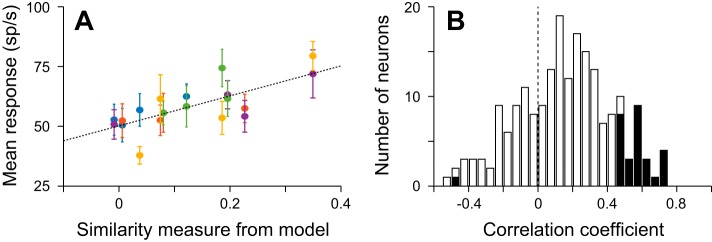
To show that the neuronal activity in LIP correlates with similarity, we need to show that the activity to a nonmatch is higher when it is paired with a similar sample than when it is paired with a sample that is not similar. Figure 4A illustrates the relationship between neuronal response and similarity for the single neuron shown in Fig. 3, A and B. It shows the responses to nonmatch stimuli on correct trials, in which a saccade was made to the match in the opposite hemifield, from a 200-ms window centered 150 ms before saccade. The responses are plotted against the similarity values from the model for the 19 stimulus pairs in which a minimum of four trials were recorded. Responses to the same nonmatch in the response field share the same color in Fig. 4A. Using the yellow points as an example, it is clear that the response to this nonmatch was lowest when it was paired with a sample that was not similar and was greatest when paired with a sample that was similar. This relationship was true for all the stimuli when they were nonmatching stimuli and results in a clear correlation between the mean response to the nonmatch and the similarity measures from the model (r = 0.7361, P = 2.16 × 10⁻⁴, n = 19). A similar correlation was not seen in the responses to match stimuli (r = 0.010, P = 0.966, n = 19), indicating that the response to the match in this neuron during this window did not vary as a function of the identity of the nonmatch stimulus.

Fig. 4.

Responses to nonmatching stimuli vary as a function of how similar they are to the sample. A: relationship between the response to each nonmatch and to the similarity measure for each match-nonmatch pair. Each point shows the mean ± SE response to a nonmatch from correct trials taken from a 200-ms window starting 250 ms before saccade onset and from trials with 200- or 400-ms SOAs. Same colors indicate responses to the same nonmatch stimulus in the response field when different sample stimuli were presented at the fovea. Dashed line is the line of best fit to all the data points (r = 0.7361, P = 2.16 × 10⁻⁴). B: distribution of correlation coefficients from all 200 neurons, based on the same 200-ms window from trials with SOAs of 200 or 400 ms. Filled and open bars show neurons with and without significant correlations (P < 0.05), respectively.

Many single neurons and the population as a whole showed a significant relationship between the response to a nonmatch and the similarity measure that stimulus had with the sample to which it was being compared. Twenty-nine of 200 neurons showed significant correlations (P < 0.05; Fig. 4B), with all but 1 showing positive correlations. As evident in Fig. 4B, there was also a trend in the majority of neurons such that the mean correlation coefficient was significantly >0 [t(199) = 7.78, P = 3.72 × 10⁻¹³, t-test; mean ± SE: 0.149 ± 0.0192]; this was even true for the subset of neurons that did not have significant correlations [t(170) = 4.95, P = 1.80 × 10⁻⁶; mean ± SE: 0.0841 ± 0.0170].

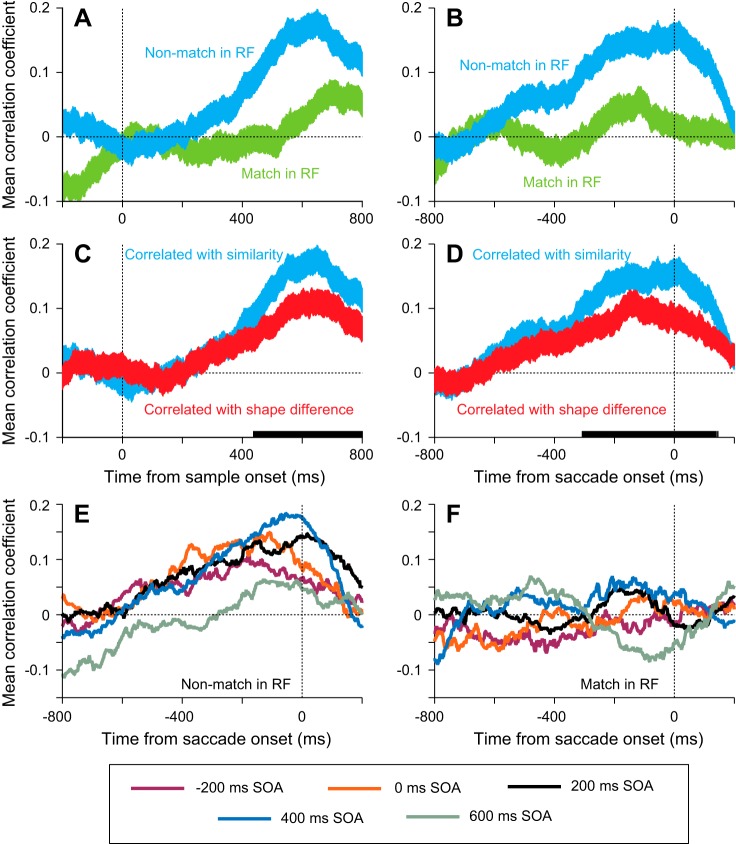
In the population, there was no correlation between nonmatch response and similarity until ~250 ms after sample onset, after which time the mean correlation coefficient became increasingly positive until 200 ms before the saccade. This can be seen in the blue traces in Fig. 5, A and B; these panels show the mean ± SE correlation coefficients taken from regressions like the example in Fig. 4A using 200-ms windows centered at the time point at which the data are plotted. While the correlation coefficients ramped up when the response to the nonmatch was examined, there was little, if any, correlation between the match response and similarity after sample onset and before saccade onset (green traces, Fig. 5, A and B), except for a brief positive correlation 100–200 ms before saccade onset.

Fig. 5.

Time course of correlation coefficients comparing responses to stimuli with similarity. A and B: mean correlation coefficients from all 200 neurons from the type of analysis illustrated in Fig. 4A plotted as a function of time, aligned by sample onset (A) or saccade onset (B). Data were taken from 200-ms windows stepped every 5 ms and are from trials with SOAs of 200 or 400 ms. Blue, correlations performed on the responses to nonmatches in the response field; green, correlations performed on the responses to matches in the response field. Width of lines shows variance (SE) across neurons. C and D: correlations performed on the responses to nonmatches in the response field to similarity (blue) and to an objective measure of shape difference (red) aligned by sample onset (C) or saccade onset (D). Solid bars on x-axis show time points where the 2 distributions were significantly different (paired t-tests, P < 0.05) E: mean correlation coefficients using stimulus similarity from all 200 neurons for each of the 5 SOAs when a nonmatch was in the response field, aligned by saccade onset. F: mean correlation coefficients from all 200 neurons for each of the 5 SOAs when a match was in the response field, aligned by saccade onset.

The positive correlation seen in the response to the nonmatch is not just a function of the individual feature differences. To test this, we replaced similarity in our correlation analyses with the parametric shape difference measure, which was a negative sum of the quantified differences at each edge (see materials and methods for details). As noted above, this metric gave a slightly better correlation with performance than the other objective measure we used (the 15-dimensional shape space). When we inserted this objective measure into the correlations (red traces, Fig. 5, C and D), we found that the coefficients were lower than when using the similarity measure (blue traces) and that the distributions of correlation coefficients were significantly different (P < 0.05, running paired t-tests, n = 200) starting ~425 ms after sample onset and continuing until after the saccade was made. This means that the activity correlated better with the similarity measure, which incorporates how much weight the animals put on particular aspects of the stimuli, than a representation built up by the individual components weighted equally.

Thus far, all our analyses have focused on trials in which the sample appeared 200 or 400 ms after the peripheral stimuli. If our hypothesis is correct, then we should see similar positive correlations of nonmatch response and similarity in all the timing conditions. Figure 5E shows the mean correlation coefficients when a nonmatch was in the response field for all five SOAs. In each condition, the correlation coefficient begins to consistently rise starting ~600 ms before saccade onset. This was true when the sample appeared before the peripheral stimuli (−200-ms SOA) and when they appeared at the same time (0-ms SOA), showing that the transient on-responses in these conditions did not negate the neurons’ processing of stimulus similarity. Conversely, we found a lack of strong correlation between the response to the match and similarity in all conditions (Fig. 5F), with none showing any consistent correlations in the 400–500 ms before saccade onset.

To confirm that the same neurons were signaling the similarity of the nonmatch in the various timing conditions, we ran an analysis in which we split the data into trials in which the sample appeared after the peripheral stimuli (SOAs of 200, 400, and 600 ms) and those in which it did not (SOAs of −200 and 0 ms). We then used a Spearman correlation to compare the order of the responses to each nonmatch as a function of the matching stimulus identity for the two timing groups. In each case, the response was from the same 200-ms window centered 150 ms before saccade onset. This provided a correlation coefficient for each nonmatch, from which we obtained a mean correlation coefficient for the neuron. If the neuron’s response to each stimulus was biased by how similar it was to the sample in a consistent way, then we would expect a positive correlation between the order of the responses in the two timing groups. It should be noted that with only four comparisons per stimulus the analysis is not particularly powerful; nonetheless, consistent results across the population would be meaningful. Figure 6 shows the distribution of the mean correlation coefficients for the 200 neurons. The distribution is shifted slightly, but significantly, to the right [t(186) = 2.92, P = 0.00398, t-test; mean ± SE: 0.0705 ± 0.0242], showing that neurons tend to have positive correlations. This implies that what we saw in the analyses with the data from the 200- and 400-ms SOAs pooled is a good representation of what the neurons do in all timing conditions.

Fig. 6.

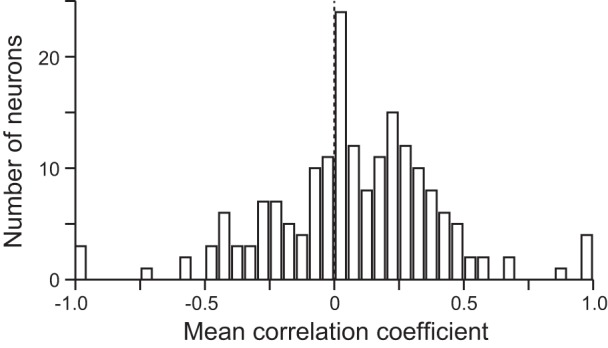
Histogram of correlation coefficients from an analysis aimed at showing response reliability. For each neuron, the data were divided into 2 timing groups based on SOA. Using a Spearman correlation, we asked whether the order of responses to each nonmatch as a function of sample identity was similar in the 2 timing groups. Histogram shows the distribution of mean correlation coefficients for all 200 neurons.

Even though we only analyzed the neuronal responses from correct trials, it is possible, because similarity correlates with behavior, that the correlation we see with the nonmatch is due to certainty or task difficulty: on easy trials, when the animal is sure which stimulus is the match, the response to the nonmatch is lower and this correlates with a lack of similarity. This would suggest that the response to the match should also correlate with difficulty or certainty, but in a negative way: on harder trials, when less certain, the response to the match should be lower. However, at no time after sample onset did we find a negative correlation between match response and its similarity to the nonmatch (Fig. 5, A and B). If anything, there was a trend in the opposite direction. The same argument can be used to refute the idea that the lower responses to the nonmatch when it is dissimilar to the match are due to the sort of ramping activity that appears in motion direction discrimination tasks. In those tasks, the activity at the target site reaches a constant level just before the saccade, while the response, when saccades go away from the response field, varies as a function of coherence, similar to the results we see at the end of the trial. However, responses to targets increase at a rate related to the strength of the signal early in the trial in both reaction time (Roitman and Shadlen 2002) and non-reaction time (Shadlen and Newsome 2001) versions of the motion decision making task. If this ramping were to explain our data, then we would expect a negative correlation associated with the match relatively early in the trial. Given that we find no evidence of such a negative correlation and, if anything, a slight positive correlation, our data do not support these hypotheses. Instead, we find that neuronal activity in LIP correlates with how similar the stimulus in the response field is to the sample: matches, being identical to the sample, tend to elicit consistent activity, whereas the responses to nonmatches depend on how similar they are to the sample.

The positive correlation we see between the response to nonmatch stimuli and similarity is not a result of eye movement planning. We have frequently argued that LIP activity is used to guide saccades (see, for example, Bisley and Goldberg 2010) rather than being driven by an externally generated eye movement plan, but it is important for us to show that this is the case in this task. To do so, we take advantage of the fact that the animals’ performance, when comparing two stimuli, could vary depending on which stimulus was the sample. If the activity in LIP represents similarity, then neurons should respond similarly to two stimuli when being compared with each other, independent of how well the animals end up being able to tell them apart. Conversely, if the activity is driven by eye movement plans, then it should vary when the animal has more or less difficulty telling two stimuli apart, depending on which is the sample. Specifically, when the performance is better with one stimulus as the sample, the response to the nonmatch stimulus should be lower, even though they are equally similar. To test whether this is the case, we compared differences in firing rate and performance for stimulus pairs. For each pair, we calculated the difference in percent correct by subtracting the worse percent correct from the better percent correct. Pairs in which the performance in any condition was below 60% correct were excluded to ensure that the animals were actually performing the task. We then calculated the difference in the response to each stimulus as a nonmatch stimulus when the other was the sample in a 200-ms window starting 150 ms before saccade onset. This was done by subtracting the response in the condition with the lower percent correct from the response in the condition with the higher percent correct. This was then normalized by dividing the difference by the maximal response of the neuron to any stimulus. If the activity in LIP reflects the similarity, then the mean response difference should be zero, independent of performance, because the pairs of stimuli are always separated by the same difference in similarity. However, if the activity is driven by a saccade plan, then there should be a negative correlation with performance, similar in strength to the correlation shown above.

Figure 7 shows the normalized response difference plotted against the difference in percent correct: Fig. 7, top, shows the raw data, and Fig. 7, bottom, shows the mean ± SD. We found that there was no correlation between the response difference and the performance difference (R² = 0.0010, P = 0.143, n = 1,511). Furthermore, the normalized response difference fluctuated around 0 with a constant variance. These data support the hypothesis that the activity represents stimulus similarity and not an externally planned eye movement that is then represented in LIP as a motor plan or an effect of attention based on the motor plan.

Fig. 7.

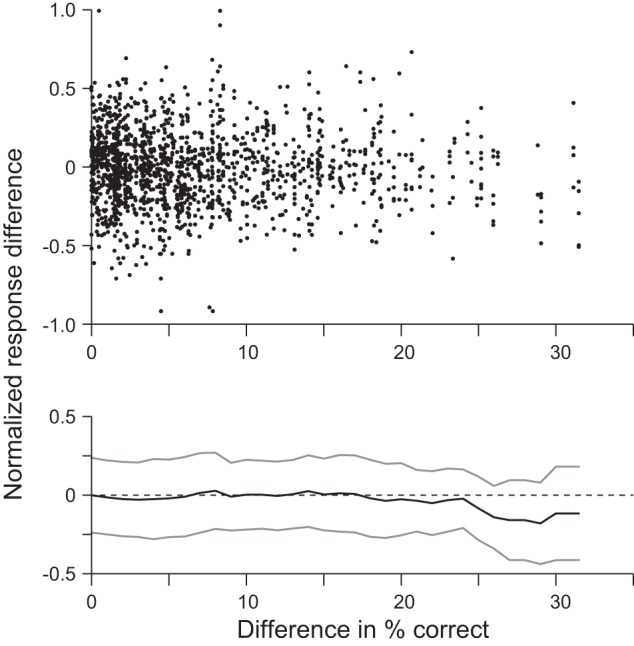
Response and performance differences for pairs of stimuli. For each pair of compared stimuli we calculated the difference in % correct when one stimulus was the sample compared with performance when the other stimulus was the sample, and the normalized difference in response to the nonmatch stimuli was calculated using the activity in a 200-ms window, 150 ms before saccade onset. Top: the 2 metrics plotted against each other. Bottom: a running average of the normalized response difference. Mean and SD (gray lines) were taken in 1% correct steps and averaging all the normalized response differences within a 5% correct window.

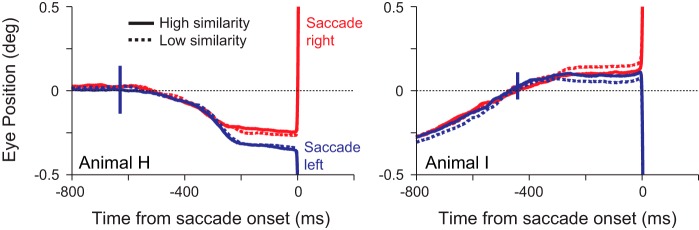
It may be argued that the lower response to a nonmatch that is less similar to the sample could be due to small eye movements biasing the eye toward the match and moving the nonmatch off the response field. Given the size of LIP response fields, we suggest that this is unlikely; nonetheless we examine it in Fig. 8. Here we show the mean eye position across sessions, with the solid vertical blue lines indicating the magnitude of the SE. For each session, we examined the eye position in the 800 ms before saccade onset in trials with SOAs of 200 and 400 ms. The results are consistent for all SOAs, but we only present data from our standard two SOAs here to limit potential differences due to different sample onset times. We compared data from the stimulus pairs that had the three highest similarities and the stimulus pairs that had the three lowest similarities. We found no consistent difference in eye position between high- and low-similarity stimulus pairs, and there were no significant differences between the two traces (P < 0.05, paired t-tests every millisecond; n = 28 for animal H, n = 21 for animal I) at any time for either direction in either animal. We did, however, find significant (P < 0.05) differences between the left and right saccade directions in the high-similarity conditions in animal H (Fig. 8, left) starting 240 ms before saccade onset and some sporadic significant differences in the low-similarity conditions, suggesting that the animal did start to indicate its choice with small eye movements, but these were independent of similarity. Although the low-similarity traces appear separated in animal I, the differences did not reach significance at the P < 0.05 level. So, overall, we found no evidence that small eye movements might explain the differences in response that correlate with stimulus similarity.

Fig. 8.

Mean eye position leading up to a correct saccade separated by saccade direction and stimulus similarity for animals H (left) and I (right). Solid traces show the mean eye position from the stimulus pairs that had the 3 highest similarities; dotted lines show the mean eye position from the stimulus pairs that had the 3 lowest similarities. Red traces show saccades made to stimuli in the right visual field, and blue traces show saccades made to stimuli in the left visual field. Solid vertical blue lines indicate the magnitude of the SE for each animal.

We have suggested that the mean response to a match, which is identical to the sample, remains constant. However, we found a slight positive correlation between the response to a match and how similar it is to the nonmatch just before the saccade (Fig. 5B). The fact that it occurs later and not in parallel with the correlation seen to the nonmatch is important, because it means that our main result cannot be due to a global increase in response due to attention or motivation on trials in which the animal finds the discrimination difficult. Instead, this result, which was obtained by only examining correct trials, can be understood by realizing that the responses to matches on error trials are likely to be lower than on correct trials. That is, if the activity in LIP indicates how similar each stimulus is to the sample, then errors should occur in trials in which the response to the nonmatch is greater than the response to the match. To test whether this occurs, we examined the mean neuronal responses to a match in the response field and a nonmatch in the response field on trials in which the animal incorrectly made a saccade to the nonmatch (Fig. 9). We found brief, but consistent, significant differences in the population response (P < 0.01, n = 200, paired t-tests) beginning around 150 ms, which became stable around 320 ms. These data are consistent with the hypothesis that if the response to the match is lower than the response to the nonmatch then an error will occur, and they support our hypothesis that LIP plays a role in deciding where to look.

Fig. 9.

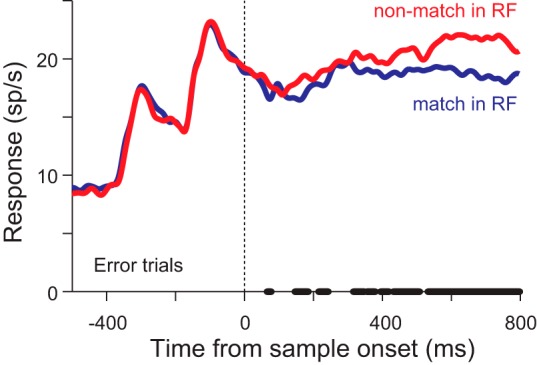
Neuronal responses from error trials in which the animal made a saccade to the nonmatch: mean neuronal response from 200 neurons when the sample appeared 200 or 400 ms after the peripheral stimuli when a match was in the response field (blue) or a nonmatch was in the response field (red). Thick line on x-axis indicates times at which the 2 traces were significantly different (P < 0.01, paired t-tests).

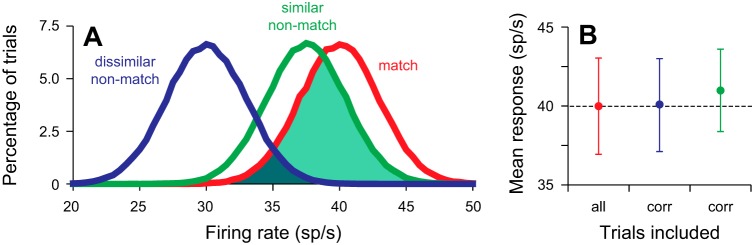
The slight positive correlation between the response to matches and similarity can now be explained by our use of correct trials. This is illustrated in Fig. 10, which shows an idealized representation of activity. For this analysis, we assumed that there was no movement component to the response, which would be added to the responses illustrated here (Ipata et al. 2009). We ran 100,000 iterations in which we randomly drew the mean response for each condition from distributions with a standard deviation of 3 sp/s and means of 30, 37.5, and 40 sp/s for the dissimilar nonmatch, similar nonmatch, and match stimuli, respectively. For each iteration and each nonmatch stimulus, we counted the “trial” as correct if the response to the match stimulus was greater than the response to the nonmatch stimulus. Figure 10A shows the resulting three distributions, and Fig. 10B shows the mean ± SD response from the entire match distribution (red), the match distribution limited to trials in which the response to the match was greater than to the dissimilar nonmatch (blue), and the match distribution limited to trials in which the response to the match was greater than to the similar nonmatch (green). When the nonmatch was dissimilar to the match, there was little overlap between the red and blue distributions (blue shaded area, Fig. 10A), so the mean response to the match on correct trials (blue point, Fig. 10B) was fairly similar to the overall mean response. This is because errors only occurred when the response to the match was unusually low and the response to the nonmatch was unusually high. When the nonmatch was similar to the match, there was more overlap between the red and green distributions (green shaded area, Fig. 10A), so more low responses to the match are likely to result in errors. This resulted in a higher mean response and lower SD (2.6 compared with 3) on correct trials (green point, Fig. 10B). Overall, these results would create a small positive correlation with similarity on correct trials: the more similar the nonmatch, the greater the response to the nonmatch and the more likely a lower response to the match would result in an error trial, resulting in a match distribution on correct trials that is skewed to the right. How far it skews would depend on how much overlap there is in the distributions of the nonmatch responses, but more similar stimuli, resulting in higher nonmatch distributions, would lead to higher mean responses to matches on correct trials. Thus, by using only correct trials in our analyses, it is not surprising to see a slight positive correlation of the match response to similarity, and this result does not conflict with our conclusion that the mean response to the match remains stable. It should be noted that the use of correct trials would tend to have the opposite effect on responses to nonmatches, giving a negative correlation with similarity. The fact that we see a strong positive correlation with similarity means that the mean responses of the whole distributions must differ substantially as a function of similarity.

Fig. 10.

Model data to show how the use of correct trials could create a positive correlation of the response to a match with similarity and to illustrate how error trials could occur. A: idealized representation of the distribution of responses to a stimulus when it is the match (red trace), a nonmatch that is similar to the sample (green trace), and a nonmatch that is not similar to the sample (blue trace). B: illustration of mean ± SD responses from the idealized representation to the match under conditions in which all trials were included (red point) and in which only correct trials were included and the nonmatch was dissimilar to the sample (blue point) or similar to the sample (green point). In all 3 cases, the mean response is calculated from the red distribution in A.

DISCUSSION

Our results have shown that when animals compare two peripheral stimuli to a sample at their fovea the responses to the stimuli vary as a function of how similar they are to the sample: the response to the matching stimulus is always high, while the response to the nonmatch positively correlates with its similarity to the sample. Because this occurred independently of the shape of the stimulus, we propose that LIP effectively computes perceived similarity across shapes. This is consistent with recent imaging work that has shown similar tuning of abstract object identity in human parietal cortex (Jeong and Xu 2016). We suggest using the term “perceptual similarity map” to describe this sort of response to differentiate it from similarity maps in visual areas that only respond to a limited set of visual stimuli. Given the parallel processing available within the visual system, the idea of a perceptual similarity map explains both simple comparisons, for example, popout (Arcizet et al. 2011; Thomas and Paré 2007), and complex comparisons, in which multiple features must be integrated (Ogawa and Komatsu 2009; Oristaglio et al. 2006).

We do not see this as a new or additional mechanistic process in LIP; rather, we see it as another use of the flexible representation that LIP forms to prioritize choices based on the current task. It combines bottom-up information, in the form of similarity signals from the ventral stream (Allred et al. 2005; Ratan Murty and Arun 2015), with top-down signals that allow it to flexibly represent the incoming similarity measures as a function of what the animal is looking for. This information is then read out downstream to form the choice of where to look. That it uses the machinery involved in guiding attention and eye movements (Andersen and Cui 2009; Bisley and Goldberg 2010; Gottlieb et al. 2009) should not be surprising, as these are the mechanisms one uses in natural conditions to find objects one is looking for.

While many studies have examined the responses to distractors in LIP, particularly during search, they have either utilized the same distractor, making the target perceptually pop out (Nishida et al. 2013; Thomas and Paré 2007), or have used multiple different distractors but have not examined the responses to different distractors or how they vary as a function of their similarity to the target (Ipata et al. 2006a; Oristaglio et al. 2006). The exceptions have mostly been studies examining responses in V4 or FEF, which have consistently shown a form of feature-based attention: when a stimulus shares a feature with the target, its response is enhanced (Bichot et al. 2005; Mazer and Gallant 2003; Zhou and Desimone 2011). In LIP, one study examined responses to nonmatching stimuli in a delayed match-to-sample task in which animals had to keep track of two stimulus features (Ibos and Freedman 2014). They found similarity-related responses, but only in neurons tuned for the to-be-matched sample stimulus, and so claimed that neuronal activity does not track sample test similarity. It is likely that the discrepancy between their interpretation of their results and our interpretation of our results comes from a key difference in task design: their animals were highly trained on the full stimulus set and, in particular, on the two possible sample stimuli, which never varied from day to day, whereas our animals were given novel stimuli in every session. Given that long-term training is known to impact the responses of neurons in LIP in a number of tasks (Ipata et al. 2006b; Law and Gold 2008; Mirpour and Bisley 2013; Sigurdardottir and Sheinberg 2015) and that in our task the animals must compare two relatively unfamiliar objects to the sample, we believe that our data better represent the responses of LIP neurons when comparing stimuli. Of note, in a separate study of dorsolateral PFC (Lennert and Martinez-Trujillo 2011), animals were trained with a rule regarding which stimulus they needed to attend. In that work, the endogenously driven changes they observed had properties similar to the results we find, and their data are also described in terms of a mechanism similar to that we envision occurring in LIP during object comparisons.

For almost a century, theoreticians and psychologists have attempted to find a general theory to explain veridical object recognition using first-order isomorphism, in which each object is uniquely and separately represented in the brain (Edelman 1999). However, modern psychophysical experiments revealed that subjects are invariably poor when it comes to veridical perception (Koenderink et al. 1996; Phillips and Todd 1996) or understanding of shape geometry per se (Jolicoeur and Humphrey 1998). Studies by Shepard and Chipman (Shepard 1962; Shepard and Chipman 1970) built a case that an intelligent system with the flexibility, efficiency, and performance of human visual object recognition needs a second-order isomorphism, in which the relationship between objects is represented in the brain, such as a representation of shape similarities. While such representations for complex shapes can be found in IT (Allred et al. 2005; Ratan Murty and Arun 2015), neurons in this area tend to be tuned to specific stimulus features and lack the spatial resolution to identify where the object is in visual space (Lehky and Tanaka 2016).

As LIP is able to represent task-relevant activity dynamically during the course of a trial, it is able to integrate incoming visual information including that of the ventral stream about object features and identity, generating a spatially specific perceptual similarity map. This response relates how similar a stimulus is to the sample, independent of the shape of that sample, and could be used to make decisions based on object identification.

GRANTS

This work was supported by National Eye Institute Grant R01-EY-019273.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

W.S.O., K.M., and J.W.B. conceived and designed research; W.S.O. performed experiments; W.S.O., K.M., and J.W.B. analyzed data; W.S.O., K.M., and J.W.B. interpreted results of experiments; W.S.O., K.M., and J.W.B. edited and revised manuscript; W.S.O., K.M., and J.W.B. approved final version of manuscript; J.W.B. prepared figures; J.W.B. drafted manuscript.