The temporal stability of visuomotor adaptation generalization

Short-term motor adaptation exhibits distinct spatial and temporal characteristics. Here we investigated the interaction of these features, utilizing a simple motor adaptation paradigm (recalibration of reaching arm movements in response to rotated visual feedback). We examined the changes in the spatial generalization of motor adaptation for different temporal manipulations and report that the spatiotemporal generalization of motor adaptation is generally local and is influenced by both passive (time dependent) and active (movement dependent) learning processes.

Abstract

Movement adaptation in response to systematic motor perturbations exhibits distinct spatial and temporal properties. These characteristics are typically studied in isolation, leaving the interaction largely unknown. Here we examined how the temporal decay of visuomotor adaptation influences the spatial generalization of the motor recalibration. First, we quantified the extent to which adaptation decayed over time. Subjects reached to a peripheral target, and a rotation was applied to the visual feedback of the unseen motion. The retention of this adaptation over different delays (0–120 s) 1) decreased by 29.0 ± 6.8% at the longest delay and 2) was represented by a simple exponential, with a time constant of 22.5 ± 5.6 s. On the basis of this relationship we simulated how the spatial generalization of adaptation would change with delay. To test this directly, we trained additional subjects with the same perturbation and assessed transfer to 19 different locations (spaced 15° apart, symmetric around the trained location) and examined three delays (~4, 12, and 25 s). Consistent with the simulation, we found that generalization around the trained direction (±15°) significantly decreased with delay and distance, while locations >60° displayed near-constant spatiotemporal transfer. Intermediate distances (30° and 45°) showed a difference in transfer across space, but this amount was approximately constant across time. Interestingly, the decay at the trained direction was faster than that based purely on time, suggesting that the spatial transfer of adaptation is modified by concurrent passive (time dependent) and active (movement dependent) processes.

NEW & NOTEWORTHY Short-term motor adaptation exhibits distinct spatial and temporal characteristics. Here we investigated the interaction of these features, utilizing a simple motor adaptation paradigm (recalibration of reaching arm movements in response to rotated visual feedback). We examined the changes in the spatial generalization of motor adaptation for different temporal manipulations and report that the spatiotemporal generalization of motor adaptation is generally local and is influenced by both passive (time dependent) and active (movement dependent) learning processes.

adaptation paradigms that alter visual feedback (via prism displacement or visuomotor manipulations; Krakauer et al. 1999; Redding et al. 2005) or movement dynamics (via imposed force-fields; Shadmehr and Mussa-Ivaldi 1994) provide a tractable method to study the features of short-term motor learning. For example, the generalization of this type of learning has been assessed across different movement speeds and extents (Goodbody and Wolpert 1998; Mattar and Ostry 2010), configurations (Malfait et al. 2002; Shadmehr and Moussavi 2000; Shadmehr and Mussa-Ivaldi 1994), effectors (Criscimagna-Hemminger et al. 2003; Joiner et al. 2013; Malfait and Ostry 2004; Poh et al. 2016; Taylor et al. 2011), and directions (Day et al. 2016; Donchin et al. 2003; Fernandes et al. 2012; Hwang et al. 2006; McDougle et al. 2017; Thoroughman and Shadmehr 2000; Thoroughman and Taylor 2005). Examining the manner in which short-term motor adaptation generalizes is a useful method for understanding the internal representations used for learning new motor abilities (Poggio and Bizzi 2004; Shadmehr 2004). Except for a few cases (Joiner et al. 2011), the transfer of motor adaptation is typically limited, with generalization locally confined around the context experienced during training. For example, the spatial transfer of adaptation generally follows a Gaussian-like relationship across different movement directions, with the amount of generalization decreasing exponentially with the distance away from the trained movement direction (Brayanov et al. 2012; Krakauer et al. 2000). However, this relationship is modified by various factors. For instance, generalization patterns change with limb configuration, revealing the interaction of intrinsic and extrinsic coordinate frames (Brayanov et al. 2012). In addition, variations in the type of visual feedback, training breadth, and uncertainty in the movement disturbance have all been shown to influence certain features of the spatial generalization patterns (Berniker et al. 2014; Fernandes et al. 2014; Taylor et al. 2013).

In addition to these effects on the spatial transfer, recent studies have demonstrated the influence of temporal manipulations on motor adaptation. For example, the temporal structure of training (intertrial interval, ITI) influences the rate and stability of adaptation (Kim et al. 2015); the initial learning rate is faster for training with a short ITI, but stability is greatest for long-ITI adaptation, a likely interaction of temporally labile and temporally stable learning processes (Sing et al. 2009). Additionally, assessing the stability of motor adaptation across nonfeedback trials and at various time points has revealed the temporal decay patterns (Criscimagna-Hemminger and Shadmehr 2008; Inoue et al. 2015; Joiner and Smith 2008). Recently, Smith and colleagues showed that motor recalibration in response to either altered visual feedback or movement dynamics has a temporal decay with a time constant of ~20 s (Hadjiosif et al. 2012; Sing et al. 2009). However, the decay of these motor memories is faster when continuously assayed throughout the same time frame, suggesting active and passive contributions to the decay process (Kitago et al. 2013).

Here we were interested in the interaction of these temporal and spatial characteristics of short-term motor adaptation and their combined effect on the generalization of adaptation. First, we established the decay of the visuomotor adaptation with the passage of time. On the basis of these observations we hypothesized how this temporal decay could potentially influence the spatial generalization of the motor adaptation. In our simulation, we assume that there are interacting local and global components (both represented by Gaussian functions) that combine during the spatial generalization of motor adaptation (Hadjiosif and Smith 2013; McDougle et al. 2017). We applied the observed proportional decrease in retention with time on the gain at the trained target location (the local component). The simulation suggested that the temporal influence would be local around the trained direction, with little effect on movement directions outside of this range. In a second experiment, we demonstrate that the temporal influence on adaptation transfer is in fact very local (within ±15° of the trained direction), with little influence beyond this extent. However, the decay of adaptation at the trained target location during the generalization experiment was faster than that predicted from a purely temporal basis, suggesting that active (movement dependent) and passive (time dependent) learning processes are concurrently engaged during adaptation transfer.

MATERIALS AND METHODS

Participants.

Forty-two healthy subjects (18 men and 24 women) without known neurological impairment were recruited from the George Mason University community to participate in the study. All participants were right-handed and performed the task with their right hand. Each individual participated in only one of the experimental sessions and experienced only one type of visuomotor rotation: 20 clockwise rotation (CW) and 22 counterclockwise rotation (CCW). The study protocol was approved by the George Mason University Institutional Review Board, and all participants gave informed written consent.

Experimental setup.

The experimental setup was similar to that used in Wu and Smith (2013) and was used in both experiments. Briefly, subjects sat at a desk facing a horizontal LCD monitor. The chair height was adjusted for each subject to ensure a comfortable viewing position. Subjects grasped a cylindrical handle (2.5 cm in diameter) that was embedded with a stylus. The stylus/hand position was represented as a screen cursor (2.5 mm in diameter). The monitor was 20 cm above a digitizing tablet (12 in. × 19 in.; Intuos3, WaCom) that recorded hand position at 200 Hz. The midline of the subject was aligned with the center of the tablet and monitor. This also served as the center of the workspace. The position of the LCD monitor obstructed vision of the tablet and the arm movements made by subjects.

Task.

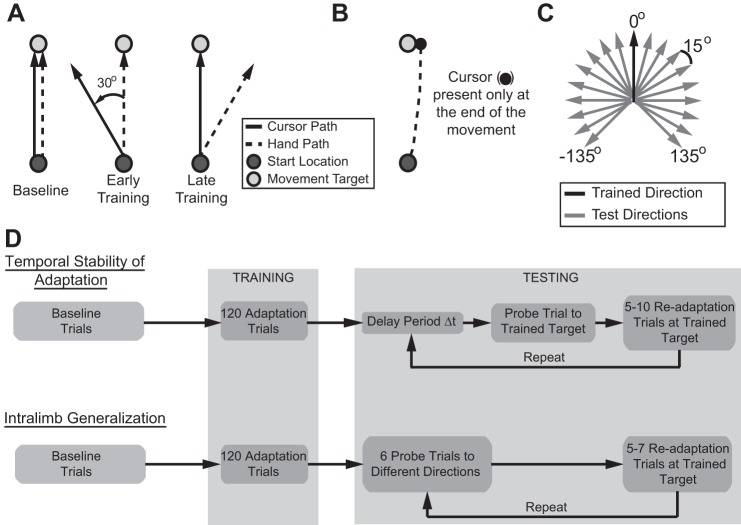
In the beginning of each experiment, each subject experienced the same basic baseline and training structure shown in Fig. 1D. Starting from an initial start target (5 mm in diameter) located in the center of the workspace, subjects moved the cursor 9 cm to a target (7 mm in diameter) also located along the midline. Subjects were instructed to “move the cursor from the initial start location through whichever outer target appears. Make fluid, uninterrupted movements as you move the cursor to the target.” During baseline trials, the cursor followed the true position of the hand while subjects made point-to-point movements to this peripheral reach target (Fig. 1B). Subjects received visual and auditory feedback on movement speed. If the movement was too slow (≥400 ms in duration), the target turned blue once the radial distance was exceeded. If the movement was too fast (≤50 ms), the target turned red. The target turned green for movement durations that were between 250 and 400 ms. In addition, a short-duration beep (at a frequency of 429 Hz) was given to signify a good trial.

Fig. 1.

Structure of experimental paradigms and overview of visuomotor adaptation, form of visual feedback, and test for spatial generalization. A: depiction of the hand and cursor movements before, during, and at the end of training. During initial baseline movements and cursor and hand position are aligned. Once the perturbation is applied there is a rotational offset between the cursor and hand movement. Late in training there is a compensatory adjustment in the hand path to guide the cursor to the target. B: end-point visual feedback for the movement is provided only once the movement exceeds the target distance, 9 cm. C: movement directions to test the spatial generalization of adaptation. There are 19 movement directions, separated by 15°, spanning ±135° from the trained direction to determine the extent of adaptation transfer. D: experimental protocol outlining the sequence of training and testing blocks for examining the temporal stability and spatial generalization of the trained visuomotor adaptation. Initial baseline and training for both experiments are similar, but the testing sequence was unique to each experiment.

After baseline, subjects were trained on a visuomotor rotation during which the cursor path was rotated around the hand path by either θ = +30° (CW) or θ = −30° (CCW) (Fig. 1B). During training subjects were only provided end-point feedback; the cursor was extinguished at movement initiation (when hand velocity exceeded 5 cm/s) and reappeared along an invisible circle once the movement exceeded the radial distance of the target (9 cm) (Fig. 1C). This feedback was presented for 1 s and then was replaced by a circle centered on the initial start target. The radius of the circle matched the distance of the hand from the start position. Subjects moved their hand back to the start position guided by the size of the circle; the circle radius decreased in proportion to the distance from the start target. This limited the spatial information of the actual movement trajectory but still provided enough information for the subjects to return to the start target. Once the hand was within 1 cm of the start position, the cursor reappeared and subjects were instructed to place the cursor in the start target for 1 s to begin the next trial.

Experiment 1: temporal decay of visuomotor adaptation.

This paradigm (Fig. 1D) was based on a task structure developed by Hadjiosif and Smith (2013). Subjects (n = 10) were trained in the visuomotor rotation of feedback described in Task. Subjects first completed a familiarization block of 20 movements to the trained target at 90° (all with full visual feedback). The next baseline block consisted of 24 movements to the trained target, with the random removal of visual feedback on 25% of the trials. Subjects completed these movements without any feedback (blank trials) for a total of six blank movements. There was only a small probability that these blank movements would occur on consecutive trials (~0.06). These no-visual feedback blank trials served as the baseline for the retention probe trials described below.

After this baseline period, subjects were trained in the visuomotor rotation with end-point visual feedback of the cursor (Fig. 1B). The rotational perturbation was abruptly applied to their hand movements. At the start of the block, there were 15 movements with no perturbation. On the 16th trial a θ = +30° or θ = −30° rotation was abruptly applied to the movement feedback and remained on for the entire block. Subjects completed 120 movements to the trained target (located at 90°) with the visuomotor perturbation.

After the training period, subjects completed a series of retention probe trials and retraining trials for eight different delay periods (0, 3, 6, 10, 20, 30, 60, and 120 s). The sequence is depicted in Fig. 1D. Throughout the duration of the delay, subjects held the cursor in the start target. After the required hold period, the reach target appeared, cuing the subject to perform the reach. During these retention probe trials, visual feedback was withheld (blank trials). Importantly, in our analysis of retention the angular bias determined from the average of the baseline trials was first subtracted from these probe movements. The single retention probe trial was followed by 5–10 retraining trials during which subjects made movements to the trained target with the visual rotation of the end-point visual feedback. This pattern (5–10 retraining movements followed by 1 retention probe movement) was repeated throughout the session, for a total of four probe movements for each delay duration. The delays were randomly selected throughout the session. Because of the randomness of the number of retraining trials, subjects made a total of 250–320 movements that were divided between three blocks. For each delay, retention of adaptation was quantified by comparing the (baseline subtracted) angular deviation on the no-visual feedback retention probe trials to the average angular deviation on the preceding retraining trials, specifically the last three trials of the 5–10 retraining sequence.

Experiment 2: intralimb spatial generalization of visuomotor adaptation.

This task (Fig. 1D), largely modeled after Brayanov et al. (2012), determined the spatial characteristics of the transfer of visuomotor adaptation. Similar to the temporal decay experiment, subjects (n = 32) first made 9-cm baseline movements to each of the 19 target positions (separated by 15°, spanning ±135° from the trained direction; Fig. 1C). The initial familiarization phase consisted of one block of 76 movements with full visual feedback, 4 to each of the 19 target locations. The baseline phase consisted of 228 movements to the 19 targets divided into three blocks of 76 trials each. During each block, movements to each target were repeated four times, with feedback removed for two of the four instances. As before, in each block blank trials were inserted at random. Over the entire baseline there were a total of six blank trials for each of the 19 target locations, and these served as the baseline for the generalization probe trials described below.

After this baseline period, subjects were trained with the rotational perturbation. As described above, the perturbation was abruptly applied to the right hand movements. The single training block started with an initial 15 movements to the trained target (located at 90°), and on the 16th movement a 30° or −30° rotation was applied. Subjects completed a total of 120 movements to the trained target with the visuomotor rotation of end-point feedback. As described in Task, subjects were guided back to the start target by the size of the circle centered on the initial start target.

After training, subjects completed a series of generalization and retraining sequences (depicted in Fig. 1D). First, subjects made movements to 6 (pseudorandomly selected) of the 19 targets (generalization probe movements). We structured the experiment so that at the end of the session each of the 19 movement directions was experienced at each of the 6 different placements within the probe sequence. That is, each movement direction was tested for generalization early (probe 1), late (probe 6), and all the times in between (probes 2–5). We chose six consecutive generalization probe movements based on the temporal decay pattern established in experiment 1 (Fig. 2B); the majority of decay occurred within 25–35 s, approximately the time frame for six consecutive movements in the task. Importantly, during these probe movements subjects received no feedback on performance (blank trials). These probe movements were followed by five to seven retraining trials during which subjects made movements to the trained target with the applied visual rotation and provided end-point feedback. This pattern (5–7 retraining movements followed by 6 generalization movements) was repeated throughout the session, for a total of six probe movements for each of the 19 targets. Because of the randomness of the number of retraining trials, subjects made a total of 209–247 movements that were divided between two blocks. Any angular bias based on the average of the baseline trials was first subtracted from these probe movements. Similar to the retention experiment, transfer of adaptation was quantified by the ratio of the (baseline subtracted) angular deviation of movements made on the blank generalization probe trials to the average angular deviation (baseline subtracted) on the preceding retraining trials, specifically the last three trials of the 5–7 retraining sequence. This ratio was then scaled to provide a percentage of adaptation transfer. Note that by computing this percentage the transfer of adaptation is relative to the angular deviation during retraining. Thus the percentage is computed the same for both CW and CCW rotations.

Fig. 2.

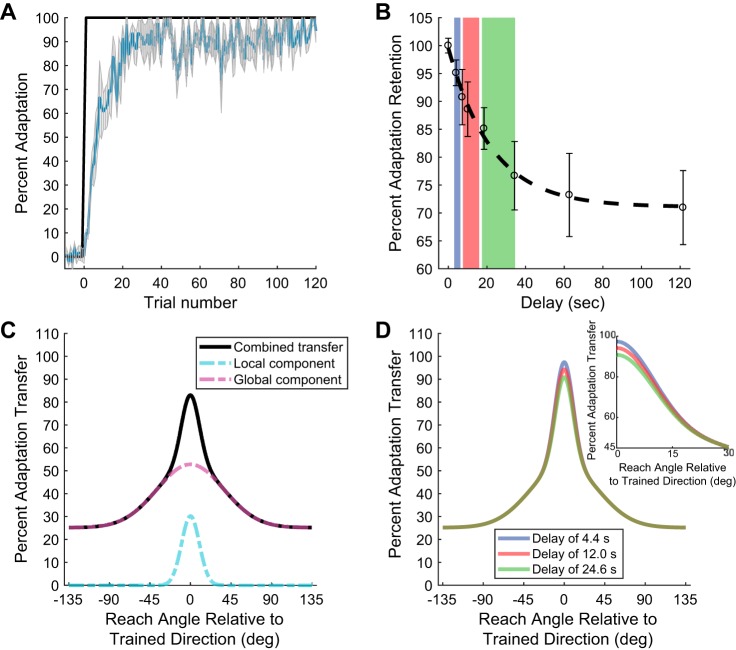
Temporal decay of visuomotor adaptation retention and predicted influence on spatial generalization. A: adaptation curve during training for the temporal delay experiment (n = 12). Blue line represents mean % of adaptation, and shaded area represents SE. Black trace represents magnitude of the visual feedback perturbation. The amount of adaptation at the end of training was significantly greater than at the beginning (20.2 ± 2.0% compared with 91.1 ± 0.3%, mean ± SE, P < 0.01, paired 2-tailed t-test). B: % adaptation retained after each temporal delay is plotted as a function of time. Delay represents the average time before the movement was executed. Circles represent the average across subjects, and vertical bars represent SE. The time constant for the fitted exponential function was 22.5 ± 5.6 s. Color shaded regions represent temporal ranges of 4.4 ± 1.6, 12.0 ± 4.2, and 24.6 ± 8.6 s (± represent 95% confidence intervals). The decay in retention was significant from 0 to 15 s (14.9 ± 3.7% decay, P < 0.05) and 30 s (23.3 ± 6.1% decay, P < 0.01) but not significant from 30 s to 120 s (5.7 ± 2.1% decay from 30 to 120 s, P = 0.31, corrected for multiple comparisons). C: depiction of the 2-component spatial generalization model. There is a local Gaussian-shaped component (dashed light blue trace) and a similar global component with offset (dashed purple trace) that sum for the total generalization (solid black trace). D: based on the exponential function derived in B, the simulated effect on the generalization if the estimated % retention is applied solely to the gain at the trained target direction (retention values of 94.9%, 87.8%, and 80.5%, respectively), keeping all other model parameters constant (k₂ = 27.7 ± 8.5%, θ₀ = 0°, c = 25.2% ± 2.4%, ${\sigma }_1$ = 9.9 ± 3.0°, and ${\sigma }_2$ = 37.1 ± 10.1°). Inset shows the decrease in adaptation transfer for the simulation over the first 30°.

From this transfer data set, for each subject we determined the time between the end of the last retraining trial and the start of each of the six generalization probe trials. From this distribution of time delays we defined three general delay periods to examine the effect of the passage of time on the amount of adaptation transfer: 4.4 ± 1.6, 12.0 ± 4.2, and 24.6 ± 8.6 s (± ranges represent the 95% confidence limits).

Two-component spatial generalization model.

There is recent evidence that there are interacting local and global components that combine during the spatial generalization of motor adaptation (Hadjiosif and Smith 2013; McDougle et al. 2017). Similar to Brayanov and colleagues (Brayanov et al. 2012), we represented these components as two modified Gaussian functions that combined represent the spatial generalization of adaptation:

$$z(\theta )=k_1\text{·}{e}^{\text{−}\frac{|{\theta -{\theta }_0|}^2}{2\text{·}{\sigma }_1^2}}+k_2\text{·}{e}^{-\frac{|{\theta -{\theta }_0|}^2}{2\text{·}{\sigma }_2^2}}\text{\hspace{0.17em}+\hspace{0.17em}}c$$ (1)

In this model (see Fig. 2C), the amount of generalization (z) to a given target direction, θ, depends on 1) the magnitudes of adaptation due to the local (k₁) and global (k₂) components at the peak movement direction, θ₀, 2) an offset term, c, that represents the amount of constant transfer to all movement directions due to the global component, and 3) the width of the respective local (σ₁) and global (σ₂) components. It should be noted that this simplified model assumes transfer based only on the angular deviation between the movement and the trained target direction in extrinsic coordinates. It is important to note that we use this model only to provide a general representation of the changes in the spatial relationships across the different delay conditions examined (Figs. 2 and 3). The learning mechanisms and reference frames that underlie the spatial generalization of adaptation are indeed complex (see Brayanov et al. 2012; McDougle et al. 2017; Poh et al. 2016), and we make no claim that this model captures these various interactions.

Fig. 3.

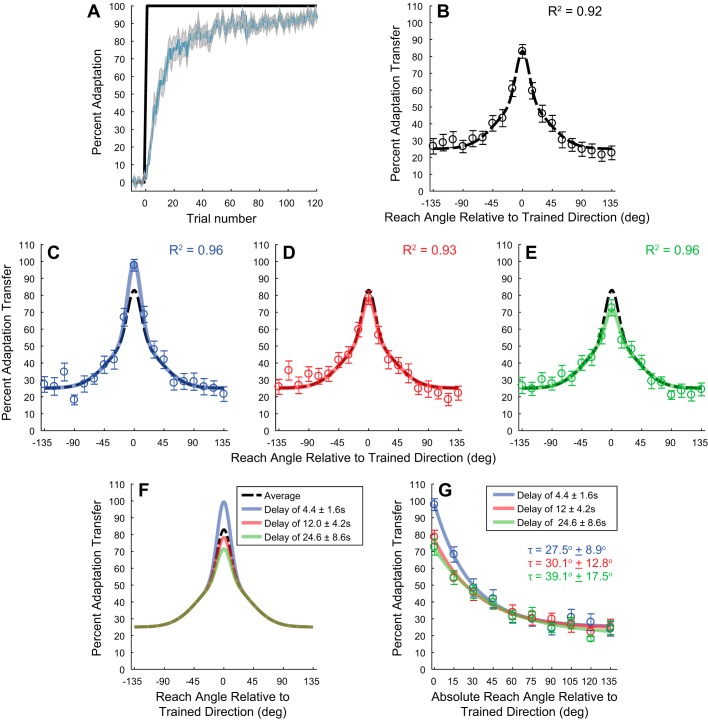
Influence of temporal delay on the spatial generalization of visuomotor adaptation. A: adaptation curve during training for the generalization experiment (n = 32). Blue line represents mean % of adaptation, and shaded area represents SE. Black trace represents magnitude of the visual feedback perturbation The amount of adaptation at the end of training was significantly greater than at the beginning (18.6 ± 1.9% compared with 92.8 ± 0.2%, mean ± SE, P < 0.01, 2-tailed t-test). B: average spatial generalization over all subjects for the entire data set. Bars represent SE. Black dashed line is the 2-component spatial generalization model fit to the experimental data (k₁ = 30.2 ± 10.6%, k₂ = 27.7 ± 8.5%, θ₀ = 0°, c = 25.2% ± 2.4%, ${\sigma }_1$ = 9.9 ± 3.0°, and ${\sigma }_2$ = 37.1 ± 10.1°). C–E: respective spatial generalization and corresponding functions for the delays of 4.4 ± 1.6 s (C), 12.0 ± 4.2 s (D), and 24.6 ± 8.6 s (E) (± represent 95% confidence intervals). Colored traces represent the 2-component spatial generalization model fits to the respective experimental data. k₁ for the different delay values are 46.6 ± 7.2%, 25.4 ± 7.7%, and 18.7 ± 5.5% for 4.4 ± 1.6, 12.0 ± 4.2, and 24.6 ± 8.6 s, respectively. F: comparison of the generalization functions from B–E. G: change in % adaptation transfer as a function of the absolute spatial distance from the trained target direction. Spatial constants for the delay of 4.4 s: 27.5 ± 8.9°, 12.0 s: 30.1 ± 12.8°, 24.6 s: 39.1 ± 17.5°.

Analysis.

We determined the direction of each movement by calculating the angle of the line connecting the hand position at 1 cm and 3 cm into the reach. The percent adaptation (Fig. 2A and Fig. 3A) was determined by the ratio of this (baseline subtracted) movement angle to the magnitude of the perturbation (30° or −30°). To determine the changes in transfer and retention across different delays and movement directions, we applied a standard exponential model with scaling, rate, and offset parameters to determine the time and spatial constants (Fig. 2B and Fig. 3G). In cases in which there was not a significant effect of delay and an exponential model was not appropriate (Fig. 4, B and C), we applied a standard linear regression model with slope and constant parameters to determine the change in transfer as a function of time for each reach direction. Except where noted, we provide the mean across subjects and the standard error of the mean.

Fig. 4.

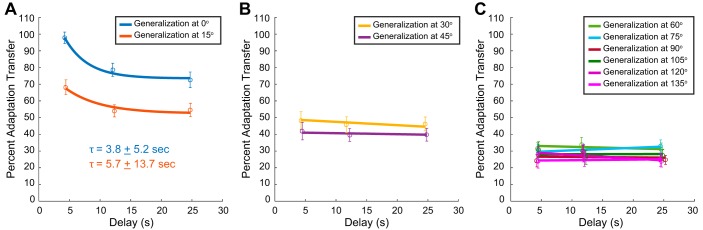
Temporal changes in the transfer of visuomotor adaptation for different distances away from the trained direction: temporal decay of visuomotor adaptation transfer to target locations local: within ±15° (A), intermediate: 30° and 45° (B), and distant: >60° (C) beyond the trained adaptation direction (n = 32). As in Fig. 2B, delay represents the average time before the movement was executed. The transfer local to the trained direction decayed across time and distance (2-way ANOVA, P < 0.001 for main effect of movement direction and P < 0.001 for main effect of delay). The time constant for transfer at 0° and 15° is 3.8 ± 5.2 s and 5.7 ± 13.7 s, respectively. Transfer to targets located at an intermediate distance showed a decay across the spatial separation but was constant across time (2-way ANOVA, P = 0.85 for main effect of delay). Generalization to distant targets was near constant across both time and space (2-way ANOVA, P = 0.2 for main effect of movement direction and P = 0.79 for main effect of delay).

We initially tested the main effect of temporal delay on the amount of retention (Fig. 2B) and transfer (Figs. 3 and 4) with a repeated-measures ANOVA. We then determined the significance of the effects of delay or movement direction with post hoc analysis. For all tests, the significance level was 0.05.

To quantify the goodness of fit for the two-component spatial generalization model, we fit the generalization function with different subsets of the five free parameters (magnitudes k₁ and k₂, width of the components σ₁ and σ₂, and offset c) and computed the corrected Akaike information criterion (AICc) for each model (Akaike 1974). We set the peak movement direction, θ₀, to the trained movement direction. First, we estimated the five parameters from the average data, allowing the parameters to vary. Next, for the generalization functions for the different delays (Fig. 3, C–E) we allowed subsets of the parameters to vary, fixing the others to the estimated values found over the average. This allowed us to determine which parameters were modified by the passage of time. The summary of this analysis is provided in Table 1. As shown in the table, we found that allowing only the magnitude of adaptation for the local component (k₁) to vary captured the temporal changes in generalization. That is, this free parameter consistently yielded the lowest AICc value among the various subsets tested.

Table 1.

AICc values for different subset fits of 2-component model for the different delay conditions (Fig. 3, C–E)

	AICc Values
Variables	Delay of 4.4 ± 1.6 s	Delay of 12 ± 4.2 s	Delay of 24.6 ± 8.6 s
k1, k2, σ1, σ2, c	−108.7693	−105.3151	−118.7197
k2, σ1, σ2, c	−111.2082	−109.6939	−116.9831
k1, k2, σ2, c	−113.0134	−109.6211	−122.0581
k1, σ1, σ2, c	−113.0158	−109.1693	−122.7968
k1, k2, σ1, c	−112.6194	−109.1407	−123.1038
k1, k2, σ1, σ2	−112.9643	−109.6516	−122.9041
k2, σ2, c	−114.5551	−113.3359	−120.7412
k1, σ1, c	−116.3046	−112.7955	−126.3679
k2, σ1, σ2	−114.1863	−113.3856	−119.8192
k1, σ1, σ2	−116.6134	−112.9063	−126.3411
k1, k2, σ2	−116.5036	−113.3555	−125.3954
k1, k2, σ1	−116.3776	−112.7045	−126.4998
k2, σ2	−117.0791	−116.5468	−123.0667
k1, σ1	−119.5159	−115.9592	−129.5881
k1	−121.2097	−118.7266	−131.3981
k2	−112.8502	−118.0780	−123.6566
σ1	−109.4387	−117.5543	−121.4832
σ2	−105.5674	−117.0642	−118.7197
c	−107.0072	−117.0223	−116.9831

Allowing the gain of the local component, k₁, to be the sole free parameter consistently resulted in the lowest AICc value (in bold).

To estimate the confidence intervals for the parameters in the generalization function, we performed a bootstrap analysis with 10³ iterations to estimate the variability of the parameter values associated with the subject-average data. For each iteration, we randomly selected 12 subjects with replacement and computed corresponding fits based on this selection. Here the ± ranges represent the 95% confidence limits.

RESULTS

Temporal decay of visuomotor adaptation.

We first trained subjects to make reaching movements when a rotation was applied to the terminal visual feedback of the unseen reaching motion (Fig. 1, A and B). Each subject experienced only one type of rotation (CW or CCW) of the visual feedback after an initial baseline period. Blank no-visual-feedback trials were used to quantify the extent to which adaptation was retained after different amounts of delay (see materials and methods). On the basis of these no-visual-feedback trials, we were able to determine the angular deviation of the reaching movement and compared that to the deviation at the end of the retraining block (see materials and methods). Similar to previous studies (Taylor et al. 2011), we observed a fast progression of adaptation early on (within the first 20 trials) that plateaued after ~50 trials (Fig. 2A). During baseline, the percentage of adaptation was 0.5 ± 0.2% and not significantly different from zero (P = 0.43). The amount of adaptation quickly increased; at the end of training the percentage of adaptation was significantly greater than at the beginning (20.2 ± 2.0% compared with 91.1 ± 0.3%, mean ± SE, P < 0.01, paired 2-tailed t-test). (The early adaptation period was determined over trials 1–5, while the late/asymptotic adaptation period was trials 105–120.)

To examine the effect of the time delay on the temporal retention of motor recalibration in response to the feedback perturbation, subjects were given hold periods of variable durations (0, 3, 6, 10, 20, 30, 60, and 120 s). During these hold periods subjects held the handle and maintained the cursor in the start target until the go signal, the appearance of the reach target. The duration of the hold period was randomly chosen such that each delay was tested four times in the experimental session. After the no-visual feedback probe trial to assess retention, subjects were retrained in the motor recalibration with 5–10 adaptation trials with end-point visual feedback (Fig. 1D). We assessed retention of visuomotor adaptation by comparing the average angular deviation over the last three retraining trials to the angular deviation on the no-visual feedback probe trial (see materials and methods). We found that over the course of 2 minutes the angular deviation applied to the reaching movement systematically decayed (Fig. 2B). When we examined the relationship between the adaptation retention and the duration of the delay period, we found that the delay length had a significant effect (1-way ANOVA, P < 0.01). At the shortest delay (Δt = 3 s), subjects applied a rotation to the movement vector that was not significantly different from the amount of recalibration during retraining (mean % of retention of 95.0 ± 2.5%, P = 0.08). However, similar to the results of Smith and colleagues (Sing et al. 2009; Hadjiosif et al. 2012), at the longer delay periods the temporal decrease in the retention of adaptation was only partial: adaptation decayed a total of 29.0 ± 6.8% at Δt = 120 s, with very little additional decay occurring beyond 30 s (Fig. 2B). More specifically, the decay in retention was significant from 0 to 15 s (14.9 ± 3.7% decay, P < 0.05) and 30 s (23.3 ± 6.1% decay, P < 0.01) but not significant from 30 s to 120 s (5.7 ± 2.1% decay from 30 to 120 s, P = 0.31, corrected for multiple comparisons). The pattern of temporal decay was well fit by a single exponential curve with an offset and decay term (black dashed line in Fig. 2B; R² = 0.99). This fit revealed a time constant, τ_Temporal, of 22.5 ± 5.6 s, suggesting that only a portion of the learned motor adaption is dependent on the passage of time.

Using this temporal relationship, we simulated the expected generalization patterns to different target directions (19 directions, separated by 15°, spanning ±135° from the trained direction of 90°) for different delays in the reaching motion. (For simplicity we now refer to the trained target direction as 0° and classify other movement trajectories relative to this direction.) We represented the spatial transfer as summation of two Gaussian functions, one representing a local component and another representing a global component (Fig. 2C). Both components depend on the magnitude of adaptation (local k₁ and global k₂) at the peak movement direction (θ₀), an offset term for the global transfer applied across the workspace (c), and the width of the respective components (local ${\sigma }_1$ and global ${\sigma }_2$) (see materials and methods; Brayanov et al. 2012; Hadjiosif and Smith, 2013; McDougle et al. 2017). Figure 2D depicts these generalization relationships if the temporal decay is applied at the trained movement direction (k₁). That is, keeping all the model parameters constant (k₂ = 27.7 ± 8.5%, θ₀ = 0°, c = 25.2 ± 2.4%, ${\sigma }_1$ = 9.9 ± 3.0° and ${\sigma }_2$ = 37.1 ± 10.1°), we scaled k₁ (30.2 ± 10.6%) by the proportion of the adaptation retention estimated in Fig. 2B. (Note that the values for the simulated fit in Fig. 2D were estimated from the average generalization data in Fig. 3B. We normalized the data to ensure that there was initially 100% transfer at the trained target.) We used three different delay periods (4.4, 12.0, and 24.6 s) depicted as the blue, red, and green regions in Fig. 2B. Based on the exponential fit these delays resulted in percent adaptation retention of 94.9%, 87.8%, and 80.5%, respectively. (Note that we chose these delay values based on the generalization experiment described below.) In this case, only the transfer local (±15°; see Fig. 2D, inset) to the trained target location (0°) appreciably decreases with delay, with less of an overall approximately constant transfer across these delays for target locations beyond this range. We next conducted an experiment to determine these spatiotemporal properties of the adaptation generalization.

Temporal influence on generalization of visuomotor adaptation.

To determine the influence of the delay on the spatial generalization of adaptation, we designed an experiment that iteratively retrained the motor recalibration and then probed the extent of transfer. Similar to the temporal decay experiment, we first trained subjects in the visuomotor task (Fig. 1). We again observed a fast progression of adaptation early on (within the first 20 trials) that plateaued after ~50 trials (Fig. 3A). Similar to the temporal decay experiment, the percentage of adaptation during baseline in the intralimb spatial generalization experiment was not significantly different from zero (0.8 ± 0.2%, P = 0.16). This amount increased quickly during training; the amount of adaptation at the end of training was significantly greater than at the beginning (18.6 ± 1.9% compared with 92.8 ± 0.2%, mean ± SE, P < 0.01, 2-tailed t-test). Again, in the intralimb spatial generalization experiment the early adaptation period was determined over trials 1–5, while the late/asymptotic adaptation period was trials 105–120. Importantly, we observed no difference in the amount of overall adaptation at the end of training compared with the temporal decay experiment, (P = 0.23, 2-tailed t-test).

We examined transfer to the 19 probe targets (separated by 15°, spanning ±135° from the trained direction, 0°; Fig. 1C). Similar to the retraining and probe sequence used in the temporal experiment, we probed adaptation transfer to 6 of the 19 different target locations after retraining in the motor recalibration (see materials and methods; Fig. 1D). After the no-visual feedback generalization probe trials to assess transfer, subjects were retrained in the motor recalibration with five to seven adaptation trials with end-point visual feedback. We assessed transfer of visuomotor adaptation by comparing the average angular deviation over the last three retraining trials to the angular deviation on the blank generalization probe trials (see materials and methods). Figure 3B shows the generalization results for the entire experimental session, and we fit a two-component spatial generalization model to capture the spatial properties of the transfer (see Eq. 1).

As described in materials and methods, we next distinguished three different time ranges within the generalization probe period (4.4 ± 1.6, 12.0 ± 4.2, and 24.6 ± 8.6 s; ± ranges represent the 95% confidence limits) and, based on the blank generalization probe trials that fell within these ranges, determined the percentage of transfer for each movement direction within each temporal range. The respective generalization curves for these three ranges are shown in Fig. 3, C–E (for 4.4 ± 1.6, 12.0 ± 4.2, and 24.6 ± 8.6 s, respectively). As with the entire data set (Fig. 3B), the two-component spatial generalization model was a sufficient representation of the spatial change in the transfer of adaptation for each temporal range (R² ≥ 0.93 for all cases). For reference, the generalization function over the entire experimental session is shown as the dashed black line in each panel. As displayed in the respective panels, the peak of the generalization for the smallest delay was above the average generalization curve, while the transfer at the longest delay was below. Generalization for the middle delay period closely matched the function when applied over the entire experimental session (black dashed line). We systematically tested the various parameters of the model and found that allowing only the magnitude of adaptation for the local component (k₁) to vary captured the temporal changes in generalization (see Table 1). Keeping all other variables fixed to the values based on the average data (Fig. 3B; k₂ = 27.7 ± 8.5%, θ₀ = 0°, c = 25.2 ± 2.4%, ${\sigma }_1$ = 9.9 ± 3.0°, and ${\sigma }_2$ = 37.1 ± 10.1°), we determined the value of k₁ for the different delay values (46.6 ± 7.2%, 25.4 ± 7.7%, and 18.7 ± 5.5% for 4.4 ± 1.6, 12.0 ± 4.2, and 24.6 ± 8.6 s, respectively). There was an ∼60% decrease in the scaling term between the delays of 4.4 and 24.6 s. Collectively, these results suggest that the percentage of adaptation applied across the different movement directions remained near constant with delay, while the percentage of transfer near the peak movement direction decreased with the passage of time.

Spatial differences in temporal decay of adaptation transfer.

A comparison of the respective fits to the generalization data is shown in Fig. 3F. As suggested by the simulations in Fig. 2C, the overall amount of decay with time is greatest at the trained target direction, 0°. Transfer to other movement directions was modulated by the time delay, but this modulation appears very local around the trained target location (within ±15° of the trained direction). Additionally, based on the fitted generalization curves, the transfer to targets beyond 45° was approximately constant across the different movement directions and temporal delays. To quantify these spatial differences in the influence of the temporal delay, we first compared the amount of transfer at each movement direction for each delay condition to determine whether there were any significant asymmetries (leftward vs. rightward). For the shortest and longest delays (Fig. 3, C and E) we found that there was a main effect of movement direction on the percentage of transfer but not a main effect of workspace location (leftward vs. rightward) (2-way ANOVA, P < 0.001 for main effect of movement direction and P > 0.26 for main effect of workspace location). On the other hand, for the middle delay (Fig. 3D) we found that there was a main effect of movement direction and workspace location on the percentage of transfer (2-way ANOVA, P < 0.001 for main effect of movement direction and P < 0.05 for main effect of workspace location). Examining the middle delay more closely, we found that only one movement direction was significantly different between the left and right workspace (the movement angle of 120°, P < 0.03). All other directions were not significantly different between the two workspace locations (P > 0.19). Because only one of the nine movement angles demonstrated a significant difference in the percent transfer (for only 1 of the 3 different delays examined), we grouped the transfer across workspace locations within each delay condition to determine the spatiotemporal differences in transfer across the absolute distances from the trained target direction.

In Fig. 3G we show how the percentage of adaptation transfer changed as a function of the delay period across the absolute distance from the trained reach direction. That is, we grouped the transfer across leftward and rightward directions (e.g., we combined the transfer for −15° and 15° together). As suggested in Fig. 3, C–E, there is a clear difference in transfer at the trained target and transfer to targets 15° away. This difference between the delay conditions decreases at reach directions of 30° and 45° and is absent for reach directions >60°. We fit a simple exponential to the decay of the percent transfer across the absolute reach directions for each delay condition (spatial constants for the delay of 4.4 s: 27.5 ± 8.9°, 12.0 s: 30.1 ± 12.8°, 24.6 s: 39.1 ± 17.5°). Consistent with Fig. 3F, there was an increase in the spatial extent to which the delay influenced the transfer of adaptation, but this temporal influence was within a very narrow range of the trained reach direction (~30–40°).

As shown by the results presented in Fig. 3, there is a clear but restricted spatial range over which there is an influence of temporal delay on the transfer of adaptation. Next, we distinguished which movement directions were significantly influenced by the temporal delay. We found that there was a significant effect of delay at the trained target and transfer to targets 15° away (1-way ANOVA, P < 0.05 in both cases). Conversely, we found that there was not a significant effect of delay for transfer to targets ≥30° away (1-way ANOVA, P > 0.40 in all cases). In light of this difference we closely examined the temporal decay of adaptation transfer within ±15° of the trained target direction and outside of this range. In Fig. 4A we plot the percent transfer across time for the two movement directions at which we found a significant effect of delay (0° and 15°). The amount of adaptation transfer was significantly greater at 0°, and transfer was significantly different across time for both directions (2-way ANOVA, P < 0.001 for main effect of movement direction and P < 0.001 for main effect of delay). For each case we fit simple exponential functions to the percentage of transfer across the delay periods. The time constant of the exponential increased as a function of distance away from the trained target direction: τ₀ = 3.8 ± 5.2 s and τ₁₅ = 5.7 ± 13.7 s.

In Fig. 4B we plot the percent transfer across time for intermediate movement directions (30° and 45°). The amount of adaptation transfer was not significantly different between the two movement directions or across time (2-way ANOVA, P = 0.1 for main effect of movement direction and P = 0.85 for main effect of delay). However, the amount of adaptation transfer for these two directions was significantly different from directions local (within ±15°) and distant from the trained target direction (60–135°) (P < 0.01, corrected for multiple comparisons). The change in transfer over the delay period for these intermediate distances was well described as a linear function (30°: slope of −0.002; 45°: slope of −0.0006). The slopes in both cases were not significantly different from zero, suggesting that for this range of movement directions the percentage of transfer was not only distinct from local and distant targets but also near constant across time (P > 0.31 in both cases).

Figure 4C plots the percent transfer across time for distant movement directions (60°, 75°, 90°, 105°, 120°, and 135°). As observed for the intermediate movement directions of 30° and 45°, the amount of adaptation transfer was not significantly different across time. However, unlike the intermediate movement directions, transfer was not significantly different across the movement directions (2-way ANOVA, P = 0.2 for main effect of movement direction and P = 0.79 for main effect of delay). For each case we performed a linear regression of the percentage of transfer across the delay periods. The slope in each case was not significantly different 1) from zero or 2) between the different movement directions, suggesting that for this range of movement directions the percentage of transfer was near constant across time and space (P > 0.65 in all cases). Note that although we see significant spatial and temporal differences between these three groupings, this does not necessarily mean that there are three distinct mechanisms underlying generalization. As described above, the finding that the magnitude of adaptation for the local component, k₁, explains the temporal differences in the generalization patterns suggests that these relative spatial and temporal changes may be simply attributed to the target/movement proximity to the trained direction.

We were also interested in the retention of adaptation at the trained target. That is, did the decay in the amount of retention based purely on the passage of time match the decay when subjects made several movements to other targets within the same time period? Interestingly, the decrease in the retention at the trained target location (0° in Fig. 3) was faster in the generalization experiment than when subjects were instructed to hold at the start location for the same amount of time (Fig. 5). (Note that in Fig. 3 we represent movements in the trained 90° direction as 0° for simplicity. Thus the comparison of the two experiments in Fig. 5 is for movements in the 90° direction. In addition, because of the across-subject variability in the timing of the probe movements, we grouped the data in the generalization experiment by delay amount rather than the number within the sequence. Thus, as in Fig. 3, the three points in Fig. 5 represent the three delay groups: 4.4 ± 1.6, 12.0 ± 4.2, and 24.6 ± 8.6 s.) The time constant of the decay in the generalization experiment was 3.8 ± 5.2 s, whereas the time constant of the temporal decay was 22.5 ± 5.6 s—an approximate sixfold increase when movements were not executed during the same time frame. This suggests that the movements made within the same temporal window actively contributed to the reduction of the memory of the motor recalibration. However, because of the pseudorandom selection of the probe movements (see materials and methods) it is not possible within the present data set to determine whether the direction of the movements (e.g., in the trained vs. untrained movement direction) plays a differential role in this decay process.

Fig. 5.

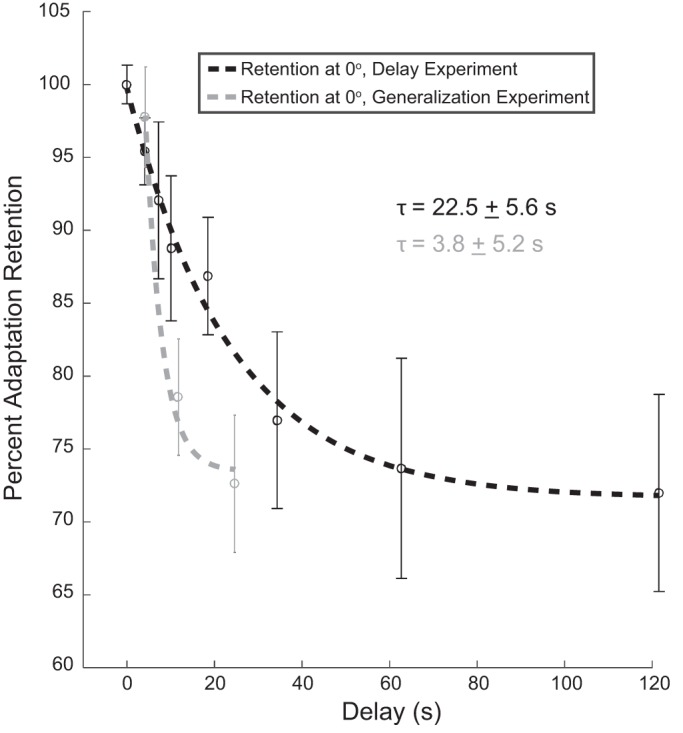
Differences in decay rate of visuomotor adaptation retention at the trained target direction. Data from Fig. 2B (decay with the passive passage of time, black dashed line and symbols, n = 12) are plotted with the decay of adaptation at the trained target direction during the generalization experiment from Fig. 4A (movement-dependent active decay combined with passive passage of time decay, gray dashed line and symbols, n = 32). As in Figs. 2B and 4, delay represents the average time before the movement was executed. Because of the across-subject variability in the timing of the probe movements, we grouped the data in the generalization experiment by delay amount rather than the number within the sequence. These delays were divided into 3 groups (4.4 ± 1.6, 12.0 ± 4.2, and 24.6 ± 8.6 s). Circles represent the average across subjects, and vertical bars represent SE. The time constant for the purely temporal case (black dashed line) is 22.5 ± 5.6 s. The time constant of the decay of adaptation retention during the generalization experiment (gray dashed line) is 3.8 ± 5.2 s.

DISCUSSION

Numerous studies have investigated the spatial extent of visuomotor adaptation generalization (Berniker et al. 2014; Brayanov et al. 2012; Fernandes et al. 2014; Krakauer et al. 2000; Taylor et al. 2013). By examining the average transfer, one common assumption across these studies is that the transfer of adaptation is stable, across both successive trials and time. However, there is also evidence that visuomotor adaptation decays from trial to trial and with the passage of time, challenging this assumption (Cohen et al. 2004; Fernández-Ruiz et al. 2004; Hadjiosif et al. 2012; Inoue et al. 2015; Kitago et al. 2013; Rubin and Wenzel 1996; Scheidt et al. 2000). In this study we determined the influence of the passage of time on the spatial generalization of visuomotor adaptation. In experiment 1, we assessed the temporal decay of adaptation over the course of 2 minutes. Similar to a previous study (Hadjiosif et al. 2012), we found that the adaptation decayed with a time constant of 22.5 ± 5.6 s. On the basis of these results we hypothesized how the spatial transfer would be modified by the passage of time. In experiment 2, we tested this hypothesis by assessing the spatial generalization for different temporal intervals. We found that as the delay increased there was a decrease in the percentage of transfer to movement directions local to the trained adaptation direction (≤|15°|). However, the temporal influence beyond this spatial range was minimal, with a near-constant transfer of the adaptation across both time (between ~4 and 25 s) and space (60–135° away from the trained movement direction). Similar to distant targets, intermediate distances (30° and 45°) showed constant transfer across time but, as observed for local targets, the amount of transfer was influenced by the movement direction; although there was not a significant difference in the amount of transfer between these two directions, this amount was significantly different from the local and distant reach directions. In addition, the temporal decay of the adaptation at the trained movement direction was faster when multiple movements to other targets were performed within the same time window, suggesting that in addition to the passage of time these actions contributed to the decay of the motor memory.

Decay and transfer of different learning mechanisms.

One question the present results raise is why the temporal decay of adaptation transfer is only observed for movements within a small region around the trained target. A possible explanation may be found in recent work examining the different learning mechanisms that underlie visuomotor adaptation to altered visual feedback. Previous work by Taylor and colleagues (Taylor et al. 2014) has distinguished the contribution of concurrent explicit and implicit learning processes during the adaptation to altered visual feedback. Explicit learning is assessed by the intended/reported aiming direction and is updated by the target error: the difference between the actual consequences of the movement (in this case the displayed cursor position) and target location. Alternatively, implicit learning is driven by the sensed difference between the expected and actual consequences of movement (the cursor location). The resulting sensory prediction error is theoretically used to update the internal model that predicts the expected movement consequences.

Based on this framework, a recent study by Day et al. (2016) examined the portion of implicit learning that transferred to different spatial locations. Specifically, the authors asked whether this generalization was centered on where subjects intended to reach (the aim of the movement) or where the cursor moved (the target). The results suggested that generalization was centered on the location at which subjects most frequently aimed (the explicitly reported movement plan) and not the target location. Similar to the present results, generalization in this study was also local (±15°), with approximately constant transfer to farther target locations. [Note that the generalization pattern was in fact asymmetric, but this may be due to not counterbalancing the rotation direction. Although the examination of only one rotation direction was justified in Day et al. (2016), it is likely that averaging across opposing perturbation directions (as in the present study; see the process to determine the percentage of adaptation transfer in materials and methods) would produce symmetric generalization around the trained direction similar to Fig. 3.]

In a follow-up study McDougle et al. (2017) finely assayed the spatial generalization of implicit and explicit learning (over 360° in steps of 22.5°). Here implicit learning was found to transfer in a Gaussian manner (average width, σ, of 37.76°), while explicit learning was applied approximately uniformly/globally over the workspace, ±180° (see also Heuer and Hegele 2011). Interestingly, the shapes of the local implicit and global explicit components of the generalization are similar to the components of the model we used to capture the spatial generalization in the present study (see materials and methods and Fig. 2C). In fact, the authors state that the global explicit component may not be a uniform offset but perhaps also Gaussian in shape.

Miyamoto et al. (2014) examined the temporal stability of implicit learning concurrent with an explicit strategy in a similar motor adaptation experiment. The authors were specifically interested in the temporal stability in order to probe the error signals that respectively drove the different learning components. On each trial the authors required the subjects to select an aiming direction strategy for the reaching movement. Importantly, during training the location of the target was shifted by a small, random angle (0 ± 3°), requiring subjects to readjust the aiming direction. This served as a way to assess whether the subjects were actively considering the aim point they reported. One-minute breaks were inserted between the blocks of trials used to assess the learning aftereffects in order to determine the temporal stability of the different components. These breaks allowed the authors to eliminate temporally labile components of learning and measure the remaining temporally stable learning during the subsequent probe period. In the following probe period subjects made movements without visual feedback to targets presented at 1 of 19 different directions (−135° to 135° around the trained target direction every 15°). Interestingly, by decomposing the motor adaptation into temporally stable and temporally labile components, the authors found that explicit learning was largely stable over the break while implicit learning reflected both temporally stable and temporally labile mechanisms.

In light of the McDougle et al. (2017) and Miyamoto et al. (2014) results above, it is possible that the local range where we see temporal decay mostly involves temporally labile implicit learning. Rather than largely diminishing its contribution as in Miyamoto et al. (2014), the temporal intervals used in the present study (~4–25 s compared with 1 min) may moderately decrease the local implicit learning. However, over the same intervals the global temporally stable explicit learning would be largely unaffected. Therefore, it is possible that there is a trade-off of explicit and implicit learning processes to these local and distant movement directions, and perhaps an associated change in the temporal stability of the respective transfer. However, we should state that in our study we did not 1) directly evaluate the contributions of explicit and implicit learning to the generalization or 2) instruct subjects to make a distinct plan before movement (see materials and methods). Therefore, these connections are purely hypothetical based on the present and previous behavioral results. Rigorous future experiments must be conducted to determine the true spatiotemporal relationships of these different learning mechanisms.

Alternatively, the adaptation transfer could involve the differential remapping of features of the movement plan: the target (goal) location and movement vector. Possibly the most complete model-based description of this remapping was provided in a recent study by Wu and Smith (2013). The authors posit that visuomotor adaptation can be described as a weighted combination of the remapping of three separable components: the movement start location, movement vector, and movement goal location. It is possible that these components of visuomotor adaptation (goal location, start location, movement vector) could demonstrate different levels of temporal stability and transfer (Wu and Smith 2013). However, 1) the extent to which these learning mechanisms generalize to other target locations and 2) the temporal stability of each component are currently unknown. In light of the evidence above it would be interesting to determine the spatiotemporal properties of these different learning mechanisms in relation to the spatial transfer of adaptation.

Active vs. passive decay of motor adaptation.

The decay of motor adaptation has been shown to occur with 1) the removal of the perturbation feedback (movement error) and 2) the passage of time. This suggests that there is a complex interaction between active, movement-based decay (Cohen et al. 2004; Fernández-Ruiz et al. 2004; Ingram et al. 2013; Inoue et al. 2015; Scheidt et al. 2000) and passive temporal-based fading of the motor memory (Cohen et al. 2004; Fernández-Ruiz et al. 2004; Hadjiosif et al. 2012; Huang and Shadmehr 2007; Rubin and Wenzel 1996). Recently, Kitago and colleagues (Kitago et al. 2013) examined the decay of visuomotor adaptation for different types of assessments, including the passage of time and when the movement errors were visually clamped to zero. Similar to the present results, the slowest decrease in adaptation level occurred with the passage of time (Fig. 5); in the present study the decay of adaptation at the trained target location was faster when subjects made nonfeedback movements than when subjects waited for the same duration of time (time constant of 3.8 ± 5.2 vs. 22.5 ± 5.6 s). This suggests that the movements made within the same time frame exerted an additional influence on the stability of the motor memory.

Although studies have varied in experimental techniques and computational approaches, there is consensus that short-term motor adaptation is the culmination of different learning mechanisms operating along multiple timescales (Criscimagna-Hemminger and Shadmehr 2008; Inoue et al. 2015; Joiner and Smith 2008; Kording et al. 2007; Mawase et al. 2014; McDougle et al. 2015; Smith et al. 2006). The finding that single exponentials sufficiently describe the decay of adaptation at the trained target may seem at odds with different learning mechanisms operating along multiple timescales (Fig. 5). However, because of the various mechanisms, properties, and timescales involved, the stability of adaptation is often differentially affected by the passage of time. For example, Sing et al. (2009) hypothesized that there is an interaction of temporally labile and temporal stable learning mechanisms (represented by fast and slow learning processes; Smith et al. 2006) that compete during adaptation. The temporally labile fast learning process decreases with the passage of time (passive decay) but remains stable over consecutive movements executed without the error feedback (active decay). In contrast, the temporally stable slow component is not modified with the passage of time but decreases with active decay. Thus such a multitimescale framework may account for the decay in the present results (Fig. 5). That is, the slower decay of adaptation at the trained target with the passage of time may represent simply the stability of the temporally labile fast process, while the faster decay that accompanies the concurrent probe movements may reflect the combined fading of both the slow and fast learning mechanisms.

The multitimescale framework may also provide some insight into the temporal modification of spatial generalization (Fig. 3). As described above, the decay of the fast (with the passage of time) and slow (with the sequences of generalization probe movements) learning processes may modify the shape of the generalization pattern (through the gain at the trained target), largely influencing transfer local to the trained direction (Tanaka et al. 2012). This assumes that the influence of the two processes is confined to a local component of generalization. Utilizing the multitimescale framework, it would be interesting to quantify the amount of passive (fast process) and active (slow process) decay and how their combined interaction influences the spatiotemporal generalization patterns reported here. For example, in the present study the generalization probe movement directions were selected pseudorandomly, resulting in a number of different movement sequences before the target location was probed for adaptation retention (see materials and methods). In our future studies we plan to examine the extent to which, within a given time frame, the number of movements and where the movements are directed (the context of the movements—in the trained vs. untrained movement direction; Ingram et al. 2013) influence the magnitude of the overall motor memory decay and subsequent transfer. Such systematic experiments may be able to bridge two common, but largely separate frameworks (multitimescale models and Gaussian spatial generalization models) used to describe motor adaptation.

Potential neural mechanisms during passive and active motor adaptation decay.

There are ample behavioral, patient, neurostimulation, and neurophysiological data that support the partially dissociable roles of the cerebellum and posterior parietal and motor cortices during the adaptation, retention, and generalization of motor adaptation to rotated visual feedback (Della-Maggiore and McIntosh 2005; Diedrichsen et al. 2005; Galea et al. 2011; Hadipour-Niktarash et al. 2007; Inoue et al. 2000; Krakauer et al. 2004; Paz et al. 2003; Paz and Vaadia 2004; Tseng et al. 2007; Wise et al. 1998; Yavari et al. 2016). Centered on the evidence noted above, Tanaka et al. (2009) proposed that this short-term motor recalibration is initiated by a sensory prediction error initially formed in the cerebellum. This error signal then modulates neurons in the posterior parietal and motor cortices, with an adjustment of the respective synaptic weights to reduce the sensory prediction error. These collective neural modulations eventually result in a remapping between the movement reach trajectory and the cursor movement direction. Corresponding to this organization, Kitago et al. (2013) hypothesized that a cerebellum-based mechanism could explain the active decay of motor adaptation in the absence of feedback. The authors posit that when no sensory feedback is available to validate the sensory prediction made by the cerebellum there is a reduction in complex spikes but an increase in the generation of movement-related simple spike activity. The simultaneous lack and occurrence of these respective signals could induce synaptic changes (e.g., long-term potentiation) that are comparable both when error feedback is present and when performance is presumed perfect, as is the case when errors are visually clamped to zero. In both cases (no feedback and clamped feedback), the synaptic changes and subsequent decay of the remapping require movement. Presumably, there could be a reduction in these synaptic changes with the passage of time, but this decay would potentially be slower compared with the movement-induced decay from the presence of simple spikes and concurrent absence of complex spikes. One hypothesis would be that cerebellar disruption immediately following training would limit the spatial generalization of adaptation, but this has yet to be systematically tested, at least in the comparison of temporal vs. movement-dependent influences (see Yavari et al. 2016).

Conclusions.

We investigated the influence of the passage of time on the spatial generalization of visuomotor adaptation. We found that transfer local to the trained direction (within ±15° of the adaptation direction) decayed across time (between ~4 and 25 s) and distance. Transfer to targets located at an intermediate distance (30° and 45°) showed a difference in transfer to other movement directions, but this generalization was constant across time. Finally, generalization to targets beyond this range (60–135° away from the trained direction) was near constant across both time and space. In light of previous studies, these differences in the spatiotemporal features of transfer suggest the possible involvement of different learning mechanisms (implicit vs explicit) or alternatively the differential remapping of movement variables (the movement goal or vector). In addition, the finding that the decay of adaptation at the trained target was six times faster than that estimated by the decay over time suggests that there are both active (movement dependent) and passive (temporal dependent) processes involved in the stability of this local component. Future work will focus on the extent to which these respective learning mechanisms influence the spatial properties and temporal stability of motor adaptation transfer.

GRANTS

This work was supported by grants from the National Eye Institute (EY-021252) and the National Science Foundation (1553895) to W. M. Joiner.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

W.Z., J.F., K.C.-C., and K.G.M. analyzed data; W.Z., J.F., and W.M.J. prepared figures; W.Z. and W.M.J. drafted manuscript; W.Z., K.G.M., and W.M.J. edited and revised manuscript; W.Z., J.F., K.C.-C., K.G.M., and W.M.J. approved final version of manuscript; J.F. and W.M.J. conceived and designed research; J.F., K.C.-C., and K.G.M. performed experiments; J.F. and W.M.J. interpreted results of experiments.