Deep Learning Based Binaural Speech Separation in Reverberant Environments

Abstract

Speech signal is usually degraded by room reverberation and additive noises in real environments. This paper focuses on separating target speech signal in reverberant conditions from binaural inputs. Binaural separation is formulated as a supervised learning problem, and we employ deep learning to map from both spatial and spectral features to a training target. With binaural inputs, we first apply a fixed beamformer and then extract several spectral features. A new spatial feature is proposed and extracted to complement the spectral features. The training target is the recently suggested ideal ratio mask. Systematic evaluations and comparisons show that the proposed system achieves very good separation performance and substantially outperforms related algorithms under challenging multi-source and reverberant environments.

I. INTRODUCTION

EVERYDAY listening scenarios are complex, with multiple concurrent sound sources and their reflections from the surfaces in physical space. Separating the target speech in such an environment is called the ”cocktail party problem” [6]. A solution to the cocktail party problem, also known as the speech separation problem, is important to many applications such as hearing aid design, robust automatic speech recognition (ASR) and mobile communication. However, speech separation remains a technical challenge despite extensive research over decades.

Since the target speech and background noise usually overlap in time and frequency, it is hard to remove the noise without speech distortion in monaural separation. However, the speech and interfering sources are often located at different positions of the physical space, one can exploit the spatial information for speech separation by using two or more microphones.

Fixed and adaptive beamformers are common multi-microphone speech separation techniques [29]. The delay-and-sum beamformer is the simplest and most widely used fixed beamformer, which can be steered to a specified direction by adjusting phases for each microphone and adds the signals from different microphones. One limitation of a fixed beamformer is that it needs a large array to achieve high-fidelity separation. Compared with fixed beamformers, adaptive beamformers provide better performance in certain conditions, like strong and relatively few interfering sources. The minimized variance distortionless response (MVDR) [10] beamformer is a representative adaptive beamformer, which minimizes the output energy while imposing linear constraints to maintain energies from the direction of the target speech. Adaptive beamforming can be converted into an unconstrained optimization problem by using a Generalized Sidelobe Canceller [12]. However, adaptive beamformers are more sensitive than fixed beamformers to microphone array errors such as sensor mismatch and mis-steering, and to correlated reflections arriving from outside the look direction [1]. The performance of both fixed and adaptive beamformers diminishes in the presence of room reverberation, particularly when target source is outside the critical distance at which direct-sound energy equals reverberation energy.

A different class of multi-microphone speech separation is based on Multichannel Wiener Filtering (MWF), which estimates the speech signal of the reference microphone in the minimum-mean-square-error sense by utilizing the correlation matrices of speech and noise. In contrast to beamforming, no assumption of target speech direction and microphone array structure needs to be made, while exhibiting a degree of robustness. The challenge for MWF is to estimate the correlation matrices of speech and noise, especially in non-stationary noise scenarios [26].

Another popular class of binaural separation methods is localization-based clustering [22] [38]. In general, two steps are taken. The localization step is to build the relationship between source locations and interaural parameters, such as interaural difference (ITD) and interaural level difference (ILD), in individual time-frequency (T-F) units. The separation step is to assign each T-F unit into a different sound source by clustering or histogram picking. In [22], these two steps are jointly estimated by using an expectation-maximization algorithm.

Although studied for many years, binaural speech separation is still a challenging problem, especially in multi-source and reverberant conditions. In contrast, the human auditory system is capable of extracting an individual sound source from a complex mixture with two ears. Such perceptual organization is called auditory scene analysis (ASA) [2].

Inspired by ASA, computational auditory scene analysis (CASA) [31] aims to achieve source separation based on perceptual principles. In CASA, target speech is typically separated by applying a T-F mask to the noisy input. The values of this mask indicate how much energy of a corresponding T-F unit should be retained. The value of the ideal binary mask (IBM) [30] is 1 or 0, where 1 indicates that the target signal dominates the T-F unit and unit energy is entirely kept, and 0 indicates otherwise. Speech perception research shows that IBM separation produces dramatic improvements of speech intelligibility in noise for both normal-hearing listeners and hearing-impaired listeners. In this context, it is natural to formulate the separation task as a supervised, binary classification problem where the IBM is aimed as the computational goal [30]. In the binaural domain, this kind of formulation is first done by Roman et al. [24], in which a kernel density estimation method is used to model the distribution of the ITD and ILD features and classification is done in accordance with the maximum a posterior (MAP) decision rule.

Treating speech separation as a supervised learning problem has become popular in recent years, particularly since deep neural networks (DNNs) were introduced for supervised speech separation [32]. Extensive studies have been done on features [33], training targets [15] [34–37] and deep models [15] [32] [36] [39] in the monaural domain. Compared with the rapid progress in monaural separation, the studies on supervised binaural separation are few. Recently, however, Jiang et al. [17] extract binaural and monaural features and train a DNN for each frequency band to perform binary classification. Their results show that even a single monaural feature can improve separation performance in reverberant conditions when interference and target are very close to each other.

In this study, we address the problem of binaural speech separation in reverberant environments. In particular, we aim to separate reverberant target speech from spatially diffuse background interference; such a task is also known as speech enhancement. The proposed system is supervised in nature, and employs DNN. Both spatial and spectral features are extracted to provide complementary information for speech separation. As in any supervised learning algorithm, discriminative features play a key role. For spectral feature extraction, we incorporate a fixed beamformer as a preprocessing step and use a complementary monaural feature set. In addition, we propose a two-dimensional ITD feature and combine it with the ILD feature to provide spatial information. Motivated by recent analysis of training targets, our DNN training aims to estimate the ideal ratio mask (IRM), which is shown to produce better separated speech than the IBM, especially for speech quality [34]. In addition, we conduct feature extraction on fullband signals and train only one DNN to predict the IRM across all frequencies. In other words, the prediction of the IRM is at the frame level, which is much more efficient than subband classification in [17].

In the following section, we present an overview of our DNN-based binaural speech separation system and the extraction of spectral and spatial features. In Section III, we describe the training target and DNN training methodology. The evaluation, including a description of comparison methods, is provided in Section IV. We present the experimental results and comparison in Section V. We conclude the paper in Section VI.

II. SYSTEM OVERVIEW AND FEATURE EXTRACTION

The proposed speech separation system is illustrated in Fig. 1. Binaural input signals are generated by placing the target speaker in a reverberant space with many other simultaneously interfering talkers forming a spatially diffuse, speech babble. In such an environment, the background noise is non-stationary and diffuse. To separate the target speech from the background noise, the left-ear and right-ear signals are first fed into two modules to extract the spectral and spatial features separately. In the upper module, a beamformer is employed to preprocess the two-ear signals to produce a single signal for spectral feature extraction. In the lower module, the left-ear and right-ear signals are each first decomposed into T-F units independently. Then, cross correlation function (CCF) and ILD are extracted in each pair of corresponding left-ear and right-ear units, and regarded as spatial features. The spectral and spatial features are then combined to form the final input feature. Our computational goal is to estimate the IRM. We train a DNN to map from the final input feature to the IRM. After obtaining a ratio mask from the trained DNN, the waveform signal of the target speech is synthesized from the sound mixture and the mask [31].

Fig. 1.

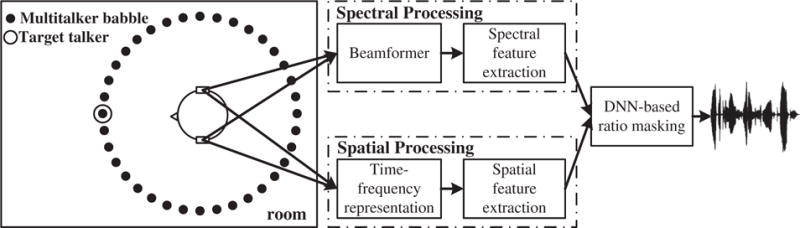
Schematic diagram of the proposed binaural separation system.

A. Spectral Features

We employ the delay-and-sum (DAS) beamformer to process the left-ear and right-ear signals into a single signal before extracting monaural spectral features. Beamforming is a commonly used spatial filter for microphone array processing. As sounds coming from different directions reach the two ears with different delays, this fixed beamformer is steered to the direction of the target sound by properly shifting the signal of each ear and then sums them together. As the noises coming from other directions are not aligned, the sum will reduce their amplitudes relative to the target signal, hence enhancing the target. The rationale for proposing beamforming before spectral feature extraction is twofold. First, beamforming enhances the target signal, and second, it avoids an adhoc decision of having to choose one side for monaural feature extraction, as done in [17] for instance.

After beamforming, we extract amplitude modulation spectrum (AMS), relative spectral transform and perceptual linear prediction (RASTA-PLP) and mel-frequency cepstral coefficients (MFCC). In [33], these features are shown to be complementary and have been successfully used in DNN-based monaural separation. It should be mentioned that the complementary feature set originally proposed in [33] is extracted at the unit level, i.e. within each T-F unit. We extract the complementary feature set at the frame level as done in [34].

B. Spatial Features

We first decompose both the left-ear and right-ear signals into cochleagrams [31]. Specifically, the input mixture is decomposed by the 64-channel gammatone filterbank with center frequencies ranging from 50 Hz to 8000 Hz on the equivalent rectangular bandwidth rate scale. The output of each channel is divided into 20-ms frame length with a 10-ms frame shift and half-wave rectified. With a 16 kHz sampling rate, the signal in a T-F unit has 320 samples.

With binaural input signals, we extract two primary binaural features of ITD and ILD. The ITD is calculated from the normalized CCF between the left- and right-ear signals, denoted by subscript l and r respectively. The CCF of a T-F unit pair, indexed by time lag τ, is defined as,

$$\mathit{CCF}\left(c,m,\tau \right)=\frac{{\displaystyle {\sum }_k{x}_{\mathit{cm},l}\left(k\right)x_{\mathit{cm},r}\left(k-\tau \right)}}{\sqrt{{\displaystyle {\sum }_k{x}_{\mathit{cm},l}^2\left(k\right)}}\sqrt{{\displaystyle {\sum }_k{x}_{\mathit{cm},r}^2\left(k-\tau \right)}}}$$ (1)

In the above formula, τ varies between −1 ms and 1 ms, x_cm,l and x_cm,r represent the left- and right-ear signals of the unit at channel c and frame m, respectively, and k indexes a signal sample of a T-F unit. For the 16 kHz sampling rate, the dimension of CCF is 33. In [17], CCF values are directly used as a feature vector to distinguish the signals coming from different locations.

Here, we propose a new 2-dimensional (2D) ITD feature. The first dimension is the CCF value at an estimated time lag $\stackrel{\sim }{\tau }$, corresponding to the direction of the target speech. The second dimension is the maximum value of CCF, which reflects the coherence of the left and right ear signals, and has been used for selecting binaural cues for sound localization [9]. The reasons for proposing these two features are as follows. The maximum CCF value is used to distinguish directional sources from diffuse sounds. For a directional source, the maximum CCF value should be close to 1, whereas for a diffuse sound it is close to 0. The CCF value at the estimated target direction is to differentiate the target speech and the interfering sounds that come from different directions. Specifically, we have

$$\mathit{ITD}\left(c,m\right)=\left(\begin{array}{c}\mathit{CCF}\left(c,m,\stackrel{\sim }{\tau }\right)\\ \underset{\tau }{max}\mathit{CCF}\left(c,m,\tau \right)\end{array}\right)$$ (2)

ILD corresponds to the energy ratio in dB, and it is calculated for each unit pair as below

$$\mathit{ILD}\left(c,m\right)=10lo{g}_{10}\frac{{\displaystyle {\sum }_k{x}_{cm,l}^2\left(k\right)}}{{\displaystyle {\sum }_k{x}_{cm,r}^2\left(k\right)}}$$ (3)

To sum up, the spatial features in each T-F unit pair are composed of 2D ITD and 1D ILD. We concatenate all the unit-level features at a frame to form the frame-level spatial feature vector. For 64-channel cochleagrams, the total dimension is 192 for each time frame.

III. DNN-BASED SPEECH SEPARATION

A. Training Targets

The ideal ratio mask (IRM) is defined as [34]

$$\mathit{IRM}\left(c,m\right)=\sqrt{\frac{S^2\left(c,m\right)}{S^2\left(c,m\right)+N^2\left(c,m\right)}}$$ (4)

where S²(c, m) and N²(c, m) denote the speech and noise energy, respectively, in a given T-F unit. This mask is essentially the square-root of the classical Wiener filter, which is the optimal estimator in the power spectrum [20]. The IRM is obtained using a 64-channel gammatone filterbank.

As discussed in Sect. I, the IRM is shown to be preferable to the IBM [34]. Therefore, we employ the IRM in a frame as the training target, which provides the desired signal at the frame level for supervised training.

B. DNN Training

A DNN is trained to estimate the IRM using the frame-level features described in Section II. The DNN includes 2 hidden layers, each with 1000 units. We find that this relatively simple DNN architecture is effective for our task. Recent development in deep learning has resulted in new activation functions [7] [13] [23] and optimizers [3] [8]. Here, the rectified linear unit (ReLU) activation function [23] is used for the hidden layers and the sigmoid activation function is used for the output layer. The cost function is mean square error (MSE). Weights of the DNN are randomly initialized. The adaptive gradient algorithm (AdaGrad) [8] is utilized for back propagation, which is an enhanced version of stochastic gradient descent (SGD) that automatically determines a per-parameter learning rate. We also employ the dropout technique [27] on hidden units to avoid overfitting. The dropout rate is 0.5. The total number of training epochs is 100. The batch size is 512.To incorporate temporal context, we use an input window that spans 9 frames (4 before and 4 after) to predict one frame of the IRM.

IV. EXPERIMENTAL SETUP

A. Dataset

For both training and test datasets, we generate binaural mixtures by placing the target speaker in a reverberant space with many interfering speech sources simultaneously. A reverberant signal is generated by convolving a speech signal with a binaural room impulse response (BRIR). In this study, we use two sets of BRIRs. One is simulated by software, called BRIR Sim Set. The other is measured in real rooms, called BRIR Real Set. These sets were generated or recorded at the University of Surrey¹.

The BRIR Sim Set is obtained from a room simulated using CATT-Acoustics modeling software [4]. The simulated room is shoebox-shaped with dimensions of 6m × 4m × 3m (length, width, height). The reverberation time (T60) was varied between 0 and 1 second with 0.1s increments by changing the absorption coefficient of all six surfaces. The impulse responses are calculated with the receiver located at the center of the room at a height of 2 m and the source at a distance of 1.5 m from the receiver. The sound source was placed at the head height with azimuth between −90° and 90° spaced by 5°.

The BRIR Real Set is recorded in four rooms with different sizes and reflective characteristics, and their reverberation times are 0.32s, 0.47s, 0.68s and 0.89s. The responses are captured using ahead and torso simulator (HATS) and a loudspeaker. The loudspeaker was placed around the HATS on an arc in the median plane with a 1.5 m radius between ±90° and measured at 5° intervals.

To generate a diffuse multitalker babble (see [21]), we use the TIMIT corpus [11] which contains 6300 sentences, with 10 sentences spoken by each of 630 speakers. Specifically, 10 sentences of each speaker in the TIMIT corpus are first concatenated. Then, we randomly choose 37 speakers, one for each source location as depicted in Fig. 1. A random slice of each speaker is cut and convolved with the BRIR corresponding to its location. Finally, we sum the convolved signals to form the diffuse babble, which is also non-stationary. The IEEE corpus [16] is employed to generate reverberant binaural target utterances, and it contains 720 utterances spoken by a female speaker. The target source is fixed at azimuth 0^circ, in front of the dummy head (see Fig. 1). To generate a reverberant target signal, we convolve an IEEE utterance with the BRIR at 0^circ. Finally, the reverberant target speech and background noise are summed to yield two binaural mixtures.

For the training and development sets, we respectively select 500 and 70 sentences from the IEEE corpus and generate binaural mixtures using BRIR Sim Set with 4 T60 values of 0s, 0.3s, 0.6s and 0.9s; T60 = 0s corresponds to the anechoic condition. The development set is used to determine the DNN parameters. So, the training set includes 2000 mixtures. The remaining 150 IEEE sentences are used to generate the test set. To evaluate the proposed method, we use three sets of BRIRs to build test sets called simulated matched room, simulated unmatched room and real room. For the simulated matched-room test set, we use the same simulated BRIRs as the ones in the training stage. For the simulated unmatched-room test set, the BRIR Sim Set with T60’s of 0.2s, 0.4s, 0.8s and 1.0s are used. The real-room test set is generated by using BRIR Real Set. The SNR of the mixtures for training and test is set to −5dB, which is the average at the two ears. It means that the SNR at a given ear may vary around −5dB due to the randomly generated background noise and different reverberation times. In SNR calculations, the reverberant target speech, not its anechoic version, is used as the signal.

B. Evaluation Criteria

We quantitatively evaluate the performance of speech separation by two metrics, which are conventional SNR and short-time objective intelligibility (STOI) [28]. SNR is calculated as

$$\mathit{SNR}=10lo{g}_{10}\frac{{\displaystyle {\sum }_t{S}^2\left(t\right)}}{{\displaystyle {\sum }_t{\left(S\left(t\right)-O\left(t\right)\right)}^2}}$$ (5)

Here, S(t) and O(t) denote the target signal and the synthesized one from an estimated IRM, respectively. STOI measures objective intelligibility by computing the correlation of short-time temporal envelopes between target and separated speech, resulting in a score in the range of [0, 1], which can be roughly interpreted as the percent-correct predicted intelligibility. STOI is widely used to evaluate speech separation algorithms aiming for speech intelligibility in recent years.

C. Comparison Methods

We compare the performance of the proposed method with several other prominent and related methods for binaural speech separation. The first kind is beamforming and we choose DAS and MVDR beamformers for comparison. As described earlier, the DAS beamformer is employed as a preprocessor in our system. The MVDR beamformer minimizes the output energy while imposing linear constraints to maintain the energy from the direction of the target speech. Both the DAS and MVDR beamformer need the target DOA (direction of arrival), which should be estimated in general. Because the location of the target speaker is fixed in our evaluation, we provide the target direction to the beamformers, which facilitates the implementation.

The second method is MWF [25]. For this method, the correlation matrices of the speech and noises need to be estimated by using voice activity detection (VAD) and speech detection errors will degrade its performance. To avoid the VAD errors, we calculate the noise correlation matrix from the background noise directly. The same is done for MVDR, which also needs to calculate the noise correlation matrix. Therefore, the actual results for MWF and MVDR are expected to be somewhat lower.

The next one is MESSL [22] that uses spatial clustering for source localization. Given the number of sources, MESSL iteratively modifies Gaussian mixture models (GMMs) of interaural phase difference and ILD to fit the observed data. Across frequency integration is handled by linking the GMMs models in individual frequency bands to a principal ITD.

The fourth comparison method employs DNN to estimate the IBM [17]. First, input binaural mixtures are decomposed into 64-channel subband signals. At each frequency channel, CCF, ILD and monaural GFCC (gammatone frequency cepstral coefficient) features are extracted and used to train a DNN for subband classification. Each DNN has two hidden layers each containing 200 sigmoidal units, which is the same as in [17]. Weights of DNNs are pre-trained with restricted Boltzmann machines. The subband binaural classification algorithm is referred as SBC in the following. It should be mentioned that, even though each DNN is small, SBC uses 64 DNNs.

V. EVALUATION AND COMPARISON

A. Simulated-room Conditions

In this test condition, we intend to evaluate the performance of the proposed algorithm in the simulated rooms, which are divided into two parts: matched and unmatched conditions. As mentioned earlier, for matched-room conditions, test reverberated mixtures are generated by using the same BRIRs as in the training stage, where the T60s are 0.3s, 0.6s and 0.9s. For the unmatched-room conditions, the BRIRs for generating reverberated mixtures are still simulated ones, but the T60s are different from those in training conditions and take the values of 0.2s, 0.4s, 0.8s and 1.0s.The results of STOI and SNR are shown in Table I and Fig. 2, respectively. The “MIX_L” and “MIX_R” refer to the unprocessed mixtures at the left and right ear respectively.

TABLE I.

Average STOI scores (%) of different methods in simulated matched-room and unmatched-room conditions.

	T60	MIXL	MIXR	DAS	MVDR	MWF	MESSL	SBC	PRO.
Matched room	0.0s	58.00	58.04	63.56	63.75	66.86	65.92	63.65	74.66
	0.3s	53.13	52.64	58.61	58.78	64.06	58.66	62.79	74.88
	0.6s	44.08	41.00	50.82	50.84	57.72	51.89	55.08	68.53
	0.9s	44.58	43.31	48.20	48.15	57.38	48.46	53.37	65.39
	Avg.	49.05	49.65	55.30	55.38	61.51	56.23	58.72	70.87
Unmatched room	0.2s	55.28	57.20	61.80	61.91	65.35	60.52	64.68	74.95
	0.4s	47.98	48.82	54.46	54.64	61.21	55.91	59.02	70.40
	0.8s	39.99	41.59	47.06	47.01	56.86	47.12	54.27	65.92
	1.0s	39.05	40.95	45.21	45.01	55.55	46.05	51.64	62.82
	Avg.	45.58	47.14	52.13	52.14	59.74	52.40	57.40	68.52

Fig. 2.

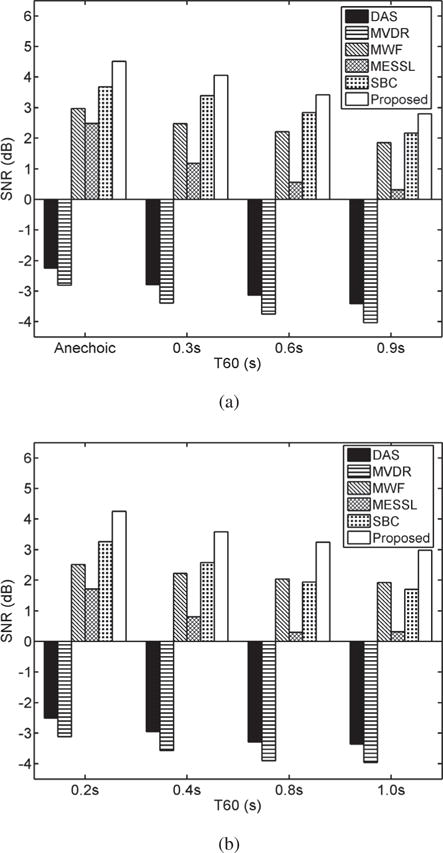
Average SNRs of different methods in simulated room conditions. (a) SNR results in simulated matched-room conditions. (b) SNR results in simulated unmatched-room conditions.

Compared the unprocessed mixtures, the proposed system obtains the absolute STOI gain about 22% on average in the simulated matched-room conditions and 23% in the simulated unmatched-room conditions. From Table I, we can see that the proposed system outperforms the other comparison methods in anechoic and all reverberation conditions. The second-best system is MWF. DAS and MVDR have similar results, because the background noise is quite diffuse; it can be proven that MVDR and DAS become identical when noise is truly diffuse. For the supervised learning algorithms, both SBC and the proposed algorithm exhibit good generalization in the unmatched-room conditions.

As shown in Fig. 2, the proposed algorithm also obtains the largest SNR gains in all conditions. It can be seen that SBC outperforms MWF in the matched-room and less reverberant unmatched-room conditions. The SNR gains obtained by MESSL are much larger than those of DAS and MVDR, while these three methods have similar STOI scores. The main reason is that SNR does not distinguish noise distortion and speech distortion, which affect speech intelligibility in different ways.

B. Real-room Conditions

In this test condition, we use the BRIR Real Set to evaluate the proposed separation system and compare it with other methods. The STOI and SNR results are given in Table II and Fig. 3, respectively. The proposed system achieves the best results in all four room conditions. Compared with unprocessed mixtures, the average STOI gain is about 20% (i.e. from 43% to 63%), which is consistent with that in simulated room conditions.

TABLE II.

Average STOI scores (%) of different methods in real room conditions.

Room	MIXL	MIXR	DAS	MVDR	MWF	MESSI	SBC	PRO.
A (0.32s)	47.49	49.02	53.71	53.84	59.50	54.39	53.37	66.70
B (0.47s)	41.29	42.55	48.10	48.08	55.01	48.61	42.95	61.96
C (0.68s)	44.33	45.06	51.31	50.86	58.39	52.11	54.13	64.78
D (0.89s)	39.61	39.18	45.48	45.58	55.22	45.35	48.52	60.57
Avg.	43.18	43.95	49.65	49.59	57.03	50.12	49.74	63.50

Fig. 3.

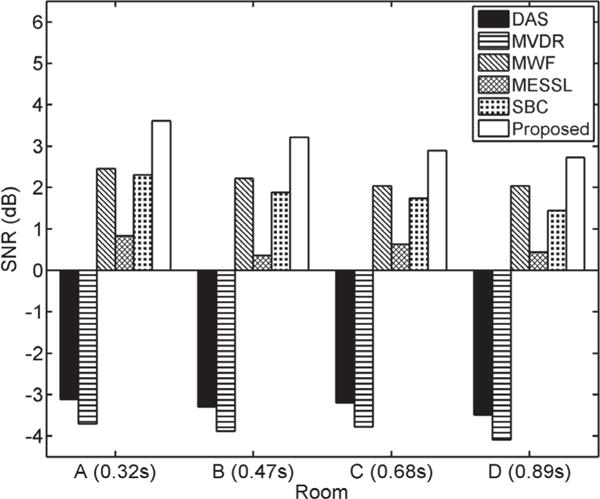
Average SNRs of different methods in real room conditions.

From the above experimental results, we can see that the proposed algorithm outperforms SBC which is also a DNN-based separation algorithm. One of the differences is that the proposed algorithm employs ratio masking for separation, while SBC utilizes binary masking. As described earlier, binary masking is not as preferable as ratio masking. A simple way to turn a binary mask to a ratio mask in the context of DNN is to directly use the outputs of the subband DNNs, which can be interpreted as posterior probabilities with values ranging from 0 to 1. With such soft masks, SBC’s average STOI scores are 63.25% for matched-room conditions, 61.96% for unmatched- room conditions and 55.80% for real-room conditions. These results represent significant improvements over binary masks, but they are still not as high as those of the proposed algorithm.

Fig. 4 illustrates the spectrograms of separated speech using different methods on a test utterance mixed with the multitalker babble noise at −5dB in a highly reverberant condition with T60=0.89s. As shown in the figure, the spectrogram of the separated speech using the proposed method is close to that of clean reverberant speech.

Fig. 4.

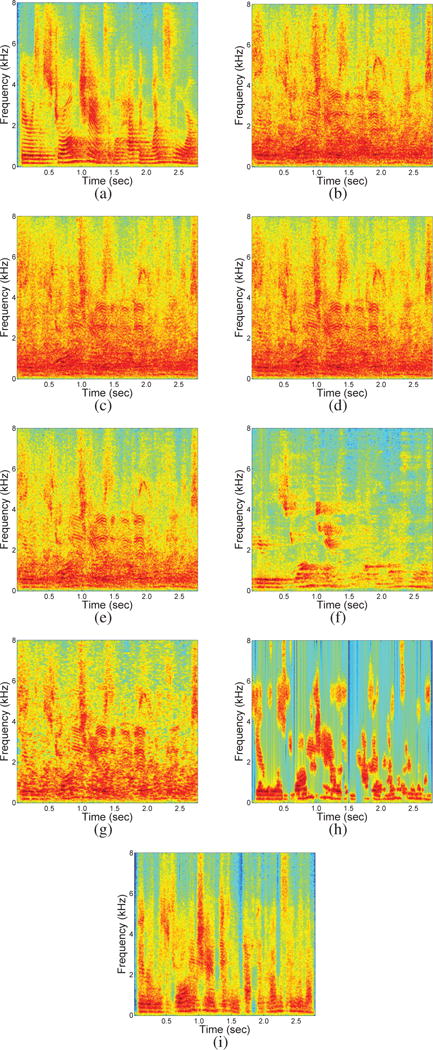
Spectrograms of separated speech using different algorithms in a recorded room condition (Room D with T60=0.89s). The input SNR is −5 dB. (a) Clean speech. (b) Mixture at the left ear. (c) Mixture at the right ear. (d) Result of DAS. (e) Result of MVDR. (f) Result of MWF. (g) Result of MESSL. (h) Result of SBC. (i) Result of the proposed algorithm.

C. Further Analysis

Our binaural speech separation system uses both spectral and spatial features. For spectral features, the DAS beamformer is employed as a preprocessor. The spatial features are formed by combining the proposed 2D ITD and ILD. Previous work [17] shows that binaural separation can benefit from joint spectral and spatial features. In fact, several reasonable spectral and spatial features could be constructed. In this subsection, we further analyze several alternatives. Also we compare with alternative training targets.

1) Spectral features

One simple way to combine spectral and spatial analyses is to directly concatenate the left- and right-ear monaural features. In this case, we extract the complementary feature set from the left- and right-ear signals independently and concatenate them to form the input feature vector for DNN. We compare this feature vector with the proposed beamformed features and also single-ear monaural features (left-ear as in [17]). The interaural features are excluded here. The same DNN configuration and training procedure are used (see Section III-B). The test datasets are also the same. Average STOI results are shown in Fig. 5. From the figure, we can see that extracting the spectral features on the output signal of the beamformer is better than concatenating the spectral features of the left- and right-ear signals. The beamformed and concatenated features are more effective than the single-ear feature.

Fig. 5.

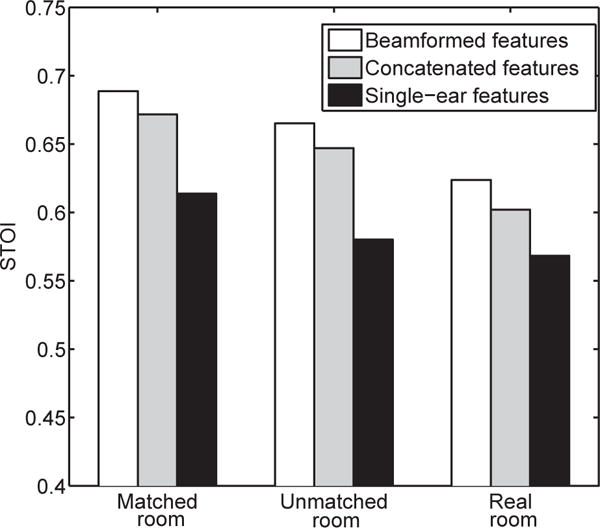
Comparison of DNN-based speech separation using different spectral features.

2) Spatial features

ITD and ILD are the most commonly used cues for binaural separation. While ILD is typically calculated in the same way (see Eq. 3), the representation of ITD information varies in different algorithms. In [24], ITD was estimated as the lag corresponding to the maximum of CCF. Jiang et al. [17] directly used CCF to characterize the interaural time difference. They also show that the CCF is more effective than ITD as a unit-level feature. In contrast, only two values of CCF in each T-F unit are selected in our system.

We compare the performances of using conventional ITD [24], CCF and the proposed 2D ITD as the spatial features. To make the comparison, the frame-level features are formed by concatenating ITD, CCF and 2D ITD in each T-F unit. Since concatenating unit-level CCF vectors directly leads to a very high dimension, we perform principal component analysis (PCA) to reduce the dimension to 128, equal to the size of 2D ITD frame-level feature. Three DNNs with the same configuration are trained using these different spatial features. The STOI results are shown in Fig. 6. We can see that the results with the conventional ITD are much worse than CCF plus PCA and the proposed 2D ITD. This indicates that the conventional ITD is not discriminative in reverberant conditions. While proposed 2D ITD yields essentially the same results as CCF, it has an advantage of relative invariance to different target directions in addition to computational efficiency. As CCF changes with target speech direction, the DNN has to be trained for multiple target directions as done in [17]. On the other hand, our 2D ITD feature requires target direction to be estimated.

Fig. 6.

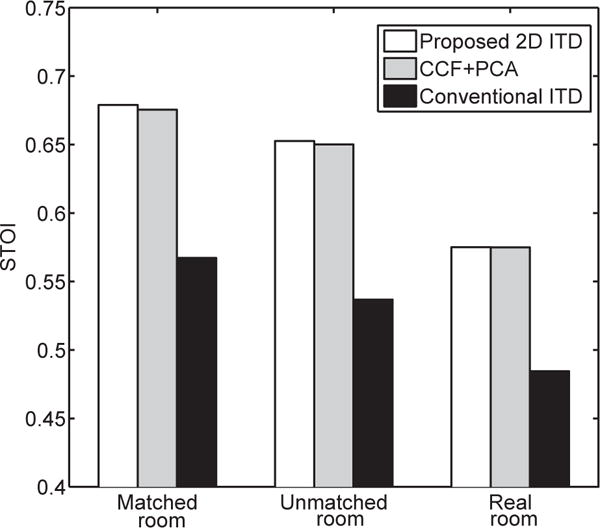
Comparison of DNN-based speech separation using different spatial features.

3) Fullband vs. subband separation

Early supervised speech separation algorithms [17] [18] typically perform subband separation. In contrast, the proposed algorithm employs fullband separation. Earlier in this section, the proposed algorithm has been demonstrated to perform much better than the SBC algorithm of Jiang et al. [17]. To what extent can the better performance be attributed to fullband separation? This question is not addressed in earlier comparisons since the features and the training target of the SBC algorithm are different from ours, and also the DNN for each frequency channel is relatively small in [17]. Here, we make a comparison between subband and fullband separation by using the same features and the same training target.

For subband separation, DAS beamforming is first applied to convert the left- and right-ear signals into a single-channel signal. Then, we decompose the signal into 64 channels by using the gammatone filterbank. For each frequency band, we extract the complementary feature set [33], 2D ITD and ILD. The same temporal context is utilized by incorporating 9 frames (4 before and 4 after). The training target is the IRM. The configuration of DNN for each frequency channel is the same as described in section III-B.

The STOI results are shown in Fig. 7. We can see that fullband separation still performs better with the same features and training target. Of course, another disadvantage of subband separation is its computational inefficiency with a multitude of DNNs to be trained.

Fig. 7.

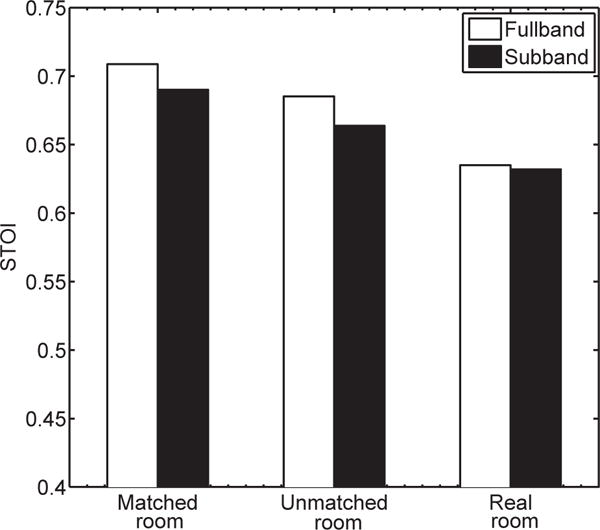
Comparison of DNN-based speech separation using different spatial features.

4) Training targets

This study uses the IRM as the training target, and a more direct target is the spectral magnitude of the target speech [37]. However, such spectral mapping is many-to-one and more difficult to estimate than the IRM [34]. Signal approximation (SA) [15] [36] is a training target that can be viewed as a combination of ratio masking and spectral mapping. SA-based speech separation has been shown to yield higher signal-to-distortion ratio compared to masking-based or mapping-based methods. The difference between Huang et al. [15] and Weninger et al. [36] is that the former makes use of both target and interference signals.

In this subsection, we compare IRM estimation and the two SA-based methods mentioned above. For this comparison, the input features, DNN configurations and training procedures (seen in Section II-B) are the same for all the three methods. The STOI scores are shown in Fig. 8. We can see that ratio masking produces the highest scores. Due to its inclusion of interference signal, Huang et al.’s method outperforms Weninger et al.’s. The SNR results are given in Fig. 9. It can be seen that the SA-based methods obtain higher SNR, particularly Huang et al.’s version. Higher SNRs are expected as signal approximation aims to maximize output SNR [36]. Similar results are obtained with different DNN configurations (with larger or smaller hidden layers, and one more hidden layer).

Fig. 8.

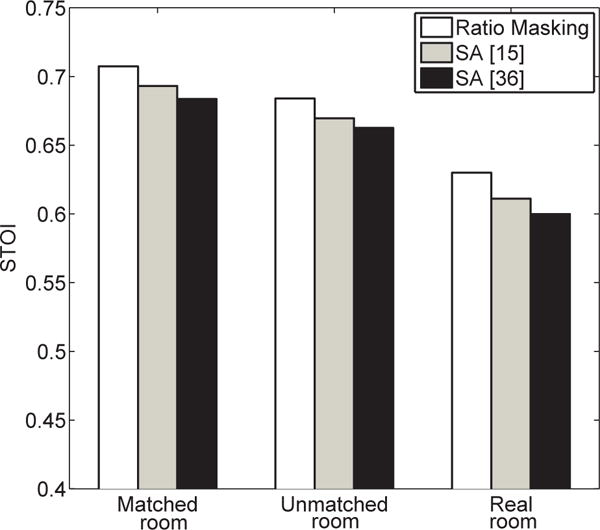
Average STOI scores of using different targets.

Fig. 9.

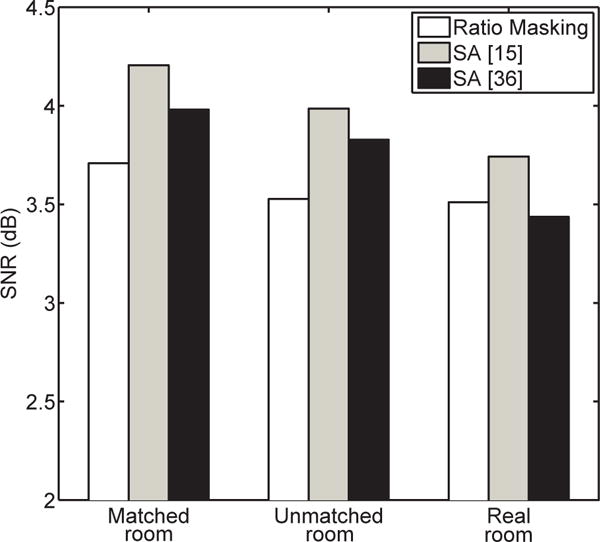
Average SNR of using different targets.

We close this section by discussing computational complexity. Compared to the training-based algorithms of SBC and MESSL, the proposed algorithm is faster, as SBC uses a DNN for each of 64 subbands and MESSL utilizes the slow expectation maximization algorithm. The DAS, MVDR and MWF beamformers have much lower computational complexities than the proposed algorithm with the given target direction, because feature extraction in our algorithm is time consuming, especially the CCF calculation. On the other hand, the beamformers need DOA estimation when target direction is unknown, and CCF-based DOA estimation [19] is a representative method. In other words, the beamforming techniques and the proposed algorithm have the same level computational complexity when DOA estimation is performed.

VI. CONCLUDING REMARKS

In this work, we have proposed a DNN-based binaural speech separation algorithm which combines spectral and spatial features. DNN-based speech separation has shown its ability to improve speech intelligibility [32] [14] even with just monaural spectral features. As demonstrated in previous work [17], binaural speech separation by incorporating monaural features represents a promising direction to further elevate separation performance.

For supervised speech separation, input features and training targets are both important. In this study, we make a novel use of beamforming to combine left-ear and right-ear monaural signals before extracting spectral features. In addition, we have proposed a new 2D ITD feature. With the IRM as the training target, the proposed system outperforms representative multichannel speech enhancement algorithms and also a DNN-based subband classification algorithm [17] in non- stationary background noise and reverberant environments.

A major issue of supervised speech separation is generalization to untrained environments. Our algorithm shows consistent results in unseen reverberant noisy conditions. This strong generalization ability is partly due to the use of effective features. Although only one noisy situation is considered, the noise problem can be addressed by involving large-scale training data [5].

In the present study, the target speaker is fixed to the front direction and sound localization is not addressed. For the proposed algorithm, two parts need the target direction. One is DAS beamforming and the other is calculation of 2D ITD. Sound localization is a well-studied problem [31]. Recently, DNN is also used for sound localization [21], although only spatial features are considered. We believe that incorporating monaural separation is a good direction to improve the robustness of sound localization in adverse environments with both background noise and room reverberation. One way to incorporate monaural separation is to employ spectral features for initial separation, from which reliable T-F units are selected for sound localization. Moreover, separation and localization could be done iteratively as in [39].

Biographies

Xueliang Zhang received the B.S. degree from the Inner Mongolia University, Hohhot, China, in 2003, received the M.S. degree from the Harbin Institute of Technology, Harbin, China, in 2005 and received the Ph.D. degree from the Institute of Automation, Chinese Academy of Sciences, Beijing, China, in 2010. From August 2015 to September 2016, he was a Visiting Scholar in the Department of Computer Science and Engineering, Ohio State University (OSU), Columbus

Currently, he is an associate professor at the Department of Computer Science, Inner Mongolia University. His research interests include speech separation, computational auditory scene analysis and speech signal processing.

DeLiang Wang received the B.S. degree in 1983 and the M.S. degree in 1986 from Peking (Beijing) University, Beijing, China, and the Ph.D. degree in 1991 from the University of Southern California, Los Angeles, CA, all in computer science.

From July 1986 to December 1987 he was with the Institute of Computing Technology, Academia Sinica, Beijing. Since 1991, he has been with the Department of Computer Science and Engineering and the Center for Cognitive Science at The Ohio State University, Columbus, OH, where he is currently a Professor. From October 1998 to September 1999, he was a visiting scholar in the Department of Psychology at Harvard University, Cambridge, MA. From October 2006 to June 2007, he was a visiting scholar at Oticon A/S, Copenhagen, Denmark. From October 2014 to De 2007, he was a visiting scholar at Oticon A/S, Copenhagen, Denmark.

DeLiang Wang received the NSF Research Initiation Award in 1992 and the ONR Young Investigator Award in 1996. He received the OSU College of Engineering Lumley Research Award in 1996, 2000, 2005, and 2010. His 2005 paper, “The time dimension for scene analysis”, received the IEEE Transactions on Neural Networks Outstanding Paper Award from the IEEE Computational Intelligence Society. He also received the 2008 Helmholtz Award from the International Neural Network Society, and was named a University Distinguished Scholar in 2014. He was an IEEE Distinguished Lecturer (2010–2012), and is an IEEE Fellow.