Estimating treatment effects in observational studies with both prevalent and incident cohorts

Abstract

Registry databases are increasingly being used for comparative effectiveness research in cancer. Such databases reflect the real-world patient population and physician practice, and thus are natural sources for comparing multiple treatment scenarios and the associated long-term clinical outcomes. Registry databases usually include both incident and prevalent cohorts, which provide valuable complementary information for patients with more recent diagnoses in the incident cohort as well as patients with long-term follow-up data in the prevalent cohort. However, utilizing such data to derive valid inference poses two major challenges: the data from a prevalent cohort are not random samples of the target population, and there may be substantial differences in the baseline characteristics of patients between treatment arms, which influences the decisions about treatment selection in both cohorts. In this article, we extend propensity score methodology to observational studies that involve both prevalent and incident cohorts, and assess the effectiveness of radiation therapy in SEER-Medicare patients diagnosed with stage IV breast cancer. Specifically, we utilize the incident cohort to estimate the propensity for receiving radiation therapy, and then combine data from both the incident and prevalent cohorts to estimate the effect of radiation therapy by adjusting for the propensity scores in the model. We evaluate the proposed method with simulations. We demonstrate that the proposed propensity score method simultaneously removes sampling bias and selection bias under several assumptions.

1. Introduction

The focus of comparative effectiveness research when using observational data is to assess the use of an intervention on a more general patient population outside of controlled clinical trials. Observational data cohorts such as national cancer registries and the Surveillance, Epidemiology and End Results (SEER)-Medicare databases are natural choices for conducting comparative effectiveness research. Due to advances in both breast cancer screening programs and adjuvant systemic therapy, fewer breast cancer cases (5.6%, www.seer.cancer.gov) are metastatic (stage IV) at diagnosis than ever before, especially for women aged 65 years and older. There are only a few standards of care in the management of stage IV breast cancer (Cardoso et al., 2012) and the role of radiation therapy (RT) remains controversial for women aged 65 years and older who had stage IV breast cancer. On the other hand, a randomized clinical trial is unlikely to assess the role of RT for this cohort of patients.

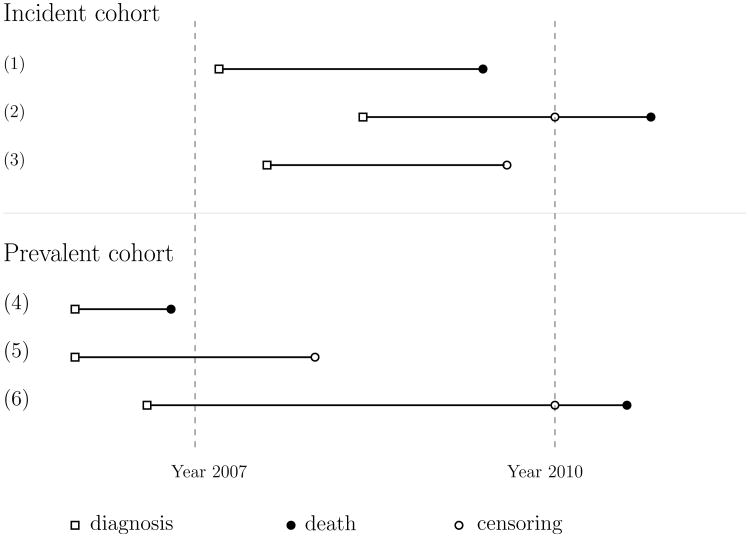
Using the recent SEER-Medicare breast cancer database of 2007-2010, it is of great interest to evaluate the effectiveness of receiving RT versus not receiving RT in elderly patients with stage IV breast cancer based on the incident cohort. This cohort consists of patients who were diagnosed with breast cancer from 2007 on, and who died or were right-censored at last follow-up. An incident cohort study is not typically an efficient design for evaluating the treatment effect on the failure event of interest due to relatively short follow-up times and, in this example, the moderate size of the population of patients with stage IV breast cancer. Therefore, from the SEER-Medicare claims data, we also retrieved information on patients who were diagnosed with stage IV breast cancer prior to 2007 and who were alive in 2007. This represents a prevalent cohort consisting of patients who had already experienced the initiating event but had not experienced the failure event at the time of ascertainment. Figure 1 illustrates the difference in sampling scheme between a prevalent and an incident cohort study. By combining the data from the two cohorts with stage IV breast cancer, we may have a sufficiently large number of patients for a better assessment of the effect of RT.

Figure 1. Incident and prevalent cohort sampling schemas.

Although we can take advantage of data from both prevalent and incident cohorts for more efficient statistical inference, we face two challenges. The first challenge is that the patients in the prevalent cohort often have longer survival times and the distribution of their covariates is not representative of the target population (i.e., incident cohort), as patients with longer survival times are preferentially sampled (Vardi, 1982; Wang et al., 1993; Gail and Benichou, 2000; Rothman et al., 2008; Zelen, 2006). The conventional estimator of the treatment effect from an outcome regression model using data from a prevalent cohort can be biased due to sampling bias related to the outcomes.

Moreover, the treatment of interest, such as RT, is not randomly assigned, and baseline patient characteristics are confounded with the treatment decision. Thus, the baseline characteristics are often imbalanced between patients who receive RT and those who do not, in either the incident or prevalent cohort. The propensity score method, introduced by Rubin (1973) and Rosenbaum and Rubin (1985), addressed this concern by reducing multiple baseline covariates to a single statistic that summarizes the collective information. Using this statistic, the imbalance in the baseline covariates between two treatment groups can be adjusted to reduce bias (D'Agostino, 1998). However, the existing methods are applicable to the incident cohort only. Prevalent cohorts suffer additional selection bias related to the length of the outcomes, since the patients in the cohort have all survived until their enrollment in the study, and those who did not survive until that time were automatically excluded.

Much progress has been made in the area of regression analysis to associate failure time and covariates given data from a prevalent cohort after adjusting for the sampling bias (Wang et al., 1993; Shen et al., 2009; Qin and Shen, 2010; Ning et al., 2011). However, little has been done regarding propensity score analysis using both prevalent and incident cohorts. Cheng and Wang (2012) and Chan (2013) developed statistical methods for propensity score analysis using prevalent cohort data only, in which some restrictive model assumptions had to be imposed.

Our strategy is to use the incident cohort to estimate the propensity for receiving RT and then use both cohorts to estimate the effectiveness of receiving RT versus not receiving RT in elderly patients with stage IV breast cancer, by using an outcome regression model (e.g., Cox model) involving the propensity scores. The sampling bias in the prevalent cohort has been corrected in the estimation of the treatment effect.

The remainder of this article is organized as follows. In Section 2, we present the proposed estimating equations and inference procedure to simultaneously estimate the regression parameters in models for the propensity score and survival outcome. In Section 3, we develop procedures to check whether the propensity scores estimated from the incident cohort can be applied to the prevalent cohort to balance the covariate distributions between the treatment arms. In Section 4, we report the simulation studies to assess the finite sample performance of the proposed method. We apply our method to the SEER-Medicare data in Section 5, and provide concluding remarks in Section 6. We provide details for the proofs of the asymptotic properties in the Appendix.

2. Model and Estimation

2.1. Notations and Model

We consider data from the incident cohort to represent the target population. Let T, Z and X respectively represent the failure time, treatment indicator (RT versus no RT), and a q × 1 vector of covariates in the incident cohort. Define the censoring time and censoring indicator to be C and δ = I(T < C), respectively. Then the observed data from the incident cohort are {Y_i, Z_i, X_i, δ_i; i = 1, ⋯, m}, where Y_i is min(T_i, C_i), m is the sample size of the incident cohort, and I(.) is the indicator function.

In the prevalent cohort, patients with the diagnosis of stage IV breast cancer prior to 2007, the time of enrollment to the study cohort, who were still at risk for the failure event (e.g., breast cancer-specific death) in 2007 were included (e.g., subjects 5 and 6 in Figure 1). The observed truncation time W is the duration from the initial diagnosis of the disease to 2007. Thus, the prevalent cohort excludes patients with T < W (e.g., subject 4 in Figure 1).

Data from the prevalent cohort represent a valuable augmentation to the incident cohort; the observed survival times from the prevalent cohort tend to be longer than those in the incident cohort. Moreover, the distributions of the baseline variables can differ between the incident and prevalent cohorts. We need a slightly different notation to define the observed data in the prevalent cohort. Let T̃, W̃, Z̃ and X̃ respectively be the failure time, truncation time, treatment indicator, and a vector of the covariates. Denote the residual survival time by Ṽ, so that T̃ = W̃ + Ṽ. The observed data are recorded as {Ỹ_i, W̃_i, Z̃_i, X̃_i, δ̃_i; i = 1, ⋯, n}, where Ỹ_i = min{W̃_i + Ṽ_i, C̃_i}, δ̃_i = I(W̃_i + Ṽ_i < C̃_i) and n is the sample size of the prevalent cohort. The propensity score method is used to mitigate the treatment selection bias arising from non-random treatment assignment in observational studies (Rosenbaum and Rubin, 1983; Kang and Schafer, 2007; Austin, 2008). We assume that the propensity score, i.e., the probability of receiving the treatment, is associated with the baseline patient characteristics via a logistic regression model,

$$e(\mathbf{X};\mathit{\gamma })=P(Z=1|\mathbf{X};\mathit{\gamma })=\frac{exp\{{\mathit{\gamma }}^{\top }(1,\mathbf{X})\}}{1+exp\{{\mathit{\gamma }}^{\top }(1,\mathbf{X})\}},$$ (1)

where γ is a vector of regression coefficients, and the interaction terms of X may be included to increase the flexibility of the propensity score model. As shown by D'Agostino (1998), Rosenbaum and Rubin (1985) and Rubin (1979), using the propensity score as a covariate in an outcome regression analysis can effectively reduce the bias in the estimation of the treatment effect in observational studies. To determine the association between the survival outcome T and RT treatment, the Cox proportional hazards model is used to adjust for the effects of baseline covariates by including the propensity score as a covariate:

$$\lambda (t|Z,\mathbf{X})={\lambda }_0(t)exp[\alpha Z+g\{e(\mathbf{X},\mathit{\gamma });\mathit{\beta }\}],$$ (2)

where λ₀(.) is an unspecified baseline function, α is the log-hazard ratio of the RT treatment after the propensity score adjustment, β is a vector of parameters in g(.) and g(.) is a flexible and differentiable function.

One major advantage of using the propensity score as a covariate in the outcome regression is to avoid over-parameterizing or mis-specifying the model with a large number of covariates. By collapsing all covariates into a single propensity score and incorporating the plausible nonlinear and interaction terms of the covariates into the propensity score, one can greatly reduce the possibility of outcome model misidentification (D'Agostino, 1998). Regression adjustment with the propensity score was used by Cheng and Wang (2012) to analyze prevalent survival data. Although the propensity score analysis introduces an additional assumption of a propensity score model, that assumption can be reinforced by assessing the balance in the covariate distributions between the two groups. The propensity score model can be reformulated until adequate balance is achieved. From this perspective, the propensity score analysis involves weaker assumptions than direct regression on the outcomes using a large number of covariates, and the estimation of α is more robust than an estimation that is conditional on all the covariates.

2.2. Estimating Equation Methods

Without loss of generality, we use a simple linear form of g(.) for illustration, g{e(X; γ); β} = βe(X; γ). Using the data from the incident cohort, we estimate the propensity score by solving the score equations under the logistic regression model,

$$U_1(\mathit{\gamma })=\sum _{i=1}^m{(1,{\mathbf{X}}_i)}^{\top }[Z_i-\frac{exp\{{\mathit{\gamma }}^{\top }(1,{\mathbf{X}}_i)\}}{1+exp\{{\mathit{\gamma }}^{\top }(1,{\mathbf{X}}_i)\}}]=0$$ (3)

The score equation under the Cox model using the incident cohort is

$$\sum _{i=1}^m{\delta }_i[{\{Z_i,e({\mathbf{X}}_i;\mathit{\gamma })\}}^{\top }-\frac{{\sum }_{j\in R_1(Y_i)}{\{Z_j,e({\mathbf{X}}_j;\mathit{\gamma })\}}^{\top }exp\{\alpha Z_j+\beta e({\mathbf{X}}_j;\mathit{\gamma })\}}{{\sum }_{j\in R_1(Y_i)}exp\{\alpha Z_j+\beta e({\mathbf{X}}_j;\mathit{\gamma })\}}]=0,$$ (4)

where R₁(t) = {j : Y_j ≥ t} is the at-risk function for the incident cohort. We estimate γ, α and β by solving (3) and (4) when using the incident cohort only.

Next, we describe how to combine the data from the prevalent cohort to improve statistical efficiency. In our motivating example, the incident cohort and prevalent cohort are derived from the same target population but with different sampling schema. Thereby, the propensity scores estimated from the incident cohort can be applied to the prevalent cohort to balance the baseline variables. The Cox model structure assumed for the incident cohort can be different from the one for the observed data from the prevalent cohort. Therefore, we need to adjust for biased sampling due to left-truncation when modeling the treatment effect on the survival outcome by using a modified at-risk function (Lai and Ying, 1991; Wang et al., 1993). We extend score equation (4) to incorporate the information from the prevalent cohort:

$$U_2(\mathit{\gamma },\alpha ,\beta )=\sum _{i=1}^m{\delta }_i[{\{Z_i,e({\mathbf{X}}_i;\mathit{\gamma })\}}^{\top }-\frac{{\sum }_{j\in R_1(Y_i)}{\{Z_j,e({\mathbf{X}}_j;\mathit{\gamma })\}}^{\top }exp\{\alpha Z_j+\beta e({\mathbf{X}}_j;\mathit{\gamma })\}}{{\sum }_{j\in R_1(Y_i)}exp\{\alpha Z_j+\beta e({\mathbf{X}}_j;\mathit{\gamma })\}}]+\sum _{i=1}^n{\stackrel{\sim }{\delta }}_i[{\{{\stackrel{\sim }{Z}}_i,e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma })\}}^{\top }-\frac{{\sum }_{j\in R_2({\stackrel{\sim }{Y}}_i)}{\{{\stackrel{\sim }{Z}}_j,e({\stackrel{\sim }{\mathbf{X}}}_j;\mathit{\gamma })\}}^{\top }exp\{\alpha {\stackrel{\sim }{Z}}_j+\beta e({\stackrel{\sim }{\mathbf{X}}}_j;\mathit{\gamma })\}}{{\sum }_{j\in R_2({\stackrel{\sim }{Y}}_i)}exp\{\alpha {\stackrel{\sim }{Z}}_j+\beta e({\stackrel{\sim }{\mathbf{X}}}_j;\mathit{\gamma })\}}]=0,$$ (5)

where R₂(t) = {j : W̃_j ≤ t ≤ Ỹ_j} is the modified at-risk function for the left-truncated and right-censored data for the prevalent cohort. Then, estimating equations U₁(γ) and U₂(γ, α, β) are simultaneously solved to estimate the parameters of interest, γ, β and α. The first component of U₂(.) uses data from the incident cohort, which often has shorter follow-up outcomes than the prevalence cohort but is not subject to biased sampling; whereas the second component of U₂(.) uses data from the prevalent cohort, which often has longer follow-up outcomes but requires an adjustment of biased sampling.

Define θ̂ = (γ̂^⊤, α̂, β̂)^⊤ as the solution of U(θ) = (U₁(γ)^⊤, U₂(θ)^⊤)^⊤ = 0 and θ₀ as the true value of θ. We show in the Appendix that U(θ) = 0 asymptotically has a unique solution θ̂, and then derive the consistency of θ̂. Moreover, based on Taylor expansions of U(θ) around θ₀, the central limit theorem, and the martingale central limit theorem, we can prove that θ̂ is asymptotically normally distributed under certain regularity conditions. We summarize these results in the following theorem, whose proof is presented in the Appendix.

Theorem 1: Under the logistic regression model for the propensity score and the Cox model for the survival time and regularity conditions [C.1-C.6] listed in the Appendix, the estimator θ̂ converges to θ₀ in probability. Moreover, √n(θ̂ − θ₀) converges in distribution to a normal distribution with mean 0 and covariance matrix defined in the Appendix.

2.2.1. Special Case: Length-biased Data

If the onset of the disease follows a Poisson process, the observed survival data from the prevalent cohort are considered to be length-biased data (Wang et al., 1993). The aforementioned set of estimating equations can be modified to increase statistical efficiency by incorporating the distributional information of the truncation time. Using the weight in a manner similar to the approach of Shen et al. (2009) and Qin and Shen (2010), we restructure unbiased estimating equations for estimating γ by using the baseline covariate data from the prevalent cohort: U_LB1(γ) = 0, where

$$U_{LB1}(\mathit{\gamma })=\sum _{i=1}^m{(1,{\mathbf{X}}_i)}^{\top }\{Z_i-\frac{exp\{{\mathit{\gamma }}^{\top }(1,{\mathbf{X}}_i)\}}{1+exp\{{\mathit{\gamma }}^{\top }(1,{\mathbf{X}}_i)\}}\}+\sum _{j=1}^n\frac{{\stackrel{\sim }{\delta }}_j{(1,{\stackrel{\sim }{\mathbf{X}}}_j)}^{\top }}{w({\stackrel{\sim }{Y}}_j)}\{{\stackrel{\sim }{Z}}_i-\frac{exp\{{\mathit{\gamma }}^{\top }(1,{\stackrel{\sim }{\mathbf{X}}}_i)\}}{1+exp\{{\mathit{\gamma }}^{\top }(1,{\stackrel{\sim }{\mathbf{X}}}_i)\}}\},$$ (6)

$w(t)={\int }_0^t{S}_c(u)\mathit{\text{du}}$, and S_c(.) is the survival distribution for the residual censoring time C̃ − W̃ which can be consistently estimated by the Kaplan-Meier estimator. The second component of (6) is similar to the first one, but is inversely adjusted by the weight w(Ỹ_j) for data from the prevalent cohort (Ertefaie, 2014).

Similarly, the second set of estimating equations under the Cox model can be reconstructed to efficiently utilize the length-biased data: U_LB2(γ, α, β) = 0, where

$$U_{LB2}(\mathit{\gamma },\alpha ,\beta )=\sum _{i=1}^m{\delta }_i[{\{Z_i,e({\mathbf{X}}_i;\mathit{\gamma })\}}^{\top }-\frac{{\sum }_{j\in R_1(Y_i)}{\{Z_j,e({\mathbf{X}}_j;\mathit{\gamma })\}}^{\top }exp\{\alpha Z_j+\beta e({\mathbf{X}}_j;\mathit{\gamma })\}}{{\sum }_{j\in R_1(Y_i)}exp\{\alpha Z_j+\beta e({\mathbf{X}}_j;\mathit{\gamma })\}}]+\sum _{i=1}^n{\stackrel{\sim }{\delta }}_i[{\{{\stackrel{\sim }{Z}}_i,e({\stackrel{\sim }{\mathbf{X}}}_i,\mathit{\gamma })\}}^{\top }-\frac{{\sum }_{j\in R_1({\stackrel{\sim }{Y}}_i)}{\stackrel{\sim }{\delta }}_j{\{w({\stackrel{\sim }{Y}}_j)\}}^{-1}{\{{\stackrel{\sim }{Z}}_j,e({\stackrel{\sim }{\mathbf{X}}}_j;\mathit{\gamma })\}}^{\top }exp\{\alpha {\stackrel{\sim }{Z}}_j+\beta e({\stackrel{\sim }{\mathbf{X}}}_j;\mathit{\gamma })\}}{{\sum }_{j\in R_1({\stackrel{\sim }{Y}}_i)}{\stackrel{\sim }{\delta }}_j{\{w({\stackrel{\sim }{Y}}_j)\}}^{-1}exp\{\alpha {\stackrel{\sim }{Z}}_j+\beta e({\stackrel{\sim }{\mathbf{X}}}_j;\mathit{\gamma })\}}].$$ (7)

In the second component of (7), the subjects in the risk sets are weighted to adjust for the length-biased sampling constraint. By using derivations similar to those of Qin and Shen (2010), (7) has mean zero and can be combined with (6) for estimating θ. The consistency and weak convergence of the resultant estimators can be established using techniques similar to those for Theorem 1.

3. Testing the Balancing Property

Unlike the motivating example, the incident cohort and prevalent cohort may not be generated from the same target population in some applications. In this case, we need to check the assumptions for the proposed method to determine whether the propensity scores estimated from the incident cohort can balance the covariate distributions of the two treatment arms in the prevalent cohort. This test is conducted under the following modeling assumption:

$$E({\stackrel{\sim }{\mathbf{X}}}_i)-\mathit{\xi }\mu \{e({\stackrel{\sim }{X}}_i;\widehat{\mathit{\gamma }})\}+\mathit{\zeta }{\widehat{Z}}_i,$$

where μ(.) is a pre-specified flexible function (e.g., fractional polynomial function or spline function), and ξ and ζ are vectors with the same dimension of X̃_i.

Under this model specification, testing the null hypothesis of the covariate being independent of the treatment assignment is equivalent to testing for H₀ : ζ = 0 vs H₁ : ζ ≠ 0. This test can also be viewed as a test for the specification of the propensity score model (1) (Imai et al., 2008; Li and Greene, 2013). Rejection of the null hypothesis indicates that the propensity score model derived from the incident cohort is not applicable to the prevalent cohort.

Under the assumption that the initial event has stationary incidence, we construct an unbiased estimating equation for estimating the unknown parameters and making inference on ζ:

$$\sum _{i=1}^n\frac{{\stackrel{\sim }{\delta }}_i}{w({\stackrel{\sim }{Y}}_i)}\{{\stackrel{\sim }{\mathbf{X}}}_i-\mathit{\xi }\mu \{e({\stackrel{\sim }{\mathbf{X}}}_i;\widehat{\mathit{\gamma }})\}-\mathit{\zeta }{\stackrel{\sim }{Z}}_i\}=0$$ (8)

The unknown weight function w(Ỹ_i) involved in (8) can be readily estimated by the Kaplan-Meier estimator. In the Appendix, we have derived the asymptotic normality of estimator ζ̂, the solution of (8). We propose a Wald-type test statistic to test for H₀ by T_test = ζ̂^⊤V̂⁻¹ ζ̂, where V̂ is the variance-covariance matrix of ζ̂. The following theorem summarizes the limiting distribution of the test statistics. A sketch of the proof is provided in the Appendix.

Theorem 2: Under regularity conditions [C.1-C.7] listed in the Appendix and the null hypothesis, T_test converges weakly to a chi-squared distribution with a degree of freedom of q.

The weight function in (8) can be generalized to accommodate general left-truncated data for which the stationarity assumption is not satisfied. If the truncation time follows a density function h_θA with a finite dimensional vector of parameters θ_A, the generalized weight function is $w({\stackrel{\sim }{Y}}_{\top })={\int }_0^{{\stackrel{\sim }{Y}}_i}{h}_{{\mathit{\theta }}_A}(a)S_c(Y_i-a)\mathit{\text{da}}$. Similarly, the weight can be estimated consistently by plugging in consistent estimators for the censoring survival function and θ_A.

4. Simulation Study

We conducted simulation studies to evaluate the finite sample performance of the proposed methods. We simulated two cohorts from the same target population: m = 200, 400 or 600 subjects in the incident cohort and n = 200 patients in the prevalent cohort. For both cohorts, we generated the treatment assignment Z_i via the propensity score function

$$e({\mathbf{X}}_i,\mathit{\gamma })=exp({\mathit{\gamma }}^{\top }(1,{\mathbf{X}}_i))/\{1+exp({\mathit{\gamma }}^{\top }(1,{\mathbf{X}}_i))\},$$

where the baseline covariates X_i = (X_i1, X_i2, X_i3) followed the standard normal distribution and γ = (0.1, 0.4, 0.4, 0.4). Given (Z_i, X_i), the failure time T_i was generated from an exponential distribution with a rate of exp{0.5Z_i + e(X_i; γ)}. The censoring times were independently generated from the uniform distribution [0, τ_c], where τ_c = 0.52 in Scenario I and τ_c = 1.3 in Scenario II. The sampling constraint in the prevalent cohort was introduced by a uniform truncation time; only patients satisfying W_i < T_i were included in the prevalent cohort. We considered different combinations of sample sizes and censoring rates to cover a wide range of scenarios. We used estimating equations U₁(γ) and U₂(γ, α, β) to fit the propensity score and survival outcome, where g{e(X;γ); β} = βe(X; γ).

Table 1 summarizes the empirical biases, empirical standard errors, average asymptotic standard errors and coverage probabilities of the 95% confidence intervals based on 1, 000 simulations. As shown, the parameters in both the propensity score model and the Cox model were estimated reliably by the proposed method. The empirical biases were close to zero, and the model-based standard errors were close to their empirical values. Furthermore, the coverage probabilities of the 95% confidence intervals were close to the nominal level. As expected, the standard errors decreased with increasing sample sizes, and the standard errors of parameter estimates in the Cox model increased with increasing rates of censoring. For comparison (but not reported here), we also calculated the standard errors of α̂ and β̂ by ignoring the additional variation due to the estimated propensity score. We found that the standard errors were underestimated and the associated coverage probabilities were much smaller than the nominal value. For example, in the scenario with a sample size of 200 from each cohort, the estimated standard error of β̂ was 0.409, which is substantially lower than its empirical standard deviation of 0.576 in Table 1. We compared the small sample performance of the estimators from the estimation equations U₁(γ) and U₂(γ, α, β), and the estimation equations U_LB1(γ) and U_LB2(γ, α, β). As expected, by incorporating the distribution information of the truncation time, the estimators obtained from estimation equations U_LB1(γ) and U_LB2(γ, α, β) are more efficient than those from estimation equations U₁(γ) and U₂(γ, α, β), which are for general left-truncated data. More details are provided in the Supplementary Materials.

Table 1.

Summary of 1, 000 simulations of the proposed method by combining incident and prevalent cohorts: empirical bias (Bias), empirical standard error (ESE), asymptotic standard error (ASE), and coverage probability (CP).

Sample Size (m,n)		Scenario I: C1% = 60%, C2% = 40%						Scenario II: C1% = 40%, C2% = 20%
		γ = (0.1, 0.4, 0.4, 0.4)				(α, β) = (0.5,1)		γ = (0.1, 0.4, 0.4, 0.4)				(α, β) = (0.5,1)
(200, 200)	Bias	-.003	.021	.008	.018	.028	-.007	-.003	.021	.008	.018	.023	-.021
	ESE	.163	.157	.156	.155	.155	.576	.163	.157	.156	.155	.127	.482
	ASE	.152	.158	.159	.159	.160	.583	.152	.158	.159	.159	.134	.498
	CP	.938	.958	.956	.970	.964	.962	.938	.958	.956	.970	.964	.962
(400, 200)	Bias	.000	.014	-.003	-.005	.012	-.013	.000	.014	-.003	-.005	.012	.006
	ESE	.102	.114	.118	.114	.136	.463	.102	.114	.118	.114	.112	.395
	ASE	.106	.110	.111	.110	.133	.460	.106	.110	.111	.110	.111	.392
	CP	.960	.946	.912	.944	.940	.960	.960	.946	.912	.944	.952	.952
(600, 200)	Bias	.002	.010	.008	.007	.018	.002	.002	.010	.008	.007	.015	-.004
	ESE	.086	.090	.090	.086	.125	.402	.086	.090	.090	.086	.105	.338
	ASE	.087	.090	.090	.090	.117	.389	.087	.090	.090	.090	.097	.328
	CP	.948	.954	.948	.958	.932	.946	.948	.954	.948	.958	.930	.948

C₁% and C₂%: the respective censoring rates of the incident cohort and prevalent cohort

We conducted some sensitivity studies to evaluate robustness of the proposed method with violations of model assumptions. The simulation results and findings are summarized in the Supplementary Materials.

Table 2 lists the simulation results of two naive methods: one uses the incident cohort data only, the other uses the prevalent cohort data only without adjusting for the sampling bias. As expected, the first naive method was valid, with small empirical biases and coverage probabilities close to the nominal value, but was much less efficient than the proposed method, which combined data from the two cohorts. In contrast, the second naive method produced biased estimates and misleading inference by ignoring that neither the baseline covariate distribution nor the survival outcomes were representative of the target population.

Table 2.

Summary of 1, 000 simulations of naive methods: empirical bias (Bias), empirical standard error (ESE), asymptotic standard error (ASE), and coverage probability (CP).

Sample Size		Scenario I: C1% = 60%, C2% = 40%						Scenario II: C1% = 40%, C2% = 20%
		γ = (0.1, 0.4, 0.4, 0.4)				(α, β) = (0.5, 1)		γ = (0.1, 0.4, 0.4, 0.4)				(α, β) = (0.5, 1)
Method using data from incident cohort only
200	Bias	-.003	.021	.008	.018	.005	-.001	-.003	.021	.008	.018	.011	-.029
	ESE	.163	.157	.156	.155	.248	.876	.163	.157	.156	.155	.192	.704
	ASE	.152	.158	.159	.159	.249	.867	.152	.158	.159	.159	.203	.720
	CP	.938	.958	.956	.970	.958	.970	.938	.958	.956	.970	.954	.966
400	Bias	.000	.014	-.003	-.005	.006	-.024	.000	.014	-.003	-.005	.009	-.007
	ESE	.102	.114	.118	.114	.170	.568	.102	.114	.118	.114	.142	.481
	ASE	.106	.110	.111	.110	.174	.583	.106	.110	.111	.110	.141	.487
	CP	.960	.946	.912	.944	.952	.974	.960	.946	.912	.944	.956	.960
600	Bias	.002	.010	.008	.007	.014	-.015	.002	.010	.008	.007	.010	-.009
	ESE	.086	.090	.090	.086	.149	.478	.086	.090	.090	.086	.119	.381
	ASE	.087	.090	.090	.090	.142	.463	.087	.090	.090	.090	.115	.384
	CP	.948	.954	.948	.958	.938	.938	.948	.954	.948	.958	.940	.948
Method using data from prevalent cohort only
200	Bias	-.503	.011	.012	.019	.315	.638	-.503	.011	.012	.019	.262	.555
	ESE	.170	.166	.165	.174	.205	.783	.170	.166	.165	.174	.177	.683
	ASE	.158	.162	.163	.163	.209	.836	.158	.162	.163	.163	.180	.731
	CP	.120	.944	.944	.940	.664	.950	.120	.944	.944	.940	.694	.950
400	Bias	-.506	.007	.006	.006	.303	.581	-.506	.007	.006	.006	.258	.505
	ESE	.111	.126	.108	.111	.140	.559	.111	.126	.108	.111	.124	.469
	ASE	.110	.114	.114	.114	.146	.548	.110	.114	.114	.114	.125	.479
	CP	.002	.916	.958	.968	.470	.866	.002	.916	.958	.968	.472	.904
600	Bias	-.495	.001	.001	.002	.292	.612	-.495	.001	.001	.002	.251	.516
	ESE	.084	.092	.099	.095	.119	.422	.084	.092	.099	.095	.104	.370
	ASE	.090	.092	.092	.092	.118	.442	.090	.092	.092	.092	.102	.387
	CP	.000	.950	.944	.938	.298	.764	.000	.950	.944	.938	.320	.786

C₁% and C₂% respectively denote the censoring rate of the incident cohort and prevalent cohort

The second set of simulations evaluates the finite sample performance (size and power) of the proposed test for determining the covariate balance in the prevalent cohort under various scenarios. We used 5000 replications of the tests to calculate the size and power, and let μ{e(X̃_i; γ̂)} = e(X̃_i; γ̂). We generated data for the incident cohort from the same model described in the first set of simulations. Under the null hypothesis, the propensity score of the prevalent cohort is the same as that of the incident cohort, e(x_i) = P(Z_i|X_i) = expit(0.1 + 0.4X_i1 + 0.4X_i2 + 0.4X_i3), where expit(.) = exp(.)/{1 + exp(.)}. Under the alternative (power I), we set the propensity score of the prevalent cohort as $e({\mathbf{x}}_i)=P(Z_i|{\mathbf{X}}_i)=\text{expit}(0.1+0.4X_{i1}^2+0.4X_{i2}^2+0.4X_{i3}^2)$, which has a different form than the propensity score function of the incident cohort. For another alternative (power II), we chose the propensity score of the prevalent cohort as e(x_i) = P(Z_i|X_i) = expit(0.1 + 0.8X_i1 + 1.2X_i2 + 1.6X_i3), which has the same function form but different coefficients from that in the incident cohort.

Table 3 lists the rates of rejecting the null hypothesis at a significance level of 0.05. The type I error rates were well maintained in the null scenario, especially for larger sample sizes. The power of the test increased with increasing sample sizes and did not change with the censoring rate. However, the proposed test performed differently for the two alternative settings. The test was very powerful for detecting different function forms between the two propensity scores (power scenario I); but, it had only mild power to detect the difference when the propensity scores shared the same model form but had different regression coefficients (power scenario II). Because the proposed test has relatively low power under power scenario II, we applied the proposed estimation method to the data generated from power scenario II when the difference in propensity score models was ignored. The resulting treatment estimators were reasonably robust to such model misspecification, and did not have substantial biases; for example, the bias was 0.05 (true value=0.5) and the associated coverage probability was 0.933 when m = 400 and n = 200.

Table 3. Simulation results: rates of rejection of the null hypothesis.

	C1% = 60%, C2% = 40%			C1% = 40%, C2% = 20%
(m, n)	Type I	Power1	Power2	Type I	Power1	Power2
(200,200)	0.070	0.672	0.213	0.063	0.704	0.256
(400,200)	0.043	0.683	0.173	0.058	0.711	0.220
(400,400)	0.049	0.873	0.223	0.058	0.877	0.272
(600,600)	0.046	0.945	0.240	0.053	0.949	0.296

5. Data Application

We used data from the SEER-Medicare database, which links the National Cancer Institutes SEER registry with Medicare claims and enrollment files. The SEER-Medicare database connects 94% of patients aged 65 years or older. Using this population-based database, we identified a prevalent cohort and an incident cohort to evaluate the effect of RT in patients of age ≥ 66 who were diagnosed with stage IV breast cancer as the first primary cancer. The incident cohort consisted of 1867 patients who were diagnosed with breast cancer after 2007, and the prevalent cohort included 1106 patients who were diagnosed with breast cancer prior to 2007 and were alive in 2007. Patients in both cohorts were followed until death or the last observation time as of December 31, 2010.

The clinical question of interest was whether RT had any benefit on the overall survival time measured from the date of breast cancer diagnosis. We extracted each patient's baseline covariates, including comorbidity, race, region of residence, age at diagnosis, estrogen-receptor status, progesterone-receptor status, and tumour size. We used Medicare claims to identify RT received within 12 months of breast cancer diagnosis. Table 4 summarizes the patient characteristics by cohort. Using the Kaplan-Meier method, the estimated median survival times for the prevalent cohort were much longer than those for the incident cohort, which suggested that the observed outcome data from the prevalent cohort were sampled with bias. We used the t-test or chi-square test to detect the difference in the covariate distributions between the two cohorts. Except for race, all covariates had different distributions between the two cohorts, which implied that the observed covariates in the prevalent cohort likely did not represent the target population.

Table 4. Distribution of patient characteristics by cohort.

Variable	Incident (m = 1867)	Prevalent (n = 1106)	P-value
Median survival time (years)	3.6	7.6
Age at diagnosis (years)	77.2	75.9	< 0.0001
Race
Non-Hispanic white	1494 (80.0%)	893 (80.7%)	0.6678
Non-Hispanic black	206 (11.0%)	117 (10.6%)	0.7149
Hispanic and other	167 (8.9%)	96 (8.7%)	0.8413
Comorbidity
0	1207 (64.6%)	808 (73.1%)	< 0.0001
1	406 (21.7%)	185 (16.7%)	< 0.0008
≥2	254 (13.6%)	113 (10.2%)	0.0068
ER
Positive	1136 (60.8%)	784 (70.9%)	< 0.0001
Negative	349 (18.7%)	152 (13.7%)	0.0005
Other	382 (20.5%)	170 (15.4%)	0.0005
PR
Positive	871 (46.7%)	606 (54.8%)	< 0.0001
Negative	588 (31.5%)	307 (27.8%)	0.0349
Other	408 (21.9%)	193 (17.5%)	0.0039

For patients older than 65 years who had stage IV breast cancer, those who received RT might differ from those who did not receive RT. For example, it is likely that patients who received RT were healthier than patients who did not, regardless of whether there was any clinical benefit of RT in that age group. Hence, we included the propensity score in the Cox model to balance the covariate distributions between the RT and no-RT patient groups. We first used the baseline covariates from the 1867 patients in the incident cohort to estimate the propensity scores of a patient receiving RT, and then used the combined cohort to fit the Cox model while controlling for and not controlling for the propensity score. As seen in Table 5, a much larger beneficial effect of RT (hazard ratio=0.66) was found in the Cox model when we ignored the covariate imbalance between the RT and no-RT groups, which was likely to be overestimated. When controlling for the covariate imbalance by the propensity score, the hazard ratio of receiving RT was 0.76, with a standard error of 0.05.

Table 5.

Estimation results by Cox models using the cohorts from the SEER-Medicare linked data. HR: hazard ratio; SE: standard error

	Incident cohort			Combined cohort
	HR	SE	P-value	HR	SE	P-value
Radiation effect without adjusting by propensity score*	0.657	0.033	< 0.001	0.700	0.028	< 0.001
Radiation effect adjusted by propensity score	0.756	0.045	< 0.001	0.748	0.030	< 0.001

^*the model does not include covariates X.

Our next step was to combine the prevalent and incident cohorts to gain statistical efficiency. Using the test in Section 3, we checked whether the estimated propensity scores from the incident cohort can be applied to the prevalent cohort to balance the covariate distribution between the RT and no-RT groups. The p-value was 0.99, which suggested that the RT and no-RT groups within the prevalent cohort had comparable baseline covariate distributions after applying the propensity score from the incident cohort. We then included the prevalent data to fit the Cox models after adjusting for baseline covariates and sampling bias in the prevalent cohort. The results indicated that the use of RT had a significant benefit for the overall survival time (hazard ratio=0.75;p-value< 0.001), and the combined data yielded a similar RT effect, but with a smaller standard error (0.03 vs 0.05) compared to that from the incident cohort only.

6. Discussion

Propensity score analysis is a valuable and convenient approach to the analysis of observational data. If data come from a prevalent cohort study, the propensity score analysis encounters significant difficulty because of sampling bias. However, prevalent cohorts contain valuable information on clinical outcomes, usually with longer periods of follow-up compared with incident cohorts. In this article, we propose a propensity score method based on the joint analysis of the incident and prevalent cohorts, which allows for adjustment for both the covariate imbalance between treatment arms and the sampling bias in the prevalent cohort. We assume both cohorts come from the same target population so that the joint analysis of both cohorts would provide more efficient results than the analysis of the incident cohort alone.

We develop a test procedure to check whether the propensity score model estimated with the incident cohort can balance the covariates between treatment groups in the prevalent cohort. Once the balance property of the prevalent cohort is confirmed by the test, we include the estimated propensity score in the Cox model and propose estimating methods, in which the modified at-risk function or the inverse weighting method is adopted to handle the biased sampling issue in the prevalent cohort. Given additional distribution assumptions on the truncation time, the data from the prevalent cohort can be utilized to estimate the propensity score and improve statistical efficiency.

It has been argued that a specification test can be used to check the adequacy of the propensity score model (Li and Greene, 2013; Imai et al., 2008; Hansen and Bowers, 2008). In this article, we present an implementation of this idea in the context of the joint analysis of prevalent and incident cohorts. For the proposed test, we restrict our attention to the setting where the censoring time and truncation time are independent of the covariates. To accommodate the possibility of covariate-dependent censoring and covariate-dependent truncation, we can adopt regression analysis or a local Kaplan-Meier estimator (González-Manteiga and Cadarso-Suarez, 1994) to estimate the covariate-specific distributions, denoted as h_θA(a|z, x) and S_c(t|z, x). The test procedure can be generalized to incorporate covariate-dependent censoring and covariate-dependent truncation, by replacing the weighting function in (8) by $w({\stackrel{\sim }{Y}}_i|Z_i,{\mathbf{x}}_i)={\int }_0^{{\stackrel{\sim }{Y}}_i}{h}_{{\mathit{\theta }}_A}(a|z_i,{\mathbf{x}}_i)S_c(Y_i-a|z_i,{\mathbf{x}}_i)\mathit{\text{da}}$. After the replacement we plug the estimated covariate-specific distributions in the implementation of the test.

Appendix

A.1. Regularity conditions

• C.1) Given the observable covariate X, potential outcomes are independent of the treatment assignment.

• C.2) The propensity score e(x) ∈ (0, 1), such that subjects with the same covariate values have a positive probability of being assigned to either of two treatment arms.

• C.3) The parameter space of θ is a compact subset of ℝ^q+3, and the true parameter value θ₀ is in the interior of the parameter space.

• C.4) X is a q × 1 vector of bounded covariates, not contained in a (q − 1)-dimensional hyperplane.

• C.5) The censoring time C is not degenerate at 0 given any (z, x), and P(T > C|Z, X) > 0.

• C.6) The conditional survival function of C̃ satisfies t₀ ≤ sup{t : S̃_c(t|Z̃, X̂) > 0} ≤ t₁ uniformly in (Z̃, X̃) for some positive constants t₀ and t₁. Furthermore, P(Ṽ > C̃|Z̃, X̃) > 0.

• C.7) ${\int }_0^{{\tau }_0}[{\{{\int }_t^{{\tau }_0}{S}_c(u)\mathit{\text{du}}\}}^2/\{S_c{(t)}^2{S}_{\upsilon }(t)\}]d{S}_c(t)<\infty$, where S_υ(.) is the survival function for the residual failure time.

Condition C.1, referred to as ignorability assumption, implies that all variables that influence treatment assignment and potential outcomes are observed. Condition C.2 rules out the phenomenon of perfect predictability of the treatment received given X. Condition C.3 ensures the compactness of the parameter space, and Condition C.4 is for model identifiability in the regression analysis. Conditions C.5 and C.6 state assumptions for the censoring time of the incident cohort and the residual censoring time of the prevalent cohort such that there is a probability of observing uncensored observations in both cohorts. Condition C.7 is a required assumption for the weak convergence of the Kaplan-Meier estimator of the residue censoring.

A.2. Proof of Theorem 1

Note that the estimating equation U₁(γ) = 0 is the score estimating equation under the logistic regression model. Under regularity conditions C.3 and C.4, the maximum likelihood estimator γ̂ is consistent.

Under the Cox model, the estimating equation U₂(θ) = 0 is the sum of the partial score equation for the data from the incident cohort and the conditional score equation for the data from the prevalent cohort. Hence the solution to U₂(θ) = 0, denoted as θ̂, is the maximum of the likelihood L(θ) = L₁(θ) × L₂(θ), where L₁(θ) is the partial likelihood of the data from the incident cohort and L₂(θ) is the conditional likelihood for the data from the prevalent cohort. For simplicity of notation, let θ₀ = 0. For any δ = 0, since the intersection of the parameter space of θ and the closure of a δ-neighborhood of origin is closed, log L(θ) has a local maximum on this set. If we can show that the maximum lies in the parameter space of θ at a distance from the origin less than δ in probability, then the existence and consistency of θ̂ will follow immediately. This can be shown by proving that log L(θ) < log L(0) with probability tending toward 1 for all θ in its parameter space that are at a distance δ from the origin. Such a fact can be established by using the Taylor expansion of log log L(θ) around 0. For simplicity, we assume θ is one-dimensional, then we have

$$\frac{1}{n}\{L(\delta )-L(0)\}=\frac{1}{n}\frac{\partial logL(0)}{\partial \theta }+\frac{1}{2n}\frac{{\partial }^{2}logL({\delta }^{\ast })}{\partial {\theta }^2}{\delta }^2,$$

where δ* is a point between the origin and δ. Note that when n and m go to infinity,

$$\frac{1}{n}\frac{\partial logL(0)}{\partial \theta }{\to }^{p}0\text{and}\frac{1}{2n}\frac{{\partial }^{2}logL({\delta }^{\ast })}{\partial {\theta }^2}{\to }^{p}a<0.$$

Then we have {L(δ) − L(0)} < 0 in probability. Consistency follows.

For the asymptotic normality, apply the Taylor expansion of U(θ) around θ₀:

$$\sqrt{N}(\widehat{\mathit{\theta }}-{\mathit{\theta }}_0)={\{-\frac{1}{N}\frac{\partial \mathit{U}({\mathit{\theta }}_0)}{\partial \mathit{\theta }}\}}^{-1}\frac{1}{\sqrt{N}}\mathit{U}({\mathit{\theta }}_0)+o(1),$$

where N = n + m. By the strong law of large numbers, $\frac{\partial \mathit{U}(\widehat{\mathit{\theta }})}{\partial \mathit{\theta }}/N$ converges to

$$\mathit{A}=[\rho E\{\partial {\mathit{U}}_{i1}(\mathit{\theta })/\partial \mathit{\theta }\},\rho E\{\partial {\mathit{U}}_{i21}(\mathit{\theta })/\partial \mathit{\theta }\}+(1-\rho )E\{\partial {\mathit{U}}_{i22}(\mathit{\theta })/\partial \mathit{\theta }\}]$$ (9)

almost surely, where ρ = lim_{n→∞,m→∞}m/(m + n),

$${\mathit{U}}_{i1}(\mathit{\theta })={(1,{\mathbf{X}}_i)}^{\top }\{Z_i-\frac{exp\{{\mathit{\gamma }}^{\top }(1,{\mathbf{X}}_i)\}}{1+exp\{{\mathit{\gamma }}^{\top }(1,{\mathbf{X}}_i)\}}\}{\mathit{U}}_{i21}(\mathit{\theta }(={\delta }_i[{\{Z_i,e({\mathbf{X}}_i;\mathit{\gamma })\}}^{\top }-\frac{{\sum }_{j\in R_1(Y_i)}{\{Z_j,e({\mathbf{X}}_j;\mathit{\gamma })\}}^{\top }exp\{\alpha Z_j+\beta e({\mathbf{X}}_j;\mathit{\gamma })\}}{{\sum }_{j\in R_1(Y_i)}exp\{\alpha Z_j+\beta e({\mathbf{X}}_j;\mathit{\gamma })\}}]{\mathit{U}}_{i22}(\mathit{\theta }(={\stackrel{\sim }{\delta }}_i[{\{{\stackrel{\sim }{Z}}_i,e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma })\}}^{\top }-\frac{{\sum }_{j\in R_2({\stackrel{\sim }{Y}}_i)}{\{{\stackrel{\sim }{Z}}_j,e({\stackrel{\sim }{\mathbf{X}}}_j;\mathit{\gamma })\}}^{\top }exp\{\alpha {\stackrel{\sim }{Z}}_j+\beta e({\stackrel{\sim }{\mathbf{X}}}_j;\mathit{\gamma })\}}{{\sum }_{j\in R_2({\stackrel{\sim }{Y}}_i)}exp\{\alpha {\stackrel{\sim }{Z}}_j+\beta e({\stackrel{\sim }{\mathbf{X}}}_j;\mathit{\gamma })\}}].$$

The matrix A can be empirically estimated by definition. Applying the classical central limit theorem and martingale central limit theorem, as n → ∞ and m → ∞, we have

$$\mathit{U}({\mathit{\theta }}_0)/\sqrt{N}{\to }^{d}N(\mathbf{0},\sum ),$$ (10)

where $\sum =\left(\begin{array}{cc}{\mathit{\sigma }}_{11}^2& 0\\ 0& {\mathit{\sigma }}_{22}^2\end{array}\right)$, ${\mathit{\sigma }}_{11}^2=\rho E{\{{\mathit{U}}_{i1}(\mathit{\theta })\}}^{\otimes 2}$, and ${\mathit{\sigma }}_{22}^2=\rho var\{{\mathit{U}}_{i21}(\mathit{\theta })\}+(1-\rho )var\{{\mathit{U}}_{i22}(\mathit{\theta })\}$. The covariance matrix that corresponds to estimating equation U₁(θ₀) can be consistently estimated by

$${\widehat{\sigma }}_{11}^2=\rho \frac{1}{m}\sum _{i=1}^m\{{\mathit{U}}_{i1}(\widehat{\mathit{\theta }}){\mathit{U}}_{i1}{(\widehat{\mathit{\theta }})}^{\top }\},$$

and the covariance matrix associated with estimating equation U₂(θ₀) can be consistently estimated by

$${\widehat{\sigma }}_{22}^2=\frac{\rho }{n}\sum _{i=1}^n\frac{{\delta }_i{\sum }_{j\in R_1(Y_i)}^n[{\{Z_j,e({\mathbf{X}}_j;\widehat{\mathit{\gamma }})\}}^{\top }-{\mathit{\mu }}_i]exp\{\alpha Z_j+\widehat{\beta }e({\mathbf{X}}_j;\widehat{\mathit{\gamma }})\}}{{\sum }_{j\in R_1(Y_i)}^{n}exp\{\alpha Z_j+\widehat{\beta }e({\mathbf{X}}_j;\widehat{\mathit{\gamma }})\}}+\frac{(1-\rho )}{m}\sum _{i=1}^m\frac{{\widehat{\delta }}_i{\sum }_{j\in R_2({\stackrel{\sim }{Y}}_i)}^n[{\{{\stackrel{\sim }{Z}}_j,e({\stackrel{\sim }{\mathbf{X}}}_j;\widehat{\mathit{\gamma }})\}}^{\top }-{\stackrel{\sim }{\mathit{\mu }}}_i]exp\{\alpha {\stackrel{\sim }{Z}}_j+\widehat{\beta }e({\stackrel{\sim }{\mathbf{X}}}_j;\widehat{\mathit{\gamma }})\}}{{\sum }_{j\in R_2({\stackrel{\sim }{Y}}_i)}^{n}exp\{\alpha {\stackrel{\sim }{Z}}_j+\widehat{\beta }e({\stackrel{\sim }{\mathbf{X}}}_j;\widehat{\mathit{\gamma }})\}},$$

where

$$\begin{array}{c}{\mathit{\mu }}_i=\frac{{\sum }_{k\in R_1(Y_i)}{\{Z_k,e({\mathbf{X}}_k;\widehat{\mathit{\gamma }})\}}^{\top }exp\{\alpha Z_k+\widehat{\beta }e({\mathbf{X}}_k;\widehat{\mathit{\gamma }})\}}{{\sum }_{k\in R_1(Y_i)}exp\{\alpha Z_k+\widehat{\beta }e({\mathbf{X}}_k;\widehat{\mathit{\gamma }})\}},\\ {\stackrel{\sim }{\mathit{\mu }}}_i=\frac{{\sum }_{k\in R_2({\stackrel{\sim }{Y}}_i)}{\{{\stackrel{\sim }{Z}}_k,e({\stackrel{\sim }{\mathbf{X}}}_k;\widehat{\mathit{\gamma }})\}}^{\top }exp\{\alpha {\stackrel{\sim }{Z}}_k+\widehat{\beta }e({\stackrel{\sim }{\mathbf{X}}}_k;\widehat{\mathit{\gamma }})\}}{{\sum }_{k\in R_2({\stackrel{\sim }{Y}}_i)}exp\{\alpha {\stackrel{\sim }{Z}}_k+\widehat{\beta }e({\stackrel{\sim }{\mathbf{X}}}_k;\widehat{\mathit{\gamma }})\}}.\end{array}$$

Summarizing equations (9) and (10), we have the asymptotic normality for θ̂

$$\sqrt{N}(\widehat{\mathit{\theta }}-{\mathit{\theta }}_0)\to N(0,{\mathit{A}}^{-1}\sum {\mathit{A}}^{-1}).$$

A.3. Proof of Theorem 2

Without loss of generality, we assume μ{e(X̃_i; γ̂)} = e(X̃_i; γ̂) in the proof of Theorem 2. Let η = (ξ, ζ) with true value η₀, and

$${\mathit{U}}_{\mathit{\text{test}}}(\mathit{\eta })=\sum _{i=1}^n\frac{{\stackrel{\sim }{\delta }}_i{\{e({\stackrel{\sim }{\mathbf{X}}}_i;\widehat{\mathit{\gamma }}),{\stackrel{\sim }{Z}}_i\}}^{\top }}{\widehat{w}({\stackrel{\sim }{Y}}_i)}\{\stackrel{\sim }{\mathbf{X}}-\mathit{\xi }e({\stackrel{\sim }{\mathbf{X}}}_i;\widehat{\mathit{\gamma }})-\mathit{\zeta }{\stackrel{\sim }{Z}}_i\}.$$

Applying the Taylor expansion of U_test(η) around η₀:

$$\sqrt{n}(\widehat{\mathit{\eta }}-{\mathit{\eta }}_0)={\{-\frac{1}{n}\frac{\partial }{\partial \mathit{\eta }}{\mathit{U}}_{\mathit{\text{test}}}({\mathit{\eta }}_0)\}}^{-1}\frac{1}{\sqrt{n}}{\mathit{U}}_{\mathit{\text{test}}}({\mathit{\eta }}_0)+o(1).$$

By the law of large numbers, $\frac{\partial }{\partial \mathit{\eta }}{\mathit{U}}_{\mathit{\text{test}}}({\mathit{\eta }}_0)/n$ converges in probability to its expectation, denoted as A_η. The remaining task is to check the asymptotic behavior of U_test(η₀). It can be shown that

$${\mathit{U}}_{\mathit{\text{test}}}(\mathit{\eta })=\frac{1}{\sqrt{n}}\sum _{i=1}^n\frac{{\stackrel{\sim }{\delta }}_i{\{e({\widehat{\mathbf{X}}}_i;\widehat{\mathit{\gamma }}),{\stackrel{\sim }{Z}}_i\}}^{\top }}{\widehat{w}({\stackrel{\sim }{Y}}_i)}\{{\stackrel{\sim }{\mathbf{X}}}_i-\mathit{\xi }e({\stackrel{\sim }{\mathbf{X}}}_i;\widehat{\mathit{\gamma }})-\mathit{\zeta }{\stackrel{\sim }{Z}}_i\}$$

$$=\frac{1}{\sqrt{n}}\sum _{i=1}^n\frac{{\stackrel{\sim }{\delta }}_i{\{e({\widehat{\mathbf{X}}}_i;\mathit{\gamma }),{\stackrel{\sim }{Z}}_i\}}^{\top }}{w({\stackrel{\sim }{Y}}_i)}\{{\stackrel{\sim }{\mathbf{X}}}_i-\mathit{\xi }e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma })-\mathit{\zeta }{\stackrel{\sim }{Z}}_i\}$$ (11)

$$+\frac{1}{\sqrt{n}}\sum _{i=1}^n\{\frac{{\stackrel{\sim }{\delta }}_i}{\widehat{w}({\stackrel{\sim }{Y}}_i)}-\frac{{\stackrel{\sim }{\delta }}_i}{w({\stackrel{\sim }{Y}}_i)}\}{\{e({\stackrel{\sim }{X}}_i;\mathit{\gamma }),{\stackrel{\sim }{Z}}_i\}}^{\top }\{{\stackrel{\sim }{\mathbf{X}}}_i-\mathit{\xi }e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma })-\mathit{\zeta }{\stackrel{\sim }{Z}}_i\}$$ (12)

$$-\frac{1}{\sqrt{n}}\sum _{i=1}^n\frac{{\stackrel{\sim }{\delta }}_i{\{e({\widehat{\mathbf{X}}}_i;\mathit{\gamma }),{\stackrel{\sim }{Z}}_i\}}^{\top }}{w({\stackrel{\sim }{Y}}_i)}\{\mathit{\xi }e({\stackrel{\sim }{\mathbf{X}}}_i;\widehat{\mathit{\gamma }})-\mathit{\xi }e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma })\}$$ (13)

$$+\frac{1}{\sqrt{n}}\sum _{i=1}^n\{\frac{{\stackrel{\sim }{\delta }}_i}{\widehat{w}({\stackrel{\sim }{Y}}_i)}-\frac{{\stackrel{\sim }{\delta }}_i}{w({\stackrel{\sim }{Y}}_i)}\}{\{e({\stackrel{\sim }{X}}_i;\mathit{\gamma }),{\stackrel{\sim }{Z}}_i\}}^{\top }\{\mathit{\xi }e({\stackrel{\sim }{\mathbf{X}}}_i;\widehat{\mathit{\gamma }})-\mathit{\xi }e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma })\}$$ (14)

$$+\frac{1}{\sqrt{n}}\sum _{i=1}^n\frac{{\stackrel{\sim }{\delta }}_i(e({\widehat{\mathbf{X}}}_i;\widehat{\mathit{\gamma }})-e({\widehat{\mathbf{X}}}_i;\mathit{\gamma }))}{w({\stackrel{\sim }{Y}}_i)}\{{\stackrel{\sim }{\mathbf{X}}}_i-\mathit{\xi }e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma })-\mathit{\zeta }{\stackrel{\sim }{Z}}_i\}.$$ (15)

By the uniform consistency of ŵ(y) to w(y) and the martingale expression of the Kaplan-Meier estimator, (12) can be rewritten as

$$\frac{1}{\sqrt{n}}\sum _{i=1}^n\frac{w({\stackrel{\sim }{Y}}_i)-\widehat{w}({\stackrel{\sim }{Y}}_i)}{w^2({\stackrel{\sim }{Y}}_i)}{\stackrel{\sim }{\delta }}_i{\{e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma }),{\stackrel{\sim }{Z}}_i\}}^{\top }\{{\stackrel{\sim }{\mathbf{X}}}_i-\mathit{\xi }e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma })-\mathit{\zeta }{\stackrel{\sim }{Z}}_i\}=\frac{1}{\sqrt{n}}\sum _{i=1}^n\left\{\frac{{\int }_0^{t_0}\mathit{D}(t)d{M}_i(t)}{S_c(t)S_c(t)}\right\}+o(1),$$

where

$$\begin{array}{c}\mathit{D}(t)=\underset{n\to \infty }{lim}\frac{1}{n}\sum _{i=1}^{n}I(t\le Y_i){\delta }_i{\{e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma }),Z_i\}}^{\top }{\int }_t^{Y_i}{\widehat{S}}_c(u)d(u)\frac{\{{\stackrel{\sim }{\mathbf{X}}}_i-\mathit{\xi }e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma })-\mathit{\zeta }{\stackrel{\sim }{Z}}_i\}}{{\widehat{w}}^2(Y_i)},\\ M_i(t)=I(Y_i-W_i\le t,{\delta }_i=0)-{\int }_0^{t}I(Y_i-W_i\ge u)d{\mathrm{\Lambda }}_c(u),\end{array}$$

and Λ_c(u) is the cumulative hazard function of the censoring time. By the martingale central limit theorem and regularity condition C.7), (12) follows a normal distribution with variance denoted as Σ_M. The asymptotic behavior of (13) is determined by the asymptotic behavior of γ̂, because it is equal to

$$\frac{1}{\sqrt{n}}\sum _{i=1}^n\frac{{\stackrel{\sim }{\delta }}_i{(1,{\stackrel{\sim }{Z}}_i)}^{\top }}{w({\stackrel{\sim }{Y}}_i)}\mathit{\xi }\{\frac{\partial }{\partial \mathit{\gamma }}e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma })\}(\widehat{\mathit{\gamma }}-\mathit{\gamma })+o(1).$$ (16)

By Theorem 1, when m → ∞ and n → ∞, we have $\sqrt{n}(\widehat{\mathit{\gamma }}-\mathit{\gamma }){\to }^{d}N(0,{\mathit{\sigma }}_{\gamma }^2)$, where ${\mathit{\sigma }}_{\gamma }^2=(1-\rho ){\mathit{\sigma }}_{\gamma }^{\ast }$ and ${\mathit{\sigma }}_{\gamma }^{\ast }$ is the (q + 1) × (q + 1) upper submatrix of A⁻¹ΣA⁻¹. Therefore, (13) converges in distribution to a normal distribution with mean 0 and variance Σ₂, where

$${\sum }_2=E{\{\frac{{\stackrel{\sim }{\delta }}_i{(e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma }),{\stackrel{\sim }{Z}}_i)}^{\top }}{w({\stackrel{\sim }{Y}}_i)}\mathit{\xi }\frac{\partial }{\partial \mathit{\gamma }}e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma })\}}^{\top }{\sigma }_{\gamma }^{2}E\{\frac{{\stackrel{\sim }{\delta }}_i{(e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma }),{\stackrel{\sim }{Z}}_i)}^{\top }}{w({\stackrel{\sim }{Y}}_i)}\mathit{\xi }\frac{\partial }{\partial \mathit{\gamma }}e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma })\}.$$

After some algebra, we can show that (14) converges to 0 in probability. Similar to the arguments used for (13), (15) converges in distribution to a normal distribution. Summarizing the previous arguments, $\sqrt{n}\{\widehat{\mathit{\eta }}-{\mathit{\eta }}_0\}{\to }^{d}N(0,{\mathit{A}}_{\eta }^{-1}{\sum }_{\eta }{\mathit{A}}_{\eta }^{-1})$, where

$${\sum }_{\eta }=E{[\frac{{\stackrel{\sim }{\delta }}_i{(e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma }),{\stackrel{\sim }{Z}}_i)}^{\top }}{w({\stackrel{\sim }{Y}}_i)}\{{\stackrel{\sim }{\mathbf{X}}}_i-\mathit{\xi }e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma })-\mathit{\zeta }{\stackrel{\sim }{Z}}_i\}+{\mathit{A}}_3{\mathbf{U}}_{i1}(\mathit{\gamma })]}^{\otimes 2}+{\sum }_M$$

and

$${\mathit{A}}_3=E[\frac{{\stackrel{\sim }{\delta }}_i{(e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma }),{\stackrel{\sim }{Z}}_i)}^{\top }}{w({\stackrel{\sim }{Y}}_i)}\mathit{\xi }\frac{\partial }{\partial \mathit{\gamma }}e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma })+\frac{{\stackrel{\sim }{\delta }}_i}{w({\stackrel{\sim }{Y}}_i)}\{{\stackrel{\sim }{\mathbf{X}}}_i-\mathit{\xi }e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma })-\mathit{\zeta }{\stackrel{\sim }{Z}}_i\}\frac{\partial }{\partial \mathit{\gamma }}e({\stackrel{\sim }{\mathbf{X}}}_i;\mathit{\gamma })].$$

This implies that under the null hypothesis, ζ̂ converges in distribution to a normal distribution with mean 0 and variance V, where V is the submatrix of ${\mathit{A}}_{\eta }^{-1}{\sum }_{\eta }{\mathit{A}}_{\eta }^{-1}$ corresponding to ζ̂. In other words, the limit distribution of the proposed test T_test is a chi-squared limiting distribution with a degree of freedom q under the null hypothesis.