The importance of mechano-electrical feedback and inertia in cardiac electromechanics

Abstract

In the past years, a number cardiac electromechanics models have been developed to better understand the excitation-contraction behavior of the heart. However, there is no agreement on whether inertial forces play a role in this system. In this study, we assess the influence of mass in electromechanical simulations, using a fully coupled finite element model. We include the effect of mechano-electrical feedback via stretch activated currents. We compare five different models: electrophysiology, electromechanics, electromechanics with mechano-electrical feedback, electromechanics with mass, and electromechanics with mass and mechano-electrical feedback. We simulate normal conduction to study conduction velocity and spiral waves to study fibrillation. During normal conduction, mass in conjunction with mechano-electrical feedback increased the conduction velocity by 8.12% in comparison to the plain electrophysiology case. During the generation of a spiral wave, mass and mechano-electrical feedback generated secondary wavefronts, which were not present in any other model. These secondary wavefronts were initiated in tensile stretch regions that induced electrical currents. We expect that this study will help the research community to better understand the importance of mechanoelectrical feedback and inertia in cardiac electromechanics.

1. Motivation

The heart is composed of four chambers and its primary function is to circulate blood in the cardivascular system. To achieve this goal, electrical waves travel through the cardiac tissue to trigger muscle contraction and generate a coordinated movement of the ventricles that pump blood through the arteries. Despite tremendous scientific advances, heart disease is responsible for half a million deaths each year in the United States alone [39]. Many of these deaths are caused by lethal arrhythmias, which provoke an abnormal electrical activity of the heart that ultimately leads to mechanical dysfunction and death. In the case of cardiac fibrillation, arrhythmias are driven by electrical spiral waves that self-excite, preventing the coordinated contraction of cardiac tissue and diminishing the pumping capacity of the heart [45]. The electrical wave that modulates muscle contraction is influenced by the mechanical deformation. Indeed, mechanical contraction deforms the domain where the electrical wave is propagating, altering wave dynamics. Moreover, transmembrane currents are generated by the stretching of ionic channels. This mechano-electrical feedback is thought to be responsible for “commotio cordis”, a condition in which the precordial impact of an object may start ventricular fibrillation [33]. Mechano-electrical feedback is also responsible for “precordial thump”, a procedure in which the currents generated by this mechanism are used to stop fibrillation [7].

Computational modeling can help to better understand the interplay between the electrical and the mechanical behavior in the heart, that would otherwise be difficult to characterize in laboratory experiments [8, 37]. Given the complexity of these interactions, different computational studies decide to include or neglect certain components of the electromechanical system. For example, most electrophysiology simulations are performed on a fixed domain, ignoring the mechanical interaction [48, 2, 14, 11]. When the focus is on the mechanical aspects of the tissue, the influence of deformation over the electric field is not directly adressed, as the electrical and mechanical models are solved separately [50, 4]. An intermediate approach is to solve the electrical and mechanical problems staggered [53, 41, 32, 43, 29]. Another component that is often neglected is the inertia term in the balance of linear momentum. Although some studies include the influence of mass in simulations of the heart [54, 9, 51], a large majority neglects its influence [10, 41, 43, 32, 31, 5]. In this work, we explore the effect of inertia in electromechanical models. We hypothesize that additional deformations caused by inertia may alter the electrical wave dynamics via the mechano-electrical feedback. Using our fully coupled formulation [18], we assess the influence of mass in normal wave propagation and in the case of fibrillation by simulating a spiral wave. We measure electrophysiological variables including the conduction velocity and the spiral wave trajectory. We also asses the influence of mechano-electrical feedback currents and their relation with inertial effects. To our knowledge, this is the first study to systematically quantify the inertial effect in a three-dimensional electromechanical model.

This manuscript is organized as follows: Section 2 covers the continuum formulation of the electromechanics problem, Section 3 describes the computational implementation, Section 4 describes the particular models we use to study conduction velocity and spiral waves along with the results of these studies. We conclude with a critical discussion in Section 5.

2. Continuum eletromechanical model

We illustrate the continuum model of electro-mechanical coupling by briefly summarizing the kinematic equations, the balance equations, and the constitutive equations of excitation-contraction coupling.

2.1. Kinematic equations

To characterize the kinematics of finite deformation, we introduce the deformation map φ, which maps particles X from the undeformed material configuration ${\mathit{ℬ}}_0\subset {ℝ}^3$ to particles x = φ (X, t) in the deformed spatial configuration $\mathit{ℬ}={\mathit{\phi }}_t\left({\mathit{ℬ}}_0\right)\subset {ℝ}^3$ [24]. Its derivative with respect to the undeformed coordinates X defines the deformation gradient,

$$\mathit{F}=\nabla \mathit{\phi },$$ (1)

from which we characterize local volume changes by computing the Jacobian J = det(F). We further introduce the right Cauchy-Green deformation tensor,

$$\mathit{C}={\mathit{F}}^{\mathrm{t}}\cdot \mathit{F},$$ (2)

and consider the invariants,

$$I_3=\text{det}\left(\mathit{C}\right)={\text{det}}^2\left(\mathit{F}\right)=J^2\text{and}{I}_4=\mathit{C}:\left[{\mathit{f}}_0\otimes {\mathit{f}}_0\right]=\mathit{f}\cdot \mathit{f}={\lambda }^2,$$ (3)

where f₀ is the material myocardial fiber unit vector, f = F·f₀ is the spatial myocardial fiber vector with norm $\lambda =\sqrt{\mathit{f}\cdot \mathit{f}}$, and : represents the tensor contraction operator. The invariant I₃ quantifies volumetric changes and the invariant I₄ quantifies the cardiac fiber stretch. We further introduce the spatial myocardial fiber unit vector $\widehat{\mathit{f}}=\mathit{f}/\lambda$. In what follows, we denote the material time derivative as $\left\{\dot{\circ }\right\}=d\{\circ \}/\mathrm{d}t$ and the material gradient and divergence as ∇{o} = ∂{o}/∂X and Div {o} = ∂{o}/∂X : I and the spatial gradient as ∇_x{o} = ∂{o}/∂x.

2.2. Balance equations

We characterize the electrical problem through the normalized monodomain equation for the transmembrane potential $\Phi :{\mathit{ℬ}}_0\times ℝ\to ℝ$ and define the mechanical problem through the balance of linear momentum for the deformation φ,

$$\begin{array}{l}\dot{\Phi }=\text{Div}\left(\mathit{Q}\right)+F^{\Phi }\mathrm{in}{\mathit{ℬ}}_0\times ℝ\\ {\rho }_0\ddot{\phi }=\text{Div}\left(\mathit{F}\cdot \mathit{S}\right)+{\mathit{F}}^{\phi }\mathrm{in}{\mathit{ℬ}}_0\times ℝ.\end{array}$$ (4)

Here, Q is the material electrical flux, F^Φ is the material ionic current, ρ₀ is the material density, S is the second Piola-Kirchhoff stress, and F^φ is the external mechanical force vector. We note that the deformation mapping allow us to compute the spatial transmembrane potential $\varphi :\mathit{ℬ}\times ℝ\to ℝ$ through mapping composition, i.e. ϕ(x,t) = Φ(φ⁻¹(x,t),t).

2.3. Constitutive equations

To close the set of equations, we specify the constitutive equations for the electrical flux Q, the ionic current F^Φ, the second Piola-Kirchhoff stress S, and the external forces F^φ Following Fick’s law, we assume that the electrical flux proportional to the gradient of the transmembrane potential in the spatial configuration,

$$\mathit{q}=-\mathit{d}\cdot {\nabla }_{\mathit{x}}\varphi ,$$ (5)

where $\mathit{d}=d^{\text{iso}}\mathit{I}+d^{\text{ani}}\widehat{\mathit{f}}\otimes \widehat{\mathit{f}}$ denotes the conductivity tensor, which consists of an isotropic contribution d^iso and an anisotropic contribution d^ani to account for faster conductivity along the current fiber direction $\widehat{\mathit{f}}$ [12]. Using the Piola transform Q = F⁻¹ q/J, we express the material electrical flux,

$$\mathit{Q}=-\mathit{D}\cdot \nabla \Phi ,$$ (6)

where D = D^iso C⁻¹ + D^anif₀ ⊗ f₀/λ² is the conductivity tensor in the material configuration. The material and spatial conductivity parameters are related as D^iso = J d^iso and D^ani = J d^ani. For the ionic current, we consider a purely electrochemical component $F_{\mathrm{e}}^{\Phi }$ plus a mechano-electrical feedback component $F_{\mathrm{m}}^{\Phi }$,

$$F^{\Phi }=F_{\mathrm{e}}^{\Phi }+F_{\mathrm{m}}^{\Phi }.$$ (7)

For the purely electrochemical component, we adopt a modified version of the Aliev-Panfilov model for ionic current [2, 27, 49],

$$F_{\mathrm{e}}^{\Phi }=c_1\Phi \left[\Phi -\alpha \right]\left[\Phi -1\right]-c_{2}r\Phi ,$$ (8)

where the cubic polynomial term controls the fast upstroke of the action potential through the parameters c₂ and α [15, 40], and the coupling term controls the slow repolarization through the recovery variable r [2]. We treat the recovery variable as an internal variable, which evolves according to the kinetic equation,

$$\dot{r}=\left[\gamma +r{\mu }_1/\left[{\mu }_2+\Phi \right]\right]\left[-r-c_2\Phi \left[\Phi -b-1\right]\right],$$ (9)

where the recovery parameters γ, μ₁,μ₂ and b control the restitution behavior [2]. The mechano-electrical feedback reflects the effects of ionic current of stretch-activated ion channels, which we assume to the proportional to the stretch in fiber direction [18, 43, 54],

$$F_{\mathrm{m}}^{\Phi }=G_{\mathrm{s}}\theta \left[\lambda -1\right]\left[{\Phi }_{\mathrm{s}}-\Phi \right].$$ (10)

Here, Φ_s is the resting potential of this current and θ(λ) with θ(λ) = 0 for λ < 1 and θ(λ) = 1 for λ ≥ 1 is a step function that only activates this current in tension. Finally, we map the resulting fields and source terms into the physiological domain via $\widehat{\Phi }=100\Phi -80\mathrm{mV}$ and τ = 12.9 t ms, to create physiologically realistic transmembrane potentials $\widehat{\Phi }$ that range from −80 mV to +20 mV.

For simplicity, we do not consider a kinematic approach towards active muscle contraction in the sense of the generalized Hill model [19], but rather follow the standard Hill model in which the tissue stress consists of passive and active contributions,

$$\mathit{S}={\mathit{S}}^{\text{pas}}+{\mathit{S}}^{\text{act}}.$$ (11)

For the passive stress, we assume a nearly incompressible, fiber reinforced, neo-Hookean behavior [17],

$${\mathit{S}}^{\text{pas}}=\frac{1}{2}\left[\lambda \ln \left(I_3\right)-2\mu \right]{\mathit{C}}^{-1}+\mu \mathit{I}+2\eta \theta \left[I_4-1\right]{\mathit{f}}_0\otimes {\mathit{f}}_0.$$ (12)

The parameters λ and μ are the Lamé constants, η controls the stiffness in the fiber direction, and θ activates the fiber stiffness only in the case of fiber tension, i.e., λ ≥ 1. For the active stress, we assume that contraction acts primarily along the fiber direction f₀,

$${\mathit{S}}^{\text{act}}=T^{\text{act}}{I}_4^{-1}{\mathit{f}}_0\otimes {\mathit{f}}_0\text{with}{\dot{T}}^{\text{act}}=\epsilon \left(\Phi \right)\left[k_T\left[\Phi -{\Phi }_{\mathrm{r}}\right]-T^{\text{act}}\right].$$ (13)

In this model, the active muscle traction T^act is driven by changes in the electrical potential and the parameters k_T and Φ_r control the maximum active force and the resting potential [41]. The activation function, $\epsilon ={\epsilon }_0+\left[{\epsilon }_{\infty }-{\epsilon }_0\right]\exp \left(-\exp \left(-\xi \left[\Phi -\overline{\Phi }\right]\right)\right)$, ensures a smooth activation of the muscle traction T^act in terms of the limiting values ε₀ at Φ → −∞ and and ε_∞ at at Φ → +∞, the phase shift $\overline{\Phi }$, and the transition slope ξ [18]. In the following, we consider the case of no external forces and set F^φ = 0.

3. Computational model

In this section, we illustrate the finite element discretization of the governing equations, demonstrate their consistent linearization, discuss the handling of their internal variables [6] and present the most relevant sensitivities.

3.1. Strong and weak forms

To derive the weak form of the governing equations, we reformulate the electrical and mechanical balance equations (4) in their residual forms and introduce the electrical and mechanical residuals R^Φ and R^φ throughout the entire cardiac domain ${\mathit{ℬ}}_0$.

$$\begin{array}{l}{\mathrm{R}}^{\Phi }=\dot{\Phi }-\text{Div}\left(\mathit{Q}\right)-F^{\Phi }\dot{=}0\\ {\mathbf{R}}^{\phi }={\rho }_0\ddot{\phi }-\text{Div}\left(\mathit{F}\cdot \mathit{S}\right)-{\mathit{F}}^{\phi }\dot{=}0.\end{array}$$ (14)

We prescribe Dirichlet boundary conditions $\Phi =\overline{\Phi }$ and $\phi =\overline{\phi }$ on the Dirichlet boundary and Neumann boundary conditions $\mathit{Q}\cdot \mathit{N}={\overline{t}}^{\Phi }$ and $\mathit{F}\cdot \mathit{S}\cdot \mathit{N}={\overline{\mathit{t}}}^{\phi }$ on the Neumann boundary with outward normal N. For simplicity, we assume homogeneous Neumann boundary conditions, i.e., ${\overline{t}}^{\Phi }=0$ and ${\overline{t}}^{\phi }=0$. We multiply the residuals (14) by the scalar- and vector-valued test functions, δΦ and δ_φ, integrate them over the domain ${\mathit{ℬ}}_0$, and integrate the flux terms by parts to obtain the weak forms of the electrical and mechanical problems,

$$\begin{array}{l}{\mathrm{G}}^{\Phi }={\displaystyle {\int }_{{\mathit{ℬ}}_0}\delta \Phi \dot{\Phi }\mathrm{d}v}+{\displaystyle {\int }_{{\mathit{ℬ}}_0}\nabla \delta \Phi \cdot \mathit{Q}}\mathrm{d}V-{\displaystyle {\int }_{{\mathit{ℬ}}_0}\delta \Phi F^{\Phi }}\mathrm{d}V\dot{=}0\\ {\mathrm{G}}^{\phi }={\displaystyle {\int }_{{\mathit{ℬ}}_0}\delta \phi \cdot {\rho }_0\ddot{\mathit{\phi }}}\mathrm{d}V+{\displaystyle {\int }_{{\mathit{ℬ}}_0}\nabla \delta \phi :\left[\mathit{F}\cdot \mathit{S}\right]}\mathrm{d}V-{\displaystyle {\int }_{{\mathit{ℬ}}_0}\delta \phi \cdot {\mathit{F}}^{\phi }\mathrm{d}V}\dot{=}0,\end{array}$$ (15)

for admisible variations δΦ and δ_φ.

3.2. Temporal and spatial discretization

To discretize the weak forms (15) in time, we partition the time interval of interest $\mathcal{T}$ into n_step discrete subintervals [t_n,t_n+1] of length Δt = t_n+1 − t_n,

$$\mathcal{T}={\displaystyle \underset{\mathrm{n}=1}{\overset{n_{\text{step}}}{\cup }}\left[t_n,t_{n+1}\right]}.$$ (16)

For the electrical problem, we adopt an implicit Euler backward scheme to determine the electrical potential Φ at the current time point t_n+1, and approximate its time derivatives as

$$\dot{\Phi }\approx \left[\Phi -{\Phi }_{\mathrm{n}}\right]/\mathrm{\Delta }t.$$ (17)

For the mechanical problem, we adopt a Newmark time discretization to approximate the mechanical acceleration and velocity $\ddot{\mathit{\phi }}$ and $\dot{\mathit{\phi }}$ at the current time point t_n+1,

$$\begin{array}{l}\ddot{\mathit{\phi }}\approx 1/\left[\beta \mathrm{\Delta }{t}^2\right]\left[\mathit{\phi }-{\mathit{\phi }}_{\mathrm{n}}\right]-1/\left[\beta \mathrm{\Delta }t\right]{\dot{\mathit{\phi }}}_{\mathrm{n}}-\left[1-2\beta \right]/\left[2\beta \right]{\ddot{\mathit{\phi }}}_{\mathrm{n}}\\ \dot{\mathit{\phi }}\approx \gamma /\left[\beta \mathrm{\Delta }t\right]\left[\mathit{\phi }-{\mathit{\phi }}_{\mathrm{n}}\right]+\left[1-\gamma /\beta \right]{\dot{\mathit{\phi }}}_{\mathrm{n}}+\left[1-\gamma /\left[2\beta \right]\right]\mathrm{\Delta }t{\ddot{\mathit{\phi }}}_{\mathrm{n}}.\end{array}$$ (18)

Typical values for the Newmark parameters are β = 0.25 and γ = 0.5, for which Newmark’s method is stable and second order accurate for linear problems. To discretize the weak forms of the electrical and mechanical problems (15.1) and (15.2) in space, we partition the domain of interest ${\mathit{ℬ}}_0$ into n_el discrete subdomains ${\mathit{ℬ}}_0^e$,

$${\mathit{ℬ}}_0={\displaystyle \underset{\mathrm{e}=1}{\overset{n_{\mathrm{el}}}{\cup }}{\mathit{ℬ}}_0^e},$$ (19)

and adopt a finite element discretization in combination with a classical Bubnov-Galerkin scheme to discretize the test functions δΦ and δφ and trial functions Φ and φ in space within the element domain ${\mathit{ℬ}}_0^{\mathrm{e}}$ [18],

$$\begin{array}{cc}\delta {\Phi }^{\mathrm{e}}={\displaystyle {\sum }_{i=1}^{n_{\mathrm{el}}}{N}_i}\delta {\Phi }_i^{\mathrm{e}}& \delta {\phi }^{\mathrm{e}}={\displaystyle {\sum }_{j=1}^{n_{\mathrm{el}}}{N}_j}\delta {\phi }_j^{\mathrm{e}}\\ {\Phi }^{\mathrm{e}}={\displaystyle {\sum }_{k=1}^{n_{\mathrm{el}}}{N}_k}{\Phi }_k^{\mathrm{e}}& {\phi }^{\mathrm{e}}={\displaystyle {\sum }_{l=1}^{n_{\mathrm{el}}}{N}_l}{\phi }_l^{\mathrm{e}}.\end{array}$$ (20)

where N represent the standard isoparametric shape functions and n_e1 represents the number of nodes per element.

3.3. Residuals and consistent linearization

With the discretizations in time (17,18) and space (20), we can reformulate the weak forms (15) as the discrete algorithmic residuals of the electrical and mechanical problems,

$$\begin{array}{l}{\mathrm{R}}_I^{\Phi }=\underset{\mathrm{e}=1}{\overset{n_{\mathrm{el}}}{A}}{\displaystyle {\int }_{{\mathit{ℬ}}_0^{\mathrm{e}}}{N}_i}\frac{\Phi -{\Phi }_{\mathrm{n}}}{\mathrm{\Delta }t}+\nabla N_i\cdot \mathit{Q}-N_i{F}^{\Phi }\mathrm{d}{V}_{\mathrm{e}}\dot{=}0\\ {\mathbf{R}}_J^{\phi }=\underset{\mathrm{e}=1}{\overset{n_{\mathrm{el}}}{A}}{\displaystyle {\int }_{{\mathit{ℬ}}_0^{\mathrm{e}}}{N}_j}{\rho }_0\ddot{\mathit{\phi }}\left(\mathit{\phi }\right)+\nabla N_j\cdot \mathit{F}\cdot \mathit{S}-N_j{\mathit{F}}^{\phi }\mathrm{d}{V}_{\mathrm{e}}\dot{=}0.\end{array}$$ (21)

The operator A symbolizes the assembly of all element residuals at the element nodes i and j to the global residuals at the global nodes I and J. To solve for the unknown nodal electrical potential Φ_I and mechanical deformation φ_J, we could, for example, adapt an incremental interative Newton-Raphson solution strategy based on the consistent linearization of the governing equations,

$$\begin{array}{l}{\mathrm{R}}_I^{\Phi }+{\displaystyle \sum _K{\mathrm{K}}_{IK}^{\Phi \Phi }}\mathrm{d}{\Phi }_K+{\displaystyle \sum _L{K}_{IL}^{\Phi \phi }}\cdot \mathrm{d}{\mathit{\phi }}_L\dot{=}0\\ {\mathbf{R}}_J^{\phi }+{\displaystyle \sum _K{K}_{JK}^{\phi \Phi }}\mathrm{d}{\Phi }_K+{\displaystyle \sum _L{K}_{JL}^{\phi \phi }}\cdot \mathrm{d}{\mathit{\phi }}_L\dot{=}0.\end{array}$$ (22)

The solution of this system of equations (22) with the discrete residuals (21) and the iteration matrices,

$$\begin{array}{l}\begin{array}{ccc}{\mathrm{K}}_{IK}^{\Phi \Phi }=\underset{\mathrm{e}=1}{\overset{n_{el}}{A}}{\int }_{{\mathit{ℬ}}_0^{\mathrm{e}}}& N_i\left[\frac{1}{\mathrm{\Delta }t}-{\mathrm{d}}_{\Phi }{F}^{\Phi }\right]N_k+\nabla N_i\cdot \mathit{D}\cdot \nabla N_k& \mathrm{d}{V}_{\mathrm{e}}\\ K_{IL}^{\Phi \phi }=\underset{\mathrm{e}=1}{\overset{n_{el}}{A}}{\int }_{{\mathit{ℬ}}_0^{\mathrm{e}}}& \left[N_i\cdot {\mathrm{d}}_{\mathit{C}}{F}^{\Phi }+\nabla N_i\cdot {\mathrm{d}}_{\mathit{C}}\mathit{Q}\right]\cdot {\left[{\mathit{F}}^{\mathrm{t}}\cdot \nabla N_l\right]}^{\text{sym}}& \mathrm{d}{V}_{\mathrm{e}}\\ K_{JK}^{\phi \Phi }=\underset{\mathrm{e}=1}{\overset{n_{el}}{A}}{\int }_{{\mathit{ℬ}}_0^{\mathrm{e}}}& \nabla N_j\cdot {\mathrm{d}}_{\Phi }{\mathit{S}}^{\text{act}}\cdot N_k& \mathrm{d}{V}_{\mathrm{e}}\end{array}\\ K_{JL}^{\phi \phi }=\underset{\mathrm{e}=1}{\overset{n_{el}}{A}}{\displaystyle {\int }_{{\mathit{ℬ}}_0^{\mathrm{e}}}{N}_j\frac{{\rho }_0}{\beta \mathrm{\Delta }{t}^2}{N}_l\mathit{I}+{\left[\nabla N_j\cdot \mathit{F}\right]}^{\text{sym}}:2{\mathrm{d}}_{\mathit{C}}\mathit{S}}:{\left[{\mathit{F}}^{\mathrm{t}}\cdot \nabla N_l\right]}^{\text{sym}}+\nabla N_j\cdot \mathit{S}\cdot {\nabla }_{l}N\mathit{I}\mathrm{d}{V}_{\mathrm{e}},\end{array}$$ (23)

defines the iterative update of the global vector of electrical and mechanical unknowns Φ_I ← Φ_I + dΦ_I and φ_J ← φ_J + dφ_J. Here we have used the symmetric operator ${\{\circ \}}^{\text{sym}}=\frac{1}{2}\left[\{\circ \}+{\{\circ \}}^{\mathrm{t}}\right]$ and the total derivative d_{●}{◦} = d{◦}/d{●}. It remains to specify the sensitivities of the fluxes Q and S and the source term F^Φ with respect to the primary unknowns Φ and φ for the iteration matrices (23.1) to (23.4) [13, 18].

3.4. Internal variables

To integrate the evolution equations of the recovery variable r and the active muscle traction T^act in time, we treat both as internal variables and update and store them locally on the integration point level [18, 36]. To solve the nonlinear evolution equation (9) for the recovery variable r, we locally adopt an implicit Euler backward scheme [17, 28],

$$\dot{r}=\left[r-r_k\right]/\mathrm{\Delta }t,$$ (24)

and introduce the local residual R^r,

$${\mathrm{R}}^r=r-r_k-\gamma \mathrm{\Delta }t+\frac{{\mu }_{1}r}{{\mu }_2+\Phi }\left[r+c\Phi \left[\Phi -b-1\right]\right]\mathrm{\Delta }t=0,$$ (25)

and its algorithmic linearization K^τ,

$${\mathrm{K}}^r=1+\frac{{\mu }_1}{{\mu }_2+\Phi }\left[2r-c\Phi \left[\Phi -\beta -1\right]\right]\mathrm{\Delta }t.$$ (26)

We iteratively update the recovery variable as r ← r − R^r/K^r [34]. To solve the linear evolution equation (13.2) for the active muscle traction T^act, we again adopt a finite difference discretization in time together with an implicit Euler backward scheme,

$${\dot{T}}^{\text{act}}=\left[T^{\text{act}}-T_k^{\text{act}}\right]/\mathrm{\Delta }t,$$ (27)

and solve the resulting equation directly to calculate the active muscle traction at the current point in time,

$$T^{\text{act}}=\left[T_k^{\text{act}}+\epsilon k_T\left[\Phi -{\Phi }_r\right]\mathrm{\Delta }t\right]/\left[1+\epsilon \mathrm{\Delta }t\right].$$ (28)

Once we have determined the recovery variable r and the active muscle traction T^act, we calculate the electrical flux Q from equation (6), the electrical source $F_{\mathrm{e}}^{\Phi }$ from equation (7), the passive stress S^pas from equation (12), and the active stress S^act from equation (13) to evaluate the electrical and mechanical residuals (21).

3.5. Sensitivities

Last, we calculate the sensitivities d_CF^Φ, d_CQ, d_ΦS^act, and d_CS for the electrical and mechanical iteration matrices (23),

$$\begin{array}{l}{\mathrm{d}}_{\mathit{C}}{F}^{\Phi }=\frac{1}{2}\theta G_{\mathrm{S}}[{\Phi }_{\mathrm{S}}-\Phi ]I_4^{-1/2}[{\mathit{f}}_0\otimes {\mathit{f}}_0]\\ {\mathrm{d}}_{\Phi }{\mathit{S}}^{\text{act}}={\mathrm{d}}_{\Phi }{T}^{\text{act}}{I}_4^{-1}{\mathit{f}}_0\otimes {\mathit{f}}_0\\ {\mathrm{d}}_{\mathit{C}}\mathit{Q}=[D^{\text{iso}}\frac{1}{2}[{\mathit{C}}^{-1}\overline{\otimes }{\mathit{C}}^{-1}+{\mathit{C}}^{-1}\underset{\_}{\otimes }{\mathit{C}}^{-1}]+D^{\text{ani}}{I}_4^{-2}[{\mathit{f}}_0\otimes {\mathit{f}}_0]\otimes [{\mathit{f}}_0\otimes {\mathit{f}}_0]]\cdot \nabla \Phi \\ {\mathrm{d}}_{\mathit{C}}\mathit{S}=\lambda {\mathit{C}}^{-1}\otimes {\mathit{C}}^{-1}-[\frac{1}{2}\lambda \text{ln}\left(I_3\right)-\mu ]\frac{1}{2}[{\mathit{C}}^{-1}\overline{\otimes }{\mathit{C}}^{-1}+{\mathit{C}}^{-1}\underset{\_}{\otimes }{\mathit{C}}^{-1}]+[2\eta \theta -T^{\text{act}}{I}_4^{-2}][{\mathit{f}}_0\otimes {\mathit{f}}_0]\otimes [{\mathit{f}}_0\otimes {\mathit{f}}_0],\end{array}$$ (29)

where ${\left\{\circ \overline{\otimes }\bullet \right\}}_{\mathit{ijkl}}={\{\circ \}}_{ik}{\{\bullet \}}_{jl}$ and ${\left\{\circ \underset{\_}{\otimes }\bullet \right\}}_{\mathit{ijkl}}={\{\circ \}}_{il}{\{\bullet \}}_{jk}$ Finally, d_ΦF^Φ and d_ΦT^act can be found in [34] and [17], respectively.

4. Model problem

In this section we summarize the model problems and their results used to assess the influence of mass and mechano-electrical feedback on the conduction velocity of the electrical wave, and the electromechanical behavior in general. Then, we consider the influence of inertial and mechano-electrical parameters on spiral waves. For each of these studies we considered five cases, plain electrophysiology (EP), electromechanics (EM), electromechanics with mass (EMM), electromechanics with mechano-electrical feedback (EM+MEF), and electromechanics with mass and mechano-electrical feedback (EMM+MEF) as summarized in Table 1.

Table 1.

Cases considered in the numerical study. The ✔symbol marks the components present in each model.

case/component	Electrophysiology	Mechanics	Mass	Mechano-electrical feedback
EP	✔
EM	✔	✔
EMM	✔	✔	✔
EM+MEF	✔	✔		✔
EMM+MEF	✔	✔	✔	✔

Table 2 summarizes the electrical, mechanical, and electro-mechanical parameters of these models. To obtain realistic mass-to-stiffness ratios, we calibrated the parameters of the neo-Hookean material model to fit the Holzapfel model [25] in the range of 0 to 15% tensile strain. In these two models, fiber stiffness is only activated when in tension. Given that we are simulating the contraction of cardiac tissue that results mainly in compressive strains in the fiber direction, we consider this neo-Hookean material a good first approximation. We also calibrated the active contraction parameters to obtain strains on the order of 12%, which agree with strains measured in vivo [52].

Table 2.

Model parameters used in all simulations.

electrical
conduction	diso = 0.0952 mm2/ms	dani = 0.03 mm2/ms	[42]
excitation	α = 0.05	γ = 0.002	[27]
	c1 = 52	c1 =8	[34]
	μ1 = 0.1	μ2 = 0.3	[27]
	b = 0.35
mechanical
passive	ρ0 =1.1 g/cm3	λ = 100 kPa
	μ = 3.91 kPa	η = 4.02 kPa
active	kT = 0.015 kPa/mV	Φr = −80 mV
coupling
activation	ε0 =0.01/mV	ε∞=1/mV	[18]
	ξ = 0.5/mV	$\overline{\Phi }=-75\text{mV}$	[18]
MEF	Gs = 20	Φs= 0.6	[54]

4.1. Conduction velocity study

To study conduction velocity, we consider 5 mm × 5 mm × 10 mm rectangular bar (Figure 1) using time steps of Δt = {0.005,0.01,0.05} ms and mesh sizes of Δx = {0.1, 0.25,0.5} mm. We take advantage of the symmetry of the problem by simulating one fourth of the cross section. As mechanical boundary conditions, we fix the plane x = 0 mm in the x direction, the plane y = 0 mm in the y direction, and the plane z = 0 mm in the z direction. To initiate a planar wave front, we apply a surface flux of 30 mV/(ms mm²) in the plane x = 0 mm at time t₀. We compute the conduction velocity in the reference configuration with the activation times at x = 2.5 mm and x = 7.5 mm. We define the activation time as the moment when the action potential reaches 0mV. To better approximate the activation times, we linearly interpolate between two discrete time points.

Figure 1.

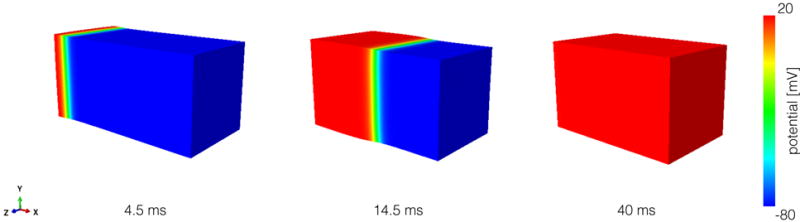
Simulation protocol to study conduction velocity. We apply a stimulus at the x = 0 mm plane to generate a planar wavefront. Then, we allow the entire bar to activate in 40 ms.

Figure 2 and Tables 3 and 4 summarize the results from the conduction velocity study. As presented in Figure 2, refining the time discretization decreases the conduction velocity and refining the mesh size increases the conduction velocity. The conduction velocities range between 0.374 m/s for Δx = 0.5 mm, Δt = 0.005 ms to 0.431 m/s for Δx = 0.1 mm, Δt = 0.05 ms. The variations in conduction velocity, however, can be considered small, falling below 5% for all models when compared to the smallest time step and mesh size for each model. We observe that the biggest impact on conduction velocity is caused by including mechano-electrical feedback in the model (EM+MEF). The addition of this mechanism leads to an increase of 6% in conduction velocity when compared to the purely electrophysiological model (EP). The inclusion of inertia in the electromechanical model (EMM+MEF) further exacerbates the effect of mechano-electrical feedback, increasing the conduction velocity by 8% when compared to the EP case. We explain this difference by the additional displacements caused by the inertial effect, which are translated into additional current via the mechano-electrical feedback. This observation is further supported by the small difference in conduction velocity between the electromechanics model with mass (EMM) and without mass (EM). In this case, the inertial displacements do not generate additional currents, and the difference in conduction velocity can be attributed to the coupling between the electrical flux and the deformation. With this in mind, we can quantify the cumulative contributions to the increment in conduction velocity as a 2% caused by electrical flux coupling, 4% caused by the mechano-electrical feedback and a final 2% caused by the inertial effect.

Figure 2.

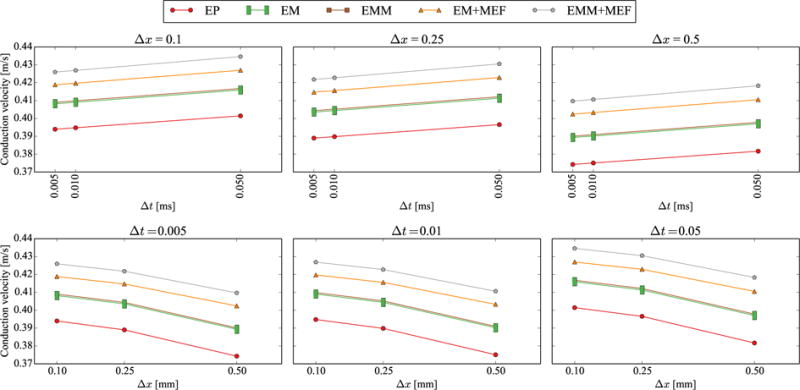
Results of the conduction velocity study. In the upper row, we observe that refining the time increment reduces the conduction velocity for a given mesh size. In the lower row, we see that refining the mesh size produces the opposite effect, increasing the conduction velocity.

Table 3.

Results from the conduction velocity study.

Δt [ms]	Δx = 0.1 [mm]			Δx = 0.25 [mm]			Δx = 0.5 [mm]
	0.005	0.01	0.05	0.005	0.01	0.05	0.005	0.01	0.05
EP	0.394	0.395	0.401	0.389	0.390	0.397	0.374	0.375	0.382
EM	0.408	0.409	0.416	0.404	0.404	0.411	0.389	0.390	0.397
EMM	0.409	0.410	0.417	0.404	0.405	0.412	0.390	0.391	0.398
EM+MEF	0.419	0.420	0.427	0.415	0.416	0.423	0.402	0.403	0.411
EMM+MEF	0.426	0.427	0.435	0.422	0.423	0.431	0.410	0.411	0.418

Table 4.

Percentage differences in conduction velocity for the different models using Δx = 0.1 mm, Δt = 0.005 ms. The differences are calculated as (row - column)/row.

	EP	EM	EMM	EM+MEF	EMM+MEF
EP	–	3.62%	3.82%	6.31%	8.12%
EM	−3.49%	–	0.20%	2.60%	4.35%
EMM	−3.68%	−0.20%	–	2.40%	4.14%
EM+MEF	−5.94%	−2.54%	−2.34%	–	1.70%
EMM+MEF	−7.51%	−4.16%	−3.97%	−1.67%	–

Figure 3 illustrates the sensitivity of the conduction velocity to the mechano-electrical feedback. We systematically vary the parameter G_s from 0 to 25 using the same geometry with Δx = 0.5 mm and Δt = 0.05 ms. Figure 3 shows that the conduction velocity increases with G_s for the cases with and without mass. However, this effect is more prominent in the case with mass. The differences in conduction velocity between the case with mass and without mass increases from 0.2% for G_s = 0 to 2.6% for G_s = 25.

Figure 3.

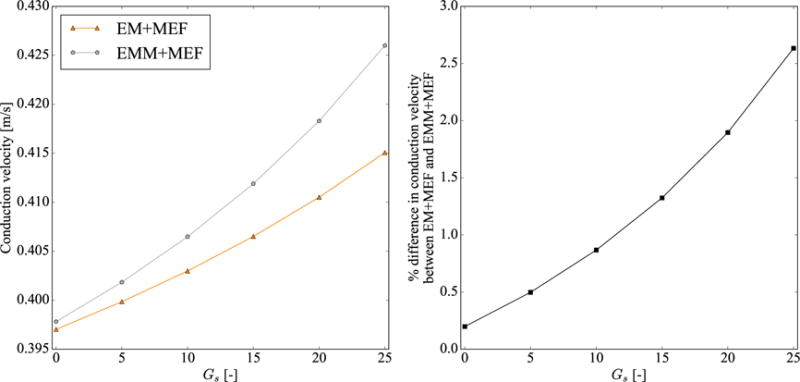
Effect of mechano-electrical feedback parameter G_s on conduction velocity. The left panel shows the conduction velocity values for the cases without mass (EM+MEF) and with mass (EMM+MEF). The right panel shows the percentual differences in conduction velocity between both cases, using the case without mass (EM+MEF) as reference.

Figure 4 highlights the response of the different models for a segment of the cardiac wall excited in three regions. The simulation covers the isovolumetric contraction phase during the cardiac cycle. Figure 4, left, illustrates the 20 mm ×20 mm × 10 mm block to represent a region of the cardiac wall, which we excite in three arbitrary elements on the endocardial surface with a body flux of 300 mV/(ms · mm³). This boundary condition mimics the activation by the Purkinje network, which is only connected at discrete points to the myocardial tissue [49]. We fix all faces of the block in their normal direction except the epicardial surface and we set Δx = 0.5 mm and Δt = 0.05 ms. As an indicator of conduction velocity in this irregular activation pattern, we use the time to completely activate the block. The results show that the differences in conduction velocity now can be mainly attributed to the mechano-electrical feedback. The electromechanics coupling (EM) and inertia (EMM) have little impact on the total activation time, with differences lower that 0.3% when compared to the plain electrophysiology case (EP). The addition of mechano-electrical feedback (EM+MEF, EMM+MEF) leads to a reduction of more than 8% in the total activation time when compared to the other cases (EP, EM, EMM). There is virtually no difference, <0.1%, in the total activation time between the mechano-electrical feedback cases without mass (EM+MEF) and with mass (EMM+MEF), which suggests that inertia does not play a significant role in this simulation.

Figure 4.

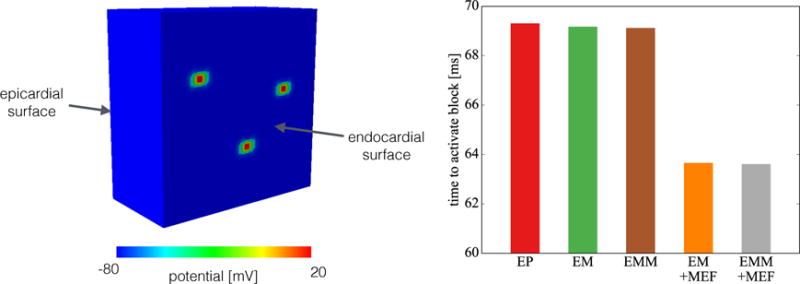
Simplified model of in vivo conditions. We simulate the isovolumetric contraction phase of the cardiac cycle by fixing all faces of the block except the epicardial surface. We activate three arbitrary elements to simulate the Purkinje network interaction with the tissue. We observe the total time to activate the entire block is mainly dependent on the presence of mechano-electrical feedback, which increases the conduction velocity.

4.2. Spiral wave trajectory

Figure 5 illustrates a slab of tissue with dimension 50 mm × 50 mm × 5 mm in which we study the effect of mass on spiral waves. We set the element size to 0.5 mm and an adaptive time step limited to 0.5 ms. We connect all the boundary of the tissue with springs pointing in the normal direction of the surface and set the stiffness of these springs to 4.5 · 10⁻⁸ N/mm to ensure convergence while leaving the tissue fairly unconstrained. To create the spiral wave, we adopt an S1–S2 protocol. We first apply a stimulus S1 of 12mV/(ms mm²) for 2ms in the plane x = 0mm to create a planar wave front. After 290ms, we apply a stimulus S2 of 15mV/(ms mm³) in the quadrant {x < 25, y < 25} mm for 5ms. Finally, we simulate the spiral wave for 1000 ms. As a post-processing step, we track the spiral tip through the entire timespan of the simulation. We calculate the position of the spiral tip as the intersection of two isopotential lines at Φ = −30 mV of two consecutive time points at the z = 0 plane in the reference configuration [14]. For each rotation, we compute the spiral center position as the mean of all points on the trajectory. We calculate the spiral center velocity by taking the norm over the difference of two consecutive center positions and dividing it by the rotation time.

Figure 5.

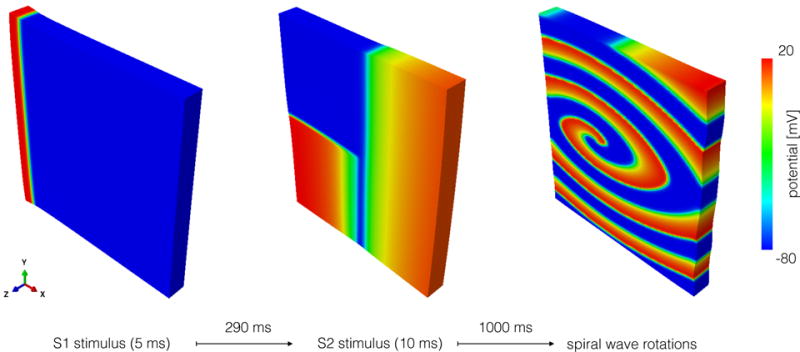
Simulation protocol to study spiral waves. First, a stimulus S1 is applied in the x = 0 plane to generate a planar wavefront. Later, a stimulus S2 is applied in the tail of the wave to trigger the formation of a spiral wave.

Figure 6 shows the transmembrane potential and fiber stretch fields for all cases during the planar wave propagation stage and by the end of the simulation, when spirals are present. At time 50 ms, compressive stretches are produced in the activated regions, where the action potential is high. We observe that the inclusion of mass alters the stretch distribution in the upper and lower boundaries. The differences are accentuated when the spiral wave develops. In the cases with mass, considerable regions of the tissue experience tensile stretch not present in the cases where mass is neglected.

Figure 6.

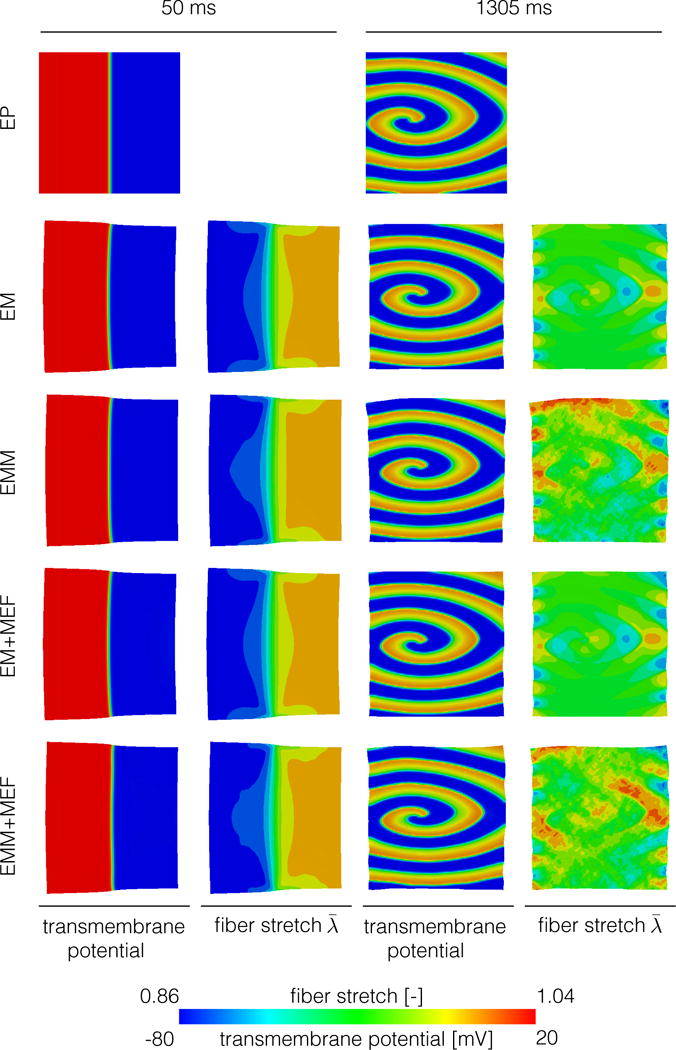
Planar wave propagation (left) and spiral wave (right) for all cases considered. The inertial effect creates tensile fiber stretch during the spiral wave stage that are not present when mass is not considered.

Figure 7 illustrates a consequence of mechano-electrical feedback, where wave fronts are generated in secondary locations when the combination of mass and mechano-electrical feedback is included. The high tensile stretch observed in the upper boundary of the case with mass and mechano-electrical feedback is followed by the activation of this region 10 ms later. This wavefront later collides with the existing spiral at time 144 ms, while another wavefront appears in the lower boundary. In the absence of inertial effects, the tensile stretches generated solely by the active contraction are lower in magnitude and are not able to generate additional wave fronts.

Figure 7.

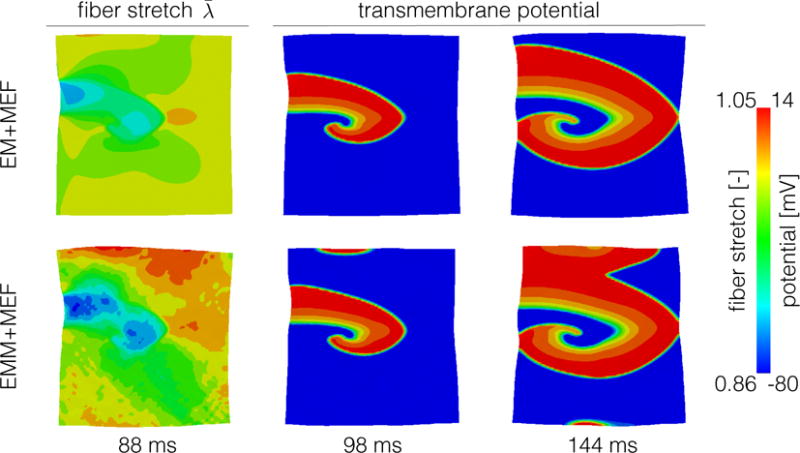
Effect of mechano-electrical feedback on spiral waves. When we include mass (lower row), there are regions of high tensile fiber stretch that create mechano-electrical currents. These currents later translate into secondary activation fronts at times 98 ms and 144 ms. This effect is not present when we neglect inertia (upper row).

Figure 8 shows the emergent spiral wave dynamics by means of the spiral wave center trajectories for all models. All trajectories show different directions and lengths, displaying an important model dependency of this variable. The spiral waves in the electrophysiology (EP) and mass and mechano-electrical feedback (EMM+MEF) cases drift to the left while they drift to the right for the remaining three cases (EM, EM+MEF, EMM). We also observe two trends: first, mechano-electrical feedback tends to decrease the trajectory length with or without mass. Figure 6 shows that in the vicinity of the spiral tip, there are regions of tensile fiber stretch. The mechano-electrical current generated in this region could stabilize the spiral wave. Second, we see that the cases when mass was included have longer trajectories for the same amount of time. When we compare the spiral center speed in Figure 9 we observe that, for most rotations, the speed is higher when mass is considered. Towards the end, the speed increases for the cases with mass, suggesting that the spiral would continue drifting. For the cases without mass, we see the opposite: the spiral center speed tends to zero, suggesting that spiral would continue to be stable.

Figure 8.

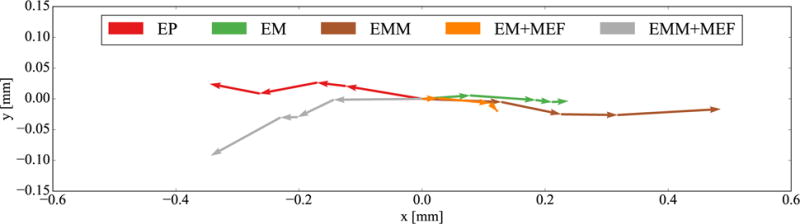
Trajectories of the spiral wave center. We observe that cases with mecho-electrical feedback tend to have shorter trajectories and cases with mass tend to have longer trajectories.

Figure 9.

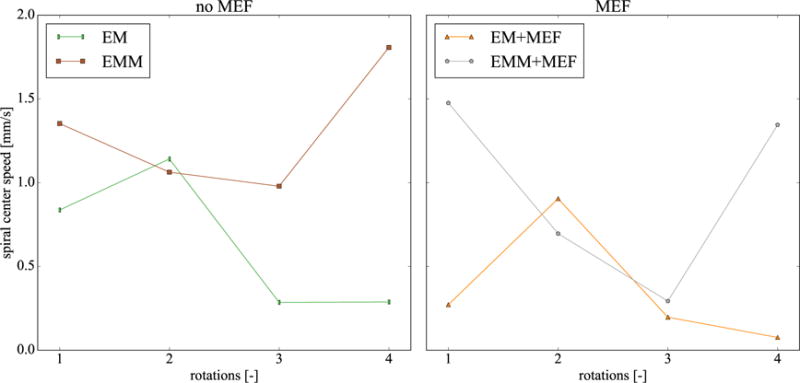
Speed of spiral wave center. The cases with mass have greater speeds for most rotations, particularly towards the end. This trend suggest that the spiral would continue drifting, while in the cases without mass, the spiral would stabilize in one position.

5. Discussion

In this work, we systematically studied the role of inertia and mechano-electrical feedback in cardiac electromechanics models. As a first step, we considered simple geometries to accurately assess the impact on electrophysiological and mechanical metrics. However, we believe our results translate directly into more realistic models, despite the inherent geometrical complexities [30] or boundary conditions [3]. In these sophisticated models, we expect to see a major influence in the electrical propagation of the mechano-electrical feedback and a minor influence of the inertia term in both the electrical and mechanical behavior. Nonetheless, we plan to incorporate our findings into a four-chamber, high resolution heart simulator [4] and explore the influence of inertia and mechano-electrical currents on clinically relevant variables such as electrocardiograms [34, 35, 26, 49] and pressure-volume loops [16]. We also plan to include a more sophisticated material model and study the effects of viscosity [22, 44]. Additionally, we would like to include the effect of stretch and velocity in the active contraction model [21, 47, 50, 38], to simulate relevant macroscopic characteristics of the heart, such as the Frank-Starling effect. Our modular approach allows us to easily incorporate these changes in our model.

In this study, we explored the differences between including mass and/or including mechano-electrical feedback using our fully coupled finite element electromechanical formulation. Our major finding is that the additional deformation caused by inertia alters the electrical wave dynamics when mechano-electrical currents are present. We observed that the inclusion of mass and mechano-electrical feedback lead to highest increase in conduction velocity. However, the inclusion of mass solely did not alter the conduction velocity compared to the plain electromechanics case. Taken together, this suggests that inertia is generating tensile stretches that initiate mechano-electrical currents, which add to the wave propagation. This observation was further confirmed by our spiral wave study. Figure 6 shows higher tensile stretches for both cases with mass. Moreover, Figure 7 shows the extreme case when the tensile stretches are large enough to create mechano-electrical currents that lead to an additional wave front. We also observed that the inclusion of mass leads to a larger and faster spiral drift, which is associated with polyformic ventricular tachycardia, a precursor of ventricular fibrillation [20, 54]. Recent studies have shown that knowing the precise position of the spiral wave center is critical when attempting to terminate atrial fibrillation through localized ablation [46].

From a computational point of view, our model showed little sensitivity to the spatial and temporal discretization. In the conduction velocity study, the maximum difference was less than 5% for all cases, which is considerable smaller than the 50% of variation that other formulations exhibit for the same range of time increments and mesh sizes [42]. Our model is able to handle the anisotropic architecture of cardiac tissue at the electrical and mechanical levels, with complex wave spiral waves and heterogeneous deformations induced by inertial effects. Ultimately, our model will help the research community to better understand the complex interactions that govern the heart’s function.

Highlights.

• ►Modeling cardiac electromechanics is critical to predict mechanisms of cardiac dysfunction
• ►We study two commonly neglected effects of cardiac electromechanics: mechano-electrical feedback and inertia
• ►We show that conduction velocities and spiral wave dynamics are sensitive to these effects
• ►Mechano-electrical feedback and inertia may initiate secondary waves and shift trajectories
• ►Correctly identifying the trajectories of spiral wave centers can improve ablation therapies

A. Appendix: Abaqus Implementation

In this Appendix, we illustrate the specific implementation of the electromechanics problem into the finite element software package Abaqus/Standard [1]. We took advantage of the existing coupled thermal-displacement procedure in Abaqus. By setting the density and the specific heat to unity, we recover the balance equations (4). However, this procedure neglects the inertia term in equation (4.2). To analyze the effect of mass, we superimposed a user element to the standard element as is explained in (A.3). In the following, we explain the different subroutines used to create the electromechanical model.

A.1. User material - UMAT

In this subroutine, we calculate the passive stress, the active stress, and the mechanical transmembrane current with their corresponding sensitivities. We use the left Cauchy-Green deformation tensor,

$$\mathit{b}=\mathit{F}\cdot {\mathit{F}}^t.$$ (30)

Abaqus/Standard uses the Cauchy stresses, σ^pas and σ^act, which follow from the push forward, σ = F · S · F^t/J, of the Piola-Kirchhoff stresses, S^pas and S^act, in equations (12) and (13),

$$\begin{array}{l}{\mathit{\sigma }}^{\text{pas}}=\left[\left[\frac{1}{2}\lambda \text{ln}\left(I_3\right)-\mu \right]\mathit{I}+\mu \mathit{b}+2\theta \eta \left[I_4-1\right]\mathit{f}\otimes \mathit{f}\right]/J\\ {\mathit{\sigma }}^{\text{act}}=T^{\text{act}}{I}_4^{-1}\mathit{f}\otimes \mathit{f}/J.\end{array}$$ (31)

For the stress sensitivity, Abaqus uses the Jauman stress rate of the Kirchhoff stress divided by the Jacobian, ${ℂ}^{\text{abaqus}}=ℂ+ℂ\prime$ [23], where $ℂ$ is the Eulerian elasticity tensor, which follows from the push forward, $ℂ=\left[\mathit{F}\overline{\otimes }\mathit{F}\right]:ℂ:\left[{\mathit{F}}^{\mathrm{t}}\underset{\_}{\otimes }{\mathit{F}}^{\mathrm{t}}\right]/J$ of the Lagrangian elasticity tensor, $ℂ=2\mathrm{d}\mathit{S}/\mathrm{d}\mathit{C}$, from equation (29.4),

$$ℂ=[\lambda \mathit{I}\otimes \mathit{I}-[\frac{1}{2}\lambda \text{ln}\left(I_3\right)-\mu ][\mathit{I}\overline{\otimes }\mathit{I}+\mathit{I}\underset{\_}{\otimes }\mathit{I}]+[4\eta \theta -2T^{\text{act}}{I}_4^{-2}][\mathit{f}\otimes \mathit{f}]\otimes [\mathit{f}\otimes \mathit{f}]]/J,$$ (32)

and ¢′ is a correction for the Jauman rate

$$ℂ\prime =\frac{1}{2}[\mathit{I}\overline{\otimes }\mathit{\sigma }+\mathit{I}\underset{\_}{\otimes }\mathit{\sigma }+\mathit{\sigma }\overline{\otimes }\mathit{I}+\mathit{\sigma }\underset{\_}{\otimes }\mathit{I}].$$ (33)

A crucial step in this subroutine is the computation of the spatial fiber vector f. When using local orientations, Abaqus rotates the local coordinate system using the rotation matrix R of the polar decomposition of the deformation gradient, F = v · R, where v is the left stretch tensor. We now seek to compute f′, which is the spatial fiber vector in the rotated coordinate system. We define ${\widehat{\mathit{f}}}_0={\mathit{R}}^t\cdot {\mathit{f}}_0$ as the fiber vector rotated only by rigid body motion. These two vectors have the same components, but in different coordinate systems, such that ${\widehat{f}}_{0i}^{\prime }=f_{0i}$ We start from the definition of f = F · f₀, or equivalently, $\mathit{R}\cdot \mathit{f}\prime =\mathit{F}\cdot \mathit{R}\cdot {\mathit{f}}_0^{\prime }$ Premultiplying this equation with R ⁻¹ = R^t yields, $\mathit{f}\prime ={\mathit{R}}^{\mathrm{t}}\cdot \mathit{F}\cdot \mathit{R}\cdot {\mathit{f}}_0^{\prime }=\mathit{F}\prime \cdot {\mathit{f}}_0^{\prime }=\mathit{F}\prime \cdot {\mathit{R}}^t\cdot {\widehat{\mathit{f}}}_0^{\prime }=v\prime \cdot \mathit{R}\cdot {\mathit{R}}^t\cdot {\widehat{\mathit{f}}}_0^{\prime }=v\prime \cdot {\widehat{\mathit{f}}}_0^{\prime }$ We can now proceed to calculate the spatial fiber vector in the rotated coordinate system using the polar decomposition of the deformation gradient, F′ = v′ · R. Finally, we can directly implement the mechano-electrical source term in the form of equation (10),

$$F_{\mathrm{m}}^{\Phi }=\theta G_{\mathrm{S}}\left[\lambda -1\right]\left[{\Phi }_{\mathrm{S}}-\Phi \right],$$ (34)

and calculate the push forward, ${\mathrm{d}}_{\mathit{g}}{F}_{\mathrm{m}}^{\Phi }={\mathrm{d}}_{\mathit{b}}{F}_{\mathrm{m}}^{\Phi }\cdot \mathit{b}=\mathit{F}\cdot {\mathrm{d}}_{\mathit{C}}{F}_{\mathrm{m}}^{\Phi }\cdot {\mathit{F}}^{\mathrm{t}}/J$, of its sensitivity, ${\mathrm{d}}_{\mathit{C}}{F}^{\Phi }=\frac{1}{2}\theta G_{\mathrm{S}}\left[{\Phi }_{\mathrm{S}}-\Phi \right]{\lambda }^{-1}\left[{\mathit{f}}_0\otimes {\mathit{f}}_0\right]$, from equation (29.1),

$${\mathrm{d}}_{\mathit{g}}{F}_{\mathrm{m}}^{\Phi }={\mathrm{d}}_{\mathit{b}}{F}_{\mathrm{m}}^{\Phi }\cdot \mathit{b}=\frac{1}{2}\theta G_{\mathrm{S}}\left[{\Phi }_{\mathrm{S}}-\Phi \right]{\lambda }^{-1}\mathit{f}\otimes \mathit{f}/J.$$ (35)

A.2. Nonlinear source term - HETVAL

This subroutine is designed to define thermal body flux, which can depend on internal variables [1]. In our formulation, we can use this body flux to represent the transmembrane current $F_{\mathrm{e}}^{\Phi }$. In this subroutine, we evaluate equations (24) to (26) with a local Newton-Raphson solver to update the internal variable r and the magnitude of the current $F_{\mathrm{e}}^{\Phi }$ (using equation (8).

A.3. User element - UEL

To include the effects of inertia, we superimpose user elements that share their nodes with the coupled thermaldisplacement elements of Abaqus/Standard. To compute the accelerations and velocities, we adopt Newmark’s method (18) and store these quantities as internal variables in the user element. To superpose these effects to the quasi-static solution, we add an inertia term to the mechanical residual,

$${\mathbf{R}}_J^{\phi }\underset{\mathrm{e}=1}{\overset{n_{\mathrm{el}}}{A}}{\displaystyle {\int }_{{\mathit{ℬ}}_0^{\mathrm{e}}}{N}_j{\rho }_0\ddot{\mathit{\phi }}\mathrm{d}{V}_{\mathrm{e}}},$$ (36)

and the corresponding linearization term, the consistent mass matrix, to the mechanical tangent operator,

$$K_{JL}^{\phi \phi }=\underset{\mathrm{e}=1}{\overset{n_{\mathrm{el}}}{A}}{\displaystyle {\int }_{{\mathit{ℬ}}_0^{\mathrm{e}}}{N}_j\frac{{\rho }_0}{\beta \Delta t^2}{N}_l\mathit{I}\mathrm{d}{V}_{\mathrm{e}}.}$$ (37)

We specify the tissue density ρ₀ as an element property.