Spectral unmixing techniques for optoacoustic imaging of tissue pathophysiology

Abstract

A key feature of optoacoustic imaging is the ability to illuminate tissue at multiple wavelengths and therefore record images with a spectral dimension. While optoacoustic images at single wavelengths reveal morphological features, in analogy to ultrasound imaging or X-ray imaging, spectral imaging concedes sensing of intrinsic chromophores and externally administered agents that can reveal physiological, cellular and subcellular functions. Nevertheless, identification of spectral moieties within images obtained at multiple wavelengths requires spectral unmixing techniques, which present a unique mathematical problem given the three-dimensional nature of the optoacoustic images. Herein we discuss progress with spectral unmixing techniques developed for multispectral optoacoustic tomography. We explain how different techniques are required for accurate sensing of intrinsic tissue chromophores such as oxygenated and deoxygenated haemoglobin versus extrinsically administered photo-absorbing agents and nanoparticles. Finally, we review recent developments that allow accurate quantification of blood oxygen saturation (sO₂) by transforming and solving the sO₂ estimation problem from the spatial to the spectral domain.

This article is part of the themed issue ‘Challenges for chemistry in molecular imaging’.

1. Introduction

Spectral unmixing of optoacoustic images combines high-resolution visualization of optical contrast with spectral specificity, granting unique imaging abilities [1]. Nevertheless, the optoacoustic spectral unmixing problem is a unique computational problem. Spectral unmixing methods have been mainly investigated in the context of two-dimensional planar optical imaging, typically epi-illumination imaging, for remote sensing [2] and optical microscopy [3] applications. Two-dimensional spectral unmixing commonly adopts a linear mixture model (LMM) [2], which assumes that the measured spectrum at each image location M(r, λ) (r denoting position and λ the optical wavelength) is a linear combination of the spectral signatures S_i(λ) of K distinct materials, weighted by their relative abundance or concentration at that specific image location c_i(r):

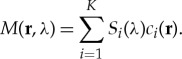1.1

Given knowledge of the spectral signatures S_i(λ), the relative concentrations c_i(r) can be straightforwardly estimated by means of linear regression (linear unmixing).

Conversely, unmixing of three-dimensional optical images is challenged by light fluence attenuation as a function of tissue depth and wavelength employed and is fundamentally a nonlinear inversion problem. The unknown depth- and wavelength-dependent fluence Φ(r, λ) introduces depth-dependent changes to the detected optoacoustic spectra P(r, λ), a phenomenon commonly termed ‘spectral colouring’ [4]:

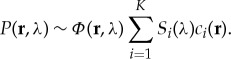1.2

Therefore, in contrast to conventional reflection spectroscopy where each photo-absorbing moiety is associated with a unique spectrum, the detected spectrum in three-dimensional optoacoustic imaging will vary according to its location in tissue, influenced by the combination of optical properties along the optical path that photons travelled to reach that location. It has been experimentally shown that the complex and nonlinear nature of the optoacoustic spectral unmixing problem leads to depth-dependent quantification errors of greater than 40% for sO₂ estimation in small animals [5], as well as substantial false-positive artefacts in the process of resolving extrinsically administered molecular targets in tissue [6], when Φ(r, λ) is considered constant and spectral colouring is not accounted for.

Overall, the accuracy of multispectral optoacoustic visualization of tissue pathophysiology, cells and molecules relies on the spectral analysis technique used. One approach proposed for solving the optoacoustic spectral analysis and quantification problem is to explicitly account for light fluence attenuation in tissue by estimating tissue optical properties. If the light fluence in tissue is recovered and accounted for, the optoacoustic spectral unmixing problem becomes a linear unmixing problem which can be straightforwardly solved. Inversion schemes that explicitly model light fluence in tissue using a light propagation model have been widely investigated for light fluence correction [4]. Nevertheless, even if theoretically correct, the application of explicit fluence modelling to experimental data is generally challenging because it depends on the accurate estimation of the light and sound propagation properties of the tissue, i.e. metrics that are never precisely known in vivo. For example, the experimental application of inverse light propagation methods require high-quality optoacoustic reconstructions of the entire three-dimensional illuminated volume, calibration of scaling factors such as the Gruneissen coefficient, accurate knowledge of the incident light fluence on tissue surface and the solution of a large scale and ill-posed inverse problem for estimating tissue optical and acoustic properties [7]. Correspondingly, the use of explicit fluence modelling methods may lead to solution bias and errors when applied to noisy experimental data [8]. Therefore, due to the complexity of the problem, explicit light fluence correction of experimental in vivo optoacoustic images is still considered an open problem.

To overcome the challenge of explicitly modelling light propagation in tissues, two classes of spectral analysis methods have been considered, which avoid the estimation of light fluence in tissue. Emphasis in these methods is put on overcoming the effects of spectral colouring by modelling spectral fluctuations based on available prior knowledge. Depending on their theoretical development and assumptions made, one class of these methods is based on statistical spectral detection and is better suited for sensing tissue-extrinsic spectral moieties. These methods are appropriate for molecular imaging applications whereby a target molecule is present in local disease foci. A second class of methods based on the low-dimensional representation of light fluence spectra has been developed for resolving contributions of molecules that are broadly distributed throughout the tissue, and it is better suited for studying tissue physiology. Herein we review these two classes of spectral analysis methods, explain their performance with experimental in vivo data and discuss their potential for accurate physiological and molecular optoacoustic imaging.

2. Molecular imaging: statistical detection methods

Optoacoustic molecular imaging can be formulated as a detection problem aiming to reveal the distribution of a target moiety (fluorochrome, dye, nanoparticle) with a distinct spectrum, which is distributed in a localized manner in certain tissue or disease foci, typically at low amounts (concentrations). The detection problem is formulated to sense this target moiety in the presence of strong tissue absorption background, the latter due to other photoabsorbers present in abundance. In this case, statistical sub-pixel detection methods used in remote sensing hyperspectral imaging [9], like the adaptive matched filter (AMF) [10], were found to substantially outperform linear unmixing approaches under the condition that the molecular target is sparsely present within the tissue [6]. The AMF models the background tissue spectral variability as a multivariate Gaussian distribution and computes the statistics of this distribution (i.e. the mean µ and the covariance matrix G) from the available data, i.e. the multispectral optoacoustic tomography (MSOT) image under investigation. The so-derived statistical model of the background accounts for spectral fluctuations due to both spectral colouring and additional noise sources. Based on these statistics (i.e. µ and G), a simple formula is derived to detect a molecular target with a distinct spectrum s from the tissue background:

2.1

where D_AMF(x_i) is the detection value for a specific pixel i, x_i is the optoacoustic spectrum of this pixel and N is the number of pixels in the MSOT image under investigation that have been used for the computation of the background statistics. If the detection value D_AMF(x_i) is larger than a threshold then this pixel likely contains the molecular target of interest.

AMF offers good performance in the case of sparsely distributed molecular targets, but its performance degrades when such targets appear in high spatial extent or high intensity within tissue. This performance degradation is caused due to the inaccurate computation of the background covariance matrix G due to the target presence. In an effort to make statistical detection robust in MSOT applications, a novel statistical sub-pixel detection framework was developed, termed the robust statistical detection framework (RSDF), where additional MSOT data of background tissues were employed as training data, along with the MSOT image under investigation, for the computation of the background covariance matrix G in a robust manner. RSDF was evaluated on both simulated and experimental in vivo data and achieved sensitive and accurate detection of molecular targets independently of the target sparsity assumption [11].

Simulations and experimental in vivo studies showed that optoacoustic imaging using statistical sub-pixel detection could detect targets at five times lower concentrations compared with linear unmixing methods [6,11] and up to 30 times lower concentrations compared to monochromatic optoacoustic imaging [12]. Essentially, statistical sub-pixel detection methods do not explicitly account for spectral colouring but overcome its effects by modelling the background and target spectral variability in a data-driven, statistical manner.

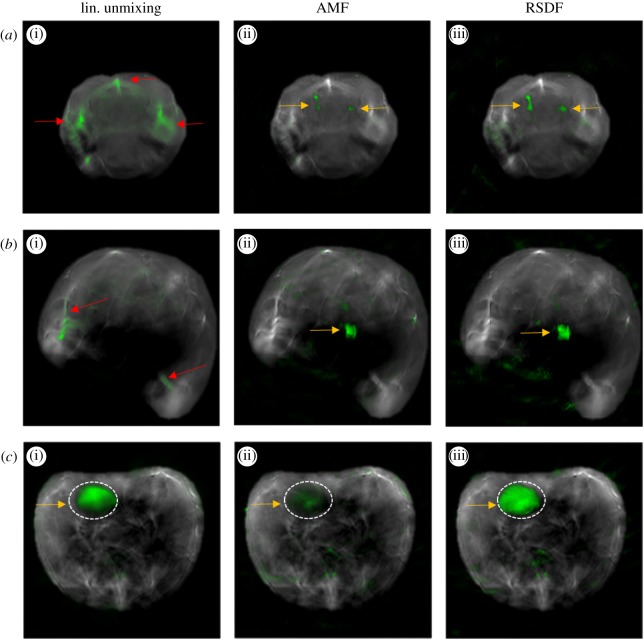
Figure 1 presents examples of MSOT animal imaging with fluorescent targets introduced within tissue and analysed with different spectral unmixing methods. Figure 1a corresponds to brain images with DiR labelled macrophages introduced in the left and right brain hemisphere (25 000 and 10 000 cells, respectively) [13]. The position of the labelled cells (yellow arrows) is accurately detected by AMF and RSDF but not by linear unmixing which yields substantially stronger false-positive detection artefacts. Figure 1b corresponds to an MSOT image from the abdominal area of an animal where a capillary tube containing the fluorochrome Alexa Fluor 790 has been introduced in tissue (yellow arrow). The location of the fluorochrome is detectable by AMF and RSDF, but not by linear unmixing. Both examples demonstrate the superiority of statistical detection methods in resolving weak molecular targets that are sparsely present within tissue. Figure 1c presents a different case where the molecular target is present in high amount within tissue. The MSOT image corresponds to the abdominal region of an animal that has been systemically injected with the fluorochrome Alexa Fluor 750 (AF750). AF750 accumulates in the bladder which is highlighted with a dashed line. In this example, the detection performance of AMF is compromised due to the high amount of the target. Both linear unmixing and RSDF offer a better detection performance.

Figure 1.

Comparison of the spectral analysis result of linear unmixing (a(i),b(i),c(i)), AMF (a(ii),b(ii),c(ii)) and RSDF (a(iii),b(iii),c(iii)) in the case of experimental MSOT images of animals with extrinsically administered fluorescent targets. (a) MSOT image of the brain with DiR labelled macrophages introduced in the left and right brain hemisphere (yellow arrows). (b) MSOT image of the abdominal region of an animal with an insertion of AF790 (yellow arrow). (c) MSOT image of the abdominal area of an animal after systemic injection of 1.2 nmoles of AF750. AF750 accumulates in the area of the bladder (dashed line and yellow arrow). In all cases, the detection result in overlaid onto the anatomical image with green pseudocolour. Red arrows indicate false-positive detection artefacts. The image is reproduced and edited with permission from [11].

3. Imaging of tissue physiology: spectral representation of light fluence

A second class of methods seeks to explicitly account for spectral colouring by introducing a representation of the light fluence spectrum in tissue. Using such a representation, a nonlinear spectral unmixing problem can be formulated. Solving this nonlinear spectral unmixing problems allows for correcting for spectral colouring and separating the relative contribution of tissue absorbers. This method is better suited for quantifying the relative concentrations of different moieties in tissue and is particularly useful for estimating blood oxygen saturation, a value of substantial significance for measuring tissue pathophysiology.

A particular class of nonlinear spectral unmixing methods relates to quantifying tissue oxygenation by means of obtaining quantified images of blood sO₂. Quantitative optoacoustic imaging of blood sO₂ presents a challenging problem where spectral colouring needs to be explicitly accounted for to estimate the relative concentrations of oxy- and deoxyhaemoglobin. A novel concept recently introduced models the spectrum of light fluence as an affine function of basis spectra [5]. Termed eigenspectra MSOT (eMSOT), the method computes a mean fluence spectrum Φ_M(λ) and three fluence eigenspectra (Φ_i(λ), i = 1..3) by applying principal component analysis on a selected training dataset of simulated light fluence spectra derived from simulations of light propagation in tissues of varying oxygenation levels. The method is based on the unique observation that any normalized light fluence spectrum Φ′(r, λ) can be accurately modelled with only three basis spectra, using the following equation, irrespective of the spatial distribution of tissue optical properties of oxygenation values:

3.1

where m₁(r) m₂(r) and m₃(r) are scalars, termed Eigenfluence parameters. The Eigenspectra model is used for formulating the blood sO₂ estimation problem as a nonlinear spectral unmixing problem:

3.2

where P(r, λ) is the multispectral optoacoustic image intensity obtained at a position r and wavelength λ, 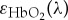and ϵ_Hb(λ) are the spectra, and 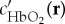and c′_Hb(r) are the relative concentrations of oxygenated and deoxygenated haemoglobin, respectively. For each pixel, five unknowns, namely m₁(r), m₂(r), m₃(r), 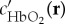and c′_Hb(r) need to be estimated by minimizing the difference between the measured data P(r, λ) and the model. This is achieved through a constrained nonlinear inversion scheme that incorporates spectral information from multiple pixels distributed in the image domain and enforces a number of constraints on the expected spatial behaviour of the Eigenfluence parameters m₁(r), m₂(r) and m₃(r).

Eigenspectra MSOT (eMSOT) showed the ability to substantially enhance the sO₂ estimation accuracy of deep tissue optoacoustic imaging in simulations, phantoms and experimental in vivo data. Effectively, eigenspectra MSOT converts optoacoustic sO₂ imaging from a problem that is spatially dependent on light propagation [4] to a problem solved in the spectral domain. This reformulation offers a number of advantages over inverse light propagation schemes. Most notably the analysis can be focused on a well reconstructed part of a two-dimensional optoacoustic image and the inversion requires only normalized spectra (calibration for scaling factors, like the Gruneissen parameter is not required). Effectively, these features allow for an easier application on experimental in vivo data. eMSOT was applied for quantifying blood sO₂ gradients in the hind-limb muscle and tumours of animals undergoing an O₂–CO₂ challenge [5]. The results obtained in deep tissue areas appeared consistent with the expected physiological state, which was not the case for previously used linear unmixing methods.

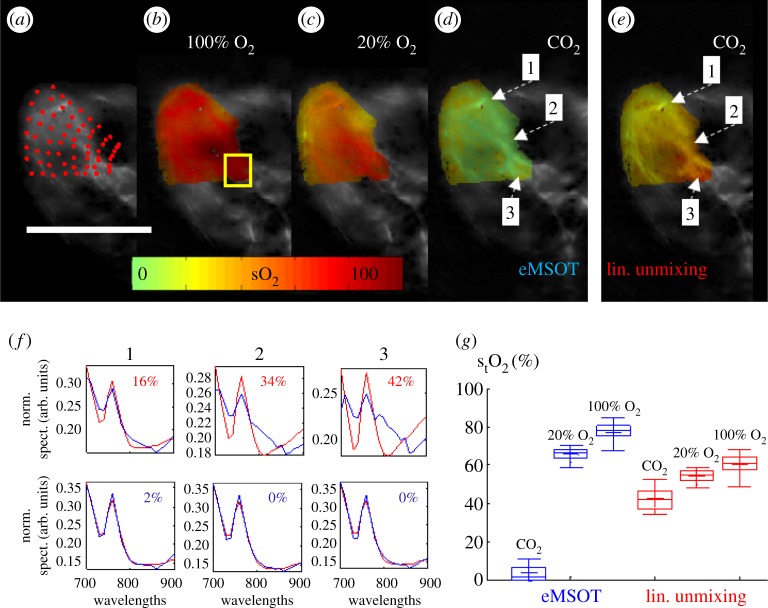
Figure 2 presents a comparison between eMSOT and linear unmixing in quantifying blood sO₂ in the hindlimb muscle area of an animal imaged in vivo and post-mortem. Figure 2a presents a grid of points applied in the area of the muscle. The spectral information of all pixels corresponding to the grid points is simultaneously used by eMSOT to estimate the Eigenfluence parameters m₁(r), m₂(r), m₃(r) at each grid point location by minimizing the difference between the spectral data and the model (equation (3.2)). In the following the Eigenfluence parameters in the convex hull of the grid are computed using cubic interpolation. The estimation of the Eigenfluence parameters m₁(r), m₂(r), m₃(r) allows for computing the normalized spectrum of the optical fluence at each pixel as per equation (3.1) and thus correcting the MSOT image for spectral colouring. Once spectral colouring has been accounted for, blood sO₂ can be computed by fitting the corrected spectra with the absorption spectra of oxy- and deoxy-haemoglobin. Figure 2b–d presents spatial sO₂ maps computed with eMSOT in vivo when the animal is breathing 100% O₂ (figure 2b), 20% O₂ (figure 2c) and post-mortem (figure 2d) after CO₂ breathing. In the post-mortem case, the sO₂ levels in the muscle are expected to approach 0%. The post-mortem deoxygenated muscle served herein as a control experiment and was also analysed with linear unmixing for comparison (figure 2e). Linear unmixing overestimated the sO₂ as a function of tissue depth as a consequence of spectral colouring, which is not accounted for in this case. Figure 2f further presents the spectral fit of linear unmixing (upper) and eMSOT (lower) for three points in the image indicated in figure 2d. Linear unmixing yielded large errors in matching the tissue spectra, especially in deep tissue areas where spectral colouring is more prominent, while eMSOT offered a low-residual spectral fit independently of tissue depth. Finally, figure 2g tabulates the estimated blood sO₂ values corresponding to a deep tissue area (yellow rectangle in figure 2b) for eMSOT and linear unmixing and depicts that the values recovered by eMSOT match better the expected physiological state.

Figure 2.

Comparison of spectral analysis methods for the estimation of blood sO₂ in experimental MSOT images of an animal obtained in vivo and post-mortem. (a–d) eMSOT grid applied on the area of the hindlimb muscle (a) and eMSOT tissue blood sO₂ estimation in the case of 100% O₂ breathing (b), 20% O₂ breathing (c) and post-mortem after CO₂ breathing (d). (e) sO₂ estimation using linear unmixing in the post-mortem case after CO₂ breathing. (f) Normalized spectra, spectral fitting and sO₂ values of linear unmixing (upper row) and eMSOT (lower row) for the three points indicated in (d) and (e). (g) Estimated blood sO₂ of a deep tissue area (yellow box in b) using eMSOT (blue) and linear unmixing (red) under different breathing conditions of CO₂, 20% O₂ and 100% O₂. Image reproduced with permission from [5].

4. Discussion: advantages and limitations

Spectral unmixing methods play a major role on the accuracy of the pathophysiological measures derived by optoacoustic imaging. Nevertheless, optoacoustic spectral unmixing presents a unique and challenging problem, mainly due spectral colouring but also due to a multitude of noise sources such as electronic noise, image reconstruction artefacts, laser power fluctuation and animal motion.

Since accurate correction of light fluence in experimental data is not yet feasible, spectral unmixing methods need to consider its effects in order to yield accurate results. Early multispectral optoacoustic imaging studies have mainly considered linear spectral unmixing methods [14,15], which disregard spectral colouring, due to their simplicity and wide adoption in the fields of remote sensing and optical microscopy. Wavelength selection methods have also been investigated to optimize the results of the linear model [16]. However due to the particular nature of the optoacoustic problem, such methods are suboptimal and may yield results of compromised accuracy.

Another class of methods that has been investigated and applied in a number of experimental studies is blind source separation through Independent Component Analysis (ICA) [17,18] and Vertex Component Analysis [19]. ICA has been shown to reveal the distribution of molecular targets in cases where linear unmixing fails [17,18]. However, a quantitative comparison using simulated and experimental data indicated that ICA does not offer better performance than AMF while blind source separation further introduces the undesirable step of component selection, which can make its application biased and non-automatic. Moreover, blind source separation is typically not appropriate for quantification as it adopts an LMM which cannot account for the spatially varying effects of spectral colouring.

The two classes of methods discussed in this paper seek to overcome the effects of spectral colouring for providing better accuracy in the specific applications of molecular imaging and physiological imaging. The class of statistical spectral detection algorithms, which focus on the detection of a tissue-extrinsic molecular target, has been shown to outperform linear unmixing substantially in numerous experimental studies and its application is simple and robust. A limitation of these algorithms is that they focus solely on the detection of a single extrinsic molecular target and they do not allow for the quantification of its concentration, which is another highly desirable parameter in molecular imaging applications.

By explicitly modelling and accounting for spectral colouring, eMSOT has shown the ability to offer substantially enhanced quantification accuracy when compared with linear unmixing in experimental in vivo data. Nevertheless, the routine quantification of in vivo tissue pathophysiology with optoacoustics can still be a challenging task. Aside to spectral colouring, the recorded optoacoustic spectra of tissue can be further corrupted by a multitude of noise sources, animal motion or image reconstruction artefacts, which may in turn compromise the performance of spectral analysis methods. Therefore, the in vivo application of eMSOT was restricted so far to high intensity, high signal-to-noise ratio regions of high-quality optoacoustic images. With the advent of advanced image reconstruction techniques that yield less artefacts and noise [20], it is expected that elaborate spectral analysis methods will also be used in a more routine basis. An additional limitation of eMSOT is that it assumes haemoglobin as the sole tissue absorber, not accounting for the potential presence of other absorbing molecules (e.g. extrinsic molecules, melanin, lipids, etc.). The prominent presence of such molecules in tissue areas may reduce the eMSOT sO₂ estimation accuracy. Overall, the development of elaborate spectral analysis methods that can accurately quantify blood sO₂ in vivo, drives the need for the collection of large in vivo datasets with available gold standard for the evaluation and optimization of the algorithmic performance. Owing to the lack of other imaging modalities that can quantify tissue blood sO₂ in high resolution, such datasets are currently limited and require invasive procedures and complex experimentation. Nevertheless, compiling a large pool of such data is important towards further developing and establishing spectral optoacoustic methods for tissue pathophysiology quantification.

Authors' contributions

Stratis Tzoumas and Vasilis Ntziachristos wrote the manuscript.

Competing interests

V.N. is a shareholder in iThera-Medical GmbH, Munich, Germany.

Funding

V.N. acknowledges funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme under grant agreement no. 694968 (PREMSOT) and from the Deutsche Forschungsgemeinschaft (DFG) as part of the CRC 1123 (Z1) and the Gottfried Wilhelm Leibniz Prize 2013 (NT 3/10-1).