Dynamic Scaling Analysis of Molecular Motion within the LAT:Grb2:SOS Protein Network on Membranes

Abstract

Biochemical signaling pathways often involve proteins with multiple, modular interaction domains. Signaling activates binding sites, such as by tyrosine phosphorylation, which enables protein recruitment and growth of networked protein assemblies. Although widely observed, the physical properties of the assemblies, as well as the mechanisms by which they function, remain largely unknown. Here we examine molecular mobility within LAT:Grb2:SOS assemblies on supported membranes by single-molecule tracking. Trajectory analysis reveals a discrete temporal transition to subdiffusive motion below a characteristic timescale, indicating that the LAT:Grb2:SOS assembly has the dynamical structure of a loosely entangled polymer. Such dynamical analysis is also applicable in living cells, where it offers another dimension on the characteristics of cellular signaling assemblies.

Introduction

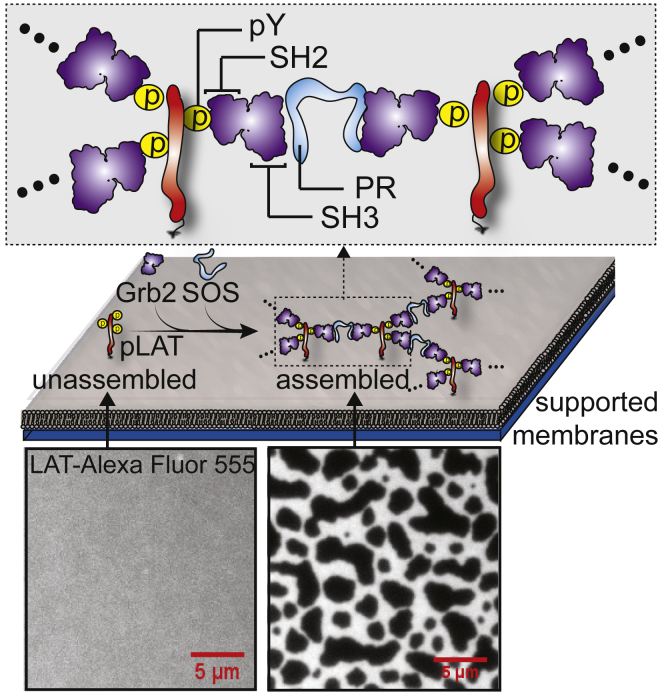
The assembly of cellular proteins into organized structures through modular binding domains is a broadly significant theme in biological signal transduction (1, 2). Hallmark examples include P granules (3), the nuclear pore complex (4, 5), receptor tyrosine kinases (6), actin cytoskeleton regulation (7, 8), and immune cell receptor signaling (2, 9, 10, 11). Common to all of these systems are multivalent protein-protein interactions, such as SH2 domain binding to phosphorylated tyrosine (pY) residues, SH3 domain binding to proline-rich regions, and interactions between FG-rich repeat domains (5, 8, 9). Multivalency enables networked assembly of proteins into extended structures via bond percolation (Fig. 1). In a number of cases, assembly is reversibly governed by tyrosine phosphorylation, which is one of the primary mechanisms of transmitting information in signal transduction cascades (1). Various functional consequences of such assemblies in signal transduction have been envisioned (10, 11). However, detailed understanding of their physical properties as well as how these modulate the molecular logic of signaling remains vague.

Figure 1.

Molecular assembly of LAT:Grb2:SOS by bond percolation. These bonds are transient and reversible modular protein-protein interactions (inset). Membrane-anchored LAT is cross-linked by membrane-recruited cytosolic proteins, Grb2 and SOS. The probability of cross-linking adjacent LAT is determined by the binding kinetics between each molecular species. The dissociation constants of SH2:pY and SH3:PR (proline-rich domain) are ∼300 and 400 nM, respectively (9). In the reconstitution experiments, addition of Grb2 and SOS in solution drives LAT assemblies on supported membranes. The images of fluorescently labeled LAT (Alexa Fluor 555) are shown before (bottom, left) and after (bottom, right) assembly.

Extensive networks of weak and rapidly reversible (e.g., ∼500 ms for SH2:pY) interactions have manifested in both 2D and 3D apparent phase transitions in reconstituted systems (7, 8, 10, 11). The static connectivity of molecular assembly is analogous to a polymer, and assembly formation has been proposed to exhibit a gelation phase transition (12) (a transition in connectivity in which a polymer can proliferate into an infinite network (13, 14)). Alternatively, the rapid turnover of individual molecules within the assembly, along with the visible macroscopic physical property of surface or line tension, has led to their description as viscous fluids (3, 8). These different possibilities have distinct dynamical properties with correspondingly different potential effects on chemical kinetics of signaling reactions. Detailed examination of the dynamic scaling of molecular mobility offers one approach to determine the molecular-scale structural identity of the assembly. In particular, the dynamical scaling law, defined as k in 〈r²〉 ∝ t^k, where r is distance traveled by an individual molecule (13), is an experimentally measurable property relating to both molecular structure as well as the diffusion process within the biochemical reaction itself. The dynamical scaling law exhibits different characteristics for gels (13), viscous fluids (15), and other forms of molecular organization.

In this study, the translational motion of individual LAT proteins engaged in the LAT:Grb2:SOS networked molecular assembly on supported membranes is comprehensively studied by single-molecule tracking. LAT is a scaffold protein in the T cell receptor signaling system with nine tyrosine residues, three of which are known to recruit Grb2 after phosphorylation (9, 16). Activation of T cell receptors by ligand leads to activation of the Zap70 kinase, which phosphorylates LAT. This occurs against a background of LAT dephosphorylation by phosphatase activity. The overall degree of LAT phosphorylation is dynamically regulated by this kinase-phosphatase balance, which ultimately tunes the threshold for propagating a signal from the T cell receptor to downstream components of the signaling pathway. Phosphorylation of LAT then leads to LAT assemblies mediated by interactions with multivalent cytosolic proteins such as Grb2 and SOS. Grb2 contains SH2 and SH3 domains, enabling it to simultaneously bind pY residues on LAT and the proline-rich region on SOS. SOS can bind to at least two Grb2 molecules, enabling extended network assembly as long as the LAT proteins are sufficiently phosphorylated (Fig. 1). This phosphotyrosine-mediated network assembly was initially proposed based on cellular imaging experiments (9) and subsequently analyzed theoretically (12). Recently, a reconstitution approach with purified proteins and artificial membranes was developed to provide a well-controlled system (10, 11) for detailed examination of the molecular identity of LAT assembly. Here we take advantage of this approach in combination with single-molecule tracking to analyze the dynamical structure of LAT assembly.

Phosphorylated LAT proteins reconstituted on supported membranes are laterally fluid and coalesce into assembled structures upon addition of Grb2 and SOS. This phase transition is reversible by addition of phosphatase and the structure is dynamically controlled by the degree of LAT phosphorylation (10, 11). We measure the dynamical scaling law of LAT movement on membranes and observe subdiffusive motion (〈r²〉 ∝ t^k, where k < 1) of LAT in the assembly only below a characteristic timescale. Multiple subdiffusive timescales can be resolved with faster image acquisition rates. Comparing these results with Monte Carlo simulations and classical polymer theory reveals that the LAT:Grb2:SOS networked assembly has a dynamical structure similar to a loosely entangled polymer.

Materials and Methods

This section is detailed in Supporting Material (11, 13, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26).

Results and Discussion

Diffusion analysis of LAT molecules within LAT:Grb2:SOS assemblies

We reconstituted the LAT:Grb2:SOS assembly on supported membranes using the cytoplasmic domain (residues 30–233) of LAT with an N-terminus 6-His tag, which was chelated onto DOPC bilayers containing 4% Ni-NTA lipids (Fig. 1) (11, 23). Typical LAT densities on the membrane surface for these experiments, measured by fluorescence correlation spectroscopy (26, 27), were ∼2400 molecule/μm². LAT was phosphorylated by inclusion of dilute Src family kinase, Hck, on membranes (typically with densities of <100 molecule/μm²). No phosphatase was included in these experiments, thus LAT is fully phosphorylated, as inferred from the extent of Grb2 recruitment (11). Under these experimental circumstances, Hck kinase activity is indistinguishable from Zap70, and corresponds to the physiological situation of strong receptor activation (11). Single-molecule trajectories from individual LAT molecules were tracked by labeling a trace fraction (∼0.1%) with Alexa Fluor 555 fluorescent dye and imaging on a total internal reflection fluorescence microscopy setup.

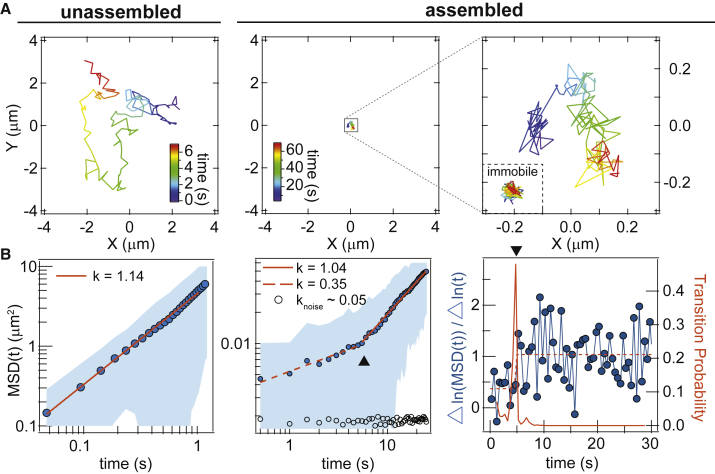
In the absence of assembly, single-molecule trajectories of LAT on the supported membrane reveal simple diffusive motion, with a linear scaling of mean-squared displacement (MSD) with time (Fig. 2 A). MSD analysis is performed on each time trajectory of positions, {x(t), y(t)}, by the time-averaging protocol: $MSD\left(n\delta t\right)=1/(N-n-1){{\sum }_{j=1}^{N-n-1}\left\{{\left[x\left(j\delta t+n\delta t\right)-x\left(j\delta t\right)\right]}^2+\left[y\left(j\delta t+n\delta t\right)-y\left(j\delta t\right)\right]\right\}}^2$, where δt is the time between frames, N is the total number of frames in a single trajectory, and n and j are positive integers (21). MSD traces from single trajectories >100 frames were analyzed in terms of a power law, MSD(t) = At^k. For unassembled LAT on the supported membrane, fitted values of k were around unity over all timescales, indicating simple Brownian motion. In this case, the diffusion coefficient (D) is well defined and A = 4D for 2D motion. Fit values of D were ∼1–1.5 μm²/s (Fig. 2 B), which are typical for a monomeric protein on supported membranes (26, 27).

Figure 2.

Dynamic scaling of LAT:Grb2:SOS assembly. (A) Single-molecule tracking of dilute labeled LAT before and after assembly. The time axis is color-coded in the trajectory. The inset of the right plot shows a trajectory of an immobilized LAT particle on a glass substrate tracked under identical imaging conditions, to quantify the extent of instrumental noise (circles in (B)). (B) Time-averaging MSD analysis for the trajectories in (A), fitted to a power law in a log-log plot. The fitted A for k = 1.14, 1.04, and 0.35 are 4.5, 0.0017, and 0.0054, respectively. The shaded area is the SD calculated from a single trajectory. The characteristic timescale (triangle) is estimated with a Bayesian change-point algorithm (right). Analysis in (B) is applied to the same trajectory shown in (A).

To trigger networked assembly of LAT, Grb2 and the proline-rich domain of SOS were added in the solution at 5.8 and 1.45 μM, respectively. We take advantage of the reconstitution approach to use a higher concentration of proteins to drive the formation of stable and extended LAT assembly of sufficient size (∼μm) for single-molecule tracking (Fig. 1). Smaller submicron LAT assemblies formed within minutes can also be achieved by tuning the protein concentrations (10). Single-molecule dwell time analysis suggests that assemblies of different sizes exhibit similar kinetic features (11), suggesting that LAT assemblies are similar regardless of their sizes. Under this basis, we drive the reconstituted system to extended LAT:Grb2:SOS network assemblies formed over the course of ∼30 min, after which the system reaches a semistationary state (Fig. 2 A). The micron-size assemblies are spatially convenient for single-molecule characterization of dynamics within LAT assemblies.

Single-molecule imaging of LAT in the assembled state, acquired at a relatively slow frame rate of 2 Hz, reveals highly constrained and localized motion (Figs. 2 A and S1; Movie S1). This slow acquisition strategy allows individual molecules to be tracked for 100 s before photobleaching. MSD analysis shows that below a characteristic timescale of a few seconds, LAT is subdiffusive (k ∼ 0.1–0.4). Over longer time intervals, linear scaling of MSD with time (k → 1) is restored, albeit with slow diffusion coefficients of <0.01 μm²/s (Fig. 2 B). The characteristic timescales are determined using a Bayesian change-point algorithm (20) to evaluate if and where transition occurs (Supporting Materials and Methods). Observations over many trajectories confirm that the transition between subdiffusive and normally diffusive motion exists in the time domain only, all tracked molecules reside within the LAT gel, and mobility is spatially homogeneous. Membrane-bound Grb2 and SOS (imaged with dilute Alexa Fluor 647-labeled construct) also exhibit similar transitions from subdiffusive to diffusive dynamics on short timescales (Fig. S2). Errors from tracking due to instrument stability and the tracking algorithm are assessed using LAT molecules immobilized directly on glass surfaces. Immobile molecules result in weak power dependence (k < 0.1), low amplitudes of <0.003 μm², and absence of a characteristic transition timescale within 100 s (Fig. 2). Therefore, we conclude that the observed transitions are dominated by genuine molecular motion.

Time-dependent subdiffusion of LAT is similar to the viscoelastic motion of a polymer

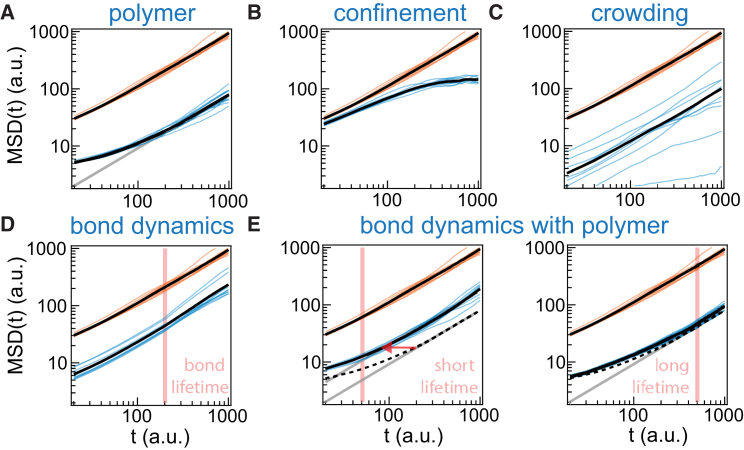
The binding relationship of LAT:Grb2:SOS hints that the assemblies can maintain an effective structure of a polymer (13, 28). However, the reversibility of the bonds introduces an additional layer of dynamics different from a conventional polymer (29). We first compare the basic feature of experimental observation, the subdiffusion-to-diffusion motion, with Monte Carlo simulations of random walks (13, 17, 19, 25) on 2D lattices. The role of the simulations, together with the accompanying discussion of classical literature in polymer physics, are meant to help evaluate how different subdiffusion mechanisms may be distinguishable in experimentally acquired MSD analyses. We specifically compare polymer bonding to two other commonly described subdiffusion mechanisms of membrane proteins—confinement from compartmentalization (30) and crowding effects (31). A purely random walk on a lattice yields a scaling of k → 1 (Fig. 3 A). Simple polymer constraints (see Supporting Materials and Methods) (13, 17, 19) recreate subdiffusive motion over short timescales whereas diffusive motion is observed on longer timescales (Fig. 3 A). Confinement by an impassable square box results in a plateau in the MSD curve (Fig. 3 B). Crowding effects are considered by trapping of molecules with a heavy-tail waiting time. In this case, the ensemble MSD follows subdiffusion whereas MSD from individual trajectories does not exhibit subdiffusion (Fig. 3 C); (18, 25). Although there can be other possible microscopic crowding mechanisms, we exclude trapping of proteins in a dynamic crowding environment as the reason for the observed subdiffusion.

Figure 3.

Time-averaging MSD from Monte Carlo simulations of 2D random walk. Molecular motions are constrained by (A) polymer bonding, (B) confinement, (C) crowding effect, (D) binding to immobile sites, and (E) binding to polymers. Orange (upper, faster) and blue (lower, slower) curves correspond to 10 simulated trajectories by the Brownian and the labeled mechanisms, respectively. Black curves are the averaged values. Gray curves are guidelines for linear scaling of MSD with time. Dashed lines in (E) are references to pure polymer constraints in (A). Pink vertical lines denote the bond lifetimes of the molecule binding to an immobile site or a polymer. In (C) and (D), the MSDs for the associated mechanisms are multiplied by a factor of 10 for clarity. To see this figure in color, go online.

The LAT:Grb2:SOS assembly does not form a conventional polymer. It differs by the fact that individual bonds are rapidly forming and breaking and some of the system dynamics result from these bond rearrangements (29). The bond dynamics themselves will increase the overall molecular turnover within the system as individual molecules may join and exit the assembly or move within it via a bind-unbind-rebind mechanism. However, random binding to and escaping from immobile sites alone is insufficient to cause subdiffusion on any characteristic timescale (Fig. 3 D; Supporting Materials and Methods). Binding to and escaping from a mobile polymer network (Supporting Materials and Methods) recreates the time-dependent subdiffusion with increased mobility, but the characteristic timescale depends on the relative timescale between the bond lifetimes and polymer constraints—the faster timescale will determine the value of the characteristic timescale (Fig. 3 E) (29). In the case of LAT, the effective bond lifetime depends on simultaneous breakage of all multivalent interactions (Fig. 1), which is estimated to be >10 s (11). Given that the observed characteristic timescales are 1–10 s (Figs. 2 and S1), this corresponds to the scenario where mean bond breakage time exceeds polymer relaxation time such that the dominating motion is then that of polymer constraints. This is further supported by the observation that Grb2 and SOS trajectories (which are terminated when the molecule escapes the assembly) both show similar characteristic transition timescales (Fig. S2). Bond rearrangements may facilitate the overall mobility. Taken with the evidence that the modular domains of LAT:Grb2:SOS (9) can form aggregated assemblies (12), the experimentally observed dynamical scaling of LAT mobility within the condensed assembly best resembles the viscoelastic motion of a polymer. Additional evidence emerges when imaging LAT motions with faster acquisitions and comparing with classical polymer theory.

Multiple time-dependent subdiffusion of LAT: entanglement within molecular assemblies

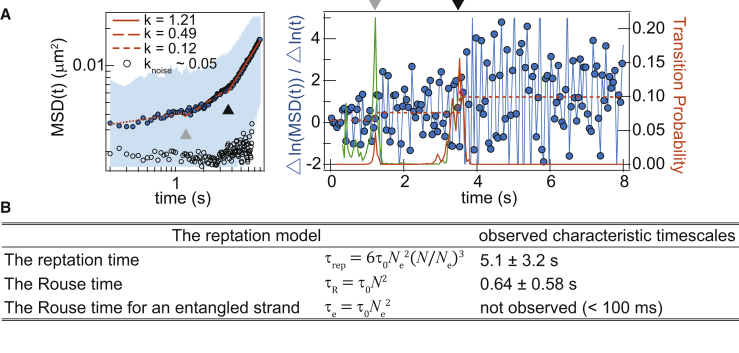
In experimental trajectories imaged at a 21-Hz frame rate, multiple relaxation timescales can be resolved for LAT motion within the assembly (k₁ ∼ 0.1, k₂ ∼ 0.4) (Fig. 4 A). This provides evidence for effective entanglement. The viscoelastic motion of a polymer arises from its relaxation modes, first analytically calculated by Rouse (28) and expanded to entangled polymers by Degennes (32). Entanglement of polymers in a condensed phase describes network chains imposing topological constraints to each other, promoting timescales of different subdiffusive dynamics (13). The reptation model for entangled linear polymers predicts multiple timescales of subdiffusion due to neighboring bond and topological constraints. In order of increasing timescale, these can be broken down as the Rouse time of an entangled strand (τ_e), the Rouse time (τ_R), and the reptation time (τ_rep). For LAT assemblies, the average number of bonds at a given time is most likely between 2 and 3 (LAT has a multivalency of three for Grb2, whereas each bond has a subsecond lifetime) (11, 16). To gain some estimations of the entanglement effects, we compare the single-molecule data with the reptation model (13), which assumes effective bonds of two; the result is summarized in Fig. 4 B. Assignment of the observed timescales to the model is established by first recognizing that only the reptation time exhibits a temporal transition from subdiffusive to diffusive motion, whereas the Rouse time defines a transition between subdiffusive motions with different characteristic scaling. The observed scaling follows the prediction of the reptation model $\left(k_{{\tau }_R>t>{\tau }_e}<k_{{\tau }_{\text{rep}}>t>{\tau }_R}<k_{t>{\tau }_{\text{rep}}}\approx 1\right)$. Although the original reptation model is considered in the case of 3D, the reptation motion itself is confined in 1D—the polymer occupies and moves in a snakelike motion along a tube (13). This effective entanglement is maintained in the case of LAT assemblies (Fig. 4), which is most likely structured in a quasi-2D geometry.

Figure 4.

Multiple subdiffusive timescale. (A) MSD analysis of LAT mobility was acquired at a frame rate of 21 Hz. The shaded area is the SD of statistics from a single trajectory. Each timescale is fitted by a power law, with the characteristic timescales denoted by triangles. The fitted A for k = 1.21, 0.49, and 0.12 are 0.021, 0.011, and 0.0041, respectively. The orange and green curves of the right plot correspond to the transition probability calculated from the full timescale and the partial timescale before the slower (black triangle) characteristic timescale, respectively. (B) Given here is a comparison of the relaxation timescales between LAT assembly and the reptation model. The value τ₀ is the relaxation time of a monomer (not determined from experiments). The symbol ± denotes the SD. Statistics for the reptation and the Rouse time are both n = 32. To see this figure in color, go online.

For an ideal polymer, the timescale of relaxation is determined by the longest relaxation mode, which reflects the total size and entanglement of the polymer strand (13). Within the 38 × 38 μm field of view, the distribution of observed relaxation timescales for individual trajectories within the LAT assembly is broad (τ_rep = 5.1 ± 3.2, τ_R = 0.64 ± 0.58 s) (Fig. 4 B). In some trajectories, subdiffusion persists without a characteristic transition timescale, indicating the existence of larger local assemblies. LAT assemblies of different sizes evidently coexist. Averaging the measurements provides estimations about the mean extent of connectivity within the assembly. The relative size of entanglement, N/N_e, where N_e is the number of monomers in an entangled strand and $N$ is the total number of monomers in the polymer, is ∼1–5 for LAT assembly (Fig. 4 B; Supporting Materials and Methods), suggesting a rather loose entanglement. The unobserved τ_e is estimated to be ∼100 ms, which is at the limits of our MSD analysis resolution.

LAT gelation

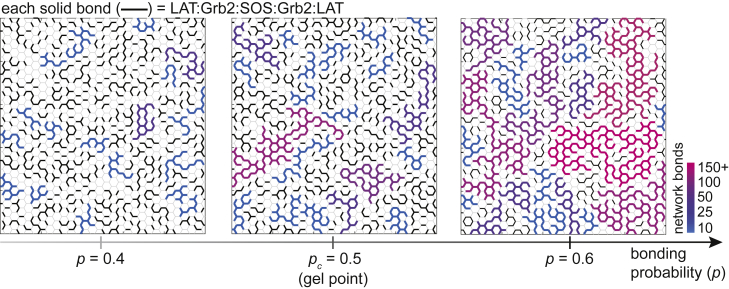
Based on the multivalent interactions of LAT, the assemblies have been suggested to resemble a gelation phase transition (12). For LAT to form a gel phase, it must be capable of forming a polymer network—the single-molecule tracking of LAT supports that it shares entangled polymerlike features. Given a multivalency of three, LAT can form a macroscopically assembled network if the bonding probability (p) between adjacent LAT (e.g., through the LAT:Grb2:SOS:Grb2:LAT motif) exceeds the critical threshold (p_c = 1/(f−1), where f is the multivalency) (13, 14). This is illustrated in Fig. 5. Qualitatively, entanglement of large polymers is prominent near the gel point, suggesting that the reconstituted LAT assemblies are possibly close to that condition.

Figure 5.

LAT gelation. LAT has a minimum multivalency of three, which can be represented by honeycomb lattices. Each intersection represents a LAT molecule, whereas each edge represents a possible bond of LAT:Grb2:SOS:Grb2:LAT with a bonding probability (p). Black and gray bonds denote bonding and nonbonding interactions, respectively. Escaping a networked assembly for a LAT molecule requires simultaneous breakage of all bonds. The color gradients represent network sizes that are >10 assembled LAT molecules.

Conclusions

Single-molecule tracking of LAT within the phosphotyrosine-mediated assembly reveals a dynamic scaling law similar to that of an entangled polymer. Although the assembly is distinct from a classical polymer in that all of its individual bonds are rapidly breaking and reforming, the mean connectivity within the structure still manifests in a characteristic dynamical scaling law. The elastic feature of LAT assembly is distinctively different from a pure viscous fluid (15). In living cells, subdiffusive motion is commonly observed and often attributed to confinement or crowding effects (33, 34). Here, we demonstrate that organization of proteins into networked assemblies leads to timescale-dependent subdiffusion. Moreover, this type of analysis could be performed in live cells (34, 35), providing a way of characterizing the molecular-scale organization of visible signaling structures based on dynamics.

Author Contributions

W.Y.C.H. and J.T.G. conceived the study. W.Y.C.H. designed the experiments. W.Y.C.H. and H.-K.C. performed the experiments. W.Y.C.H. analyzed data and carried out the simulations. W.Y.C.H. and J.T.G. wrote the manuscript. J.T.G. supervised the project.

Editor: Joseph Falke.

Supporting Material

Movie S1. Single-Molecule Imaging of LAT

Imaging of LAT-AlexaFluor 555 is at a frame rate of 2 Hz. Most of the particles are mobile over longer timescales (>10 s).