Abstract
Recent studies show the remarkable power of fine-grained information disclosed by users on social network sites to infer users' personal characteristics via predictive modeling. Similar fine-grained data are being used successfully in other commercial applications. In response, attention is turning increasingly to the transparency that organizations provide to users as to what inferences are drawn and why, as well as to what sort of control users can be given over inferences that are drawn about them. In this article, we focus on inferences about personal characteristics based on information disclosed by users' online actions. As a use case, we explore personal inferences that are made possible from “Likes” on Facebook. We first present a means for providing transparency into the information responsible for inferences drawn by data-driven models. We then introduce the “cloaking device”—a mechanism for users to inhibit the use of particular pieces of information in inference. Using these analytical tools we ask two main questions: (1) How much information must users cloak to significantly affect inferences about their personal traits? We find that usually users must cloak only a small portion of their actions to inhibit inference. We also find that, encouragingly, false-positive inferences are significantly easier to cloak than true-positive inferences. (2) Can firms change their modeling behavior to make cloaking more difficult? The answer is a definitive yes. We demonstrate a simple modeling change that requires users to cloak substantially more information to affect the inferences drawn. The upshot is that organizations can provide transparency and control even into complicated, predictive model-driven inferences, but they also can make control easier or harder for their users.
Keywords: : predictive modeling, transparency, privacy, comprehensibility, inference, control
Introduction
Successful pricing strategies, marketing campaigns, and political campaigns depend on the ability to optimally target consumers and voters. This generates incentives for firms, political parties, and governments to exploit information related to people's personal characteristics, such as their gender, marital status, religion, sexual or political orientation, and personality. The boom in availability of online data has accelerated efforts to do so. However, personal characteristics often are hard to determine with certainty because of privacy restrictions or simply because they are not directly observed. As a result, online marketers increasingly depend on statistical inferences based on available information. A predictive model can be used to give each user a score that ranks users by the estimated probability of having a certain personal trait, such as being gullible, introverted, female, a drug user, or gay.1 Users then can be targeted based on these inferred propensities and their relationship to particular content or advertising campaigns. Alternatively, such inferred characteristics can be used implicitly in advertising campaigns or other systems, via models trained on feedback from those who responded positively. In practice, usually a combination of model confidence and a budget for showing content or advertisements leads to targeting users in some top percentile of the score distribution given by predictive models.2
Online user targeting systems, particularly in digital advertising, increasingly are trained using information on users' web browsing behavior.2 In addition, when possible, targeters include information disclosed by users on social networks. For instance, to target ads Facebook uses a combination of your social activity on their network (pages you and your friends Like), web browsing history, interactions with various businesses (such as loyalty program information shared with Facebook), and your location.* Recently, Facebook has extended this type of targeting to work outside of direct Facebook properties; third-party mobile applications can take advantage of Facebook's advertising tools through the use of Facebook Audience Network.†
While some online users may benefit from being targeted based on inferences of their personal characteristics, others may find such inferences unsettling. Not only may these inferences be incorrect due to a lack of data or inadequate models, some users may not wish to have certain characteristics inferred at all. To many, privacy invasions via statistical inferences are at least as troublesome as privacy invasions based on personal data.3
In response to an increase in demand for privacy from online users, suppliers of browsers such as Chrome and Firefox have developed features such as “Do Not Track,” “Incognito,” and “Private Windows” to control the collection of information about web browsing. However, these features provide neither clear transparency into what inferences are drawn and why, nor easy, fine-grained control over what information may be used for inference. Furthermore, as of now, social networks such as Facebook do not have a strong analog to these privacy features that would allow for transparency and control in how user information is used to decide on the presentation of content and advertisements.‡
In this article,§ as a means for providing transparency into the reasons why a particular inference is drawn about an individual, we draw on an idea introduced for explaining the reasons behind instance-level document classifications.7 Specifically, what is a minimal set of evidence such that if it had not been present, the inference would not have been drawn? Let's call this an evidence counterfactual. The evidence counterfactual can be applied beyond document classification to the sorts of inference that interest us here.
As a concrete example, consider that Manu has been determined by the system's inference procedure to be gay, based on the things that Manu has chosen to Like.** Note that the inference of the personal trait may be direct or may be subtle—for example, a prediction that Manu would be a good target for a particular ad, where the inference of an associated personal trait is implicit. The system subsequently delivers to Manu an advertisement for a local LGBTQ activism group. Although Manu actively supports the LGBTQ community, he prefers to keep certain aspects of his personal life between him and his friends, and not have the system using these aspects to make ad targeting decisions. What is a minimal set of Manu's Likes such that if they were not used for inference Manu would no longer receive the ad, or alternatively be classified by the system as being gay?
We introduce the idea of a “cloaking device” as a vehicle to provide, and to study, control over inferences. Specifically, the cloaking device provides a mechanism for users to inhibit the use of particular pieces of information in inference. Combined with the transparency provided by the evidence counterfactual, a user could be given control over model-driven inferences. So, continuing our example, Manu would be given the ability to request that the Likes responsible for this inference not be used by the system for future inferences. Importantly, the user can cloak particular information from inference, without having to stop sharing the information with his social network friends. Thus, hopefully, this combination will allow control with a minimal amount of disruption to the user's normal activity. This hope rests on the relationship between the evidence and the behavior of the predictive models.
Importantly, cloaking the information used to draw inferences provides users with deeper control than simply inhibiting individual inferences, such as would be achieved by blocking particular content, ads, or advertisers. The cloaking device essentially tells the system: “do not draw inferences like this about me”—or more practically, “do not show me ads or content for the same reasons that you decided to show me this.”
We use these mechanisms as analytical tools to answer two main questions: (1) How much information must users cloak to significantly affect inferences about their personal traits? We find that generally a user does not need to cloak the majority of his or her information to inhibit inference. In fact, we find that for the most common online inference setting, users need to cloak only a small portion of the information recorded about them. We also find that, encouragingly, false-positive (FP) inferences are generally easier to cloak than true-positive (TP) inferences.
The second question we address is (2) Can firms change their modeling behavior to make cloaking more difficult? The answer is a definitive yes. In our main results we replicate the methodology of Kosinski et al.1 for modeling personal traits; then we demonstrate a simple modeling change that still gives accurate inferences of personal traits, but requires users to cloak substantially more information to affect the inferences drawn. The upshot is that firms can provide transparency and control even into very complicated, predictive model-driven inferences, but they also can make modeling choices to make control easier or harder for their users.
We also discuss that transparency and control can be separated. For example, firms could provide users with “one-click” cloaking, through which the fine-grained information responsible for a particular inference would be cloaked without the users needing to or even being able to see the specific information. An individual targeted with content that makes him or her uncomfortable could simply click the “cloak” button, and the system would hide the fine-grained data from its future inference procedures.
Background and Related Work
Online privacy is becoming an increasing concern for consumers, regulators, and policy makers.8,9 Treatments of privacy in the analytics literature often focus on the issue of confidentiality of personal characteristics.10,11 However, with the rapid increase in the amount of social media data available, statistical inference about personal characteristics is drawing attention.3,9,12 Several articles have shown the predictive power of information disclosed on Facebook to infer users' personal characteristics.1,13,14 Specifically, the set of Facebook pages that users choose to “Like” on the platform can predict their gender, religion, sexual or political orientation, and many more personal traits. As a result, recent studies have begun to examine the implications of the use of large-scale behavioral data.
Shmueli15 discusses the growing trend in both academia and industry to collect behavioral data on a large scale, and presents several difficulties related to acquiring and analyzing big behavioral data. A particular problem arises when big data is used to create black box predictive models that are often misleadingly described using causal interpretations. These massive models are used to drive decisions for millions of individuals; they can learn trends that are incorrect, or perpetuate social biases, and result in social and emotional outcomes that are harmful to people and social groups. Barocas et al.9 develop a research agenda to begin approaching these types of problems by building awareness of various machine learning methods, enhancing transparency in model interpretation, and assessing the possible sources of bias that can be introduced in modeling.
A study surveyed Facebook users and found that they did not feel that they had the appropriate tools to mitigate their privacy concerns when it comes to social network data.16 In an online experiment utilizing a Facebook social recommender system for music that gives users control over recommendations and explains how they were derived, Knijnenburg et al. show that inspectability and control of the system increased users' ratings for recommendations and their satisfaction with the system.17 A related study finds that different types of explanations by a recommendation agent enhance users' trust in the system.18 Furthermore, there is evidence that when given the appropriate tools, people will choose to give up some of the benefits they derive from their social network activity to meet their privacy concerns.19 Besides being a conceptual tool to help with the analysis of control, the cloaking device can be a practical tool to achieve it.
The term “evidence counterfactual”5,6 focuses on the causal nature of explanations for data-driven inferences.* Before digging deeper, it is important to clarify that we are considering specifically explanations for why a classification (or other decision) was made, in contrast to explanations of other phenomena in the world. Robnik-Sikonja and Kononenko22 discuss the difference between explanations at the “model level” and explanations at the “domain level”; not considering this distinction can lead to confusion. So, for example, we would consider an explanation for why a data-driven predictive model classified an individual as being introverted—what evidence caused the predictive model to issue this classification? This is the phenomenon that we want to provide transparency into.22 Explaining instance-level classifications by assessing the (causal) influence of data inputs is receiving increasing attention in research and practice for improving the transparency of algorithmic decision-making.5–7,20–24
A Model of Cloaking
We can now describe the core design, use, and value of the cloaking device. Given an individual, and a specific model-based inference about the individual, the evidence counterfactual explanation reveals the particular evidence (features of the individual, e.g., Likes) that caused the inference to be made. Recalling our example from the Introduction section, a targeting model inferred that Manu would be a good target for specific content based on the items that he had Liked on Facebook. The cloaking device allows the individual to hide (to “cloak”) particular evidence, for example, one or more Likes, from the inference procedure. Once a Like is cloaked, the inference (decision-making) procedure would remove it from its input, and therefore treat the user as if he had not Liked this item. The evidence counterfactual presents the user with a minimal set of Likes to cloak to change an inference made about him.
More generally, consider any domain where the features can be seen as evidence for or against a particular nondefault* inference. Consider also the increasingly common scenario25 where there are a vast number of possible pieces of evidence, but any individual normally only exhibits a very small number of them—such as when drawing inferences from Likes on Facebook.†
Now consider the task of predicting whether or not a user is gay using Facebook Likes. While some users might choose to take actions on the social platform that suggest or reveal that they are gay, some may not wish for this information to be available to advertisers or others drawing automatic inferences based on online user behavior. Users who prefer not to share this personal status even with their friends may not want it to be predicted by the system. Furthermore, a user who is in fact not gay may not want an incorrect inference to be drawn about him or her. Figure 1 illustrates two users, their probabilities of being gay as predicted by a model-based inference procedure, and the effect of removing evidence from their data. As evidence is removed by cloaking Likes, we see that removing fewer than 15 Likes for one user results in a dramatic drop in the predicted probability of being gay, whereas for the same number of removals the probability is reduced hardly at all for the other user.
FIG. 1.
For two users, the lines track the predicted probability of being gay as a function of cloaking Likes. For each line, the leftmost point shows the estimated probability of being gay for the user before any cloaking. Moving left to right, for each user, Likes are removed one-by-one from consideration by the inference procedure in order of greatest effect on the estimated score (before the score is converted to a probability estimate). One user's probability drops dramatically with cloaking fewer than 15 Likes (blue solid-circle line); the other's is hardly affected at all (red dashed-diamond line).
The cloaking device thus has two important dimensions of value. First, it provides a practical device that could be implemented by social media sites (and others) to provide such transparency and control to their users. Second, it provides us with a means for studying the relationship between evidence and model-based inference, and thereby transparency and control, in settings such as these. This article focuses on the latter, both for its own intrinsic interest and also as potential support for the former.
Technically, cloaking is defined in the context of a particular predictive model. We assume for this article that the model is fixed, such as in situations where new models are put into production infrequently. Scenarios where the system relearns models after cloaking would be an interesting line of future study. (Note that to minimize “rediscovering” cloaked traits, Likes can be cloaked from inference but not from learning.) For this article, we consider classification or ranking tasks, where the inferences are made by a linear model with the presence/absence of each Like being the features. The procedure can be extended to nonlinear models (see Martens and Provost7). All of the features and targets in these models are assumed to be binary. In particular, for our results the main model replicates the predictive modeling used by Kosinski et al.1 and we use their data on predicting personal traits from Facebook Likes. More specifically, the modeling procedure first reduces modeling dimensionality by computing the singular-value decomposition (SVD) of the matrix of users and their Likes, and choosing the top-100 SVD dimensions' vectors as the modeling dimensions (as has become standard practice with such high-dimensional data). Then, logistic regression models are built on these dimensions to predict a variety of personal traits, as detailed below.
For inference we simulate what is to our understanding the most common method of taking online actions based on such models. Specifically, we assume that a positive inference is drawn—for example, a user would be subject to targeting—if the model assigns the user a score placing him or her in a specified top quantile 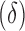 of the score distribution produced by the predictive model.*
of the score distribution produced by the predictive model.*
More formally, let  be an indicator equal to 1 if user i has Liked a piece of information j and 0 otherwise. For the main results we build the SVD-logistic regression model described above; then, we convert it to a mathematically (and functionally) equivalent linear logistic regression singular-value decomposition (LRSVD) model in the original features, via the transformation described in Appendix A. This transformation facilitates direct manipulation of the original Likes. From now on unless stated otherwise we will consider this linear logistic model.
be an indicator equal to 1 if user i has Liked a piece of information j and 0 otherwise. For the main results we build the SVD-logistic regression model described above; then, we convert it to a mathematically (and functionally) equivalent linear logistic regression singular-value decomposition (LRSVD) model in the original features, via the transformation described in Appendix A. This transformation facilitates direct manipulation of the original Likes. From now on unless stated otherwise we will consider this linear logistic model.
Let 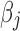 be the coefficient in the (linear) model associated with feature
be the coefficient in the (linear) model associated with feature 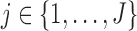 . Without loss of generality, assume that these are ranked by decreasing value of
. Without loss of generality, assume that these are ranked by decreasing value of 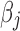 . Each such coefficient corresponds to the marginal increase in a user's score if he or she were to choose to Like feature j. Consider the following model output score given to user i, which ranks users by their estimated probability of having a characteristic s.
. Each such coefficient corresponds to the marginal increase in a user's score if he or she were to choose to Like feature j. Consider the following model output score given to user i, which ranks users by their estimated probability of having a characteristic s.
 |
For simplicity, let us call those users for whom the positive inference is made the “targeted” users. For a particular set of users, define the cutoff score 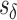 to be the score of the highest ranked user in the quantile directly below the targeted users. Thus, the set of targeted, top-ranked users Ts for classification task s is
to be the score of the highest ranked user in the quantile directly below the targeted users. Thus, the set of targeted, top-ranked users Ts for classification task s is
 |
To analyze the difficulty or ease of cloaking for each user in the targeted group, we iteratively remove Likes from his or her profile until he or she is successfully cloaked. For our linear models, we do this by iteratively subtracting from his or her score the coefficient of the feature that is present (non-zero) in his or her data instance that has the largest coefficient in the model. Figure 1 shows two examples. A user is considered to be successfully cloaked when his or her score falls below 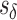 .*,†
.*,†
Figure 2 shows the discriminative power associated with each Like in our data individually (i.e., not in the context of the predictive model) for the task of predicting if male users are gay. The 10 points with associated text labels are the Likes that have the largest coefficients from the LRSVD model. The top-10 highest-coefficient Likes for the user shown by the red dashed-diamond line in Figure 1 are shown here as large red points. Six out of this user's top-10 Likes overlap with the top 10 for the entire task. This highlighted user is the user that the LRSVD model predicts as having the highest probability of being gay.
FIG. 2.
The discriminative power of Likes on Facebook when determining if a user is gay 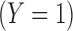 . Each point represents one Like; the axes represent the probabilities of having that Like for the two classes in the data set. Labels are given to the top 10 Likes as sorted by their corresponding coefficients in the LRSVD model. The large points colored in red are the top 10 pages Liked by the user with the highest probability of being gay as predicted by the LRSVD model. This is the same user who appeared as the red dashed-diamond line in Figure 1. LRSVD, logistic regression singular-value decomposition.
. Each point represents one Like; the axes represent the probabilities of having that Like for the two classes in the data set. Labels are given to the top 10 Likes as sorted by their corresponding coefficients in the LRSVD model. The large points colored in red are the top 10 pages Liked by the user with the highest probability of being gay as predicted by the LRSVD model. This is the same user who appeared as the red dashed-diamond line in Figure 1. LRSVD, logistic regression singular-value decomposition.
To quantify the difficulty of cloaking via Like removal, we let 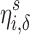 represent the effort to cloak user i from the top
represent the effort to cloak user i from the top 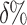 of the score distribution for a characteristic s.
of the score distribution for a characteristic s. 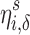 is defined precisely in Algorithm 1; it is the minimum number of Likes that must be removed to move i below the threshold. All else being equal, the effort to cloak a user is smaller when (1) the coefficients of his or her removed features are larger, (2) the threshold score is larger, and/or (3) his or her predicted score is smaller.
is defined precisely in Algorithm 1; it is the minimum number of Likes that must be removed to move i below the threshold. All else being equal, the effort to cloak a user is smaller when (1) the coefficients of his or her removed features are larger, (2) the threshold score is larger, and/or (3) his or her predicted score is smaller.
Algorithm 1:
Algorithm to determine the amount of effort needed to cloak a user for a particular predictive task.
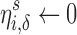 |
Let 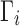 = { = { | |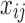 >0} >0} |
Sort 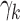 ∈ ∈ 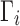 in descending order as 1…| in descending order as 1…| | | |
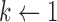 |
while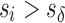 do do
|
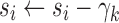
|
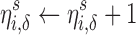
|
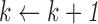
|
| end |
The absolute effort to cloak a particular classification task s is given by averaging  across users in Ts,
across users in Ts,
 |
The relative effort to cloak a task for user i is defined by normalizing the absolute effort by the total quantity of information revealed by the user,
 |
We can then define the relative effort to cloak a classification task s by averaging this measure across users in Ts,
 |
For the rest of this article, we use 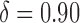 to indicate that the top 10% of users are being targeted. (For other values of
to indicate that the top 10% of users are being targeted. (For other values of  , the results hold qualitatively.)
, the results hold qualitatively.)
Results
Let us now examine the effort required to cloak the inferences of a variety of personal characteristics, based on data on Facebook users. We first describe the data and then proceed to assess the effort required to cloak user characteristics.
Data
Our data were collected through a Facebook application called my Personality.* It contains information on 164,883 individuals from the United States, including their responses to survey questions and a subset of their Facebook profiles. Users can be characterized by their sexual orientation, gender, political affiliation, religious view, IQ, alcohol and drug consumption behavior, personality dimensions, and lifestyle choices. Users do not necessarily reveal all of these personal characteristics. For these users we also know their Facebook Likes.
The personal characteristics are the target variables for the various modeling and inference problems. Some personal characteristics were extracted directly from users' Facebook profiles, whereas others were collected by survey. Binary variables are kept without change. Variables that fall on a Likert scale are separated into two groups, users who have the largest Likert value and users who have any other value. Continuous variables are represented as binary variables using the 90th percentile as a cutoff. Multicategory variables are subsampled to only include the two most frequent categories, with the instances representing the other categories discarded for the corresponding inference task. Notice also that the feature data are very sparse; for each characteristic, a user on average displays less than  of the total set of Likes. Table 1 presents summary statistics of the data.
of the total set of Likes. Table 1 presents summary statistics of the data.
Table 1.
Summary statistics of the data set
| Task | Number users | Number pages |
 positive positive
|
Average likes |
|---|---|---|---|---|
Age  37 37 |
145,400 | 179,605 | 12.7 | 216 |
Agreeableness  5 5 |
136,974 | 179,440 | 1.4 | 218 |
Conscientiousness  5 5 |
136,974 | 179,440 | 1.8 | 218 |
Extraversion 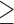 5 5 |
136,974 | 179,440 | 3.3 | 218 |
IQ 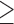 130 130 |
4540 | 136,289 | 13.0 | 186 |
IQ  90 90 |
4540 | 136,289 | 7.3 | 186 |
| Is democrat | 7301 | 127,103 | 59.6 | 262 |
| Is drinking | 3351 | 118,273 | 48.5 | 262 |
| Is female | 164,285 | 179,605 | 61.6 | 209 |
| Is gay | 22,383 | 169,219 | 4.6 | 192 |
| Is homosexual | 51,703 | 179,182 | 3.5 | 257 |
| Is lesbian | 29,320 | 175,993 | 2.7 | 307 |
| Is Muslim | 11,600 | 148,943 | 5.0 | 238 |
| Is single | 124,863 | 179,605 | 53.5 | 226 |
| Is smoking | 3376 | 118,321 | 23.7 | 261 |
Life satisfaction 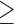 6 6 |
5958 | 141,110 | 12.5 | 252 |
Network density 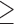 65 65 |
32,704 | 178,737 | 1.2 | 214 |
Neuroticism  5 5 |
136,974 | 179,440 | 0.4 | 218 |
Num friends  585 585 |
32,704 | 178,737 | 14.0 | 214 |
Openness  5 5 |
136,974 | 179,440 | 4.3 | 218 |
| ss belief = 1 | 13,900 | 169,487 | 17.8 | 229 |
| ss belief = 5 | 13,900 | 169,487 | 7.9 | 229 |
| Uses drugs | 2490 | 105,001 | 17.2 | 264 |
Number of pages indicates how many unique Facebook pages have at least one Like by users who have a label for the given trait. Percent positive are how many positive instances there are for each trait. Average Likes indicate the average number of Likes a user associated with the given task has.
Replicating the prior prediction results
We first replicate the predictive modeling and inference procedure reported by Kosinski et al.1 Specifically, we build predictive models on the SVD dimensions in Python using logistic regression as implemented in the scikit-learn package. For each model, we choose the regularization parameter by (five-fold) cross-validation, as is the state-of-the-art practice.26 Appendix B reports the predictive performance across the set of tasks. The results concur with those reported by Kosinski et al.1 As in the original article, the predictive performance is quite strong across the classification tasks.
Main result: how hard is it to cloak?
Table 2 reports the efforts to cloak users who belong to the target group, that is, those users in the top 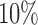 of users as ranked by model score. First, we will focus on the “All” columns (in the next section we break down the results by TPs and FPs). The results show that although users on average display hundreds of Likes, on average they need to cloak fewer than 10 to successfully inhibit inference. This corresponds to cloaking only about 2%–3% of a user's Likes on average. Digging a little deeper, the prediction tasks are sorted in Table 2 by
of users as ranked by model score. First, we will focus on the “All” columns (in the next section we break down the results by TPs and FPs). The results show that although users on average display hundreds of Likes, on average they need to cloak fewer than 10 to successfully inhibit inference. This corresponds to cloaking only about 2%–3% of a user's Likes on average. Digging a little deeper, the prediction tasks are sorted in Table 2 by 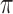 , showing that the averages give a fair picture: with only a couple of exceptions, the proportion of information needed to inhibit inference is around 2%–4%. The actual numbers of Likes that must be removed vary more, as the top-decile users have different total numbers of Likes, but nevertheless we see no extreme outliers.
, showing that the averages give a fair picture: with only a couple of exceptions, the proportion of information needed to inhibit inference is around 2%–4%. The actual numbers of Likes that must be removed vary more, as the top-decile users have different total numbers of Likes, but nevertheless we see no extreme outliers.
Table 2.
The amount of Likes one needs to remove (effort) to cloak different users' traits predicted by the LRSVD models
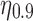 |
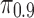 |
|||||
|---|---|---|---|---|---|---|
| Task | All | TP | FP | All, % | TP, % | FP, % |
Age 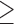 37 37 |
10.3 | 13.0 | 5.8 | 7.7 | 9.7 | 4.4 |
Agreeableness  5 5 |
5.0 | 6.5 | 5.0 | 2.3 | 3.3 | 2.3 |
Conscientiousness  5 5 |
4.7 | 6.7 | 4.7 | 3.9 | 4.7 | 3.9 |
Extraversion  5 5 |
4.4 | 5.9 | 4.3 | 1.9 | 2.4 | 1.8 |
IQ  90 90 |
6.9 | 16.3 | 4.6 | 4.5 | 9.0 | 3.5 |
IQ  130 130 |
6.6 | 3.4 | 7.3 | 2.8 | 3.5 | 2.6 |
| Is democrat | 8.5 | 8.5 | 2.0 | 1.7 | 1.7 | 0.3 |
| Is drinking | 6.8 | 7.5 | 3.9 | 2.0 | 2.2 | 1.2 |
| Is female | 10.0 | 10.0 | 5.5 | 1.9 | 1.9 | 1.3 |
| Is gay | 5.7 | 10.9 | 3.2 | 3.8 | 7.4 | 2.2 |
| Is homosexual | 3.5 | 6.6 | 2.9 | 2.4 | 4.7 | 1.9 |
| Is lesbian | 3.1 | 5.4 | 2.8 | 1.9 | 3.5 | 1.7 |
| Is Muslim | 11.7 | 27.8 | 2.9 | 9.6 | 20.2 | 3.9 |
| Is single | 13.7 | 15.5 | 7.9 | 3.4 | 3.8 | 2.1 |
| Is smoking | 8.4 | 9.8 | 5.6 | 2.8 | 3.2 | 1.9 |
Life satisfaction 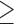 6 6 |
5.1 | 7.2 | 4.6 | 2.2 | 3.2 | 2.0 |
Network density  65 65 |
10.5 | 15.3 | 10.4 | 2.1 | 2.6 | 2.1 |
Neuroticism 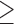 5 5 |
9.1 | 5.7 | 9.2 | 2.2 | 1.6 | 2.2 |
Num friends 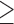 585 585 |
5.0 | 6.6 | 4.2 | 2.1 | 2.5 | 1.9 |
Openness 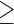 5 5 |
6.7 | 7.7 | 6.6 | 2.3 | 2.8 | 2.3 |
| ss belief = 1 | 5.7 | 6.9 | 4.9 | 2.9 | 3.6 | 2.4 |
| ss belief = 5 | 8.3 | 11.1 | 7.8 | 2.1 | 2.5 | 2.1 |
| Uses drugs | 12.2 | 12.1 | 12.2 | 2.7 | 3.3 | 2.2 |
| Mean | 7.5 | 9.9 | 5.6 | 3.1 | 4.5 | 2.3 |
| Median | 6.8 | 7.7 | 4.9 | 2.3 | 3.3 | 2.1 |
Absolute efforts (numbers of Likes removed) are presented in the left panel, and relative efforts (percentages of Likes removed) are in the right panel. For each panel, we show in the first column, the full set of users with data for the trait, in the second column only the TP users, and in the third column only the FP users.
FP, false positive; LRSVD, logistic regression singular-value decomposition; TP, true positive.
To put these results in context, it would be useful to understand how strongly the cloakability of a trait is related to the statistical dependency structure of the data-generating process. One might think that people who indeed hold a particular trait would exhibit it throughout their behavior, and in particular throughout the things that they Like. How do these cloakability results compare to what one would expect if Likes and the trait were not actually interrelated?
To draw this comparison, we conduct a randomization test to assess both qualitatively and quantitatively whether cloakability for these individuals is indeed harder than it would be in the absence of this statistical interdependency. We first create a sampling distribution to be used to randomly assign Likes to individuals. We want only to remove the interdependency between the Likes and the dependency between the target and the Likes, so we retain the general popularity of Likes as follows (otherwise, due to the skew in popularity, individuals would have collections of oddly unpopular Likes). For each personality trait prediction task, we assign to each Like a weight equal to the fraction of users for that task who have that particular Like. We then normalize the set of weights so that their sum is equal to one to create a sampling distribution. Then, for each user, we draw from this distribution a set of Likes without replacement. For each user, we draw the same number of Likes as the user had in the original data set. Thus, in the resultant population, the popularity distribution over the Likes is the same as in the original data, and the numbers of Likes that people have are the same, and the relationship between the number of Likes and the target trait is the same. However, there are no statistical dependencies among the Likes or between the Likes and the trait. This procedure is repeated 1000 times and each time we apply the same procedure as above to the new population, computing the values of 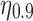 and
and 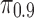 . This results in a distribution over
. This results in a distribution over 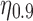 and
and  when the dependencies are removed.
when the dependencies are removed.
Figure 3a shows the difference between  in the no-dependency population and the true
in the no-dependency population and the true  . Quantitatively, for all tasks, we find that the actual absolute effort to cloak is always higher (
. Quantitatively, for all tasks, we find that the actual absolute effort to cloak is always higher (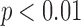 , sign test) than cloaking would be if Likes were randomly assigned. Qualitatively, we see that indeed cloaking seems very easy in the random case. In all but three cases, one needs to cloak fewer than two Likes on average to inhibit inference. In all cases, inference can be inhibited by cloaking fewer than four Likes on average. The figure shows that generally the statistical dependency structure renders cloaking several times harder than it would otherwise be.
, sign test) than cloaking would be if Likes were randomly assigned. Qualitatively, we see that indeed cloaking seems very easy in the random case. In all but three cases, one needs to cloak fewer than two Likes on average to inhibit inference. In all cases, inference can be inhibited by cloaking fewer than four Likes on average. The figure shows that generally the statistical dependency structure renders cloaking several times harder than it would otherwise be.
FIG. 3.
Comparison between the efforts needed to cloak predictions for the populations of real users, and for users for whom the statistical interdependencies among the Likes and between the Likes and the personal trait have been removed. (a) Absolute (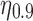 ) and (b) relative (
) and (b) relative (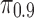 ) efforts are shown for the LRSVD model. Error bars depict 95% confidence intervals. The upshot is that the presence of the statistical dependencies makes it significantly harder to cloak, although the total amount of effort still is small. The differences are more striking for absolute effort than for relative effort, because the real users who are in the top deciles have substantially more likes in total.
) efforts are shown for the LRSVD model. Error bars depict 95% confidence intervals. The upshot is that the presence of the statistical dependencies makes it significantly harder to cloak, although the total amount of effort still is small. The differences are more striking for absolute effort than for relative effort, because the real users who are in the top deciles have substantially more likes in total.
Figure 3b shows the difference in the relative effort to cloak, 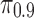 , between the randomized setting and the true setting. Here the highest level result is the same: in every case, the relative effort is no worse than in the true setting (
, between the randomized setting and the true setting. Here the highest level result is the same: in every case, the relative effort is no worse than in the true setting (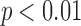 , sign test). However, some of the differences quantitatively are not as striking as in the comparison of absolute effort. In fact, in one case (“is lesbian”) the difference is essentially zero. This seeming paradox is explained by the fact that the numbers of Likes for the true top-decile individuals can be quite different from the numbers of Likes for the top-decile individuals in the no-dependency setting. So, for example, the actual top-decile individuals for “is lesbian” have twice as many Likes on average as the top-decile individuals in the randomized setting.
, sign test). However, some of the differences quantitatively are not as striking as in the comparison of absolute effort. In fact, in one case (“is lesbian”) the difference is essentially zero. This seeming paradox is explained by the fact that the numbers of Likes for the true top-decile individuals can be quite different from the numbers of Likes for the top-decile individuals in the no-dependency setting. So, for example, the actual top-decile individuals for “is lesbian” have twice as many Likes on average as the top-decile individuals in the randomized setting.
The upshot is that although in an absolute sense it is relatively easy to inhibit inference by cloaking Likes, the statistical dependence structure among the Likes and the predicted trait makes it more difficult than it would be without such structure.
Cloaking TPs versus FPs
At the outset, we introduced the idea that there are multiple settings where one might want to inhibit inference. Possibly the most important distinction is between inhibiting an inference that is in fact true (a TP inference) and inhibiting an inference that is false (an FP inference).
Based on the prior results, one might expect that an FP inference would be easier to cloak because the statistical dependency to the (positive) trait is by definition missing. Thus, in a sense, the FP user “accidentally” was targeted, similarly to how the top-decile randomized users “accidentally” were targeted. In neither case was the presence of the trait reflected in the behavior of the user. However, there is an important distinction: in the randomized setting, the statistical dependencies also were broken among the Likes, as opposed to simply between each Like and the target trait. For FPs, intuitively there still may be strong statistical interdependencies between the Likes—so if one has some Likes that trigger the inference by the predictive model, one may have many Likes that trigger the inference.
Thus, in addition to measuring the cloakability across all users in the targeted group, Table 2 also reports the same results for TP and FP users separately. The results show that cloaking is indeed generally more difficult for TP users than for FP (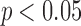 , sign test). The differences in cloakability between TP and FP users are shown in Figure 4.
, sign test). The differences in cloakability between TP and FP users are shown in Figure 4.
FIG. 4.
Differences in cloaking effort required ( and
and 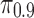 ) for true-positive versus false-positive users, based on the LRSVD model. Bars above the zero level indicate that true positives are harder to cloak; bars below the zero level indicate that false positives are harder to cloak. Error bars depict the 95% confidence interval.
) for true-positive versus false-positive users, based on the LRSVD model. Bars above the zero level indicate that true positives are harder to cloak; bars below the zero level indicate that false positives are harder to cloak. Error bars depict the 95% confidence interval.
These results may provide some intuitive satisfaction. It is relatively easier to “fix” an incorrect classification, than to “hide” from a correct inference. The most striking example of this is in prediction for the “is Muslim” trait. On average, to inhibit the positive inference for someone who actually is Muslim, 28 Likes have to be cloaked. This is almost twice as many as for any other trait. On the contrary, to inhibit the “is Muslim” classification for a non-Muslim, only three traits need to be cloaked. This suggests a line of future inquiry: does this illustrate a case of a strong dependency between a personal trait and the individual's choice of actions? Or is there some alternative explanation having to do with the subtleties of predictive modeling? Other such examples can be seen, although to a lesser extent, for “age 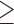 37,” “IQ
37,” “IQ 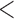 90,” and “is gay.”
90,” and “is gay.”
A comprehensive analysis of this question is beyond the scope of this article; however, we can offer an initial view. Besides the statistical dependency relationships discussed above, the observed differences in cloakability for the TP and FP users can also be attributed to the interaction between two factors: variance in predicted probability and the order in which each model ranks the users subject to prediction. For some tasks, we find that the predicted probabilities for all users in the targeted group are tightly clustered; other tasks have a wide range of probabilities. Within the targeted group, each model finds itself discriminating between TP and FP users differently. Some models see a majority of TP users being ranked above FP users, while others find TP and FP to be mixed. If a majority of FP users find themselves ranked below their TP counterparts, ceteris paribus they will be easier to cloak simply because they are closer to the threshold. In addition, if the variance in predicted probability is large, and many FP users fall at the lower end of the targeted range, again the FP users will find it easier to cloak themselves from inference.
Making cloaking more difficult
In the previous section, we showed that inhibiting inference requires cloaking only a relatively small amount of personal information—in the prediction setting used above, only around seven (3%) out of one's hundreds of Likes on average need to be cloaked—and that the statistical dependence structure among the Likes and the predicted trait makes cloaking more difficult than it would be without such dependency structure. However, we showed this for a particular predictive model and modeling procedure; even though it is a best-practices modeling procedure, we did not show that cloaking would be easy using any predictive model.
Could it be that organizations could make different modeling decisions that would allow them still to predict accurately and offer transparency and control with a cloaking device, but make it much harder for the users actually to cloak themselves? Those who run some organizations may be quite happy to provide transparency and easy control, either because they believe it is simply the right thing to do, or because they believe that it will increase user/customer satisfaction, or even because they believe it will be more profitable as the targeting actually will be better. Others may want to give the semblance of transparency and control, but actually dissuade users from manipulating their profiles to cloak. To explore whether a targeter can manipulate cloakability through modeling choices, let us briefly examine two alternative model choices.
The Naive Bayes (NB) model is a linear model quite similar to logistic regression,* but with a certain particularity. NB assumes that the pieces of evidence taken as input (the Likes) are conditionally independent of each other given the target (the trait). Mechanically, the algorithm for inducing the NB model from data treats each Like independently. When the Likes in fact are highly correlated, this creates a pathology in predictive behavior: the resulting inference model will tend to “double count” when users present correlated Likes.† However, our unscrupulous targeter may decide to use this pathology to its advantage. The model will tend to give extra high scores when correlated evidence is presented and will tend to give the highest scores to users with large numbers of such Likes. Because of the double counting, a top-ranked user would have to cloak many more Likes to achieve the same effect as a user ranked highly by a model that does not exhibit this pathology (like the LRSVD model).
For completeness, in addition to the LRSVD model and the NB model, we also will examine a straightforward logistic regression model trained on the full (non-SVD) raw Like feature space. We would expect the results for LRSVD and LR to be similar, but the NB model would require significantly more cloaking to inhibit inference.
Table 3 presents the values for our cloaking measure across different models.‡ As expected, the cloaking efforts required for the LR and LRSVD models are similar. In contrast, cloaking is indeed substantially more difficult for NB. Rather than needing to cloak only a half-dozen or so Likes, for the NB models users on average have to cloak 57 Likes. This is on average 15% of a user's Like set. At the extreme, an average person classified as “is Muslim” has to cloak 50% of her or his Likes! A person classified as “conscientiousness 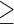 5” has to cloak 44% of her or his Likes. Classified as “is female,” with the NB model? You will have to cloak over 377 (25%) of your Likes to escape that classification.
5” has to cloak 44% of her or his Likes. Classified as “is female,” with the NB model? You will have to cloak over 377 (25%) of your Likes to escape that classification.
Table 3.
The effort to cloak different users' characteristics using a logistic regression with 100 singular-value decomposition components, a logistic regression, and Naive Bayes model
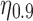 |
 |
|||||
|---|---|---|---|---|---|---|
| Task | LRSVD | LR | NB | LRSVD, % | LR, % | NB, % |
Age  37 37 |
10.3 | 7.3 | 37.7 | 7.7 | 7.4 | 17.9 |
Agreeableness 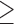 5 5 |
5.0 | 2.9 | 7.2 | 2.3 | 4.3 | 12.6 |
Conscientiousness 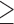 5 5 |
4.7 | 3.4 | 16.1 | 3.9 | 4.8 | 44.1 |
Extraversion 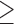 5 5 |
4.4 | 3.6 | 58.0 | 1.9 | 2.5 | 10.2 |
IQ  90 90 |
6.9 | 3.7 | 21.6 | 4.5 | 7.3 | 7.2 |
IQ  130 130 |
6.6 | 2.9 | 14.4 | 2.8 | 3.3 | 9.4 |
| Is democrat | 8.5 | 9.4 | 61.7 | 1.7 | 2.0 | 10.6 |
| Is drinking | 6.8 | 5.4 | 17.1 | 2.0 | 2.1 | 8.2 |
| Is female | 10.0 | 11.6 | 377.4 | 1.9 | 2.0 | 25.9 |
| Is gay | 5.7 | 9.1 | 20.6 | 3.8 | 15.0 | 15.3 |
| Is homosexual | 3.5 | 3.4 | 8.2 | 2.4 | 3.9 | 10.8 |
| Is lesbian | 3.1 | 2.5 | 7.4 | 1.9 | 3.9 | 13.6 |
| Is Muslim | 11.7 | 8.9 | 31.1 | 9.6 | 10.1 | 46.5 |
| Is single | 13.7 | 10.2 | 105.8 | 3.4 | 2.8 | 12.5 |
| Is smoking | 8.4 | 7.0 | 26.2 | 2.8 | 3.2 | 13.5 |
Life satisfaction  6 6 |
5.1 | 4.1 | 10.3 | 2.2 | 7.2 | 8.3 |
Network density  65 65 |
10.5 | 2.6 | 75.7 | 2.1 | 3.9 | 7.7 |
Neuroticism  5 5 |
9.1 | 2.3 | 254.5 | 2.2 | 3.6 | 18.0 |
Num friends  585 585 |
5.0 | 4.7 | 52.6 | 2.1 | 2.5 | 10.6 |
Openness  5 5 |
6.7 | 3.7 | 28.6 | 2.3 | 2.5 | 11.1 |
| ss belief = 1 | 5.7 | 4.5 | 24.2 | 2.9 | 3.6 | 10.4 |
| ss belief = 5 | 8.3 | 4.7 | 18.4 | 2.1 | 4.1 | 6.2 |
| Uses drugs | 12.2 | 8.2 | 31.5 | 2.7 | 3.4 | 9.0 |
| Mean | 7.5 | 5.5 | 56.8 | 3.1 | 4.6 | 14.8 |
| Median | 6.8 | 4.6 | 26.2 | 2.3 | 3.6 | 10.8 |
Absolute efforts are presented in the left panel, and relative efforts are in the right panel.
LR, logistic regression; LRSVD, logistic regression singular-value decomposition; NB, Naive Bayes model.
In summary, a targeter wishing to make cloaking more difficult could do so without imposing any restrictions on the users by changing the predictive model choice. While it is clear that Like pages do not conform to the independence assumption inherent to NB, we find that across all tasks (with the exception of “is female”), the difference in predictive performance (measured by the area under the ROC curve [AUC] as in Kosinski et al.1) between LRSVD/LR and NB models is 10% on average. Thus, by taking a measured loss in predictive performance, it is possible to make cloaking significantly more difficult.
However, this increased difficulty presumes that the user must manually choose Likes to cloak—one by one. In the next section we discuss how, if users are willing to trust the system to cloak for them, the difficulty vanishes. Moreover, we can give cloakability even in cases where we cannot or choose not to provide transparency.
Discussion and Limitations
The conclusion that cloaking may be more or less difficult based on the number of features (Likes) that one would need to cloak is based on several assumptions. First, there is a presumption that the individual and/or the firm would like to have some inferences made—for example, the individual may be interested in receiving some targeted content; the firm may be interested in showing some targeted ads even if an individual does not want to see all. Otherwise, simply toggling inferences on or off would suffice. Under this presumption, there is the further assumption that individuals would like to be given and/or the firm would like to give its users explicit fine-grained control over which features (Likes) are cloaked. In many situations, this assumption is reasonable: Facebook may want as many Likes as possible to remain viable for inference, while still allowing users to cloak particularly concerning ones.
If we were to relax this latter assumption, then the cloaking mechanism could be used easily regardless of the number of features that need to be cloaked. For example, “one-click cloaking” could be offered. Specifically, when faced with an undesired inference, an individual could click the “cloak me from stuff like that” button. Behind the scenes, the system could apply the evidence counterfactual, determine a minimal set of features (Likes) to cloak to inhibit the inference, and cloak these particular features. Then, these features would not be available for future inferences, and thus, the system would provide more than just “don't show me that content again”—it would not show other contents for the same reasons. The system could even provide the list of cloaked features, if this were deemed valuable.
One-click cloaking separates control from transparency—a firm could give either, neither, or both. There are some important, real situations where this separation is important. Firms may not want to give away the fine-grained details of their predictive modeling. The reasons for such reluctance range from issues of competitive advantage (someone may be able to reverse engineer the model-in-use with enough probes), to reluctance to divulge the data used for drawing inferences, to the actual technical inability to show the specific features used in a human-digestible manner. For example, perhaps the features being used are actually higher level features, constructed by the machine learning mechanism (e.g., by a deep learning system). A particularly ironic instance of the latter problem comes with the use of “doubly anonymized” data for drawing inferences in production.28 The idea behind doubly anonymized data is that not only are the identities of the individuals anonymized but the identity of the features are anonymized (e.g., irreversibly hashed) for use in drawing inferences from a predictive model as well. The predictive models will operate identically regardless of whether the feature is “likes dogfood” or “2A3#99HSW5B.” However, one cannot offer transparency if one cannot access human-comprehensible versions of the features.* However, even in cases where a firm cannot or prefers not to give transparency, it can give control via one-click cloaking: there is no need to reveal or even to be able to understand the features to apply the evidence counterfactual and the associated cloaking.
One reason why one would want to cloak the underlying features, rather than simply to inhibit particular inferences, is because doing so will also inhibit future inferences made for the same reasons. If I cloak “likes dogfood,” then no ads or content will be shown to me because of this. How well this cross-target cloaking actually works is an open question. As is illustrated by the NB results above, it may be that there is a wealth of redundant information in a sparse, ultrahigh-dimensional feature set. Furthermore, it may be that slightly different sets of Likes are most predictive for different targets. If the cloaking does not “cover” closely associated features, then one may end up being targeted in the future—not for identical reasons, but for closely associated reasons. Future research could examine the effectiveness of cross-target cloaking systematically and possibly suggest better cloaking mechanisms if the exact mechanism introduced above is insufficient.
One direction toward that end is to cloak on higher-level features, rather than on the ultrafine-grained features, as suggested briefly above. In the modeling we did earlier, we follow the methodology of Kosinski et al.1 and first run unsupervised dimensionality reduction to create higher-level features, essentially 100 vectors of weights across the space of Likes, then learn a logistic regression model using these high-level features. However, the cloaking that we perform is on the fine-grained features—cloaking the Likes themselves. Instead, we could provide cloaking across the high-level features (e.g., SVD dimensions, deep-learned intermediate features). We may or may not be able to provide reasonable transparency, but as with one-click cloaking, if we have separated control from transparency, we could in principle allow cloaking over the higher-level space.† Our conjecture is that cloaking on the higher-level features will further reduce undesired inferences, and that it also will reduce inferences that are not undesired.
In this article, we have assumed that features are cloaked from inference but not from learning/model building. If we also were to cloak from model building, then given the redundancy in the relationship between features and target, it is likely with enough cloaking the modeling would learn to predict the target based on some other features. The individual could then have similar or even the same inferences drawn in the future. This could be undesirable from a user-experience point of view, and also could lead to an arms race between a machine learning system and the cloaking users. It would be interesting to study the properties of such a dynamic system, for example, from a game-theoretic perspective.
A number of articles study preserving individual privacy in the presence of high-dimensional fine-grained data. For example, Ghinita et al.29 address the anonymization of sparse high-dimensional data under the notion of k-anonymity and l-diversity. Chen et al.30 discuss differentially private high-dimensional data publication. These works focus on preserving sensitive individual information from being revealed to an adversarial party. In this article, we have adopted an alternative approach designed for situations where a cooperative data manager/service provider wants to provide transparency and control over inferences drawn from models applied to (high-dimensional) data on individuals.
Conclusion
In this article, we developed a method—what we call the cloaking device—to provide individuals with control over the inferences made about them by statistical models. The cloaking device makes use of the evidence counterfactual to provide transparency into the particular information on which inferences are based and enables users to inhibit the use of particular pieces of information for drawing future inferences. As a result, this understanding and transparency allow users to control the final inferences made about them in a precise and unobtrusive way.
Using the cloaking device, we answer two questions: (1) how difficult is it for users to cloak themselves from inference and (2) can organizations making inferences make them harder to hide from? Using data from Facebook and a common targeting strategy, we find that users only need to cloak a small portion of their Facebook Likes to successfully inhibit particular inferences of personal traits. In addition, we find that it is easier to hide from an FP inference than from a TP. These results provide some level of intuitive satisfaction. When a user is targeted due to an incorrect inference about some personal trait, they need to hide a smaller number of Likes when compared to someone in the targeted group that does indeed exhibit the trait. On investigating the patterns of Likes that occur in Facebook profiles, we find that the combinations of Likes that exist for an individual are not random. This interrelated nature of Likes results in cloaking becoming more difficult than if Likes occurred independently.
While we find that cloaking with our modeling setup is not difficult, we show that simple changes to modeling can result in significant changes in a user's ability to hide from inference. When compared to logistic regression models, whose inferences are relatively easy to cloak, using an NB model results in inferences that are far more difficult to mask. The predictive accuracy of our NB models is on average 10% worse than logistic regression, but the result is a significant increase in cloaking difficulty. However, this example is only comparing two simple predictive models. In reality, an organization intent on making cloaking more difficult could explore other modeling options that provide better predictive performance while still increasing the difficulty of cloaking. A calculated trade-off can be made in terms of predictive power and cloaking effort.
In the Discussion and Limitations section, we outline several implications of our research and provide some of its limitations. The concepts we discuss suggest several possible directions for future research. For example, one-click cloaking would require less effort from users and thereby give them added control. On the contrary, it may be less desirable from the firm's point of view, as users may end up cloaking more features.
As digital data become increasingly centered on the inherent network structure of many online platforms and online inferences are incorporating social network data into their models, expanding cloaking to utilize network-based techniques can have a dramatic effect on inference and cloakability.31 In our setting, utilizing network data could lead to not only cloaking features but to also suggesting the cloaking of friends to avoid being targeted.
Abbreviations Used
- AUC
area under the ROC curve
- FP
false positive
- LRSVD
logistic regression singular-value decomposition
- NB
Naive Bayes model
- SVD
singular-value decomposition
- TP
true positive
Appendix A: Singular Value Decomposition
The performance of a logistic regression model can be improved by reducing the set of features if it is very large or if the data are sparse. A common technique is to use a singular value decomposition (SVD).
Let M be a feature matrix that contains n records and m features. M can be decomposed into:
 |
In the above decomposition, U is an 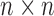 unitary matrix,
unitary matrix, 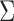 is an
is an 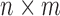 diagonal matrix composed of the singular values of M sorted in descending order, and
diagonal matrix composed of the singular values of M sorted in descending order, and 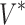 is the
is the 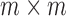 conjugate transpose of the unitary matrix V. To reduce the space, we can choose to only include a subset of the first k features from the matrix
conjugate transpose of the unitary matrix V. To reduce the space, we can choose to only include a subset of the first k features from the matrix 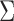 when training a new model.
when training a new model.
A model trained on this reduced feature space will not directly yield coefficients for each of the original features. A simple transformation will allow for a mapping between a model trained on the SVD space to the original set of features before the reduction. Let 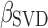 be the set of coefficients from the linear model trained on the SVD space and let
be the set of coefficients from the linear model trained on the SVD space and let 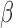 be the coefficients on the original set of features. We map from one to the other by the following:
be the coefficients on the original set of features. We map from one to the other by the following:
 |
Appendix B: Classification Performance
Table 4 reports the area under the ROC curve and lift at 10% across classification tasks and across different predictive models.
Table 4.
Area under the ROC curve and lift at 10% for each classification task using a logistic regression with 100 singular-value decomposition components, a logistic regression, and a Naive Bayes model
| AUC | Lift at 10% | ||||||
|---|---|---|---|---|---|---|---|
| Task | % positive | LRSVD | LR | NB | LRSVD | LR | NB |
Age 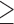 37 37 |
12.7 | 0.868 | 0.904 | 0.816 | 4.92 | 5.82 | 3.81 |
Agreeableness 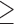 5 5 |
1.4 | 0.604 | 0.590 | 0.587 | 1.85 | 1.82 | 2.06 |
Conscientiousness 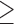 5 5 |
1.8 | 0.677 | 0.670 | 0.626 | 2.53 | 2.64 | 2.28 |
Extraversion  5 5 |
3.3 | 0.680 | 0.671 | 0.590 | 2.48 | 2.55 | 1.90 |
IQ  90 90 |
7.3 | 0.631 | 0.625 | 0.571 | 2.42 | 2.78 | 2.60 |
IQ  130 130 |
13.0 | 0.620 | 0.636 | 0.619 | 1.97 | 2.37 | 1.98 |
| Is democrat | 59.6 | 0.889 | 0.888 | 0.822 | 1.65 | 1.65 | 1.58 |
| Is drinking | 48.5 | 0.782 | 0.790 | 0.683 | 1.70 | 1.74 | 1.66 |
| Is female | 61.6 | 0.922 | 0.967 | 0.667 | 1.61 | 1.62 | 1.38 |
| Is gay | 4.6 | 0.890 | 0.904 | 0.784 | 6.92 | 7.64 | 7.56 |
| Is homosexual | 3.5 | 0.788 | 0.839 | 0.694 | 4.76 | 6.25 | 4.84 |
| Is lesbian | 2.7 | 0.729 | 0.797 | 0.605 | 3.50 | 5.19 | 2.88 |
| Is Muslim | 5.0 | 0.949 | 0.949 | 0.894 | 8.40 | 8.71 | 8.50 |
| Is single | 53.5 | 0.637 | 0.665 | 0.644 | 1.40 | 1.44 | 1.28 |
| Is smoking | 23.7 | 0.785 | 0.792 | 0.673 | 2.46 | 2.81 | 2.18 |
Life satisfaction  6 6 |
12.5 | 0.594 | 0.579 | 0.570 | 1.62 | 1.66 | 1.50 |
Network density  65 65 |
1.2 | 0.609 | 0.575 | 0.518 | 3.00 | 3.52 | 2.24 |
Neuroticism  5 5 |
0.4 | 0.673 | 0.603 | 0.523 | 2.40 | 2.12 | 1.67 |
Num friends 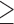 585 585 |
14.0 | 0.717 | 0.734 | 0.625 | 2.66 | 2.95 | 2.45 |
Openness 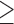 5 5 |
4.3 | 0.665 | 0.660 | 0.635 | 2.27 | 2.49 | 2.20 |
| ss belief = 1 | 17.8 | 0.689 | 0.700 | 0.651 | 2.26 | 2.50 | 2.02 |
| ss belief = 5 | 7.9 | 0.641 | 0.616 | 0.546 | 1.94 | 2.22 | 1.93 |
| Uses drugs | 17.2 | 0.781 | 0.772 | 0.683 | 3.12 | 3.18 | 2.83 |
| Mean | 0.731 | 0.736 | 0.653 | 2.95 | 3.29 | 2.75 | |
| Median | 0.689 | 0.700 | 0.635 | 2.42 | 2.55 | 2.18 | |
AUC, area under the ROC curve.
Acknowledgments
The authors thank Michal Kosinski, David Stillwell, and Thore Graepel for sharing their data. We thank Wally Wang for helpful discussions at the outset of this project. We also thank Yannis Bakos, Solon Barocas, Vasant Dhar, Carlos Fernandez, Bart Knijnenburg, Claudia Perlich, the Detectica Data Science Discussion Group, and our anonymous reviewers for helpful feedback and suggestions. F.P. thanks Andre Meyer for a Faculty Fellowship. The authors also thank the Moore and Sloan Foundations for their generous support of the Moore-Sloan Data Science Environment at NYU.
Author Disclosure Statement
No competing financial interests exist.
Facebook introduced a feature called “Why am I seeing this ad?” (www.facebook.com/ads/preferences), which gives users partial transparency on why they are being targeted. Users can select not to be targeted with particular categories of ads or advertisers; they can modify their “ad preferences” to hide categories of information from being used for targeting, and they can see a high-level overview of some inferences being made about them (e.g., liberal political affiliation, traveled recently).
We will capitalize “Like” when referring to the action or its result on Facebook.
Martens and Provost7 focused on document classification but conjecture that the method they introduce could be used for other domains with similar data. It subsequently has been used to explain inferences for fraud detection20 and online ad targeting,6,21 in addition to the present problem.
The inference not being the default is important for explaining the reasons for model-based prediction. The default prediction is the prediction that is given when there is not enough evidence for predicting anything else, for example, predicting that there is no fraud on a particular account. Thus, the explanation for a default prediction—that there is no evidence for any alternative—often will be viewed as either trivial or unsatisfying. Usually the default inference is either the most common alternative or the least costly alternative, and very often these two concur. See Martens and Provost7 for further discussion and other nuances of explaining model-based inferences.
As with predictive modeling projects generally, engineering the right representation often is key to achieving top-notch performance. So, for example, one might code the lack of a particularly popular Like as positive evidence. We will only consider the presence of a Like in our results, but our qualitative results should generalize across such alternative representations.
For example, for targeting online ads, a typical value for 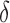 would range between 90% and 100%. Perlich et al.2 describe in detail online targeting with predictive models based on fine-grained user data.
would range between 90% and 100%. Perlich et al.2 describe in detail online targeting with predictive models based on fine-grained user data.
If the targeted group is defined by a fixed threshold score (such as the estimated probability being above a fixed threshold), this is straightforward. If the targeted group is defined instead based on the actual quantile, then when a user is removed from the targeted group another user takes his or her place. In this article, we consider users in isolation and do not consider the effects of cloaking on sets of users.
More generally, for nonlinear models, the evidence counterfactual would reveal a minimal set of Likes such that their removal would successfully cloak the individual.7
Thanks to the authors of the prior study1 for sharing the data.
Indeed equivalent under certain assumptions.27
Technically, since many Likes that supply evidence of a user being part of the positive class are highly correlated with one another, the NB modeling will essentially assign all of these Likes high coefficients, whereas the LR modeling spreads the overall impact across the coefficients of the correlated Likes (in one way or another depending on the type and degree of regularization).
The predictive (generalization) performance for the NB model is slightly lower than that for the logistic regression models. For details, see Appendix B.
The irony is that a firm that has tried to improve its privacy friendliness via double anonymization may no longer be able to offer transparency into the reasons why a particular inference has been made.
We would need to define how exactly to compute the evidence counterfactual on this space, as it is no longer sparse binary. For example, we could set variables to a chosen value other than zero, such as the population mean, median or mode, or the mean in the nontargeted population.
References
- 1.Kosinski M, Stillwell D, Graepel T. Private traits and attributes are predictable from digital records of human behavior. Proc Natl Acad Sci U S A. 2013;110:5802–5805 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Perlich C, Dalessandro B, Raeder T, et al. Machine learning for targeted display advertising: Transfer learning in action. Mach Learn. 2014;95:103–127 [Google Scholar]
- 3.Barocas S. Panic Inducing: Data Mining, Fairness, and Privacy. Phd dissertation, New York University, 2014 [Google Scholar]
- 4.Chen D, Fraiberger S, Moakler R, Provost F. Enhancing transparency and control when drawing data-driven inferences about individuals. NYU Working Paper No. 2451/33969. 2015 [DOI] [PMC free article] [PubMed]
- 5.Chen D, Fraiberger S, Moakler R, Provost F. Enhancing transparency and control when drawing data-driven inferences about individuals. In: 2016 ICML Workshop on Human Interpretability in Machine Learning (WHI 2016) New York: 2016, pp. 21–25 [Google Scholar]
- 6.Provost F. Understanding decisions driven by big data: From analytics management to privacy-friendly cloaking devices. Keynote Lecture, Strata Europe. 2014
- 7.Martens D, Provost F. Explaining documents' predicted classifications. MIS Q. 2014;38:73–99 [Google Scholar]
- 8.White House Report. Consumer Data Privacy in a Networked World: A Framework for Protecting Privacy and Promoting Innovation in the Global Digital Economy. Journal of Privacy and Confidentiality. 2013;4(2):Article 5. Available at: http://repository.cmu.edu/jpc/vol4/iss2/5 [Google Scholar]
- 9.Barocas S, Bradley E, Honavar V, Provost F. Big data, data science, and civil rights. Computing Community Consortium White Paper. Available at: http://cra.org/ccc/resources/ccc-led-whitepapers/
- 10.Smith HJ, Dinev T, Xu H. Information privacy research: An interdisciplinary review. MIS Q. 2011;35:989–1016 [Google Scholar]
- 11.Pavlou PA. State of the information privacy literature: Where are we now and where should we go. MIS Q. 2011;35:977–988 [Google Scholar]
- 12.Schoen H, Gayo-Avello D, Metaxas PT, et al. The power of prediction with social media. Internet Res. 2013;23:528–543 [Google Scholar]
- 13.Bachrach Y, Kosinski M, Graepel T, et al. Personality and patterns of facebook usage. In: Proceedings of the 3rd Annual ACM Web Science Conference, Evanston, IL, ACM, 2012. pp. 24–32. [Google Scholar]
- 14.Schwartz HA, Eichstaedt JC, Kern ML, et al. Personality, gender, and age in the language of social media: The open-vocabulary approach. PLoS One. 2013;8:e737–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Shmueli G. Research dilemmas with behavioral big data. Big Data. 2017;5:98–119 [DOI] [PubMed] [Google Scholar]
- 16.Johnson M, Egelman S, Bellovin SM. Facebook and privacy: It's complicated. In: Proceedings of the Eighth Symposium on Usable Privacy and Security (SOUPS), New York: ACM, 2012. pp. 9:1–9:15. [Google Scholar]
- 17.Knijnenburg BP, Bostandjiev S, O'Donovan J, Kobsa A. Inspectability and control in social recommenders. In: Proceedings of the Sixth ACM Conference on Recommender Systems, Dublin Ireland, ACM, 2012. pp. 43–50. [Google Scholar]
- 18.Wang W, Benbasat I. Recommendation agents for electronic commerce: Effects of explanation facilities on trusting beliefs. J Manag Inf Syst. 23:217–246, 2007 [Google Scholar]
- 19.Knijnenburg BP, Kobsa SM, Jin H. Counteracting the negative effect of form auto-completion on the privacy calculus. In: Thirty Fourth International Conference on Information Systems, Milan, Italy, 2013, pp. 1–21. [Google Scholar]
- 20.Junqué de Fortuny E, Stankova M, Moeyersoms J, et al. Corporate residence fraud detection. In: Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining, New York, ACM, 2014. pp. 1650–1659. [Google Scholar]
- 21.Moeyersoms J, d'Alessandro B, Provost F, Martens D. Explaining classification models built on high-dimensional sparse data. In: 2016 ICML Workshop on Human Interpretability in Machine Learning (WHI 2016) New York, 2016, pp. 36–40. [Google Scholar]
- 22.Robnik-Šikonja M, Kononenko I. Explaining classifications for individual instances. IEEE Trans Knowl Data Eng. 2008;20:589–600 [Google Scholar]
- 23.Datta A, Sen S, Zick Y. Algorithmic transparency via quantitative input influence: Theory and experiments with learning systems. In: 2016 IEEE Symposium on Security and Privacy (SP), San Jose, CA, IEEE, 2016. pp. 598–617. [Google Scholar]
- 24.Bohanec M, Borštnar MK, Robnik-Šikonja M. Explaining machine learning models in sales predictions. Expert Syst Appl. 2017;71:416–428 [Google Scholar]
- 25.Junqué de Fortuny E, Martens D, Provost F. Predictive modeling with big data: Is bigger really better? Big Data. 2013;1:215–226 [DOI] [PubMed] [Google Scholar]
- 26.Provost F. and Fawcett T. Data Science for Business: What you need to know about data mining and data-analytic thinking. California: O'Reilly Media, Inc., 2013. [Google Scholar]
- 27.Mitchell Thomas M. Machine learning—Additional chapters, 1st ed. New York, NY: McGraw-Hill, Inc; 1997 [Google Scholar]
- 28.Provost F, Dalessandro B, Hook R, et al. Audience selection for on-line brand advertising: Privacy-friendly social network targeting. In: Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, KDD'09, Paris, France, ACM, 2009. pp. 707–716. [Google Scholar]
- 29.Ghinita G, Tao Y, Kalnis P. On the anonymization of sparse high-dimensional data. In: 2008 IEEE 24th International Conference on Data Engineering (ICDE 2008), Cancun, Mexico, IEEE, 2008. pp. 715–724. [Google Scholar]
- 30.Chen R, Xiao Q, Zhang Y, Xu J. Differentially private high-dimensional data publication via sampling-based inference. In: Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining KDD'15, Sydney, Australia, ACM, 2015. pp. 129–138. [Google Scholar]
- 31.Macskassy SA, Provost FJ. Classification in networked data: A toolkit and a univariate case study. J Mach Learn Res. 2007;8:935–983 [Google Scholar]
References
Cite this article as: Chen D, Fraiberger SP, Moakler R, Provost F (2017) Enhancing transparency and control when drawing data-driven inferences about individuals. Big Data 5:3, 197–212, DOI: 10.1089/big.2017.0074.






