The Detection of Nanoscale Membrane Bending with Polarized Localization Microscopy

Abstract

The curvature of biological membranes at the nanometer scale is critically important for vesicle trafficking, organelle morphology, and disease propagation. The initiation of membrane bending occurs at a length scale that is irresolvable by most superresolution optical microscopy methods. Here, we report the development of polarized localization microscopy (PLM), a pointillist optical imaging technique for the detection of nanoscale membrane curvature in correlation with single-molecule dynamics and molecular sorting. PLM combines polarized total internal reflection fluorescence microscopy and single-molecule localization microscopy to reveal membrane orientation with subdiffraction-limited resolution without reducing localization precision by point spread function manipulation. Membrane curvature detection with PLM requires fewer localization events to detect curvature than three-dimensional single-molecule localization microscopy (e.g., photoactivated localization microscopy or stochastic optical reconstruction microscopy), which enables curvature detection 10× faster via PLM. With rotationally confined lipophilic fluorophores and the polarized incident fluorescence excitation, membrane-bending events are revealed with superresolution. Engineered hemispherical membrane curvature with a radius ≥24 nm was detected with PLM, and individual fluorophore localization precision was 13 ± 5 nm. Further, deciphering molecular mobility as a function of membrane topology was enabled. The diffusion coefficient of individual DiI molecules was 25 ± 5× higher in planar supported lipid bilayers than within nanoscale membrane curvature. Through the theoretical foundation and experimental demonstration provided here, PLM is poised to become a powerful technique for revealing the underlying biophysical mechanisms of membrane bending at physiological length scales.

Introduction

Nanoscale membrane curvature is essential for many biological functions (1), including the regulation of lipid rafts (2), exocytosis/endocytosis (3), viral fusion/egress (4), nanotherapeutics (5), membrane remodeling (6), and the shedding of circulating microvesicles (7). Membrane curvature can be induced by the line tension between coexisting liquid-lipid phases, the aggregation of curvature preferring molecules, the steric pressure between crowded proteins, and the molecular shape of either lipids or proteins (8, 9, 10). However, quantifying the relative contributions of these curvature-generating mechanisms at physiological length scales remains elusive due to limited experimental capabilities for detecting nanoscale bending. Here, we report the development of polarized localization microscopy (PLM), which combines single-molecule localization microscopy (SMLM) with polarized total internal reflection fluorescence microscopy (TIRFM). Polarized TIRFM distinguishes between membranes (11) and molecules (12) of varying orientation by measuring the overlap between the fluorophore’s transition dipole moment and linearly polarized incident excitation light. Indocarbocyanine dyes (e.g., 1,1'-didodecyl-3,3,3′,3′-tetramethylindocarbocyanine perchlorate (DiI)) maintain their transition dipole moment in the plane of the membrane such that DiI in membranes parallel to the coverslip is preferentially excited by incident s-polarized light and DiI in membranes vertical to the coverslip is preferentially excited by incident p-polarized light (Fig. 1) (13, 14, 15). Diffraction-limited polarized TIRFM has advanced the detection of membrane curvature despite lateral resolution being limited to >200 nm (16), as demonstrated by presynaptic vesicle fusion (17) and endocytosis/exocytosis (11, 18).

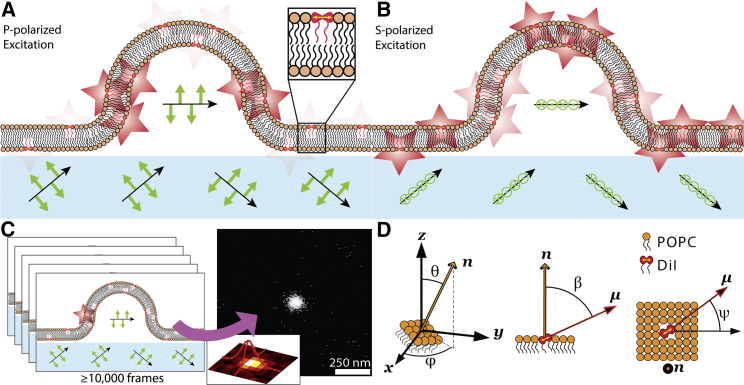
Figure 1.

Polarized localization microscopy combines the techniques of polarized TIRFM and SMLM. By controlling the linear polarization of incident excitation light, the electric field (green arrows) of the evanescent wave for fluorescence excitation can be either (A) vertical with p-polarized light or (B) horizontal with s-polarized light. This results in differential excitation of rotationally confined fluorophores dependent on the local membrane orientation. (C) Imaging and localizing individual blinking fluorophores in separate frames enables the reconstruction of superresolution images with embedded information on membrane orientations. (D) The probability of localizing a DiI depends on the direction of the normal vector to the membrane (n) relative to the coverslip, as described by θ and φ, as well as and the angle of the DiI dipole moment (μ) within the membrane, as described by β and ψ. To see this figure in color, go online.

Superresolution SMLM, such as fluorescence photoactivated localization microscopy and direct stochastic optical reconstruction microscopy, have overcome the diffraction-limited resolution of traditional optical microscopy to provide images with a lateral resolution of <20 nm (19, 20, 21, 22). SMLM depends on the computational localization of individual fluorophores that sparsely blink in sequential diffraction-limited images for the reconstruction of a superresolution image. The resolution of the resulting reconstructed image depends on the localization imprecision, systematic inaccuracies, and localization density (23, 24). Three-dimensional (3D) SMLM has been implemented through the insertion of a cylindrical lens into the emission light path (25), single-fluorophore interference in a 4π configuration (26), biplane imaging (27), and emission phase manipulations (28). For these methods, information about the fluorophore vertical location requires either incorporating a precisely aligned, multicamera interferometric detection path, or sacrificing precision in lateral localization through the manipulation of the point spread function (PSF) to yield localization precisions along the z-direction (σ_z) typically double that of the xy-plane (σ_xy), approximately equal to 40 and 20 nm, respectively. Similarly, single-fluorophore orientations have been measured precisely by combinations of image defocusing, emission phase modulations, steerable filters, birefringent wedges, and advanced fitting routines (28, 29, 30, 31, 32, 33, 34, 35, 36, 37). However, the optical and computational challenges of these methods limit their applicability to multicolor superresolution imaging.

PLM provides fluorophore orientation with conventional detection optics, no sacrifice of localization precision by PSF manipulation, minimal adjustment of the excitation optics, and the use of commercial fluorophores. Total internal reflection fluorescence (TIRF) SMLM setups can perform PLM by the sole addition of a liquid-crystal variable waveplate (LCC1111-A; Thorlabs), which controls the polarization of the excitation with computer control and minimal power lost. PLM depends on the use of rotationally confined fluorophores that maintain an orientation relative to the membrane normal (38), and photoswitch between fluorescent bright and transient dark states (39, 40), such as the indocarbocyanine dye DiI. Superresolution images from PLM reveal the membrane vertical to the coverslip via p-PLM and membranes parallel to the coverslip via s-PLM. This approach enables resolving dynamic nanoscale membrane curvature and curvature-induced variations in membrane organization and dynamics in aqueous, physiological conditions.

Here, PLM was used to detect engineered nanoscale membrane curvature and correlate curvature to single-molecule trajectories. PLM provided visualization of nanoscale curvature in agreement with theoretical predictions. PLM was demonstrated to provide order-of-magnitude improvements in detection and resolution of membrane curvature. Curvature in model membranes was engineered by draping supported lipid bilayers (SLBs) over nanoparticles (NPs) of known sizes, ranging in radius (r_NP) from 24 to 70 nm. The resulting membrane curvature and curvature-influenced diffusion of individual lipids were resolved. In summary, our study demonstrates the capabilities of PLM to advance optical imaging capacities and provide order-of-magnitude improvements in spatial and temporal resolution over comparable SMLM techniques.

Materials and Methods

Sample dish preparation

Glass-bottomed dishes (MatTek) were immersed in 7× detergent overnight, rinsed with deionized water (18.2 MΩ-cm; EMD Millipore), bath sonicated for 30 min, dried with nitrogen gas, and cleaned by air plasma (Harrick Plasma). NPs were diluted in deionized water, sonicated for 15 min, and deposited onto a glass coverslip. NP sedimentation occurred for 10 min to achieve a density of 0.02 NPs/μm². Separate polystyrene NPs were used for both engineering membrane curvature and tracking stage drift. The index of refraction of bulk polystyrene is 1.59. NPs for creating membrane curvature were either 26 nm radius and λ_ex = 647 nm (FluoSpheres; Life Technologies), 51 nm radius and λ_ex = 405 nm (FluoSpheres; Life Technologies), or 70 nm radius and λ_ex = 488 nm (Fluoro-Max; Fisher Scientific). NPs for detecting stage drift (100 nm diameter, TetraSpeck; Life Technologies) were fluorescent in all color channels. Dishes were placed on a 55°C hotplate for 5 min to ensure their stability on the coverslip. NP shape after exposure to the hotplate was confirmed by scanning electron microscopy (Fig. S1).

SLB formation

Giant unilamellar vesicles (GUVs) of primarily 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC; Avanti Polar Lipids) labeled with 0.3 mol % DiI (Life Technologies) were prepared by electroformation, as described previously (41). Details on the GUV formation method are provided in the Supporting Material. This fluorophore density yielded 110 nm² of bilayer per DiI molecule. The interaction between the GUVs with the plasma-cleaned glass coverslip resulted in bursting of the GUVs and the formation of patches of SLB over the glass and NPs. This method of SLB creation proved to create more uniform SLBs over the NPs than SLBs formed by the fusion of large unilamellar vesicles (LUVs). The detailed methods for LUV creation are provided in the Supporting Material.

Optical setup

PLM was performed with an inverted IX83 microscope with Zero-Drift Correction and a 100×, 1.49 NA objective (Olympus) on a vibration-isolated optical table. Four continuous wave diode lasers were incorporated at wavelengths 405, 488, 561, and 647 nm, each with at least 120 mW maximal power for fluorescence excitation. The excitation polarization was rotated with a computer-controlled liquid-crystal waveplate (LCC1111-A; Thorlabs). The extinction ratio for each polarization at a certain liquid-crystal input voltage is shown in Fig. S2. The ratio of the laser polarization for P/S and S/P incident on the sample was 207:1 and 54:1, respectively, at the optimal liquid-crystal waveplate voltages for each imaging condition.

The different emission wavelengths are individually selected with a filter wheel (LB10-W32-Y73; Sutter Instruments) capable of 40-ms changes between filters specific for the emission ranges between the laser wavelengths. Image acquisition was performed with an iXon-897 Ultra EMCCD camera (Andor Technology) proceeded by emission filters (BrightLine single-band bandpass filters; Semrock), a 4-band notch filter (ZET405/488/561/640m; Chroma), and a 2.5× magnification lens (Olympus). This setup provided high laser power (>80 mW) at each polarization and integrated computer control of all equipment via custom LabVIEW routines (National Instruments).

Imaging procedure

Exposure of the sample to >80 mW of excitation light with λ_ex = 561 nm for 3 s resulted in converting most of the DiI from the fluorescent state “on” to the transient, nonfluorescent dark state “off,” and provided steady-state fluorophore blinking. The “on” fluorophores were imaged at a density of <1 fluorophore/μm². Sequential movies were acquired with alternating p-polarized TIRF (p-TIRF) excitation at λ_ex = 561 nm for p-PLM and s-polarized TIRF (s-TIRF) excitation at λ_ex = 561 nm for s-PLM. Between 10,000 and 30,000 frames were acquired for a cropped region of interest in each polarization, at a frame rate of 50 Hz and 18 ms acquisition time per frame. Details of the imaging buffer are provided in the Supporting Material.

Single-fluorophore localizations

The analysis of the raw, diffraction-limited images included low-pass Gaussian filtering, median background subtraction, lateral stage drift correction, and fitting each isolated fluorophore image via the ImageJ plug-in ThunderSTORM (42). ThunderSTORM provided the single-fluorophore positions, localization uncertainty, and photon per fluorophores for further analysis. A threshold value of 100 photons per fluorophores was used to keep only the bright localizations for further analysis. Single-molecule DiI localizations had 13 ± 5 nm precision (Fig. S3; Table S1). The localizations from s-TIRF and p-TIRF excitation were analyzed separately to reconstruct separate superresolution images for each polarization.

Single-particle tracking

The sequential localizations of single fluorophores were analyzed to reveal the diffusion rate of individual molecules versus membrane topography. The individual fluorophore trajectories projected onto the imaging plane were identified with custom MATLAB code. Single-fluorophore localizations were linked as a trajectory if they were in sequential frames, within 500 nm of each other, and there was no alternative localization for linking within 1 μm. The single-molecule step lengths (v) were grouped based on their distance from the NP center, and their normalized distribution was fit to a two-dimensional (2D) Maxwell-Boltzmann distribution (Eq. 1), as would be expected for 2D Brownian diffusion, to find the fit diffusion coefficient (D_fit)

$$P\left(v\right)=\frac{v}{2D_{fit}\Delta t}{e}^{\frac{-v^2}{4D_{fit}\Delta t}}.$$ (1)

The projection of the lipid trajectories onto the imaging plane yielded a decrease in their apparent step lengths depending on the membrane tilt (θ); this effect is considered in the simulations of single-molecule trajectories described below. The localization imprecision (σ_r = 13 ± 5 nm) increased the apparent step lengths. A camera blur was caused by the single-frame exposure time (t_exp) being a significant fraction of the time between frames (Δt) (43, 44). The diffusion coefficient (D) was calculated from D_fit, according to

$$D=\left(D_{fit}-\frac{{\sigma }_r^2}{2\mathit{\Delta }t}\right)/\left(1-\frac{t_{exp}}{3\mathit{\Delta }t}\right),$$ (2)

with σ_r = 13 nm, Δt = 20 ms, and t_exp = 18 ms. If D_fit = 0.5 μm²/s then D = 0.7 μm²/s, or if D_fit = 0.1 μm²/s then D = 0.13 μm²/s. Because the microscopy methods used here reveal only the z-projection of the diffusion, D calculated from Eq. 2 is reported as D_xy to emphasize that only the diffusion through the xy-plane has been measured. Diffusion coefficients from single-particle tracking (SPT) are typically extracted by fitting the mean-squared displacement versus Δt. However, fitting a whole trajectory to a single diffusion coefficient blurs the effects of nanoscale curvature, with the lipid trajectory sampling both curved and flat membranes (44). Therefore, in this study, a single-step analysis approach was adopted to study the dynamics of lipids diffusing between curved and flat membrane.

Modeled membrane topography and diffusion

The membrane topography was simulated by smoothly connecting the spherical NP coating to a planar sheet with no less than a 20-nm radius of curvature. With custom MATLAB routines, a random distribution of points on these simulated topographies mimicked the possible 3D locations of localized fluorescent lipids. These points were used to reconstruct simulated PLM images and lipid trajectories by incorporating the localization probabilities and localizations impressions and inaccuracies detailed in the Supporting Material.

Results

Theory of PLM

PLM depends on the relative orientation between the DiI fluorescence dipole moment (μ) with the fluorescence excitation light (E). The coordinate frame was defined such that the coverslip-water interface is in the xy-plane with z = 0. The local membrane orientation is represented by the polar (θ) and azimuthal (φ) angles of the membrane normal vector relative to the microscope coordinate frame. Relative to the membrane normal, the DiI fluorescence dipole moment experiences a polar tilt (β) and azimuthal rotation (ψ) (Fig. 1 D). Therefore, the Cartesian components of μ are

$$\begin{array}{c}{\mathit{\mu }}_x=\text{cos}\theta \text{cos}\varphi \text{sin}\beta \text{cos}\psi -\text{sin}\varphi \text{sin}\beta \text{sin}\psi +\text{sin}\theta \text{cos}\varphi \text{cos}\beta ,\\ {\mathit{\mu }}_y=\text{cos}\theta \text{sin}\varphi \text{sin}\text{β}\text{cos}\psi +\text{cos}\varphi \text{sin}\text{β}\text{sin}\psi +\text{sin}\theta \text{sin}\varphi \text{cos}\beta ,\\ {\mathit{\mu }}_z=\text{cos}\theta \text{cos}\beta -\text{sin}\theta \text{sin}\beta \text{cos}\psi ,\end{array}$$ (3)

as shown previously (14). The polar tilt of DiI in the membrane has been previously measured to be β = 69°. Changing β by 5° has a <5% effect on these results (18). The azimuthal rotation of DiI samples all angles within 0.2 ns (14), resulting in an averaging over ψ for the hundreds of excitation events that occur during the 18 ms single-frame exposure time. The high numerical objective used in these experiments (NA = 1.49) yields collection efficiency consistent within 10% for the emission of all fluorophore orientations (18).

Within our experimental setup, the p-polarized evanescent field (E_p) is elliptically polarized in the xz-plane and the s-polarized evanescent field (E_s) is linearly polarized in the y-plane according to

$$\begin{array}{c}{\mathit{E}}_{\mathit{p}}=E_p^o\left(0.5\mathit{x}+1.9i\mathit{z}\right)\times \text{exp}\left(\frac{-z}{2d}\right),\\ {\mathit{E}}_{\mathit{s}}=E_s^o\left(1.7\mathit{y}\right)\times \text{exp}\left(\frac{-z}{2d}\right),\end{array}$$ (4)

where $E_p^o$ and $E_s^o$ represent the magnitude of the p-polarized and s-polarized incident electric field, respectively (14, 45). The penetration depth of the evanescent field (d) was 124 nm, as determined by the excitation incident angle (θ_i = 65°), excitation wavelength (λ_ex = 561 nm), and the indices of refraction of the sample and glass (1.33 and 1.52, respectively). Approximating E_p to have no x-component induces 7% error and simplifies the intensity of excitation for each DiI molecule as a function of the membrane orientation. The corresponding intensities are then set equal to I_p = ${\left({\mu }_z·{\mathit{E}}_p\right)}^2$ and I_s = ${\left({\mu }_y·{\mathit{E}}_s\right)}^2$ for p-polarized and s-polarized excitation, respectively.

Diffraction-limited polarized TIRFM compares I_p and I_s directly. PLM incorporates these intensities into the localization probability and provides increased sensitivity to changes in fluorophore orientation. Individual fluorophores demonstrated an exponential distribution of detected brightness with the average fluorophore brightness proportional to I_p or I_s (Fig. S3). Only fluorophores with a detected brightness greater than a detection threshold (B₀) were localized for inclusion in the PLM results. The probability of detecting a DiI molecule as a function of membrane orientation (θ, φ), DiI orientation with the membrane (β, ψ), and height above the coverslip (z) was approximated as

$$\begin{array}{c}{P}_p=\text{exp}\left(\frac{-B_0}{3.6\langle {\mu }_z^2\rangle \text{exp}\left(-z/d\right)}\right),\\ P_s=\text{exp}\left(\frac{-B_0}{2.9\langle {\mu }_y^2\rangle \text{exp}\left(-z/d\right)}\right),\end{array}$$ (5)

for p-polarized and s-polarized excitation, respectively, where the brackets represent the average overall ψ. Because the variation in membrane height throughout this study was smaller than the width of the objective focal plane (200 nm), no change in detection probably as a function of distance from the focal plane of the objective was incorporated into this analysis. B₀ was set to match these theoretical results to the experimental results. Increasing the brightness threshold increases p-PLM sensitivity to θ. p-PLM yields the magnitude of θ and no information on φ. s-PLM results depend on both θ and φ. Neither the sign of θ nor the value of φ may be determined with only the z-polarized and y-polarized excitations; however, resolving changes to θ across a sample is sufficient for detecting membrane curvature.

P_s and P_p were compared to the expected detection probability for hypothetical unpolarized total internal reflection illumination (P_uTIR) and unpolarized epifluorescence illumination (P_uEPI). The unpolarized illumination assumes all fluorophore orientations had a 50% overlap between the fluorescent dipole moment and exciting electric field direction, such that there is no θ, φ, β, or ψ dependence on P_uTIR or P_uEPI. In these simulations of unpolarized illumination, we assume that the fluorophore is randomly tumbling as if bound by a long, flexible linker. Accordingly, P_uEPI is a constant for all sample variables with no z-dependence, and

$$P_s=\text{exp}\left(\frac{-B_0}{2.3\text{exp}\left(-z/d\right)}\right).$$ (6)

The presence of membrane curvature affects the local density of localizations in the z-projection for unpolarized illumination due to the local increase in membrane area per pixel in the xy-plane.

Comparison between SMLM methods

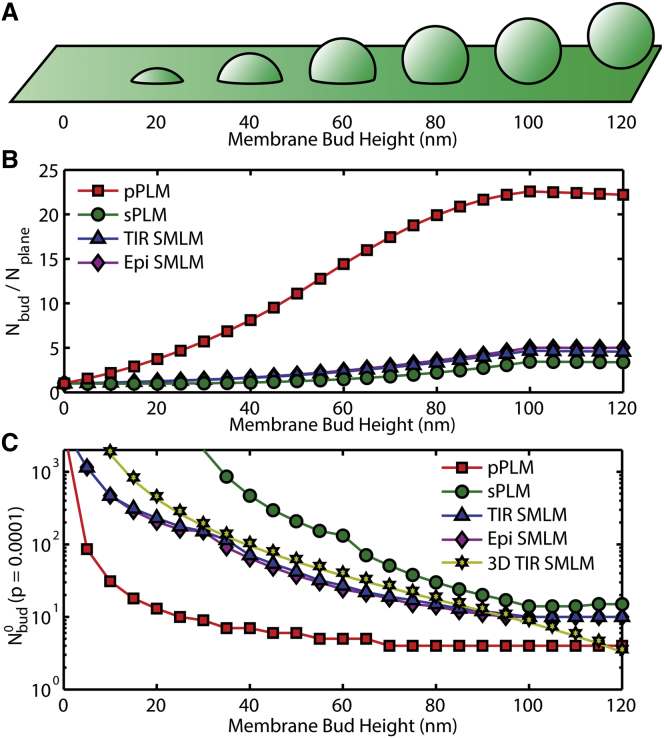
Membrane topologies were simulated with these detection probabilities to demonstrate the effects of polarization and total internal reflection (TIR) in superresolution imaging. The sensitivity of p-PLM, s-PLM, unpolarized TIR-SMLM, unpolarized epifluorescence-SMLM, and unpolarized 3D TIR-SMLM to membrane budding was calculated. A 50 nm radius membrane vesicle was simulated budding from a planar SLB (Fig. 2 A), the expected number of localizations increases for all polarizations because the area of the membrane and the number of fluorophores increase at the site of budding. Illumination modes were compared by predicting the increase in the expected number of localizations for vesicle budding (Fig. 2 B). The number of localizations from p-polarized excitation increased more than other polarizations because the new membrane had large θ. Upon the formation of a hemispherical membrane bud, when the top of the bud was 50 nm above the surrounding SLB, 11× more localizations would be detected by p-PLM because of the presence of the bud. When the bud top was 100 nm away from the SLB and a complete vesicle had formed, p-PLM would yield 23× more localizations whereas other illumination methods would reveal at most, 5× more localizations (Fig. 2 B).

Figure 2.

Theoretical estimates of the localization probabilities reveal the sensitivity of PLM compared to other optical methods. (A) Membranes containing buds of 50 nm radii of curvature were analyzed at varying protrusion distances from the surrounding connected planar membrane. The fractional increase in localizations due to the bud is plotted. (B) The increased number of localizations expected due to nonplanar membrane shape relative to the number of localizations expected from a planar membrane demonstrated a 23× increase in localization density with p-PLM, which is over 4× larger than expected for s-PLM, unpolarized epifluorescence SMLM, and unpolarized total internal reflection (TIR) illumination SMLM. The fraction increase in localizations due to the bud in 3D TIR SMLM is similar to the TIR SMLM results. (C) The required number of localizations to identify a membrane bud from the surrounding SLB $\left(N_{bud}^0\right)$ with p = 0.0001 are plotted for p-PLM, s-PLM, unpolarized TIR, and unpolarized epifluorescence SMLM from Eq. 7 and for 3D SMLM from Eq. 8. To see this figure in color, go online.

A membrane bud is identified with the statistical significance of given p-value (p) when the number of localizations at the membrane bud (N_bud) is greater than the average number of localizations over the planar membrane (N_plane), according to

$$p=e^{-N_{plane}}\sum _{i=N_{bud}}^{\infty }\frac{{\left(N_{plane}\right)}^i}{i!},$$ (7)

assuming the planar membrane provides a Poisson distribution of localizations per area. The minimum value of N_bud that satisfies this equation $\left(N_{bud}^0\right)$ varies with the N_bud/N_plane ratio, which depends on the membrane topography and excitation polarization. For instance, N_bud is up to 23× greater than N_plane for p-PLM (Fig. 2 B).

3D SMLM provides a minimal advantage in the N_bud/N_plane ratio, but it does provide the height of each fluorophore with an associated uncertainty (σ_z ≈ 40 nm). For 3D SMLM, statistically significant bud detection occurs when the average z-value of the localizations at the bud (<z_bud>) has a mean ± SE sufficiently small, such that the bud may be distinguished from the surrounding planar membrane at z = 0, according to

$$p=0.5erfc\left(\langle z_{bud}\rangle \frac{\sqrt{N_{bud}^0}}{{\sigma }_z\sqrt{2}}\right),$$ (8)

where erfc is the complementary error function. The integer $N_{bud}^0$ that satisfies Eqs. 7 and 8 for the various bud detection methods were calculated and plotted (Fig. 2 C). 3D SMLM can reveal membrane bending by measuring the height of each localization rather than the change in a number of localizations. However, the uncertainty of each fluorophore height requires the averaging the height of multiple fluorophores in a given region to confidently detect the membrane height. Due to this uncertainty, 3D SMLM requires more localizations for detecting membrane curvature than p-PLM until the bud has fully undergone vesicle fission. Further, p-PLM requires only 10% of the total number of localizations required for 3D SMLM, with p = 0.0001 when the bud top is 50 nm above the surrounding planar membrane. This corresponds to detecting membrane budding 10× faster via p-PLM than 3D SMLM. Membrane curvature detection with 3D SMLM requires data averaging that further reduces sensitivity and resolution, whereas p-PLM localization density itself is correlated with membrane bending. A further discussion comparing localization rate and time required to detect local membrane bending is discussed below.

The relatively small change in the number of localizations that are detected by s-PLM on membrane budding (<3.5×) provides an internal control for other possible membrane topographies. Whereas p-PLM may yield a significant increase in localizations due to the bud, s-PLM shows minor fluctuations across the sample. A high local density of p-PLM localizations is more confidently associated with membrane bending when coincident with a nearly uniform distribution of s-PLM localizations.

Resolution and sensitivity of PLM

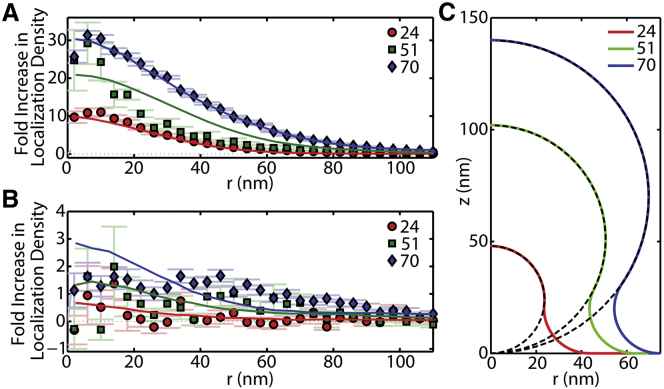
To demonstrate the ability of PLM to detect membrane curvature, we created membrane bending by three different methods: SLBs draped over NPs (Figs. 3, S4, and S5), LUVs above an SLB (Fig. S6), and unfused GUVs adhered to the glass coverslip (Fig. S7). The best control consistency came from SLBs composed of 99.7 mol % POPC and 0.3 mol % DiI that were draped over NPs of known size to engineer a model membrane topography. Continuity of the SLB over the NP was verified with fluorescence recovery after photobleaching (FRAP) (Fig. S8). This procedure was reproduced for 37, 29, and 175 NPs of r_NP = 24, 51, and 70 nm, respectively. p-PLM provided an increased density of localizations at the site of membrane curvature, and the size of the nanoscale membrane bud was measured (Figs. 4 and S9). For example, the density of localizations at the curved membrane over the 70 nm NP in p-PLM was (2.2 ± 1) × 10⁻⁶ localizations/nm² per frame, a 27× increase over the (8.2 ± 3) × 10⁻⁸ for flat SLB (Fig. 5). As an important internal control, no significant increase in the number of s-PLM localizations was observed with NP-induced membrane curvature (Fig. 3 J), which provides a second verification that chromatic bleed-through from the NP was not present and the high index of refraction of the polystyrene NP did not adversely affect the polarization of the fluorescence excitation (Fig. S10).

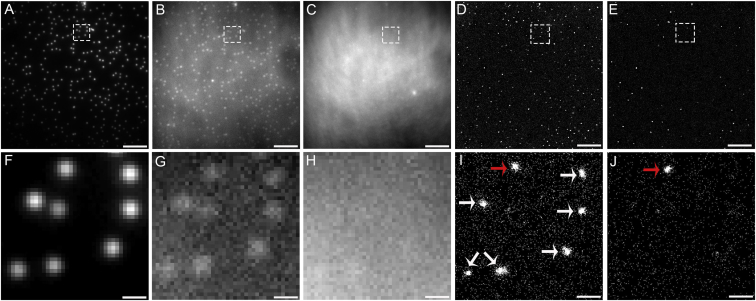
Figure 3.

Membrane curvature was engineered by draping a supported lipid bilayer over NPs. (A) The 70 nm radius fluorescent NPs on glass were imaged with λ_ex = 488 nm. (B–E) The membrane was imaged with λ_ex = 561 nm and the differences between the polarizations provide internal controls. (B and C) Diffraction-limited p-polarized and s-polarized TIRFM image, respectively. (D and E) Reconstructed images of the membrane over the NPs presented as 2D histograms of the localizations in p-PLM and s-PLM, respectively. (F–J) Magnified views of the dashed regions from (A–E) show membrane curvature coincident with the NPs. (I) The detected membrane curvature over the 70 nm NPs is indicated by white arrows. (I and J) A multicolored fiduciary mark is indicated by red arrows. Scale bars represent (A–E) 5 μm and (F–J) 400 nm. The Supporting Material provides similar results for other size and color NPs (Figs. S4 and S5), LUVs (Fig. S6), GUVs, (Fig. S7), and other magnifications of these data (Fig. S13). To see this figure in color, go online.

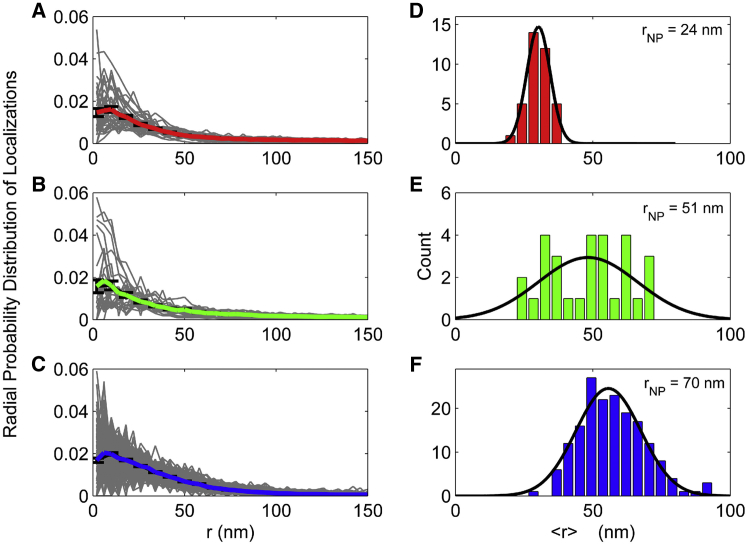
Figure 4.

(A–C) Radial probability distribution of localizations versus distance from the center of the curved membrane (r) over NPs of r_NP = 24, 51, and 70 nm, respectively. Gray lines represent individual events and the colored lines represent the averages. Error bars represent the mean ± SE at a given r. (D–F) Histograms of the radius for each membrane curvature event (<r>) for r_NP = 24, 51, and 70 nm. Black lines represent the Gaussian fits to guide the eye. The mean of the events radii was 32 ± 4, 50 ± 14, and 60 ± 13 nm for r_NP = 24, 51, and 70 nm, respectively. To see this figure in color, go online.

Figure 5.

The density of localizations vs. distance from the center of the curved membrane (r) observed via (A) p-PLM and (B) s-PLM. Data points show the experimental results and the theoretical results are plotted as solid lines. The theoretical results assumed the membrane topography shown in (C) with a single B₀ value and out-of-focus magnitude for anisotropic inaccuracy were fit to all six data sets from Eq. 5. To see this figure in color, go online.

Comparisons between the diffraction-limited images of the fluorescent polystyrene NP, the diffraction-limited polarized TIRFM images, and the reconstructed PLM images of the membrane reveal the increased resolution and detection sensitivity provided by PLM (Fig. 3). The diffraction-limited images demonstrated the PSF of the microscope more so than the physical size of the NP or membrane curvature. However, the radius of each membrane bud $\left(r\right)$ was calculated from p-PLM images by averaging the distance between each localization and the center of the bud (r). This calculation yielded <r> of 32 ± 4, 50 ± 14, and 60 ± 13 nm for membranes draped over NPs of 24, 51, and 70 nm radii, respectively (Fig. 4). Greater consistency in <r> calculations was provided when more localizations per area were detected, as expected (Fig. S9).

The sensitivity of PLM for detecting membrane curvature was especially apparent for the SLBs draped over NPs of 24 nm radius. The faint signal from the membrane curvature in diffraction-limited p-polarized total internal reflection fluorescence microscopy (p-TIRFM) images could have gone undetected, whereas the increased density of localizations p-PLM is readily apparent (Figs. 5 and S4). p-PLM provided a 6× increase in the signal/noise ratio (SNR) over diffraction-limited p-TIRFM with SNR of 11 ± 9 and 1.9 ± 0.7, respectively, where these uncertainties represent the standard deviation between events.

LUVs of with 0.3 mol % DiI were imaged with PLM. From diffraction-limited images of polarized TIFM excitation, flat SLBs were 1.8 ± 0.3× brighter with s-polarized total internal reflection fluorescence microscopy (s-TIRFM) than p-TIRFM, with the primary variability coming from laser alignment and SLB quality. Unfused LUVs above an SLB yielded 1.8 ± 0.7× more signal from p-TIRFM than s-TIRFM, with the variability coming primarily from the LUV size. The combination of these factors yielded a 3.2 ± 0.8× increase in signal for LUV detection via diffraction-limited p-TIRFM versus s-TIRFM. p-PLM yielded a 7.6× increase in localization rate when an LUV was present over an SLB with (50 ± 20) vs. (6.6 ± 0.8) × 10⁻⁷ localizations/nm² per frame in p-PLM versus s-PLM. The mean and SD of the LUV radii was <r> = 54 ± 29 and 57 ± 21 nm, as measured by p-PLM and s-PLM, respectively. As a demonstration of the increased sensitivity provided by PLM, 81% of the 122 LUVs that were detected in both s-PLM and p-PLM were not apparent with diffraction-limited p-TIRFM or s-TIRFM (Fig. S11). The LUVs only detected by PLM had radii shifted to smaller values of <r> of 62 ± 20 nm, whereas LUVs detected in PLM and TIRF possessed <r> of 72 ± 10 nm.

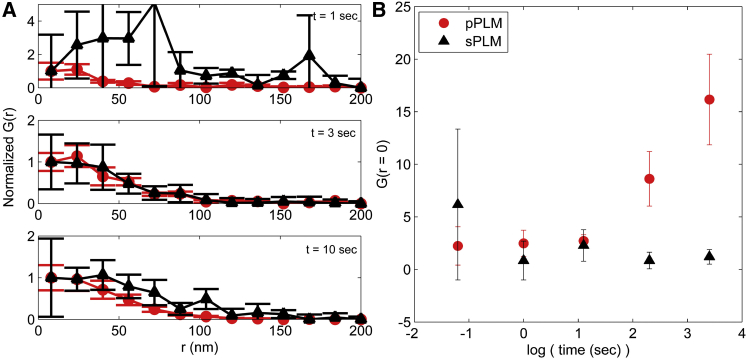
To reveal PLM temporal resolution, an autocorrelation analysis was performed on the PLM data. Correlation analysis was performed on both s-PLM and p-PLM images with increasing acquisition time interval to find PLM temporal resolution for detecting membrane bending. Results reveal the increased correlation between localizations due to the curvature detection in p-PLM in comparison to the more uniform localization distributions from s-PLM. Localization density rate of (1.2 ± 0.1) × 10⁻⁶ localizations/nm² per frame enabled early detection of local membrane bending over the 70 nm NPs within 1 s in p-PLM with a p-value of 0.0239; for a 3 s acquisition interval, the curvature region is detected in p-PLM with a p-value of 0.0002 (Fig. 6).

Figure 6.

Autocorrelation analysis for s-PLM and p-PLM for different acquisition time intervals. (A) Data were normalized to the first G(r) value to show the detection of curvature in p-PLM (red) with smaller error bars as time interval increases in comparison to s-PLM (black). (B) Autocorrelation G(r) value at r = 0. The s-PLM analysis provides an internal control to show the uniform bilayer analysis. An acquisition time of 1 s is sufficient to indicate the presence of curvature in p-PLM. To see this figure in color, go online.

Localization imprecision was limited primarily by the number of photons collected from each fluorophore in each frame. The localization software ThunderSTORM accounted for the camera quantum efficiency and imaging noise to estimate the number of photons and the localization precision for each detected fluorophore. 1200 ± 800 photons per fluorophore per frame were acquired, yielding a localization precision of 13 ± 5 nm. Further information regarding the acquired number of photons per fluorophore and the uncertainty for the different NPs sizes are provided in the Fig. S3 and Table S1.

Membrane bending affects lipid mobility

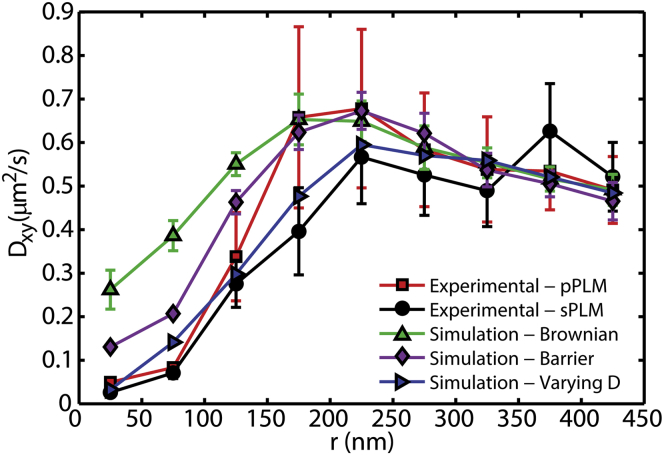
The same raw data from PLM that reveals nanoscale membrane bending through image reconstruction also can be interpreted to provide single-lipid trajectories relative to the membrane bending. High-throughput SPT was performed on the raw PLM data by tracking of individual fluorophores that were localized in sequential frames. Single-molecule DiI diffusion was observed with p-PLM and s-PLM to reveal the apparent diffusion coefficient in the xy-plane (D_xy). DiI that was detected in more than one frame was detected in 3.8 sequential frames on average. Analyzing D_xy as a function of location on the sample revealed the effects of membrane topology to lipid dynamics. In particular, D_xy versus distance from the center of the NP (r) revealed the curvature-induced slowing of the single-lipid diffusion (Fig. 7). SPT of DiI yielded D_xy = 0.55 ± 0.1 μm²/s, far from the 70 nm radius NP; however, within 50 nm of the center of the NP, D_xy = 0.03 ± 0.01 μm²/s when detected with either p-polarized or s-polarized excitation.

Figure 7.

Single-particle tracking of DiI molecules reveals slowed diffusion at the site of nanoscale membrane curvature equally while imaged with p-polarized or s-polarized excitation. SLBs were draped over 70 nm radius NPs. Particle locations were projected on the xy-plane and the apparent fluorophore diffusion was affected by both the 3D membrane topology and the influences of membrane curvature on DiI mobility. The fit of the distribution of step lengths to Eq. 1 yielded the apparent diffusion coefficient and the 95% confidence range, as indicated by the error bars. Neither a locally Brownian diffusion nor a simulated barrier to free diffusion surrounding the bud reproduced the experimental results. However, on simulating a decreased local D for curved SLB slower than that of the planar SLB, the resulting simulated D_xy matched the experimentally observed D_xy. Simulations matched experimental data when the planar SLB had a D that was 25 ± 5× faster than the curved SLB. To see this figure in color, go online.

The geometrical effects of diffusing on a nonplanar membrane can cause the observed diffusion rate through the xy-plane to be significantly different from the true, local diffusion rate. For example, a simple tilt of the membrane can decrease the apparent D_xy by up to 50%. With localization imprecision, long imaging frame rates, sample averaging, and increased membrane area per imaging pixel, even greater ratios of D/D_xy are possible. By simulating the diffusion of individual DiI on the estimated membrane topography (Fig. 5 C) with a constant in-membrane diffusion rate, the simulated nonplanar membrane topography was unable to reproduce the experimental results when assuming a locally Brownian diffusion.

Another hypothesis tested was that a barrier to diffusion was preventing the lipids from transitioning between the planar SLB and the membrane bud. However, the incorporation of a diffusion barrier into our simulations that prevented single-lipid trajectories from crossing between the curved membrane bud and surrounding SLB was insufficient to reproduce the experimental data. With a 50 Hz frame rate, a local D_xy = 0.55 μm²/s, and r_NP = 70 nm, a simulated diffusion barrier yielded only half of the observed decrease in D_xy necessary to get from the Brownian simulation to the experimental results. Additionally, FRAP results demonstrate the continuity of the membrane between the bud and the SLB (Fig. S8) and show no apparent barrier to diffusion.

Alternatively, the hypothesis was tested that the membrane curvature induced a local change in the effective membrane viscosity. This could be caused by variations in the curvature-induced changes to the lipid packing and/or the lateral membrane tensions. This hypothesis was tested via simulations with a lipid diffusion coefficient that was slower in curved membranes than planar membranes. Simulations of lipids diffusing on a planar membrane 25 ± 5× faster than their local diffusion on the curved membrane comfortably reproduced our experimental data from both s-PLM and p-PLM SPT (Fig. 7).

Discussion

Engineered membrane curvature

The method of creating SLBs primarily used in these studies incorporated draping the burst GUVs over the glass coverslip and polystyrene NPs. Draping a bilayer over NPs of known radii provided a model of physiologically similar dimensions to clathrin- and caveolin-mediated endocytosis. SLBs created by bursting GUVs were more intact and contained fewer pores than creating a bilayer via LUV fusion. However, such holes within the SLB were still feasible with this GUV-fusion method, especially when GUVs were more violently ruptured via application of GUVs to plasma-cleaned glass coverslips or dilution with hypotonic solutions. The continuity of the membrane between the SLB and the curvature over the NP was confirmed FRAP and long single-lipid trajectories. Both FRAP and long trajectories demonstrated that the lipids coating the NP can exchange with the lipids directly on the coverslip (Fig. S8), as also shown previously (46). Examination of the continuity of the bilayer over NPs was performed by assessing the p-PLM data, where 94% of 290 NPs surrounded by an SLB had curved membrane draping over the NP, and 60% of the NPs were well isolated from other NPs for further analysis. NPs without membrane curvature could be due to the NP being on top of the bilayer rather than under it, or the formation of a hole in the SLB directly surrounding the NP. The rare occasions in which membrane curvature did not appear at a NP gives confidence that the data we interpret as membrane curvature was not an artifact caused inherently by the presence of the NP (i.e., chromatic bleed-through).

An alternative membrane topography examined is that of the LUVs bound to an underlying SLB, which resembles vesicle docking in endocytosis and the later stage of exocytosis that precedes vesicle fission in cells. The variation of LUV sizes obtained by extrusion was demonstrated by PLM (Fig. S11). Other studies of vesicle sizes produced by extrusion through 100 nm pores have found the average diameter of extruded LUVs to be 65 ± 30 nm (47), indicating that the extrusion process produces a variation of LUV sizes with an upper diameter limit comparable to the extruder filter pore size. Taking advantage of PLM sensitivity and resolution, our reported values are in agreement with previous reports of LUV size distributions imaged via scanning electron microscopy (47).

Membrane topography over NPs

The demonstration of PLM performed here measured nanoscale hemispherical membrane curvature of an SLB draped over NPs ranging in radii from 24 to 70 nm. Prior methods of inducing nanoscale curvature utilized nanoengineered wavy glass substrates (48), microfabricated structures (49, 50), membrane tubule pulled from GUVs (51), and SLBs on deformable substrates (52, 53). However, wavy glass substrates, thick polymer structures, and lipid tubules are not compatible with TIRF excitation. The method of draping a membrane over fluorescent NPs of known size, as done here and previously (46, 54, 55), was effective for engineering nanoscale membrane curvature, testing the capabilities of PLM, and revealing the effects of curvature on lipid mobility.

A comparison between s-PLM and p-PLM results provided confirmation of numerous aspects of our results. At the location of the NP-induced membrane curvature, a near uniform density of localizations in s-PLM was detected whereas >5× increase of localizations in p-PLM was observed (Figs. 3 and 5 A). This confirms that there was no significant chromatic bleed-through from the fluorescence emission of the NP, that the refraction of the excitation light by the NP did not catastrophically alter the excitation light polarization, and that there was no significant Förster resonance energy transfer between DiI and the NP disrupting the polarization dependence of the signal. However, refraction by the NP may have influenced the direction of the DiI emission, as discussed below, but incorporation of the high index of refraction of the polystyrene NP was not necessary for theoretical reproduction of our experimental results, as further described in the Supporting Material.

The membrane topology over the NPs depended on the adhesion between the lipids and the polystyrene NP, the adhesion between the lipids and the glass coverslip, the size of the NP, the membrane-bending rigidity, the lateral membrane tension and pressure, and the packing properties of lipids (55, 56). POPC, the dominant lipid in these experiments, has no intrinsic curvature and forcing a POPC bilayer to bend would cause an unfavorable packing of the lipids. For a positive membrane curvature, the lipid tails are crowded whereas the headgroups are stretched over more area. For a negative membrane curvature, the lipid headgroups are crowded whereas the lipid tails are given more volume to occupy. Both configurations are unfavorable for POPC and apparently result in slowing the diffusion of a fluorescent lipid through the crowded environments.

We modeled the shape of the membrane over the NPs to be primarily spherical, with a smooth 20 nm radii of curvature bend to connect to the planar SLB (Fig. 5 C). This consistent radius of curvature for the connection of the SLB on the NP to the SLB on the coverslip resulted in a tent-like transition from the top of the small NPs to the glass substrate, and a neck-like feature at the transition from the large NPs to the coverslip. The tent-like membrane structure would have a bigger size than the small NPs; the neck-like membrane structure would have a smaller size than the large NPs (Figs. 4 and 5 C) (55). The tent-like model may represent the initial stages of membrane bending on the initiation of endocytosis or conclusion of exocytosis; the neck-like model represents the later stage of endocytosis or early stage of exocytosis. The agreement between the experimentally measured and theoretically predicted radial density profiles suggest the accuracy of both the membrane model and the theoretical analysis of localization probabilities (Fig. 5; Eq. 5).

Limitations to resolution

The distribution of localizations around the NP-induced membrane buds was influenced by multiple effects that limit the experimental determination of the membrane topography, including 1) localization imprecision of the individual fluorophores, 2) anisotropic emission from the membrane-confined DiI, 3) finite localization rates, 4) NP-induced emission lensing, 5) the fitting of multiple “on” fluorophores as if they were a single fluorophore, and 6) membrane curvature motion within the sample (i.e., NP or LUV drift) (Fig. S12). Each of these contributions has been theoretically tested in attempts to match theoretical predictions to the experimental observations, as described below and in the Supporting Material. It was found that the single-fluorophore localization imprecision, anisotropic emission effects, and bud center identification proved to be the only error sources needed to theoretically reproduce the experimental data. Matching the experimental data with theoretical estimates required no NP-induced emission lensing nor multiple “on” fluorophore misassessements.

The inherent inability of DiI to tumble freely within the membrane is a necessary component for polarization sensitivity and membrane orientation detection; however, it also results in an anisotropic emission and systematic inaccuracies of DiI localization. Although the DiI is not rigid in one location and can explore all ψ values in addition to a tilt of β = 69°, some orientation averaging occurs for each DiI image. Still, the anisotropic emission results in a systematic shift up to 100 nm of the single-fluorophore localizations toward the center of the NP. Numerical integration yielded the magnitude and direction of the shift in localization position due to the single-fluorophore orientation and height above the focal plane, following the framework of Agrawal et al. (57). The expected PSF and lateral shift were estimated as a function of membrane orientation (θ and φ) after considering the expected fluorophore orientations within the membrane (ψ and β). Accordingly, the expected lateral shifts as a function of membrane orientation and height were calculated. This systematic shift was incorporated into our simulated image reconstruction and SPT results, and was critical for matching the experimental data.

The upper limit on localization rates in all SMLM methods is based on the camera frame rate and the length scale of diffraction-limited imaging. Localization rates could be increased above those reported here by increasing density of DiI in the sample, or optimizing the DiI “on” and “off” rates with further buffer or incident light optimization. Further, the limited final number of localizations yields uncertainty in analyzing the precise local membrane orientation and the center of the membrane bud. Here, 200 ± 100 localizations per membrane bud were collected, each with a radius of 30–60 nm, which resulted in uncertainty in identifying the bud center by 3 ± 1 nm, by mean ± SE analysis.

SMLM is based on localizing single fluorophores that are sufficiently separated for computational fitting (>200 nm apart); however, if multiple fluorophores were proximal to each other (<100 nm) and falsely interpreted as a single fluorophore, then systematic errors could be incorporated. Typically, this error is predictable by assuming a uniform time-averaged fluorophore density, estimating the mean separation distance between fluorophores, and calculating the probability of multiple fluorophores being within the diffraction-limited range from each other. However, for p-PLM, the assumption of a uniform time-averaged fluorophore density may not be appropriate. Because the horizontal membrane comprises the majority of the sample and DiI within the horizontal membrane absorbs less excitation light, it would follow that the sample-averaged fluorescence “off” rate would be slower with p-polarized than with s-polarized excitation. This could yield more “on” fluorophores on the curved membrane than seemingly apparent. For the curved membranes examined here, if multiple fluorophore images were averaged simultaneously, the resulting localization will be shifted toward the center of the feature. The inclusion of this error caused worse fitting of our simulations to the experimental data, suggesting that the multiple “on” fluorophore misassessements were not a significant component of our image reconstruction and data analysis.

Curvature-affected lipid diffusion

Analyzing D_xy versus distance from the NP center demonstrated how the lipid diffusion slowed at the membrane buds equivalent to the membrane bending causing an increase in effective viscosity (r). With greater experimental sampling densities, rates, and precision, a more sophisticated simulation and analysis routine would be warranted (44). The sequential frame linking and analysis performed here resulted in the average single-lipid step sampling a distance between 60 and 200 nm, depending on the local diffusion coefficient, which is comparable to the size of the NPs. However, the curvature-dependent single-lipid step length observed here is dramatic and was able to be modeled computationally by incorporating the experimental data conditions, such as frame rate, localization precision, anisotropic inaccuracies, and membrane topography.

The diffusion of DiI apparently slowed when the membrane was curved over the NP. The change in membrane topography from flat to the curved membrane over the NP alters DiI diffusion observed in both s-polarization and p-polarization, resulting in a decrease in the observed diffusion coefficient within the membrane (Fig. 7). Because the diffusion analysis from the s-PLM and p-PLM data yielded indistinguishable effects of membrane curvature on lipid mobility, the illumination polarization did not apparently affect the observed diffusion coefficients. When a membrane is tilted (θ > 0), a 2D Brownian diffuser apparently moves slower when imaged in the xy-plane; however, this geometric effect alone was not sufficient to reproduce diffusion rates extracted from experimental data.

To account for the 20× slowing of the single-lipid trajectories at the site of nanoscale membrane budding, two hypotheses were tested. A diffusion barrier between the membrane bud and the surrounding planar SLB was not sufficient in matching the modeled and experimental data. However, combining both the geometric effects of the tilted membrane and a curvature-dependent effective membrane viscosity yielded a strong agreement between the modeled and experimental SPT results. This analysis supports the hypothesis that DiI diffuses slower on more curved membranes due to changes in membrane properties, such as effective membrane viscosity or lipid packing, as suggested previously (46).

Neither the experimental data nor the simulated theoretical reproduced data for D_xy distinguishes between the two leaflets of the lipid bilayer. The SLBs were symmetrically labeled through the addition of DiI to the lipid mixture before GUV electroformation, and both bilayer leaflets contributed to the observed DiI diffusion rates. DiI in the outer leaflet would have minimal direct substrate interaction, whereas DiI in the inner leaflet would be proximal to the supporting polystyrene NP or glass coverslip. However, our control experiments have failed to find a substrate-induced slowing of the single-lipid diffusion. We have created stacked SLB structure with between one and five bilayers layered over the coverslip and we have not detected any difference in the distribution of single-lipid step lengths versus number of bilayers present; the cushioning of an SLB by additional SLBs did not apparently affect the single-lipid diffusion. Accordingly, this suggests that the substrate differences between the glass coverslip and the polystyrene NP are unlikely to affect the single-lipid step lengths reported here. Further, single-lipid diffusion has been observed to be slower when nanoscale membrane buds are formed by cholera toxin subunit B rather than a NP (58 (this issue of Biophysical Journal)).

Diffusion rates measured by SPT, FRAP, and fluorescence correlation spectroscopy show systematic variations in the measured diffusion coefficients depending on the analysis method. Comparison between these techniques requires accounting for their difference in sensitivity to detecting mobile versus immobile diffusers, length scale- and timescale-dependent processes, and subpopulations of diffusers (43, 44). The SPT results presented here are consistent with prior SPT results and, as expected, report a slower diffusion rate than FRAP or fluorescence correlation spectroscopy measurements (54, 59).

Future improvements to PLM

PLM is able to provide superresolution detail on membrane orientation with improved sensitivity and resolution from comparable methods. Because PLM requires no manipulation of the fluorescence emission path or the PSF, the incorporation of PLM with SMLM in additional complementary color channels is straightforward. For example, the simultaneous superresolution membrane orientation detection via PLM with the curvature-sorting and curvature-induction effects of cholera toxin subunit B is the focus of a companion article in this issue of Biophysical Journal (58).

It is feasible that the local membrane orientation could be evaluated by the direct mapping of acquired localizations per pixel to the PLM theory. To perform such analysis, a minimal localization density of 0.05 localizations/nm² would be required. PLM has the advantage of observing lipids that diffuse into the region of view from the surrounding membrane to effectively achieve unlimited labeling densities, similar to what has been previously utilized in point accumulation for imaging in nanoscale topography (60). Greater sampling statistics would enable finer details of membrane topology to be extracted, with more statistically significant comparisons between p-PLM and s-PLM localization densities.

With a faster frame rate and/or decreased localization imprecision, more sophisticated SPT analyses could be performed (44). It could be instructive to analyze the single-molecule trajectories to extract the component of the molecular diffusion radial from the center of the bud, as opposed to the diffusion component around the bud. If some membrane components accumulate at the bud neck, it is feasible that the single molecules could diffuse quickly around the bud while slowly changing its radial distance from the bud center. Unfortunately, this analysis is not feasible at current imaging frame rates, but it will be the focus of future work using PLM to reveal the nanoscale effects of membrane curvature.

Conclusions

PLM is capable of detecting and resolving nanoscale membrane curvature with super resolution and correlating this curvature to single-molecule diffusion and molecular sorting. PLM requires no alteration of the emission path from traditional single-molecule fluorescence microscopes and incorporates no inherent sacrifice in the signal or localization precision for observing the membrane orientation. Distinct identification between membrane topology of LUVs, GUVs, and curved SLBs over NPs was observed. The NP-patterned substrate provided a means to engineering nanoscale membrane curvature of physiologically relevant dimensions. Local membrane-bending regions with radii of curvature ≥24 nm were detected. PLM detected membrane curvature and resolved membrane topography with 1 s of acquisition time at (1.2 ± 0.1) × 10⁻⁶ localizations/nm² per frame.

Radial line scans of p-PLM localizations reveal radii of curvature of 32 ± 4, 50 ± 14, and 60 ± 13 nm for membranes over NP radii of 24, 51, and 70 nm, respectively. Further, a 6× increase in the SNR is obtained by PLM over traditional TIRFM. The theoretically estimated localization probabilities versus membrane orientation reproduced experimental data. The unique spatiotemporal resolution of PLM is suited to monitor membrane structure variation with lipid and protein dynamics. We envision that this microscopy technique will provide information for previously untestable nanoscale processes coupled with a change in membrane topography. This is demonstrated by the observation of time-dependent membrane budding initiation and growth induced by cholera toxin subunit B in quasi-one component lipid bilayers, revealing a possible mechanism of cholera immobilization and cellular internalization described further in the accompanying article (58). Fundamental questions regarding nanoscale cellular processes such as clathrin-independent endocytosis, viral infections, endocytosis/exocytosis, and immunological responses are soon to be addressed with PLM. The feasibility of performing PLM on model membranes or live cells on timescales suitable for observing cellular processes permits this technique to be adopted and broadly used to probe cellular dynamics.

Author Contributions

A.M.K. and C.V.K. designed the experiments, analyzed the data, and prepared the manuscript. A.M.K. performed the experiments. C.V.K. performed the simulations.

Editor: Tommy Nylander.