Confocal Rheology Probes the Structure and Mechanics of Collagen through the Sol-Gel Transition

Abstract

Fibrillar type I collagen-based hydrogels are commonly used in tissue engineering and as matrices for biophysical studies. Mechanical and structural properties of these gels are known to be governed by the conditions under which fibrillogenesis occurs, exhibiting variation as a function of protein concentration, temperature, pH, and ionic strength. Deeper understanding of how macroscopic structure affects viscoelastic properties of collagen gels over the course of fibrillogenesis provides fundamental insight into biopolymer gel properties and promises enhanced control over the properties of such gels. Here, we investigate type I collagen fibrillogenesis using confocal rheology—simultaneous confocal reflectance microscopy, confocal fluorescence microscopy, and rheology. The multimodal approach allows direct comparison of how viscoelastic properties track the structural evolution of the gel on fiber and network length scales. Quantitative assessment and comparison of each imaging modality and the simultaneously collected rheological measurements show that the presence of a system-spanning structure occurs at a time similar to rheological determinants of gelation. Although this and some rheological measures are consistent with critical gelation through percolation, additional rheological and structural properties of the gel are found to be inconsistent with this theory. This study clarifies how structure sets viscoelasticity during collagen fibrillogenesis and more broadly highlights the utility of multimodal measurements as critical test-beds for theoretical descriptions of complex systems.

Introduction

Type I collagen is the most abundant protein in the mammalian extracellular matrix and plays a role in a broad variety of critical functions in mammals including tissue scaffolding, cell adhesion and migration, and wound healing (1, 2, 3). In recent years, collagen I matrices have regularly been prepared in vitro for use in biophysical experiments and bioengineering applications (4, 5, 6, 7, 8). For example, reconstituted collagen hydrogels have been employed as physiologically relevant, tunable environments for investigating how cells respond to environments of different stiffness in three dimensions. For such studies, characterization of mechanical properties and structure of the matrix is critical, as cells may alter their behavior in response not only to altered gel stiffness but also independently to accompanying changes in gel network structure (9, 10, 11, 12, 13).

The self-assembly of collagen has primarily been described with and tested against nucleation and growth theories (12, 14, 15, 16, 17). Indeed, it has been shown that a degree of independent control over structural and mechanical properties of collagen gels can be obtained through exploiting the putative nucleation and growth based self-assembly of these systems (12). Within nucleation-based models, three distinct regimes are expected in the self-assembly of collagen from a set of monomers to a fully assembled fibrous hydrogel. These are the lag, growth, and plateau phases: during the lag phase, collagen monomers form critical nuclei that develop into fibrillar structures during the growth phase until monomers are depleted, the plateau phase. This model predicts sigmoidal development of various experimental observables and was initially suggested based on the development of turbidity during collagen self-assembly (14, 15).

Whereas nucleation and growth theory correctly predicts turbidity development during collagen self-assembly, the theory (and turbidity measurements) cannot distinguish between a final structure consisting of, for example, a set of disconnected collagen fibers and a spanning network of the same. In contrast, both imaging and rheological measurements indicate that at concentrations typically used in experiments employing reconstituted collagen, fibrillar collagen structures do form a spanning network that can withstand stress. To describe the sol-gel transitions that occur in such self-assembling systems common in biology, nucleation and growth theories are insufficient and additional theories such as those of phase transitions, including geometric and rigidity percolation transitions, have been invoked (18, 19, 20, 21, 22, 23).

Percolation theory describes gelation within the framework of critical phenomena, as a phase transition due to gradual interconnection of clusters to form a single system-spanning cluster (a network) (20, 24). Critical gelation as formulated by Winter and co-workers (24, 25, 26, 27, 28, 29, 30, 31) predicts a variety of rheological behaviors, including power-law scaling of loss and storage moduli with frequency in the vicinity of the sol-gel transition (or gelation point)—behavior that has been observed in some chemical and physical gels, including biological ones. Through connections with and extensions of percolation theory, the predicted structure of networks going through critical gelation has also been described (32, 33, 34, 35, 36, 37). Understanding whether network structure and mechanical properties of collagen networks can be explained through critical gelation theory or other relatively simple approaches could enhance control over these properties in such systems, in analogy to the manner in which nucleation and growth has been exploited.

To assess whether the sol-gel transition in self-assembling collagen systems occurs through critical gelation, the evolution of structure and viscoelasticity in the system must be followed during self-assembly. Although a few studies have attempted to do so through side-by-side imaging and rheology studies (19, 38), multimodal, simultaneous interrogation of these properties is needed for unambiguous comparison. Such studies could provide a critical test-bed for theories describing collagen gelation as well as those predicting collagen mechanical properties from structure (39, 40, 41, 42, 43, 44, 45, 46).

Here, we use a multimodal confocal rheology apparatus to monitor structural and viscoelastic evolution of collagen during its self-assembly and through the sol-gel transition. This approach allows comparison of the sol-gel transition to predictions of critical gelation theory. We show that the collagen system displays a network spanning structure at a gelation time defined through rheology as well as a scaling relationship consistent with gelation through percolation. However, other rheological and structural predictions of critical gelation theory do not hold in the collagen system under study. These findings highlight the power of the simultaneous tracking of structure and viscoelasticity to critically assess theoretical approaches to describing complex systems.

Materials and Methods

Chemicals and materials

High concentration type I acid-solubilized (AS) collagen (8.5–10 mg/mL, in 0.02 M acetic acid, pH = 2, rat tail), 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid (1 M), sodium hydroxide (1 M), and sodium bicarbonate (7.5%) were purchased from Corning (Corning, NY) and used without further purification. Dulbecco’s modified Eagle’s medium (10×), ATTO 647N (with n-hydroxysuccimide-ester functionality, λ_ex = 646 nm, λ_em = 664 nm), dimethyl sulfoxide, and acetic acid (99.7%) were purchased from Sigma-Aldrich (St. Louis, MO) and used without further purification. Dialysis tubing (Side-A-Lyzer, 20 k molecular weight cutoff; Sigma-Aldrich) was used for purification of labeled collagen.

Fluorophore labeling of collagen monomers

Type I AS collagen monomers were conjugated with ATTO 647N fluorescent dye molecules following a procedure reported previously (47, 48). Briefly, ATTO dye stock in dimethyl sulfoxide was prepared and added to a 3.0 mg/mL collagen solution in 0.01 M sodium bicarbonate (pH = 9). The conjugation reaction was carried out at 4°C in the dark for 1 day. For purification, the product was dialyzed against 0.02 M acetic acid for 3 days (or until the acetic acid was colorless) at 4°C in the dark using mini-dialysis tubing. The acetic acid solution in the tubing was changed twice a day. The final product was stored at 4°C in the dark at pH = 2 until use.

Preparation of ATTO-doped collagen gels

Collagen gels of 1.0 mg/mL were prepared by diluting a 3.0 mg/mL stock solution (prepared from high concentration stock, in 0.02 M acetic acid) with 10% Dulbecco’s modified Eagle’s medium, 2.5% 4-(2-hydroxyethyl)-1-piperazineethanesulfonic acid, and deionized H₂O. The stock solution was then doped with 3.0 mg/mL ATTO-labeled collagen (in 0.02 M acetic acid). The final ratio of labeled to unlabeled collagen was 1:20. All solutions were prepared and held on ice (∼10 min) to allow air bubbles induced by mixing to dissipate. To initiate collagen fibrillogenesis, 10 μL of 1 M NaOH was added to 700 μL solution for neutralization (pH ≈ 7.4). The ionic strength of all gel solutions was I ≈ 0.13.

Confocal rheology instrumentation

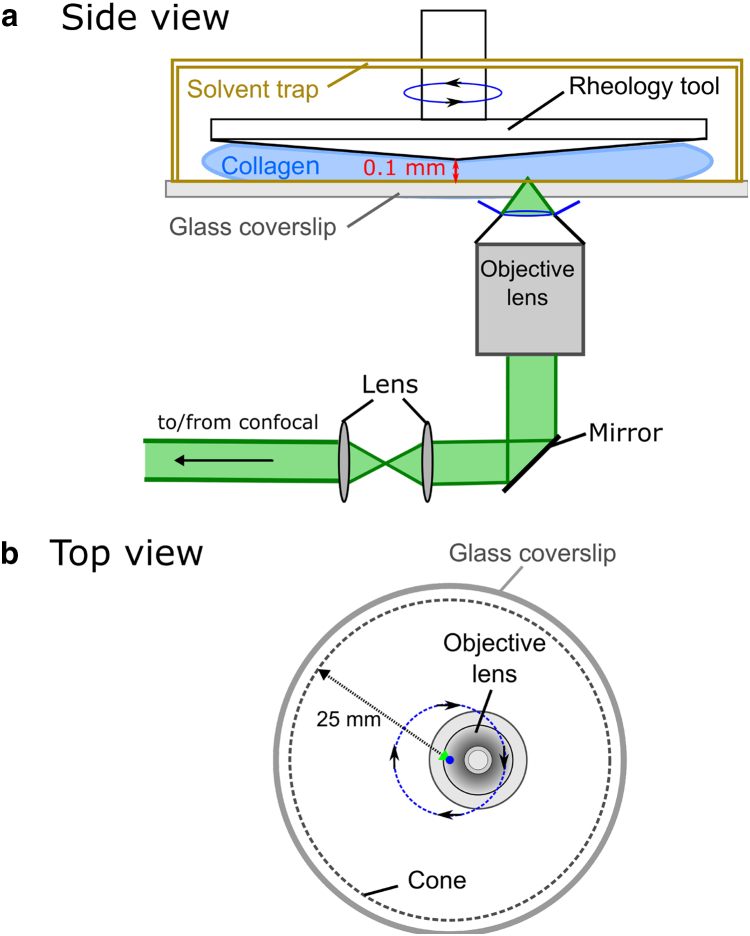
Confocal rheology experiments were conducted on a modified rheometer (MCR 302; Anton Paar, Graz, Austria) with an open bottom configuration that allows for placement of a 60×, water-immersion objective lens (UPLAPO, 60XW3, N.A. = 1.2; Olympus, Tokyo, Japan) under the lower plate, with height controlled with a manual micrometer. This configuration allowed for simultaneous confocal imaging and rheology (Fig. 1) in a manner similar to that described by Besseling et al. (49). The rheometer was equipped with a solvent trap to minimize sample evaporation. Peltier temperature control was provided from both the bottom of the rheometer stage and the top, where a heating element is present in the inner hood of the solvent trap, to limit possible temperature gradients in the sample. The temperature was set to 25°C for 15 min to equilibrate and maintained at 25°C during the measurements. A polycarbonate cone (CP50-1/PC; 1° tilt angle, 50 mm diameter, 100 μm truncation gap; Anton Paar) was used for cone-plate rheology measurements in oscillatory mode. Glass coverslips were custom made (UQG Optics, Cambridge, United Kingdom) to fit the round bottom of the rheometer stage. Samples were illuminated using Helium-Neon lasers (λ_ex = 543 and 633 nm; Melles Griot, Carlsbad, CA) directed out the back of an inverted confocal laser scanning microscope (Fluoview 300; Olympus) through a custom multiple lens/mirror system to ensure the same magnification as if imaged on the confocal stage. The objective, which was modified with a homebuilt heater, was placed slightly off-center to avoid imaging directly at the truncation point of the cone. The truncation gap was 100 μm in height, and the thickest portions of the samples were ∼530 μm. At the objective focal point in the xy plane of the sample, the gap was ∼210 μm. This sample configuration and thickness is not expected to give rise to sample size effects in loss or storage modulus (50). Light reflected or emitted from the sample was collected in the epi-direction by the objective, directed back to the confocal scan head through a confocal pinhole and to photomultiplier tube detectors. All measurements were performed ∼10–20 μm above the bottom glass to minimize visualized motion imparted by the oscillating cone during imaging.

Figure 1.

Schematic of the confocal rheometer showing the (a) side view of the instrument and (b) top view of the rheology tool. The experimental setup integrates a commercial confocal microscope and a commercial rheometer through optical elements, thus allowing simultaneous collection of confocal microscopy and oscillatory rheology data. To see this figure in color, go online.

Confocal rheology measurements

Collagen solutions were prepared as described above, and ∼600 μL sample volume was added to the rheometer stage as quickly as possible after gelation was initiated by solution neutralization. Samples were not trimmed to minimize delay (1.0 min) before the start of imaging. The solvent trap hood was lowered as soon as the sample was applied to limit evaporation and to equilibrate the solution at the measurement temperature. For reproducible rheological measurements during the early stages of fibrillogenesis, it was imperative to avoid air bubbles in the sample. However, despite the use of solution preparation procedures meant to minimize bubbles, some inevitably remained. These bubbles caused inconsistent rheological results at the earliest time points. As such, for all data presented here, rheology measurements were begun with a delay of 7.0 min relative to sample neutralization with NaOH.

Upon neutralizing the collagen solution, the sample was mixed, placed on the rheometer coverslip preequilibrated to 25°C, and confocal imaging began. Time zero (t = 0 min) was defined as time when the collagen solution was neutralized by NaOH. Confocal imaging began at t = 1.0 min whereas oscillatory rheology began at t = 7.0 min. Rheological data was collected using the software Rheoplus/32 (v6.62; Anton Paar), and storage (G′) and loss (G″) moduli measurements were taken every 15 s at 1% strain and at different frequencies (ω = 0.5, 1.0, 2.5, 5.0, and 10.0 rad/s) for 20 min (from t = 7.0 to 27.0 min). A strain of 1% was verified to be within the linear regime for collagen gels. Confocal reflectance microscopy (CRM) and confocal fluorescence microscopy (CFM) data were also recorded every 15.0 s (3.26 s per scan with 11.74 s between scans) for 120 frames (from t = 1.0 to 31.0 min). A 543-nm laser (60 μW at the objective lens) and 633-nm laser (115 μW at the objective lens) were used for CRM and CFM, respectively. A dichroic mirror (DM 630) was used to separate the CRM and CFM signal and a long-pass filter (660 LP) was employed in the CFM detection channel. In all cases, scans were 1024 × 1024 pixels (235 × 235 μm), and 12-bit images were collected. Both photomultiplier tubes for CFM and CRM were set to maximize signal without saturation, and the same detector settings were used to collect all data. Simultaneous CRM and CFM were performed for all imaging experiments.

Determination of key time points during gelation

Because we were interested in identifying the time at which the sol-gel transition occurred, we quantified several time points and time-dependent quantities from confocal imaging and rheology.

Structural characterization. From CRM, the arrest time $\left(t_{\text{ARR}}^{\text{CRM}}\right)$ was qualitatively identified from time-lapse images as the time at which visualized fibers were fixed relative to each other, as described previously (38, 51). A second time point was also assessed qualitatively: CFM images were used to determine the time at which small features—likely representing oligomers of labeled collagen—were fully incorporated into the fiber network. We denote the time at which this occurs as the incorporation time, $t_{\text{INC}}^{\text{CFM}}$. Because $t_{\text{ARR}}^{\text{CRM}}$ and $t_{\text{INC}}^{\text{CFM}}$ were identified qualitatively, two researchers independently determined these times, and they differed by no more than two frames (30 s).

The qualitative assessment of network structure development captured by identifying arrest and incorporation time were supplemented with quantitative image assessment. For analysis of CRM images, the central portion of each image was replaced by a copy of the upper-left corner of the image before further analysis, as these images have an artifact due to reflection from optical elements in the microscope. From these center-replaced CRM images, total intensity (I^CRM) was obtained by summing all individual pixel intensity values. Cross-correlation image analysis was also performed on CRM and CFM images. Correlation coefficients, r^CRM and r^CFM, between subsequent images were computed via $r=\sum _m\sum _n\left(A_{\text{mn}}-\overline{A}\right)\left(B_{\text{mn}}-\overline{B}\right)/\left({\sum _m\sum _n\left(A_{\text{mn}}-\overline{A}\right)}^2\right){\left({\sum _m\sum _n\left(B_{\text{mn}}-\overline{B}\right)}^2\right)}^{0.5}$, with $A{\left(B\right)}_{\text{mn}}$ as the pixel intensity value of the first (second) image in the mth row and nth column and $\overline{A}\left(\overline{B}\right)$ as the mean pixel value of the images.

The fractal dimension of images collected during confocal rheology was also assessed for comparison of collagen gelation to structural predictions of percolation through critical gelation. Fractal dimension was calculated with the Fractal Count ImageJ plugin, which uses the box-counting method and provides the Minkowski-Bouligand dimension as output. We employed this method on CRM images and refer to the output as d_f,slice. Images were first thresholded, with the threshold value for distinguishing features from noise analytically determined using the isodata-threshold routine in ImageJ (National Institutes of Health, Bethesda, MD). For time-lapse CRM images collected during gelation, the threshold was determined from the last frame. This threshold was then used to analyze the full set of images with box-counting. Each image (1024 × 1024 pixels) was divided into squares of 256 × 256 pixels, and the number of boxes that contained at least one pixel with intensity higher than the threshold value was counted. The size of the box was then decreased by a factor of 1.2, and the counting procedure was repeated. This cycle continued until the box size reached 6 × 6 pixels. Fractal dimension was then calculated via a linear fit to $d_{f,\text{slice}}=\text{log}\left(c\right)/-\text{log}\left(x\right)$ , where x is the length of the box and c is the number of boxes with at least one pixel above threshold.

CRM intensity curves (I^CRM), CRM and CFM correlation curves (r^CRM and r^CFM), and CRM fractal dimension (d_f,slice) curves all displayed sigmoidal shapes. The first derivative of the sigmoidal fit was used to extract time points of interest, where 5, 50, and 95% of the final value was present. We term these lag, inflection, and plateau times in accordance with the sigmoidal shape and the nucleation and growth interpretation of turbidity curves in collagen fibrillogenesis (12, 15, 51, 52).

Rheological characterization. Oscillatory rheology was used to determine other key time points in the gelation process. The crossover time, $t_{\text{CO}}^{\text{RHEO}}$, was defined as the time at which the storage and loss moduli crossed, which may depend on the frequency at which oscillatory rheology is performed (53). The crossover time was determined by fitting straight lines to the three G′ and G″ data points surrounding the time point at which G′ was first larger than G″. The gel point, $t_{\text{GEL}}^{\text{RHEO}}$, was determined within the critical gelation model described previously (20, 24, 26, 27, 54). For percolation through critical gelation, the gel point is a characteristic that, unlike the crossover time, does not depend on applied frequency (53). Thus, $t_{\text{GEL}}^{\text{RHEO}}$ was obtained by identifying the time at which the slope, Δ, of the viscoelastic impedance spectra of storage, G′(ω), and loss moduli, G″(ω), were the same, such that G′(ω) ∝ G″(ω) ∝ ω^Δ (54), as will be discussed further in Results.

Results

Qualitative description of gelation probed by confocal rheology

In advance of simultaneous confocal imaging and oscillatory rheology measurements, control experiments on 1.0 mg/mL collagen samples gelled at 25°C were performed to confirm that the intrinsic collagen gelation characteristics were not perturbed by confocal microscopy at low laser power, rheology at low strain, or sample confinement (as imposed by the rheometer tool) (Supporting Material, Table S1). Then, simultaneous confocal imaging and oscillatory rheology measurements were performed to monitor and systematically study fibrillogenesis and gelation of 1.0 mg/mL collagen I samples at 25°C. The concentration and gelation temperature were chosen primarily to limit crowding in the system that can obscure identification of network presence and to assure gelation kinetics were sufficiently slow to monitor key events during the gelation process with imaging and rheology.

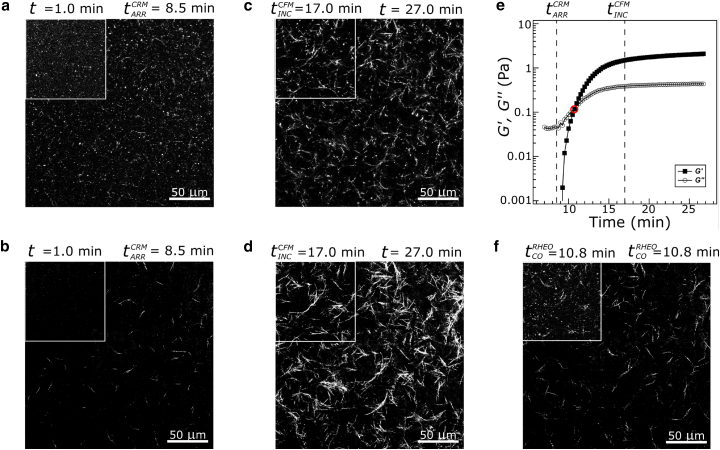
Movie S1 shows a representative set of confocal rheology data with rheology performed at 10.0 rad/s. Time-lapse imaging reveals key events during fibrillogenesis and gelation. Initially (t = 1.0 min), CFM images show the presence of many diffraction-limited features on a uniform low intensity background (Fig. 2 a, inset). Given the microscope configuration and detectors, single molecule sensitivity is not present, and these features reflect the presence of oligomers in the solution. In contrast, CRM images show a uniform dark background with no clear features (Fig. 2 b, inset), as expected given CRM’s limited sensitivity relative to CFM (51, 55). At later times, fibrillar structures become visible in both CFM and CRM. Fig. 2, a and b, reflects the arrest time $t_{\text{ARR}}^{\text{CRM}}$ as visualized in CFM and CRM images, respectively. Arrest time was determined as described previously, as the time point at which fibers observed in CRM do not exhibit motion relative to each other. It has been suggested that this represents the time at which the fibers form a system-spanning structure (38). After this time, additional fibrillar structures become evident and they grow brighter in CRM, with CRM intensity reflecting increasing fiber width (51). In CFM, features also are seen to assemble into fibers on the same timescale. Due to the photostability of ATTO 647N, fluorescence images could be collected through the entirety of the gelation process, which had not been possible with FITC-labeled collagen used in a previous study (51). This allowed visualization of the time point shown in Fig. 2 c (inset), where small features present in the initially visualized solution are fully associated with fibers and exhibit no additional motion, $t_{\text{INC}}^{\text{CFM}}$. After this time, CRM images continue to brighten to a certain extent (Fig. 2 d). Fig. 2, c and d, shows CFM and CRM images near the conclusion of the experiment, where a fully developed gel is present and negligible further evolution of structure or mechanical properties occurs. The final collagen structure, despite being formed on the rheometer and during oscillatory rheology, shows prototypical microstructure for a collagen gel formed at 25°C, with both single and bundled fibers. As in previous reports, the labeling of collagen monomers with fluorophores somewhat diminishes bundling that otherwise occurs in low temperature AS collagen gelation (39, 51).

Figure 2.

Representative (a) CFM and (b) CRM images were recorded at (inset) the initial time point imaged (t = 1 min) and at (full image) $t_{\text{ARR}}^{\text{CRM}}$ during fibrillogenesis of 1.0 mg/mL collagen at 25°C. (c) CFM and (d) CRM images were recorded at (inset) $t_{\text{INC}}^{\text{CFM}}$ and at (full image) the end of the experiment (t = 27 min) of the same gel. (e) Storage, G′, and loss, G″, moduli of collagen gelation were probed at 10.0 rad/s. The G′-G″ crossover, $t_{\text{CO}}^{\text{RHEO}}$, is highlighted with a circle. $t_{\text{ARR}}^{\text{CRM}}$ and $t_{\text{INC}}^{\text{CFM}}$ are indicated with dashed lines. (f) CRM and (inset) CFM images were recorded at $t_{\text{CO}}^{\text{RHEO}}$. All images and data were obtained from a single representative sample also shown in Movie S1. To see this figure in color, go online.

The simultaneously collected rheology is shown for the representative sample in Fig. 2 e. Initially (t = 7.0 min), the loss modulus, G″, is very small (∼0.05 Pa) and the storage modulus, G′, is undetectable, consistent with the presence of a Newtonian liquid. As gelation proceeds, G′ becomes detectable and G′ and G″ increase, with G′ increasing faster than G″: this leads to a crossover point, $t_{\text{CO}}^{\text{RHEO}}$ where G″ = G′, as denoted in Fig. 2 e. The CRM and CFM images at the crossover time are shown in Fig. 2 f and inset, respectively.

Comparison of rheological features to critical gelation predictions

The crossover time, $t_{\text{CO}}^{\text{RHEO}}$, may be expected to be similar to $t_{\text{ARR}}^{\text{CRM}}$, as both have been associated with the sol-gel transition and the existence of a sample-spanning network, but that was not found here. Instead, the crossover time was found to be consistently later than arrest time, a finding echoing our earlier results with nonsimultaneous imaging and rheology (38). Crossover time is expected to be frequency dependent: measurements probing viscoelasticity with high frequency oscillatory rheology probe shorter timescales and shorter length scales than low frequency measurements (56). As such, the sol-gel transition cannot be determined directly from oscillatory rheology at a given frequency (53).

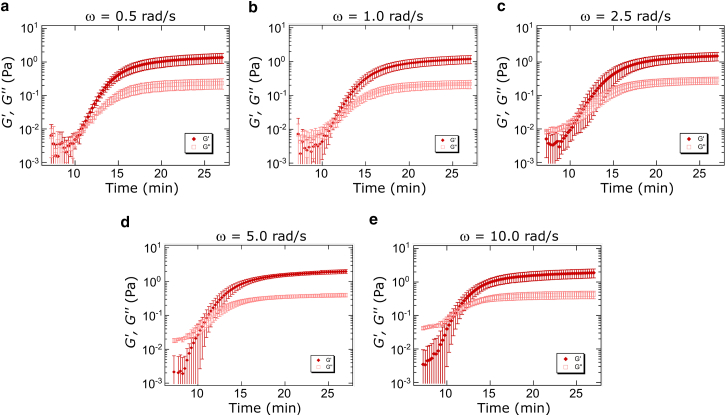
Given the potential frequency-dependence of the crossover time and the possibility of identifying a frequency-independent gelation time through comparison to percolation theory, additional imaging and rheology measurements were performed at ω = 0.5, 2.5, and 10.0 rad/s. In all cases, gel structure and key time points of interest obtained from imaging did not differ significantly as a function of oscillatory rheology frequency with or without accompanying confocal microscopy (Supporting Material, Table S2). Additional measurements were taken without simultaneous imaging, and Fig. 3 shows the time-course of average storage and loss moduli during fibrillogenesis of collagen samples measured at five angular frequencies (ω = 0.5, 1.0, 2.5, 5.0, and 10.0 rad/s). Despite potential frequency dependence, we find that $t_{\text{CO}}^{\text{RHEO}}$ ∼ 11 min for all frequencies with no clear trend as a function of frequency (Supporting Material, Table S2). The lack of frequency dependence may be due to the relatively small frequency range investigated. This frequency range is related to depth of penetration or characteristic length by $l_c={\left(2v/\omega \right)}^{1/2}$, with v as the kinematic viscosity of the medium and ω as the oscillatory frequency (56) (Supporting Material). For the frequency range interrogated here, the penetration depths explored are 1–5 mm. The length scales probed are thus all larger than any dimension of the fibers and the axial dimension of the sample. As such, the crossover time over the frequency range investigated may be assumed to be probing similar structures, those associated with the presence of a network spanning the axial dimension of the sample.

Figure 3.

Time-course of average storage (G′, solid diamonds) and loss (G″, open squares) moduli recorded during fibrillogenesis of 1.0 mg/mL collagen at 25°C. Rheology measurements were performed at five angular frequencies: (a) 0.5 rad/s, (b) 1.0 rad/s, (c) 2.5 rad/s, (d) 5.0 rad/s, and (e) 10.0 rad/s. At each frequency, 4–6 samples were interrogated and error bars represent SD of the measurements. To see this figure in color, go online.

Next, we quantitatively assess the rheological gel point using the critical gelation model (20, 24, 26, 27, 54). Critical gelation through percolation is based on a power-law equation, the gel equation, which describes the relaxation of the modulus of the system near the gelation time, G(t) = St^-Δ, with S a measure of system strength and Δ a power-law scaling exponent. Using this expression together with standard assumptions of viscoelastic theory and a Kramers-Kronig relationship yields the following expressions for the storage and loss moduli:

$$G^{\mathit{\text{'}}}\left(\omega \right)=\frac{\pi }{2\Gamma (\Delta )\text{sin}\left(\frac{\Delta \pi }{2}\right)}S{\omega }^{\Delta }\mathrm{and}{G}^{\mathit{”}}\left(\omega \right)=\frac{\pi }{2\Gamma (\Delta )\text{cos}\left(\frac{\Delta \pi }{2}\right)}S{\omega }^{\Delta },$$ (1)

with Γ as the gamma function (25, 29, 54). These relationships require that around the gelation time, storage and loss moduli will exhibit identical scaling as a function of frequency.

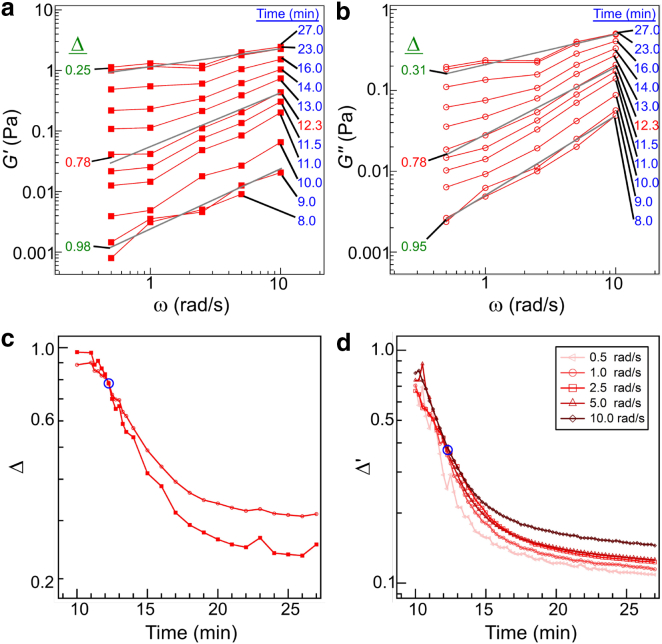
First, gel point was determined as the time point at which viscoelastic impedance spectra of storage, G′(ω), and loss moduli, G″(ω), exhibited the same frequency dependence (20). Fig. 4, a and b, shows log-log plots of the average G′(ω) and G″(ω) curves at multiple time points (t = 8.0–27.0 min) and for five frequencies (ω = 0.5, 1.0, 2.5, 5.0, and 10.0 rad/s), respectively. G′(ω) and G″(ω) curves were fit to a power law (y = aω^Δ). At the gel point, Δ is expected to be identical for G′(ω) and G″(ω). Both the storage and loss moduli as a function of frequency show their steepest slopes (G′ ∼ ω^0.98, G″ ∼ ω^0.95) at the earliest times measured and decrease with increasing time. By 27 min, the slopes have plateaued at G′ ∼ ω^0.25 and G″ ∼ ω^0.31. Similar frequency dependence of storage modulus of fully formed collagen gels has been previously reported (G′ ∼ ω^0.17–0.20) (39, 57). At the earliest times probed, G″ evolves linearly with frequency, consistent with a simple Maxwell model of a viscoelastic material; however, the scaling of G′ is shallower than expected from that model, as has been noted previously in collagen (19) and is distinct from behavior seen in gelatin (31).

Figure 4.

Log-log plot of the average viscoelastic impedance spectra of (a) storage, G′(ω) and (b) loss, G″(ω), moduli at multiple time points (t = 8–27 min) were recorded during fibrillogenesis of 1.0 mg/mL collagen at 25°C obtained from the data also shown in Fig. 3. Lines (gray) represent best fits to G′(ω) and G″(ω) using a power law (y = aω^Δ). (c) Exponent, Δ, of the power law was extracted from G′(ω) and G″(ω) curves as a function of fibrillogenesis time. The intersection at 12.3 min is highlighted (blue circle) and represents the rheological gel point, $t_{\text{GEL}}^{\text{RHEO}}$. (d) Scaling exponent, Δ′, was derived from analysis of tan(δ) curves, which also intersect at 12.3 min. The curve at 0.5 rad/s was noisier than, and deviated from, the other curves, likely due to limited data averaging, as at this frequency only one oscillation is performed for each time point. This curve was thus not considered when finding the intersection point and the value of Δ′. To see this figure in color, go online.

This analysis revealed a time point at which the frequency dependence of the storage and viscous modulus was identical. Here, G′(ω) and G″(ω) both showed a slope of Δ ≈ 0.78 at t = 12.3 min, with this time then defining the rheological gelation point of this network, $t_{\text{GEL}}^{\text{RHEO}}$ (Fig. 4 c). Although within percolation theory such scaling is required, power-law scaling over a small frequency range such as that probed here is not necessarily a robust test; moreover, additional constraints on relative values of G′ and G″ at the gel point are required by Eq. 1. In particular, from Eq. 1 and the definition of phase angle, $\tan \left(\delta \right)=G^{\mathit{”}}\left(\omega \right)/G^{\mathit{\text{'}}}\left(\omega \right)$, it is required that at the gel-point the critical phase angle, δ_c, is given by ${\delta }_c=\Delta \pi /2$. As such, at the gelation time, δ will be frequency independent, and tan(δ) curves plotted versus time will intersect (54). Although the gelation time found in this manner is concurrent with that found using the G′ and G″ scaling shown in Fig. 4, a and c (t = 12.3 min), the exponent (Δ′) is different, with Δ′ = 0.37 (Fig. 4 d).

Given that the scaling exponent may only range from 0 to 1 and has typically been found to vary between 0.5 and 0.8 in physical and chemical gels where percolation theory holds (20, 26, 28, 29, 30, 58, 59), the values obtained from the two approaches are notably different. The discrepancy between the two approaches requires that the prefactor ratio for G′ and G″ is inconsistent with Eq. 1. Because collagen gelation dynamics are highly sensitive to sample concentration and gelation temperature and because early time measurements of the storage moduli were quite noisy, particularly for low frequency measurements, we considered whether the discrepancy between Δ and Δ′ could be related to these issues. However, neither including additional measurements nor excluding measurements that diverged most from the average at early times changed the outcome: in all cases, power-law scaling of storage and loss moduli yielded Δ > 0.70 but the same exponent extracted from tan(δ_c) data was notably lower (<0.45).

Comparison of structural features to critical gelation predictions

Given the inconsistency in identified scaling exponents (Δ versus Δ′) and the potential frequency dependence of crossover time, we cannot identify the sol-gel transition unambiguously using rheology. However, we note that each approach to determining gel point through rheology leads to identification of time points in rather close vicinity, with $t_{\text{CO}}^{\text{RHEO}}$ occurring at ∼11 min and $t_{\text{GEL}}^{\text{RHEO}}$ at 12.3 min. Although $t_{\text{CO}}^{\text{RHEO}}$ and $t_{\text{GEL}}^{\text{RHEO}}$ occur in close vicinity, the arrest time identified through imaging $t_{\text{ARR}}^{\text{CRM}}$ is earlier (∼9 min). The arrest time has previously been associated with the emergence of a system-spanning structure (38) and would thus be expected to occur concurrent with gelation as defined rheologically. It is possible the visual identification of this time point does point to a spanning structure; however, it is also possible it instead represents an earlier event in the gelation process, when fibers are sufficiently large such that their relative motion cannot be detected by eye but a spanning structure is not yet present.

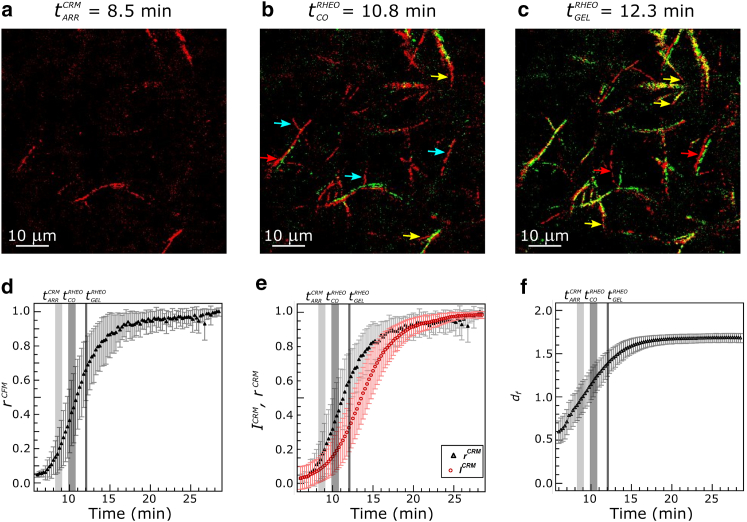
The lack of concordance among $t_{\text{ARR}}^{\text{CRM}}$, $t_{\text{CO}}^{\text{RHEO}}$, and $t_{\text{GEL}}^{\text{RHEO}}$ encourages further investigation of the structure of the network at these times and comparison to structural predictions of percolation theory. Fig. 5, a–c, shows regions of the representative collagen system also shown in Fig. 2 at these key time points and Fig. 5, d–f, shows quantitative assessment of correlation curves of CFM and CRM (r^CFM and r^CRM), intensity of CRM (I^CRM), and fractal dimension of CRM (d_f,slice) averaged over all (n = 9) confocal rheology measurements. Fig. 5 a shows that at $t_{\text{ARR}}^{\text{CRM}}$ some fibers are present, but quantitative assessment shows that no more than 20% of the final value of the correlation coefficients or intensity is present at this time (Fig. 5, d and e). This is true also of the storage modulus, which is <0.01 Pa for lower frequency measurements at this time and smaller (sometimes undetectable) for frequencies >5 rad/s (Fig. 3). These observations suggest that no spanning structure is in place at this time. By the crossover time, further fiber development is evident (red in Fig. 5 b), with some new fibers visualized, some that have increased in length, and some that have shifted position. At this point, ∼20% of the final CRM intensity and ∼40% of the maximum correlation coefficients have developed. Correlation analysis compares intensity of each pixel at each time point to intensity of that pixel at the subsequent time point normalized by the average intensity of the image. This measure is thus sensitive to the initial appearance of structures as well as to changes in the position of structures. It will not be sensitive to changes in intensity that affect the full field of view, such as the increase in CRM signal due to fiber thickening. This is consistent with the faster rise of the correlation coefficients, r^CRM and r^CFM, relative to I^CRM, as well as the similarity of $t_{\text{INC}}^{\text{CFM}}$ and the plateau times of r^CRM and r^CFM (Table 1). At $t_{\text{GEL}}^{\text{RHEO}}$, few new fibers are seen relative to the gel at the crossover time, but the fibers are both longer and brighter than those at crossover, with fiber thickening continuing until ∼20 min, the plateau time associated with I^CRM (Table 1).

Figure 5.

(a–c) Region of the images also shown in Fig. 2 and Movie S1 at (a) $t_{\text{ARR}}^{\text{CRM}}$, (b) $t_{\text{CO}}^{\text{RHEO}}$, and (c) $t_{\text{GEL}}^{\text{RHEO}}$. In each case, on-pixels (defined as intensity count >49) are shown, with red indicating a new on-pixel, green indicating an on-pixel in the image to the left (or, in (a), for the image at t = 1.0 min), and yellow indicating an on-pixel in both images. Blue arrows point to representative new fibers, yellow arrows to lengthening fibers, and red arrows to shifted fibers. (d–f) Time-course of the (d) normalized CFM correlation coefficient, r^CFM; (e) normalized CRM correlation coefficient, r^CRM (solid triangles); normalized CRM intensity, I^CRM (open circles); and (f) d_f,slice obtained from CRM. All were averaged over nine confocal rheology measurements (three at 0.5, 2.5, and 10.0 rad/s each). Error bars are SD. Mean ± SD (n = 9) of $t_{\text{ARR}}^{\text{CRM}}$ and $t_{\text{CO}}^{\text{RHEO}}$ times across samples and $t_{\text{GEL}}^{\text{RHEO}}$ are indicated by gray vertical lines. To see this figure in color, go online.

Table 1.

Key Time Points Associated with Collagen Gelation

Average Time (min ± SD)
	$t_{\text{LAG}}$	$t_{\text{ARR}}^{\text{CRM}}$	$t_{\text{CO}}^{\text{RHEO}}$	$t_{\text{INF}}$	$t_{\text{GEL}}^{\text{RHEO}}$	$t_{\text{INC}}^{\text{CFM}}$	$t_{\text{PL}}$
rCFM	6.3 ± 0.6	—	—	11.2 ± 1.1	—	17.1 ± 1.7a	16.1 ± 2.2
rCRM	6.3 ± 1.2	8.7 ± 0.6b	—	11.5 ± 1.1	—	—	16.8 ± 2.0
ICRM	7.5 ± 1.1	—	—	13.1 ± 1.2	—	—	19.7 ± 1.4
df,slice	2.0 ± 1.1	—	—	8.9 ± 1.1	—	—	15.6 ± 1.5
GRHEO	—	—	10.6 ± 1.1	—	12.3	—	—

Mean ± SD of nine samples monitored with confocal rheology during fibrillogenesis of 1.0 mg/mL collagen at 25°C. All data were obtained from curves indicated in the leftmost column unless otherwise noted, with r^CFM and r^CRM as the CFM and CRM image correlation curves, I^CRM as the CRM intensity curve, d_f,slice as the CRM fractal dimension, and G^RHEO as the rheological storage modulus curve. t_LAG, t_INF, and t_PL correspond to lag, inflection, and plateau time points at which the curves rise to 5, 50, and 95% of their final value, respectively. $t_{\text{CO}}^{\text{RHEO}}$ is the crossover time and $t_{\text{GEL}}^{\text{RHEO}}$ is the gel point extracted from frequency dependent rheology. The p values obtained from two-tailed, unequal variance t-tests comparing all time points are provided in the Supporting Material and Table S4.

^a$t_{\text{INC}}^{\text{CFM}}$ is the time at which oligomeric structures are fully incorporated into fibrillar structures and was extracted from CFM video data.

^b$t_{\text{ARR}}^{\text{CRM}}$ is the time at which fibrillar structures are apparently fixed in position and was extracted from CRM video data.

The multimodal measurements here also allow comparison to structural predictions of percolation theory in and around the gel point. In particular, classical percolation theory predicts the critical gel will have a 3D fractal dimension, d_f,3D, of 2.5 at the gel point (32, 37). Extensions of this theory have led to the prediction

$$d_{f,3D}=\frac{5}{2}\left(2\Delta -3\right)/\left(\Delta -3\right),$$ (2)

for critical gels in 3D (28, 60). The box-counting method of determining fractal dimension on 2D confocal reflectance images returns the d_f,slice evolution shown in Fig. 5 f. At time points before $t_{\text{ARR}}^{\text{CRM}}$, no or very few features are present, and d_f,slice assessment returns an unphysical result <1. However, starting at approximately $t_{\text{ARR}}^{\text{CRM}}$, d_f,slice grows from ∼1.0 to 1.7 by ∼16 min. We interpret these changes as due to the appearance of fibers and their growth in length. The value of d_f,slice increases rapidly across the time regime associated with the sol-gel transition as identified through imaging ($t_{\text{ARR}}^{\text{CRM}}$ ∼9 min) and rheology ($t_{\text{CO}}^{\text{RHEO}}$∼11 min and $t_{\text{GEL}}^{\text{RHEO}}$ = 12.3 min). This continuing evolution suggests that the incipient network associated with the transition evolves rapidly until at least the rheological identification of gelation, with d_f,slice with values of 1.0, 1.26, and 1.44, respectively, at these three time points. As for correlation coefficients and distinct from CRM intensity growth curves, we expect little change in fractal dimension during fiber thickening, explaining the similar plateau times for correlation coefficients and d_f,slice evolution (Table 1).

From Eq. 2, the expected fractal dimension of the collagen networks at the gel point assuming the scaling exponent found from the approach depicted in Fig. 4, a–c (Δ = 0.78), is d_f,3D = 1.6 whereas that obtained from the approach depicted in Fig. 4 d (Δ = 0.37) is d_f,3D = 2.1. Although there is a known relationship between d_f,3D and d_f,slice for the Hausdorff dimension, an alternative approach to describing fractal objects that is computationally challenging to calculate, there is no such established relationship for the Minkowski-Bouligand dimension (61, 62). As such, one cannot immediately compare the fractal dimension obtained through 2D confocal imaging to those predicted from percolation theory. Although the rapidity of gelation does not allow 3D stacks to be collected during the process, we analyzed 2D slices and 3D reconstructions from fully formed gels to find typical relationships between d_f,3D and d_f,slice in these systems (Supporting Material). We note that previous studies have shown correlation between d_f,3D and d_f,slice dimensions, with d_f,3D typically 0.7–1.0 higher than d_f,slice, with the upper limit recalling the relationship between Hausdorff dimension as obtained from 2D and 3D information (61, 62, 63). Our own analysis suggests d_f,3D = d_f,slice + 0.9 (Supporting Material; Fig. S1; Table S3). As such, we conclude that d_f,3D of the gel at $t_{\text{GEL}}^{\text{RHEO}}$ is ∼2.3. This is well over the value predicted from percolation theory (d_f,3D = 1.6) using Eq. 2 and the scaling exponent obtained from frequency dependence of the moduli as well as greater than that from the scaling exponent obtained from the convergence of tan(δ_c). This finding further emphasizes the inconsistency between predictions of percolation theory through critical gelation and measurements of collagen self-assembly.

Discussion

The multimodal measurements performed here reveal inconsistency between collagen self-assembly and the rheological and structural predictions of critical gelation through percolation, and we conclude that the sol-gel transition of collagen at the relatively low concentration of 1.0 mg/mL and relatively low temperature of 25°C does not proceed through critical gelation as described previously (20, 24, 26, 27, 54). This finding is in contrast to some previous rheology-based measurements that showed consistency with percolation theory for collagen gels (19, 64). In particular, Forgacs et al. (19) found that a 1.7 mg/mL collagen gel formed at 12°C and probed rheologically between ∼0.2 and 7.0 rad/s in a manner similar to that used in this study was consistent with percolation theory and yielded Δ = 0.70. Curtis et al. (64) studied collagen gelation through optimal Fourier rheometry, which uses chirped waveforms to probe multiple rheological frequencies simultaneously and is suitable for systems with high strain sensitivity. Using this approach and probing frequencies of ∼6.0–60.0 rad/s, Curtis et al. (64) found that collagen gels prepared at 28°C exhibited consistency with percolation theory and concentration-dependent scaling exponents, with Δ ∼ 0.82 for a 4 mg/mL gel and Δ ∼ 0.62 for an 8 mg/mL gel. We propose that discrepancy between our finding and the studies cited above can be attributed to the fact that gelation at the concentration and temperature explored in this study leads to thick fiber, large pore size, heterogeneous hydrogels compared to AS collagen gelation at higher temperatures, and/or concentrations (39, 65). The conditions used in this study were chosen to facilitate identification of the time at which a system-spanning structure was first present, a challenge in higher concentration systems and/or those gelled at higher temperature. Higher-concentration, higher-gelation temperature collagen gels are more homogeneous and have smaller pore size, structural characteristics more similar to those present in chemical gels where percolation theory has been more regularly and successfully applied. Indeed, complex networks—in particular physical and/or thermoreversible gels—have been found to show less consistency with critical gelation theory than chemically cross-linked gels. In one case, rheology was used to study the gelation of the bacterial polyester poly(β-hydroxyoctanoate). The system was found to go through the sol-gel transition in a manner consistent with critical gelation at some temperatures, but at others it apparently went through the sol-gel transition without passing through a stage with the self-similar structure of a critical gel (66). The authors proposed that at these temperatures slow nucleation led to long-range heterogeneity that in turn led to failure to pass through a critical gel, a situation highly analogous to the low-concentration, low-temperature collagen gelation studied here.

Beyond differences in concentration and gelation temperature between this and previous studies, a key difference in this study is the multimodal approach that allowed simultaneous assessment of mechanical properties and network structure during gelation, providing additional measures with which to compare the gelation process to predictions of critical gelation theory. In addition to finding collagen gelation is inconsistent with predictions of percolation theory that can be tested through rheology, simultaneous imaging provides additional evidence that collagen gelation is inconsistent with percolation through a critical gel. In particular, we find higher than expected fractal dimension for networks over the time regime when a network spanning structure is first present relative to that predicted by percolation theory extended to be applicable to polymeric gelation. Indeed, we find values for fractal dimension in this time range more similar to those predicted by classic percolation theory (d_f,3D = 2.5). Perhaps to describe collagen gelation the simpler picture of classic percolation with a set of rigid rods is more appropriate than theory developed for flexible chains with flexible bonds, as also reflected by recent modeling of the origin of strain stiffening in collagen gels (44, 46).

Conclusions

In this study, we used simultaneous CRM, CFM, and rheology to probe the structural and mechanical evolution of collagen I through the sol-gel transition. Direct comparison of data recorded by microscopy and rheology allows evolving structure on the fiber and network length scales to be correlated with evolving viscoelastic properties. Such measurements provide a detailed picture of the developing gel structurally: after neutralization, numerous fibers form and grow rapidly in length, with fiber lengthening and thickening occurring concurrently and fiber thickening continuing through the end of the gelation process. The confocal rheometer measurements also allow careful comparison to rheological and structural predictions of critical gelation theory. Rheology suggested the presence of a spanning structure for the 1.0 mg/mL collagen gels assembled at 25°C studied here at 12.3 min, with storage and loss moduli both displaying power-law scaling with a scaling exponent of Δ = 0.78 at that time; however, the ratio of the moduli at that time suggested a much lower value of the scaling exponent. This inconsistency with percolation theory was reinforced by the finding that the fractal dimension was higher than that predicted by the theory at this time point. Despite notable differences between our findings and predictions of percolation theory, aspects of the sol-gel transition described by percolation theory appear relevant for the collagen gelation process: for example, relatively early in gelation, a system-spanning structure exists that acts as a template for additional growth, through lengthening and thickening of fibers rather than through new fiber formation. The dual rheological and structural measurements performed here served as a critical test-bed for percolation theory in the case of collagen gelation. More broadly, this study demonstrates the utility of confocal rheology for quantitative characterization of evolving viscoelastic and structural properties of complex systems, measurements that can address fundamental questions and suggest paths to controlling properties of self-assembling systems.

Author Contributions

K.-H.T.-B., J.Z., and L.J.K. designed the project. K.-H.T.-B. and J.Z. collected data. K.-H.T.-B., D.J.L., J.Z., and L.J.K. contributed analytical tools. K.-H.T.-B., D.J.L., and L.J.K. analyzed data. K.P. designed and tested the confocal rheometer. K.-H.T.-B. and L.J.K. wrote the manuscript.

Editor: Celeste Nelson.

Supporting Material

Movie S1. Video Showing Simultaneous Rheology, CFM, and CRM Recorded during Gelation of a 1.0 mg/mL Collagen Gel Self-Assembling at 25°C

This sample is the same sample from which the images in Figs. 2 and 5 in the main text are obtained. The storage, G′, and loss, G″, moduli were measured at 10.0 rad/s. Each point in oscillatory rheology was collected and averaged over 15 s and the interval between images was also 15 s. Playback speed is 1 frame/s. The video reflects data recorded at t = 7–27 min. Simultaneous rheology shown in left panel, CFM shown in center panel, and CRM shown in right panel.