Molecular Simulations Suggest a Force-Dependent Mechanism of Vinculin Activation

Abstract

Focal adhesions are dynamic constructs at the leading edge of migrating cells, linking them to the extracellular matrix and enabling force sensing and transmission. The lifecycle of a focal adhesion is a highly coordinated process involving spatial and temporal variations of protein composition, interaction, and cellular tension. The assembly of focal adhesions requires the recruitment and activation of vinculin. Vinculin is present in the cytoplasm in an autoinhibited conformation in which its tail is held pincerlike by its head domains, further stabilized by two high-affinity head-tail interfaces. Vinculin has binding sites for talin and F-actin, but effective binding requires vinculin activation to release its head-tail associations. In migrating cells, it has been shown that the locations of vinculin activation coincide with areas of high cellular tension, and that the highest recorded tensions across vinculin are associated with adhesion assembly. Here, we use a structure-based model to investigate vinculin activation by talin modulated by tensile force generated by transient associations with F-actin. We show that vinculin activation may proceed from an intermediate state stabilized by partial talin-vinculin association. There is a low-force regime and a high-force regime where vinculin activation is dominated by two different pathways with distinct responses to force. Specifically, at zero or low forces, vinculin activation requires substantial destabilization of the main head-tail interface, which is rigid and undergoes very limited fluctuations, despite the other being relatively flexible. This pathway is not significantly affected by force; instead, higher forces favor an alternative pathway, which seeks to release the vinculin tail from its pincerlike head domains before destabilizing the head-tail interfaces. This pathway has a force-sensitive activation barrier and is significantly accelerated by force. Experimental data of vinculin during various stages of the focal adhesion lifecycle are consistent with the proposed force-regulated activation pathway.

Introduction

Cell migration is a fundamental process in embryonic development, wound healing, and cancer metastasis. It involves the coordination of a series of events: initiating protrusion at the cell front, forming focal adhesions (FAs) with the underlying extracellular matrix, anchoring the actin network on the adhesion, generating contractile force to pull the cell body forward, and breaking adhesions at the cell rear. FAs anchor the cell to the extracellular matrix through transmembrane adhesion receptor integrins and play a central role in cell migration (1, 2). FAs arise from small dotlike nascent adhesions within the lamellipodium that have only transient stability (3), and undergo myosin II-dependent maturation into large streaklike structures within the lamella. During FA maturation, FA proteins are hierarchically recruited to the FA sites (3) and assemble into a sophisticated network of protein-protein interactions that links integrins to the actin cytoskeleton. In this network, each discrete adhesion site functions as a mechanosensitive hub where talin interacts directly with integrins and F-actin and vinculin performs core regulatory activities through interactions with talin, F-actin, and other FA molecules. The FA lifecycle is largely regulated by cellular forces generated by the actomyosin machinery that display strong spatiotemporal variations (4, 5, 6). The areas of highest cellular tension normally correspond to sites of FA assembly. Measurements at the single-molecule level also reveal a wide range of forces from a few pN for intracellular FA proteins such as talin (7) and vinculin (8), to higher forces that can exceed 50 pN at the extracellular domains of integrin receptors (9, 10, 11).

Talin is a large protein containing an N-terminal integrin-binding domain, a C-terminal actin-binding domain, and multiple vinculin binding sites (VBSs), which are single helices normally buried within talin’s helical bundles (12, 13, 14). During the initial stage of FA formation, talin provides a weak link (∼2 pN) between integrins and the cytoskeleton (15, 16). Tension across the talin rod exposes some of its VBSs (12, 17, 18). These VBSs participate in recruiting vinculin to FA sites via low-affinity binding, and keep vinculin in place for possible associations with F-actin (19). Upon recruitment to FAs, vinculin remains in an inactive conformation (20, 21) with only low affinity for talin and F-actin. During FA maturation, vinculin undergoes activation. Active vinculin forges strong links between talin and F-actin and stabilizes integrins in a high-affinity, ligand-binding state (22, 23).

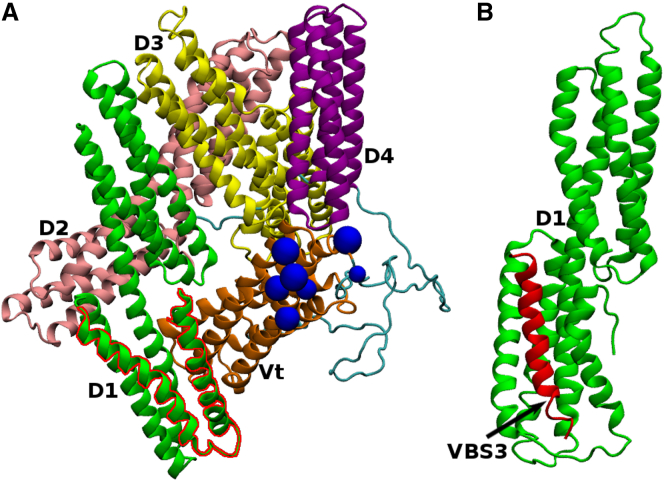
Vinculin is a globular molecule of 1066 residues (24). It consists of five α-helical bundle domains, D1, D2, D3, D4, and the vinculin tail (Vt), from the N-terminus to the C-terminus (Fig. 1 A). The first four domains, D1–D4, constitute the vinculin head (Vh), which is joined by a proline-rich linker to Vt. The N-terminal four-helix bundle of D1 binds talin VBSs to form a five-helix bundle in a process termed “helical bundle conversion”, during which the VBS is inserted into the hydrophobic groove between α1 and α2, causing a conformational change in D1 and a distortion of the D1-Vt interface (25). In native vinculin, the talin binding site on D1 is readily accessible to talin VBSs (24, 26), but the proximity of Vt to Vh allows only low-affinity talin-vinculin association. Vt contains two actin binding interfaces, of which one is exposed in native vinculin and contacts a highly charged area of actin (27). In particular, the mutation on residue 1049 of the exposed interface from arginine (basic) to glutamic acid (acidic) impairs the ability of vinculin to bind F-actin and impacts cell migration (28).

Figure 1.

Crystal structures of (A) native vinculin and (B) D1 in complex with a VBS3 peptide. (A) Shown here is native vinculin in its autoinhibited conformation (PDB: 1TR2). Individual domains D1–D4 and Vt are labeled and shown in different colors. (Blue beads) Seven residues of Vt that constitute the binding interface exposed to F-actin are as suggested in (27). (Red traces) Shown here are the first two helices α1 and α2 of D1 that open up for full VBS3 insertion. (B) Given here is vinculin domain D1 in complex with VBS3 (PDB: 1RKC). The N-terminal bundle of D1 is in a helical-bundle converted structure to accommodate full VBS3 insertion. Protein structures were rendered with the software VMD. To see this figure in color, go online.

Native vinculin adopts an inactive globular conformation, in which the first three domains (D1–D3) form a pair of pincers holding Vt tight in place, and high-affinity head-tail associations resulting from D1-Vt to D4-Vt contacts maintain vinculin in its autoinhibited state (29). Vinculin activation is the process of disrupting the head-tail associations. It is currently accepted that vinculin cannot be activated by talin (VBSs) or F-actin alone, but requires the combinatorial input of both ligands (19, 30, 31, 32). Autoinhibited vinculin has binding sites partially accessible to talin and F-actin; therefore, before activation, vinculin may bind talin with low affinity and localize at sites of FA assembly for possible weak or transient associations with F-actin. Indeed, in the leading-edge lamella, vinculin motion is directionally coupled with F-actin retrograde flow, and transient linkages across the actin-vinculin slippage interfaces are considered as a source of force transduction (5, 33, 34, 35). Furthermore, throughout the FA lifecycle, FA assembly is a stage associated with the highest tension across vinculin (8), indicating the important role of force in regulating vinculin activity during FA assembly. Thus, although talin alone is only able to weakly associate with vinculin to keep it in place, F-actin retrograde flow may generate effective tensile force through transient contacts with vinculin, which may serve as an additional input and lead to vinculin activation.

Force-induced unfolding has been widely studied on single-domain proteins experimentally (36, 37, 38, 39, 40, 41), theoretically (42, 43, 44), and by simulation (45, 46, 47, 48, 49). A commonly observed phenomenon that has drawn much attention is a marked turnover found in force-dependent unfolding rates of many proteins, suggesting that mechanical unfolding is not always a smooth distortion of the zero force free-energy landscape (46). Less has been studied for multidomain proteins, for which force-induced domain dissociation may involve a switch from the zero-force mechanism. In the case of vinculin activation, it remains to be shown if tensile force assists talin by continuously lowering the activation barrier, or diverting activation along a different pathway on the free-energy landscape by first weakening the more force-sensitive interdomain interactions.

Here, we use a structure-based model (SBM) to investigate how force across vinculin may help talin in vinculin activation. The model consists of a VBS3 (a VBS from the 10th helical bundle domain of the talin rod) and a full-length vinculin with a dual-basin potential to account for the structural difference between active and autoinhibited conformations. Partial association between VBS3 and D1 in a stable intermediate state enables force transmission across autoinhibited vinculin resulting from transient actin associations. Based on free-energy landscape theory, we show that under zero or low tensile forces, vinculin activation requires substantial destabilization of the D1-Vt interface. The kinetic bottleneck results from the fact that the strong and rigid D1-Vt interface undergoes very limited scale of fluctuations necessary for activation. Higher forces have no strong impact on the D1-Vt interface, but open up a novel pathway that seeks to destabilize the pincerlike constraints of the vinculin head on its tail. This novel activation pathway is highly sensitive to force. Based on further support from kinetic data over a range of forces, we predict that, in an environment of high mechanical tension, this force-sensitive pathway is the dominant pathway for vinculin activation. Finally, we use a cartoon model to illustrate the vinculin activation mechanisms discussed in this work, and relate them to the widely accepted combinatorial activation mechanism.

Methods

Structure-based model and dual-basin interaction potential

A structure-based model was built for a bimolecular system consisting of a full-length vinculin and a VBS3 helix with energetic minima derived from reference structures corresponding to different states of vinculin. All heavy (i.e., nonhydrogen) atoms were included and each atom was represented as a single bead of unit mass. The five vinculin domains were defined as follows: D1, residues 1–252; D2, residues 253–485; D3, residues 493–717; D4, residues 719–836; and Vt, residues 894–1066. Bond lengths, bond angles, improper dihedrals, and planar dihedrals were maintained by harmonic potentials. Proper dihedrals were given a weak torsional potential. Nonbonded atom pairs that are in contact in the reference structures were given an attractive Gaussian potential (50). All other pairwise interactions were repulsive to maintain excluded volume.

The contact pairs for nonbonded interaction were defined by the Shadow algorithm (51) using a 6 Å cutoff and 1 Å atomic radius. Torsional and nonbonded interaction potentials were parameterized with energetic minima derived from active or autoinhibited states of vinculin. The interaction parameters for autoinhibited vinculin (referred to as “topology A”) were based on the crystal structure of human vinculin (PDB: 1TR2; Fig. 1 A); (24), with the missing proline-rich loop region completed by MODELER (52). The interaction parameters for the D1-VBS3 complex (referred to as “topology B”) were taken from the crystal structure of the human vinculin D1 domain in complex with VBS3 (PDB: 1RKC; Fig. 1 B) (25). Topologies A and B were combined and a dual-basin topology was used for D1 to account for its conformational change upon binding VBS3. The resulting model has 416 contacts on the Vh-Vt interface (269 on D1-Vt, 25 on D2-Vt, 37 on D3-Vt, and 85 on D4-Vt) and 325 contacts on the D1-VBS3 interface. The interaction potential is

$$V_{\text{SBM}}=\sum _{ij\in \left\{\text{bonds}\right\}}{\mathit{ϵ}}_r{\left(r_{ij}-r_{ij}^0\right)}^2+\sum _{ijk\in \left\{\text{angles}\right\}}{\mathit{ϵ}}_{\theta }{\left({\theta }_{ijk}-{\theta }_{ijk}^0\right)}^2+\sum _{ijkl\in \left\{\text{impropers}/\text{planar}\right\}}{\mathit{ϵ}}_{\chi }{\left({\chi }_{ijkl}-{\chi }_{ijkl}^0\right)}^2+\sum _{ijkl\in \left\{\text{backbone}\right\},A\cap B}{\mathit{ϵ}}_{BB}{F}_D\left({\varphi }_{ijkl},{\varphi }_{ijkl}^A,{\varphi }_{ijkl}^B\right)+\sum _{ijkl\in \left\{\text{backbone}\right\},A-B}{\mathit{ϵ}}_{BB}{F}_D\left({\varphi }_{ijkl},{\varphi }_{ijkl}^A\right)+\sum _{ijkl\in \left\{\text{backbone}\right\},B-A}{\mathit{ϵ}}_{BB}{F}_D\left({\varphi }_{ijkl},{\varphi }_{ijkl}^B\right)+\sum _{ijkl\in \left\{\text{side}\text{chains}\right\},A\cap B}{\mathit{ϵ}}_{SC}{F}_D\left({\varphi }_{ijkl},{\varphi }_{ijkl}^A,{\varphi }_{ijkl}^B\right)+\sum _{ijkl\in \left\{\text{side}\text{chains}\right\},A-B}{\mathit{ϵ}}_{SC}{F}_D\left({\varphi }_{ijkl},{\varphi }_{ijkl}^A\right)+\sum _{ijkl\in \left\{\text{side}\text{chains}\right\},B-A}{\mathit{ϵ}}_{SC}{F}_D\left({\varphi }_{ijkl},{\varphi }_{ijkl}^B\right)+\sum _{ij\in \left\{\text{contacts}\right\},A\cap B}{V}_G\left(r_{ij},r_{ij}^A,r_{ij}^B\right)+\sum _{ij\in \left\{\text{contacts}\right\},A-B}{V}_G\left(r_{ij},r_{ij}^A\right)+\sum _{ij\in \left\{\text{contacts}\right\},B-A}{V}_G\left(r_{ij},r_{ij}^B\right)+\sum _{ij\in \left\{\text{noncontacts}\right\}}{\mathit{ϵ}}_{\text{NC}}{\left(\frac{r_{\text{NC}}}{r_{ij}}\right)}^{12}.$$ (1)

Here the single-basin dihedral potential is

$$F_{\text{D}}\left(\varphi ,{\varphi }^0\right)=\left[1-\text{cos}\left(\varphi -{\varphi }^0\right)\right]+\frac{1}{2}\left[1-\text{cos}\left(3\left(\varphi -{\varphi }^0\right)\right)\right]$$ (2)

and the dual-basin dihedral potential F_D($\varphi$,${\varphi }^{\mathit{A}}$,${\varphi }^{\mathit{B}}$) is constructed with two single-basin branches connected by fourth-order polynomials such that each basin at ${\varphi }^{\mathit{A}}$ or ${\varphi }^{\mathit{B}}$ locally resembles the single-basin potential (Eq. 2) at ${\varphi }^0$. The single-basin Gaussian contact potential is

$$V_G\left(r,r^0\right)={\mathit{ϵ}}_C\left\{\left[1+\frac{1}{{\mathit{ϵ}}_C}{\mathit{ϵ}}_{\text{NC}}{\left(\frac{r_{\text{NC}}}{r}\right)}^{12}\right]\left[1+G\left(r,r^0\right)\right]-1\right\},$$ (3)

where $G\left(r,r^0\right)=-\text{exp}\left\{-{\left(r-r^0\right)}^2/\left[2\sigma {\left(r^0\right)}^2\right]\right\}$, $\sigma \left(r^0\right)=0.2r^0/{\left[2\text{log}\left(2\right)\right]}^{\left(1/2\right)}$. The dual-basin Gaussian contact potential is

$$V_{\text{G}}\left(r,r^{\text{A}},r^{\text{B}}\right)={\mathit{ϵ}}_{\text{C}}\left\{\left[1+\frac{1}{{\mathit{ϵ}}_{\text{C}}}{\mathit{ϵ}}_{\text{NC}}{\left(\frac{r_{\text{NC}}}{r}\right)}^{12}\right]\left[1+G\left(r,r^{\text{A}}\right)\right]\left[1+G\left(r,r^{\text{B}}\right)\right]-1\right\}.$$ (4)

The superscripts A and B correspond to topology A (autoinhibited vinculin) and topology B (D1 in complex with VBS3), respectively. A–B stands for the set of dihedrals or contacts found exclusively in topology A; B–A stands for the set of dihedrals or contacts found exclusively in topology B; and A∩B stands for the dual-basin topology of the D1 domain. Because bond lengths, bond angles, and improper dihedrals are close between the two topologies, the superscript 0 in the first three terms of Eq. 1 stands for the values corresponding to either A or B and those values are taken from topology A in practice. The parameters used are: ϵ_r = 10,000ϵ/nm², ϵ_θ = 20ϵ, ϵ_χ = 10ϵ, ϵ_NC = ϵ, and r_NC = 2.1 Å, where ϵ is the reduced energy unit. The values ϵ_BB, ϵ_SC, and ϵ_C are chosen as in (49), and this choice gives k_BT_F ≈ ϵ. Here, the folding temperature T_F is defined by the peak in the heat capacity C_V of Vt in Fig. S1.

Simulation details

All the simulations were run using Langevin dynamics implemented by the stochastic dynamics integrator in the GROMACS 4.5 software package (53). The GROMACS units were interpreted as reduced units. The time step was 0.002. Temperature was controlled through stochastic dynamics with a coupling constant of 1. The GROMACS topology files for use with the SBM were generated with the SMOG webserver (54).

Constant force pulling

To implement constant force pulling, two pulling groups were defined. One group consists of the Cα atoms of VBS3. The other group consists of the Cα atoms of seven residues (963, 966, 967, 970, 978, 1049, and 1051) of Vt that constitute the actin binding interface exposed in native vinculin as suggested by Janssen et al. (27). Constant forces of the same magnitude and opposite directions were applied on the two pulling groups and evenly distributed over their Cα atoms.

Calibration of temperature and force

Temperatures in the SBM were mapped to experimental temperatures by relating the folding temperature T_F of Vt to that found experimentally. The T_F of Vt was found by simulations using the Vt topology separated from the full model to be 1.04 reduced temperature units, whereas it was determined experimentally to be 67°C (55) or 340 K. Accordingly, experimental room temperature (taken as 25°C) would correspond to 0.91 (0.88T_F) in the SBM. Thus, we performed SBM simulations at 0.88T_F, and individual vinculin domains stayed folded in all the simulations. When characterizing the thermodynamic properties of a system, force and temperature are comparable through energy. Thus, force mapping can be obtained from temperature mapping using energy as a bridge, giving the correspondence of a reduced force unit in the SBM to ∼5 pN. Details can be found in (49).

Umbrella sampling and free-energy profiles

To effectively study the thermodynamic properties, we performed umbrella sampling on four coordinates: the number of contacts N_D1-VBS3 formed on the D1-VBS3 interface, and three distances DistA, DistB, and DistC accounting for the degree of separation of the D1-Vt, D4-Vt, and D1-VBS3 interfaces, respectively (Fig. 2). DistA, DistB, and DistC were each defined using the pair of Cα atoms that has the shortest contact distance among all the Cα-Cα contacts in the bound complex (crystal structure) of the interface. All umbrella potentials were harmonic and tuned with different spring constants and minima to ensure that all the important transitions were sufficiently sampled. The reweighted free energy was then calculated using the weighted histogram analysis method (49, 56). Independent umbrella sampling simulations were carried out at no pulling force and 10 pN pulling force, respectively. The free-energy landscapes under 10 pN were then extrapolated to higher forces by perturbing the energy function using the weighted histogram analysis method. Details of the trajectories and parameters used can be found in Tables S1 and S2.

Figure 2.

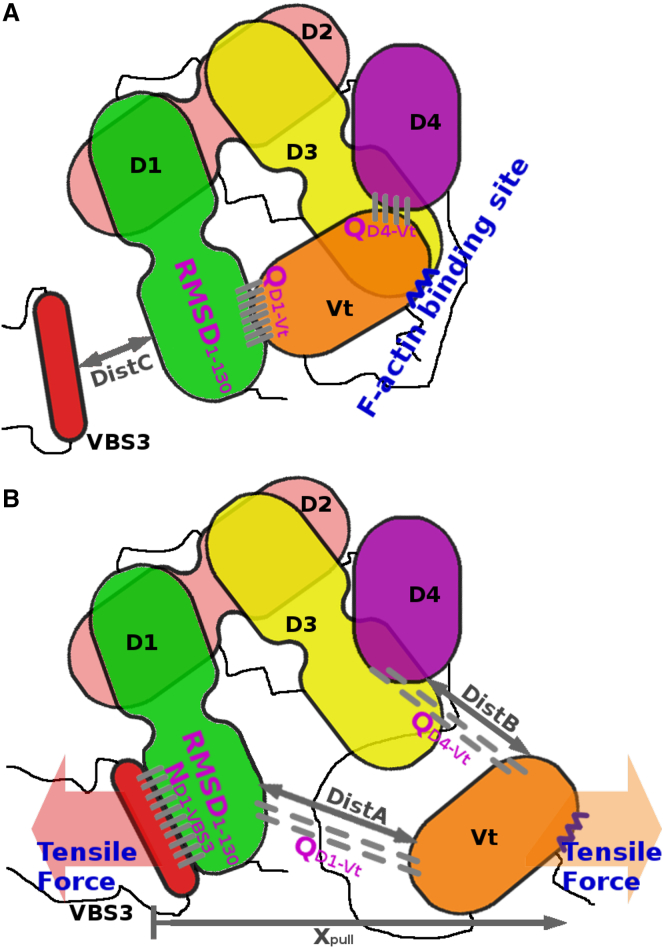
The model system in cartoon representation with reaction coordinates illustrated. The molecular system consists of a full-length vinculin molecule and a VBS3 peptide. Individual vinculin domains and VBS3 are labeled and colored consistently with Fig. 1. Two-bundle domains (D1–D3) and one-bundle domains (D4 and Vt) use different representations. Reaction coordinates are illustrated and labeled. Main reaction coordinates are labeled in magenta: N_D1-VBS3, cutoff-based number of contacts formed on the D1-VBS3 interface; RMSD_1–130, root-mean-square deviation of the backbone atoms of the N-terminal bundle of D1 from its native conformation; Q_D1-Vt, continuous fraction of contacts formed on the D1–Vt interface; and Q_D4-Vt, continuous fraction of contacts formed on the D4-Vt interface. Q_D1-Vt and Q_D4-Vt are defined for their respective binding interface to be effective for both contact formation in bound states and distance in dissociated states. Auxiliary and umbrella coordinates are also labeled: X_pull, the vector connecting VBS3 and the exposed actin binding interface of Vt projected onto the pulling direction; and DistA, DistB, and DistC, umbrella coordinates accounting for separation of the D1-Vt, D4-Vt, and D1-VBS3 interfaces, respectively. They are defined as distances between three pairs of Cα atoms from vinculin residues 25 (D1) and 945 (Vt) (DistA), vinculin residues 775 (D4) and 973 (Vt) (DistB), and vinculin residue 50 (D1) and the 13th residue of VBS3 (DistC). Coordinates are illustrated for (A) autoinhibited native vinculin and a dissociated VBS3, and (B) active vinculin with VBS3 fully bound. Some coordinates are shown in both states but have different typical values: (A) RMSD_1–130 ≈ 0.15 nm, Q_D1-Vt ≈ 0.5, and Q_D4-Vt ≈ 0.5; and (B) RMSD_1–130 ≈ 0.3 nm, Q_D1-Vt ≈ 0, and Q_D4-Vt ≈ 0. To see this figure in color, go online.

Reaction coordinates monitoring interdomain interfaces

Monitoring binding/unbinding on an interdomain interface requires two complementary indicators: the fraction of contacts formed (defined by the crystal structure of the bound state) when the two domains are in contact, and the distance between the two domains when they are dissociated. Here we aimed to design a reaction coordinate to effectively capture both indicators. Suppose that the interface has N_c native contacts, and the νth contact is associated with a native distance of r_ν⁰. Then we defined the continuous number of native contacts formed in a configuration $\mathcal{S}$ as

$$N^{\gamma }\left(\mathcal{S}\right)=\sum _{\nu }^{N_c}\frac{1}{2}\left\{1-\text{tanh}\left[\gamma \left(r_{\nu }^{\mathcal{S}}-1.2r_{\nu }^0\right)\right]\right\}$$ (5)

and the continuous fraction of native contacts is then $Q^{\gamma }\left(\mathcal{S}\right)=\left(1/N_c\right)N^{\gamma }\left(\mathcal{S}\right)$ (57). The parameter γ modulates the smoothness and steepness. Setting γ to infinity reproduces the cutoff-based discrete number of native contacts $N^{\infty }\left(\mathcal{S}\right)={\sum }_{\nu }^{N_c}\left[1-\text{Θ}\left(r_{\nu }^{\mathcal{S}}-1.2r_{\nu }^0\right)\right]$ (where Θ is the Heaviside step function) and loses unbound states, whereas using a too small γ compromises the resolution for bound states. We found that setting $\gamma =1$ effectively captures both the contact and the distance indicators of an interface, and accordingly defined two reaction coordinates Q_D1-Vt and Q_D4-Vt for the D1-Vt and D4-Vt interfaces, respectively.

Results and Discussion

To study vinculin activation, we built a model using atomic coordinates and interaction parameters from two separate crystal structures, full-length human vinculin (PDB: 1TR2; Fig. 1 A) (24) and the human vinculin D1 domain in complex with VBS3 of talin (PDB: 1RKC; Fig. 1 B) (25) for the autoinhibited and active states of vinculin, respectively. The resulting model, consisting of a full-length vinculin and a VBS3 helix, captures several important structural aspects of vinculin autoinhibition and vinculin-VBS3 binding. It contains a Vh-Vt interface of 416 contacts and a D1-VBS3 interface of 325 contacts. Individual Vh domains show distinct contact strengths with Vt, resulting in two major interfaces D1-Vt (269 contacts) and D4-Vt (85 contacts), and two minor interfaces D2-Vt (25 contacts) and D3-Vt (37 contacts). The dual-basin topology for D1 effectively accounts for the conformational change of D1 upon binding VBS3.

Parameterizing the head-tail interface for vinculin autoinhibition

The mechanism of vinculin activation is closely related to the affinities of various intramolecular or intermolecular interfaces (29, 31). Although VBS3 alone is unable to tightly bind or activate full-length vinculin (31), it has been shown that VBS3 can displace Vt from the D1-Vt complex to form a new D1-VBS3 complex (25). We therefore assessed whether our model can correctly reflect the relative affinities of the D1-VBS3, D1-Vt, and Vh-Vt interfaces by studying the free-energy profiles for binding between 1) VBS3 and full-length vinculin, and 2) VBS3 and the D1-Vt complex. The coordinates and interaction parameters for the D1-Vt complex were extracted from those of the full-length vinculin. We used the cutoff-based number of contacts formed on the D1-VBS3 interface, N_D1-VBS3, to monitor the degree of D1-VBS3 association (Fig. S2). Common to both systems (Fig. S2, A and B), the free-energy projection on N_D1-VBS3 displays three stages of D1-VBS3 association, corresponding to dissociated, partially bound and fully bound states. The partially bound state has roughly half of the D1-VBS3 contacts formed. The fully bound state matches the crystal structure of VBS3 in complex with D1. Based on experimental data for VBS3 binding to full-length vinculin (31) and to the D1-Vt complex (25), we expect 1) the partially bound state to be more likely than the fully bound state for VBS3 binding to full-length vinculin (Fig. S2 A), and 2) the fully bound state more likely than the partially bound state for VBS3 binding to D1-Vt (Fig. S2 B). Using the current interaction parameters, we found that the partially bound state is overstabilized in both systems (Fig. S2; dashed black line). Therefore, we used a scaling factor α to lower the energy per contact formed between Vt and Vh. We calculated the free-energy profiles using different values of α ranging from 1.0 to 0.5 (Fig. S2), and found that the expected relative stabilities between the partially and fully bound states are produced by using α = 0.6. Therefore, α = 0.6 became the choice to model the head-tail autoinhibitory interface of vinculin and is consistently used in this study.

Autoinhibited vinculin partially binds VBS3 to form a stable complex while further activation is prohibited

Investigation of the different stages of D1-VBS3 association and vinculin activation requires a set of reaction coordinates that consider the various structural aspects of interest (Fig. 2). Previously, we used N_D1-VBS3 to monitor the degree of D1–VBS3 association. Another structural event accompanying full D1-VBS3 binding is a helical bundle conversion of the N-terminal D1. This can be captured by RMSD_1–130, the root-mean-square deviation of the backbone atoms of the N-terminal bundle of D1 from its native conformation. Small and large values of RMSD_1–130 correspond to states before and after the helical bundle conversion, respectively. Finally, vinculin activation involves the dissociation of Vt from Vh by breaking the Vh-Vt contacts (mainly on D1-Vt and D4-Vt interfaces) and displacing Vt away from Vh. For a given interdomain interface, we looked for a reaction coordinate that could provide a measure of the fraction of contacts formed when the two domains are in contact, and the interdomain distance when the two domains are dissociated. Thus, we defined reaction coordinates Q_D1-Vt and Q_D4-Vt for the D1-Vt and D4-Vt interfaces, respectively (see Methods). Both coordinates range from zero (dissociated and far apart) to ∼0.5 (bound).

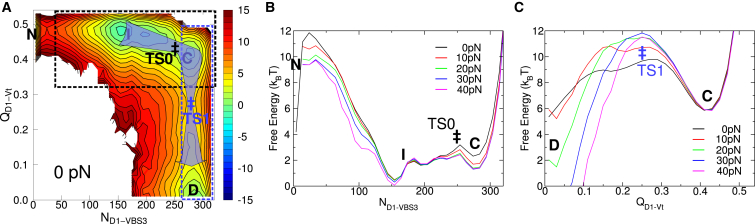
We used different combinations of the four coordinates to build 2D free-energy profiles and identified four distinct states, i.e., the native state N, the inactive intermediate state I, the helical-bundle converted state C, and the dissociated active state D (Fig. 3). Different states are easily distinguished using structural signatures provided by the reaction coordinates. State N is characterized by an almost zero N_D1-VBS3 and displays native features of vinculin (RMSD_1–130 ≈ 0.15 nm and Q_D1-Vt and Q_D4-Vt both ∼0.5). State I is characterized by N_D1-VBS3 ≈ 150 (roughly half of the total number of contacts 325) but has RMSD_1–130, Q_D1-Vt, and Q_D4-Vt unchanged from N. State C is characterized by N_D1-VBS3 ≈ 300 (close to the total number 325) associated with a larger RMSD_1–130 ≈ 0.3 nm, a slight drop of Q_D1-Vt from ∼0.5 to ∼0.4, and an unchanged Q_D4-Vt from I. State D is characterized by both Q_D1-Vt and Q_D4-Vt close to zero and has both N_D1-VBS3 and RMSD_1–130 unchanged from C.

Figure 3.

Free-energy profiles for vinculin activation by VBS3 alone, under zero force. Each 2D profile uses a coordinate monitoring D1-VBS3 association (N_D1-VBS3 or RMSD_1–130) and a coordinate monitoring Vh-Vt dissociation (Q_D1-Vt or Q_D4-Vt). Four states N, I, C, and D are labeled. Initial bimolecular binding is marked with a vertical double asterisk. Helical bundle conversion TS0 and activation transition TS1 are marked with asterisks. N_D1-VBS3 and RMSD_1–130 are similar except that N_D1-VBS3 is able to distinguish between states N and I (A and C) whereas RMSD_1–130 is not (B and D). Color bars: free energy in units of k_BT. To see this figure in color, go online.

The transitions between states from N to D can be viewed as two sequential processes of different natures. The N → I transition is a concentration-dependent bimolecular binding reaction as a result of the accessibility of the talin binding site on D1 (helices α1 and α2). The following process, I → C → D, consists of concentration-independent conformational changes within a single vinculin-VBS3 complex. The concentration of the reactants determines the population of state I, but does not change the relative populations or transitions between states I, C, and D, which was supported by studying the free-energy profiles on $DistC$ with an approximate treatment of concentration as a harmonic potential between VBS3 and D1 (Fig. S3). Therefore, we ignored the effect of concentration for the remainder of the analysis.

In intermediate state I, vinculin and VBS3 form a relatively stable complex, as a free-energy barrier of >10 k_BT prohibits the I → N transition (Fig. 3, A and C; Figs. S2 and S3). State I is stabilized by the contacts made between D1 and the N-terminal half of VBS3 (Fig. S4), in agreement with the one observed by Golji et al. (58) stabilized by hydrophobic contacts between autoinhibited vinculin and the N-terminal VBS. In state I, Vt remains tightly bound to Vh as Q_D1-Vt and Q_D4-Vt are not affected by VBS3 attachment. Further D1-VBS3 binding causes a helical bundle conversion in D1 and accordingly a slight destabilization of the D1-Vt interface (state C). Vinculin activation could proceed from state C with the destabilized Vh-Vt interface and reach state D, but this process is kinetically prohibited and thermodynamically much less favored than state I. Moreover, the metastability of state C indicates that the duration of Vh-Vt destabilization may be too short for complete dissociation to reach state D and that transition from C back to I is much more likely.

Force generation through intermediate VBS3 association creates an additional activation pathway

In the leading-edge lamella, autoinhibited vinculin localizes to FA sites through low-affinity associations between D1 and talin VBSs, and requires F-actin and force application to complete activation (19). The exposed actin binding interface on Vt allows F-actin retrograde flow to transiently engage vinculin and generate force across the talin-vinculin-F-actin linkage (5, 33, 34, 35). To incorporate the scenario of force in our model, we initiated simulations from state I of the vinculin-VBS3 complex, with constant forces of equal magnitude and opposite directions applied on two pulling groups. One pulling group consists of the Cα atoms of VBS3, and the other consists of the Cα atoms of the actin binding interface on Vt exposed in native vinculin (27) (see Methods). The use of force to study vinculin activation under the joint effect of talin and F-actin has been practiced by Golji and Mofrad (59). They applied force at the centers of mass of Vt and the N-terminal bundle of D1. Here we applied force at the binding interfaces based on available experimental results. Our effort with a more careful treatment could give us more insights.

Using the aforementioned reaction coordinates, we built 2D free-energy profiles to study activation pathways among states I, C, and D under constant force. When state N is not included, N_D1-VBS3 and RMSD_1–130 are equally capable of distinguishing the remaining states (Fig. 3). Therefore, we show the 2D free-energy profiles at a moderate force, 40 pN, using a reduced set of three coordinates RMSD_1–130, Q_D1-Vt, and Q_D4-Vt (Fig. 4, A and D). A comparison of the free-energy profiles at 40 pN (Fig. 4, A and D) with those at 0 pN (Fig. 3, B and D) clearly demonstrates the thermodynamic stabilization of the active state D by force. The activation pathway, I → C → D, exists both in the absence (Fig. 3, B and D) and presence (Fig. 4, A and D) of force. This pathway is indicated by a blue arrow in Fig. 4, A and D, and will be referred to as “Pathway 1”. Two transitions, namely a helical bundle conversion I → C (TS0, black asterisk) and the activation transition C → D (TS1, blue asterisk), correspond to the two bottlenecks of the arrow.

Figure 4.

Vinculin activation by VBS3 under 40 pN force may proceed along one of two pathways. (A and D) Given here are 2D free-energy profiles, each using a coordinate Q_D1-Vt or Q_D4-Vt characterizing one of the two head-tail interfaces. Transitions are marked with asterisks (TS0 and TS1 for Pathway 1 and TS2 for Pathway 2) and two activation pathways are indicated by arrows (blue for Pathway 1 and red for Pathway 2) of varying width. Two arrows for the same pathway are kinetically related approximately by the positions of their bottlenecks. (B and E) Given here is a kinetic trajectory activated along Pathway 1. For clarity, only the trajectory segment near the activation transition is shown. Time sequences are indicated by a continuous variation of colors from blue to red. The transition path is highlighted in dark magenta. (C and F) Shown here is a kinetic trajectory activated along Pathway 2. Color bars: free energy in units of k_BT. To see this figure in color, go online.

Notably, at 40 pN, vinculin activation can proceed along a novel pathway that bypasses state C. This pathway, referred to as “Pathway 2”, is indicated by a red arrow in Fig. 4 D. The activation transition I → D (TS2, red asterisk) corresponds to the bottleneck of the arrow. The emergence of Pathway 2 suggests a novel force-induced activation mechanism, as this pathway is not traceable at 0 pN (Fig. 3 D). Pathway 2 differs from Pathway 1 in the order of events: at TS2, the D4–Vt interface is almost completely broken, but D1 is only starting to undergo a helical bundle conversion, which is in strong contrast to Pathway 1. Before activation, Q_D4-Vt undergoes large fluctuations (from basin I (∼0.5) down to ∼0.1) over a wide range of RMSD_1–130 (from the native value up to ∼0.25 nm) (Fig. 4 D). Interestingly, this extended basin of Q_D4-Vt fluctuation is almost identical to that at 0 pN (Fig. 3 D), except that force creates an opening for activation to proceed to state D (Fig. 4 D).

Kinetic accessibility supports the two vinculin activation pathways

In the previous section, we studied free-energy projections onto two 2D reaction coordinates, q_rmsd,1 = (RMSD_1–130, Q_D1-Vt) and q_rmsd,4 = (RMSD_1–130, Q_D4-Vt), and identified two vinculin activation pathways. Pathway 1 was traced on both q_rmsd,1 and q_rmsd,4 and is made up of two separate transitions (Fig. 4, A and D, blue arrow), whereas Pathway 2 was traced on q_rmsd,4 and contains a single transition (Fig. 4 D, red arrow). Due to the complexity arising from low dimensional projections of a high dimensional system, it was necessary to further ensure that the two pathways are indeed kinetically accessible. Therefore, we initiated 50 independent kinetic trajectories from state $\mathit{I}$ at 40 pN force, and projected the kinetics onto the 2D reaction coordinates. We found that all the trajectories that reached the active state D did follow one of the two pathways. Fig. 4 shows two typical activated trajectories following Pathway 1 (Fig. 4, B and E) and Pathway 2 (Fig. 4, C and F). We note that Pathway 2 is traceable on q_rmsd,1 even though it is not prominently suggested by the free-energy profile (Fig. 4 C).

Vinculin activation along Pathway 1 is rate-limited by disrupting the D1-Vt interface

Further dissection of the activation mechanism of vinculin requires a set of kinetically relevant reaction coordinates that could capture the transition state ensemble (TSE). In this section, we aim to pinpoint the kinetic bottleneck of Pathway 1. Pathway 1 consists of two transitions: helical bundle conversion TS0 and activation transition TS1 (Figs. 3, A and B and 4 A). For TS0, although RMSD_1–130 and N_D1-VBS3 are comparably useful, N_D1-VBS3 is preferred over RMSD_1–130 because it is able to distinguish state N at 0 pN (Fig. 3, A and B). TS1 is dominated by two separate events characterized by Q_D1-Vt and Q_D4-Vt. It is therefore necessary to find the relation between these two events and determine the rate-limiting step of TS1.

The 2D free-energy profiles in the absence (Fig. 3) and presence (Fig. 4) of force both indicate that choosing Q_D1-Vt over Q_D4-Vt guarantees a much higher barrier for TS1, suggesting that disrupting the D1-Vt interface is a much slower process than disrupting the D4-Vt interface. With the additional input of information from kinetic trajectories, we show that the region on q_rmsd,1 around the free-energy saddle point is indeed the kinetic bottleneck of the activation transition TS1. First, for each successful activation transition (TS1), we identified the transition path as the trajectory segment starting from C and ending in D without reentering the region of C at intermediate times, as illustrated in Fig. 4, B and E (dark magenta segments). Then we randomly selected 12 TS1 transitions and plotted the corresponding transition paths as line segments (Fig. S5, A and C, 12 distinct colors) or as points (Fig. S5, B and D). We further assumed that the transition paths thus selected form an approximate ensemble. In Fig. S5 B, the points on transition paths spend a high fraction of time around the free-energy saddle point on q_rmsd,1, indicating that the activation rate is indeed limited by the free-energy barrier. In contrast, in Fig. S5 D, the majority of the points on transition paths fall within basin D, suggesting that the kinetic bottleneck is not captured by the free-energy saddle point on q_rmsd,4. Therefore, we conclude that q_rmsd,1 should be preferred over q_rmsd,4 to characterize the activation transition TS1, which is rate-limited by disrupting the D1-Vt interface. Also, with the kinetic signatures of transition paths on reaction coordinates q_rmsd,1 and q_rmsd,4, we describe the TSE for Pathway 1 at TS1 as having the D1-Vt interface critically disrupted and the D4-Vt interface more severely disrupted, in addition to a helical-bundle converted D1 tightly bound to VBS3.

Pathway 1 has limited sensitivity to force

We now investigate the force sensitivity of Pathway 1 by studying $\mathit{TS}0$ and $\mathit{TS}1$ separately using appropriate 1D components of q_rmsd,1 (Fig. 5). The helical bundle conversion $\mathit{TS}0$ from I to C is rate-limited by a barrier that slightly varies with force between 2 and 3 k_BT, whereas the reverse barrier from C to I is only ∼1 (Fig. 5 B, black ‡). The activation transition $\mathit{TS}1$ from C to D has a much higher barrier, from ∼4 k_BT at 0 pN, rising to ∼6 k_BT at 30 pN, then slightly drops (Fig. 5 C, blue ‡). Interestingly, not only the barrier height but also its shape and the position of the TSE change significantly with force. Overall, Pathway 1 displays strong resistance to force, at least up to a moderate level of ∼40 pN.

Figure 5.

Vinculin activation Pathway 1 is rate-limited by disrupting the D1-Vt interface and has low sensitivity to force. (A) Effective regions for helical bundle conversion TS0 (black ‡) and activation transition TS1 (blue ‡) in dashed rectangles are illustrated on a 2D free-energy profile under 0 pN force (Fig. 3 A). Color bar: free energy in units of k_BT. (B) Free-energy profiles on N_D1-VBS3 indicate low barriers for TS0 and metastability of state C. (C) Free-energy profiles on Q_D1-Vt indicate that the rate-limiting transition TS1 has limited sensitivity to force. To see this figure in color, go online.

Vinculin activation along Pathway 2 is triggered by a substantial displacement of vinculin tail from its head constraints and is accelerated by tensile force

Pathway 2 requires tensile force and has been shown to contain a single transition $\mathit{TS}2$ (Fig. 4 D, red arrow and red asterisk). Previously we described Pathway 2 as emerging from the extended basin I where Q_D4-Vt undergoes extensive fluctuations, and verified its accessibility using kinetic trajectories. Examination of the 2D free-energy profiles on q_rmsd,4 at 0 pN (Fig. 3 D), 20 pN (Fig. 6 A), and 40 pN (Fig. 6 B) shows the emergence of Pathway 2 induced by force and suggests the use of q_rmsd,4 to describe Pathway 2. Surprisingly, as the main structural event immediately before barrier crossing, the fluctuations of Q_D4-Vt are not affected by force: basin I at 40 pN shares a high degree of similarity with that at 0 or 20 pN. This suggests that the disruption of the D4-Vt interface is likely a structural event accompanying vinculin activation through Pathway 2, but the use of q_rmsd,4 may hide the true activation mechanism.

Figure 6.

Vinculin activation Pathway 2 is accelerated by force. Free-energy profiles use coordinate q_rmsd,4 = (RMSD_1–130,Q_D4-Vt) (A and B) or q_rmsd,pull = (RMSD_1–130,X_pull) (C and D), at force 20 pN (A and C) or 40 pN (B and D). The coordinate q_rmsd,pull contains a pulling component X_pull and displays the activation transition TS2 at 20 pN (C) that is poorly defined by q_rmsd,₄ (A). The activation barrier is lowered by force, and basin I moves along X_pull with force toward TS2 that stays fixed (C and D). TS2 is marked with an asterisk for q_rmsd,₄ (A and B) and a ‡ for q_rmsd,pull (C and D) to indicate the kinetic relevance of q_rmsd,pull. Color bars: free energy in units of k_BT. To see this figure in color, go online.

A natural and usually useful reaction coordinate in force-induced molecular events is the pulling direction. Here, the pulling coordinate X_pull is defined as the vector connecting the centers of mass of the two pulling groups projected onto the pulling direction (Fig. 2 B). We constructed a 2D reaction coordinate q_rmsd,pull = (RMSD_1–130, X_pull) by replacing Q_D4-Vt with X_pull in q_rmsd,4. Using q_rmsd,pull, Pathway 2 can be traced from state I with small RMSD_1–130 and small X_pull, to state D with large RMSD_1–130 and large X_pull (Fig. 6, C and D). Interestingly, the value of RMSD_1–130 at TS2 found using q_rmsd,pull (Fig. 6 D) agrees with that found using q_rmsd,4 (Fig. 6 B), and in both representations TS2 stands ∼3 k_BT above the bottom of I. To find the kinetic relevance of 2D coordinates q_rmsd,1, q_rmsd,4, and q_rmsd,pull, we selected 12 TS2 transitions and plotted their transition paths on the 2D free-energy profiles (Fig. S6). Among the three 2D coordinates, only q_rmsd,pull shows a prominent accumulation of transition path points around the free-energy saddle point (Fig. S6 F), whereas both q_rmsd,1 and q_rmsd,4 show a strong bias of the points toward states I or $\mathit{D}$ (Fig. S6, B and D). Therefore, q_rmsd,pull most appropriately captures the kinetic bottleneck of $\mathit{TS}2$ around its free-energy saddle point.

Next, we studied 2D free-energy profiles on q_rmsd,pull to understand how force modulates the free-energy landscape for vinculin activation. Notably, we found that the location of the TSE (TS2) remains unchanged from 20 pN (Fig. 6 C) to 40 pN (Fig. 6 D), whereas the location of basin I shows a well-targeted movement along X_pull toward the TSE with force, and the activation barrier height decreases from ∼6 k_BT at 20 pN to ∼3 k_BT at 40 pN. These data strongly suggest a force-dependent mechanism of Pathway 2. Force effectively reduces the kinetic cost of reaching TS2 at an elongation of ∼4.5 nm, which is prohibitive in the absence of force. This rate-limiting step corresponds to pulling Vt from the center of the pair of pincers and likely involves breaking the D2-Vt and D3-Vt contacts. More information about the structural features of TS2 can be obtained from the kinetic signatures of its transition paths on different coordinates. The reactive configurations identified using q_rmsd,pull (Fig. S6, E and F) are seen at Q_D4-Vt ≈ 0 (Fig. S6, C and D), but show a wide distribution of Q_D1-Vt from ∼0.5 to ∼0.2 (Fig. S6, A and B). Thus, the TSE can be described as Vt adequately detached from the pincerlike constraints of the head domains, with a severely disrupted D4-Vt interface and a slightly disrupted D1-Vt interface, in addition to a nativelike D1 domain with VBS3 only partially bound.

Pathway 2 competes with Pathway 1 at low forces and becomes the dominant activation pathway at high forces

We have investigated two pathways for vinculin activation using free-energy profiles on appropriate coordinates, i.e., a force-insensitive Pathway 1 and a force-accelerated Pathway 2. It is thus conceivable that, in the absence of force, due to the high activation barrier for Pathway 2 (> 6 k_BT), vinculin activation is restricted, and very unlikely, along Pathway 1, with an activation barrier of ∼4 k_BT. Because of the force sensitivity of Pathway 2, its activation barrier drops to ∼3 k_BT at 40 pN, and presumably continues to be lowered by force. This competition between the two pathways suggests that Pathway 2 will eventually become the dominant pathway for vinculin activation in a high-force environment.

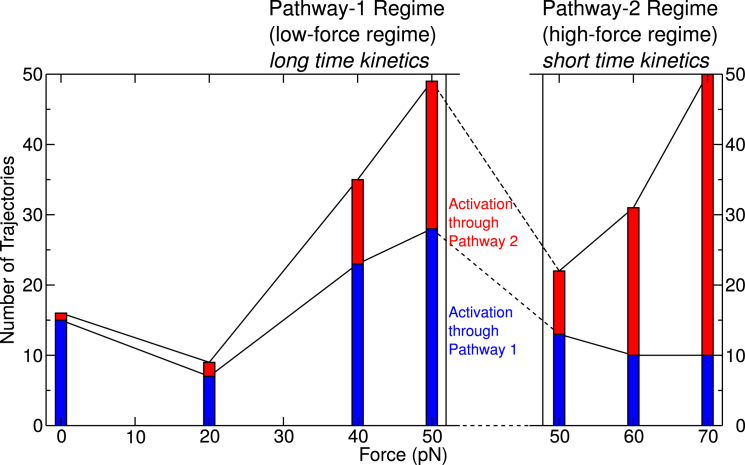
To verify this hypothesis, we initiated kinetic trajectories from state I, at forces 0, 20, 50, 60, and 70 pN, with 50 independent trajectories at each force, supplemented by those at 40 pN previously mentioned. For 60 and 70 pN, short trajectories were used, whereas for forces below 50 pN, longer trajectories were needed (six times the length of short trajectories) to obtain significant statistics. The numbers of activated trajectories through each pathway are shown in Fig. 7 as stacked histograms. Pathway 1 dominates below 50 pN whereas Pathway 2 dominates above 50 pN, resulting in a Pathway-1 regime at low forces and Pathway-2 regime at high forces.

Figure 7.

Histogram of vinculin activation along Pathway 1 (blue) or Pathway 2 (red) with 50 independent trajectories at each force. Longer trajectories are used for low forces to obtain sufficient statistics. Two force regimes are defined. To see this figure in color, go online.

Conclusions

We have used an all-heavy-atom structure-based model to study vinculin activation by talin in a high-tension context mechanically driven by F-actin. This model consists of a full-length vinculin and a VBS3 peptide from talin, and uses a dual-basin potential for D1 to account for its helical bundle conversion upon VBS3 binding. As a major difference from single-domain protein mechanical unfolding, vinculin activation involves breaking interdomain contacts. Therefore, we chose a proper set of reaction coordinates validated for kinetic relevance to account for the major structural events during vinculin activation. Based on free-energy landscape theory and transition path analysis, we obtained the following results. First, we showed that the stability of autoinhibited vinculin, and the kinetic bottleneck in vinculin activation by VBS3 alone (along Pathway 1), are mainly due to the strong and rigid D1-Vt interface. In the autoinhibited conformation (states N and I), and even in the helical-bundle converted conformation with a slightly destabilized interface (state C), the D1-Vt contacts undergo only a limited scale of fluctuations insufficient to trigger the activation transition. Next, considering the stability of the intermediate state I resulting from partial vinculin-VBS3 association, the accessibility of an actin binding site on autoinhibited vinculin, and the fact that highest tensions across vinculin are associated with FA assembly, we applied force across the vinculin-VBS3 complex to investigate vinculin activation in its physiological context in the leading edge lamella. Our results indicate that mechanical activation of vinculin can proceed along a novel pathway (Pathway 2) in addition to the original pathway (Pathway 1). We showed that tensile force plays an active role in releasing Vt from the pincerlike constraints by the vinculin head, and that Pathway 2 is highly sensitive to force. Finally, with additional data from kinetic trajectories over a range of forces, we showed that the dominance of Pathway 1 at low forces is gradually overtaken by Pathway 2 with increasing force. We predict that if vinculin activation in its physiological setting is regulated by force, it likely follows a pathway similar to Pathway 2, considering the mechanical environment during FA assembly.

Based on our results, we propose a model at the molecular level to illustrate the two vinculin activation pathways (Fig. 8). This model mimics an environment of F-actin retrograde flow in the leading-edge lamella during FA assembly and describes possible scenarios in the activation of a full-length vinculin molecule by a VBS3 helix from talin under different levels of force resulting from transient vinculin-F-actin associations. The first step is the formation of the intermediate state I with partial but stable vinculin-VBS3 association (Step 1). This step is initiated by free diffusion of the molecules and therefore concentration dependent, but once in state I, the effect of concentration becomes less important. In the absence of force, vinculin activation by VBS3 alone (Pathway 1: Steps 3–5) is highly unlikely, rate-limited mainly by achieving sufficient destabilization of the D1-Vt interface for the activation transition TS1. If transient associations of F-actin (Step 2) generate tensile force across vinculin, the most likely activation pathway depends on the level of force. If the force is small, then Pathway 1 (Steps 6–8) remains the dominant activation pathway. If the force is large, then instead of seeking to destabilize the D1-Vt interface, force adequately pulls Vt out of the pincerlike pocket formed by domains D1–D3 and brings the vinculin-VBS3 complex to transition state $\widetilde{\mathit{TS}}2$ (Step 9), and completes the high-force activation pathway (Pathway 2) with Step 10. Once in state $\tilde{\mathit{D}}$, a second actin binding site on Vt originally masked by Vh-Vt interactions is exposed, and full association between vinculin and F-actin can be made.

Figure 8.

Cartoon illustration of vinculin activation pathways regulated by force. Stable states include native state N, inactive intermediate state I, helical-bundle converted state C, and dissociated active state D. Transition states include TS1 and TS2. The notation “∼” is used to indicate the presence of F-actin association ($\tilde{\mathit{I}}$, $\tilde{\mathit{C}}$, $\tilde{\mathit{D}}$, $\widetilde{\mathit{TS}}1$, and $\widetilde{\mathit{TS}}2$) but does not distinguish the state from its counterpart without F-actin. Step 1: VBS3 partially binds D1. Step 2: F-actin retrograde flow engages vinculin by transient associations with an actin binding site exposed on Vt. Step 3: VBS3 fully inserts into D1 and causes a slight destabilization of the D1-Vt interface; this step contains a helical bundle conversion TS0 in the N-terminal bundle of D1. Steps 4 and 5: Vinculin activation TS1 is triggered by substantial destabilization of the D1-Vt interface. Steps 6–8 are similar to steps 3–5. Vinculin activation Pathway 1 follows steps 3–5 under zero force or steps 6–8 under low force. Steps 9 and 10: Along Pathway 2 under high force, vinculin activation TS2 is triggered by substantial release of Vt from the pair of pincers formed by D1–D3. A second actin binding site on Vt originally masked by Vh–Vt interactions is exposed and the molecular link is strengthened. Steps 11 and 12: When tension is released, vinculin refolds to its autoinhibited conformation by a mechanism that remains unclear. To see this figure in color, go online.

We note here that the difference in kinetic accessibilities of Pathways 1 and 2 is closely related to the intrinsic flexibility of vinculin. In a study using essential dynamics analysis to characterize the principal motions near the native state of vinculin (60), the authors found that the first two dominant modes both involve the opening and closing motions between Vt and the structural components D2 and D3 of the pincers while keeping the D1-Vt interface rigid. In the case of the two activation pathways, we find that the opening motions between Vt and domains D2 and D3 directly lead to the transition state TS2 of Pathway 2, whereas the rigidity of the D1-Vt interface explains the difficulty in reaching the transition state TS1 of Pathway 1.

Among the many possible ways to progressively open up an autoinhibited vinculin, Pathway 1 aims to destabilize the D1-Vt interface, whereas Pathway 2 aims to unplug Vt from Vh by force to loosen up the head-tail constraints. Both pathways overcome the activation barrier by releasing one of the key factors that contribute to vinculin autoinhibition. Likewise, in the widely accepted combinatorial activation mechanism, it is believed that the release of the D4-Vt contacts will allow talin to disrupt the D1-Vt interface (27, 29, 30). Experiments using a Förster resonance energy transfer probe showed that only in the presence of F-actin can either the talin rod or VBS3 activate full-length vinculin (31), suggesting that the additive energetics of the vinculin-talin and vinculin–F-actin interfaces constitute a favorable condition for vinculin activation, possibly following a pathway that aims to initiate Vt–F-actin contacts, thus releasing Vt from D4. Therefore, the combinatorial activation mechanism differs from Pathway 2 in that it is driven by the energetics of the Vt–F-actin interface and does not depend on force. During vinculin activation in the cell, however, Pathway 2 and combinatorial activation may coexist in a synergistic manner. The investigation of the combinatorial activation of vinculin requires the molecular details of the Vt–F-actin interface and is beyond the scope of this study.

A less understood but equally important process is vinculin deactivation associated with FA disassembly. A mature FA can exist under levels of cellular tension much lower than required for FA assembly. Although the active conformation of vinculin is maintained by an average tension of ∼2.5 pN in stationary FAs (8), further reducing the tension lowers the residence time of vinculin at FAs and finally vinculin is released from the adhesion sites and found diffusely distributed in the cytoplasm (23, 61). This process may involve two major steps in the framework of this model (Fig. 8). First, tension is released from active vinculin by either inhibiting myosin II activity or releasing F-actin from Vt (Step 11). Next, Vt collapses onto Vh and displaces the VBS, leaving an autoinhibited vinculin free to diffuse around (Step 12). A few questions remain to be answered to understand vinculin deactivation. Does this process follow the reversed Pathway 1? What is the mechanism involved in releasing F-actin and the VBS, considering their strong interactions with active vinculin?

Finally, it is worth mentioning that VBS3 is the only VBS used for this study. Because helical bundle conversion is a conserved conformational change in talin-vinculin binding (25, 62, 63), we believe that the mechanism proposed in this study also applies to vinculin activation involving other VBSs. However, because different VBSs differ in their affinity for D1 (62), differences may exist in activation rate and threshold force. It is also important to recognize that vinculin has binding sites for many interaction partners located on its head (talin, α-actinin, …), tail (F-actin, paxillin, PIP₂, …) domains and the proline-rich loop region (VASP, …). Many of these have been proposed to participate in vinculin activation. Specifically, it has been demonstrated that tyrosine phosphorylation at both Y100 and Y1065 is necessary for vinculin activation, possibly through inducing a conformational rearrangement and stabilizing the Vt–F-actin interaction, thus facilitating the initial weak binding of vinculin to talin and F-actin (64, 65, 66). Understanding how different binding partners cooperate in vinculin activation remains a challenge toward the full elucidation of the FA machinery.

Author Contributions

L.S., J.K.N., H.L., and J.N.O. designed research. L.S. performed research. L.S., J.K.N., H.L., and J.N.O. analyzed data. L.S., J.K.N., H.L., and J.N.O. wrote the manuscript.

Editor: Matthias Rief.