A Boltzmann Constant Determination Based on Johnson Noise Thermometry

Abstract

A value for the Boltzmann constant was measured electronically using an improved version of the Johnson Noise Thermometry (JNT) system at the National Institute of Standards and Technology (NIST), USA. This system is different from prior ones, including those from the 2011 determination at NIST and both 2015 and 2017 determinations at the National Institute of Metrology (NIM), China. As in all three previous determinations, the main contribution to the combined uncertainty is the statistical uncertainty in the noise measurement, which is mitigated by accumulating and integrating many weeks of cross-correlated measured data. The second major uncertainty contribution also still results from variations in the frequency response of the ratio of the measured spectral noise of the two noise sources, the sense resistor at the triple-point of water and the superconducting quantum voltage noise source. In this paper, we briefly describe the major differences between our JNT system and previous systems, in particular the input circuit and approach we used to match the frequency responses of the two noise sources. After analyzing and integrating 49 days of accumulated data, we determined a value: k = 1.380 642 9(69)×10⁻²³ J/K with a relative standard uncertainty of 5.0×10⁻⁶ and relative offset −4.05×10⁻⁶ from the CODATA 2014 recommended value.

1. Introduction

The pending redefinition of the unit kelvin of the International System of Units (SI) will define the Boltzmann constant k to be an exact numerical value in units of joule per kelvin, thus relating the thermodynamic temperature T directly to energy E = k T. Before the new definition of the Boltzmann constant can take place, low uncertainty measurements of k need to be performed to guarantee compatibility with the current SI definition based on the intrinsic standard ‘triple-point of water’. The Consultative Committee on Thermometry (CCT) of the International Committee for Weights and Measures (CIPM) requires that, before a definition of the Boltzmann constant can occur, the value of k needs to be determined with a relative uncertainty of less than 1×10⁻⁶, supported by a measurement using a different technique with a relative uncertainty of less than 3×10⁻⁶[1]

Currently the most precise measurement techniques for the determination of k are based on the acoustic properties of gases and yield a relative uncertainty of less than 1×10⁻⁶ [2, 3]. Alternative gas-based thermometry techniques are Doppler broadening thermometry and dielectric-constant gas thermometry [4, 5]. The latter was developed by the PTB, and a relative uncertainty of 1.9×10⁻⁶ was recently reported [6], thus meeting the goal of a relative uncertainty of less than 3×10⁻⁶for a supporting measurement.

Johnson noise thermometry (JNT) is the only technique currently being used to determine k that is not based on the thermodynamic properties of classical gases, but on the properties of a free electron gas in a conductor [7, 8, 9]. The random thermal motion of electrons results in voltage noise as described by the fluctuation-dissipation theorem [10, 11]. This voltage noise is approximated by Nyquist’s equation to be proportional to k and resistance; at frequencies below 50 MHz and temperatures above 100 K, the approximation is better than 1 part in 10¹⁰ and therefore the use of this approximation has negligible effect on the uncertainty in the determination of k [15]. The generality of the fluctuation-dissipation theorem, predicting the link between thermal voltage fluctuations and resistance, allows Johnson noise thermometry to be used as an absolute primary thermometry method.

In our JNT measurement we utilize a quantum voltage noise source (QVNS) to accurately generate synthetic noise with a calculable synthetic noise spectrum that is inversely proportional to the Josephson constant K_J (Eqn. 2, section 2). When the resistance of the thermal noise source is known in terms of the conventional value for the von Klitzing constant R_K, a measurement of the ratio of the thermal noise to the QVNS spectrum will be proportional to the ratio of the Boltzmann constant to the Planck constant, or k/h. The relative uncertainty of the measurement of the Planck constant is about 1.2×10⁻⁸, or about 50 times smaller than the relative uncertainty of the best estimate of the Boltzmann constant of 5.7×10⁻⁷[39]. Therefore, for this work we can assume a fixed value for the Planck constant of h = 6.626 070 040×10⁻³⁴ J·s [39] and use this value in the further calculations to determine k with negligible effect on the uncertainty in the determination of k.

Johnson noise thermometry has been used for many years [12, 13, 14, 15], but its application in high-precision measurements experienced many difficulties; especially the small thermal noise voltage of only $0.123\text{ nV}/\sqrt{\mathrm{\Omega }\text{ Hz}}$ (at 273 K) poses a problem that could only be solved with modern fast ADCs and custom amplifiers, new data analysis techniques involving a correlation measurement and real-time averaging of FFTs, a heavily shielded measurement environment, and by use of comparison to an absolute QVNS reference [16]. The work of Brixy et al. for measuring temperature in nuclear reactors [13] and the availability of a QVNS pushed the development of JNT forward to its status as a high-precision measurement tool. The National Institute of Standards and Technology (NIST) has been developing precision QVNS-JNT systems since 1999 in cooperation with the Measurement Standards Laboratory of New Zealand [17 to 28], and since 2009 in collaboration with the National Measurement Institute (NIM), China [29, 30]. Different versions of QVNS-JNT systems at NIST, NIM, and the National Metrology Institute of Japan (NMIJ) have produced four independent determinations of k since 2011 [31, 32, 33, 40]. The most recent measurement with the latest NIM system determined the Boltzmann constant with a relative uncertainty of 2.7×10⁻⁶, meeting the 3×10⁻⁶ requirement of the CCT [1].

In a series of experiments over the last few years, many improvements have been integrated into these systems [17 to 30]. In this paper, we briefly describe the most important recent improvements to the NIST JNT system, primarily a different approach to matching the frequency responses of the two sources. Here, we report our new measurement result for the determination of the Boltzmann constant. A more detailed description of this system, the experiment, and the data analysis will be published in the near future [34].

2. Improvements to the NIST JNT system

As in previous JNT measurements, we use a pair of data acquisition channels and a custom relay board (see Figure 1) to switch every 100 s between a cross-correlation measurement of the two noise sources, in one case measuring S_R, the sense resistor’s thermal noise power spectral density, and in the other case measuring S_Q, the QVNS-synthesized pseudo-noise power spectral density. The calculated power spectral density of the thermal noise is given by the Nyquist equation

$$S_{\mathrm{R},\text{calc}}=4kT{X}_{\mathrm{R}}{R}_{\mathrm{K}},$$ (1)

where T is the temperature of the sense resistor in a triple-point of water (TPW) cell and X_R is the resistance of the sense resistor expressed in units of the von Klitzing resistance R_K = h/e². The QVNS uses an array of N_JJ Josephson junctions (JJs) biased by a high-speed pulse generator with a pulse frequency of f_s = 5×10⁹ pulse/s; for each input pulse from the pulse generator, each JJ creates a voltage pulse with a quantized area equal to a flux quantum, that is, the inverse of the Josephson constant $K_{\mathrm{J}}^{-1}=h/2e$. We use a repeating pattern of quantized pulses of length M that is designed to create pseudo-random noise with a calculated effective power spectral density

$$S_{\mathrm{Q},\text{calc}}=M{D}^2{N}_{\text{JJ}}^2{f}_{\mathrm{S}}{K}_{\mathrm{J}}^{-2},$$ (2)

where D is a parameter that depends on the FFT of the pulse pattern.

Figure 1.

JNT schematic diagram. The sense resistor of 200 Ω is composed of two series resistors R_T = 100 Ω, while the QVNS is composed of two arrays with a total of N_JJ = 20 Josephson junctions and two pairs of resistors R_Q ~ 100 Ω. The QVNS lines have additional matching resistors R_m ~ 1 Ω and matching capacitors C_m. A custom switch board is used to determine which noise source is connected to the two signal processing channels (Ch A and Ch B). The amplifiers (Amp) are stabilized using a combination of toroidal ferrite-core inductors (light grey boxes) and resistors R_amp. The center of each source is grounded (green lines) at the amplifier input, and that ground is used to shield each differential twisted pair. After the custom high-gain low-noise amplifier [15–20, 32, 34], there is a steep 11th-order 850 kHz low-pass filter (LPF) and an AC-coupled 16-bit 2.083 Msample/s digitizer (ADC). There is an additional grounded shield surrounding the entire system (grey boxes), and the entire system is also in an electromagnetically shielded room. The switchboard and ADCs are optically controlled by a computer (PC) outside of the shielded room.

We wish to compare the ratio of calculated spectral densities

$$a_{0,\text{calc}}=\frac{S_{\mathrm{R},\text{calc}}}{S_{\mathrm{Q},\text{calc}}}=\frac{k}{h}\frac{16T{X}_{\mathrm{R}}}{M{D}^2{N}_{\text{JJ}}^2{f}_{\mathrm{S}}}$$ (3)

to the ratio of the measured power spectral densities S_R/S_Q. However, the measured power spectral densities include the effects of the different frequency-dependent transfer functions between the voltage sources and the input of the correlator amplifiers. We operate in the regime where the transfer functions for the two QVNS channels are identical and can be approximated as lumped elements. Therefore the scaling factor for the measured power spectral density S_Q is an even-order polynomial as a function of frequency, and the same holds for the thermal noise S_R for identical resistor channels. As in previous JNT measurements [17–36], we then model the measured ratio as an even-order polynomial

$$\frac{S_{\mathrm{R}}}{S_{\mathrm{Q}}}=\frac{a_{0\mathrm{R}}+a_{2\mathrm{R}}{f}^2+\dots }{a_{0\mathrm{Q}}+a_{2\mathrm{Q}}{f}^2+\dots }=a_0+a_2{f}^2+‥..$$ (4)

This model also takes into account the imperfect rejection of amplifier noise currents by the cross-correlation measurement because their contribution to the measured ratio would have an f² dependence. The consistency between the assumed value of k/h used in the calculated a_0,calc and in the JNT measurement is given by a₀ − a_0,calc. We use the CODATA 2014 recommended values for k and h.

The most important differences between the measurement reported here and earlier measurements at NIST [31] and NIM [32], as well as the recent NIM measurements [33], are the value of the sense resistor as well as both the circuit and procedure used to match the transfer functions. Compared to earlier NIST measurements, the shielding was also dramatically improved to reduce electromagnetic interference (EMI). We will briefly discuss these differences here; full details will be given in a future publication [34].

Most importantly, we used a multi-step procedure to tune the electrical circuit and reduce the frequency dependence of S_R/S_Q over the 1 MHz bandwidth of the system. This tuning started by minimizing the capacitive loading during the assembly of the QVNS probe and the probe holding the sense resistor. We also decided to increase the sense resistance from 100 Ω to 200 Ω, thereby increasing the thermal noise relative to the amplifier noise without a significant decrease in the measurement bandwidth of the system; in contrast, Qu et al. [33] reduced their sense resistance from 200 Ω to 100 Ω to increase the measurement bandwidth.

After assembly, we matched the DC resistance of the QVNS to the DC resistance of the sense resistor to within 0.2 Ω by adding matching resistors to all of the QVNS leads at the inputs to the relay board (see R_m in Figure 1). We then tuned the parallel matching capacitors on the QVNS leads (see C_m in Figure 1) to attempt to satisfy two somewhat conflicting goals: to flatten the frequency-dependence of S_R/S_Q and to reduce the required order of the even-order polynomial that best fits S_R/S_Q (see Figure 2 for S_R/S_Q with different capacitor settings).

Figure 2.

Summary of all of the ratio data S_R/S_Q − a_0,calc; each line is the average of data collected with a different QVNS transfer function, i.e., different parallel capacitances C_m (overall change is <20 pF).

We also made a small permanent change at the input to the amplifiers and relay boards on May 26 (86 days after March 1). Before May 26, we used toroidal ferrite-core inductors on the sense resistor leads as well as resistors R_amp = 10 Ω each (see Fig 1) to prevent Colpitts oscillations in the amplifiers and input circuits [32]; however ferrites can have complicated nonlinear and frequency-dependent behavior. To remove this potential source of problems, on May 26 we entirely removed the ferrite components. Instead, we increased the resistance on the input of the amplifiers R_amp = 21.1 Ω each (see Fig 1) to prevent oscillations. This additional resistance contributes a small increase in the effective noise of the amplifier.

We also made a number of small but important changes. Using an additional switchboard we were able to dynamically adjust the grounding conditions. In order to minimize the influence of EMI, the system was fully battery operated in a magnetically and high-frequency shielded room. We also improved the shielding and grounding of the electronics, including isolating the pulse generator from the measurement electronics by adding inside-outside DC blocks to the QVNS chip. In addition, the wiring was optimized to reduce differential crosstalk by using twisted pairs to each channel in separately grounded shields (see Fig. 1). This approach is intended to reduce capacitance to the shield and thus increase measurement bandwidth in comparison to the use of a pair of twisted coaxial lines to each channel, as in [33].

Finally, in an effort to improve the objectivity of the analysis of the measurement data, we implemented a cross-validation method developed by Coakley et al [35] and also implemented in [33]. This analysis technique automatically determines the bandwidth and order of the even-order polynomial, and then provides a well-defined uncertainty due to this model ambiguity which is included in the uncertainty budget. Our use of this method is described in more detail in the next section.

3. Modeling and Statistics

The data accumulated and reported in this paper were measured over a total of 93 days beginning on March 18, 2017 and ending on June 20, 2017. During that time, we collected QVNS and Johnson noise data for a total of 44 days. Data were collected nearly continuously, with hour-long interruptions every 2–3 days to measure the resistance of the sense resistor and to change batteries. A slightly longer pause was required every ~10 days to change liquid helium dewars, and there were also occasional pauses to measure and change other system parameters.

Over this time period we intentionally changed the electrical characteristics of the transfer function between the QVNS and the amplifiers, both by occasionally changing C_m and by, on May 26, removing the toroidal ferrite-core inductors. We also observed unintentional changes in the electrical characteristics after thermally cycling the QVNS while changing liquid helium dewars. Finally, the gain of the amplifiers’ input circuits drift with the temperature of the shielded room. In the end, these small system adjustments and changes in the environmental conditions induced small changes in the electrical characteristics of certain components, but the measurements and analysis method consistently yielded valid data.

Because of these changes in electrical characteristics, in the cross-validation analysis below we are averaging over a number of different transfer functions (see Figure 2 for data from different transfer functions and Figure 3 for the average). Since each of these transfer functions is an even-order polynomial with the same unobserved theoretical intercept of interest a₀, the average is also an even order polynomial and deterministic changes in the transfer functions’ higher-order terms will not affect the signal-to-noise of the average.

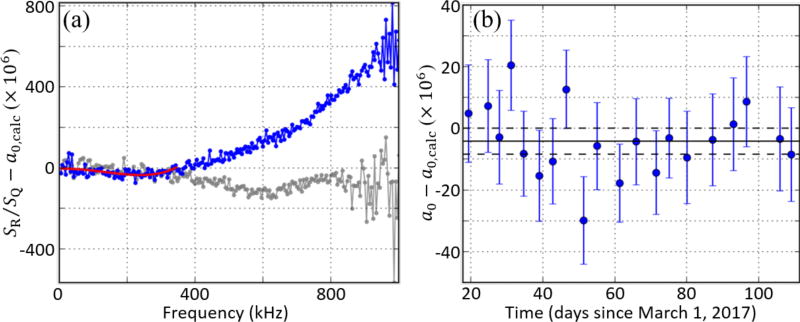
Figure 3.

(a) Average data S_R/S_Q − a_0,calc (blue) with fit to a d=4 even order polynomial from 5 kHz to 350 kHz (based on the cross-validation results, red line). The spectral densities reported by the cross-correlation measurement are complex. In this paper, S_R and S_Q are defined as the real parts of each measurement; the imaginary parts of the complex ratio (gray) are small at low frequencies but become significant at higher frequencies. We will discuss the complex analysis in more detail in [34]. (b) a₀ − a_0,calc as a function of time extracted from fits to the data divided into subsets with equal integration time as well as from the fit to the average from plot (a) (solid black line with uncertainty as dotted black line). This plot is a diagnostic tool and shows that there is minimal impact on a₀ from intentional changes to the system (in particular matching capacitors) and that there are no unknown sources of drift as a function of time.

As described in section 2, we model the ratio S_R/S_Q as a d-th order even polynomial function of frequency (further details are given in [34, 35]). We consider candidate polynomial models with orders ranging from d=2 to d=14. In the cross-validation approach, we randomly split observed spectral data into 45 equally sized subsets. Data from each run appear in just one of the 45 subsets. Each of these 45 subsets was then assigned to one of five groups. From the five groups, we constructed training and validation data for a five-fold cross-validation study, where we selected that model determined from training data that was most consistent with validation data according to a meansquare deviation criterion. Based on 20 000 random groupings of the 45 subsets, we determined model selection fractions. Given that a d-th order model is valid and d is known, asymptotic theory predicts a sampling distribution for the estimate of a₀. The standard deviation of this sampling distribution is the statistical uncertainty of the estimate.

To account for the effect of imperfect knowledge of the order of the polynomial in the model on results, we formed a mixture of the sampling distributions from the candidate models weighted by their associated model selection fractions determined by cross-validation. We estimated the uncertainty of estimated a₀ as the standard deviation of the mixture model distribution σ̂_tot. We define σ̂_stat to be the statistical uncertainty associated with the selected model, assuming the model is valid. Then the additional uncertainty associated with model ambiguity, that is, imperfect knowledge of the polynomial order d of the ratio spectrum model, is defined as ${\hat{\sigma }}_{\text{model}}=\sqrt{{\hat{\sigma }}_{\text{tot}}^2-{\hat{\sigma }}_{\text{stat}}^2}$ assuming σ̂_tot ≥ σ̂_stat (see [34] and [35] for details).

The polynomial fit is performed on data between 5 kHz and a variable maximum fit frequency f_max. We select f_max by minimizing σ̂_tot on a grid in frequency space from 200 kHz to 700 kHz with a resolution of 25 kHz. Based on scientific judgement, we restrict our search to f_max values no larger than 700 kHz to keep a sufficient distance from the corner frequency of the low pass filters (see Figure 1). However, for informational purposes, we shown results for f_max up to 800 kHz (Figure 4).

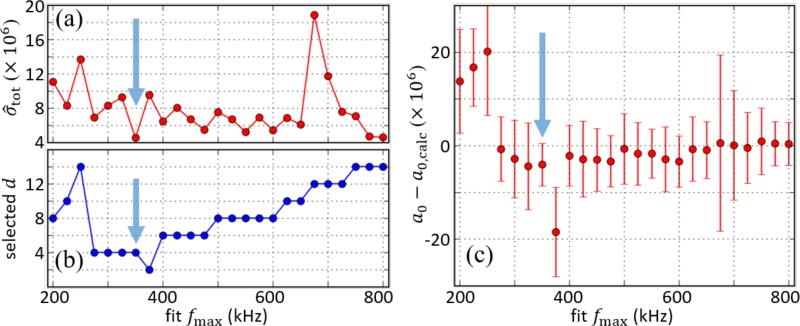
Figure 4.

Summary of cross-validation results. (a) Estimated minimum uncertainty σ̂_tot versus maximum fit frequency f_max. The arrows in each plot indicate the point selected for the k determination, that is, to the minimum value of σ̂_tot. (b) Polynomial order d which yields the minimum uncertainty given in (a) as a function of f_max. (c) Estimated a₀ − a_0,calc as a function of f_max and approximate 68% coverage interval.

The constrained grid search yields a minimum σ̂_tot = 4.55×10⁻⁶ at f_max = 350 kHz and d = 4, with σ̂_stat = 4.25×10⁻⁶ and σ̂_model = 1.63×10⁻⁶. Since the uncertainty estimates are realizations of random variables, the selected f_max is a realization of a random variable. Hence, following arguments in [33] and [35], we determine an additional component of uncertainty σ̂_fmax that accounts for uncertainty associated with imperfect performance of our selection method due to random effects, as well as possible systematic effects, including frequency-dependent physical effects. We set this component to the estimated standard deviation of the estimates that correspond to fitting bandwidths that yield the 5 lowest values of σ̂_tot for f_max no larger than 700 kHz. We determine that σ̂_fmax=1.31×10⁻⁶.

Our estimate of the Boltzmann constant from the ratio of the power spectral densities S_R/S_Q is k =1.380 642 9×10⁻²³ J/K with a combined relative standard uncertainty of 4.97×10⁻⁶ due to the combined effect of random measurement errors, model selection ambiguity and fitting bandwidth ambiguity and relative offset −4.05×10⁻⁶ from the CODATA 2014 recommended value.

4. Uncertainties

In this work, the uncertainties are similar to those reported in [32] and [33] and also dominated by statistical uncertainty. The uncertainty budget shown in Table 4.1 is divided into four main categories that are associated with the factors in Eqn. 3. These categories are: 1) the uncertainty in the measurement of the ratio of power spectral densities; 2) the uncertainties of the QVNS waveform; 3) the uncertainties in the realization of the kelvin through use of the TPW cell; and 4) the uncertainties in the resistance measurements and traceability to the QHR representation of the ohm. A more detailed description of these uncertainty components will be available in a future publication [34].

Table 4.1.

Uncertainty Budget Summary expressed in relative dimensionless units ×10⁻⁶.

Category	Component	NIST 2011	NIST 2017
Ratio of the Power Spectral Densities
	Statistical	5.2	4.25
	Model ambiguity	See text	1.63
	Bandwidth Ambiguity	-	1.31
	Spectral Aberrations	10.4	-
	Dielectric Losses	2.0	1
	EMI	2.0	1
	Non-Linearity and Offsets	1.0	0.5
	Total Ratio	12.0	4.97
QVNS Waveform
	Frequency Reference	<0.001	<0.01
	Quantization Effects	<0.5	<0.1
	Total QVNS		<0.1
TPW Temperature Realization	Chemical Impurities	0.18	0.18
	Pressure Head Correction	0.18	0.08
	Immersion Error	0.73	0.65
	Isotopic Variation	0.26	0.1
	Thermal Equilibrium	0.18	0.18
	Total Temperature	0.84	0.71
Resistance	Bridge Statistics	0.4	0.1
	Standard Resistor Calibration Stability	0.15	0.1
	Standard Resistor Temperature	-	0.05
	Sense Resistor Relaxation / Stability	0.50	0.11
	Frequency Dependence	0.10	0.05
	Second-order Thermoelectric Effects	0.10	0.1
	Total Resistance	0.67	0.22
Total Combined Uncertainty		12.1	5.0

The dominant uncertainty contributions in this work are the three estimates, σ̂_stat, σ̂_model, and σ̂_fmax,[35] from the modeling and statistical analysis in section 3 and these are shown in the first three rows of Table 4.1. The modeling ambiguity σ̂_model and bandwidth ambiguity σ̂_model will capture the non-ideal spectral characteristic that were formerly estimated as ‘spectral aberrations’ in our previous determination [31]. Hence we omit that as an explicit contribution in the present budget. Another difference in the present treatment is in the uncertainty from quasi-linear frequency dependence due to dielectric losses, which were labeled (incorrectly) as ‘model ambiguity’ in our previous work. Here this uncertainty component is more properly categorized as ‘dielectric losses’ in Table 4.1. However, we make a similar a priori equivalent-circuit-model estimate in the present system which benefits from some additional cancellation effects due to the impedance matching strategy. The resulting uncertainty estimate is 1×10⁻⁶. The EMI uncertainty of 1×10⁻⁶ is an estimate derived from comparative analysis of the QVNS spectra and the use of a separate null measurement which substitutes a four-wire short for the normal configuration in the sense resistor [36]. Finally, we include an estimate for non-linearity in the amplification and signal processing, similar to that estimated in Qu, et. al., [32], which is also negligible at 0.5×10⁻⁶.

The QVNS waveform uncertainties are shown in Table 4.1 for the sake of completeness but these are completely negligible in this measurement. These originate from small quantization effects and the uncertainty in the traceability of the 10 MHz time base and are similar to those discussed in Qu, et. al., [32].

The uncertainties in the realization of the kelvin are estimated based on the known characteristics of the working TPW cell as used during these measurements and on various comparisons made between that cell’s temperature and that of other well-characterized TPW cells used at NIST. These uncertainties include various thermophysical and chemical effects due to: the chemical purity of the water; its isotopic content; and the static pressure-head correction. Cell temperature comparisons were made with new quartz-glass TPW cells with traceable isotopic composition to bound the possible extent of those effects in the working cell. The largest and most challenging uncertainty component is the well-known ‘immersion error’ uncertainty which is a combined property of the immersion probe that holds the sense resistor, the TPW cell, and the condition of the ice mantle within the cell. This uncertainty can therefore be variable during the course of the measurements and in our case we estimate between 0.18×10⁻⁶ and 1.1×10⁻⁶ depending on the condition of the ice mantle over time. The combined uncertainty of the weighted average temperature over the entire measurement is 0.71×10⁻⁶.

The resistance measurement uncertainties are derived from the resistance bridge measurement statistics, and a collection of other systematic effects due to the instabilities and frequency characteristics of both the sense resistor and the reference resistor. The reference resistor, designated as serial number 1202T, has been used at NIST since 2005 and has a history of direct comparisons against the QHR ohm since 2007 [37, 38]. It’s estimated drift rate is 0.02 μΩ/Ω/year and the temperature coefficient of resistance varies as a weak quadratic function with temperature with a relative maximum at 24 °C. Most measurements presented here were performed at ambient room temperatures well below that, usually at 17.0(5) °C, which necessitated relative temperature corrections of approximately 1×10⁻⁶. The sense resistor used here is of the same metal-foil type as used in prior works [31–33] and subject to stress relaxation effects exhibiting time constants on the order of 100 days. This leads to drift in the resistance value at rates of order −0.02 μΩ/Ω/day. This drift is monitored at regular intervals sufficient to yield a reliable interpolation of resistance with time resulting in an estimated relative uncertainty component of 0.08×10⁻⁶ for data taken between March 25 and April 10 and 0.03×10⁻⁶ for all data taken after April 10. Prior to March 24, the uncertainty is enlarged to 0.38×10⁻⁶ to account for larger variance in the earlier data. The pooled uncertainty due to sense resistor relaxation effects is 0.11×10⁻⁶. Finally, various frequency-dependent effects have been considered from the standpoint of resistance measurement and in all cases these are found to be either indistinguishable from those already accounted for in the frequency-correction model (Eqn. 4) or otherwise negligible. The combined uncertainty of the weighted average resistance over the entire measurement is 0.22×10⁻⁶.

5. Conclusion

Based on data acquired with a significantly modified NIST QVNS-JNT system, we report an electronic-based determination of the Boltzmann constant of k = 1.380 642 9(69)×10⁻²³ J/K with a relative combined standard uncertainty of 5.0×10⁻⁶. The value is offset by −4.05×10⁻⁶ from the CODATA 2014 value assigned to the Boltzmann constant value. Improvements to the NIST system since the 2011 NIST determination, such as a different matching approach, new QVNS circuit design, grounding, and shielding, have enabled a two-fold reduction in uncertainty. The uncertainty of this measurement is twice that of the 2017 NIM-NIST determination with the NIM system. Our improved matching technique flattened the frequency response in our ratio data, which enabled us to achieve a comparable measurement uncertainty in a wide frequency bandwidth while accumulating data over a short integration period. Nevertheless, our combined uncertainty could have been improved with better measurement conditions and longer integration time.