Abstract
In the electronic measurement of the Boltzmann constant based on Johnson noise thermometry, the ratio of the power spectral densities of thermal noise across a resistor at the triple point of water, and pseudo-random noise synthetically generated by a quantum-accurate voltage-noise source is constant to within 1 part in a billion for frequencies up to 1 GHz. Given knowledge of this ratio, and the values of other parameters that are known or measured, one can determine the Boltzmann constant. Due, in part, to mismatch between transmission lines, the experimental ratio spectrum varies with frequency. We model this spectrum as an even polynomial function of frequency where the constant term in the polynomial determines the Boltzmann constant. When determining this constant (offset) from experimental data, the assumed complexity of the ratio spectrum model and the maximum frequency analyzed (fitting bandwidth) dramatically affects results. Here, we select the complexity of the model by cross-validation – a data-driven statistical learning method. For each of many fitting bandwidths, we determine the component of uncertainty of the offset term that accounts for random and systematic effects associated with imperfect knowledge of model complexity. We select the fitting bandwidth that minimizes this uncertainty. In the most recent measurement of the Boltzmann constant, results were determined, in part, by application of an earlier version of the method described here. Here, we extend the earlier analysis by considering a broader range of fitting bandwidths and quantify an additional component of uncertainty that accounts for imperfect performance of our fitting bandwidth selection method. For idealized simulated data with additive noise similar to experimental data, our method correctly selects the true complexity of the ratio spectrum model for all cases considered. A new analysis of data from the recent experiment yields evidence for a temporal trend in the offset parameters.
Keywords: Boltzmann constant, cross-validation, Johnson noise thermometry, model selection, resampling methods, impedance mismatch
2. Introduction
There are various experimental methods to determine the Boltzmann constant including acoustic gas thermometry [1],[2],[3]; dielectric constant gas thermometry [4],[5], [6], [7], Johnson noise thermometry (JNT) [8], [9], [10], and Doppler broadening [11], [12]. CODATA (Committee on Data for Science and Technology) will determine the Boltzmann constant as a weighted average of estimates determined with these methods. Here, we focus on JNT experiments which utilize a quantum-accurate voltage-noise source (QVNS).
In JNT, one infers true thermodynamic temperature based on measurements of the fluctuating voltage and current noise caused by the random thermal motion of electrons in all conductors. According to the Nyquist law, the mean square of the fluctuating voltage noise for frequencies below 1 GHz and temperature near 300 K can be approximated to better than 1 part in billion as < V2 >= 4kTRΔf, where k is the Boltzmann constant, T is the thermodynamic temperature, R is the resistance of the sensor, and Δf is the bandwidth over which the noise is measured. Since JNT is a pure electronic measurement that is immune from chemical and mechanical changes in the material properties of the sensor, it is an appealing alternative to other forms of primary gas thermometry that are limited by the non-ideal properties of real gases.
Recently, interest in JNT has dramatically increased because of its potential contribution to the “New SI” (New International System), in which the unit of thermodynamic temperature, the kelvin, will be redefined in 2018 by fixing the numerical value of k. Although almost certainly the value of k will be primarily determined by the values obtained by acoustic gas thermometry, there remains the possibility of unknown systematic effects that might bias the results, and therefore an alternative determination using a different physical technique and different principles is necessary to ensure that any systematic effects must be small. To redefine the kelvin, the Consultative Committee on Thermometry (CCT) of the International Committee for Weights and Measures (CIPM) has required that besides the acoustic gas thermometry method, there must be another method that can determine k with a relative uncertainty below 3×10−6. As of now, JNT is the most likely method to meet this requirement.
In JNT with a QVNS, [10], according to physical theory, the Boltzmann constant is related to the ratio of the power spectral density (PSD) of noise produced by a resistor at the triple point of water temperature and the PSD of noise produced by a QVNS. For, frequencies below 1 GHz, this ratio is constant to within 1 part in 109. The physical model for the PSD for the noise across the resistor is SR where
| (1) |
TW is the temperature of the triple point of water, XR is the resistance in units of the von Klitzing resistance where e is the charge of the electron and h is Planck’s constant. The model for the PSD of the noise produced by the QVNS, SQ, is
| (2) |
where , fs is a clock frequency, M is a bit length parameter, D is a software input parameter that determines the amplitude of the QVNS waveform, and NJ is the number of junctions in the Josephson array in the QVNS. Assuming that the Eq. 1 and Eq. 2 models are valid, the Boltzmann constant k is
| (3) |
In actual experiments, transmission lines that connect the resistor and the QVNS to preamplifiers produce a ratio spectrum that varies with frequency. Due solely to impedance mismatch effects, for the frequencies of interest, one expects the ratio spectrum predicted by physical theory to be an even polynomial function of frequency where the constant term (offset) in the polynomial is the value SR/SQ provided that dielectric losses are negligible. The theoretical justification for this polynomial model is based on low-frequency filter theory where measurements are modeled by a “lumped-parameter approximation.” In particular, one models the networks for the resistor and the QVNS as combination of series and parallel complex impedances where the impedance coupling in the resistor network is somewhat different from that in the QVNS network. For the ideal case where all shunt capacitive impedances are real, there are no dielectric losses. As a caveat, in actual experiments, other effects including electromagnetic interference and filtering aliasing also affect the ratio spectrum. As discussed in [10], for the the recent experiment of interest, dielectric losses and other effects are small compared to impedance mismatch effects. As an aside, impedance mismatch effects also influence results in JNT experiments that do not utilize a QVNS [13], [14], [15].
Based on a fit of the ratio spectrum model to the observed ratio spectrum, one determines the offset parameter SR/SQ. Given this estimate of SR/SQ and values of other terms on the right hand sided of Eq. 3 (which are known or measured), one determines the Boltzmann constant. However, the choice of the order d (complexity) of the polynomial ratio spectrum model and the upper frequency cutoff for analysis (fitting bandwidth fmax) significantly affects both the estimate and its associated uncertainty. In JNT, researchers typically select the model complexity and fitting bandwidth based on scientific judgement informed by graphical analysis of results. A common approach is to restrict attention to sufficiently low fitting bandwidths where curvature in the ratio spectrum is not too dramatic and assume that a quadratic spectrum model is valid (see [9] for an example of this approach).
In contrast to a practitioner-dependent subjective approach, we present a data-driven objective method to select the complexity of the ratio spectrum model and the fitting bandwidth. In particular, we select the ratio spectrum model based on cross-validation [19],[20],[21],[22]. We note that in addition to cross-validation, there are other model selection methods including those based on the Akaike Information Criterion (AIC) [16], the Bayesian Information Criterion (BIC) [17], Cp statistics [18]. However, cross-validation is more data-driven and flexible than these other approaches because it relies on fewer modeling assumptions. Since the selected model determined by any method is a function of random data, none perform perfectly. Hence, uncertainty due to imperfect model selection performance should be accounted for in the uncertainty budget for any parameter of interest [23], [24]. Failure to account for uncertainty in the selected model generally leads to underestimation of uncertainty.
In cross-validation, one splits observed data into training and validation subsets. One fits candidate models to training data, and selects the model that is most consistent with validation data that are independent of the training data. Here (and in most studies) consistency is measured with a cross-validation statistic equal to the mean square deviation between predicted and observed values in validation data. We stress that, in general, this mean square deviation depends on both random and systematic effects.
For each candidate model, practitioners sometimes average cross-validation statistics from many random splits of the data into training and validation data set [25], [26], [27]. Here, from many random splits, we instead determine model selection fractions determined from a five-fold cross-validation analysis. Based on these model selection fractions, we determine the uncertainty of the offset parameter for each fitting bandwidth of interest. We select fmax by minimizing this uncertainty. As far as we know, our resampling approach for quantification of uncertainty due to random effects and imperfect performance of model selected by five-fold cross-validation is new. As an aside, for the case where models are selected based on Cp statistics, Efron [28] determined model selection fractions with a bootstrap resampling scheme.
In [10], the complexity of the ratio spectrum and the fitting bandwidth were selected with an earlier version of the method described here for the case where fmax was no greater than 600 kHz. Here, we re-analyze the data from [10] but allow fmax to be as large as 1400 kHz. In this work, we also quantify an additional component of uncertainty that accounts for imperfect performance of our method for selecting the fitting bandwidth. We stress that this work focuses only on the uncertainty of the offset parameter in ratio spectrum model. For a discussion of other sources of uncertainty that affect the estimate of the Boltzmann constant, see [10]. In a simulation study, we show that our methods correctly selects the correct ratio spectrum for simulated data with additive noise similar to observed data. Finally, for experimental data, we quantify evidence for a possible linear temporal trend in estimates for the offset parameter.
3. Methods
3.1. Physical model
Following [10], to account for impedance mismatch effects, we model the ratio of the power spectral densities of resistor noise and QVNS noise, rmodel(f), as a dth order even polynomial function of frequency as follows
| (4) |
where d = 2imax, and f0 is a reference frequency (1 MHz in this work). Throughout this work, as shorthand, we refer to this model as a d = 2 model if imax = 1, a d = 4 model if imax = 2, and so on. The constant term, a0 in the Eq. 4 model corresponds to SR/SQ where SR and SQ are predicted by Eq. 1 and Eq 2. respectively.
3.2. Experimental data
Data was acquired for each of 45 runs of the experiment [10]. Each run occurred on a distinct day between June 12, 2014 to September 10, 2014. The time to acquire data for each run varied from 15 h to 20 h. For each run, Fourier transforms of time series corresponding to the resistor at the triple point of water temperature and the QVNS were determined at a resolution of 1 Hz for frequencies up to 2 MHz. Estimates of mean PSD were formed for frequency blocks of width 1.8 kHz. For the frequency block with midpoint f, for the ith run, we denote the mean PSD estimate for the resistor noise and QVNS noise for the ith run as SR,obs(f, i) and SQ,obs(f, i) respectively where i = 1,2, · · · 45.
Following [10], we define a reference value a0,calc for the offset term in our Eq. 4 model as
| (5) |
where k2010 is the CODATA2010 recommended value of the Boltzmann constant, R is the measured resistance of the resistor with traceability to the quantum Hall resistance, T is the triple point water temperature and SQ,calc is the calculated power spectral density of QVNS noise.
In the recent experiment the true value of the resistance, R, could have varied from run-to-run. Hence, in [10], R was measured for each run in a calibration experiment. Based on these calibration experiments, a0,calc was determined for each run. The difference between the maximum and minimum of the estimates determined from all 45 runs is 2.36 ×10−6. For the ith run, we denote the values a0 and a0,calc as a0(i) and a0,calc(i) respectively. Even though a0(i) and a0,calc(i) vary from run-to-run, we assume that temporal variation of their difference, a0(i)−a0,calc(i), is negligible. Later in this work, we check the validity of this key modeling assumption. The component of uncertainty of the estimate of a0,calc for any run due to imperfect knowledge of R is approximately 2 ×10−7. The estimated weighted mean value of our estimates, , is 1.000100961. The weights are determined from relative data acquisition times for the runs.
Following [10], for each frequency, we pool data from all 45 runs to form a numerator term and a denominator term . From these two terms, we estimate one ratio for each frequency as
| (6) |
(see Figure 1). From the Eq. 6 ratio spectrum, we estimate one residual offset term a0 − ā0,calc where ā0,calc is the weighted mean of a0,calc values from all runs.
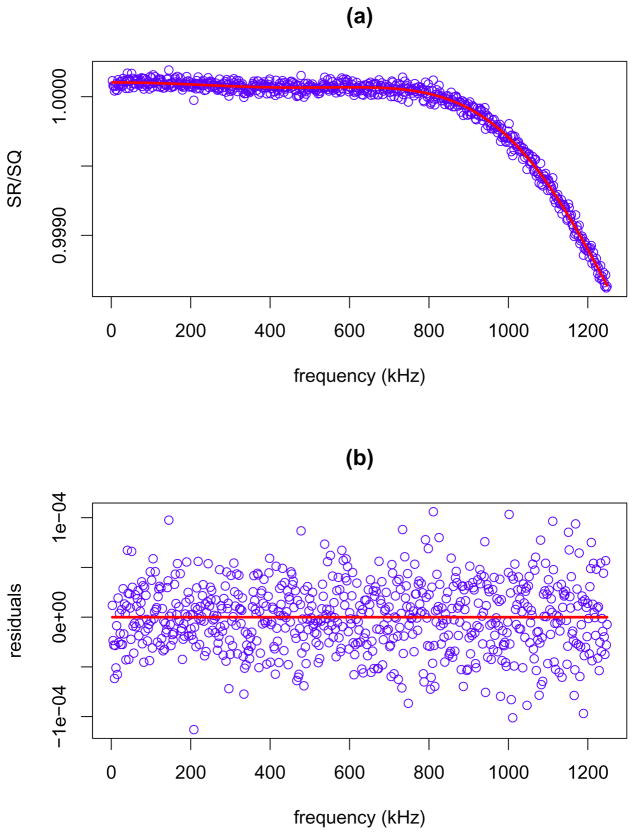
Figure 1.
Experimental data. (a) Observed (Eq. 6) and predicted ratio spectra based on selected model (d=8) and fitting bandwidth (1250 kHz) (see Table 3). (b) Residuals (observed - predicted).
3.3. Model selection method
In our cross-validation approach, we select the model that produces the prediction (determined from the training data) that is most consistent with the validation data. Since a0,calc varies from run-to-run, we correct SR,obs spectra so that our cross-validation statistic is not artificially inflated by run-to-run variations in a0,calc. The corrected ratio spectrum for the ith run is
| (7) |
where
| (8) |
In effect, given that our calibration experiment measurement of a0,calc(i) has negligible systematic error, the above correction returns produces a spectrum where the values of a0 should be nearly the same for all runs. We stress that after selecting the model based on cross-validation analysis of corrected spectra (see Eq. 7), we estimate a0 − ā0,calc from the uncorrected Eq. 6 spectrum.
In our cross-validation method, we generate 20 000 random five-way splits of the data. In each five-way split, we assign the pair of spectra, (SR,cor and SQ,obs), from any particular run to one of the five subsets by a resampling method. Each of the 45 spectral pairs appears in one and only one of the five subsets. We resample spectra according to run to retain possible correlation structure within the spectrum for any particular run. Each simulated five-way split is determined by a random permutation of the positive integers from 1 to 45. The first nine permuted integers corresponds to the runs assigned to the first subset. The second nine correspond to the runs assigned to the second subset, and so on. From each random split, four of the subsets are aggregated to form training data, and the other subset forms the validation data. Within the training data, we pool all SR,cor spectrum and all SQ,obs spectrum and form one ratio spectrum. Similarly, for the validation data, we pool all SR,obs spectrum and SQ,obs spectrum and form one ratio spectrum. We fit each candidate polynomial ratio spectrum model to the training data, and predict the observed ratio spectrum in the validation data based on this fit. We then compute the (empirical) mean squared deviation (MSD) between predicted and observed ratios for the validation data. For any random five-way split, there are five ways of defining the validation. Hence, we compute five MSD values for each random split. The cross-validation statistic for each d, CV(d), is the average of these five MSD values. For each random five-way split, we select the model that yields the smallest value of CV(d). Based on 20 000 random splits of the 45 spectra, we estimate a probability mass function p̂(d) where the possible values of d are: 2,4,6,8,10,12 or 14.
3.4. Uncertainty quantification
For any choice of fmax, suppose that d is known exactly. For this ideal case, based on a fit of the ratio spectrum model to the Eq. 6 ratio spectrum, we could construct a coverage interval for a0 with standard asymptotic methods or with a parametric bootstrap method [29]. For our application, we approximate the parametric bootstrap distribution of our estimate of a0 as a Gaussian distribution with mean â0 and variance , where is predicted by asymptotic theory. To account for the effect of uncertainty in d on our estimate of a0, we form a mixture of bootstrap distributions as follows
| (9) |
where g(x, μ, σ2) is the probability density function (pdf) for a Gaussian random variable with expected value μ and variance σ2. For any fmax, we select the d that yields the largest value of p̂(d). Given that the probability density function (pdf) of a random variable X is , and the mean and variance of a random variable Z with pdf fi(z) are μi and , the mean and variance of X are
| (10) |
and
| (11) |
Hence, the mean and variance of a random variable sampled from the Eq. 9 pdf are and respectively, where
| (12) |
and
| (13) |
where
| (14) |
and
| (15) |
For each fmax value, we estimate the uncertainty of our estimate of a0 as σ̂tot. We select fmax by minimizing σ̂tot on grid in frequency space. For any fitting bandwidth, σ̃β is the weighted-mean-square deviation of the estimates of a0 from the candidate models about their weighted mean value where the weights are the empirically determined selection fractions. The term σ̃α is the weighted variance of the parametric bootstrap sampling distributions for the candidate models where the weights are again the empirically determined selection fractions. We stress that both σ̃α and σ̃β are affected by imperfect knowledge of the ratio spectrum model.
4. Results
4.1. Analysis of Experimental data
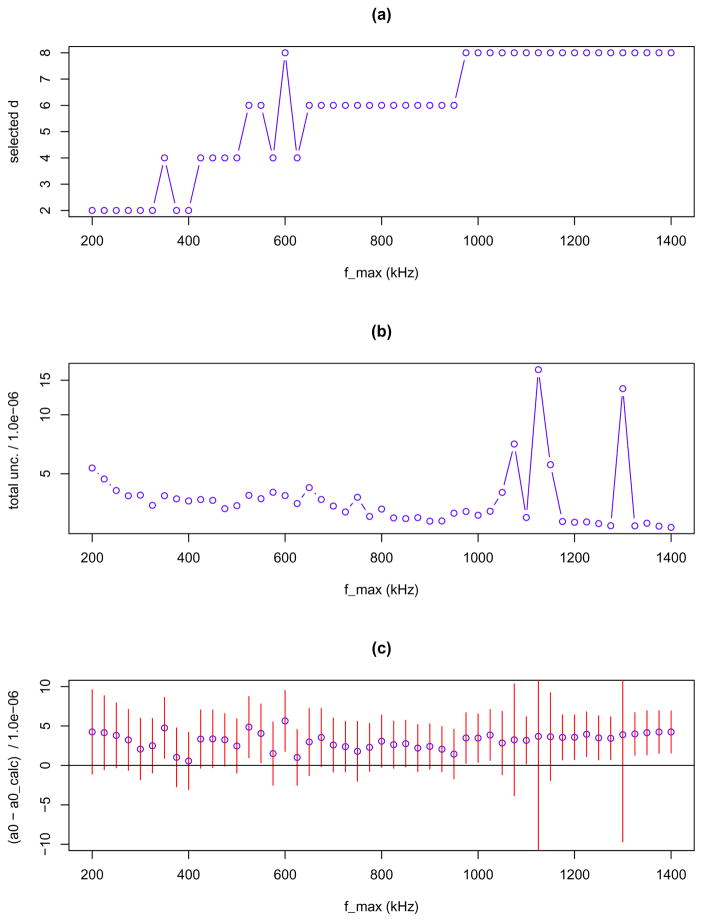
We fit candidate ratio spectrum models to the Eq. 6 observed ratio spectrum by the method of Least Squares (LS). We determine model selection fractions (Table 1) and σ̂tot (Table 2) for fmax values on an evenly space grid (with spacing of 25 kHz) between 200 kHz and 1400 kHz. In Figure 2, we show how selected d, σ̂tot and vary with fmax. Our method selects (fmax, d) = ( 1250 kHz, 8), σ̂tot,* = 3.25 ×10−6, and . In Figure 3, we show results for the values of fmax ( that yield the five lowest values of σ̂tot. For these five fitting bandwidths (900 kHz, 1150 kHz, 1175 kHz, 1225 kHz and 1250 kHz) σ̂tot values appear to follow no pattern as a function of frequency, however visual inspection suggests that the estimates of a0 − ā0,calc may follow a pattern. It is not clear if the variations in Figure 2 and 3 are due to random or systematic measurement effects. To get some insight into this issue, we study the performance of our method for idealized simulated data that are free of systematic measurement error.
Table 1.
Moodel selection fractions for polynomial models for experimental data.
| fmax (kHz) | selection fractions: p(d) | ||||||
|---|---|---|---|---|---|---|---|
| d=2 | d=4 | d=6 | d=8 | d=10 | d=12 | d=14 | |
| 200 | 0.7789 | 0.1269 | 0.0698 | 0.0046 | 0.0159 | 0.0039 | 0.0000 |
| 300 | 0.3271 | 0.2510 | 0.0000 | 0.4160 | 0.0047 | 0.0012 | 0.0000 |
| 400 | 0.0304 | 0.2234 | 0.6427 | 0.0017 | 0.0240 | 0.0716 | 0.0061 |
| 500 | 0.0249 | 0.6043 | 0.0010 | 0.2648 | 0.0701 | 0.0001 | 0.0349 |
| 525 | 0.1347 | 0.0960 | 0.0150 | 0.6758 | 0.0747 | 0.0037 | 0.0000 |
| 550 | 0.0290 | 0.7016 | 0.0000 | 0.0000 | 0.2668 | 0.0027 | 0.0000 |
| 575 | 0.0000 | 0.9446 | 0.0000 | 0.0000 | 0.0012 | 0.0513 | 0.0029 |
| 600 | 0.0000 | 0.9264 | 0.0003 | 0.0000 | 0.0002 | 0.0730 | 0.0000 |
| 625 | 0.0027 | 0.2192 | 0.1273 | 0.0746 | 0.0002 | 0.5289 | 0.0472 |
| 650 | 0.1072 | 0.0022 | 0.2342 | 0.1557 | 0.0006 | 0.0000 | 0.5001 |
| 675 | 0.0320 | 0.0287 | 0.6831 | 0.0077 | 0.0201 | 0.0000 | 0.2285 |
| 700 | 0.2659 | 0.0106 | 0.5514 | 0.0002 | 0.1718 | 0.0000 | 0.0002 |
| 725 | 0.0326 | 0.0181 | 0.8166 | 0.0159 | 0.1067 | 0.0101 | 0.0000 |
| 750 | 0.0700 | 0.0103 | 0.5985 | 0.1475 | 0.0242 | 0.1495 | 0.0001 |
| 775 | 0.0000 | 0.0863 | 0.2889 | 0.3968 | 0.1279 | 0.0980 | 0.0021 |
| 800 | 0.0000 | 0.0216 | 0.4607 | 0.4439 | 0.0017 | 0.0600 | 0.0120 |
| 825 | 0.0009 | 0.0667 | 0.8472 | 0.0320 | 0.0004 | 0.0168 | 0.0362 |
| 850 | 0.0000 | 0.0000 | 0.9294 | 0.0071 | 0.0034 | 0.0059 | 0.0541 |
| 875 | 0.0000 | 0.0000 | 0.8301 | 0.0344 | 0.0001 | 0.0000 | 0.1354 |
| 900 | 0.0278 | 0.0012 | 0.9357 | 0.0314 | 0.0030 | 0.0000 | 0.0009 |
| 925 | 0.0178 | 0.0002 | 0.6384 | 0.3411 | 0.0003 | 0.0000 | 0.0022 |
| 950 | 0.1015 | 0.0000 | 0.0135 | 0.8824 | 0.0022 | 0.0006 | 0.0000 |
| 975 | 0.0421 | 0.0212 | 0.0782 | 0.8560 | 0.0026 | 0.0000 | 0.0000 |
| 1000 | 0.0000 | 0.1072 | 0.1866 | 0.6441 | 0.0622 | 0.0000 | 0.0000 |
| 1025 | 0.0000 | 0.1704 | 0.0000 | 0.8158 | 0.0074 | 0.0029 | 0.0035 |
| 1050 | 0.0010 | 0.0000 | 0.0000 | 0.9751 | 0.0232 | 0.0007 | 0.0000 |
| 1075 | 0.0117 | 0.0001 | 0.0000 | 0.9646 | 0.0235 | 0.0000 | 0.0000 |
| 1100 | 0.0000 | 0.0021 | 0.0000 | 0.9976 | 0.0003 | 0.0000 | 0.0000 |
| 1125 | 0.0000 | 0.0000 | 0.0000 | 0.9519 | 0.0481 | 0.0000 | 0.0000 |
| 1150 | 0.0000 | 0.0000 | 0.0000 | 0.9962 | 0.0012 | 0.0016 | 0.0010 |
| 1175 | 0.0000 | 0.0000 | 0.0000 | 0.9996 | 0.0000 | 0.0003 | 0.0000 |
| 1200 | 0.0000 | 0.0002 | 0.0000 | 0.7125 | 0.1578 | 0.1269 | 0.0027 |
| 1225 | 0.0000 | 0.0000 | 0.0000 | 0.9998 | 0.0002 | 0.0000 | 0.0000 |
| 1250 | 0.0000 | 0.0000 | 0.0000 | 0.9427 | 0.0571 | 0.0003 | 0.0000 |
| 1275 | 0.0000 | 0.0000 | 0.0000 | 0.4784 | 0.5181 | 0.0034 | 0.0000 |
| 1300 | 0.0000 | 0.0000 | 0.0000 | 0.1782 | 0.5986 | 0.2231 | 0.0000 |
| 1325 | 0.0000 | 0.0000 | 0.0000 | 0.0010 | 0.1050 | 0.8885 | 0.0055 |
| 1350 | 0.1879 | 0.2538 | 0.0000 | 0.0000 | 0.0000 | 0.2315 | 0.3268 |
| 1375 | 0.0362 | 0.0322 | 0.0000 | 0.0000 | 0.1788 | 0.7038 | 0.0491 |
| 1400 | 0.2812 | 0.0593 | 0.0000 | 0.0000 | 0.4527 | 0.0060 | 0.2007 |
Table 2.
Results for experimental data.
| fmax (kHz) | d |
|
σ̂â0(d),ran ×106 |
|
σ̃α ×106 | σ̃β ×106 | σ̂tot ×106 | ||
|---|---|---|---|---|---|---|---|---|---|
| 200 | 2 | −0.57 | 4.15 | −1.97 | 4.57 | 3.173 | 5.564 | ||
| 300 | 8 | −7.58 | 5.62 | −2.71 | 4.67 | 4.348 | 6.380 | ||
| 400 | 6 | −2.09 | 4.40 | −1.35 | 4.41 | 3.041 | 5.357 | ||
| 500 | 4 | 1.88 | 3.47 | 0.39 | 4.00 | 2.133 | 4.535 | ||
| 525 | 8 | −0.42 | 4.38 | −0.75 | 4.13 | 1.255 | 4.319 | ||
| 550 | 4 | 1.90 | 3.26 | 0.51 | 3.69 | 2.179 | 4.290 | ||
| 575 | 4 | 1.81 | 3.18 | 1.48 | 3.31 | 1.360 | 3.579 | ||
| 600 | 4 | 2.21 | 3.14 | 1.79 | 3.30 | 1.473 | 3.618 | ||
| 625 | 12 | −2.65 | 4.83 | −1.04 | 4.31 | 2.295 | 4.886 | ||
| 650 | 14 | −5.09 | 5.05 | −2.35 | 4.34 | 4.384 | 6.167 | ||
| 675 | 6 | 3.55 | 3.49 | 1.36 | 3.88 | 3.455 | 5.197 | ||
| 700 | 6 | 2.88 | 3.40 | −0.95 | 3.32 | 5.318 | 6.271 | ||
| 725 | 6 | 2.63 | 3.37 | 1.92 | 3.46 | 2.345 | 4.177 | ||
| 750 | 6 | 1.99 | 3.39 | 0.97 | 3.61 | 3.270 | 4.874 | ||
| 775 | 8 | 3.88 | 3.72 | 1.78 | 3.68 | 2.422 | 4.404 | ||
| 800 | 6 | 1.15 | 3.29 | 1.96 | 3.57 | 1.699 | 3.953 | ||
| 825 | 6 | 1.64 | 3.31 | 0.92 | 3.39 | 2.454 | 4.182 | ||
| 850 | 6 | 1.61 | 3.25 | 1.50 | 3.36 | 0.545 | 3.403 | ||
| 875 | 6 | 1.29 | 3.21 | 1.07 | 3.45 | 0.735 | 3.530 | ||
| 900 | 6 | 1.44 | 3.17 | 1.36 | 3.17 | 0.769 | 3.266 | ||
| 925 | 6 | 1.03 | 3.13 | 1.49 | 3.27 | 0.656 | 3.334 | ||
| 950 | 8 | 2.85 | 3.51 | 3.12 | 3.44 | 0.994 | 3.577 | ||
| 975 | 8 | 2.35 | 3.44 | 2.04 | 3.39 | 4.020 | 5.261 | ||
| 1000 | 8 | 1.97 | 3.41 | −1.29 | 3.33 | 8.390 | 9.028 | ||
| 1025 | 8 | 2.73 | 3.44 | −2.49 | 3.41 | 11.510 | 12.010 | ||
| 1050 | 8 | 2.90 | 3.40 | 2.91 | 3.41 | 0.968 | 3.549 | ||
| 1075 | 8 | 2.94 | 3.37 | 3.38 | 3.40 | 4.185 | 5.394 | ||
| 1100 | 8 | 2.78 | 3.37 | 2.69 | 3.37 | 1.842 | 3.837 | ||
| 1125 | 8 | 3.13 | 3.34 | 3.09 | 3.36 | 0.343 | 3.372 | ||
| 1150 | 8 | 2.69 | 3.30 | 2.69 | 3.30 | 0.329 | 3.315 | ||
| 1175 | 8 | 2.82 | 3.30 | 2.82 | 3.30 | 0.012 | 3.301 | ||
| 1200 | 8 | 2.18 | 3.28 | 2.34 | 3.42 | 0.780 | 3.511 | ||
| 1225 | 8 | 2.62 | 3.25 | 2.62 | 3.25 | 0.002 | 3.253 | ||
| 1250 | 8 | 2.36 | 3.22 | 2.40 | 3.24 | 0.145 | 3.246 | ||
| 1275 | 10 | 3.13 | 3.53 | 2.56 | 3.38 | 0.592 | 3.431 | ||
| 1300 | 10 | 3.52 | 3.48 | 2.88 | 3.49 | 0.863 | 3.597 | ||
| 1325 | 12 | 2.23 | 3.76 | 2.42 | 3.73 | 0.553 | 3.774 | ||
| 1350 | 14 | 3.38 | 4.05 | 25.47 | 6.62 | 90.27 | 90.52 | ||
| 1375 | 12 | 2.82 | 3.81 | 9.22 | 4.54 | 43.23 | 43.47 | ||
| 1400 | 10 | 4.32 | 3.57 | 68.13 | 8.41 | 112.2 | 112.5 |
Figure 2.
Experimental data. (a) Estimated polynomial complexity parameter d. (b) Estimated total uncertainty σ̂tot (Eq. 13). (c) Estimated a0 − ā0,calc and approximate 68 % coverage interval.
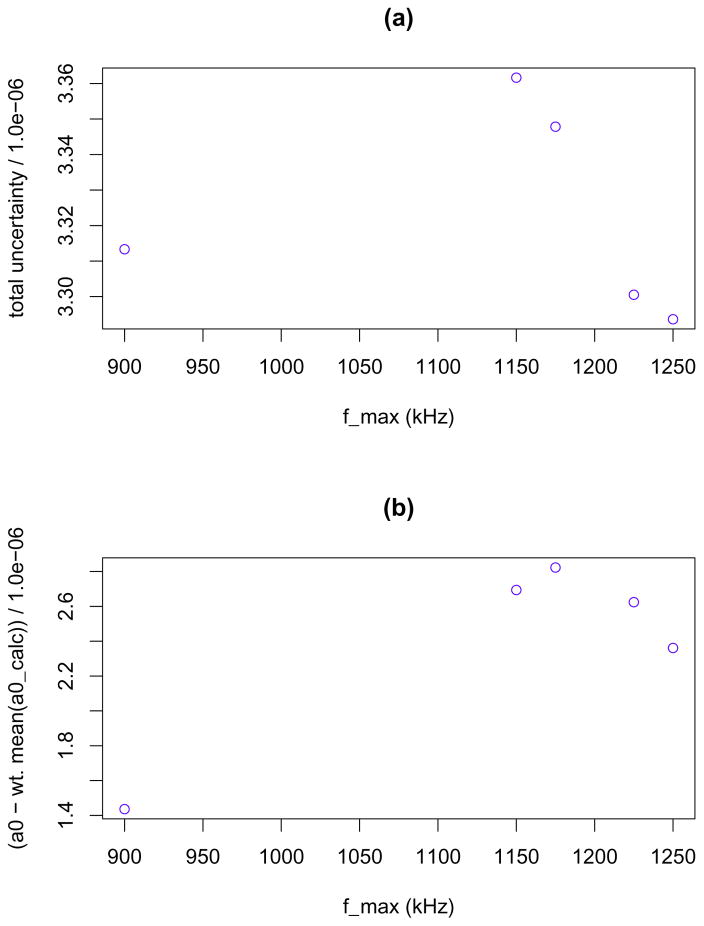
Figure 3.
Experimental data. Results for fmax values which yield the five lowest values of σ̂tot. (a) σ̂tot versus fmax. (b) Estimated a0 − ā0,calc versus fmax.
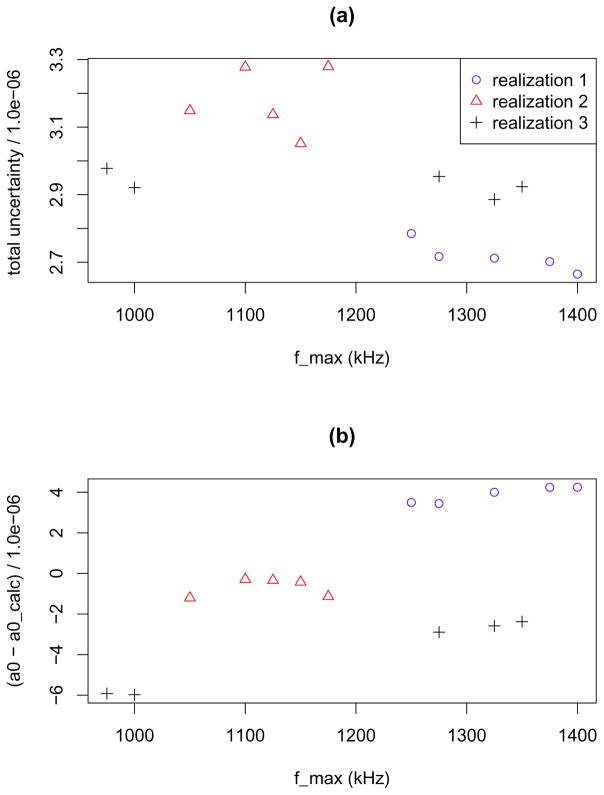
We simulate three realizations of data based on the estimated values of a2, a4, a6 and a8 in Table 3. In our simulation, for each run, we set a0 − a0,calc = 0, SQ,obs(f) = 1 and SR,obs(f) equals the sum of the predicted ratio spectrum and Gaussian white noise. For each run, the variance of the noise is determined from fitting the ratio spectrum model to the experimental ratio spectrum for that run. For simulated data, the d, σ̂tot and â0−a0,calc spectra exhibit fluctuations similar to those in the experimental data (Figures 4,5,6). Since variability in simulated data (Figures 4,5,6) is due solely to random effects, we can not rule out the possibility that random effects may have produced the fluctuations in the experimental spectra (Figures 2 and 3). For the third realization of simulated data (Figure 6), the estimated values of a0 − a0,calc corresponding to the fmax values that yield the five lowest values of σ̂tot form two clusters in fmax space which are separated by approximately 300 kHz (Figure 7). This pattern is similar to that observed for the experimental data (Figures 3). As a caveat, for the experimental data, we can not rule out the possibility that systematic measurement error could cause or enhance observed fluctuations.
Table 3.
Estimated model parameters for experimental data for fmax = 1250 kHz.
| parameter | estimate |
|---|---|
| a0 − ā0,calc | 2.36 (3.22) ×10−6 |
| a2 | −4.33 (0.41) ×10−4 |
| a4 | 1.66 (0.13) ×10−3 |
| a6 | −2.25 (0.13) ×10−3 |
| a8 | 6.26 (0.46) ×10−4 |
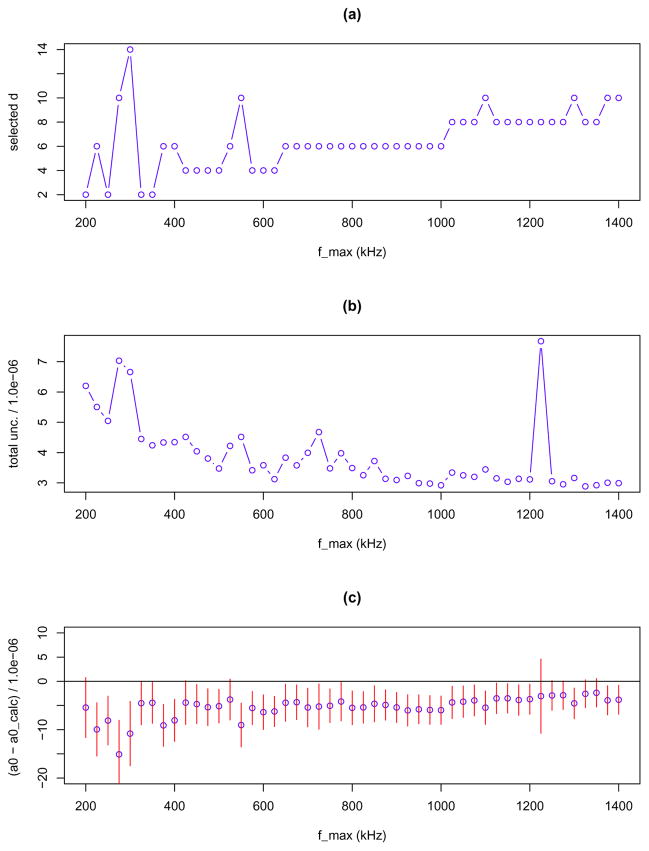
Figure 4.
Simulated data (realization 1). (a) Estimated polynomial complexity parameter d. (b) Estimated total uncertainty σ̂tot. (c) Estimated a0 − a0,calc and approximate 68 % coverage interval. The true value of a0 − a0,calc is 0.
Figure 5.
Simulated data (realization 2). (a) Estimated polynomial complexity parameter d. (b) Estimated total uncertainty σ̂tot. (c) Estimated a0 − a0,calc and approximate 68 % coverage interval. The true value of a0 − a0,calc is 0.
Figure 6.
Simulated data (realization 3). (a) Estimated polynomial complexity parameter d. (b) Estimated total uncertainty σ̂tot. (c) Estimated a0 − a0,calc and approximate 68 % coverage interval. The true value of a0 − a0,calc is 0.
Figure 7.
Simulated data. Results for fmax values which yield the five lowest values of σ̂tot. (a) σ̂tot versus fmax. (b) estimated a0 − a0,calc versus fmax. The true value of a0 − a0,calc is 0.
Our method correctly selects the d=8 model for each of three independent realizations of simulation data (Table 4). In a second study, we simulate three realizations of data according to a d=6 polynomial model based on the fit to experimental data for fmax = 900 kHz. Our methods correctly selects the d=6 for each of the three realizations.
Table 4.
Comparison of selected fmax and associated model parameters for experimental and simulated data sets. In the simulation, the true values of a0 −a0,calc and d are 0 and 8 respectively. The component of uncertainty σ̂fmax accounts for imperfect performance of our fmax selection method.
| fmax (kHz) | d |
|
σ̂â 0(d),ran ×106 |
|
σ̃α ×106 | σ̃β ×106 | σ̂tot,* ×106 | σ̂fmax ×106 | σ̂tot,final ×106 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| experimental | 1250 | 8 | 2.36 | 3.22 | 2.40 | 3.24 | 0.14 | 3.25 | 0.56 | 3.29 | ||
| realization 1 | 1400 | 8 | 4.25 | 2.64 | 4.20 | 2.66 | 0.18 | 2.67 | 0.39 | 2.69 | ||
| realization 2 | 1150 | 8 | −0.43 | 2.98 | −0.39 | 3.00 | 0.59 | 3.05 | 0.45 | 3.08 | ||
| realization 3 | 1325 | 8 | −2.59 | 2.76 | −2.88 | 2.82 | 0.60 | 2.89 | 1.83 | 3.42 |
In [10], our method selected fmax = 575 kHz and d = 4 when fmax was constrained to be less than 600 kHz. For these selected values, our current analysis yields and σ̂tot = 3.58 ×10−6. In this study, when fmax is allowed to be as large as 1400 kHz, our method selects fmax = 1250 Hz and d = 8, and and σ̂tot,* = 3.25 ×10−6. The difference between the two results, 0.55 ×10−6, is small compared to the uncertainty of either result.
We expect imperfections in our fitting bandwidth selection method for various reasons. First, we conduct a grid search with a resolution of 25 kHz rather than a search over a continuum of frequencies. Second, there are surely fluctuations in σ̂tot due to random effects that vary with fitting bandwidth. Third, different values of fmax can yield very similar values of σ̂tot but somewhat different values of . Therefore, it is reasonable to determine an additional component of uncertainty, σ̂fmax, that accounts for uncertainty due to imperfect performance of our method to select fmax. Here we equate σ̂fmax to the estimated standard deviation of estimates of a0 − ā0,calc corresponding to the five fmax values that yielded the lowest σ̂tot values (Figures 3 and 7). For the three realizations of simulated spectra, the corresponding σ̂fmax values are 0.39 ×10−6, 0.45 ×10−6, and 1.83 ×10−6. For the experimental data σ̂fmax = 0.56 ×10−6. For both simulated and experimental data, our update for the total uncertainty of estimated a0 is σ̂tot,final where
| (16) |
For the simulated data, σ̂tot,final is 2.69 ×10−6, 3.08 ×10−6, and 3.42 ×10−6. For the experimental data, σ̂tot,final = 3.29 ×10−6. As a caveat, the choice to quantify σ̂fmax as the standard deviation of the estimates corresponding to fmax values that yield the five lowest values is based on scientific judgement. For instance, if we determine based on the the fmax values that yield the ten lowest rather the five lowest values σ̂tot, for the three simulation cases and the observed data we get σ̂fmax = 0.55 ×10−6, 1.08 ×10−6, 1.42 ×10−6, and 0.73 ×10−6 respectively.
4.2. Stability analysis
From the corrected Eq.7 spectra, we estimate a0 − ā0,calc for each of the 45 runs by fitting our selected ratio spectrum model (d = 8 and fmax = 1250 kHz) to the data from each run by the method of LS (Figure 8). Ideally, on average, these estimates should not vary from run-to-run assuming that our Eq. 8 correction model based on calibration data is valid. From these estimates, we determine the slope and intercept parameters for a linear trend model by the method of Weighted Least Squares (WLS) where we minimize
Figure 8.
From the corrected ratio spectrum (Eq. 7), we estimate a0 − ā0,calc for each run by fitting a d = 8 ratio spectrum model by the method of Least Squares. The half-widths of the intervals are asymptotic uncertainties determined by the Least Squares method. The fitting bandwidth is fmax = 1250 kHz.
| (17) |
Above, for the ith run, yi and ŷi are the estimated and predicted (according to the trend model) values of a0 − ā0,calc, and wi is the inverse of the squared asymptotic uncertainty of associated with our estimate determined by the LS fit to data from the ith run. We determine the uncertainty of the trend model parameters with a nonparametric bootstrap method (see Appendix 1) following [30] (Table 5). We repeat the bootstrap procedure but set ŷi to a constant. This analysis yields an estimate of the null distribution of the slope estimate corresponding to the hypothesis that there is no trend. The fraction of bootstrap slope estimates with magnitude greater than or equal to the magnitude of the estimated slope determined from the observed data is the bootstrap p-value [29] corresponding to a two-tailed test of the null hypothesis. For the fmax values that yield the five lowest values of σ̂tot, our bootstrap analysis provides strong evidence that a0 − ā0,calc varies with time. At the value of fmax = 575 kHz, there is a moderate amount of evidence for a trend.
Table 5.
Estimated trend model parameters, associated uncertainties and p-values for testing the no-trend hypothesis (column 5). Based on and the number of degrees-of-freedom (43), we determine a p-value (column 7) for testing the hypothesis that the linear trend model is consistent with observations. The value fmax = 575 kHz corresponds to selected fitting bandwidth in [10]. The five values (ranging from 900 kHz to 1250 kHz) yield the five lowest values of σ̂tot when fmax is varied from 200 kHz to 1400 kHz on a grid. For comparison, we list results at fitting bandwidths of 200 kHz, 300 kHz, 400 kHz, 500 kHz, 700 kHz and 800 kHz. In the last column, we list estimates of a0 − ā0,calc from the pooled data and their associated σ̂tot values in parentheses. (Table 2).
| fmax (kHz) | d | intercept ×106 | slope ×106 day | p-value (trend test) |
|
p-value (model consistency test) | a0 − ā0,calc ×106 | |
|---|---|---|---|---|---|---|---|---|
| 200 | 2 | 11.98(6.50) | −0.243(0.125) | 0.050 | 33.0 | 0.864 | −0.57(5.56) | |
| 300 | 8 | 11.74(10.54) | −0.440(0.199) | 0.027 | 47.0 | 0.311 | −7.58(6.38) | |
| 400 | 6 | 10.31(6.64) | −0.247(0.126) | 0.062 | 35.8 | 0.775 | −2.09(5.36) | |
| 500 | 4 | 10.69(5.12) | −0.175(0.097) | 0.072 | 32.6 | 0.877 | 1.88(4.54) | |
| 575 | 4 | 10.13 (4.42) | −0.164 (0.084) | 0.049 | 28.2 | 0.960 | 1.81(3.58) | |
| 700 | 6 | 13.56(4.95) | −0.213(0.093) | 0.021 | 31.0 | 0.914 | 2.88(6.27) | |
| 800 | 6 | 10.49(3.94) | −0.175(0.074) | 0.018 | 22.5 | 0.996 | 1.15(3.95) | |
| 900 | 6 | 9.15 (3.49) | −0.164 (0.066) | 0.012 | 19.9 | 0.999 | 1.44(3.27) | |
| 1150 | 8 | 11.39 (3.79) | −0.179 (0.071) | 0.011 | 23.2 | 0.994 | 2.69(3.32) | |
| 1175 | 8 | 11.57 (3.81) | −0.185 (0.072) | 0.010 | 24.0 | 0.991 | 2.82(3.30) | |
| 1225 | 8 | 12.13 (3.79) | −0.204 (0.071) | 0.004 | 25.0 | 0.987 | 2.62(3.25) | |
| 1250 | 8 | 12.02 (3.78) | −0.202 (0.071) | 0.004 | 25.2 | 0.986 | 2.36(3.25) |
For each fmax choice, we test the hypothesis that the linear trend is consistent with observations based on the value of . If the observed data are consistent with the trend model, a resulting p-value from this test is realization of a random variable with a distribution that is approximately uniform between 0 and 1. Hence, the large p-values reported column 7 of Table 5 suggest that the asymptotic uncertainties determined by the LS method for each run may be inflated. As a check, we estimate the slope uncertainty with a parametric bootstrap method where we simulate bootstrap replications of the observed data by adding Gaussian noise to the estimated trend with standard deviations equal to the asymptotic uncertainties determined by the LS method. In contrast to the method from [30], the parametric bootstrap method yields larger slope uncertainties. For instance, for the 1250 kHz and 575 kHz cases, the parametric bootstrap slope uncertainty estimates are larger than the corresponding Table 5 estimates by 30 % and 23 % respectively. That is, the parametric bootstrap method estimates are inflated with respect to the estimates determined with the method from [30].
This inflation could result due to heteroscedasticity (frequency dependent additive measurement error variances). This follows from the well-known fact that when models are fit to heteroscedastic data, the variance of parameter estimates determined by the LS method are larger than the variance of parameter estimates determined by the ideal WLS method. Based on fits of selected models to data pooled from all runs, we test the hypothesis that the variance of the additive noise in the ratio spectrum is independent of frequency. Based on the Breush-Pagan method [31], the p-values corresponding to the test of this hypothesis are 0.723, 0.064, 0.006, 0.001, 0.001 and 0.001 for fitting bandwidths of 575 kHz, 900 kHz, 1150 kHz, 1175 kHz, 1225 kHz, and 1250 kHz respectively. Hence, the evidence for heteroscedasticity is very strong for the larger fitting bandwidths.
For a fitting bandwidth of 1250 kHz, the variation of the estimated trend over the duration of the experiment is 18.2 × 10−6. In contrast, the uncertainty of our estimate of a0 − ā0,calc determined under the assumption that there is no trend is only 3.29 ×10−6 (Table 4). The evidence for a linear trend at particular fitting bandwidths above 900 kHz is strong (p-values are 0.012 or less) (column 5 in Table 5). In contrast, the evidence (from hypothesis testing) for a linear trend at 575 kHz (the selected fitting bandwidth in [10]) is not as strong since the p-value is 0.049. However, the larger p-value at 575 kHz may be due to more random variability in the estimated offset parameters rather than lack of a deterministic trend in the offset parameters. This hypothesis is supported by the observation that the uncertainty of the estimated slope parameter due to random effects generally increases as the fitting bandwidth is reduced, and that fact that all of the slope parameter estimates for cases shown in Table 5 are negative and vary from −0.440 ×10−6/day to −0.164 ×10−6/day. Together, these observations strongly suggest a deterministic trend in measured offset parameters at a fitting bandwidth of 575 kHz. Currently, experimental efforts are underway to understand the physical source of this (possible) temporal trend.
If there is a linear temporal trend in the offset parameters at a fitting bandwidth of 575 kHz, with slope similar to what we estimate from data, the reported uncertainty for the Boltzmann constant reported in [10] is optimistic because the trend was not accounted for in the uncertainty budget. To account for the effect of a linear trend on results, one must estimate the associated systematic error due to the trend at some particular time. Unfortunately, we have no empirical method to do this. As a further complication, if there is a trend, it may not be exactly linear.
5. Summary
For electronic measurements of the Boltzmann constant by JNT, we presented a data-driven method to select the complexity of a ratio spectrum model with a cross-validation method. For each candidate fitting bandwidth, we quantified the uncertainty of the offset parameter in the spectral ratio model in a way that accounts for random effects as well as systematic effects associated with imperfect knowledge of model complexity. We selected the fitting bandwidth that minimizes this uncertainty. We also quantified an additional component of uncertainty that accounts for imperfect knowledge of the selected fitting bandwidth. With our method, we re-analyzed data from a recent experiment by considering a broader range of fitting bandwidths and found evidence for a temporal linear trend in offset paramaters. For idealized simulated data free of systematic error with additive noise similar to experimental data, our method correctly selected the true complexity of the ratio spectrum model for all cases considered. In the future, we plan to study how well our methods work for other experimental and simulated JNT data sets with variable signal-to-noise ratios and investigate how robust our method is to systematic measurement errors. We expect our method to find broad metrological applications including selection of optimal virial equation models in gas thermometry experiments, and selection of linewidth models in Doppler broadening thermometry experiments.
Acknowledgments
Contributions of staff from NIST, an agency of the US government, are not subject to copyright in the US. JNT research at NIM is supported by grants NSFC (61372041 and 61001034). Jifeng Qu acknowledges Samuel P. Benz, Alessio Pollarolo, Horst Rogalla, Weston L. Tew of the NIST and Rod White of MSL, New Zealand for their help with the JNT measurements analyzed in this work. We also thank Tim Hesterberg of Google for helpful discussions.
6. Appendix 1: nonparametric bootstrap resampling method
We denote the estimate of a0 − ā0,calc from the ith run as yi, and the data acquisition time for the ith run as ti. Our linear trend model is
| (18) |
where the observed data is y = (y1, y2 · · · y45)T, ε is an additive noise term, and the matrix X is
and β = (β0, β1)T where the β0 is the intercept parameter and β1 is the slope parameter. Above, we model the ith component of ε as a realization of a random variable with expected value 0 and variance κVi where Vi is known but κ is unknown. Following [30], the predicted value in a linear regression model is ŷ = Xβ̂ where the estimated model parameters β̂ are
| (19) |
where W is a diagonal weight matrix. Here, we set the jth component of W to where Vj is the estimated asymptotic variance of yi determined by the method of LS. Following [30], we form a modified residual
| (20) |
where hi is the ith diagonal element of the hat matrix H = X(XTWX)−1XTW. This transformation ensures that the modified residuals are realizations of random variables with nearly the same variance. The ith component of a bootstrap replication of the observed data is
| (21) |
where i = 1, 2, · · · 45 and ( ) is sampled with replacement from (r1− r̄, r2− r̄, · · · r45− r̄) where r̄ is the mean modified residual. From each of 50 000 bootstrap replications of the observed data, we determine a slope and intercept parameter. The bootstrap estimate of the uncertainty of the slope and intercept parameters are the estimated standard deviations of the slope and intercept parameters determined from these estimates.
7. Appendix 2: Summary of model selection and uncertainty quantification method
Based on a calibration data estimate of a0,calc for each run, correct SR,obs spectra per Eq. 8.
Set fitting bandwidth to fmax = 200 kHz.
Set resampling counter to nresamp = 1.
Randomly split SR,cor and SQ,obs spectral pairs from each of 45 runs into five subsets. Select d by five-fold cross-validation and update appropriate model selection fraction estimate.
Increase nresamp by 1.
If nresamp < 20 000, go to 4.
If nresamp = 20 000, select the polynomial model with largest associated selection fraction. Calculate estimate of residual offset and its uncertainty σ̂tot,final (Eq. 16) from pooled uncorrected spectrum (see Eq. 6).
Increase fmax by 25 kHz and go to 3 if fmax < 1400 kHz.
Select fmax by minimizing σ̂tot. Denote the minimum value as σ̂tot,*.
Assign component of uncertainty associated with imperfect performance of method to select fmax as σ̂fmax to estimated standard deviation of offset estimates corresponding to fmax values that yield the five lowest values of σ̂tot. Our final estimate of the uncertainty of the offset is .
For completeness, we note that simulations and analyses were done with software scripts developed in the public domain R [32] language and environment. Please contact Kevin Coakley regarding any software-related questions.
References
- 1.Moldover MR, Trusler JPM, Edwards TJ, Mehl JB, Davis RS. Measurement of the universal gas constant using a spherical acoustic resonator. J Res Natl Bur Stand. 1988;93:85–144. doi: 10.1103/PhysRevLett.60.249. [DOI] [PubMed] [Google Scholar]
- 2.Pitre L, Sparasci F, Truong D, Guillou A, Risegari L, Himbert ME. Determination of the Boltzmann constant using a quasi-spherical acoustic resonator. Int J Thermophys. 2011;32:1825–1886. doi: 10.1098/rsta.2011.0197. [DOI] [PubMed] [Google Scholar]
- 3.de Podesta M, Underwood R, Sutton G, Morantz P, Harris P, Mark DF, Stuart FM, Vargha G, Machin G. A low-uncertainty measurement of the Boltzmann constant. Metrologia. 2013;50:354–76. [Google Scholar]
- 4.Gavioso RM, Benedetto G, Albo PAG, Ripa DM, Merlone A, Guianvarc’h C, Moro F, Cuccaro R. A determination of the Boltzmann constant from speed of sound measurements in helium at a single thermodynamic state. Metrologia. 2010;47:387–409. [Google Scholar]
- 5.Lin H, Feng XJ, Gillis KA, Moldover MR, Zhang JT, Sun JP, Duan YY. Improved determination of the Boltzmann constant using a single, fixed-length cylindrical cavity. Metrologia. 2013;50:417–32. doi: 10.1088/1681-7575/aa7b4a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Gaiser C, Zandt T, Fellmuth B, Fischer J, Gaiser C, Jusko O, Priruenrom T, Sabuga W, Zandt T. Improved determination of the Boltzmann constant by dielectric-constant gas thermometry. Metrologia vol. 2011;48:382–390. L7–L11. [Google Scholar]
- 7.Gaiser C, Fellmuth B. Low-temperature determination of the Boltzmann constant by dielectric-constant gas thermometry. Metrologia vol. 2012;49:L4–L7. [Google Scholar]
- 8.Benz SP, White DR, Qu J, Rogalla H, Tew WL. Electronic measurement of the Boltzmann constant with a quantum-voltage-calibrated Johnson-noise thermometer. C R Physique. 2009;10:849858. [Google Scholar]
- 9.Benz SP, Pollarolo A, Qu JFH, Rogalla Urano C, Tew WL, Dresselhaus PD, White DR. An electronic measurement of the Boltzmann constant. Metrologia vol. 2011;48:142–153. [Google Scholar]
- 10.Jifeng Q, Benz S, Pollarolo A, Rogalla H, Tew W, White D, Zhou K. Improved electronic measurement of the Boltzmann constant by Johnson noise thermometry. Metrologia, vol. 2015;52:S242–S256. doi: 10.1088/1681-7575/aa781e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Bord CJ. Atomic clocks and inertial sensors. Metrologia. 2002;39:435463. [Google Scholar]
- 12.Fasci E, De Vizia MD, Merlone A, Moretti L, Castrillo A, Gianfrani L. The Boltzmann constant from the H2 18O vibrationrotation spectrum: complementary tests and revised uncertainty budget. Metrologia. 2015;52:S233S241. [Google Scholar]
- 13.Kamper RA. Survey of noise thermometry. Temperature, its measurement and control in science and industry. Instrument Society of America. 1972;4:349–354. [Google Scholar]
- 14.Blalock TV, Shepard RL. A decade of progress in high temperature Johnson noise therometry. Temperature, its measurement and control in science and industry, 5, Instrument Society of America. 1982:1219–1223. [Google Scholar]
- 15.White DR, Galleano R, Actis A, Brixy H, de Groot M, Dubbeldam J, Reesink A, Edler F, Sakurai H, Shepard RL, Gallop JC. The status of Johnson noise thermometry. Metrologia. 1996;33:325–335. [Google Scholar]
- 16.Akaike H. Information theory and an extension of the maximum likelihood principle. In: Petrov BN, Czaki F, editors. Second International Symposium on Information Theory; Akademiai Kiado, Budapest. 1973. pp. 267–81. 2010. [Google Scholar]
- 17.Schwartz G. Estimating the dimension of a model. Ann Statistic. 1978;9:130–134. [Google Scholar]
- 18.Mallows C. Some comments on Cp. Technometrics. 1973;15:661–675. [Google Scholar]
- 19.Stone C. Cross-validatory choice and assessment of statistical predictions. Journal of the Royal Statistical Society Series B (Methodological) 1974;36(2):111–147. [Google Scholar]
- 20.Stone C. An Asymptotic Equivalence of Choice of Model by Cross-Validation and Akaike’s Criterion. Journal of the Royal Statistical Society. Series B (Methodological) 1977;39(1):44–47. [Google Scholar]
- 21.Arlot S, Celisse A. Asurvey of cross-validation procedures for model selection. Statistical Surveys. 2010;4:40–79. [Google Scholar]
- 22.Hastie T, Tibshirani R, Friedman JH. The Elements of Statistical Learning. 2. Springer-Verlag; 2008. p. 763. [Google Scholar]
- 23.Burnham KP, Anderson DR. Model Selection and Multimodel Inference: A Practical Information-Theoretical Approach. 2. Springer-Verlag; New York: 2002. [Google Scholar]
- 24.Claeskens G, Hjort NL. Model Selection and Model Averaging. Cambridge University Press; New York: 2008. [Google Scholar]
- 25.Picard RR, Cook RD. Cross-validation of regression models. Journal of the American Statistical Association. 2004;79:575–583. [Google Scholar]
- 26.Shao J. Linear model selection by cross-validation. Journal of the American Statistical Association. 1993;88:486–494. [Google Scholar]
- 27.Xu QS, Liang YZ, Zu YP. Monte Carlo cross-validation for selecting a model and estimating the prediction error in multivariate calibration. Journal of Chemometrics. 2004;18:112–120. [Google Scholar]
- 28.Efron B. Estimation and accuracy after model selection. Journal of the American Statistical Association. 2014;109(507) doi: 10.1080/01621459.2013.823775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Efron B, Tibshirani RJ. Monographs and Statistics and Applied Probability. CRC Press; 1993. An Introduction to the Bootstrap; p. 57. [Google Scholar]
- 30.Davison, Hinkley . Bootstrap Methods and Their Applications. Cambridge University Press; Cambridge: 1997. [Google Scholar]
- 31.Breusch TS, Pagan AR. A simple test for heteroscedasticity and random coefficient variation. Econometrica. 1979;47:1287–1294. [Google Scholar]
- 32.R Core Team. R: A language and environment for statistical computing. R Foundation for Statistical Computing; Vienna, Austria: 2015. https://www.R-project.org/ [Google Scholar]