Mapping Cell Membrane Fluctuations Reveals Their Active Regulation and Transient Heterogeneities

Abstract

Shape fluctuations of the plasma membrane occur in all cells, are incessant, and are proposed to affect membrane functioning. Although studies show how membrane fluctuations are affected by cellular activity in adherent cells, their spatial regulation and the corresponding change in membrane mechanics remain unclear. In this article, we study how ATP-driven activities and actomyosin cytoskeleton impact basal membrane fluctuations in adherent cells. Using interference imaging, we map height fluctuations within single cells and compare the temporal spectra with existing theoretical models to gain insights about the underlying membrane mechanics. We find that ATP-dependent activities enhance the nanoscale z fluctuations but stretch out the membrane laterally. Although actin polymerization or myosin-II activity individually enhances fluctuations, the cortex in unperturbed cells stretches out the membrane and dampens fluctuations. Fitting with models suggest this dampening to be due to confinement by the cortex. However, reduced fluctuations on mitosis or on ATP-depletion/stabilization of cortex correlate with increased tension. Both maps of fluctuations and local temporal autocorrelation functions reveal ATP-dependent transient short-range (<2 μm) heterogeneities. Together, our results show how various ATP-driven processes differently affect membrane mechanics and hence fluctuations, while creating distinct local environments whose functional role needs future investigation.

Introduction

Plasma membrane deformations are associated with several of its functions such as motility, cell division, vesicle trafficking, mechanoresponse, etc. (1, 2). Fluctuation spectra of deformations capture parameters responsible for deformability of the membrane. Governed by viscoelastic properties of the membrane, fluctuations are powered by thermal energy as well as ATP-driven processes. The temporal range of fluctuations reported is quite broad. Slow (10 s) actin waves drive large wavelength fluctuations (100 nm–10 μm) at cell edges and basal membrane (3, 4, 5). They are accompanied by fluctuations with relatively smaller amplitudes (5–50 nm) that are more prominently observed at basal membrane (6, 7, 8), and are mainly thermal in nature. Although larger amplitudes are involved in cell spreading and motility (3, 4, 9), studies suggest that thermal fluctuations (<10 nm) can influence the spatial organization of molecules on membranes leading to formation of nanodomains/invaginations (10, 11).

In contrast to cell edges, fluctuations of the rest of the basal membrane of nucleated adherent cells remain lesser explored (6, 7, 8, 12, 13). However, its amenability to a variety of imaging techniques makes the basal membrane an ideal platform to study the properties and functional implications of shorter fluctuations. Dynamics of the basal membrane can be studied in terms of its height (distance from substrate in z direction) fluctuations (14). Studies demonstrate amplitudes to be 10s of nanometers and fluctuations to be affected by ATP depletion and cytoskeleton perturbation (6, 7, 8, 12, 13). However, these studies have either explored the power spectral density of fluctuations in monolayers with no spatial resolution (12, 13) or have focused on only the temporal (7) or spatial (8) aspects in single cells—rarely combining the two for broad range of timescales (5, 6). The power of combining them has already been demonstrated in red blood cells (RBCs) for differentiating nonthermal from thermal fluctuations (15, 16). To be able to understand the spatial regulation of lipid/protein organization by fluctuations, their spatial heterogeneities cannot be ignored in experiments.

At the basal membrane of nucleated adherent cells, ATP-dependent processes have been shown to increase the amplitude of fluctuations while making distributions non-Gaussian (7). However, how ATP-dependent processes alter the landscape and heterogeneity of fluctuations is yet to be established. The effect of the actomyosin network on spatio-temporal regulation of fluctuations also remains unclear with both reports of increase (6) and decrease of fluctuations (12). Unlike the spectrin network of RBCs, actin-based structures across a single nucleated adherent cell form heterogeneous patterns that modulate the height profile (undulations) of the membrane (17). How does the cortex and its activities—actin polymerization, myosin-II motor activity—affect the landscape of fluctuations and their heterogeneities? To address this, the impact of cortex on spatial distribution of fluctuations along with measurements of corresponding alteration in membrane mechanics need to be studied.

We address these issues by working with HeLa, CHO (epithelial), and C2C12 (myoblast) cells. Adapting a noninvasive imaging technique, interference reflection microscopy (IRM) (18, 19, 20, 21, 22), we measure spatio-temporal parameters of membrane z fluctuations at high z- but diffraction-limited xy-resolution. The impacts of ATP-driven processes and cortex on fluctuations are probed by drug-based perturbations and the temporal spectra are compared with existing theoretical models.

Materials and Methods

Cell culture and fixation

HeLa, CHO-K1, and C2C12 cells are grown in Dulbecco’s Modified Essential Medium (Gibco/Life Technologies, Carlsbad, CA) supplemented with 10% fetal bovine serum (Gibco/Life Technologies) and 0.4% Pen/Strep L-Glutamine mixture (Lonza, Basel, Switzerland) and maintained at 37°C in a humidified atmosphere with 5% CO₂. Cells, used between passages 3 and 17, are deposited on customized glass-bottomed dishes at a concentration of ∼20,000 cells/mL and all experiments are performed after 12–16 h of seeding. For actin labeling, cells are fixed with 4% paraformaldehyde (Sigma-Aldrich, St. Louis, MO) for 15 min, washed thoroughly with 1× phosphate-buffered saline (Sigma-Aldrich), and then incubated in 0.1 M glycine (Sigma-Aldrich) for 5 min. They are washed well and then incubated with 1 μM AlexaFluor 488 Phalloidin (Molecular Probes; Invitrogen, Carlsbad, CA) in the dark for 45 min. To visualize the nucleus in live cells, cells are incubated with 1 μg/mL Bisbenzimide Hoechst 33342 (Sigma-Aldrich) at 37°C for 30 min (23). Cells are always washed before imaging.

Pharmacological treatments

Specific agents are used to inhibit the polymerization of actin filaments, i.e., cytochalasin D and latrunculin B (Cyto D and Lat B; Sigma-Aldrich) and blebbistatin (Blebb.) to inhibit myosin-II activity (Sigma-Aldrich). Quantities of 2-deoxy D-glucose and sodium azide (Sigma-Aldrich) are used to deplete ATP, and Jasplakinolide (Jas; Molecular Probes) is used to stabilize preexisting actin filaments by favoring polymerization. Cells are grown and treated separately for 1 h with 5 μM Cyto D (24), 5 μM Lat B (25), 100 μM blebbistatin (26), and 5 μM Jas (27). Quantities of 10 mM sodium azide and 10 mM 2-deoxy D-glucose are added to cells (28) in M1 Imaging medium (150 mM NaCl; Sigma-Aldrich), 1 mM MgCl₂ (Merck, Kenilworth, NJ), and 20 mM HEPES (Sigma-Aldrich) and incubated for 60 min for ATP depletion (dep.). All the incubations are done at 37°C.

Transfection

pEGFP-MRLC1 is a gift from Tom Egelhoff (Addgene plasmid: 35680) (29). A quantity of 1 μg of the plasmid DNA is transfected into the HeLa cells to label the myosin-II in live cells by Lipofectamine 3000 (Life Technologies) as per manufacturer protocol. Cells are imaged 16 h posttransfection.

Formation of plasma membrane spheres

Cells are grown on micropatterns (clusters of 64 hexagons each with a side of 18 μm separated by 40 μm). For micropatterning, etched coverslips are first coated with PLL-g-PEG (SuSoS, Dübendorf, Switzerland) and then selectively depleted of PLL-g-PEG by UVO treatment (UVO Cleaner; Jelight, Irvine, CA) at the desired locations using Photomask (JD Photo Data, Hitchin, United Kingdom), as in (30). The coverslips are washed thoroughly and used for cell culture. Cells at ∼70% confluency are incubated for 6–8 h in phosphate-buffered saline (at pH 7.4) supplemented with 1.5 mM CaCl₂ (Sigma-Aldrich), 1.5 mM MgCl₂ (Merck), and 10 mM MG132 (Sigma-Aldrich) at 37°C (31). The sample is directly imaged for measuring fluctuations on cell-attached and cell-free plasma membrane spheres (PMSs).

Imaging techniques

An Eclipse Ti-E motorized inverted microscope (Nikon, Tokyo, Japan) equipped with adjustable field and aperture diaphragms, 60× Plan Apo (NA 1.22, water immersion), a 1.5× external magnification, and an electron-multiplying charge-coupled device camera (Evolve 512 Delta; Photometrics, Trenton, NJ) is used for imaging in differential interference contrast, epifluorescence, and IRM modes. For IRM, an additional 100 W mercury arc lamp, an interference filter (546 ± 12 nm), and a 50:50 beam splitter is used. Cells and beads (60 μm in diameter; Bangs Laboratories, Fishers, IN) are imaged in 3 mL Dulbecco’s Modified Essential Medium, No-Phenol Red in a 37°C onstage incubator at EM gain 30 and exposure time 50 ms. All movies are recorded at the same settings for 102 s at 19.91 frames/s (2048 frames).

Total internal reflection fluorescence (TIRF) images are acquired using a CMOS camera (ORCA-Flash4.0; Hamamatsu, Hamamatsu City, Japan) attached to a TIRF microscope, based on an IX-83 inverted microscope (Olympus, Melville, NY) equipped with a 100× NA 1.49 oil-immersion objective (PlanApo; Olympus) and a 488-nm laser. All images are acquired at exposure time 300 ms and penetration depth of 100 nm.

Calculation of spatio-temporal parameters

The software MATLAB (The MathWorks, Natick, MA) is used to calculate the relative height at all time-points for each pixel from the ΔI/Δh conversion factor (Supporting Discussion) of the day’s alignment. The SD from the relative heights across 144 pixels (2.16 × 2.16 μm²) in a first branch region (FBR) is calculated, averaged over 20 frames, and termed as SD_(space). For each pixel, the relative height time-series is obtained. The mean and SD of the time-series are calculated, averaged across 144 pixels in an FBR, and termed as mean relative height and SD_(time). The power spectral density (PSD) of the height time-series for each pixel is subsequently calculated from a custom-written program using the FFT algorithm provided by MATLAB and averaged across an FBR. The area under the curve of PSD is calculated each time and matched with the variance of the time-series as a check. The root of the area under the PSD curve of frequency bands of 0.01–0.1 Hz and 0.1–1 Hz are calculated and termed as $\overline{\sigma }$. The log (PSD) versus log(f) is fitted to a straight line for frequencies from 0.04 to 0.4 Hz. The slope of the fit is termed as the exponent. PSD_cell is calculated by averaging PSD curves of all FBRs in a cell. A 60 × 60 pixels noncell region is chosen to calculate PSD_background. The ratio of the background-subtracted PSD of treated cells to control cells $f=\left(PS{D}_{\text{cell}\left(\text{treated}\right)}-PS{D}_{\text{background}\left(\text{treated}\right)}/PS{D}_{\text{cell}\left(\text{untreated}\right)}-PS{D}_{\text{background}\left(\text{untreated}\right)}\right)$ is plotted as a function of frequency. Spatial autocorrelation functions (ACF) are calculated as $G\left(r\right)=\langle \Delta h\left(r^{\mathit{\prime }}\right)\Delta h\left(r^{\mathit{\prime }}+r\right)\rangle /\langle \Delta h{\left(r^{\mathit{\prime }}\right)}^2\rangle$ in long FBRs (35 × 10 pixels corresponding to 6.3 × 1.8 μm²) and averaged in 200 frames. Temporal ACFs are calculated over 2048 frames as $G\left(t\right)=\langle \Delta h\left(t^{\mathit{\prime }}\right)\Delta h\left(t\mathit{\prime }+t\right)\rangle /\langle \Delta h{\left(t^{\prime }\right)}^2\rangle$ and averaged across small FBRs of 2 × 2 pixels (0.36 × 0.36 μm²). Spatial and temporal ACFs are fitted with a three-term multiexponential function to obtain the correlation length (λ) and time (τ), respectively; PSDs are fitted with a modified theoretical model to extract mechanical parameters. Gaussian-ness of temporal fluctuations is evaluated at each pixel by Kolmogorov-Smirnov hypothesis testing (Supporting Discussion).

Analysis of heterogeneity in cells

The SD_(time) for each pixel is collated across 144 pixels in an FBR, and the SD of the series is averaged over multiple FBRs in a cell and termed as SD(SD_(time)). It is used as a measure of short length-scale heterogeneity inside an FBR. The SD_(time) of all 144 pixels in an FBR is compared to those of other FBRs in pairs, and a one-way analysis of variance (ANOVA) is performed. If p value is <0.001, SD_(time) maps are dissimilar. The number of such FBR pairs with dissimilar SD_(time) is counted and the ratio of such pairs to the total number of FBR pairs in a cell is calculated and termed as percent dissimilarity. This parameter is used as a measure of long length-scale heterogeneity.

Analysis of the amount of cortex present in cells

The periphery of an actin-stained epi-fluorescent cell is marked in the software ImageJ (National Institutes of Health, Bethesda, MD), linearized, and the total length is measured. The cortical regions in the cell having a signal-to-noise ratio >2 are marked, the lengths of each is added, and it is considered as cortex. The ratio of the amount of cortex present to the total periphery is calculated and averaged over 10 cells.

Statistical analysis

Calibration with beads and control experiment with cells without any treatment is performed with each set of experiment. During time-lapse imaging for any set, at least 10 cells are imaged for each condition and ∼20–40 FBRs analyzed for each cell. In most cases, analysis is collated over at least three sets of experiments performed on different days. For comparisons between populations of cells, a one-way ANOVA combined with a Tukey post-hoc test is performed to determine the statistical significance (^∗p < 0.05, ^∗∗ p < 0.001) whenever the parameters have similar variances and have Gaussian distributions. A Mann-Whitney U test is done whenever the parameters are not Gaussian.

Results

Using interference microscopy to map membrane dynamics

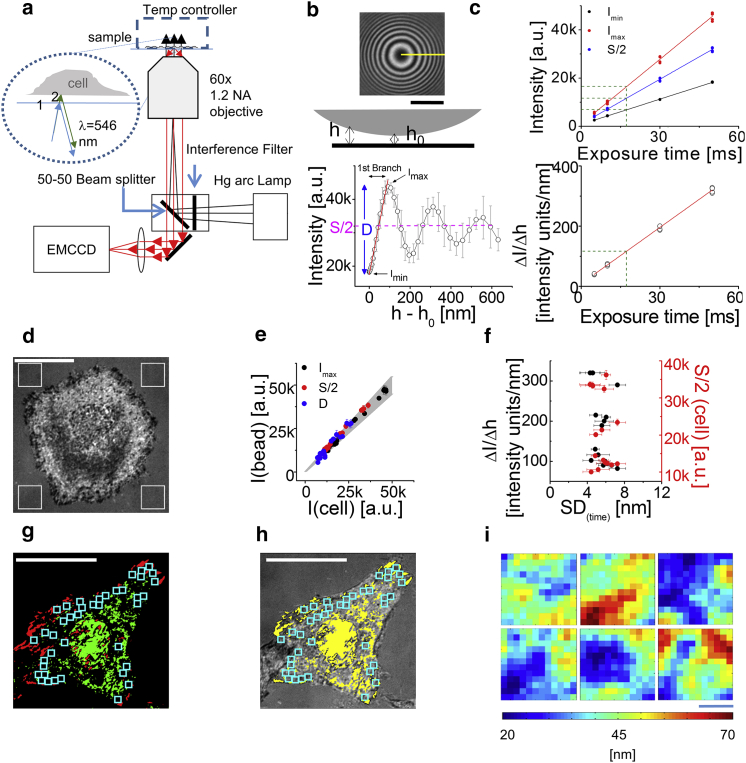
To quantify basal membrane fluctuations, adherent eukaryotic cells are imaged using IRM (Fig. 1 a). The interference pattern in an IRM image of a cell is produced by light reflected off from the coverslip and the reflected beam from the plasma membrane (due to the differences in the refractive indices). Thus, the intensity of the interference image, at any pixel and time, can be used to measure the height of the membrane patch at that pixel and time. For calculating spatio-temporal height variations, first, the intensity variation (ΔI) to height variation (Δh) is obtained by calibrating with an object whose height profile is known. Second, parts of the cell where this conversion is applicable are identified and corresponding maps of relative height (Δh + h₀) are obtained.

Figure 1.

Details of calibration of IRM. (a) Given here is an IRM setup schematic showing illumination and detection path. Zoomed-in view shows reflections at interface 1 (coverslip-medium, blue arrows) and 2 (medium-cell, green arrows), which interfere. (b) (Top) Shown here is an IRM image of a bead with a typical radial line in yellow. (Bottom) Shown here is an averaged intensity-versus-height profile (N = 10) with linear fit of the first branch in red. (c) (Top) Shown here is a plot of I_max, I_min and S/2 from profiles of same beads is imaged at different exposure times (n = 5 beads, four line scans per bead) for a particular day. (Bottom) Given here is ΔI/Δh versus exposure times for beads. (d) Shown here is a typical IRM image of a HeLa cell. White ROIs are used to calculate S/2 (cell). (e) Given here is a comparison of I_max, I_min and S/2 between beads and cells for different days (N = 20). Gray region covers y = x ± 0.1 x. (f) Shown here is the SD_(time) measured and the S/2 (cell) used for different days versus the conversion (ΔI/Δh) used. (g) Shown here are minima (red) and maxima (green) projections of an HeLa cell with FBRs overlaid in cyan. (h) Shown here, FBRs are overlaid on the corresponding IRM image. (i) Shown here are relative height maps at any given time-point of six FBRs in an HeLa cell. Scale bars represent 1 μm. Scale bars for (a–h) = 10 μm. See also Fig. S1; Supporting Discussion. To see this figure in color, go online.

For the calibration of ΔI to Δh conversion, a 60 μm polystyrene bead is imaged (Fig. 1 b, top; and Supporting Discussion). Its interference pattern displays Newtonian rings (Fig.1 b, top) due to the radial symmetry in its monotonically increasing height profile from the center. The intensity dependence on height shows periodicity (Fig.1 b, bottom) as expected (22)—leading to degeneracy in height prediction from intensity because a particular intensity is repeated at different branches and hence at different heights. We restrict our analysis to regions that lie within the first branch of the profile (Fig. 1 b) to make the conversion possible. The central part of the first branch can be approximated to have linear intensity height dependence as depicted in the linear fit (Fig. 1 b, bottom). For a given wavelength and refractive index of external medium, the slope is expected to depend on the difference (D) of intensity of maxima (I_max) and minima (I_min) of the first branch (Fig. 1 b, bottom; Supporting Discussion). Beads are imaged at various exposure times to cover a range of I_max and I_min—hence, D and S (= I_max + I_min; Fig. 1 c, top). The corresponding slopes show a linear dependence on exposure time (Fig. 1 c, bottom) that allows calculation of slopes for intermediate values of exposure times. Next, IRM images of HeLa cells (Fig. 1 d) are analyzed to obtain I_max and S/2. The S/2 value (cross-checked in three different ways, Fig. S1 a–c; Supporting Discussion) is compared with those obtained from beads and the corresponding slope read out. The corresponding D for the cell (= 2I_max − S) matches closely with that of the bead and hence justifies the conversion (Fig. 1 e; Table S1). Typically, the conversion entails ∼20,400 ± 9900 intensity units for 100 nm (∼204 units/nm). The resolution is thus ∼6 nm for relative height measurement as the noise is 1200 intensity units. However, our analysis relies on height fluctuations captured by SD_(time). SD_(time) is measured to be ∼2 nm for background regions and ∼0.5 nm for dark current (imaging without light source)—this sets the minimum resolvable SD_(time). But, variations (∼2 nm) observed in SD_(time) measured over different days have no correlation with the ΔI to Δh conversion used (Fig. 1 f), and hence reflect the inherent variability in HeLa cells.

Next, FBRs in the cell are identified (Supporting Discussion) by accepting groups of pixels that meet the two following criteria. The first is to only allow a range of intensities (I_min + 2000 to I_max − 2000) so that pixels corresponding to interference maxima and minima are excluded. However, this is not enough to filter out pixels whose heights correspond to higher-order branches. The second criterion enforced is to choose regions of interest (ROIs) any of whose edges could be physically connected (1-pixel distance) to the first minima. The projection of first minima (red pixels, Fig. 1 g) and first maxima (green pixels, Fig. 1 g) from time-lapse images are used as a guide to the eye for selecting FBRs (pixels in the cell not marked in yellow; Fig. 1 h). We find that an ∼73 ± 10% (N = 30 cells) area of the cell is FBRs. However, for consistency in analysis, we use multiple square FBRs (12 × 12 pixels) per cell that amount to ∼10 ± 4% (N = 30 cells) of the basal membrane (cyan ROIs; Fig. 1, h and i).

IRM images, without conversion, themselves reveal interesting features that qualitatively describe the membrane topology. Whereas images of RBCs show circular symmetry, adherent eukaryotic cells show a different and heterogeneous topology (Fig. S2). Focal adhesions appear commonly as dark patches and the membrane under the nucleus appears at a higher contrast—often displaying mobile particulate features (Movies S1 and S2).

Time-lapse imaging of cells reveals intensity flickering at all pixels (Fig. S3). Relative heights (Fig. 2 a(i)) obtained from intensities are compared either across space (Fig. 2 a(ii and iii)) or time (Fig. 2 a(iv–viii)) to calculate the different parameters, ACFs and PSDs. The amplitudes of spatial undulations and temporal fluctuations are quantified by SD_(space) and SD_(time), respectively. Because the PSD captures the distribution of fluctuations over various frequencies, $\overline{\sigma }$ values for frequency ranges 0.01–0.1 Hz and 0.1–1 Hz are calculated to compare fluctuation levels at lower and higher frequencies. The exponent, also computed from the PSD, reveals the power-law dependence of PSD on frequency in the 0.04–0.4 Hz band. The values λ and τ are calculated by fitting spatial and temporal ACFs to three-term multiexponentials, respectively. Mechanical parameters are extracted by fitting PSDs to theoretical models (Fig. 2 a(viii)). Finally, SD_(time) of whole cells (non-FBR regions blocked out) as well as square FBRs (used for computing the parameters; Fig. 2 b) are mapped to quantify the spatial profile of the temporal fluctuations.

Figure 2.

Quantification of temporal fluctuations and spatial undulations. (a) (i) Given here is a relative height map of a membrane patch (FBR) at two time-points. (ii) Shown here is a distribution of relative heights across the FBR at any particular time-point. (iii) Representative spatial ACF is measured at a long FBR. Solid line shows fit to three-term multiexponential function. (iv) Given here is a time-series of relative heights of a pixel in red in (i). (v) Distribution of relative heights is given for a time-series in (iv). (vi) Shown here is a representative temporal ACF of a small FBR. Solid line shows fit to a three-term multiexponential function. Black arrow points out a bump. (vii) Given here is a PSD at an FBR, and the parameters extracted from it. (viii) Fitting of a background-subtracted PSD was made to Eq. 1. (b) Shown here are SD_(time) maps of an HeLa cell (non-FBRs blocked by white; scale bars, 10 μm) and two FBRs. Scale bars, 1 μm. To see this figure in color, go online.

In HeLa cells, we find SD_(time) to be ∼4.9 ± 0.7 nm and SD_(space) to be ∼7.2 ± 1.5 nm (Figs. 2 and S4). SD_(time) and PSD (Fig. S3 b and c) remain similar over different days as well as different batches with minor variations. Similar values for spatio-temporal parameters are seen in two other cell types—CHO and C2C12 (Fig. S4). In comparison, amplitudes of temporal fluctuations reported in RBCs (32) are ∼20–30 nm and amplitudes of spatial undulations reported in MDA-MB-231 epithelial cells are ∼8–11 nm (8). The observed λ of ∼500 nm (Fig. 2 a; Table S2) is lower than predicted values (∼600 nm) (33). We find a f^−4/3 dependence of the PSD for frequency range 0.04–0.4 Hz (Fig. 2 a; Table S2), which is associated in the literature with hydrodynamic damping by a rigid wall (34, 35). The correlation between SD_(time) and mean relative height from the substrate (Fig. S3, d–f) is found to be weak, suggesting that damping by the rigid substrate is not the dominant factor controlling fluctuations.

We next investigated the role of ATP-dependent processes in regulating fluctuations.

ATP-driven activities increase temporal fluctuations and flatten out spatial undulations

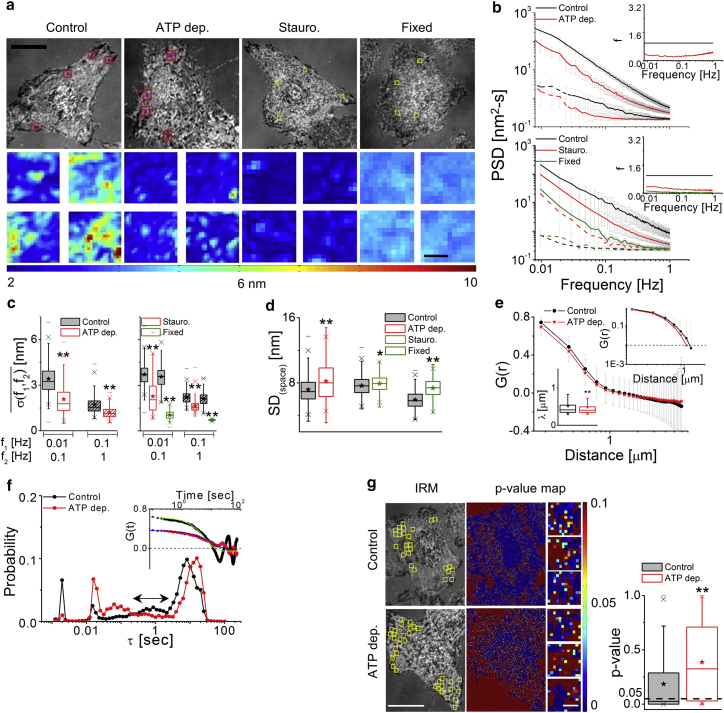
Membrane fluctuations are expected to be due to thermal as well as ATP-dependent processes (32, 36, 37). Work on fluctuations in the cytoplasm have already shown that ATP-dependent processes generate random noise (38, 39, 40). To ascertain the contribution of ATP-driven processes, cells are depleted of ATP. To strengthen this, effects of Staurosporine induced cell death and fixation is tested. Although ATP depletion and cell death block the main source of active energy in cells, fixation stops all biochemical activities and additionally rigidifies the cell without triggering biochemical responses (Figs. 3 a and S5 a). In all three cell lines, the three treatments show a net reduction in temporal fluctuations (Figs. 3, b and c; S5 b, S6, and S7; Movie S3). The complete frequency dependence of weakened temporal fluctuations is plotted as f (ratio of the background-subtracted PSD of treated set to control) in which f = 1 represents no change whereas f > 1 and f < 1 represent increased and decreased fluctuations from control cells, respectively. On ATP depletion, Staurosporine treatment, or fixation, f is reduced over a broad range of frequencies (Fig. 3 b, insets). The exponent is close to −1 and reflects increased damping on all treatments (Figs. S5 b, S6, and S7). In contrast to SD_(time), SD_(space) is seen to increase in all the treatments (Figs. 3 d, S6, and S7). The average λ of ATP-depleted cells shows a significant reduction (Fig. 3 e) and the distribution of τ shows underrepresentation of timescales ranging from 0.2–2 s (Fig. 3 f). The normality of fluctuations (evaluated for each pixel, expressed as p value) shows that ATP depletion increases the Gaussian-ness of fluctuations (Fig. 3 g). Thus, cellular activity enhances the temporal fluctuations, altering their nature while decreasing the spatial amplitudes and flattening the membrane.

Figure 3.

Effect of prevention of cellular activity on membrane fluctuations. (a) Shown here are IRM images (scale bars, 10 μm) and SD_(time) maps (scale bars, 1 μm) of FBRs in control, ATP-depleted, staurosporine-treated (Stauro., 5 μM, 60 min), and fixed HeLa cells. (b) Given here are PSDs of FBRs in treated cells and their controls (solid lines) with their backgrounds (dashed lines); inset shows the value f. (Top) Shown here are N = 50 cells each, n_control = 1083 FBRs, and n_{ATP depletion} = 880 FBRs. (Bottom) Shown here are N = 10 cells each, n_control = 412 FBRs, n_{staurosporine} = 336 FBRs, and n_fixed = 329 FBRs. (c and d) Given here are temporal and spatial parameters for (b). ^∗p < 0.05, ^∗∗p < 0.001, one-way ANOVA. (e) Shown here are averaged spatial ACFs (and their log-log plots, top inset) for control and ATP-depleted cells (N = 80 cells, n_control = 2024 FBRs, and n_{ATP depletion} = 1244 FBRs). (Bottom inset) Given here are correlation lengths. (f) Weighted distribution of correlation timescales was obtained from temporal ACFs (inset: solid line shows fits) (N = 9 cells, n_control = 3765 FBRs, and n_{ATP depletion} = 1987 FBRs). (g) Given here are IRM images (scale bars, 20 μm), with FBRs overlaid in yellow and their corresponding p-value maps (Kolmogorov-Smirnov hypothesis testing). Scale bars, 1 μm. (Right) Given here is the p value for FBRs in control versus ATP-depleted cells. Shown here are N = 30 cells, n_control = 41,760 pixels, and n_{ATP depletion} = 25,766 pixels. Asterisks in (e) and (g) indicate ^∗∗p < 0.001, Mann-Whitney U test. See also Figs. S5 and S7; Tables S2 and S3. To see this figure in color, go online.

The actomyosin cortex has dynamic connections with the membrane (41, 42), is home to various ATP-driven processes, and is the next target of our study.

Active cortex stretches out membrane but has dual effect on temporal fluctuations

Actin polymerization (can extend the membrane by ∼2.76 nm per polymerization depending on the angle of polymerization (43)) and the organization of short actin filaments by myosin-II (44) can enhance membrane fluctuations. In contrast, pinning of the membrane onto a much tensed actomyosin cortex and presence of contractile stress fibers can reduce deformability and have an opposite effect. How the cortex affects membrane fluctuations therefore depends on the locally dominant process.

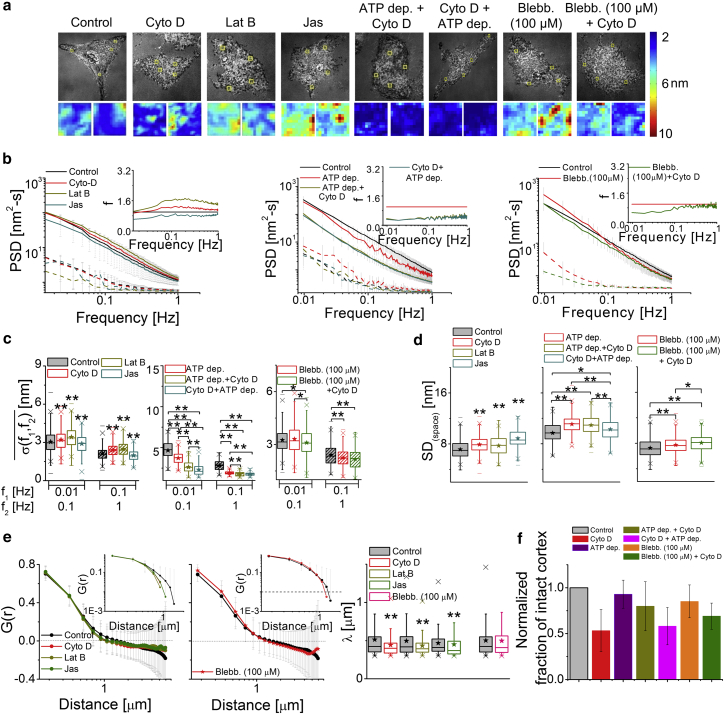
We block actin polymerization by Cyto D or Lat B, and block actin dynamics by Jas. We find that the PSDs and SD_(time) show a net enhancement of temporal fluctuations for Cyto D and Lat B but reduction for Jas (Figs. 4, a–c, and S8; Movie S3). Both f (Fig. 4 b, inset) and $\overline{\sigma }$ (Fig. 4 c) reflect that both lower and higher frequencies are affected, although the effect is not as uniform over the frequencies as in ATP depletion. However, larger amplitudes of spatial undulations (Fig. 4 d) and shorter λ-values (Fig. 4 e) are observed in all these treatments. Quantifications show that there is an ∼47 ± 22% loss of defined cortex from the vicinity of the membrane after Cyto D treatment (Figs. 4 f and S9). Thus, absence of an intact cortex enhances, but blocking actin dynamics reduces, fluctuations. To understand why reducing polymerization rates by Cyto D also does not reduce fluctuations, we study the effect of polymerization without affecting cortex integrity.

Figure 4.

Effect of the actomyosin cortex on membrane fluctuations. (a) Given here are IRM images (scale bars, 10 μm) and SD_(time) maps (scale bars, 1 μm) of HeLa cells under mentioned conditions. (b) Shown here are PSDs for cells (solid lines) and their backgrounds (dashed lines), with the inset showing the value f for all conditions. (Left) Shown here are N = 30 cells each, n_control = 741 FBRs, n_{Cyto D} = 564 FBRs, n_{Lat B} = 426 FBRs, and n_Jas = 259 FBRs. (Middle) Shown here are N = 10 cells each, n_control = 141 FBRs, n_{ATP depletion} = 158 FBRs, n_{ATP depletion + Cyto D} = 254 FBRs, and n_{Cyto D + ATP depletion} = 162 FBRs. (Right) Shown here are N = 20 cells each, n_control = 402 FBRs, n_blebbistatin = 333 FBRs, and n_{blebbistatin + Cyto D} = 193 FBRs. (c and d) The parameters of temporal fluctuations and spatial undulations of cells are given under different conditions. ^∗p < 0.05, ^∗∗p < 0.001, one-way ANOVA. (e) Given here are averaged spatial ACFs (and their log-log plots, top inset) and correlations lengths (n_control = 1085 FBRs, n_{Cyto D} = 494 FBRs, N = 40 cells each; n_control = 884 FBRs, n_{Lat B} = 495 FBRs, N = 30 cells; n_control = 300 FBRs, n_Jas = 102 FBRs, N = 20 cells; and n_control = 811 FBRs, n_blebbistatin = 729 FBRs, N = 30 cells). ^∗p < 0.05, ^∗∗p < 0.001, Mann-Whitney U test. (f) Given here is the normalized fraction of cortex clearance (N = 10 cells each). See also Figs. S8, S9, S10, S11, and S12; Tables S2 and S3. To see this figure in color, go online.

We recreate a condition in which the cortex remains intact but polymerization is blocked. Cortex clearance on Cyto D treatment requires forces generated by actomyosin contractility (45). Blocking myosin-II activity by ATP depletion or blebbistatin (100 μM) treatment before addition of Cyto D shows that only 20 ± 27% and 21 ± 14% of the cortex is cleared, respectively (Figs. 4 f and S9). The subsequent effect of Cyto D on these pretreated cells is reversed. Temporal fluctuations are now reduced instead of being amplified (Figs. 4, a–c, S10, and S12). On reversing the order of treatments (Cyto D + ATP depletion) cortex clearance (42 ± 20%) is observed along with reduction in fluctuations (Figs. 4, a–c and S10). Thus, polymerization individually can enhance fluctuations. The role of myosin-II motor activity at the cortex is investigated next.

Blocking myosin-II motors shows that blebbistatin at low concentration (5 μM, 60 min) either does not change or it decreases the temporal fluctuations (Fig. S11; Movie S3). The global actin distribution (Fig. S9 a) is not affected at this concentration, implying that local myosin-II activities have a positive contribution to fluctuations. At 100 μM, fluctuations either do not change or are significantly enhanced (Figs. 4, a–c and S12; Movie S3). The global actomyosin distribution at this concentration appears more diffused (Fig. S12 a). Hence, the positive contribution of myosin-II activity on fluctuations are measurable when the cortex is not globally altered by blebbistatin.

In all the above treatments, although the SD_(time) either increases or decreases, the SD_(space) always increases (Fig. 4 d). Additionally, λ (Fig. 4 e) decreased for Cyto D, Lat B, and Jas (although not for blebbistatin (100 μM)). Decreased SD_(space) and increased λ in unperturbed cells imply that the cytoskeleton flattens membrane undulations.

We thus show that, in interphase cells, although polymerization- or myosin-II-based activities can enhance temporal fluctuations, the net contribution of the cortex is to dampen fluctuations that are dependent on cortex integrity and contractility (Tables S2, S3, and S4). We next explore systems where the membrane is at a different mechanical state than interphase cells and the cortex is either stiffer or completely missing.

Reduced spatio-temporal fluctuations in mitotic cells and PMSs

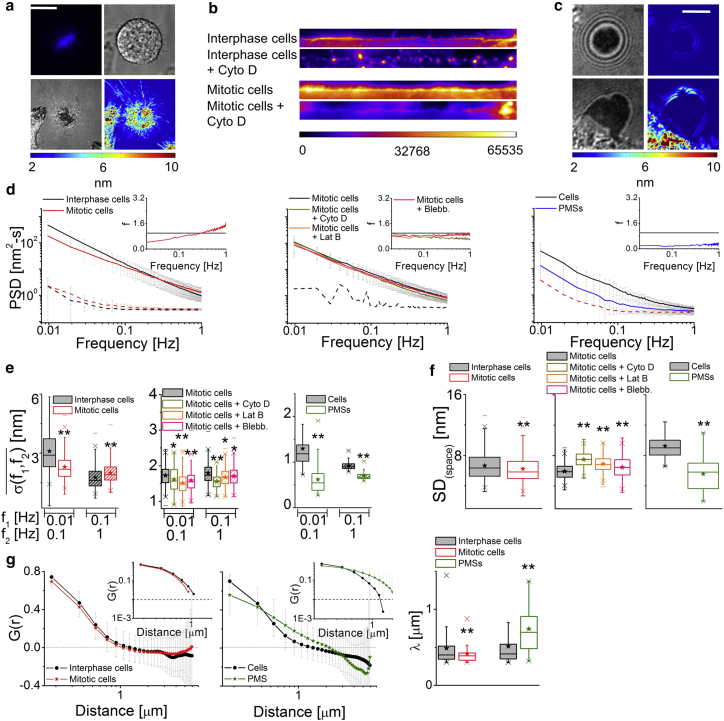
Mitotic cells, their cortex (Fig. 5, a and b), and PMSs (Fig. 5 c) are imaged to study membrane fluctuations. Mitotic cells have increased apparent membrane tension compared to interphase cells (46), which are known to not alter on cytoskeleton perturbation—thus indicating a higher level of bilayer tension than interphase cells. These cells have a more cross-linked and stiffer cortex (47, 48) than interphase cells. We see net reduction in temporal fluctuations as captured by SD_(time) (Fig. S13 a). Reduction of PSDs and $\overline{\sigma }$ (Fig. 5 e) is prominent at the lower frequencies. Both SD_(space) and λ values are smaller than interphase cells (Figs. 5, f and g and S13 a). Cyto D treatment reduced the actin intensity at the cortex but does not result in cortex clearance as previously observed in interphase cells (Figs. 5 b and S13 c). We find a reduction of temporal fluctuations on Cyto D, Lat B, or blebbistatin (100 μM) treatment (Figs. 5, d and e and S13 b) in mitotic cells that resembles the response of pretreated interphase cells where cortex clearance is stopped. The blebbistatin (100 μM) here has a similar effect to that of blebbistatin (5 μM) on interphase cells. This is probably due to the increased myosin-II concentration in mitotic cells (49). The SD_(space) increases on all treatments as seen in interphase cells (Fig. 5 f). In mitotic CHO cells, a similar trend of reduced temporal fluctuations is found. The SD_(space) is already low for interphase CHO and therefore is not reduced any further (Fig. S13 a). Spatio-temporal fluctuations are, therefore, primarily reduced under mitosis.

Figure 5.

Membrane fluctuations in mitotic HeLa cells and in PMSs. (a) Mitotic HeLa cell is observed in fluorescence (top left) (DNA stained with Hoechst 33342), IRM (bottom left), and differential interference contrast (top right) modes along with the SD_(time) map (bottom right). Scale bars, 10 μm. (b) Shown here is the linearized and color-coded cortex (60 μm × 9 μm) of actin-labeled interphase and mitotic cells in normal and Cyto D-treated conditions. (c) Given here are representative images of IRM (left) and SD_(time) maps (right) of CHO-derived PMS (cell-free PMS (top), cell-attached PMS (bottom)). Scale bars, 5 μm. (d) Given here are PSDs for cells, PMSs (solid lines), and their backgrounds (dashed lines) with the insets showing the value f; (left) N = 30 cells each, n_interphase = 639 FBRs, and n_mitotic = 352 FBRs; (middle) N = 15 cells each, n_mitotic = 105 FBRs, n_{mitotic + Cyto D} = 85 FBRs, n_{mitotic + Lat B} = 182 FBRs, and n_{mitotic + blebbistatin} = 215 FBRs. (Right) Shown here is N = 10 cells/PMSs each, n_cell = 70 FBRs, and n_PMS = 85 FBRs. (e and f) The parameters of temporal fluctuations and spatial undulations of cells/PMSs are given in the mentioned conditions. ^∗p < 0.05, ^∗∗p < 0.001, one-way ANOVA. (g) Shown here are the averaged spatial ACFs (and their log-log plots, top inset) and correlation lengths (n_interphase = 447 FBRs, n_mitotic = 199 FBRs, N = 50 cells each; n_cells = 130 FBRs, n_PMS = 39 FBRs, and N = 15 cells/PMS). ^∗p < 0.05, ^∗∗p < 0.001, Mann-Whitney U test. See also Figs. S13 and S14; Tables S2 and S3. To see this figure in color, go online.

To further explore systems in which the membrane can be debrided of its underlying cytoskeleton, we produce PMSs from CHO cells (Figs. 5 c and S14). We see reduced temporal fluctuations and spatial undulations (Figs. 5, c–f and S13 d) here. Although the mean relative height is lower for PMSs than the cells in the vicinity, for FBRs at similar mean relative heights (Fig. S13 e, dotted line) PMSs still display lower SD_(space) than cells. A concomitant increase in λ (Fig. 5 g) with respect to live control cells suggests a more flattened membrane. The reduced fluctuations are in line with reports showing adhesion-based increase in lateral tension in liposomes (50).

So far, we have explored the averaged parameters of spatio-temporal fluctuations. Because heterogeneity is key to spatial segregation and regulation of activity at the plasma membrane, we next measured the spatial heterogeneity of temporal fluctuations.

Fluctuation maps reveal transient localized events creating heterogeneity

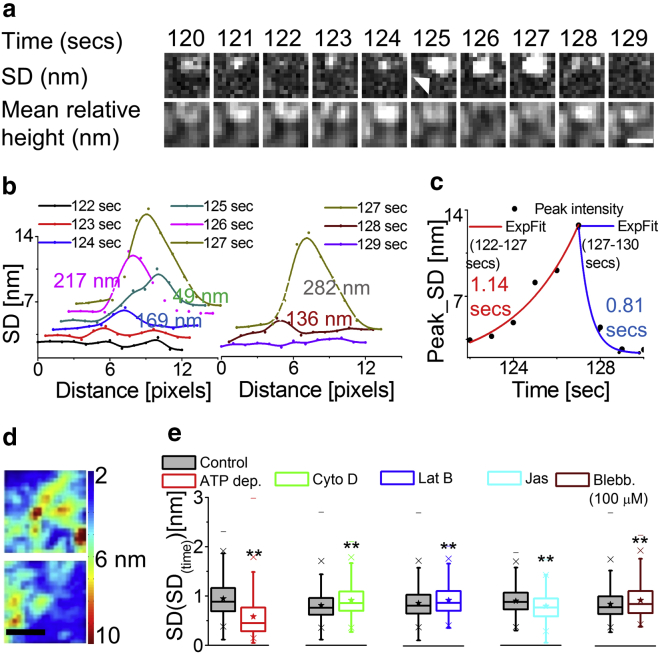
SD_(time) maps (Fig. 2 b) show that fluctuations are nonuniform across the cell, but zooming into FBRs brings out the micron-sized heterogeneities (Fig. 2 b, bottom). We explored this by mapping SD_(time) for a reduced time-interval (1 s) and capturing the evolution of fluctuations (Movie S4). In Fig. 6 a, we zoom into an FBR and highlight the transient nature of spatial heterogeneity of temporal fluctuations by following the formation and dissolution of a structure (arrow). These structures can appear and stay on for ∼1 s as depicted in the time evolution of line scans of SD_(time) maps (Fig. 6, b and c). The timescales of appearance and disappearance of these features are ∼1.02 ± 0.79 and ∼0.79 ± 0.35 s, respectively (n = 20 events from a single cell). Such events (along with those not as clearly visible as the one in Fig. 6 a) are expected to increase the intra-FBR variation of SD_(time) in the map. We hence calculate the SD(SD_(time)) for different conditions to quantify the short length-scale heterogeneity (Figs. 6, d and e and S15 a). We find that ATP depletion, mitosis, and Jas treatment reduce the heterogeneities, and the cortex disorganization by Cyto D/Lat B/blebbistatin (100 μM) increases them (Fig. 6 e; Table S2). Because a reduction in the basal (mean) SD_(time) can also lower SD(SD_(time)), to normalize out the effect of the basal value we calculate $SD\left(S{D}_{\left(\text{time}\right)}\right)/Mean\left(S{D}_{\left(\text{time}\right)}\right)$. The ratio obtained for all treatments is subtracted from that of the control set. Whereas we observe reduced values (Fig. S15 b) on treatments that affect cellular activity and on stabilized cortex (Jas), perturbations affecting the cytoskeleton either increase or do not change the short length-scale heterogeneities. At short length scales (<2 μm), therefore, cellular activity results in enhanced heterogeneities (Fig. S5 d; Supporting Discussion).

Figure 6.

Characteristics of transient heterogeneities in fluctuations. (a) Given here is the SD_(time) and mean relative height map of an FBR. Scale bars, 1 μm. (b) Shown here is a line scan of SD_(time) across the feature (white arrow) at the mentioned time-points. The numbers mentioned are the SD of the Gaussian fits to profiles. (c) Variation of peak values of SD_(time) are given at different time-points, exponential fits, and extracted timescales. (d) Given here are typical maps of SD_(time) for a pair of FBRs. Scale bars, 1 μm. (e) Shown here is SD(SD_(time)) for different conditions (N = 30 cells each). ^∗p < 0.05 and ^∗∗p < 0.001, one-way ANOVA. See also Fig. S15; Tables S2 and S3. To see this figure in color, go online.

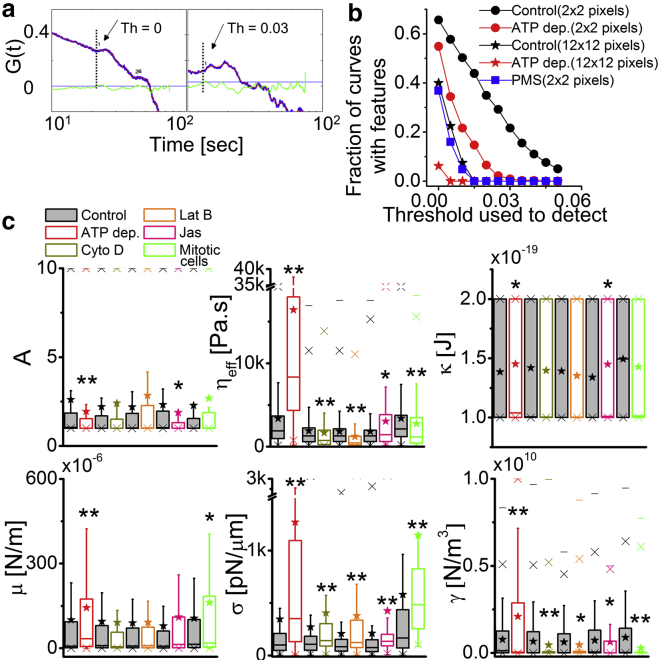
The range of timescales observed for the transient heterogeneities overlap with the range of τ (∼0.2–2 s) underrepresented in ATP depletion cells (Fig. 3 f). We also find that the temporal ACFs display peaklike features (Fig. 2 a(vi), arrow) when averaged over 0.36 × 0.36 μm², which diminish on averaging over longer distances (Fig. 7, a and b). The steeper peaks are more frequent (in 21% ACFs) in control cells than in ATP depletion cells (in 8% ACFs), and rarely present in PMSs (Fig. 7 b). However, ATP depletion does not completely abrogate the features from the ACFs.

Figure 7.

Local heterogeneities and underlying membrane mechanics. (a) Shown here are zoomed-in temporal ACFs (blue) and slopes (green) of smoothened ACFs (red). Horizontal lines denote the slope threshold (Th) set in each given to detect features (arrow). The vertical lines denote the crossovers. (b) Given here is the fraction of ACF curves with features obtained using different thresholds (N = 9 cells, n_control = 3765 FBRs, n_{ATP depletion} = 1987 FBRs; N = 10 PMSs, and n = 352 FBRs). (c) Membrane mechanical parameters A, η_eff, κ, μ, σ, and γ are obtained from fitting PSDs to a theoretical model (n_control = 1238 FBRs, n_{ATP depletion} = 811 FBRs, N = 80 cells each; n_control = 595 FBRs, n_{Cyto D} = 378 FBRs, N = 40 cells each): n_control = 488 FBRs, n_{Lat B} = 300 FBRs, N = 30 cells each; n_control = 199 FBRs, n_Jas = 106 FBRs, N = 20 cells each; and n_interphase = 329 FBRs, n_mitotic = 101 FBRs, N = 30 cells each). ^∗p < 0.05, ^∗∗p < 0.001, Mann-Whitney U test. To see this figure in color, go online.

To understand if different amplitudes of fluctuations can coexist at distal (>2 μm) regions across the same cell, we compared percent dissimilarity as a measure of long-range heterogeneity. We see that ∼60% FBR pairs are dissimilar in control cells (Fig. S15, c and d). This is reduced on fixation and ATP depletion followed by Cyto D, but there is no significant difference seen for any other treatments (Fig. S15, c and d; Table S2). The distinctly different fluctuations at distal FBRs may be caused due to short length-scale heterogeneities that are subdued but not abrogated in ATP depletion cells.

Hence, spatial mapping of temporal fluctuations reveals transient heterogeneities and shows that distal regions in the cell can have dissimilar fluctuations. We next compare the data with theoretical models to understand the underlying membrane mechanics.

Comparison with theoretical models

Fluctuations in RBCs have been compared in the literature with different models to extract membrane mechanical properties (16, 32, 35, 51). These models either explicitly incorporate effect of direct forces on membranes or use equilibrium descriptions and account for active processes by an increase in the effective temperature. Because, in our data, bumps and peaks in the ACF (Fig. 2 a(vi))—signatures of active fluctuations—are no longer distinguishable when averaged over the whole FBR, we therefore do not use models describing direct effect of active forces. Instead, we fit the PSDs (averaged over FBRs) using a description (Eq. 1) that incorporates a higher effective temperature (or, active temperature A^∗T) to account for cellular activity (35). We also consider the contribution (16, 35, 51, 52, 53) of effective cytoplasmic viscosity (η_eff), bending rigidity (κ), shear modulus (μ), membrane tension (σ), and confinement (γ). The PSDs are fit with the following equation:

$$PSD\left(f\right)=\frac{4{\eta }_{\text{eff}}A{k}_{\text{B}}T}{\pi }\underset{q_{\text{min}}}{\overset{q_{\text{max}}}{\int }}\frac{dq}{{\left[4{\eta }_{\text{eff}}\left(2\pi f\right)\right]}^2+{\left[\kappa q^3+\frac{9k_{\text{B}}T}{16\pi \kappa }\mu q+\sigma q+\frac{\gamma }{q}\right]}^2}.$$ (1)

Although other parameters fall in the expected range (Fig. 7 c), the η_eff has values much higher (∼1500 Pa.s) than that of water or cytoplasm (54). However, micropipette aspiration experiments on fibroblasts (55) and simulations of the cross-linked actin-network (56) report similar values for η_eff, implying that the cortex contributes to η_eff due to slow relaxation times of the cross-linked actin network. This is supported by the observation (Fig. 7 c) that η_eff reduces on perturbing the actomyosin cytoskeleton with Cyto D or Lat B, but increases by the action of Jas as well as on ATP depletion.

Comparing the values of σ for control cells with those obtained from imaging studies (57) or tether-pulling experiments (58, 59), we find the numbers to be in the right range (∼10–450 pN/μm). No decrease of σ is seen when fluctuations are enhanced (for Cyto D, Lat B), but increased σ correlates with decreased fluctuations (in ATP depletion, Jas, and mitosis). Decreased A (ATP depletion and Jas) and increased κ/μ (ATP depletion, Jas/mitosis) correlate with decreased fluctuations. The γ-values decreased for all cytoskeletal perturbations as well for mitosis, but increased on ATP depletion. The γ-values did not fall below 10⁸ N/m³ on cytoskeleton disruption (Supporting Discussion), implying contributions from not just the cortex but also from other sources (confinement due to the coverslip).

Discussion

Through implementation of IRM and image analysis, we successfully create spatial maps of the temporal fluctuations in three different cell lines. The study of membrane fluctuations in nucleated cells has been experimentally challenging (14) due to the complex internal architecture of cells. Firstly, because we do not use the absolute height and instead measure Δh—the variation of height in time or space—we could use beads-based calibration and avoid assumptions of internal refractive indices. Secondly, by stringently identifying pixels that remain FBRs throughout the time-lapse imaging, we hoped to have also eliminated regions where intensity reached values away from the first branch due to reflections from internal structures. Comparison with experimentally measured quantities reveal the measured amplitudes (SD_(time), SD_(space)) to range from ∼4–8 nm—similar to other reports in adherent nucleated cells (6, 60). Incorporating dual wavelength imaging, in future, will add to the stringency of identification of FBRs.

The first striking observation is about the basal level of fluctuations. In the three cell lines we chose, epithelial-like (HeLa and CHO) and a myoblast cell line (C2C12), spectra of fluctuations are not significantly different. Mitotic cells, in contrast, displayed different characteristics from interphase cells. Whether this indicates regulation of fluctuations, such as membrane tension homeostasis (61), is a relevant future application of the technique.

Activity due to membrane proteins (36) or the underlying cytoskeleton has been reported to act as fluctuating force monopole/dipoles on the membrane, enhancing fluctuations (37, 62). In our study, amplification of temporal fluctuations by cellular activity is observed to be true for all cells and cell lines used. Signatures of direct forces impacting fluctuations have been reported in RBCs and vesicles (16, 36, 37, 62). In RBCs, analyzing temporal ACFs for different spatial modes have demonstrated forces acting at ∼5 × 10⁻³ pN and ∼0.1 s (16). In our system, ACFs of control cells display peaklike features (similar to active fluctuations in RBCs) as well as extra timescales (compared to ATP-depleted ones) that are in close range to timescales of transient heterogeneities observed. Various membrane activities occur in this range of timescales—membrane trafficking, blebbing, actin protrusions—which may be responsible for this effect. Although signatures exist, the clear demarcation of active fluctuations in cells needs measurement of their mechanical response.

The surprising part of the study is that cellular activity, which is expected to increase the dynamics of the system, flattens spatial undulations. It needs to be noted that decreased SD_(space) and increased λ are signatures of membrane flattening. Because SD_(space) and λ are calculated across an ∼4 and 11 μm² area, respectively, with diffraction-limited lateral resolution, the flattening by activity reported here is at micrometer scales in contrast to the nanometer-scale temporal dynamics. This flattening is in line with reports that suggest that the contractile cytoskeleton creates coherence in the mechanical connectivity required for long-range (μm-scale) force transmission during cell spreading (63). Strong alterations to the cortex (Cyto D/Lat B) or its dynamics (Jas, ATP depletion) both affect the parameters and support the role of cytoskeleton in flattening the undulations. Mitotic cells, owing to their limited adhesion and rounding at the edges (∼6 μm apart), show decreased λ although the SD_(space) is reduced.

The study also highlights the dual role of cortex in setting the fluctuations. Actin polymerization and myosin-II based activities can individually enhance fluctuations. However, the intact cortex dampens fluctuations and this reduction is not lost until the cortex is cleared, as seen both in interphase and mitotic cells. Other actin structures may have different contributions. Stress fibers (contributing 13 ± 10% actin at the basal cortex of interphase HeLa, measured over 25 cells, and absent in mitotic cells) do not qualitatively dominate over the impact of the cortex. Short actin filaments and their myosin-II based activity can enhance fluctuations. Slow and large actin waves (wavelength: ∼2 μm, speed: ∼20 nm/s, mostly reported at cell edges of spreading cells, and may also exist at the basal membrane (5, 64)) are expected to cause low-frequency fluctuations (0.01 Hz). Although specific wavelike features are not observed in this study, the expected frequency range (0.01–0.03 Hz) shows (Fig. 4 b, inset) a relatively positive contribution to temporal fluctuations from the cortex. At a similar frequency range, mitotic cells also show reduced temporal fluctuations. Therefore, this frequency range has a contribution from actomyosin activity related to spread-out cells.

Comparing the PSDs with a theoretical description of fluctuating membranes adapted from existing models (16, 32, 35, 51) suggests the possible mechanisms behind the effect of perturbing activity or the cytoskeleton. Most values and effect of drugs are close to expectations in comparison to reports/predictions in literature (Supporting Discussion). In general, we find that loss of activity leads to increase in tension, indicating an active softening of the membrane—also observed in RBCs (16, 32, 37, 62). However, the amplification of fluctuations by activity is a combined effect of increase in active temperature, reduction of confinement, and a decrease in tension. The damping role of the cytoskeleton, on the other hand, appears to be arising due to increased confinement of the membrane. It needs to be noted that confinement may arise not only from the cortex but also from the coverslip. In mitotic cells, reduced fluctuations are found to correspond to increase in tension, and values (1146 ± 1770 pN/μm) are close to the surface tension reported in the literature (65).

Hence, by applying IRM, creating spatial maps of temporal fluctuations, and comparing with theoretical descriptions, we provide better understanding about the role of activity and cytoskeleton in setting up the state of fluctuations. We demonstrate that spatial undulations are actively diminished by the cytoskeleton whereas temporal fluctuations intricately depend on the details of the active state, cytoskeleton integrity, and contractility. Fluctuations display transient heterogeneities and long length-scale dissimilarity. The mechanical parameters extracted corroborate the interpretation of the measurements. The functional role of spatial heterogeneity observed in this study and the spatial mapping of corresponding mechanical parameters, especially through coupling of IRM to TIRF microscopy, need future investigation.

Author Contributions

B.S. conceptualized the project. B.S. and A.B. set up the system. A.B. performed and analyzed the experiments. B.S. and A.B. analyzed and interpreted the data. A.A. established and performed experiments with the PMSs. B.S. and A.B. wrote the article. All authors edited the article.

Editor: Cecile Sykes.

Supporting Material

Table S3. Statistical Parameters for Data Presented in Main Figures

The table provides details of the statistical parameters for Figs. 1, 2, 3, 4, 5, 6, and 7. Each experiment was performed on 2–5 separate days keeping a gap of at least 5 days between two. A one-way ANOVA has been used for statistical testing. Mann-Whitney U test for Figs. 3E–3G, 4E, 5G, and 7C. Here, N represents the number of cells and n signifies the number of FBRs (if not mentioned otherwise).

Table S4. Statistical Parameters for Data Presented in Supplementary Figures

The table provides details of the statistical parameters. Each experiment was performed on 2–5 separate days keeping a gap of at least 5 days between two. A one-way ANOVA has been used for statistical testing. Here, N represents the number of cells and n signifies the number of FBRs (if not mentioned otherwise).

Movie S1. Time Lapse Imaging of a Single HeLa Cell at 37°C under IRM Mode

The movie shows the time evolution of the interference pattern of the basal membrane of a single HeLa cell. Scale bar: 10 μm. Exposure time of each frame is 50 ms.

Movie S2. Time Lapse Imaging of a Single CHO Cell at 37°C under IRM Mode

The movie shows the time evolution of the interference pattern of the basal membrane of a single CHO cell. Scale bar: 10 μm. Exposure time of each frame is 50 ms.

Movie S3. Time Lapse Imaging of a Single HeLa Cell under Different Conditions at 37°C under IRM Modes

The movie shows the interference pattern of the basal membrane of single HeLa cells under the mentioned conditions. Scale bar: 10 μm. Exposure time of each frame is 50 ms.

Movie S4. Time Evolution of SD_(time) Projection of a Single Cell

The movie shows the color-coded SD_(time) projections of a HeLa cell with the FBRs overlaid, where each frame is the SD_(time) calculated over 1 s. Scale bar: 10 μm. Lower values of SDs are in black and higher ones are in white.