Metastability Gap in the Phase Diagram of Monoclonal IgG Antibody

Abstract

Crystallization of IgG antibodies has important applications in the fields of structural biology, biotechnology, and biopharmaceutics. However, a rational approach to crystallize antibodies is still lacking. In this work, we report a method to estimate the solubility of antibodies at various temperatures. We experimentally determined the full phase diagram of an IgG antibody. Using the full diagram, we examined the metastability gaps, i.e., the distance between the crystal solubility line and the liquid-liquid coexistence curve, of IgG antibodies. By comparing our results to the partial phase diagrams of other IgGs reported in literature, we found that IgG antibodies have similar metastability gaps. Thereby, we present an equation with two phenomenological parameters to predict the approximate location of the solubility line of IgG antibodies with respect to their liquid-liquid coexistence curves. We have previously shown that the coexistence curve of an antibody solution can be readily determined by the polyethylene glycol-induced liquid-liquid phase separation method. Combining the polyethylene glycol-induced liquid-liquid phase separation measurements and the phenomenological equation in this article, we provide a general and practical means to predict the thermodynamic conditions for crystallizing IgG antibodies in the solution environments of interest.

Introduction

Protein crystallization finds importance in structural biology for studying protein structure-function relationships (1), and in the pharmaceutical industry for developing crystalline protein drug formulations, e.g., insulin and antibodies, with improved injectability and stability (2, 3). On the other hand, undesirable protein crystallization can cause health problems such as cataracts, cryoglobulinemia, and hemolytic anemia (4, 5, 6), or impede protein drug development due to particle formation during manufacture, purification, formulation, and storage (7). The ability to predict and control protein crystallization would have great impacts in both basic science and in the development of protein drug products. The temperature and the protein concentration at which a protein crystallizes are each delineated by the solubility line, also known as the “liquidus” line, in the phase diagram (Fig. 1). However, to determine the solubility line, protein crystals must be first obtained, ideally under the solution conditions of interest. Protein crystallization, if it ever occurs, usually takes a long time due to the slow nucleation processes. Therefore, a rational estimation of the solubility line is highly desirable, and would be superior to the widely used trial-and-error crystallization screening methods.

Figure 1.

A typical temperature-concentration phase diagram of protein solutions. T_s and T_c are the temperatures on the solubility line and coexistence curve at the critical concentration, respectively.

From the theoretical perspective, phase behavior of protein solutions is similar to that of colloids (8, 9, 10, 11, 12). A typical phase diagram of protein solutions, as shown in Fig. 1, consists of three phase boundaries: the solubility line, the solidus line, and the liquid-liquid coexistence curve. The solubility and solidus lines encompass the solution conditions for crystallization. The coexistence curve, located within the crystallization region, is the boundary for liquid-liquid phase separation (LLPS). Unlike crystallization, protein-rich droplets almost instantaneously form when the solution temperature drops below the LLPS coexistence curve. Thus, the coexistence curve measurement does not have a long lag-time. If the metastability gap, i.e., the distance between the solubility line and the coexistence curve, is known, the position of the solubility line in the phase diagram can be determined from the experimental coexistence curve. Previous theoretical studies have revealed that the metastability gap reflects the entropic components, i.e., spatial nonuniformity, of interprotein interactions (8, 12, 13, 14). Near-spherical proteins with isotropic long-range interactions essentially have the same metastability gap (15), whereas the short-range and aelotopic interactions broaden the metastability gap (8, 13, 14). Similarly, nonspherical proteins should have large metastability gaps due to their anisotropic geometry.

In this work, we examine the experimental metastability gap of an important class of nonspherical proteins: IgG antibodies. Antibodies are present in blood and play a central role in the humoral immunity (16). In the modern pharmaceutical industry, monoclonal (single idiotype) IgG antibodies are developed to treat cancers and autoimmune and infectious diseases (17). Antibody crystals find many important applications, e.g., the crystals can be used to determine the antibody-antigen interactions by x-ray crystallography (18, 19, 20); antibody crystalline suspension is a promising type of drug formulation that has high overall protein concentration but low viscosity (3). IgGs are also of particular interest in the theoretical studies of phase diagrams because different IgG molecules share the same Y-shaped structure and the majority of their amino-acid sequence. Due to their common molecular structures, the phase diagrams of most IgGs should have phase boundaries with similar layouts and shapes. Previous studies demonstrate that several IgGs indeed have coexistence curves with the same shape (21, 22, 23). On the other hand, different antibodies have hypervariance in their amino-acid sequence at the tips of the two arms (the antigen-binding Fab domains) of the Y-shaped molecule. This local difference of amino acids may lead to strong interaction contacts for some IgGs (24, 25). Therefore, it is necessary to evaluate to what extent the metastability gap of IgGs is universal, and how it differs from that of near-spherical proteins with isotropic interactions. Despite the extensive studies on phase behavior of antibody solutions (5, 21, 22, 23, 26, 27), the full experimental phase diagram, which is required for evaluating the metastability gap, has not yet been reported. Here, we experimentally determine the full phase diagram of a monoclonal IgG antibody. Using this phase diagram, we show that the metastability gaps of IgG antibodies are similar to each other, but are twice as broad as that of near-spherical proteins. By quantitatively examining the metastability gap of IgG antibodies, we present a method to estimate the solubility line based on a simple critical temperature measurement and a phenomenological equation.

Materials and Methods

Protein and solution preparation

IgGX, a human IgG1 subclass monoclonal antibody, was produced and purified by MedImmune (Gaithersburg, MD). The purity of IgGX, examined by size-exclusion HPLC (Superdex 200 10/300 GL; GE Healthcare, Little Chalfont, United Kingdom), is higher than 98%. The molar mass of IgGX was determined by ESI-TOF MS (microOTOF II; Bruker, Billerica, MA) to be 148,236 Da. The isoelectric point of IgGX is 8.1 (MedImmune internal data). Other chemicals including histidine >98% (ACROS Organics, Morris Plains, NJ), 6 M HCl (Thermo Fisher Scientific, Fairlawn, NJ), NaCl > 99% (BDH, PA), and PEG3350 >98% (Thermo Fisher Scientific) were purchased and used without further purification.

Using gas-pressured diafiltration (Amicon Stirred Cell; EMD Millipore, Billerica, MA), the protein was dialyzed exhaustively against a 20-mM histidine hydrochloride buffer at pH 6.0 with 70 mM NaCl. The protein solution was concentrated using diafiltration followed by centrifugal ultrafiltration (Amicon 50-kDa Centrifugal Filter; EMD Millipore). The concentrated protein stock solution was used to prepare samples at specific protein concentrations. The final protein concentration in each sample was measured by UV absorbance at 280 nm with an extinction coefficient 1.35 mL/mg·cm. A quantity of 50% (w/w) PEG3350 stock solutions was prepared by directly dissolving PEG solid into the buffer. The masses of PEG and buffer were weighed with an analytical balance (model No. AT261 DeltaRange Microbalance; Mettler, Toledo, OH) to calculate the accurate PEG concentrations of the stock solutions. The final PEG concentrations in the samples were determined by weighing the masses of protein stock solution, PEG stock solution, and buffer used during sample preparation.

Clouding-point measurements of liquid-liquid coexistence curve

In the clouding-point measurements, the liquid-liquid phase separation temperature of the samples with various protein and PEG concentrations were determined using a custom-made turbidimeter to construct the coexistence surface of the protein-PEG-buffer ternary system. The sample test tube was placed in a thermostated light-scattering stage. The initial temperature was set high enough so that the solution was homogenous. A 4-mW 633-nm laser beam (R-30988; Research Electro-Optics, Boulder, CO) was directed through the sample. The transmitted intensity was detected by a photodiode and registered to a power meter (1936-C; Newport, Irvine, CA). The temperature of the sample was lowered by 0.2°C every 5 min. At a temperature, T_cloud, the sample became cloudy due to liquid-liquid phase separation. The temperature was then increased until the sample became clear again at a given temperature, T_clear. The average of T_cloud and T_clear was taken as the LLPS temperature, T_ph. The temperature hysteresis between T_cloud and T_clear of IgGX solutions was within 1°C.

Quasielastic light scattering measurements

For quasielastic light scattering (QLS) measurements, ∼100 μL protein samples were filtered by 0.2-μm syringe filter (13 mm 0.2 μm PTFE filter; VWR International, Radnor, PA) into small test tubes. The light scattering experiments were conducted using a custom-made thermostated light scattering apparatus with a coherent He-Ne laser (35 mW, 632.8 nm; Coherent, Santa Clara, CA) and a PD4047 correlator (Precision Detectors, Bellingham, MA). Scattering at 90° was measured to determine the correlation functions. The apparent diffusion coefficients were calculated from the correlation functions using the Precision Deconvolve 6.0 software (Precision Detectors) with a regulated algorithm.

Solubility measurements

The crystals of IgGX were obtained in a 150 mg/mL protein solution after 2 weeks of incubation at 4°C. The crystals were placed in a small amount of fresh histidine buffer to measure the protein solubility at various temperatures. At each temperature, three crystal suspension samples were incubated in a water bath. In the solubility measurement, the samples were centrifuged at 4000 × g for 2 min (Centrifuge 5804R; Eppendorf, NY) at the given incubation temperature. An aliquot of each supernatant was taken to measure protein concentration by UV absorbance at 280 nm. The crystals were resuspended immediately by vortexing and placed back in the incubation water bath. When the supernatant protein concentrations stopped increasing, the average equilibrium concentration of the triplicates was taken as the solubility of IgGX at the incubation temperature.

Results and Discussion

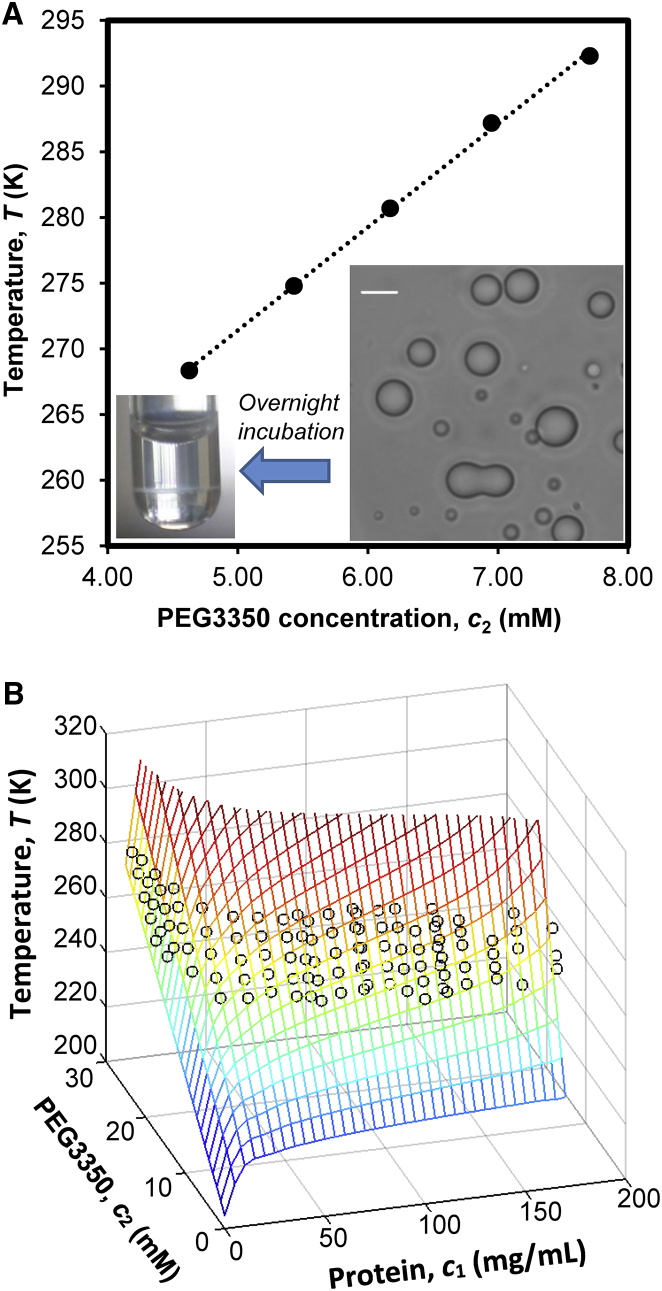
We experimentally studied the phase diagram of a pharmaceutical monoclonal IgG antibody (IgGX, a human IgG1 subclass antibody with molar mass 148,236 Da and isoelectric point 8.1) in a 20 mM histidine hydrochloride buffer at pH 6.0 with 70 mM NaCl. To investigate the metastability gap, we first determined the coexistence curve of IgGX using clouding-point measurements. For most IgG antibodies, LLPS cannot be directly observed because the coexistence curves are located at temperatures well below the freezing point of solution (22, 23). Previous studies demonstrate that LLPS in antibody solutions can be induced at elevated temperatures by addition of a nonionic polymer: polyethylene glycol (PEG) (23, 28). PEG causes an additional interprotein attraction known as “depletion force” (29, 30, 31). Furthermore, the experimental LLPS temperatures for various proteins increase linearly with PEG concentration over broad ranges of protein and PEG concentrations (23, 28). For IgGX, we also found that LLPS can be induced by addition of PEG and the change of LLPS temperature is proportional to PEG concentration (Fig. 2 A). We determined the LLPS temperature as a function of PEG concentration at various protein concentrations from 0.2 mg/mL up to 170 mg/mL (Fig. S1). The LLPS coexistence surface of the IgGX-PEG solution was then constructed by linear regression of the experimental data at given protein concentrations (Fig. 2 B; Table S1). The coexistence surface shows the coexistence curves at various PEG concentrations.

Figure 2.

(A) Given here is the LLPS temperature of 100-mg/mL IgGX solutions as a function of PEG3350 concentration. The inset shows a bright-field micrograph of the protein-rich droplets formed below the LLPS temperature. The white bar is 10 μm. The droplets coalesced into the bottom phase in test tube with a clear meniscus after overnight incubation at room temperature. (B) Given here is the LLPS coexistence surface of the IgG-PEG solutions constructed by linear regression of the experimental data (circles) with respect to PEG concentration. The color gradient from red to blue corresponds to LLPS temperatures from high to low. To see this figure in color, go online.

Our focus in this work is the coexistence curve without PEG. However, it is interesting to notice that in Fig. 2 B the coexistence curves with PEG rapidly increase at protein concentrations higher than 150 mg/mL, i.e., the PEG-induced depletion force increases exponentially with protein concentrations in concentrated IgG solutions. Because the depletion force also promotes protein crystallization, the PEG-induced LLPS of IgGX was preempted by the fast crystallization at concentrations higher than 170 mg/mL. If the depletion force in other IgG solutions also exhibits strong protein-concentration dependence, addition of PEG in concentrated protein solutions could provide an efficient method to prepare IgG crystals. However, note that aggregation may compete with crystallization at high protein concentration in the presence of PEG.

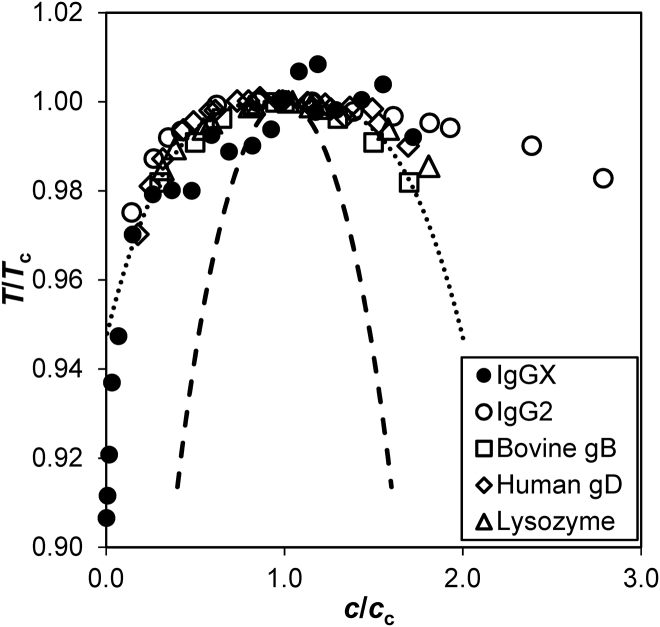
We then compared the coexistence curve of IgGX without PEG to that of other proteins (21, 32, 33, 34). In Fig. 3, the coexistence curves of different proteins were brought together by plotting them in the scale of their temperature and concentration at the critical point, i.e., the maxima of coexistence curves. Fig. 3 shows that the coexistence curve of IgGX indeed has a shape similar to that of other proteins, including another IgG (namely IgG2), which exhibits LLPS without addition of PEG (21). The direct LLPS measurements of IgG2 allowed its critical concentration to be determined (90 ± 5 mg/mL) with high accuracy (21). Other IgGs have a similar critical concentration, whereas near-spherical proteins have much higher critical concentrations (∼260 mg/mL) (21, 22, 35). Like other IgGs, the coexistence curve of IgGX also rises to a plateau at protein concentrations above 90 mg/mL. The universal shape of the coexistence curve of IgGs is consistent with their common molecular geometry (35).

Figure 3.

The scaled LLPS coexistence curve of IgGX in comparison with that of another IgG (21) and various other proteins (32, 33, 34). The dotted line is a fit to the experimental coexistence curve of the near-spherical proteins in (32). The dashed curve is the theoretical coexistence curve of spherical particles with mean-field interaction calculated using the Carnahan-Starling equation of state.

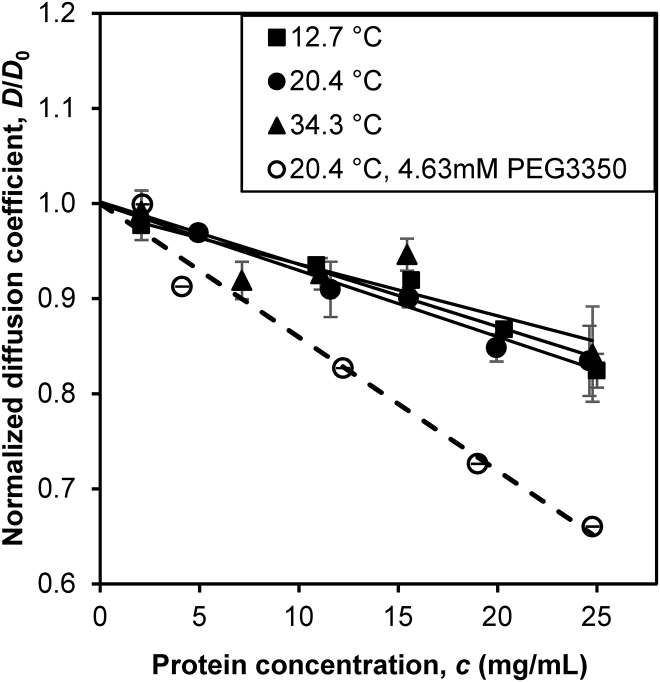
Both LLPS and crystallization require attractive interprotein interactions. To verify the attractive interaction in the IgGX solutions without the presence of PEG, we conducted QLS experiments. Fig. 4 shows the apparent diffusion coefficient of IgGX as a function of protein concentration at various temperatures. The diffusion coefficients are normalized by the extrapolated values of infinite dilute solutions (Table S2). The negative slopes in Fig. 4 indicate attractive interprotein interactions in the IgGX solutions. Fig. 4 also shows that addition of PEG increases the attraction. The results of QLS experiments are consistent with that of the LLPS study: IgGX has weak native attractive interactions, and PEG adds the depletion force resulting in increased protein attractions.

Figure 4.

The normalized apparent diffusion coefficient of IgGX as a function of protein concentration at various temperatures and in the presence of PEG.

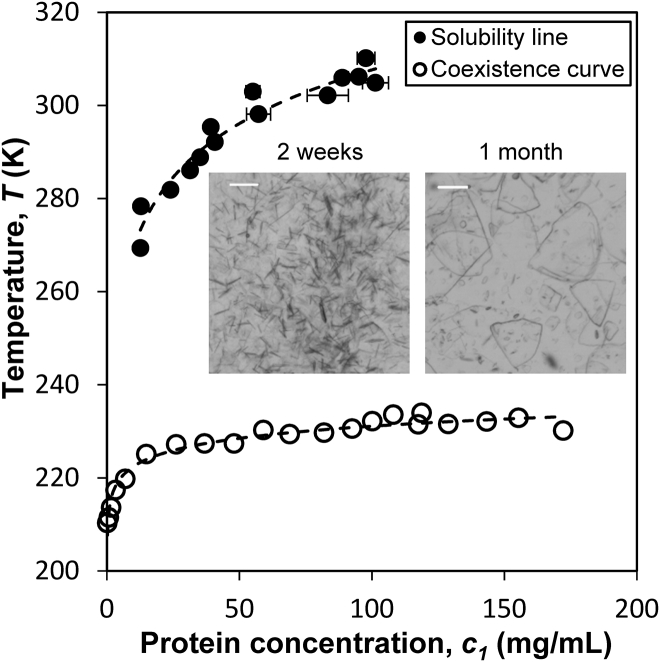
We completed the phase diagram of IgGX by determining the solubility line. Without the presence of PEG, we obtained IgGX crystals in a 150-mg/mL solution at 4°C (Fig. 5). The needlelike crystallites formed in the solution after 2 weeks of incubation, and grew into thin sheets of large crystals in one month. Using these crystals, we measured the protein solubility at various temperatures from 4 to 37°C (Fig. 5). The experimental solubility line of IgGX covers a broad range of protein concentration, including that at the critical point (∼90 mg/mL), which allows analysis of the metastability gap. In a phase diagram (Fig. 1), the metastability gap can be quantified by δ_c ≡ (T_s – T_c)/T_c, where T_c is the critical temperature and T_s is the temperature on the solubility line at the critical concentration (8). Whereas the critical temperature T_c of IgG solutions can be readily determined by PEG-induced LLPS experiments (23), the crystallization temperature at the critical concentration T_s of most IgGs cannot be measured because their interprotein interactions are either too weak or too strong. Without sufficient interprotein attraction, the protein will not crystallize at temperatures above the freezing point of solution. In contrast, strong attraction will lead to low solubility in the temperature range where protein’s structure remains stable (typically <40°C). Because of its apt attractive interprotein interaction, the IgGX solution provides a suitable system for evaluating the experimental metastability gap.

Figure 5.

The full phase diagram of the IgGX solution, consisting of a solubility line and a coexistence curve. The dashed lines are guides to the eye through the experimental data. Below the solubility line, the IgG crystallizes. Inset micrographs show the crystals formed in a 150-mg/mL IgG solution after incubation at 4°C for two weeks and one month, respectively. The white bars are 100 μm.

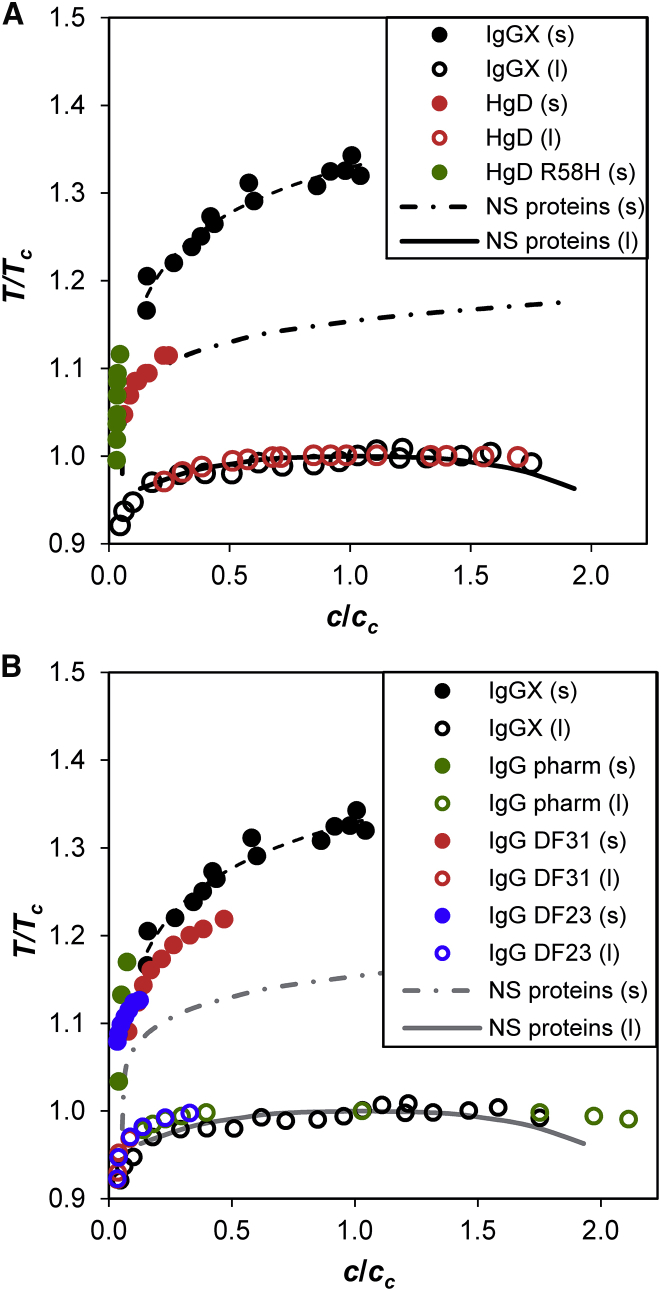
Using the experimental phase diagram, we quantitatively compared the metastability gap of IgGX to that of other proteins. Fig. 6 A shows the scaled phase diagrams of IgGX and several near-spherical proteins including lysozyme, bovine γD eye-lens crystallin (BgD), human γD eye-lens crystallin (HgD), and a cataractogenic mutant of HgD (HgD R58H). Previous studies showed that the experimental phase boundaries of the near-spherical proteins, such as lysozyme and BgD, completely overlap in the scaled phase diagram and thus have the same metastability gap (15). In Fig. 6 A, the metastability gap of IgGX, δ_c = T_s/T_c − 1 = 0.33, is approximately twice as large as that of the near-spherical proteins, δ_c = 0.16. The broad metastability gap of IgGX is consistent with its nonspherical molecular geometry. Interestingly, a similar difference in the metastability gap is observed for another near-spherical protein, HgD, and its cataractogenic mutant HgD R58H (4). Even though the solubility of HgD at temperatures below 40°C is much lower than the critical concentration, the experimental solubility data clearly fall on the solubility line of the other near-spherical proteins. In contrast, the solubility of HgD R58H is much lower than that of HgD and projects to the solubility line of IgGX. The similarly broad metastability gaps of IgGX and HgD R58H can be attributed to the anisotropicity of the interprotein interactions. The single amino-acid mutation of HgD R58H creates strong local interaction contacts and renders the overall interaction of the near-spherical protein aeolotopic (orientation-dependent) in nature (8, 14). Apparently, highly anisotropic interprotein interactions can also be expected for nonspherical molecules like IgGX.

Figure 6.

The scaled phase diagrams of IgGX and other proteins. (A) Shown here is the scaled phase diagram of IgGX in comparison to that of the near-spherical proteins. The NS proteins curve is a guide to the eye through solubility data of lysozyme and bovine γD crystallin (15). HgD is human γD crystallin, and HgD R58H is a cataractogenic mutant of HgD (4). The dashed line is the fit of the IgGX solubility line using the phenomenological equation presented in this work. (B) Shown here is the scaled phase diagram of IgGX in comparison to that of previously reported IgGs (22, 23). In the legend, s and l stands for solubility line and coexistence curve, respectively.

We then examined to what extent the broad metastability gap of IgGX is universal for the IgG-class antibodies. In Fig. 6 B, we compared the phase diagram of IgGX to that of other monoclonal IgG antibodies, including one pharmaceutical and two human myeloma (cancer) IgGs (22, 23). The metastability gaps of the other IgGs cannot be directly determined from the limited solubility data. However, Fig. 6 B clearly shows that all the IgGs have metastability gaps much broader than those of the near-spherical proteins. Theoretically, metastability gaps of different IgGs may vary depending on the number of interaction contacts in both crystal and solution phases (8, 14). Although some variation does appear in Fig. 6 B, the scaled solubility lines of these IgGs are close to each other.

Finally, we present a phenomenological equation to describe the scaled solubility lines of the proteins. The theoretical description of solubility lines requires analytical expressions of the IgG chemical potentials in the solution and crystal phases (8). Nevertheless, we can use a simple logarithmic equation to fit the experimental solubility data in Fig. 6:

$$\frac{T}{T_c}=b\text{ln}\left(\frac{c}{c_c}\right)+{\delta }_c+1.$$ (1)

The values of phenomenological parameters b and δ_c for IgGX, IgG DF31, and the near-spherical proteins are listed in Table 1. By definition, δ_c is the metastability gap. In the frame work of the Lennard-Jones-Devonshire cell model, b is related to the difference between the interprotein interaction energies in the crystal and the solution phases (8).

Table 1.

The Phenomenological Parameters of the Scaled Solubility Line for Three Proteins

	δc	b
IgGX	0.331 ± 0.005	0.072 ± 0.005
IgG DF31	0.271 ± 0.003	0.059 ± 0.002
Near-spherical proteins	0.155 ± 0.002	0.032 ± 0.002

In practical applications, Eq. 1 can be used to estimate the location of the solubility line for other IgG solutions before crystallization screening. As discussed before, most IgGs have similar critical concentrations, c_c ∼ 90 mg/mL. Because the top of the IgG coexistence curve is very flat, the critical temperature, T_c, of any IgG solution can be quickly determined with good accuracy by conducting PEG-induced LLPS measurements at a single protein concentration larger than ∼30 mg/mL (23). Knowing the critical temperature and concentration, one can then plot the solubility line of the IgG solution of interest using Eq. 1 with the parameters obtained for IgGX. When applying this method, we need to be aware of its limitations: 1) The solubility line estimated using the phenomenological parameters for IgGX will be approximate; some variation of the metastability gap of IgGs may be expected. 2) Although the solubility line delineates the thermodynamic conditions for crystallization, kinetic factors govern the time and likelihood of protein crystallization. 3) Equation 1 does not quantitatively describe the high-concentration extreme of the solubility line. As illustrated in Fig. 1, at extremely high protein concentrations, the theoretical solubility line would rise rapidly instead of leveling off as predicted by Eq. 1. In such rare conditions, Eq. 1 still produces a lower limit of the crystallization temperature. With the above considerations in mind, our method provides a useful way to estimate the solubility lines of IgG antibodies.

Conclusion

In this work, we experimentally determined the phase diagram of a monoclonal IgG antibody. Unlike the previously reported phase diagrams of other IgG antibodies, the solubility line in our phase diagram spans a broad range of protein concentration including the critical concentration. We also employed the PEG-induced LLPS method to determine the liquid-liquid coexistence curve located at temperatures below the freezing point of solution. The full experimental phase diagram allows the metastability gap of IgG antibodies to be quantitatively evaluated, to our knowledge, for the first time. By comparing our data and the partial phase diagrams of other antibodies in literature, we found that the metastability gaps of the Y-shaped IgG antibodies are similar in the scale of critical temperature and concentration. Therefore, we can use a single phenomenological equation to estimate the scaled solubility line for different IgG antibodies. Because the critical temperature and concentration of antibodies can be readily determined by the PEG-induced LLPS experiments, our equation can be used to predict antibody solubility at various temperatures. Despite the possible errors of prediction due to individual differences in IgG antibodies, our method provides a practical approach to select the thermodynamic conditions for antibody crystallization. This rational approach could transform the protein crystallization screening experiments for the crystallographic studies of antibody-antigen interactions and preparation of crystalline antibody drug formulations. Also, in the development of antibody drugs, the solution conditions that prompt undesired crystallization can be predicted and avoided. To deepen our understanding of antibody crystallization and extend the usefulness of our method, future studies will be conducted to examine how metastability gaps of other IgGs may vary with the local mutations in the antigen-binding sites. In addition, theoretical and simulation studies will be performed to develop a nonspherical aeolotopic (or patched-particle) model, which describes the experimental metastability gaps of IgG antibodies.

Author Contributions

J.B.R., J.Z., and Y.W. designed research. J.B.R., R.A.C., T.D.E., and R.P.F. performed research. J.B.R., J.Z., and Y.W. analyzed data. J.B.R., S.P., J.A.S., J.Z., and Y.W. wrote the manuscript.

Editor: James Cole.