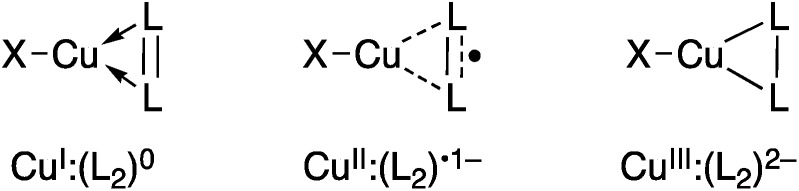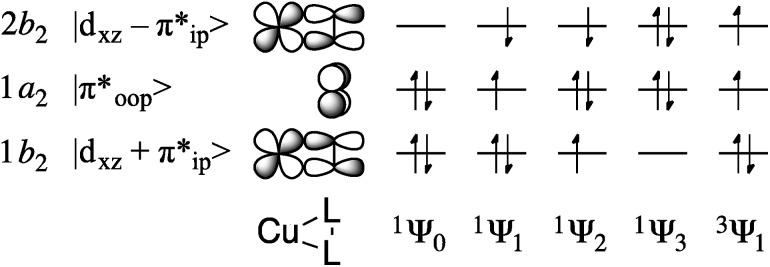Re-evaluating the Cu K pre-edge XAS transition in complexes with covalent metal–ligand interactions

Covalent metal–ligand interactions can lead to Cu K pre-edge transitions that result from metal-to-ligand charge transfer, instead of 1s → 3d, character.

Abstract

Three [Me₂NN]Cu(η²-L₂) complexes (Me₂NN = HC[C(Me)NAr]₂; L₂ = PhNO (2), (3), PhCH CH₂ (4); Ar = 2,6-Me₂-C₆H₃; Ar^F = 3,5-(CF₃)₂-C₆H₃) have been studied by Cu K-edge X-ray absorption spectroscopy, as well as single- and multi-reference computational methods (DFT, TD-DFT, CASSCF, MRCI, and OVB). The study was extended to a range of both known and theoretical compounds bearing 2p-element donors as a means of deriving a consistent view of how the pre-edge transition energy responds in systems with significant ground state covalency. The ground state electronic structures of many of the compounds under investigation were found to be strongly influenced by correlation effects, resulting in ground state descriptions with majority contributions from a configuration comprised of a Cu(ii) metal center anti-ferromagentically coupled to radical anion O₂, PhNO, and ligands. In contrast, the styrene complex 4, which displays a Cu K pre-edge transition despite its formal d¹⁰ electron configuration, exhibits what can best be described as a Cu(i):(styrene)⁰ ground state with strong π-backbonding. The Cu K pre-edge features for these complexes increase in energy from 1 to 4, a trend that was tracked to the percent Cu(ii)-character in the ground state. The unexpected shift to higher pre-edge transition energies with decreasing charge on copper (Q _Cu) contributed to an assignment of the pre-edge features for these species as arising from metal-to-ligand charge transfer instead of the traditional Cu_1s → Cu_3d designation.

Introduction

Interactions between 2p elements and copper ions in metalloenzymes are central to the biological processing of small molecules (e.g. O₂, NO). In particular, the enzymes galactose oxidase, peptidylglycine-α-hydroxylating monooxygenase, dopamine-β-monooxygenase, and amine oxidase rely on the coordination of dioxygen to copper ions in their active sites, as they either introduce an oxygen atom into a substrate or utilize O₂ as a terminal oxidant to form water.¹

This theme reoccurs in inorganic and materials chemistry, where the use of O₂ and related small molecules (herein referred to by the general term L₂) to oxidize low-valent Cu species is crucial to catalytic turnover. The nature of the Cu:L₂ interaction has important implications for the mode of reactivity following coordination by L₂. Understanding these interactions will lead to improved catalyst design and functionality.

Research into the molecular coordination chemistry of Cu:O₂ interactions has linked specific experimental observables to changes in the oxidation states of the metal(s) and ligating O₂.² This information has been critical for mapping the mode of O₂-activation to the function of the coordinated ion, be it in an enzyme active site, networked material, or molecular coordination complex. Dioxygen and related small molecules L₂ (nitrosoarenes, diazenes, and imines) are known to coordinate to metal centers as neutral (L₂ ⁰), monoanionic (L₂˙^1–), or dianionic (L₂ ^2–) ligands (Fig. 1), but while the L–L bond length can be a useful predictor of oxidation state, changes in coordination mode (η¹ vs. η²) and other ligand field effects can complicate this interpretation, which is further impeded in the case of Cu:L₂ complexes by the diamagnetism of most of these species.

Fig. 1. Limiting valence bond electronic structures of Cu:(η²-L₂) complexes. X represents a monoanionic ligand.

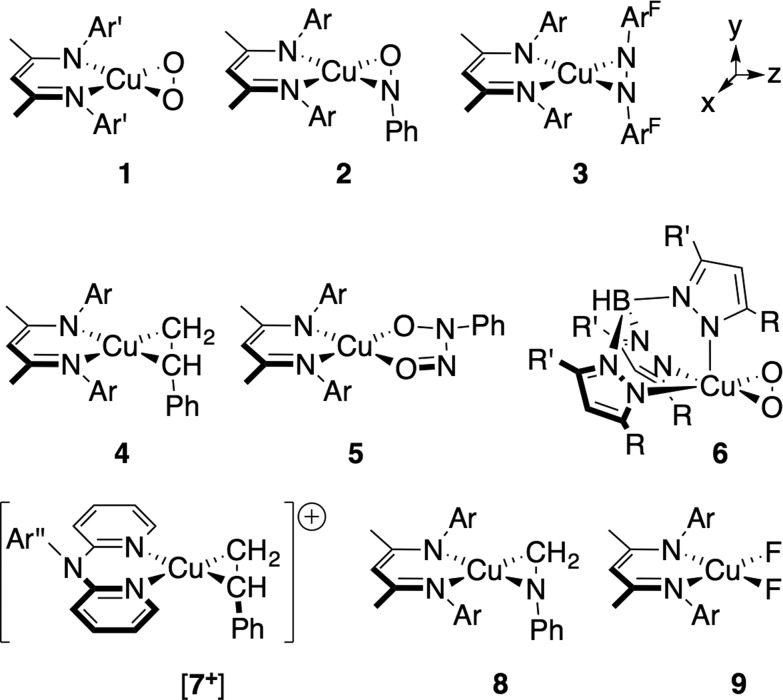
As an example of the difficulty that accompanies oxidation state assignments in such Cu:L₂ systems, we consider the Cu:O₂ species [ⁱPr₂NN]Cu(η²-O₂) (1, Fig. 2). First prepared and characterized by Tolman, Cramer and coworkers, ^3,4 compound 1 was later described in a DFT-supported study as possessing a leading Cu(iii):(O₂)^2– ground-state electronic structure.⁵ This contrasts with the closely related five-coordinate η²-O₂ complex Tp′Cu(η²-O₂) (6, Tp′ = hydrotris(3-R-5-ⁱPr-1-pyrazolyl)borate; R = ^t Bu, adamantyl), which was assigned a Cu(ii):(O₂)˙^1– ground state in related work. ^5,6 Since then, computational studies on 1 and 6 have appeared in the literature, ^7–15 many of which suggest that treatment of these systems with density functional theory (DFT) may be insufficient for accurately modeling their ground states. Gherman and Cramer provided a detailed account of the Cu(iii):peroxide and Cu(ii):superoxide character of model complexes of 1,⁹ using multireference second-order perturbation theory (CASPT2). More recent work by Zapata-Rivera et al. described 1 using the multireference configuration interaction method DDCI-3 (MR-DDCI3). ^12,13 In both cases, significant anti-ferromagnetic coupling (a.k.a. static, or left-right, correlation) in the Cu–O₂ σ-bonding led to a Cu(ii):(O₂)˙^1– description of the ground state. As detailed below, expression of the lowest-energy singlet state in terms of localized orbital representations has allowed for a valence-bond-type description of the bonding, ^16–18 providing a measure of the degree to which Cu(i):(O₂)⁰, Cu(ii):(O₂)˙^1–, and Cu(iii):(O₂)^2– valence bond configurations contribute to the ground state. In the cases in which this analysis has been performed, the results have overwhelmingly favored a Cu(ii):(O₂)˙^1– description for both 1 and 6.

Fig. 2. Depictions of compounds 1–9; the connectivity is not intended to reflect the ground state electronic structures (see text). The following abbreviations were used: Ar = 2,6-(CH₃)₂-C₆H₃; Ar′ = 2,6-[CH(CH₃)₂]₂-C₆H₃; Ar^F = 3,5-(CF₃)₂-C₆H₃; R = C(CH₃)₃, adamantyl; R′ = CH(CH₃)₂; Ar′′ = 2-(CH(CH₃)₂)-C₆H₄.

Recent advances in spectroscopic and computational techniques, especially as applied to metalloproteins, have added new dimensions to the study of oxidation states in transition metal chemistry. In particular, X-ray absorption spectroscopy (XAS) has emerged as a valuable tool, due to the atom-specificity and the wide range of structural information available from this technique.¹⁹ Both the energies and cross-sections of pre-edge and rising-edge absorptions have been used to assign, variously, the physical oxidation states of the metals and ligands, the geometries of binding, and the degree of covalency in the metal–ligand bonds. A detailed understanding of the X-ray absorption spectra of species in biologically relevant interactions is thus of importance for developing accurate models of enzymatic action.

Hodgson, Solomon, and co-workers have made seminal contributions to the study of molecular systems by X-ray absorption near-edge spectroscopy (XANES). ^20–25 For the present work, we are interested in the study of the Cu K-edge (Cu_1s → valence) for identifying the physical oxidation states of Cu ions bound by ligands from the 2p-elements. In this area, the aforementioned researchers have examined Cu complexes with varying coordination numbers and formal oxidation states as a means of delineating the K-edge spectral features common to each oxidation state assignment. ^21,26 A substantial portion of their work has focused on the initial pre-edge transition, which can be found in the range of 8978–8982 eV. In the case of complexes that are comprised of metal centers coordinated by closed-shell ligands, i.e. ligands that form largely ionic bonds with the metal ion, this transition is well-described as a dipole-forbidden (Δl ≠ ±1), quadrupole allowed 1s → 3d transition, which is understood to gain intensity primarily through the admixture of 4p character into the final state.²⁷ Consistent with the d¹⁰ electron configuration for Cu(i), this pre-edge feature has not been observed for cuprous species. Spectra of closed-shell d⁹, Cu(ii) complexes, however, display a low-energy, low-intensity feature at ∼8979 eV (+0.4/–0.6 eV) corresponding to 1s excitation into the Cu-centered 3d-hole.

For other first-row transition metals, shifts in the pre-edge feature of ca. 1 eV has indicated a unit change in the oxidation state of the metal; however, of the few complexes that have been referred to as containing Cu(iii) ions, the pre-edge transition was found to have shifted by ∼2 eV to higher energy (∼8981 ± 0.5 eV).²⁶ Importantly, these Cu compounds are expected to exhibit extensive mixing with the frontier ligand manifold, but much less is understood about the XANES spectra of metal centers that undergo covalent bonding with ligands. The dioxygen compounds 1 and 6 certainly fall in this class, but so do a wide range of Cu complexes that form covalent bonds between the metal ion and its ligands.

An open question thus remains as to how one may reconcile the data from high-level computational studies with the experimental trends in the XANES pre-edge transition energies for not only the dioxygen compounds 1 and 6 but also for related molecules that involve high ground-state covalency. This study seeks to address this question by (i) making judicious choices of oxidation state standards, (ii) examining ground-state and excited-state trends across a series of closely related molecular complexes, and (iii) performing high-level ab initio computations on all complexes under study.

In addition to the η²-dioxygen species 1 and 6, we have studied the η²-nitrosobenzene (2),²⁸ η²-diazene (3), η²-styrene (4 (ref. 29) and [7⁺ ] (ref. 30)), η²-imine (8), and difluoride (9) complexes (Fig. 2), which together provide a modular change in the electronegativity of the ligating atoms. Both the similarity and the high energy of the in-plane-π* orbitals (π*ip) on these ligands provide a means for examining the effects of extensive mixing between the Cu d-manifold and ligand-based fragment orbitals. The Cu K-edge XANES data on these complexes provide a trend that is ultimately tied to the percent contribution of Cu(ii) configurations to the ground state as determined by multireference computational techniques. This trend leads to a re-evaluation of the nature of the pre-edge transition in complexes with covalent metal–ligand interactions, providing a new metric for judging copper ion oxidation states in complexes with covalent bonds to the metal center.

Results and discussion

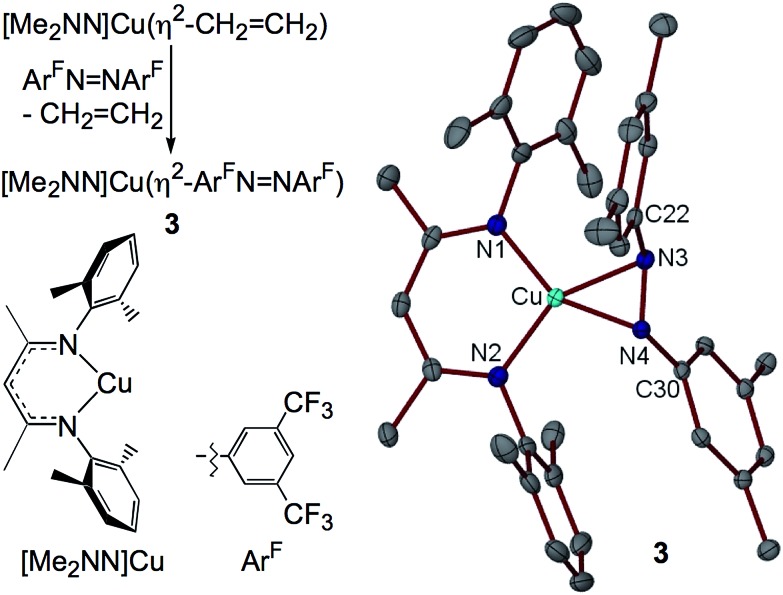
I. Synthesis of the η²-diazene adduct [Me₂NN]Cu(η²-Ar^FN NAr^F) (3)

The syntheses of most of the compounds discussed in this study have been previously reported. [Me₂NN]Cu(η²-Ar^FN NAr^F) (3), however, represents a rare example of a simple diazene complex of copper. Addition of Ar^FN NAr^F to [Me₂NN]Cu(η²-CH₂CH₂)²⁹ in toluene followed by crystallization from pentane affords red-orange crystals of 3 in 78% yield (Fig. 3).

Fig. 3. Synthesis and X-ray structure of 3 (F atoms of CF₃ groups omitted for clarity).

The X-ray structure of 3 reveals symmetrical η²-binding of the diazene to the Cu center with Cu–N3 and Cu–N4 distances of 1.9430(17) and 1.9438(17) Å (Fig. 3). The β-diketiminato Cu–N1 and Cu–N2 distances of 1.8940(17) and 1.8939(18) Å are somewhat contracted relative to those in [Me₂NN]Cu(η²-CH₂CH₂) (1.917(2) and 1.908(1) Å (ref. 29)) indicating a more electron-poor Cu center in 3. The diazene N3–N4 distance of 1.352(2) Å is much longer than that found in the free diazene Ar^FN NAr^F (1.249(2) Å, see ESI†), suggesting electron density transfer from the [Me₂NN]Cu fragment to the diazene. While in most structurally characterized copper–diazene complexes, the diazene is bound κ¹-N as part of a larger chelate, ^31–34 Fujisawa and Lehnert have reported simple mono- and binuclear diazene adducts employing the tris(pyrazolyl)borate complex ^iPr₂ TpCu. ^35,36 Both the parent diazene HN NH and MeN NMe exhibit trans-μ-1,2-binding in {^iPr₂ TpCu}₂(μ-RN NR) with diazene N–N distances of 1.13(1) Å (R = H) and 1.27(2) Å (R = Me).³⁵ These N–N distances, particularly for the HN NH derivative, may be anomalously short due to librational disorder in the diazene N positions.

II. Ground state geometric and electronic structures

II.a. Structural data

All compounds described in this study (except for the five-coordinate dioxygen complex 6) exhibit square-planar geometries in the solid state. For ease of comparison, the nitrogen donor atoms on the auxiliary ligands (R₂NN, Tp′, dipyridylamine) will be referred to as N_eq (and N_ax in the case of Tp′), while the other metal-bound atoms will be referred to either generically as L(1) and L(2) or specifically by their atom identity. The Cu–N_eq bond lengths vary modestly across the series (1.856(6)–1.931(3) Å; see ESI†), except for (i) the Tp′ complex 6, with Cu–N_eq = 1.99(2) Å, which will be discussed in detail below and (ii) the dipyridylamine (dpa) cation [7⁺ ] (Cu–N_eq = 1.958(3) and 1.973(3) Å). The longer Cu–N_eq bond lengths in [7⁺ ] are consistent with the neutral charge of dpa when compared to the monoanionic R₂NN ligand.

The four-coordinate complex [Me₂NN]Cu(κ²-O ₂–O N–N(Ph)–O) 5, which has been previously synthesized and concomitantly described by one of our research groups as a Cu(ii)-containing species with a monoanionic nitrosylated aniline oxide ligand, ^28,37 serves as an oxidation state standard for square-planar [R₂NN]Cu(ii). The description is supported by the isotropic EPR spectrum for this species, which indicated large hyperfine coupling to Cu (A _Cu = 79 G) and significant deviation of the isotropic g-tensor (g _iso = 2.10) from the free electron g-value of 2.002, both consistent with a metal-based S _tot = 1/2 system.

Complexes 1–4, 6 and [7⁺ ] are diamagnetic, complicating the interpretation of the physical oxidation states of the metal centers in this series. The intraligand L(1)–L(2) bond lengths, however, provide an initial indication that many of the complexes under investigation exhibit electron distributions consistent with Cu(ii):(L₂)˙^1– valence bond descriptions. Comparisons are made presently to the DFT geometry optimized L(1)–L(2) bond lengths, the details of which will be provided in the following section.

The experimental and computed O–O distances in [ⁱPr₂NN]Cu(O₂) (1) are 1.392(12) and 1.386 Å, midway between the O–O distances of 1.208 Å in O₂ and 1.47 Å in H₂O₂.³⁸ Notably, the O–O bond in 1 lies within experimental error (3σ) of those calculated for gas phase O₂˙^1–, LiO₂, and NaO₂ (1.363–1.369 Å).⁷ While the experimental O–O bond distance in 6 has been reported as 1.22(3) Å, subsequent reports suggested that the original study significantly underestimated the O–O distance; ^5–7 our computational work predicts an O–O distance of 1.361 Å.

In [Me₂NN]Cu(PhNO) (2), the 1.333(4)/1.333 Å (exp./calc.) N–O bond length is nearly equidistant from the N O distance of 1.20 Å in PhNO³⁹ and the 1.47(1) Å N–O bond in hydroxylamine.⁴⁰ Recent studies suggest that while the N–O distance in 2 is longer than for a metal-bound η¹-N-PhNO˙^1– ligand,³⁹ the additional coordination of O to a metal center can lengthen the N–O distance in the radical anion to ca. 1.33 Å. ^39,41

The N–N distance in the diazene portion of 3, 1.352(2)/1.347 Å lies within experimental error of the 1.345(7) Å N–N bond distance in the monocationic, dinuclear Cu(i) complex of azobis(5-chloropyrimidine)˙^1–.⁴² Again, these values are partway between those of the neutral diazene (1.250(3) Å, see ESI†) and related diarylhydrazines (1.45–1.47 Å). ^43,44

For the styrene complexes 4 and [7⁺ ], the C–C bond distances within the η²-bound alkene (1.373(6)/1.398 Å for 4 and 1.395(6)/1.397 Å for [7⁺ ]) show only modest lengthening compared to a styrenyl C C distance of ca. 1.34 Å and are much shorter than a typical alkane C–C single bond of 1.54 Å.

While a majority of the compounds under study exhibit L(1)–L(2) bond lengths consistent with covalent Cu–L₂ bonds, it is neither clear from these simple structural arguments how strong the overlap in these bonds may be nor how the overlap changes across the series.¶ To aid in understanding these trends, we have performed extensive computational investigations of the molecular ground states as well as low- and high-energy excited states, using a combination of DFT and TD-DFT as well as multiconfigurational and multireference ab initio levels of theory.

II.b. DFT calculations

Density functional theory (DFT) geometry optimization calculations at the BP86 level of theory provided coordinates about the metal center for all species in agreement with those determined crystallographically (see ESI† for full details). Complete molecular (or cationic) structures were used for all complexes except the dioxygen species 1, for which the ligand ⁱPr groups were truncated to CH₃. Since this substitution appears to have a minimal effect on the valence bond structure, the compounds [ⁱPr₂NN]Cu(η²-O₂) (experimental) and [Me₂NN]Cu(η²-O₂) (DFT) are referred to interchangeably in the text.

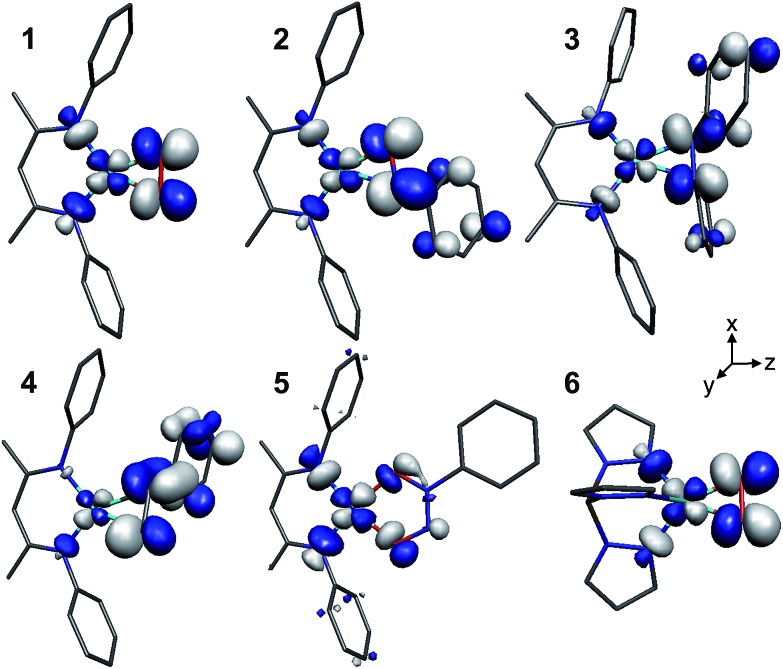
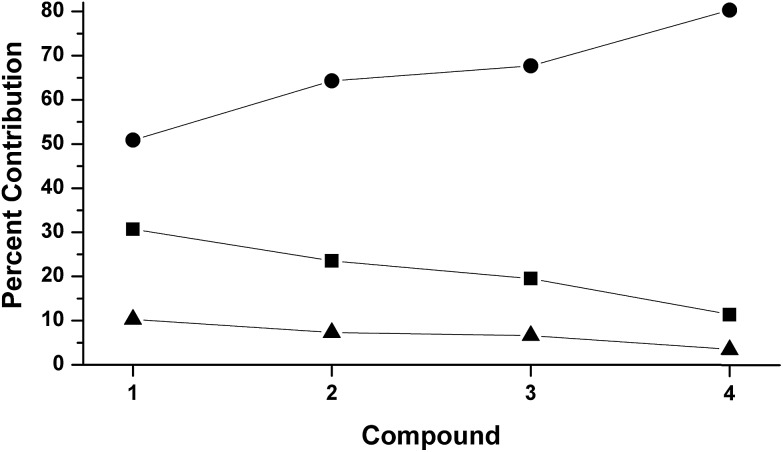
The LUMOs of 1–4 exhibit b ₂ symmetry (assuming an idealized C _2v point group) and comprise the anti-bonding combinations of d _xz with both the π*ip of L₂ and a σ-donating ligand group orbital (LGO) from the diketiminate nitrogens (Fig. 4). The relative contributions of these three fragments to the LUMOs of 1–4 are plotted in Fig. 5. Similar to the computational results reported by Solomon and co-workers,⁵ we find a 30.7% contribution from d _xz to the LUMO of the dioxygen complex 1. This percent contribution decreases across the series to the styrene complex 4 for which the metal contributes 11.3% d _xz character. The decrease in metal character is accompanied by an increase in L₂, from 50.9% O₂ in 1 to 80.3% styrene in 4.

Fig. 4. Graphical representations of the DFT-derived LUMOs for complexes 1–6. The [ⁱPr₂NN] (1), [Me₂NN] (2–5), and Tp′ (6) ligands have been graphically truncated for clarity.

Fig. 5. DFT-derived (B3LYP, Loewdin population analysis) percent contribution to the molecular LUMOs of complexes 1–4 from L₂ (O₂, PhNO, , styrene; ), d _xz (■), and the two nitrogens of [R₂NN] (▲).

Complexes 1–4 provide a nearly monotonic change in the identities of the ligating atoms in L₂, from O O → O NAr → ArN NAr → H₂C CHAr. Missing from this series are the hypothetical η²-imine complexes, where L₂ = ArN CHR (R = H, Ar). No such η²-imine adducts of copper have been crystallographically characterized, as imines have been shown to exhibit κ¹-N binding in such complexes,⁴⁵ exemplified by the recently reported β-diketiminato complex [Cl₂NN]Cu(κ¹-NH CHCH₂Ph).⁴⁶ Nonetheless, while a κ¹-N-isomer of [Me₂NN]Cu(η²-PhN CH₂) was computationally determined to be the ground state geometry, we were also able to locate a local minimum for the η²-bound imine complex at +0.3 kcal mol^–1 (see ESI†).

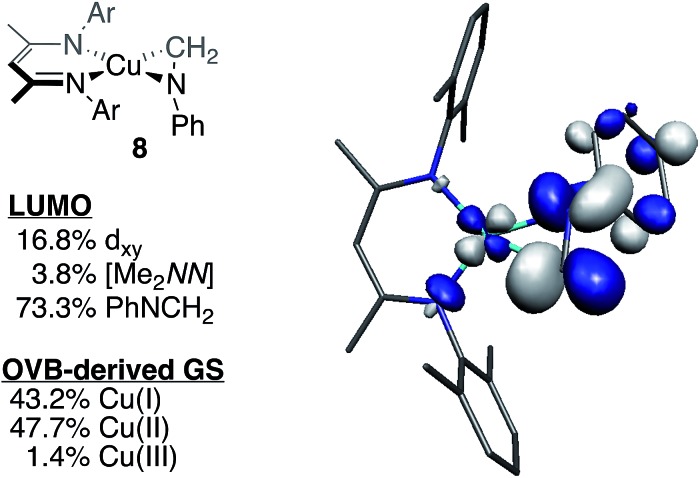
Starting from the optimized geometry of [Me₂NN]Cu(styrene) (4) and substituting the α-CH moiety with a nitrogen, geometry optimization calculations converged on the η²-imine complex [Me₂NN]Cu(η²-PhN CH₂) (8, Fig. 2). Complex 8 is square-planar at Cu and exhibits an elongated C N distance (1.339 Å) compared to a free imine (ca. 1.27 Å), consistent with electron density transfer into the C N π* orbital (π*ip). A B3LYP single-point energy calculation on the BP86 optimized coordinates provides a molecular LUMO comprised of 16.8% d _xz (18.3% total Cu), 5.7% [Me₂NN], and 73.3% L₂ π*ip. These data are consistent with the trend observed for complexes 1–4 (Fig. 5), which indicated an increase in the contribution from π*ip as the sum electronegativity of the ligating atoms decreased.

We have also applied these computational methods to the two known complexes Tp′Cu(η²-O₂) (6) and the cationic portion of [(dpa)Cu(η²-styrene)][BF₄] ([7⁺ ]) (see Fig. 2). The dioxygen complex 6 has been compared to [Me₂NN]Cu(O₂) (1) in previous studies.⁵ Tp′Cu(η²-O₂) is five-coordinate, with a facially-bound Tp′ ligand and an η²-coordinated O₂ ligand. In addition to the two equidistant Cu–N_eq distances of 1.99(2) Å mentioned above, the Tp′ ligand also makes a long Cu–N_ax contact at 2.25(2) Å.⁴⁷ As suggested by the structural data and supported by computational work, this species approximates the geometry of 1, forming a square plane comprising Cu, O₂, and the two N_eq, with N_ax coordinating normal to the plane formed by the Cu–O₂ interaction. Importantly, since the interaction between N_ax and y ²/p _y lacks the symmetry to mix with either the π*oop or the b ₁ LUMO, this additional coordination would not be expected to perturb the Cu–O₂ bonding in 6 with respect to 1. Indeed, the DFT-calculated ground state predicts a LUMO comprised of 33.6% d _xz and 47.4% π*ip, with a further 8.2% contributed by the two N_eq σ-donors, nearly identical to the composition of the LUMO for 1 (Fig. 5).

The cationic dipyridylamine–styrene complex [7⁺ ] (ref. 30) provides a modular change from the neutral [Me₂NN] styrene complex 4, illustrating the generality of the XANES and TD-DFT assignments described below for 4. The styrene-bound cation [7⁺ ] (Fig. 2) crystallizes in a square-planar geometry, with an outer-sphere BF₄ ^– counterion. The LUMO+2 of [7⁺ ] was calculated using the crystallographically determined coordinates and found to be qualitatively identical to the LUMO of 4, with 11.7% Cu-d _xz, 59.4% styrene, 1.8% Cu-4p _x , and modest contributions from the η²-N₂ dpa ligand.

II.c. CASSCF and MR-DDCI3 calculations

While the DFT computational results clearly point to significant covalency in the ground states of compounds 1–8, the inability of DFT to model static correlation in weak-overlap covalent bonds (i.e. bonds that result from fragment orbitals with similar energies that cannot overlap strongly with one another) prompted us to pursue a more quantitative analysis of the physical oxidation states of Cu ions bound by π-acidic ligands. In particular, the combination of the small radial extension of the Cu-d manifold with the high covalency in these systems, as well as the significant static correlation found previously for 1 (ref. 9, 12, 13, and 15) suggested that most, if not all, of the compounds under investigation would be better described by a ground state that allows for mixing between various electron configurations of suitable symmetry.

Typically, the broken-symmetry methodology of Noodleman ^17,18 has performed well at modeling multiconfigurational character within the single-determinate framework of DFT, but for species 1–4, we were either unable to locate a broken symmetry solution (2–4) or the broken-symmetry solution was found to be higher in energy than the closed-shell solution (1, see ESI†). We thus turned to multiconfiguration (MC) and multireference (MR) ab initio methods. These calculations were attractive for not only their more rigorous theoretical treatment of static correlation effects but also for their ability to quantify the contributions to the ground state electronic structure from various limiting, valence-bond descriptions.

MC and MR calculations were performed using atomic coordinates derived from the DFT geometry optimization calculations. The C₆-rings of the aryl groups for complexes 1–5 where left in place due to mixing of the aryl π-systems with the σ-donor orbitals on the [R₂NN] nitrogens, but the aryl-methyl groups were truncated to hydrogens. The Tp′ ligand of 6 was truncated to tris-pyrazolylborate (Tp), and 8 was calculated as the full molecule. Optimization of the positions of the hydrogen atoms provided the model compounds of 1–6. Since the cores of the molecules were unchanged from the truncation, we will refer to these model compounds by the numerical scheme given in Fig. 2. In the ESI,† the numbers 1′–6′ are used to distinguish the MC/MR model compounds from 1–6.

The multiconfigurational ground states of model compounds of 1 have been previously described as resulting from admixture of the doubly-excited singlet state ¹Ψ₃ = (1b ₂)⁰(1a ₂)²(2b ₂)² into the lowest-energy configuration, ¹Ψ₀ = (1b ₂)²(1a ₂)²(2b ₂)⁰ (Fig. 6). ^9,12,13,15 This static correlation can be equivalently described, by way of a linear combination of these two configurations, as the antiferromagnetic coupling of a superoxide radical anion (O₂)˙^1– with an S = 1/2 Cu(ii) metal center to provide the experimentally-observed S _tot = 0 ground state.⁴⁸

Fig. 6. Key frontier orbitals and partial occupations of relevant singlet and triplet CASSCF wavefunctions.

For complexes 1–4, the ¹Ψ₁ configuration is of B ₁ symmetry and is therefore unable to mix with the A ₁ configurations ¹Ψ₀ and ¹Ψ₃, allowing for the exclusion of 1a ₂ (π*) from the active space during computations of the ground state electronic structure. This truncation provides a CAS(2,2) reference space (where CAS(i,k) refers to an active space comprised of i electrons in k valence orbitals), with two electrons in the bonding and anti-bonding combinations of d _xz and π*ip. For complexes 2–4, the qualitative CAS(2,2) descriptions were found to be identical to those given previously for 1 (ref. 9, 12, 13, and 15) and qualitatively invariant to increases in the size of the active space. This treatment revealed a decrease in multiconfigurational character as the electronegativity of the L₂ ligands decreases. Thus, the contribution of ¹Ψ₃ to the ground state dropped from ca. 20% for 1–3 and 6 to 8.2% for 4 (Table 1).

Table 1. Percent contributions of ¹Ψ₀ and ¹Ψ₃ to the ground state wavefunctions for 1–4, 6 and 8, as determined by CAS(2,2) and CAS(2,2)/MR-DDCI3 computational methods.

Compound	CASSCF		MR-DDCI3
	%1Ψ0	%1Ψ3	%1Ψ0	%1Ψ3
1	82.08	17.92	83.51	8.27
2	79.84	20.16	83.30	8.54
3	82.69	17.31	85.35	6.33
4	91.82	8.18	89.87	2.39
6	80.36	19.64	83.43	8.28
8	88.35	11.65	88.73	2.19

Multireference-DDCI3 treatments of the CASSCF-derived wavefunctions provided an evaluation of the extent to which contributions from alternative reference spaces (i.e. those other than the CAS(2,2) reference described above) contributed to the ground state. These second-order perturbation calculations confirmed that the CAS(2,2) basis was an appropriate choice for a first-order approximation of the ground state; ca. 90% of the MR ground states arose from configurations involving the CAS(2,2) reference described above. Table 1 shows that the MR-DDCI3 data are qualitatively identical to those derived by CASSCF methods, with the main difference being a regular decrease in the percent contribution from ¹Ψ₃ with decreasing net electronegativity of the ligating atoms.

A useful analysis that may be performed with CASSCF and multireference calculations is to localize the orbitals in the active space and evaluate the resulting wavefunction for the relative contributions of various limiting valence bond pictures. The output of this method has been termed the Orthogonal Valence Bond (OVB) description of the wavefunction, and this methodology has been used previously in the literature to convey a more intuitive, while equally rigorous, description of molecular ground states. ^{16,18,46,49,50} Using this technique, Zapata-Rivera et al. have previously identified the Cu(ii):(O₂)˙^1– valence bond description as accounting for 64% of the ground state of 1, with <5% being contributed from a Cu(iii):(O₂)^2– configuration when employing a CAS(4,3) reference space.¹² We obtain similar data for 1 (Table 2; full OVB results provided in the ESI†), and for the nitrosobenzene (2) and diazene (3) complexes, OVB analyses revealed %Cu(ii)/%Cu(iii) contributions of 67.0/2.3 and 59.9/1.8, respectively. The styrene complex 4 was found to be comprised of 44.0% Cu(ii) and 46.1% Cu(i) configurations, with an additional 1.4% from Cu(iii). The plurality Cu(i) character for 4 is consistent with traditional descriptions of Cu–styrene bonding, with the substantial Cu(ii) component representing the effect of a π-backbonding interaction between the metal and the π*ip orbital of the styrene. Thus, we observe a trend in leading valence bond configurations to decreasing Cu(ii) character across the series from 1 to 4, and more specifically, to a Cu(ii) description for 1–3 and a Cu(i) description for 4. The OVB-derived atomic charges (Mulliken) on the metal centers support these descriptions, with a cluster near +0.6 for complexes 1–3 and 5 but a value of +0.37 for the styrene complex 4 (Table 2).

Table 2. Tabulated contributions from various valence bond pictures to the ground states of complexes 1–6 .

Compound	OVB-derived character			Q Cu
	%Cu(i)	%Cu(ii)	%Cu(iii)
1	17.2	70.2	4.3	0.698
2	22.4	67.9	2.2	0.607
3	29.9	60.2	1.8	0.531
4	48.6	42.3	1.3	0.366
5	— a	89.0	— a	0.665
6	17.0	71.8	3.1	0.656

^aNo configurations greater than the printing threshold (0.3%).

II.d. Modeling electronic excitations with CASSCF and MR-DDCI3 calculations

To evaluate the multiconfigurational ground states against experimental data, we extended the computational work to the prediction of low energy electronic excitations – specifically the lowest-energy triplet state (¹Ψ_0/3 → ³Ψ₁; where ¹Ψ_0/3 represents the ground state obtained by admixture of ¹Ψ₀ with ¹Ψ₃) and lowest-lying singlet excited state (¹Ψ_0/3 → ¹Ψ₁).

Doing so requires an expansion of the reference to a CAS(4,3) space, i.e. one comprised of the CAS(2,2) manifold described above and the π* orbital on the L₂ ligand (see Fig. 6). The transition energies vary significantly across the series due to perturbations in the π*oop fragment orbital in complexes [Me₂NN]Cu(PhNO) (2) and 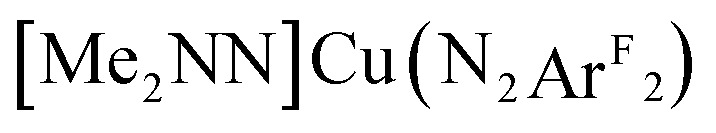(3). The calculated ¹Ψ_0/3 → ¹Ψ₁ energies thus increase from 4691 cm^–1 for [ⁱPr₂NN]Cu(O₂) 1 to 16 903 cm^–1 for 2 on substitution of one oxygen atom for an [NPh] group; substitution of the remaining oxygen to form the diazene complex 3 results in a further increase of this transition to 23 336 cm^–1 (Table 3). The orbital of π*oop character in the styrene complex 4 is mixed heavily with the three hydrogens and the aryl group of styrene, causing a further blue-shift in the “¹Ψ_0/3 → ¹Ψ₁” transition energy to outside the visible region, thus accounting for the colorless appearance of 4; this transition was not modeled computationally.

Table 3. CAS(4,3), CAS(4,3)/MR-DDCI3, and experimental absorption energies from the ground state to the lowest energy singlet (left) and triplet (right) states.

Compound	1Ψ0/3 → 1Ψ1/cm–1			1Ψ0/3 → 3Ψ1/cm–1
	CAS(4,3)	MR-DDCI3	Exp.	CAS(4,3)	MR-DDCI3	Exp.
1	4691	5653	—	3960	2771	—
2	16 903	17 951	17 007	8084	11 137	—
3	23 336	21 616	23 753	10 926	14 993	—
6	3427	4469	4200 a	2754	1804	1500 a

^aValues obtained from ref. 6.

The lowest-energy singlet excited state (¹Ψ₁) and lowest-energy triplet (³Ψ₁) states were similarly evaluated by MR-DDCI3 calculations for their compositions and relative energies. In concurrence with the results obtained by Zapata-Rivera et al.,¹² MR-DDCI3 treatment of the CAS(4,3) wavefunctions of 1 and 6 found ¹Ψ_0/3 → ¹Ψ₁ transition energies of 5653 and 4469 cm^–1, respectively, and singlet–triplet gaps ΔE(³Ψ₁ – ¹Ψ_0/3) of 2771 cm^–1 for 1 and 1804 cm^–1 for 6. Experimental detection of the triplet state of 1 is hampered by the low thermal stability of this species in solution, a problem that also complicates direct observation of the predicted lowest-energy electronic excitation, but experimental data are available for both transitions within complex 6, with the computational data exhibiting an error of ca. 300 cm^–1 (Table 3).

For the nitrosobenzene complex 2, ¹Ψ₁ was calculated to lie at +17 951 cm^–1, which is in agreement with the lowest-energy experimental vis-NIR spectral feature for this compound at 17 007 cm^–1.²⁸ As for 1, this transition is best described as excitation from π*oop (1a ₂) of the PhNO ligand to the d _xz – π*ip (2b ₂) LUMO. For 2, the calculated singlet–triplet gap can be characterized by the same transition (with spin-flip), but the 11 137 cm^–1 gap is diminished by exchange-coupling in the triplet state, which stabilizes ³Ψ₁ by 6800 cm^–1 relative to ¹Ψ₁. The magnitude of this exchange-stabilization is similar in the diazene complex 3 (see Table 3) but ca. 2.5 times greater than for 1 and 6, due to the steric-induced overlap between π*oop and d _xz for compounds 2 and 3 that is absent for the dioxygen species. As seen for the PhNO complex 2, the calculated ¹Ψ₀ → ¹Ψ₁ transition energy for 3 of 21 616 cm^–1 correlates well with the experimentally observed value of 23 753 cm^–1.

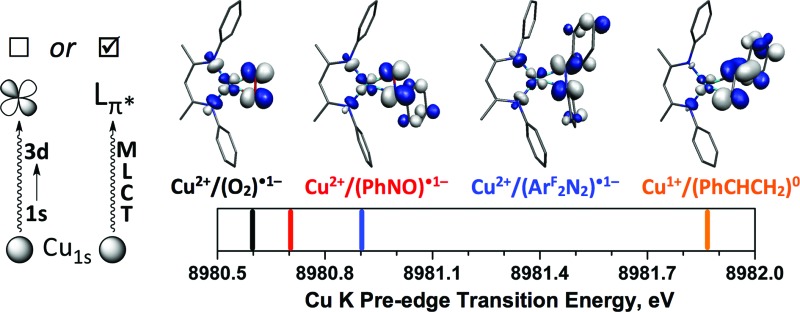
III. Cu K-edge X-ray absorption spectroscopy

III.a. Cu K-edge XANES data

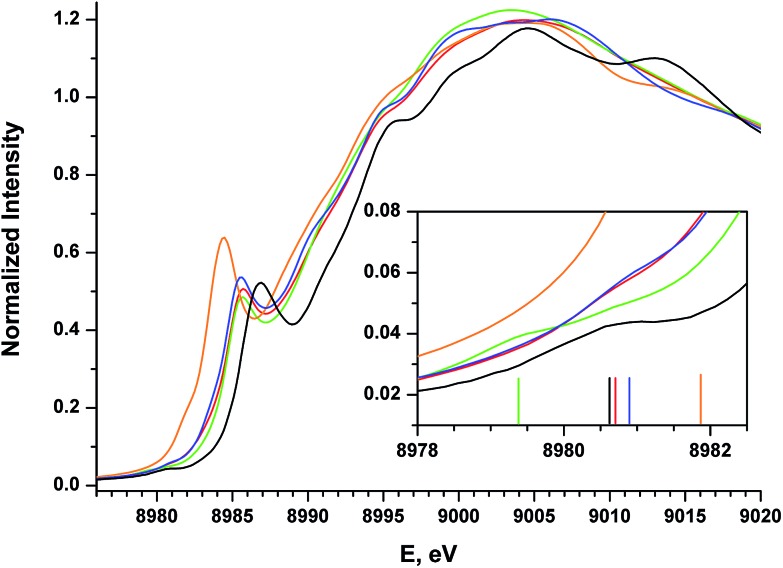
Cu K-edge XANES data were collected on complexes 2–5 (Fig. 2); the spectra are shown in Fig. 7. All four complexes display similar pre- and rising-edge features, consistent with the similar coordination environment for all four metal ions. This similarity thus allows for direct comparisons of the energies and intensities of the spectral features as modest changes are made to the coordination environment about the metal center.

Fig. 7. Experimental XANES spectra for compounds 1 (black), 2 (red), 3 (blue), 4 (orange), and 5 (green). The inset shows an expanded view of the pre-edge region, with vertical bars providing the approximate positions of the pre-edge features.

The Cu K-edge XANES spectrum of 5 (Fig. 7, green), our standard for Cu(ii) in a square-planar coordination environment, exhibits a pre-edge transition at 8979.5 eV (Fig. 7, inset) and a rising-edge transition at 8985.4 eV. Both features are in agreement with those reported previously for four-coordinate Cu(ii) ions bound by closed-shell ligands.²¹

The Cu XANES spectrum of the dioxygen complex 1 has been reported previously.⁵ The apparent position of the edge transition for 1 is at higher energy than that of the Cu(ii) complex 5, and the intense rising-edge feature is shifted to 8986.4 eV. In particular, the appearance of the low-intensity pre-edge feature at 8980.6 eV has been invoked when describing this species as a Cu(iii) metal center coordinated by an η²-O₂ ^2– ligand.

The pre-edge transitions for the nitrosobenzene complex 2 and the diazene complex 3 appear at 8980.7 and 8980.9 eV, respectively; however, the intense rising-edge 1s → 4p ^21,51,52 or 1s → {4p + shakedown} ^21,53–55 transitions lie at 8985.5 eV and 8985.3 eV, lower in energy than the analogous transition for 1 and nearly identical to that of 5. Thus, while the position of the pre-edge feature would suggest Cu(iii) oxidation states for 2 and 3, the energies of the 1s → 4p transitions and apparent edge positions are consistent with those found for the veritable Cu(ii) species 5.

The styrene complex 4 is of interest in that it is formally a Cu(i)-d¹⁰ complex that exhibits a square-planar geometry in the solid state. The Cu K-edge XANES spectrum of this complex exhibits the lowest apparent edge energy, with red-shifted rising-edge features compared to analogous transitions for complexes 1–3 and 5. As the edge energy is most closely tied to the charge on the copper atom in the molecule (Q _Cu), 4 can thus be identified as the complex with the most Cu(i) character within this series. The greater intensity and lower energy of the rising-edge feature at 8984.3 eV has been shown to be characteristic of Cu(i).

In contrast to the Cu(i) complexes studied previously, however, a pre-edge transition can be clearly identified in the spectrum of 4 at 8981.8 – 1.2 eV higher than the analogous feature for the dioxygen complex 1. Deconvolution of the low-energy region of the spectrum suggests an increase in the intensity of this feature compared to those of complexes 1–3 and 5 (Table 4, see ESI† for spectral fits).

Table 4. Experimental and calculated energies and intensities of pre-edge (E ₁) and rising-edge (E ₂) absorption features.

	Transition energies/eV				Pre-edge peak intensities
	Exp. E 1 a	Calc. E 1	Exp. E 2 a	Calc. E 2	Exp. I b	Exp. I rel	Calc. I rel
1	8980.65	8980.79	8986.4	8987.22	1.6(0.11)	1.3(0.09)	0.3
2	8980.7	8980.85	8985.5	8986.33	1.9(0.13)	1.6(0.11)	0.6
3	8980.9	8980.89	8985.3	8986.23	1.2(0.47)	1.0(0.39)	1.0
4	8981.8	8981.91	8984.3	8985.21	8.0(0.72)	6.7(0.60)	4.0
5	8979.3	8978.86	8985.4	8986.70	1.3(0.03)	1.1(0.03)	1.1
6	8978.6	8980.19	—	—	—	—	0.6
[7+ ]	—	8981.90	—	8985.04	—	—	6.0
8	—	8981.64	—	8985.23	—	—	2.7
9	—	8980.20	—	8988.15	—	—	0.5

^aFrom the second derivative of the experimental data.

^bSee ESI for method of calculation.

Together, the XANES spectral data represent competing trends. The clear decreases in the energies of both the main rising-edge transitions and the apparent edge positions from the dioxygen complex (1) to the styrene complex (4) are consistent with a decrease in Q _Cu from 1 across the series to 4. As expected, this trend tracks with the combined electronegativity of the ligating atoms;⁵⁶ i.e. a decrease in the combined electronegativity of L₂ corresponds to a lower Q _Cu. However, based on a traditional analysis of the 1s → 3d pre-edge feature, one would further expect a concurrent decrease in the energy of the pre-edge, but the experimental data trend in the opposite direction. Thus while the analysis of pre-edge features on closed-shell, ionic first-row transition metal complexes is well established, the data presented above appear to re-open the question of how to interpret the electronic structure origin of the pre-edge features in species that display significant ground state covalency.

III.b. TD-DFT calculations of Cu K-edge XANES spectra

Time-dependent-DFT (TD-DFT) calculations of the Cu 1s absorption energies were performed on the optimized coordinates using the B3LYP functional and the CP(PPP) basis set on Cu, the latter of which provided greater flexibility for the core electron density.

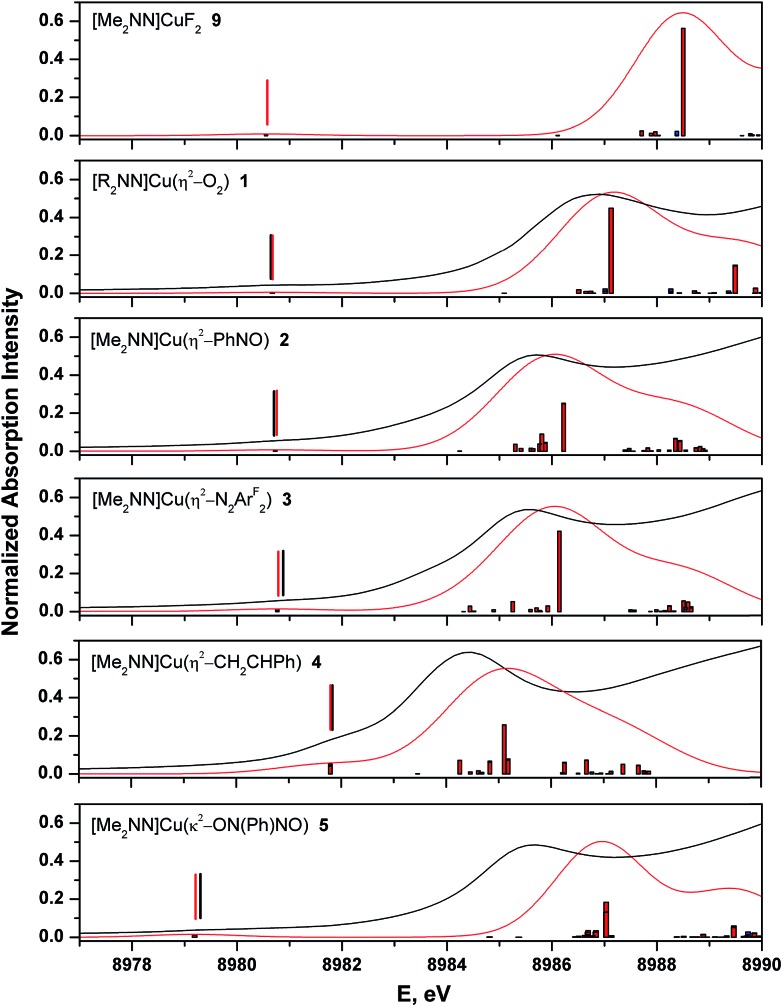
The calculated spectra adequately reproduce the trends in both the pre- and rising-edge features of the experimental spectra (Fig. 8 and ESI†). In general, the computations showed that the pre-edge features (<8982 eV) for all complexes are calculated to result from core excitation into |d _xz – π*ip>, the molecular LUMO in most complexes (Fig. 4). The calculated pre- and rising-edge transition energies are given in Table 4 alongside the experimental data.

Fig. 8. Comparison of experimental (black) and TD-DFT calculated (red) Cu K-edge XANES spectra for complexes 1–5 and 9. Broad vertical bars from the baseline represent individual calculated transitions. Vertical bars above the pre-edge transitions provide calculated and experimental peak positions.

For two compounds described thus far ([7⁺ ] and 8), experimental data are not available with which to compare the calculated spectra, but the consistent accuracy of the TD-DFT methodology lends support to our use of these purely theoretical results. Of note are the observations that (i) the calculated XANES spectrum of [7⁺ ] contains a low-intensity 1s → LUMO+2 transition within 0.1 eV of that calculated for 4, suggesting that this transition is common to Cu(i)–alkene complexes in this geometry; and (ii) TD-DFT calculations on the imine complex 8 predict a pre-edge feature at 8981.6 eV. As expected, this latter feature is characterized as Cu_1s → LUMO, with a calculated relative intensity of 2.7, partway between that of complexes 3 and 4 (Table 4).

TD-DFT is unable to account for shakedown (mutli-electron) transitions, so it is worth noting that the main calculated rising-edge features for 1–5 were modelled well considering these features have often been described as originating from 1s → {4p + shakedown} transitions. This observation suggests that intensity in this region may instead arise from 1s → 4p character.⁵⁷ Cu-4p _y is found to be the prime contributor (ca. 40%) to the acceptor states of compounds 1, 3, and 5; this plurality p character also accounts for the observed intensity (Δl = 1). Like the dioxygen (1), diazene (3), and N-nitroso-nitrosobenzene (5) complexes, the PhNO (2) and styrene (4) complexes also exhibit significant 4p _y character in the main rising-edge transition, but the contribution from 4p _y is tempered by the out-of-plane distortion of the L₂ σ-donors imposed by the asymmetrically substituted L₂ ligand. This distortion turns on mixing with 4p _y , distributing Cu 4p _y character among multiple final states that contribute to intensity along the rising-edge.

For evaluating oxidation states in these complexes, the main rising-edge transition appears to better reflect changes in Q _Cu. These intense features track with the apparent edge energies, which result from 1s → continuum excitations, and represent excitations into states that lack the symmetry to mix with the L₂ valence manifold, thereby making them more immune to ligand field effects. For the sake of comparison, we have performed DFT calculations on the hypothetical compound [Me₂NN]CuF₂ (9, Fig. 2, see ESI†). This species represents an extension of the trend in L₂ donor atoms across the 2p block and may reasonably be expected to represent a species with the most Cu(iii) character among compounds 1–9. Using the methods described above, a C _2v-symmetric energetic minimum was located, for which the metal adopts a square-planar geometry. The Cu–F bond lengths are short, at 1.803 Å, and the d(F–F) (2.529 Å) and ∠(F–Cu–F) (89.1°) are most consistent with a ([Me₂NN]Cu)²⁺/(F^–)₂ description of the molecule. The B3LYP-calculated LUMO is composed of greater d _xz character (40.4%) than the dioxygen complex 1 (30.7%), and importantly, whereas the O₂ ligand accounts for 50.9% of the LUMO of 1, the fluoride ligands provide only 21.7% of the LUMO in 9, consistent with a lower fragment orbital energy for the fluorides than for the π*ip of O₂.

TD-DFT calculations on 9 predict a 1s → LUMO transition at 8980.2 eV and a main rising-edge transition at 8988.2 eV. The pre-edge transition is closest to that of 1 (8980.6 eV), but the rising-edge transition is blue-shifted by ca. 1 eV. As with compounds 1, 3, and 5, the rising-edge transition is plurality 4p _y in character (40%).

In this scenario, if 5 is used as a Cu(ii) reference, with the difluoride as Cu(iii), then a unit change in oxidation state is reflected by a change of 1.5 eV in 1s → 4p transition energy. With this metric as a guide, the placement of the main rising-edge transitions for 1–3 within ca. 0.5 eV of the Cu(ii) complex 5 leads to a bonding model for the dioxygen, nitrosobenzene and diazene complexes in which electron density in the Cu–L₂ σ-bonds is shared equally the metal centers and L₂, generating a metal-based electron density comparable to that of an unambiguous Cu(ii) ion, as predicted by the ground state descriptions provided above.

III.c. Comparison of MR-DDCI3 and Cu XANES data

In complexes with such covalent metal–ligand interactions, quantitative computational analyses can also be of significant value, especially in cases for which static correlation plays a role in the description of the ground state. As described above, the 1s → 4p and estimated edge transition energies will provide the most reliable measure of a copper ion's oxidation state in this geometry, but the repeated use of the pre-edge feature in this analysis, combined with its energetic isolation from other spectroscopic features, necessitates further analysis of what information might be contained in the low energy region of the XANES spectrum.

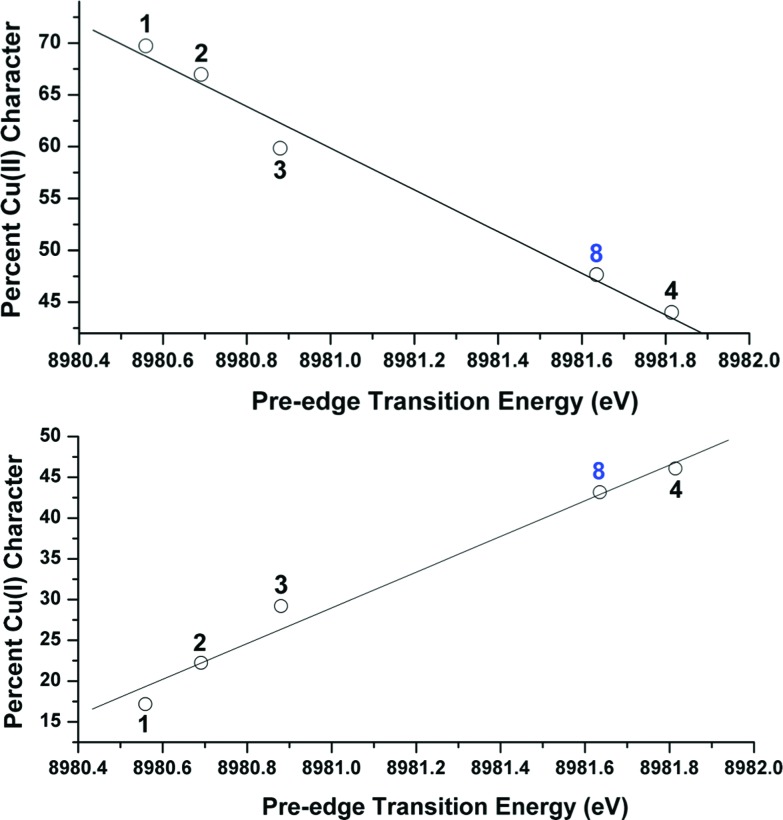
OVB analyses were found to provide a linear correlation between the percent Cu(ii) character in the ground state of complexes 1–4 and the energy of each complex's experimentally-determined Cu K pre-edge transition energy (Fig. 9). This relationship, which similarly holds both for the %Cu(i) character (Fig. 9) and for the DFT-computed pre-edge energies [R ² = 0.90 for Cu(ii) and 0.91 for Cu(i)], thereby allows one to use the pre-edge transition energy as a direct measure of the relative contributions from Cu(i) and Cu(ii) valence bond configurations to the ground states. A similar comparison between the pre-edge energy and the OVB-derived percent Cu(iii) character reveals only modest correlation (R ² = 0.46; see ESI†), likely due to the low weight of Cu(iii) configurations compared to the unaccounted reference space.

Fig. 9. Top: Plot relating the experimental Cu K pre-edge transition energy to the OVB-derived percent Cu(ii) character in the molecular ground states of complexes 1–4 and 8. The trendline was generated from the data points from complexes 1–4: y = 180 686 – 20.112x; R ² = 0.98. Bottom: Plot relating the experimental Cu K pre-edge transition energy to the OVB-derived percent Cu(i) character in the molecular ground states of complexes 1–4 and 8. The trendline was generated from the data points from complexes 1–4: y = 21.895x – 196 607; R ² = 0.97.

To test the predictive capacity of this analysis, we consider the η²-imine compound 8, for which inputting the TD-DFT-calculated pre-edge energy (8981.64 eV) into the trendlines associated with the plots given in Fig. 9 lead to a predicted ground state composition of 47.3% Cu(ii) and 46.0% Cu(i). Performing the relevant CAS(2,2)/MR-DDCI3/OVB calculations on the full structure of 8 revealed a ground state comprised of 47.7% Cu(ii) and 43.2% Cu(i) configurations (Fig. 10), validating the coherence of the model across multiple computational techniques.

Fig. 10. Depiction of the skeletal structure and B3LYP-calcuated molecular LUMO of 8, along with tabulated compositions of both the LUMO and the OVB-derived ground state.

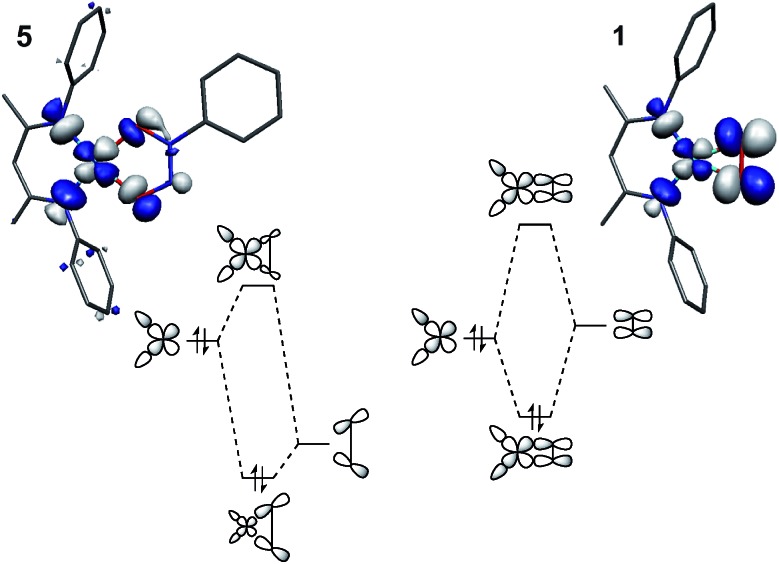
Importantly, this trend only holds for ligand fields of closely analogous compositions. Compound 5 is not appropriate to include in this analysis because the long O–O distance weakens the anti-bonding interaction between the oxygen donor orbitals compared to that in 1, leading to a fundamentally different description of the fragment orbital interactions as compared to 1–4 (Fig. 11). The same rationale applies to the difluoride complex 9, if experimental data were available. The Tp′-bound dioxygen complex 6 will be discussed in greater detail below.

Fig. 11. Comparison of the fragment orbital interactions in 5 and 1, illustrating the different fragment orbital energies of the σ-donor LGO in N₂O₂Ph and the π*ip of O₂.

IV. Comparison of [ⁱPr₂NN]Cu(O₂) and Tp′Cu(O₂)

Our CASSCF and MR-DDCI3 calculations on model compounds of 1 and 6 revealed similar results to those reported previously by Zapata-Rivera et al. ¹² As discussed, similarities in the calculated ground state compositions, lowest energy electronic excitation energies, and singlet–triplet gaps between complexes 1 and 6 suggest that it would be most appropriate to describe both species with the same Cu(ii):(O₂)˙^1– ground state valence bond description. Our MR-DDCI3 calculations further provide a Mulliken atomic charge on Cu of +0.656 for 6, nearly identical to those of 1 (+0.698) and the veritable Cu(ii) complex 5 (+0.665). The similarities between the calculated ground states of 1 and Tp′Cu(η²-O₂) (6), however, are incongruous with the varying shifts in the Cu K pre- and rising-edge data for these species – differences that are unexplained by the CASSCF and MR-DDCI3 computations alone.

The strong interaction between the axial Tp′ nitrogen and Cu-4p _y is expected to shift the main rising-edge transition to higher energy than those observed in the spectra for complexes 1–5. The calculated XANES spectrum for 6 (see ESI†) is consistent with this interpretation, as no clear feature corresponding to excitation into a (1s)¹(4p _y )¹ state is visible within the investigated energy range. Thus, while this region is again modeled reasonably well by TD-DFT in terms of gross spectral features, intense core-to-valence transitions on the rising-edge resulting from the change in coordination number and ligand identity has diminished the validity of comparing the metal-based oxidation states using the rising-edge features alone (see ESI,† Section 17).

The pre-edge transitions, on the other hand, allow for a comparison of energies that originate from transitions of the same character. For 1, the pre-edge signal lies at 8980.6 eV, 2.0 eV higher in energy than the analogous feature for 6, a trend that has been reproduced by TD-DFT calculations (ΔE = 0.6 eV).⁵ The CASSCF and MR-DDCI3 calculations, however, suggest that both complexes are best described by a Cu(ii):(O₂)˙^1– valence bond structure, indicating that rather than a change in Cu and L₂ oxidation states, a change in LF strength may be responsible for the shift in pre-edge transition energy.⁵

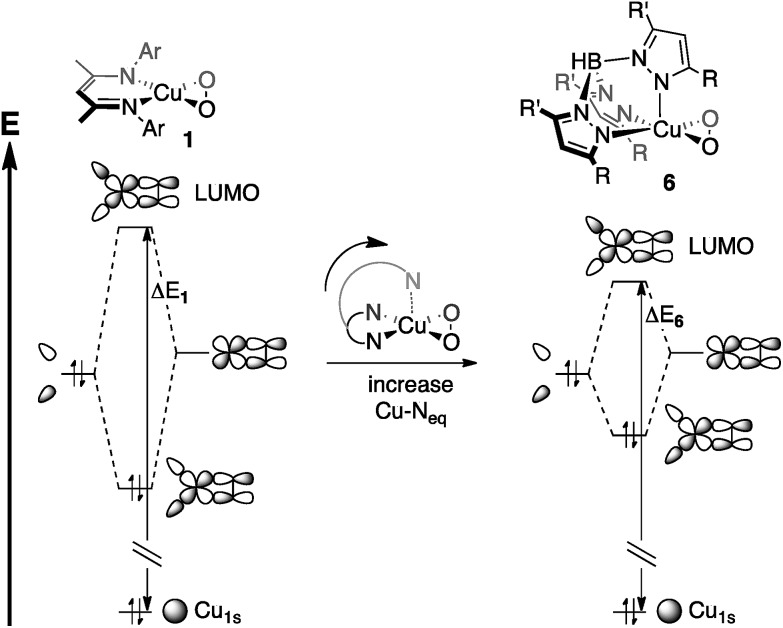
The bidentate coordination of [ⁱPr₂NN] in 1 allows for tight binding of the monoanionic ligand to the metal center, resulting in short Cu–N distances of 1.856(6) Å. For 6, however, the Cu–N_eq interactions are modulated by the Cu–N_ax bond. As a result, the interaction between the metal center and the axial nitrogen pulls the equatorial nitrogens away from the metal, leading to the lengthened Cu–N_eq bonds of 1.99(2) Å in 6, despite the monoanionic charge of Tp′. This stereoelectronic effect, invoked by Cramer et al. when describing the effects of ligand binding strength on dioxygen coordination,¹⁵ would then be expected to decrease the fragment orbital interaction energy that gives rise to the LUMO (Fig. 12), driving the pre-edge transition to lower energy.⁵⁸

Fig. 12. Stereoelectronic effects on ligand field strength, as applied to Cu-1s → LUMO transition energies (ΔE ₁ and ΔE ₆). The Cu-1s orbitals are assumed to be at the same energy, making ΔE ₁ > ΔE ₆.

V. Characterizing the Cu–K pre-edge feature in complexes with covalent metal–ligand interactions

For changes in oxidation state of largely ionic complexes, blue-shifted metal K pre-edge transitions result from a disproportionately large stabilization of the core metal-1s orbitals compared to the valence orbitals following oxidation of the metal center. This effect accounts for the ca. 1 eV increase in pre-edge transition energy per unit increase in oxidation state that is observed when comparing spectra of analogous M(ii) and M(iii) Werner-type complexes (M = first-row transition metal). The accumulated data for 1–4 suggest that a Werner-type bonding model for these complexes is inadequate. The pre-edge data on 1–4 revealed a trend to lower transition energies as the oxidation state of the metal center increased (as gauged by the electron-withdrawing ability of the ligating atoms within L₂). This change was most apparent for the styrene complex 4, for which the transition energy of 8981.8 eV lies both 1.2 eV higher than the analogous feature in the spectrum of the dioxygen complex 1 and 2.5 eV higher in energy than that of the Cu(ii) complex 5, suggesting the need for an alternative to the traditional 1s → 3d description of this feature.

Instead, a molecular orbital view that includes substantial mixing between the π*ip and d _xz provides a more accurate description of the bonding in these more covalent species. The L₂-based π*ip fragment will increase in energy from O₂ to styrene, meaning the LUMO (2b ₂, Fig. 6) of the styrene complex 4 will exhibit the most L₂-character (ca. 80%, Fig. 5) and have the highest energy, while 2b ₂ of the dioxygen complex 1 will exhibit the least L₂-character (ca. 50%) and have the lowest energy. This description is supported by the MR-DDCI3 computational results which revealed, when compared to complexes 1–3, a significant increase in Cu(i) character for 4, as one would expect for a species in this geometry with an L₂-based LUMO. Complex 4 also exhibits the least multiconfigurational character, in line with greater energetic separations of {d _xz + π*ip} and {d _xz – π*ip}. As such, an assignment of the initial pre-edge features as metal-to-ligand charge transfer (MLCT) excitations (Cu_1s → L_2π^* ), rather than the typical C_1s → Cu_3d characterization, provides a better interpretation of the data.

A recent evaluation of calculated MLCT transitions in the low energy region of transition metal XANES spectra found a significant dependence on the degree of hybridization in the utilized functional.⁵⁹ Pure DFT functionals (e.g. TPSS and BP86) proved unsatisfactory in modeling pre-edge trends, but the incorporation of ca. 20% Hartree–Fock character (e.g. B3LYP) led to results that accurately reproduced experimental data. Our computational results using B3LYP provided excellent agreement in both the 1s → LUMO and 1s → 4p transitions (Fig. 8). Plots of experimental transition energies vs. the uncorrected, calculated energies for compounds 1–4 had linear coefficients of determination of 0.974 (1s → LUMO) and 0.996 (1s → 4p). Use of the BP86 functional led to a similar linear correlation for the 1s → 4p transitions (R ² = 0.983), as expected for an excitation that does not involve charge transfer, but the BP86-calculated 1s → LUMO transitions exhibited low correlation with the experimental data (R ² = 0.117), thus underpinning the MLCT description of these transitions.

The low intensities of the pre-edge features are unusual for traditional MLCT transitions but are more common in X-ray absorption spectroscopy, due, in part, to the localization of the initial state on the metal atom (M_1s). In the present case, where the final states include non-negligible contributions from the metal, excitation from the a ₁-symmetric initial states to the (formally) b ₂ final states are forbidden. In such an instance, the oscillator strength of the transition becomes largely dependent on the extent of Cu-4p mixing, as a Laporte forbidden 1s → 3d transition would gain only modest intensity from electric quadrupole coupling.²⁰ While the intensities of the pre-edge features for 1–5 are difficult to determine with certainty, both the TD-DFT predicted transition dipole moments and the intensity estimates from the deconvoluted spectra suggest an approximate three-fold increase from complexes 1–3 to complex 4 (Table 4). This trend may be explained by the polarization of the ligand field with changing L₂. The 4p _z (b ₁) and 4p _y (a ₁) are precluded from mixing with the b ₂-symmetric LUMO. The 4p _x is of b ₂-symmetry, but its contribution will be modulated by the presence of a dipole in the ligand field. This dipole thus serves as a measure of the difference in energy between the ligand-based fragment orbitals that contribute to the LUMO; greater energy differences will increase 4p _x /d _xz mixing.

From both the computational and experimental data, it appears that the donor strength of the monoanionic [R₂NN] ligand is matched by the monoanionic (O₂)˙^1–, (PhNO)˙^1–, 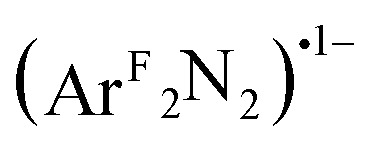, and (PhN₂O₂)^1– ligands to form an effectively-centrosymmetric ligand field, as evidenced by the low degree of 4p _x character (∼0.1%) in the LUMOs of 1–3 and 5 as well as the low intensities of the observed transitions (Table 4). By extension, should 1 exhibit a Cu(iii):(O₂)^2– ground state, then the intensity of the pre-edge feature would be expected to again increase relative to those of complexes 2 and 3, as the (O₂)^2– ligand would create an energetically asymmetric ligand field capable of incorporating more 4p _x character into the final state. For 4, which is best characterized as a Cu(i) complex with a neutral styrene donor, (PhCHCH₂)⁰, the ligand field dipole leads to greater LUMO 4p _x character (1.0%), thereby decreasing the degree to which parity is conserved during excitation.

Conclusions

In the absence of a series of related complexes and extensive computational data, analysis of the Cu K pre-edge transitions for complexes 2–4 would have led to Cu(iii) oxidation state assignments for these species. This is based on the high pre-edge energies (ca. 8980.5–8982 eV) for these complexes when compared to those of veritable Cu(ii) reference compounds (ca. 8979 eV). This view would be consistent with the traditional conception that Cu 1s energies drive changes in the pre-edge region of the XANES spectrum. However, the similar coordination environments of the dioxygen (1), nitrosobenzene (2), diazene (3), and styrene (4) complexes allowed for a comparison of the often-obscured edge positions for these compounds, which, as expected, showed a trend to lower copper oxidation states as the combined electronegativity of the coordinating atoms decreased (1 → 4). Considering that the edge position solely reflects the Cu 1s binding energy, an investigation of the incongruity between the trend in the pre-edge data and that of the rising edge energies turned to a re-evaluation of the origin of the pre-edge feature, one that could more readily be influenced by ligand field effects.

In all cases, the final state associated with the pre-edge transition was dominated by the π*ip character of the η²-L₂ ligand (L₂ = O₂, PhNO, 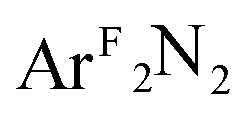, CH₂CHPh), receiving only modest contributions from the Cu 3d manifold. The low-intensity pre-edge features for 1–4 were thus assigned as MLCT transitions, which gained intensity via an asymmetry in the ligand field. In a traditional analysis, this interaction would lead to a Cu(i):(L₂)⁰ description of the ground state. As discussed here and in prior research (see above), however, this analysis fails to account for static correlation in the ground states of complexes that exhibit weak-overlap covalency. MR-DDCI3 calculations in conjunction with OVB analyses of the resulting wavefunctions led to majority Cu(ii):(L₂)˙^1– descriptions of 1–3 and a plurality Cu(i):(L₂)⁰ ground state for the styrene complex 4. The Cu K pre-edge XAS feature was found to respond linearly to the percent Cu(ii) character of the complex as determined by an OVB analysis of the MC/MR ground state.

While the shift in the apparent edge positions between complexes 1–4 likely represents greater ionicity in the ground state of the dioxygen species, the accumulated data presented above would suggest that the characterization of the metal ions in 1–4 as Cu(iii) is incorrect. Rather, we believe that this series of compounds represents a progressing tradeoff between Cu(i) and Cu(ii), meaning that the styrene complex 4 is the species with the most Cu(i) character and the dioxygen complex 1 is that with the greatest Cu(ii) character, even though all four species exhibit a mixture of both oxidation states. Only the difluoride species 9 shows a degree of ionicity consistent with a Cu(iii) oxidation state assignment. Considering the similar pre-edge energies for 1 and 9, however, we conclude that transitions in this region (∼8980.5 eV) may represent a tipping point between Cu(iii) bound by low-energy closed-shell ligands (e.g. 9) and Cu(ii) bound by high-energy π-acceptor-type ligands (e.g. 1–3). Still, studies on a wider range of related compounds are needed to further disentangle the complex bonding situation between copper and π-acidic ligands with respect to both their most accurate ground state electronic structures and their K-edge XANES spectroscopic features.

Overall, the data suggest that covalency in the final state of Cu K-edge XANES transitions can dramatically change the manner in which pre-edge features are interpreted. Variations in Cu 1s orbital energies have traditionally been thought to be the primary force behind differing pre-edge features, but our work supports the view that covalency can up-end this interpretation. The diminishing Cu d-character of the molecular LUMO leads to what can best be described as MLCT states following 1s excitation. This re-interpretation accounts for the unexpected trend in the pre-edge transition energies, leading ultimately to a new metric for evaluating electronic structures in K-edge XANES spectroscopy.