The Neural Basis of Aversive Pavlovian Guidance during Planning

Abstract

Important real-world decisions are often arduous as they frequently involve sequences of choices, with initial selections affecting future options. Evaluating every possible combination of choices is computationally intractable, particularly for longer multistep decisions. Therefore, humans frequently use heuristics to reduce the complexity of decisions. We recently used a goal-directed planning task to demonstrate the profound behavioral influence and ubiquity of one such shortcut, namely aversive pruning, a reflexive Pavlovian process that involves neglecting parts of the decision space residing beyond salient negative outcomes. However, how the brain implements this important decision heuristic and what underlies individual differences have hitherto remained unanswered. Therefore, we administered an adapted version of the same planning task to healthy male and female volunteers undergoing functional magnetic resonance imaging (fMRI) to determine the neural basis of aversive pruning. Through both computational and standard categorical fMRI analyses, we show that when planning was influenced by aversive pruning, the subgenual cingulate cortex was robustly recruited. This neural signature was distinct from those associated with general planning and valuation, two fundamental cognitive components elicited by our task but which are complementary to aversive pruning. Furthermore, we found that individual variation in levels of aversive pruning was associated with the responses of insula and dorsolateral prefrontal cortices to the receipt of large monetary losses, and also with subclinical levels of anxiety. In summary, our data reveal the neural signatures of an important reflexive Pavlovian process that shapes goal-directed evaluations and thereby determines the outcome of high-level sequential cognitive processes.

SIGNIFICANCE STATEMENT Multistep decisions are complex because initial choices constrain future options. Evaluating every path for long decision sequences is often impractical; thus, cognitive shortcuts are often essential. One pervasive and powerful heuristic is aversive pruning, in which potential decision-making avenues are curtailed at immediate negative outcomes. We used neuroimaging to examine how humans implement such pruning. We found it to be associated with activity in the subgenual cingulate cortex, with neural signatures that were distinguishable from those covarying with planning and valuation. Individual variations in aversive pruning levels related to subclinical anxiety levels and insular cortex activation. These findings reveal the neural mechanisms by which basic negative Pavlovian influences guide decision-making during planning, with implications for disrupted decision-making in psychiatric disorders.

Introduction

Most important decisions are difficult as they involve sequences of consequential choices. For example, to go to university, where, and what to study? Such planning is complex as the outcomes of earlier decisions (e.g., degree) can affect the availability of later options (e.g., income), and the resulting tree of future possibilities to be evaluated grows quickly with decision sequence length. To manage this intricacy, we often have to abandon rational calculation in favor of hard-wired approximations. We recently identified one such powerful Pavlovian heuristic that humans ubiquitously use during complex planning, which we term “aversive pruning” (Huys et al., 2012). Aversive pruning entails excising from consideration decision tree branches that contain important negative events (here, large monetary losses; Fig. 1A,B). Individual variation in aversive pruning levels predicted the severity of subclinical depressive symptoms (Huys et al., 2012), suggesting a possible role in depression (Dayan and Huys, 2008, Eshel and Roiser, 2010). These behavioral and computational studies raise the question as to how aversive pruning is implemented in the brain. Therefore, we sought to identify the neural basis of aversive pruning using fMRI.

Figure 1.

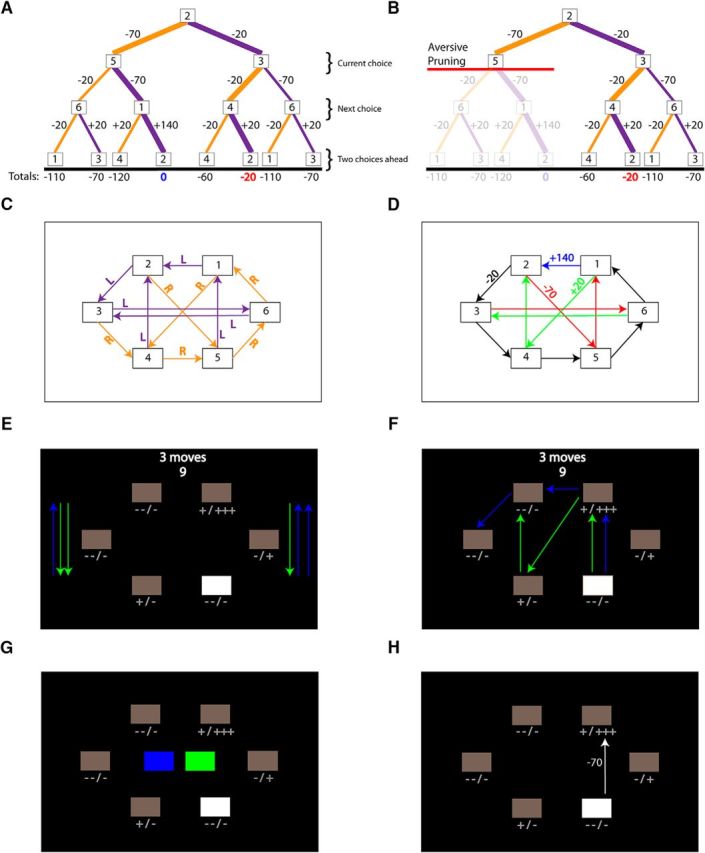
Aversive pruning example and fMRI task design. A, Decision tree and monetary outcomes up to a depth of three from starting state 2. Purple- and orange-colored lines indicate pressing the left and right buttons, respectively. The totals earned for the two best paths (thicker lines; breaking even and losing 20 pence) are shown in blue and red. B, An example of disadvantageous aversive pruning. The red line shows the curtailment of the search within the decision tree upon encountering a large monetary loss (−70 pence), such that the more advantageous break-even sequence is not considered. C, Button presses and transitions within the maze. D, Monetary outcomes within the maze. E, Free plan trial. Beginning in a selected white box, participants had 9 s to plan a sequence of moves (3–5 moves, indicated at the top of the screen) to maximize income. Plusses and minuses below each box indicate the potential outcomes possible from moving from there but are not indicative of directionality. Colored sidebar arrows were included to match visual input with restricted plan trials. F, Restricted plan trial. Participants had 9 s to decide between two maze routes (green and blue), one of which provided higher net income. G, For restricted plan trials, the selection of either the blue or green route involved choosing either the left or right button. H, After entering their moves or path selection, participants were shown their selected path with the corresponding monetary outcome for each box-to-box transition for both free and restricted plan trials. Summed path totals were not shown.

Aversive pruning is reflexive, akin to Pavlovian responses, as it persists above and beyond loss aversion, even when it is highly suboptimal (Huys et al., 2012). Our central expectation therefore was that aversive pruning would be mediated via regions known to be involved in orchestrating emotional reactions to aversive events. Thus, our predictions focused first on the subgenual anterior cingulate cortex (SGC; part of the ventromedial prefrontal cortex). The SGC is anatomically well placed to subserve the impact of affective aversive values on planning. It is connected to areas involved in mediating Pavlovian behavioral inhibition such as the periaqueductal gray (PAG) and amygdala, as well as regions involved in the evaluation required for planning (Schultz, 2015), such as orbitofrontal cortex (OFC) and dorsolateral prefrontal cortex (DLPFC; Johansen-Berg et al., 2008, Ongür et al., 2003). The SGC is known both to represent aversive stimuli and mediate their impact: neurons in the homologous region of the macaque brain (ventral bank of the pregenual anterior cingulate) specifically represent negatively valenced motivational value (Amemori and Graybiel, 2012). These neurons increased in activity during decisions to avoid a punishment (facial air puff), which also entailed forsaking a reward (food). Importantly, the stimulation of these neurons triggered maladaptive decision-making, increasing levels of avoidance even when potential concomitant rewards were high.

There is also evidence that the SGC participates in aversive processing in humans (Talmi et al., 2009). Additionally, and consistent with some theoretical accounts of the role that Pavlovian inhibition plays in the development of affective disorders (Dayan and Huys, 2008, Eshel and Roiser, 2010, Huys et al., 2015b), the SGC has consistently been shown to be overactive in patients with mood disorders (Drevets et al., 1997, 2008), with its degree of activation to negative stimuli predicting treatment response in depression (Roiser et al., 2012). Since aversive pruning is a form of reflexive behavioral inhibition, we additionally expected the involvement of regions directly implicated in this process, notably the PAG and amygdala. The PAG participates in fear (Mobbs et al., 2007) and increases in activation with anxiety in humans (Mobbs et al., 2010). The amygdala has been reported to be recruited during human conditioned inhibition (Geurts et al., 2013). Both structures have also been implicated in affective disorders (Krishnan and Nestler, 2008).

Finally, as planning depends on multiple cognitive systems, we anticipated that the neural architecture subserving aversive pruning would operate in addition to, yet distinct from, established networks governing other cognitive processes. Specifically, we expected to distinguish the neural correlates of aversive pruning from those associated with executive functioning (Newman et al., 2003) and mnemonic processes (Tolman, 1948; DLPFC, parietal cortex, dorsal striatum), sequence planning [Matsuzaka et al., 2012; Fermin et al., 2016; pre-supplementary motor area (SMA), SMA, motor cortex, cerebellum], as well as goal-directed evaluation [Schultz, 2015; ventral striatum (VS), OFC, insula].

Materials and Methods

Participants

Forty-one healthy volunteers [21 females; mean (M) = 23.30 years, SD = 3.70] were recruited via the University College London Psychology participant pool. Participants were screened for past and present psychiatric disorders, including substance/alcohol dependence/abuse, using the Mini International Neuropsychiatric Inventory (Sheehan et al., 1998). Past or present psychopathology was an exclusion criterion, and one participant was excluded on this basis (previous substance dependence), leaving 40 participants in the analysis. Participants completed the State-Trait Anxiety Inventory [STAI; Spielberger et al., 1970; state: M = 9.50, SD = 7.20; trait: M = 14.00, SD = 7.53; Beck Depression Inventory (BDI); Beck et al., 1961; M = 3.13, SD = 4.21], the revised Neuroticism-Extraversion-Openness Personality Inventory (Costa and McCrae, 1992; openness: M = 33.28, SD = 5.84; conscientiousness: M = 29.90, SD = 7.88; extraversion: M = 31.45, SD = 6.54; agreeableness: M = 34.18, SD = 4.84; neuroticism: M = 17.98, SD = 8.13), and the Wechsler Test of Adult Reading (Wechsler, 2001), which was used to evaluate intelligence quotient (IQ; M = 111, SD = 4.2). The study was approved by the UCL Graduate School Ethics Committee, and all participants provided written, informed consent. Participants were compensated based on task performance, up to a maximum of £40, with a minimum payment of £15.

Task

The reinforced sequential planning task was adapted for fMRI from one described in detail previously (Huys et al., 2012) and programmed in Cogent 2000 (www.vislab.ucl.ac.uk/Cogent), a stimulus presentation toolbox for MATLAB (version 7.1). Participants moved throughout a hexagonal maze via button presses (U/I during training, left/right in the scanner; Fig. 1C) in an attempt to maximize earnings. Possible outcomes (Fig. 1D) comprised one large reward (Fig. 1D, +140 pence, top blue arrow), three large losses (Fig. 1D, −70 pence, red arrows), and several small gains and losses [Fig. 1D, 20 pence each, green (+) and black (−) transitions, respectively]. During free plan trials (of which there were 90; Fig. 1E), participants had 9 s to devise a sequence of moves so as to maximize their earnings (planning phase); a countdown timer from 9 to 1 indicated the amount of time left in seconds. Following this planning phase, participants had 2.5 s to input their responses, via a series of button presses on an MRI-compatible button box. We biased the free plan trials by starting position and difficulty, such that for 60 trials it was optimal to transition through the large loss, while for the remaining 30, the optimal sequence avoided the large loss.

During restricted plan trials (40; Fig. 1F,G), participants were presented with two possible multistep routes (equal length; three to five moves) through the maze, one colored blue and the other green (Fig. 1F), and had to choose between just these. As in the free plan trials, participants had 9 s to evaluate the best route (one path always yielded more money than the other). Subsequently, two colored boxes appeared, one blue, the other green, and the participant then selected their chosen route with a single button press (Fig. 1G, either left or right option; again, as per ad libitum plan trials, participants had 2.5 s to input their response). Twenty of the restricted plan trials involved deciding between two routes that both transitioned through a large loss (restricted plan large loss). In the other 20 restricted plan trials, both paths avoided the large loss (restricted plan no large loss).

For both free plan and restricted plan trials, participants were then shown the selected sequence of moves and their corresponding monetary outcome (0.8 s for each move; Fig. 1H). Every trial finished with a fixation cross, which varied in duration depending on the number of moves (0.5–2.1 s), such that the trial duration was always 16 s. Twenty fixation trials, also 16 s in duration, were included to constitute an implicit baseline in the fMRI analysis. Trials were randomized into three runs of 50 trials, each lasting 13.5 min and with the constraint that no trial (i.e., number of moves, starting position, and trial type) was repeated consecutively. Participants were paid according to their earnings, but the running net income was not displayed until the end of each run. Not entering enough moves on free plan trials, or failing to respond on restricted plan trials, incurred a £2 loss on each occasion.

Participants received extensive training on the task before entering the scanner: 30 trials without reinforcement, followed by a test, to learn the transitions (Fig. 1C); and 34 trials to learn the transition values (Fig. 1D), including 18 free plan and 2 restricted plan trials with no time restriction, and 14 with the same time restriction as in the scanner, 2 of which were restricted plan trials.

Behavioral analyses

Basic behavioral outcome measures

Free plan trials were classified according to the following categories: correct decisions (participants executed the best possible sequence); suboptimal decisions (participants did not execute the best possible sequence); and misses (participants failed to enter enough moves). Correct decisions were further subcategorized as “optimal large loss” (OLL) correct trials, on which the participant transitioned through at least one large loss to gain the maximum amount of money, and “optimal no large loss” (ONLL) correct trials, where the maximum was attained by avoiding large losses. Suboptimal decisions were further classified into aversive pruning trials and “error” trials. Aversive pruning trials were defined when it was optimal to transition through the large loss, but participants selected the best available option that avoided the large loss (Fig. 1A,B). Errors were defined as all other instances of suboptimal choices and were subdivided into trials where the optimal decision would avoid (ONLL error, though these occurred very rarely) or entail (OLL error, excluding aversive pruning trials) transitioning through a large loss. Restricted plan trials were classified as either correct or errors. Please see Table 1 for a list of trial outcome classifications.

Table 1.

Basic behavioral outcome measures

Type	Abbreviation	Explanation
Optimal no large loss correct	ONLL correct	Optimal sequence chosen where this does not include a large loss
Optimal large loss correct	OLL correct	Optimal sequence chosen where this includes a large loss
Aversive pruning		The best sequence that avoids large losses chosen when the optimal sequence includes at least one
Optimal no large loss error	ONLL error	Suboptimal sequence chosen for this trial type, not including aversive pruning
Optimal large loss error	OLL error	All suboptimal sequences chosen for this trial type

The main behavioral outcome measures were proportion of correct (OLL and ONLL) scores (after removing the small number of missed trials: mean = 4.65%; SD = 2.55%) and reaction times (calculated at the time of the first move entered). We determined a proxy (trial-based) measure of each individual's sensitivity to large losses by calculating the difference between ONLL and OLL correct scores (averaged across depth). We excluded three participants who scored <50% correct across all ONLL trials, indicating an inability to perform the task.

Basic behavioral data analyses

Behavioral data from the scan (i.e., excluding training trials) were analyzed using SPSS (version 21, IBM). Only free and restricted plan trials on which participants entered the correct number of moves were included in this analysis. Accuracy, reaction time (RT), and earnings data across conditions were analyzed using paired-sample t tests and ANOVA. Due to low trial numbers, RT and earnings data were not analyzed for ONLL error trials. Where appropriate, RT data were log transformed to meet parametric assumptions (assessed using the one-sample Kolmogorov–Smirnov test). Where transformations were not sufficient to correct normality violations, nonparametric tests were applied, including the Friedman test and Wilcoxon signed-rank test. To test the relationship between psychometric variables and task performance, we used multiple linear regression, with the following variables included in the model: age, sex, IQ, STAI trait, STAI state, and BDI. For all analyses, p < 0.05 was considered significant and 0.05 < p < 0.1 was a trend toward significance. Where appropriate, Greenhouse–Geisser correction of df was used to accommodate violations of sphericity.

Model-based behavioral data analyses

Overview of model-based behavioral data analyses.

Here, we focused our analyses specifically on aversive pruning and fMRI; detailed analyses of alternate planning strategies are described previously (Huys et al., 2015a). Computational modeling was based on our previous approach (Huys et al., 2012). Only free plan trials on which participants entered sufficient moves were included; restricted plan trials were not modeled. Following model fitting, models were compared using the integrated Bayesian information criteria (iBIC; Huys et al., 2012), in which models of greater complexity are penalized more strongly, and thus are required to have higher log likelihoods for the choices than simpler models.

We initially provide a brief overview of our modeling approach and explain this in more detail in the section below. Our analyses focused on the creation of four distinct computational models and their evaluation in relation to our behavioral data based on our previous results with this task reported in Huys et al. (2012). First, we constructed an optimally performing model, called “lookahead,” which fully evaluated each sequence within the maze and chose the path with the highest net total value. As optimal sequence planning is unrealistic, especially at higher decision depths, we next calculated a “discount” model, in which sequence planning is probabilistically terminated at each depth, with the likelihood of termination determined by the “general discount” parameter. Most relevant to the hypothesis examined here, we then created a “pruning” model, in which participants stopped planning sequences specifically if they contained a large monetary loss, in addition to general discounting. This tendency is governed by the pruning (specific discount) parameter. Finally, we constructed a “loss-sensitive” model to control for any overweighting of negative relative to positive outcomes, a phenomenon commonly known as loss aversion.

For the fMRI analyses, we exploited the best-fitting, “pruning” model, to quantify the “inclination to prune” on a trial-by-trial basis. This involved computing the distribution of probabilities over all possible paths for a particular problem (starting state and depth), given that individual's pruning parameter. This distribution was calculated from the pruning model. We also computed this distribution assuming that the pruning parameter was identical to the general discount parameter—in other words, assuming no specific discounting when encountering large monetary losses, equivalent to the “discount” model. The difference between these two distributions, calculated for every trial, was our metric of the inclination to prune in our model-based fMRI analyses, which is called the Kullbach–Leibler (KL) divergence.

Details of model-based behavioral data analyses.

Compared with our previous approach (Huys et al., 2012), the models were adapted to take into account the fact that participants had to emit an entire action sequence at once; the models therefore had to specify distributions over entire action sequences. That is, rather than choosing from one of the two actions d times (Huys et al., 2012), participants chose one sequence from the entire set of 2^D (where D corresponds to decision depth) available sequences. We write the probability of emitting sequence aⁱ as follows:

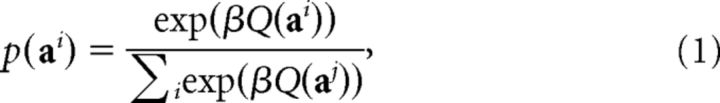where β is the inverse temperature that determines the steepness of the softmax function.

The Q value was defined as follows. For model lookahead, a standard tree-search algorithm was used. This completely evaluates each possible sequence according to the sum of all D outcomes r_d(aⁱ) that would be encountered, as follows:

However, it is computationally unrealistic for human participants to perform such a search, given the large number of possible sequences (8, 16, or 32 sequences, for three-, four-, and five-move trials, respectively). Thus, we fitted a discount model, which captures the tendency not to plan fully, forcing the tree search to terminate at each depth with probability 1 − γ (hence, γ here represents the continuing probability; note that in Huys et al., 2012 it was formulated as the complementary stopping probability). The discount model captured such uniform search curtailment with a single γ parameter, as follows:

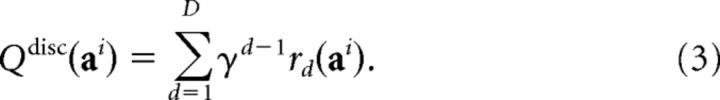The next model, pruning, is central to the hypothesis we aimed to test here: it splits the γ parameter into γ_G (“general pruning”), representing the general tendency not to plan (as in model discount), and γ_S (termed “specific pruning” in our previous report; Huys et al., 2012; aversive pruning in this article), the probability of tree-search continuation specifically on encountering a large loss. The pruning model incorporated these two separate γ parameters, as follows:

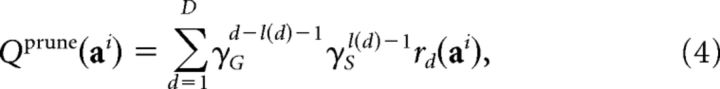with l(d) indexing the number of times a large loss outcome had been encountered up to the point d in the sequence. That is, a probabilistic reduction in planning beyond a large loss is captured by a lower continuing probability (γ_S) after a large loss.

Next, a “loss-sensitive” model with values Q^prune+LA (a) additionally allowed the sensitivities to each of the outcomes r in Equation 4 to be fitted separately for every participant. For this model, β in Equation 1 was fixed at unity. This ensured that any aversive pruning was not simply due to a relatively stronger weighting of losses compared with rewards (i.e., loss aversion, the well known tendency for humans to overweight losses relative to gains of equivalent magnitude; Tversky and Kahneman, 1991).

Finally, we considered an additional Pavlovian attraction parameter that had proved important in the behavioral study (Huys et al., 2012). This captured the attraction of states based on their average future consequences, regardless of whether sufficient choices remained on a trial to exploit those consequences. Most critically, this captured the tendency of participants to move from state 6 to state 1 (−20 pence) rather than to state 3 (+20 pence) when there was only one choice left at this state. We found this effect in our current data too, with participants choosing the transition from state 6 to state 1 on 53% of trials when only one choice remained, despite the relative 40 pence cost entailed. However, there were fewer such trials in the current version of the task, thus weakening its evidentiary basis.

The reader is referred to Huys et al. (2012) for a detailed discussion of these models. The fitting procedures and the rationale for the group-level iBIC are also discussed there.

Additional behavioral modeling was performed to generate parameter estimates to approximate the aversive pruning on each particular trial, including in model-based fMRI analyses (O'Doherty et al., 2007). As a marker for the engagement of the neural circuits that are involved, we examined the inclination the subject had to aversively prune on each trial, whether or not this behavior actually occurred. This inclination should depend on the trial type (being greater when there are more opportunities for aversive pruning; e.g., on deeper trials) and should be higher the stronger the individual's overall tendency to engage in aversive pruning. Short of a validated process model for aversive pruning, we considered a surrogate measure of trial- and subject-specific propensity that at least exhibits these two critical properties. Specifically, we computed (using a set of parameters tailored to each subject) two probability distributions over all possible sequences for every trial: first, the distribution assuming that aversive pruning had no influence (i.e., fixing γ_S at zero); and second, the distribution calculated using their fitted γ_S. The difference between these two distributions, the KL divergence, is our index of the likely predilection to engage in aversive pruning on any given trial. Note that we do not assume that subjects actually compute the distributions with and without γ_S; they are simply used here as a tractable proxy of the trial-by-trial variation in inclination to engage in aversive pruning. The KL divergence was calculated between the action distribution probability for models with and without aversive pruning. If p(α|s_o, d, γ) is the probability of all possible action sequences of length d starting from state S₀ given by Equation 3 (the discount model, with only one γ) and p(α|s_o, d, γ_G, γ_S) is the same for Equation 4 (the pruning model, where γ is split), the KL divergence D_KL is then as follows:

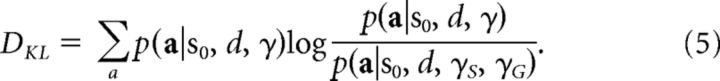This KL divergence value was calculated for each successfully completed free plan trial, including the training trials, and then Z-transformed such that the mean was equal to zero and the SD was equal to 1 for each individual. Importantly, the summed KL divergence value across trials for each participant was highly correlated with the difference between their γ_G and γ_S values (r₍₃₇₎ = 0.74, p < 0.001). Note that the KL divergence measure should be high on trials where the possibility of aversive pruning is likely to have influenced subjects' behavior to a greater degree (e.g., with increased complexity), given their estimated overall tendency to engage in aversive pruning.

MRI data acquisition

Brain images were acquired using a Siemens 1.5 tesla Avanto MRI scanner with a 32-channel sense head coil at the Birkbeck-UCL Neuroimaging Centre.

The task was presented via a head coil mirror and a front-of-bore projection system. Two hundred twenty-five T2*-weighted echoplanar imaging (EPI) volumes [42 slices per volume; slice repetition time (TR) = 87 ms; volume TR = 3.654 s, echo time (TE) = 50 ms; slice tilt = −30°; flip angle = 90°; field of view = 192 mm] were collected per run. The EPI sequence used was optimized to reduce signal dropout in both OFC and amygdala regions (Weiskopf et al., 2006). Phase oversampling (12%) was applied. Slices were positioned to maximally encompass ventral prefrontal and subcortical regions as these included our a priori hypothesized regions of interest (ROIs). Following task completion, field maps (short TE = 10 ms; long TE = 14.76 ms) were acquired to assess the inhomogeneity of the magnetic field. Finally, a 3D T1-weighted anatomical scan (magnetization prepared rapid gradient echo; 176 slices; slice thickness = 1 mm; gap between slices = 0.5 mm; TR = 2730 ms; TE = 3.57 ms; field of view = 256 × 256 mm²; matrix size = 256 × 256; voxel size = 1 × 1 × 1 mm resolution) was acquired at the end of each scanning session.

fMRI preprocessing

EPIs were preprocessed before analysis using Statistical Parametric Mapping (SPM) 8 (release 4010; www.fil.ion.ucl.ac.uk/spm) in MATLAB (version 7.1). The first three volumes from each run were discarded to allow for T1 equilibrium effects, leaving 222 volumes per run. Images were spatially realigned to the fourth volume of the session and unwarped (using field maps) to correct for motion and geometric distortions caused by inhomogeneities in the magnetic field, respectively. Volumes corrupted due to movement (0.01% of all volumes) were excluded and replaced by linear interpolation of the surrounding images. Images were then normalized to Montreal Neurological Institute (MNI) coordinate space and smoothed with a Gaussian kernel of 4 mm full-width at half-maximum (FWHM).

fMRI statistical analyses

All fMRI analyses were conducted using SPM.

First-level modeling

Model-based fMRI—aversive pruning.

We first constructed an fMRI model to explore the impact of aversive pruning on planning on a trial-by-trial basis using the computationally derived KL divergence estimates, Z-transformed within each subject (i.e., model-based fMRI). In this model, all valid free plan trials were included in a single regressor, which was modulated first by difficulty (i.e., the number of sequences to evaluate; 2^d = 8, 16, or 32 for 3-, 4- and 5-move problems, respectively, where d = depth) to account for the linear effects of the expanding tree upon the KL divergence value. The difficulty-modulated regressor was then parametrically modulated by the KL divergence value. This, and all other models (except the model examining value itself), contained a separate parametric regressor representing the net monetary outcome of the chosen sequence across all trials (also time locked to the planning period with the same duration). Specifically, the linear effect of the anticipated reward on planning-related responses was modeled via a parametric regressor, with magnitude proportional to the net outcome provided by the chosen sequence. The inclusion of such a regressor removes value-related response variance from the analysis; this is important because aversive pruning is, by definition, monetarily disadvantageous. We also examined the effect of depth on KL divergence-related responses by computing the interaction of the KL divergence value and difficulty (again, 2^d) and entering it as a third parametric modulator.

Distinguishing aversive pruning from planning and value-related networks.

To confirm established findings and the distinctiveness of our aversive pruning fMRI results from other networks and processes elicited by the task, we also constructed further models testing for the neural effects of planning and valuation. To examine responses related to difficulty during complex planning, we examined the first parametric modulator (difficulty: 2^d), which modulated the regressor containing all successfully completed free plan trials [time locked to the planning period with the same duration (9 s)]. The aim here was to locate the regions of the brain that scaled with the increasing cognitive demands of planning in our task. We constructed an additional model to explore outcome value-related networks. This value model contained a further parametric modulator time locked to the outcome phase (2.4–4 s following the end of response input), which allowed us to examine value-related responses during both the planning and outcome phases (each in a separate regressor); we parametrically modulated the relevant portions of the trial by the net monetary outcome of each trial.

Trial-based fMRI—aversive pruning.

For the trial-based fMRI analyses, the subject-level design matrix included separate regressors for the different trial types (defined according to participants' in-scanner choices; see “Basic behavioral analyses” above; Table 1) corresponding to the planning phase of the task. The following regressors of interest were included: OLL correct; ONLL correct; aversive pruning; OLL error; correct restricted plan large loss; and correct restricted plan no large loss. ONLL error trials were not included due to low trial numbers for this category and were included in a separate regressor of no interest. To model increasing cognitive demands with increasing depth, we entered trial difficulty as a parametric modulator. This parametric regressor on OLL correct, ONLL correct, aversive pruning, and OLL error entailed a modulation by the number of sequences that needed to be evaluated (i.e., difficulty, 2^d). Contrasting conditions parametrically modulated by depth should yield a more sensitive analysis of neural responses because the likelihood of aversive pruning grows with the branching or complexity of the decision tree.

Model- and trial-based fMRI.

For both model-based and trial-based fMRI analyses, we also included regressors to model the response input phase (duration, 2.5 s; in a single regressor for all trials) and outcome phase (duration, 2.4–4 s). The outcome phase was categorized into the same six regressors as the planning phase for the trial-based fMRI analysis (free plan: OLL correct, ONLL correct, aversive pruning, and OLL error; restricted plan: correct restricted plan large loss and correct restricted plan no large loss), again separately modeling the linear effect of net outcome across trial types. Additionally, to assess the impact of receiving a large loss, we contrasted OLL and ONLL correct trials during the outcome phase of the task. For both the model- and trial-based fMRI analyses, regressors of no interest included missed/no-response trials, ONLL error trials, and incorrect restricted plan trials combined into a single regressor (whole-trial duration, 16 s), as well as regressors modeling null scans for the two scans immediately before and after the second run, and interpolated images following removal of corrupted scans (if any). Fixation trials were not modeled explicitly and constituted an implicit baseline. The six realignment parameters were also included in the model. All regressors were modeled as boxcars time locked to the trial phase (planning, input, and outcome) with the corresponding duration (9, 2.5, and 2.4–4 s, respectively) and convolved with the SPM canonical hemodynamic response function.

Estimation incorporated a high-pass filter at 1/128 Hz, and serial correlations intrinsic to the fMRI time series were accounted for using an AR(1) model. The three runs were modeled as a single concatenated run to avoid nonestimation of entire runs for participants with low numbers of event types.

Second-level modeling

Following estimation, subject-level contrast images were smoothed with a 7 mm FWHM kernel and entered into group-level one-sample t tests. Activations were localized with reference to the group-averaged anatomical scan and the atlas of Mai et al. (2003). Given our a priori hypotheses regarding the neural basis of aversive pruning (Dayan and Huys, 2008), we applied an initial threshold of p = 0.005 and applied family-wise error (FWE) correction for multiple comparisons at the voxel-level, adjusted for small volume correction (SVC) across our ROIs. For the planning-phase analysis, the SGC ROI was defined as an 8 mm box centered on of the peak coordinate from a study reporting altered glucose metabolism in patients with depression (MNI coordinates: x = −2; y = 32; z = −2; Drevets et al., 1997). The PAG ROI was defined as an 8 mm box centered on the peak coordinate previously identified as activating to increasing threat using fMRI in healthy human participants (MNI coordinates: x = −3; y = −25; z = −11; Mobbs et al., 2007). A bilateral amygdala ROI was created from the Wake Forest University (WFU) Pickatlas toolbox for SPM (http://www.fmri.wfubmc.edu/download.htm) with the Automated Anatomical Labeling atlas. We anticipated very robust responses for the more general planning and value-related networks; thus, for the purposes of inference, outside our ROIs, we increased our threshold such that only voxels surviving whole-brain (WB) voxel-level FWE correction <0.05 survived. All second-level analyses incorporated an explicit binary gray matter mask.

For the trial-based analyses, the main contrasts we report are derived from linear combinations of the ONLL correct, OLL correct, and aversive pruning regressors, which are comparable in terms of visual input during the planning and outcome phases, and the correct restricted plan trials. Since trials were categorized according to participants' decisions, some participants had fewer than four trials in a given condition; these participants were excluded from the relevant contrasts, resulting in slightly different numbers of subjects across analyses. For the outcome phase analysis, we anticipated that activation in the insula would be elicited during the receipt of large losses (Garrison et al., 2013). Therefore, for this analysis we created a bilateral insula ROI from the WFU Pickatlas and applied SVC as described above.

For the trial-based planning analyses, our primary contrast of interest was the comparison of aversive pruning trials (on which participants avoided the optimal sequence that contained a large loss and instead chose the best available large-loss-free sequence), relative to OLL correct trials (on which participants chose an optimal sequence transitioning through a large loss). To control for the effects of transitioning through a large loss per se on OLL correct trials, we included the restricted plan trials to create the following contrast: aversive pruning + restricted plan large loss > OLL correct + restricted plan no large loss. We ensured that difficulty was matched across this contrast by selecting trials that provided an equal ratio of 3:4:5 move problems for each participant across the aversive pruning and OLL correct conditions. For restricted plan trials, the inclusion threshold was set at chance level (50%); two participants failed to meet this criterion due to a failure to understand trial instructions and were excluded from analyses including this trial type. To control for possible difficulty differences between restricted plan trials (because there were more divergent arrows in the restricted plan large loss condition), trials were chosen to match the number of divergent arrows between the two restricted plan trial types.

Finally, we constructed additional contrasts to test how the above planning contrasts were modulated by difficulty (2^d). These contrasts are derived from linear combinations of the OLL correct, ONLL correct, and aversive pruning parametric modulator regressors but exclude the restricted plan trials; the latter are unnecessary here as the parametric modulator already entails a contrast (between more difficult and easier trials) within each condition, controlling for the transition through the large loss per se on OLL correct trials. As above, the following three main contrasts were examined: (1) aversive pruning parametric modulator > OLL correct parametric modulator; (2) OLL correct parametric modulator > ONLL correct parametric modulator; and (3) ONLL correct parametric modulator > aversive pruning parametric modulator.

Results

We describe two broad collections of behavioral analysis and, through this, associated fMRI responses. Following a brief description of the broad patterns of behavior observed on the task, which paralleled our previous findings (Huys et al., 2012), we initially consider a computational model-based treatment that aimed to characterize the whole structure of behavior using a parsimonious model whose parameters are intended to capture the general tendencies of each subject. Imaging analyses associated with this model duly indicated the general architecture of control. We then explore the specificity of our imaging analyses in the context of other known neural architecture underlying the cognitive components implicated in our task. Finally, for completeness, we provide complementary behavioral and fMRI analyses based on categorizations of trials (Table 1).

Behavioral and modeling evidence for pruning

Participants chose the correct sequence on average 78% (SD = 18%) of the time in free plan trials on which the optimal sequence did not include a large loss (ONLL); on these trials, aversive pruning would not be disadvantageous. By contrast, on free plan trials on which the optimal sequence did include a large loss (OLL), for which aversive pruning would be disadvantageous, performance was impaired for every participant (mean OLL correct = 37%; SD = 18%). The difference between performance on these trial types was substantial and highly significant (mean difference = 41%, SD = 20%; t₍₃₆₎ = 12.51; p < 0.001; d = 2.06; Fig. 2A), confirming our previous findings (Huys et al., 2012). As expected, performance also became worse with increasing difficulty (F_(2,72) = 132.75, p < 0.001, η_p² = 0.787; Fig. 2B) but remained high even for depth 5 choices, where there are 32 different paths. Critically, there was a significant interaction between trial type and difficulty (F_(2,72) = 5.58, p = 0.009, η_p² = 0.134). Planned contrasts revealed that the requirement to transit through a large loss to attain the optimal amount had an increasingly detrimental effect on decision-making at higher difficulty (depth 3: mean difference = 34%, SD = 25%; t₍₃₆₎ = 8.26; p < 0.001; d = 1.36; depth 4: mean difference = 40%, SD = 22%; t₍₃₆₎ = 11.29; p < 0.001; d = 1.86; depth 5: mean difference = 49%, SD = 29%; t₍₃₆₎ = 10.33; p < 0.001; d = 1.70). Note, though, that this analysis does not examine where the loss appeared in the tree.

Figure 2.

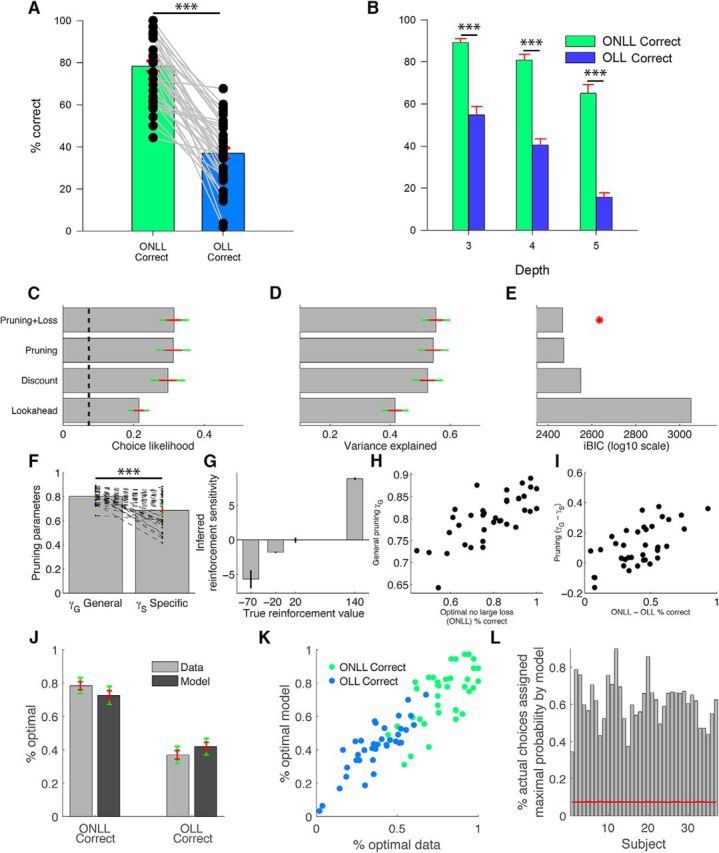
Initial model-free and computational model-based results, model comparison, and model validation analyses. A, Percentage of trials on which the correct sequence was chosen, split by whether it did not include a large loss (green: ONLL) or did (blue: OLL). Black dots represent individual performance and gray lines connect the two trial types. B, ONLL and OLL performance split by decision depth. C, Average likelihood of participants' choices. Chance model performance level is shown by the black dashed line; Lookahead represents optimal planning; Discount incorporates random stopping of the tree search; Pruning additionally incorporates a specific chance of stopping when a large loss (−70 pence) is encountered; and Pruning+Loss additionally incorporates individual reinforcement value sensitivities to account for loss aversion. D, Proportion of variance explained by the different models. E, Model evidence measured by group-level iBIC; red star indicates the best-performing (i.e., lower iBIC) model. F, Pruning parameters (values indicate the probability of continuing to evaluate the decision tree). Black dots in F show individual data (parameters taken from the Pruning+Loss model), connected by black dashed lines. G, Reinforcement sensitivity parameter estimates. H, Relationship between the trial-based measure of general planning ability, ONLL, and its computational equivalent γ_G. I, Relationship between the trial-based measure of aversive pruning (ONLL − OLL) and its computational equivalent, the difference between γ_G and γ_S. J, Comparison of ONLL and OLL correct trials between the observed data and the data generated from our winning model. K, Observed and generated data for each individual subject plotted for ONLL and OLL correct trials. L, The fraction of times the winning model gave the highest probability to the action chosen by the subject; red line shows chance level. Red and green error bars indicate one SE and 95% confidence intervals of the mean, respectively. ***p < 0.001.

Model-based aversive pruning behavior and associations with psychometric variables

Consistent with our previous report (Huys et al., 2012), there was substantial evidence for aversive pruning based on our computational model (Fig. 2C,D, Pruning and Pruning+Loss models). That is, the most parsimonious model (smallest negative model evidence iBIC; Fig. 2E, red star; Table 2, for model performance overview) incorporated aversive pruning, with steeper discounting after large losses than after other outcomes [γ_G is significantly larger than γ_S; t₍₃₆₎ = 5.12; p < 0.001; d = 0.84; Fig. 2F; improvement in log₁₀ model evidence between model discount and model pruning (ΔiBIC) = 77.5, indicative of decisive evidence in favor of the pruning model]. Loss aversion was also evident (Fig. 2G), such that the best model incorporated fitted reward and loss sensitivities [ΔiBIC between model Pruning and Pruning+Loss) = 5.8]. It is important to distinguish between these two loss-related processes that are included in our model. Aversive pruning, as instantiated in the model, is not simply a discounting of the value associated with transitions (or subsequent paths). Instead, the aversive pruning parameter controls whether paths following large losses are actually explored at all, regardless of the possible gains that lie behind them. We consider such a reflexive avoidance of even considering options to be Pavlovian in nature, as it is elicited automatically and not related to the overall value of the path. Excessive discounting of the value of negative transitions (equivalent to loss aversion) does occur in our data, but this is controlled by a different set of parameters and is conceptually separate from pruning.

Table 2.

Model performance values

Model	Number of parameters	Choice log likelihood	Variance explained (%)	iBIC
Pruning + loss	6	1151	55.3	2466
Pruning	3	1173	54.4	2472
Discount	2	1221	52.5	2549
Lookahead	1	1502	41.7	3052

Importantly, our computationally derived general planning parameter (γ_G) was positively correlated with its trial-based equivalent (ONLL percentage correct: r₍₃₇₎ = 0.73, p < 0.001; Fig. 2H). The difference between OLL and ONLL percentage correct was strongly correlated with the equivalent metric derived from the computational analyses (γ_G − γ_S: r₍₃₇₎ = 0.63, p < 0.001; Fig. 2I), providing convergent validity for the two approaches. However, due to the uncertainty attached to both choice frequency and model parameter estimates, this correlation is not perfect, and some subjects with small or even negative difference between γ_S and γ_G values still show a positive difference between ONLL and OLL frequencies. It would be interesting to examine subjects who do and do not show aversive pruning separately or, indeed, to look for changes over time in the strength of pruning. Unfortunately, the present sample size does not allow for this; therefore, we concentrate here on correlational analyses. Finally, further validation of the model comes from sampling surrogate data (Fig. 2J–L).

Overall, these results are consistent with our previous report in an independent sample (Huys et al., 2012) and provide complementary evidence for the presence of aversive pruning. The slow degradation of performance with depth on the ONLL trials is compatible with the fact that the number of trials without a large loss increases slowly with depth and that aversive pruning allows the concentration of resources on these paths.

A multiple regression analysis revealed that state anxiety, but no other included variable (i.e., IQ, sex, age, depression, and trait anxiety), correlated with the difference between ONLL and OLL percentage correct (t₍₃₇₎ = 2.12, p = 0.042); variance inflation factor values were <3.0 for all independent variables, suggesting an adequate lack of collinearity. Contrary to our expectations, however, no psychometric variables correlated with the computationally derived aversive pruning estimate (γ_G − γ_S). In particular, we did not replicate our previous finding that this statistic was correlated with subclinical depression scores, though we note that the range of scores in the present study was relatively low.

Aversive pruning recruits the subgenual cingulate cortex

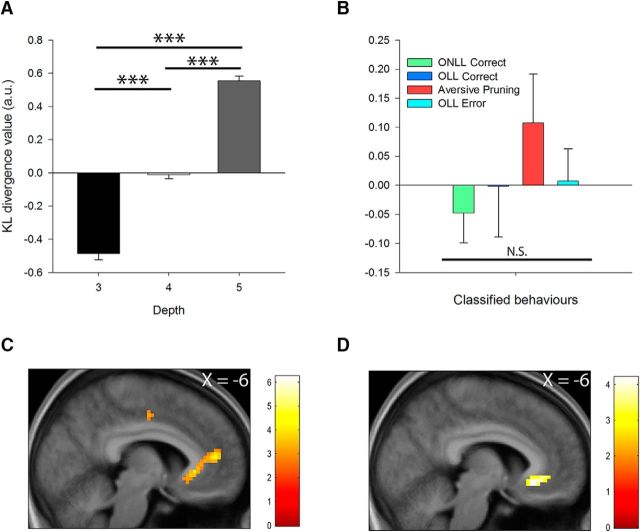
We used the computational model to construct, separately for each participant's maximum a posteriori parameters, a measure of the inclination to engage in aversive pruning on each trial. This is the KL divergence between the distributions of trajectories assuming discounting based on depth alone (discount model) versus discounting based on losses encountered (pruning model). Figure 3A confirms that the KL divergence increases with depth (F_(2,72) = 223.82, p < 0.001, η_p² = 0.86), with all three levels significantly different from each other (p < 0.001), as expected from the likely extra opportunities for aversive pruning with longer sequences. Figure 3B shows that the measure was indeed higher on aversive pruning trials (based on participant choices; Table 1); however, there were no significant differences between trial types (F_(3,108) = 0.74, p = 0.48, η_p² = 0.02). Negative KL divergence values shown here arise due to the mean correction applied to the metric used for fMRI analyses.

Figure 3.

Neural responses during aversive pruning: model-based fMRI results. A, B, KL divergence value increased linearly with depth (A) and, based on participant behavior, was highest on trials classified as aversive pruning trials (B). C, Activation in pregenual ACC and SGC increased linearly with KL divergence value. D, There was an interaction between KL divergence value and difficulty in the SGC, with greater impact of the former on more difficult trials. Overlays are presented at a threshold of p < 0.005 (uncorrected). Error bars represent 1 SEM, and color bars indicate t values. N.S., Non-significant; ***p < 0.001.

We entered the KL divergence value on each trial as a parametric regressor across all successfully completed free plan trials, controlling for difficulty (which was entered as the first parametric regressor) and trial net value. Consistent with our primary hypothesis, this analysis revealed that SGC activation increased with our metric of inclination to engage in aversive pruning, the KL divergence (MNI coordinates: x = −6; y = 29; z = −2; t₍₃₆₎ = 3.87, p_SVC = 0.004; Fig. 3C). The interaction between KL divergence and difficulty also revealed a greater modulation of SGC activation by inclination to engage in aversive pruning at higher depth (MNI coordinates: x = −6; y = 35; z = −5; t₍₃₆₎ = 3.47, p_SVC = 0.009; Fig. 3D).

In summary, our computational fMRI analyses revealed that SGC activation was higher on trials in which our model indicated that there was a greater inclination to indulge in aversive pruning, and this was particularly the case on more difficult trials. In the following analyses, we show that this activation in the SGC is separate to responses related to planning and valuation.

Planning and valuation responses

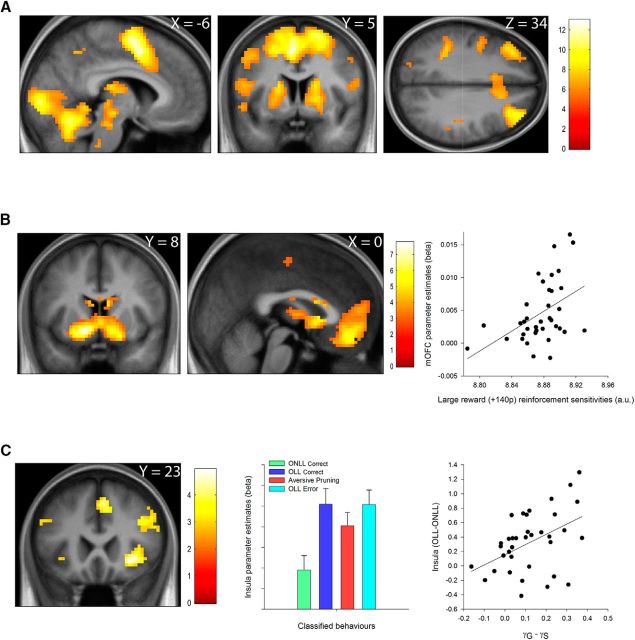
We next explored the specificity of our aversive pruning results relative to other neural networks known to be associated with cognitive processes required during successful undertaking of our task, namely planning and valuation. We first explored the effect of planning by examining the first parametric modulator, which indexed difficulty (2^d). As expected, increasing difficulty robustly activated a network of regions identified in previous studies of planning. This included the bilateral dorsal cerebellum, primary visual, supplementary motor, and DLPFC, thalamus, dorsal caudate, and putamen, all of which survived WB voxel-level correction for multiple comparisons (all t₍₃₆₎ > 5.45, p_WB < 0.05; Fig. 4A).

Figure 4.

Neural responses to increasing difficulty and value and relationship between aversive pruning and loss receipt at outcome. A, Bilaterally, cerebellum (left), motor cortex (left), dorsal striatum (middle), and dorsolateral prefrontal cortex (right) activation increased linearly with task difficulty during the planning phase. Overlays are presented at a threshold of p_WB < 0.05. B, VS (left) and mOFC (middle) activation increased linearly with the net monetary value during the outcome phase. Overlays are presented at a threshold of p < 0.005 (uncorrected), but VS and mOFC results survive voxel-level p_WB < 0.05. Peak voxel mOFC activation to increasing reward (B, right) correlated with the sensitivity to a large rewards (+140 pence) parameter derived from our computational model. C, Contrasting feedback on the correct trial types (OLL vs ONLL correct) revealed responses in the right insula (left), and right DLPFC (left). Response in the insula was driven by increased activation during OLL correct outcomes (C, middle). The difference in insula activation between OLL and ONLL correct trials at outcome correlated with γ_G − γ_S, our computationally derived measure of overall aversive pruning (C, right). Overlays are presented at a threshold of p < 0.005 (uncorrected). Error bars represent 1 SEM, and color bars indicate t values.

To examine responses related to the receipt of outcomes, we constructed a separate model in which the net monetary value of the chosen sequence was entered as a parametric regressor, time locked to the outcome period. Increasing monetary outcome robustly activated the VS (MNI coordinates: left: x = −12; y = 8; z = −8; t₍₃₆₎ = 7.74, p_WB < 0.001; right: x = 12; y = 8; z = −8; t₍₃₆₎ = 5.52, p_WB = 0.027; Fig. 4B, left), the mOFC (MNI coordinates: x = 0; y = 44; z = −14; t₍₃₆₎ = 5.88, p_WB = 0.013; Fig. 4B, middle), and the head of the caudate (MNI coordinates: x = −6; y = 20; z = 7; t₍₃₆₎ = 7.17, p_WB < 0.001; Fig. 4B). Given the wealth of research establishing the existence of value signals in the VS and OFC (Schultz, 2015), we correlated the large reward (+140 pence) sensitivity parameter from our winning computational model with the net outcome-related activation at the peak voxel within these regions. This was significant in the mOFC (r₍₃₇₎ = 0.46, p = 0.004; Fig. 4B, right), but not in the VS (r₍₃₇₎ = 0.13, p = 0.45).

Neural response to large losses is associated with aversive pruning tendency

During the outcome phase, participants would no longer have any reason to plan but, instead, had just to observe their executed plan being replayed with feedback on the monetary consequence of each box-to-box move. We next asked whether the tendency to engage in aversive pruning might impact on activation during this phase. To do this, we examined trials on which volunteers could have aversively pruned but (correctly) chose not to. Thus, again controlling for net objective outcome, we compared trials on which subjects correctly avoided aversively pruning, therefore receiving at least one large loss during the entire sequence (OLL correct), with correct trials that avoided all large losses (i.e., aversive pruning was helpful, ONLL correct; note that all of the trials in this contrast involved optimal decisions).

This contrast revealed activation in our insula ROI (MNI coordinates: x = 33; y = 23; z = −5; t₍₃₆₎ = 4.70, p_SVC = 0.011; Fig. 4C, left), as well as robust responses that survived whole-brain correction in the inferior parietal lobule (IPL; MNI coordinates: x = 39; y = −52; z = 46; t₍₃₆₎ = 4.78, p_WB = 0.01) and DLPFC (MNI coordinates: x = 45; y = 44; z = 4; t₍₃₆₎ = 4.32, p_WB < 0.001). We next asked whether the tendency to engage in aversive pruning might be related to activation to the receipt of large losses (Fig. 4C, middle). Activation in the insula (r₍₃₇₎ = 0.47, p = 0.003; Fig. 4C, right) and DLPFC (r₍₃₇₎ = 0.35, p = 0.034), but not in the IPL (r₍₃₇₎ = 0.22, p = 0.20), correlated significantly with our computationally derived measure of aversive pruning, γ_G − γ_S [although the correlations between activation in the insula (Z = 1.58, p = 0.113) and DLPFC (Z = 0.85, p = 0.39) and aversive pruning behavior were not significantly greater than that in the IPL].

Confirmatory trial-based behavioral and fMRI analyses

Trial-based behavior provides further evidence of pruning

Further evidence consistent with aversive pruning comes from a finer classification of suboptimal choices. Of course, it is not possible to be definitive as to the processes that underlie any particular suboptimal (or indeed optimal) choice. However, trials for which it would have been optimal to transition through a large loss, but in which participants selected the best available option that avoided large losses (Fig. 1B), are at least suggestive of aversive pruning-influenced planning. We call these aversive pruning trials. All other instances of suboptimal selection we term as errors (separated into trials for which the optimal decision entailed (OLL error; excluding aversive pruning trials; i.e., this category did not include trials where the next best available option that did not entail transitioning though a large loss was chosen) or avoided (ONLL error) transitioning through a large loss: see Table 1). Due to low trial numbers, ONLL errors were not considered further.

A clear example of aversive pruning occurs in the scenario depicted in Figure 5A. Placed in state 2 with three moves to plan, the optimal solution is to go from state 2 to state 5 (−70 pence), from state 5 to state 1 (−70 pence), and from state 1 back to state 2 (reaping the only large reward in the maze, +140 pence). This sequence results in breaking even, and participants chose it 41% (SD = 33%) of the time (Fig. 5A, blue outcome). However, despite the relative ease of the problem (only eight sequences needed evaluating), participants had a strong tendency to engage in aversive pruning, presumably because the optimal sequence contains two large losses. The best available option that avoided the large loss involved moving from state 2 to state 3 (−20 pence), from state 3 to state 4 (−20 pence), and from state 4 back to state 2 (+20 pence; resulting in a net loss of 20 pence). Such aversive pruning arose on 37% (SD = 31%; aversive pruning percentage) of trials (Fig. 5A, red outcome; i.e., nearly as often as the optimal choice). By way of comparison, subjects selected the optimal and the next best available sequence 80% (SD = 23%) and 14% (SD = 20%) of the time, respectively, on the ONLL trial requiring three moves to plan from state 5.

Figure 5.

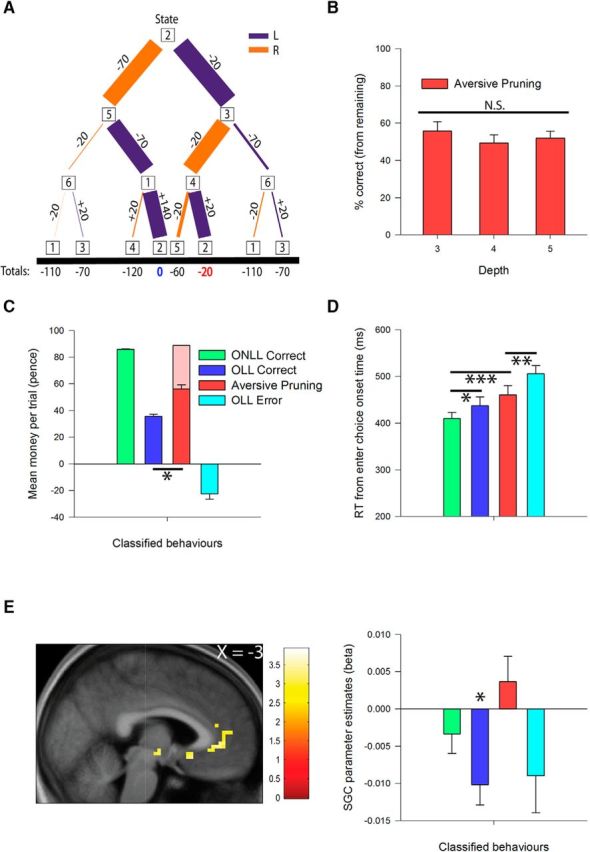
Confirmatory trial-based behavioral and fMRI results. A, Decision tree showing path selection starting from state 2 with three moves to go; line width is proportional to selection frequency. The optimal route (break-even, blue) and the suboptimal aversive pruning route (net income −20p, red) were selected with similar frequency. B, Aversive pruning percentage [aversive pruning/(aversive pruning + OLL error) * 100], split by depth. C, Mean trial earnings across the four conditions. The light red bar behind aversive pruning depicts the possible earnings if participants had performed optimally on the trials classified as aversive pruning. OLL error represents incorrect choices on OLL trials that could not be classified as aversive pruning. D, Reaction times for the first button press across trial types. E, Difficulty-related response in the SGC (left) contrasting aversive pruning trials against OLL correct trials. Overlay is presented at a threshold of p < 0.005 (uncorrected). The finding in the SGC was driven by a negative modulation by difficulty for OLL correct trials (p = 0.001), with no significant effect of difficulty on aversive pruning trials (p = 0.285, right). Error bars represent 1 SEM, and the color bar indicates t values. N.S., Non-significant; *p < 0.05; **p < 0.01; ***p < 0.001.

Participants displayed a strong tendency toward aversive pruning, choosing the best sequence that avoided a large loss on ∼52% (SD = 23%) of OLL trials in which they chose suboptimally (chance = approximately 11% across depths). All subjects engaged in aversive pruning; however, the extent of the predilection was highly variable across the sample (4–93%); nevertheless, the aversive pruning percentage was very consistent within subjects between the first and second halves of the trials (r₍₃₇₎ = 0.69, p < 0.001). Interestingly, this fraction, which we call the aversive pruning percentage, did not depend on depth (F_(2,72) = 1.15, p = 0.32, η_p² = 0.03; Fig. 5B), thus supporting the hypothesis that aversive pruning acts as an adaptive heuristic to reduce the number of options to be considered, allowing participants to maintain reasonable, if not perfect, planning performance across depths (Huys et al., 2012). We also examined the average earnings, which revealed a significant main effect of trial type (Fig. 5C; F_(3,108) = 320.538, p < 0.001, η_p² = 0.90). Perhaps surprisingly, aversive pruning choices earned participants significantly more money than OLL correct choices (t₍₃₆₎ = 6.74, p < 0.001, d = 1.11). Although by definition optimal choices would have earned more on aversive pruning trials (Fig. 5C, light red bar; mean difference = 33 pence, SD = 9 pence), this pattern arises because aversive pruning occurred more frequently with increasing depth (while it was rarer for OLL correct trials to be performed at higher depth), and the average net value largely increases with depth (OLL correct: depth 3 = 33 pence; depth 4 = 67 pence; depth 5 = 93 pence; aversive pruning: depth 3 = −20 pence; depth 4 = 13 pence; depth 5 = 50 pence; OLL error: depth 3 = −84 pence; depth 4 = −59 pence; depth 5 = −47 pence), although this is not the case for ONLL correct trials (depth 3 = 100 pence; depth 4 = 80 pence; depth 5 = 60 pence).

If aversive pruning is indeed a heuristic that reduces the number of evaluated sequences, then we might see an effect on RTs (Fig. 5D; note though, that subjects could not enter choices until the 9 s of planning had elapsed, which could reduce the magnitude of this effect). There was a main effect of trial type (Friedman χ²(3) = 33.876, p < 0.001). Post hoc tests revealed that ONLL correct RTs were significantly shorter than OLL correct RTs (Z = 2.105, p = 0.035) and aversive pruning RTs (Z = 4.413, p < 0.001). However, contrary to our expectations, the difference in RT between OLL correct and aversive pruning choices was nonsignificant (Z = −1.335, p = 0.182). Nevertheless, aversive pruning choices were made significantly faster than OLL error trials (Z = 2.844, p = 0.004).

Finally, we note that the difficulty in planning transitions through large losses was even evident on the much easier restricted plan trials (on which only two sequences required evaluation). Participants made the optimal choice significantly more often on restricted plan trials that did not feature large losses (mean = 90%, SD = 9%) than on those that did (mean = 84%, SD = 8%; t₍₃₄₎ = 3.74, p < 0.001, d = 0.63). However, there was no effect on RT (correct trials only: t₍₃₄₎ = 1.12, p = 0.27, d = 0.19).

Trial-based fMRI confirms a role for the SGC in aversive pruning

A contrast between aversive pruning and OLL correct trials during the planning period (incorporating restricted plan control trials, controlling for net outcome; N = 31) revealed no significant activation in our ROIs, and no cluster survived whole-brain correction for multiple comparisons. However, an analysis of the parametric modulation of aversive pruning trials by difficulty (contrasted against the parametric modulation of OLL correct trials by difficulty, again controlling for net income: N = 33) revealed a cluster in the SGC extending into pregenual ACC (MNI coordinates: x = −3; y = 35, z = −2; t₍₃₂₎ = 3.08, p_SVC = 0.023; Fig. 5E, left). We also note the presence of a cluster in the right amygdala, though this did not survive correction for multiple comparisons; therefore, we do not consider it further (MNI coordinates: x = 21; y = 2; z = −20; t₍₃₂₎ = 2.85, p_SVC = 0.144). The result in the SGC was driven by a progressive reduction in response with increasing difficulty on OLL correct trials (i.e., a negative modulation by difficulty; one-sample t test against zero: t₍₃₂₎ = 3.72, p = 0.001), while difficulty did not affect activation on aversive pruning trials (t₍₃₂₎ = 1.09, p = 0.285; Fig. 5E, right). This finding that aversive pruning elicits a (relative) increase in SGC activation as depth increases, complements the one arising in our computationally motivated analysis based on the KL divergence, where a robust modulation by difficulty was also identified. Together, these results suggest that inhibiting aversive pruning may require deactivation of the SGC, particularly when decisions are more complex.

None of our other comparisons yielded significant activation in our ROIs or activation in other regions that survived whole-brain correction for multiple comparisons. Contrasting the parametric effect of difficulty between aversive pruning and ONLL correct trials (N = 35) did not reveal any effect surviving correction for multiple comparisons. The equivalent parametric contrast between ONLL and OLL correct trials (N = 35) revealed an effect in the right amygdala that narrowly missed significance (MNI coordinates: x = 33; y = −1; z = −20; t₍₃₄₎ = 3.25, p_SVC = 0.062).

Discussion

Multistep decision-making is fundamental to human behaviors. However, fully solving complex planning problems is often too arduous, thus necessitating heuristics. We used a combination of neuroimaging and computational modeling of behavior to characterize the neural basis of one such simple approximation, aversive pruning. This is the inflexible, reactive curtailment of a search when a large loss is encountered during planning. Aversive pruning represents a computationally well defined influence of a Pavlovian inhibitory response on high-level cognitive manipulations during planning. We replicated previous findings that aversive pruning was ubiquitous across subjects (Huys et al., 2012). As expected, it served to preserve computational resources, being more prevalent on harder problems, and was associated with faster responses than other suboptimal decisions. Both computational model-based and trial-based neuroimaging analyses showed that aversive pruning was associated with hemodynamic responses in the SGC during planning. By contrast, distinct circuits were activated by planning and valuation. Further, the responses to the receipt of large losses in the insula and DLPFC correlated with one of our computationally derived behavioral measures of overall aversive pruning. Our results reveal the neural and computational architecture underlying a profoundly influential heuristic that enables humans to make complex planned decisions with reasonable speed and accuracy.

The aversive pruning-related activation that we identified in the SGC through both computational and categorical analyses exists over and above planning-related and value-related responses. Closer examination of the parametric modulation by difficulty sheds further light on the nature of this finding. Compared with correct decisions that transitioned through a large loss, aversive pruning was associated with higher SGC activation, especially on more difficult problems. Intriguingly, our trial-based analyses suggest that this effect was largely driven by a relative decrease in SGC response on correct decisions that transitioned through a large loss as planning complexity increased (Fig. 5E). This is consistent with studies examining the trade-off between appetitive and aversive outcomes. In humans, Talmi et al. (2009) also found SGC inhibition when participants chose to endure a punishment to obtain a gain. In nonhuman primates, Amemori and Graybiel (2012) reported that neurons in the homologous area of the ACC in the macaque (BA24b) responded to aversive stimuli in an approach–avoidance decision task; localized microstimulation of these neurons increased the negative impact of aversive consequences on choice. Thus, it appears that planning through a negative outcome to achieve an overall positive outcome is facilitated when the SGC is deactivated.

Importantly, the SGC is a key node where cognition and emotion are thought to interact pathologically, for example, in mood disorders (Drevets et al., 2008, Roiser et al., 2012). The anatomical correspondence between resting-state findings in depressed patients, punishment-driven anticipatory responses in healthy humans, and aversive signals in nonhuman primates is striking. The SGC may be an important mediator of the inhibitory effect of aversive expectations not just on behavior, but also on higher-level cognitive function in mood disorders. In the context of depression, it has been suggested that inhibitory control is impaired and that this underlies some of depressed subjects' inability to disengage from aversive information (Dayan and Huys, 2008, Joormann and Gotlib, 2010). However, the SGC appears to be hyperactive during rumination, and in depression more generally (Cooney et al., 2010), possibly suggesting a reduced efficiency of these mechanisms rather than a lack of engagement.

Complex decision-making processes recruit a diverse set of hierarchical cognitive components (Solway and Botvinick, 2012) and neural structures (Newman et al., 2003). We note here at least two neural network processes on top of which aversive pruning occurs. First, planning a complex sequence of actions requires considerable cognitive control. Unsurprisingly, as planning difficulty increased in our task, structures such as the cerebellum, DLPFC, dorsal striatum, motor cortex, and thalamus were increasingly activated (Fig. 4A). These brain regions are frequently implicated in planning tasks that require cognitive control (Newman et al., 2003) and in goal-directed approaches to problem solving (Solway and Botvinick, 2012). A second important component process of decision-making is the evaluation of outcomes associated with action sequences. Increasing net monetary outcome was associated with activation in a network of structures commonly activated in reinforcement learning tasks and thought to underlie valuation, including the VS and the mOFC (Schultz, 2015). Interestingly, activation in mOFC, but not in VS, at the time of outcome was associated with our computationally derived behavioral measure of sensitivity to large reinforcements. This finding is consistent with the hypothesis that mOFC is critical for processing outcomes per se, while VS is more closely aligned with prediction error signaling (Schultz, 2015).

When we focused our analysis on the outcome phase (contrasting optimal decisions with and without large losses), we found that a number of regions (insula, IPL, and DLPFC) were significantly more activated during the receipt of large losses, even after accounting for trial-by-trial monetary earnings. Even though the actual planning would have terminated before this point, activations in the structures that responded positively to large losses (insula and DLPFC) also correlated positively with our computationally derived estimate of overall aversive pruning (γ_G − γ_S). Of particular relevance is the insula, which is thought to play a role in interoceptive perception and the production of subjective negative feeling states (Medford and Critchley, 2010) and has been reported to influence decision-making (Yu et al., 2010). For example, individuals with insula damage have been reported to exhibit a selective impairment in avoiding stimuli associated with monetary losses (Palminteri et al., 2012). We had not predicted activation of DLPFC and IPL in the outcome phase, but this pattern would be consistent with the engagement of inhibitory processes during cognitive control (Guitart-Masip et al., 2012). We speculate that these results may indicate a similar involvement in aversive pruning, though this needs to be tested in future studies. The activation of the DLPFC is particularly noteworthy with respect to depression. Fales et al. (2008) showed a failure to activate the DLPFC during the suppression of irrelevant aversive information in depression. As aversive pruning might relate to the ability to inhibit the processing of aversive information, and hence correlate negatively with rumination (Gotlib and Joormann, 2010), a clear prediction is that a similar pattern would be observed when depressed patients aversively prune.

Taking the above results together, a possible model accounting for our fMRI results is that the DLPFC and insula might coordinate to mark parts of the decision tree that contain large losses. Once the tree is demarcated, these signals may then be used during the planning phase where SGC responses drive the decision to prune. Meanwhile, deactivation of the SGC appears critical to choosing to engage with the large loss to make an optimal decision. The consistency of the SGC response between our computational and categorical fMRI analyses during planning supports the notion that this region participates in curtailing the decision tree search on encountering a large loss. Although we cannot directly exclude an additional causal influence, whereby it is the overloading of cognitive control that leads to the release of the pruning reflexes, the structure of the findings still argue for a shaping influence of the pruning reflexes on the process of evaluation.

A limitation of the current work is that the aversive pruning time-points during planning are not clearly temporally delineated; we therefore cannot make temporal causality claims about the neural effect. Aversive pruning is a meta-reasoning process involving multiple repeated decisions about what to evaluate next (Russell and Wefald, 1991). The ambiguity surrounding the precise point at which aversive pruning occurs could be resolved more directly, possibly using a combination of eye-tracking and neuroimaging methods with higher temporal resolution such as EEG or MEG. A further limitation is that our study was performed in healthy participants and was not designed to detect correlations with symptoms of mood or anxiety disorders. In a previous study (Huys et al., 2012), aversive pruning correlated with subclinical measures of depression, while in the current study it correlated with state anxiety. We originally hypothesized (Dayan and Huys, 2008) that aversive pruning might relate to both symptoms of depression and anxiety because features of impaired inhibition of aversive processing are prominent in both disorders. The failure to confirm our previous finding of a correlation with depressive symptoms might be due to a restricted range of scores in the present sample.

In summary, it is tremendously difficult to plan optimally in complex problems; heuristics are frequently mandatory. We confirmed the pervasive influence of one such shortcut, aversive pruning, over goal-directed behavior, distinguishing its impact from those of other decision-making biases. Our neuroimaging results revealed that aversive pruning recruits neural structures implicated in decision-making and mood disorders, specifically the SGC. DLPFC and insula responses to large losses and anxiety levels, an established risk factor for mood disorders, were related to the degree of aversive pruning across participants. Together, our results suggest a novel circuit in which emotionally salient information is used to facilitate decision-making, albeit only approximating optimality. Activation of this circuit could prevent optimal decision-making during planning and may contribute to psychopathological conditions characterized by aberrant decision-making.