Fused Lasso Approach in Regression Coefficients Clustering – Learning Parameter Heterogeneity in Data Integration

Abstract

As data sets of related studies become more easily accessible, combining data sets of similar studies is often undertaken in practice to achieve a larger sample size and higher power. A major challenge arising from data integration pertains to data heterogeneity in terms of study population, study design, or study coordination. Ignoring such heterogeneity in data analysis may result in biased estimation and misleading inference. Traditional techniques of remedy to data heterogeneity include the use of interactions and random effects, which are inferior to achieving desirable statistical power or providing a meaningful interpretation, especially when a large number of smaller data sets are combined. In this paper, we propose a regularized fusion method that allows us to identify and merge inter-study homogeneous parameter clusters in regression analysis, without the use of hypothesis testing approach. Using the fused lasso, we establish a computationally efficient procedure to deal with large-scale integrated data. Incorporating the estimated parameter ordering in the fused lasso facilitates computing speed with no loss of statistical power. We conduct extensive simulation studies and provide an application example to demonstrate the performance of the new method with a comparison to the conventional methods.

1. Introduction

Combining data sets collected from multiple studies is undertaken routinely in practice to achieve a larger sample size and higher statistical power. Such information integration is commonly seen in biomedical research, for example, the study of genetics or rare diseases where data repositories are available. The motivation of this paper arises from the consideration of data heterogeneity during data integration. Although data integration has different meanings, in here, we consider the concatenation of data sets of similar studies over different subjects, where the number of integrated data sets can be very large.

Inter-study heterogeneity can result from the differences in study environment, population, design and protocols (Leek and Storey, 2007; Sutton and Higgins, 2008; Liu et al., 2015). Data heterogeneity is likely attributed to population parameter heterogeneity, where the association of interest can differ across different study populations from which data sets are collected. Examples include multi-center clinical trials when participant data from different sites are combined (Shekelle et al., 2003) and genetics studies when genomic data from multiple similar studies are combined (Lohmueller et al., 2003; Sullivan et al., 2000). Discrepancies in treatment effect or trait-gene association may arise due to the differences in facilities, practices and patient characteristics across studies, albeit the adjustment of confounding (Leek and Storey, 2007). The parameter heterogeneity introduced in data integration compromises the power of the larger sample size and may even lead to biased results and misleading scientific conclusions. Thus, counterintuitively, the model obtained from the combined studies may not serve as a proper prediction model for each individual study in the case of heterogeneous study populations.

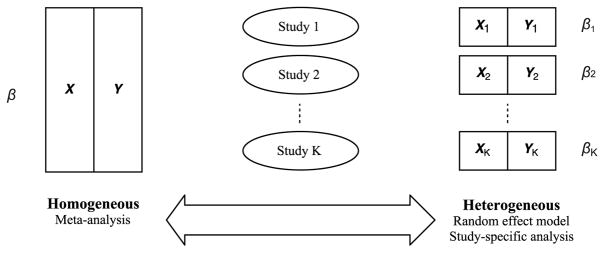
Traditional treatments of parameter heterogeneity are not optimal. Meta-analysis methods such as combining summary statistics (Glass, 1976), estimating functions (Hansen, 1982; Qin and Lawless, 1994) or p-values functions (Xie et al., 2012) are built upon the assumption of complete parameter homogeneity, as shown in the left panel of Figure 1. This assumption is hardly valid in practice. When individual participant data from multiple data sets are available, a retreat to the classical meta-analysis methods is necessary, because in this case assessing the assumption of inter-study homogeneity becomes possible. The two most common approaches to handling parameter heterogeneity include (i) specifying study-specific effects by including interaction terms between study indicator and covariates (e.g., Lin et al. (1998)), and (ii) utilizing random covariate effects by allowing variations across studies as random variables (e.g., DerSimonian and Kacker (2007)). Both approaches essentially assume fully heterogeneous covariate effects, namely, each study having its own set of regression coefficients, as shown in the right panel of Figure 1.

Figure 1.

Homogeneous assumption (left) versus heterogeneous assumption (right).

When study-specific effects are of interest, the interaction-based formulation may lead to over-parameterization, which impairs statistical power. The most straightforward way to reduce the number of parameters is to identify clusters of homogeneous parameters through exhaustive tests for the differences between every pair of study-specific coefficients. However, when the number of data sets is large, the use of hypothesis testing to determine parameter clusters becomes untrackable in addition to the multiple-testing problem. One may draw different or even conflicting conclusions due to different orders of hypotheses performed.

In reality, covariate effects from multiple studies are likely to form groups, a scenario falling in between the complete heterogeneity and the complete homogeneity. This leads to the following two essential yet related analytic tasks: (i) to assess the inter-study heterogeneity, so to determine an appropriate form of parsimonious parameterization in model specification; and (ii) to identify and merge groups of homogeneous parameters for better statistical power for parameter estimation and inference based on a more parsimonious model. Along the idea of lasso shrinkage estimator (Tibshirani, 1996), fused lasso methods (Tibshirani et al., 2005; Friedman et al., 2007; Yang et al., 2012) have been introduced to achieve covariate grouping, where covariate adjacencies are naturally defined by a metric of time, location or network structure. In our problem of data integration, there does not exist a natural metric to define the ordering of regression coefficients from different studies. Shen and Huang (2010) proposed the grouping pursuit via penalization of all pairwise coefficient differences in a single study, where covariate orderings are not considered. To reduce the computational burden in the all-pairs based regularization, Wang et al. (2016) and Ke et al. (2015) used the initial coefficient estimates to establish certain ordering and then to define parameter adjacencies. However, most of these studies have been entirely focusing on a single cohort of subjects from a single study. For example, Shin et al. (2016) proposed to fuse regression coefficients of different loss functions obtained from a single study, such as coefficients from different quantile regression models. Limited publication of fusion learning and grouping pursuit has been available in the literature, except Wang et al. (2016), to assess the differences and similarities among regression coefficients across multiple studies in the scenario of data integration.

In this paper, we propose an agglomerative clustering method for regression coefficients in the context of data integration, named as the Fused Lasso Approach in Regression Coefficients Clustering (FLARCC). FLARCC is proposed to identify heterogeneity patterns of regression coefficients across studies (or data sets) and to provide estimates of all regression coefficients simultaneously. It is interesting to draw a connection between our method and Pan et al. (2013) where they consider a classic clustering problem of individual responses by pairwise coefficient fusion via penalized regression. Their method aims at clustering subjects, while our method focuses on clustering regression coefficients across multiple data sets, and these two methods coincide only in a special case where each study is composed of only one subject. FLARCC achieves clustering of study-specific effects by penalizing the ℓ₁-norm differences of adjacent coefficients, with adjacency defined by the estimated ranks. Our method extends the bCARDS method in Ke et al. (2015) from one study to multiple studies as well as from the linear model to the generalized linear models, and focuses on simultaneous clustering of regression coefficients of individual covariates from multiple studies in data integration. An R package metafuse is created as part of our methodology development to perform the proposed integrated data analysis which can be downloaded from the Comprehensive R Archive Network (web link https://cran.r-project.org/web/packages/metafuse).

In the proposed method, tuning parameter is used to determine the clustering pattern of coefficients across data sets. Specifically, let λ be the tuning parameter of regularization. If λ = 0 (i.e., no penalty), FLARCC becomes a method under the setting of complete heterogeneity, so that study-specific regression coefficients for each covariate are assumed different across data sets. If λ is large enough that all differences of regression coefficients are shrunk to zero, FLARCC reduces to a homogeneous model in that a common regression coefficient for each covariate is assumed for all studies. In light of the hierarchical clustering scheme, these two extreme cases above correspond to the start and end of an agglomerative clustering, respectively; however, the reality is believed to reside in between. Analogous to dendrograms in the hierarchical clustering, we propose a new tree-type graphic display, named as fusogram, which presents tree-based coefficient clusters according to solution paths obtained from FLARCC. The selection of optimal λ pertains to pruning of clustering trees, which can be based on certain model selection criterion. We use the extended Bayesian information criterion (EBIC) proposed by Chen and Chen (2008) as our model selection criterion and show that EBIC exhibits better performance than BIC when the number of studies (or data sets) is large. In addition, we propose a scaling strategy to “harmonize” solution paths by covariate-wise adaptive weights to allow flexible tuning, which further improves the clustering performance.

The rest of this paper is organized as follows. Section 2 describes FLARCC in detail under the generalized linear models (GLM) framework. Section 3 presents the theoretical properties of the proposed method (with technical proofs presented in the Appendix). Section 4 discusses the interpretation and selection of the tuning parameter. In Section 5, we use simulation studies to evaluate the performance of our method. A real data analysis is given in Section 6 with interpretation of coefficient estimates and illustration of fusograms. Discussion and concluding remarks are in Section 7.

2. Method of Parameter Fusion

In this section, we present the method and algorithm of FLARCC.

2.1 Notations and Method

We start by introducing necessary notations. Throughout this paper, i, j and k are used to index subject, covariate and study, respectively. For instance, $X_{j,k}^{(i)}$ denotes the measurement of the jth covariate from the ith individual from study k, and $Y_k^{(i)}$ is the measurement of a response variable from the ith individual from study k. The total number of studies is denoted as K and the number of covariates involved is p. The sample size for study k is n_k, k = 1, …, K, and the combined sample size is $N={\sum }_{k=1}^K{n}_k$. The collection of all coefficients (covariates-wise) is denoted as $\mathit{\beta }={({\mathit{\beta }}_{1,•}^{\top },{\mathit{\beta }}_{2,•}^{\top },\dots ,{\mathit{\beta }}_{p,•}^{\top })}^{\top }$ with β_j,· = (β_j,1, …, β_j,K)^⊤ for j = 1, …, p. An indicator vector c = (c₁, …, c_p)^⊤ is used to flag heterogeneous covariates, namely if the jth covariate is treated as heterogeneous (i.e., all different coefficients across K studies) then c_j = 1 and as homogeneous (a common coefficient across K studies) otherwise. Thus c_j = 0 for some j ∈ {1, …, p} implies that coefficient vector β_j,· reduces to a common scalar parameter β_j for all K studies.

For illustration, let us consider a simple scenario of c = (1, 1, 0, …, 0)^⊤, in which the first two covariates are set as heterogeneous and the remaining p − 2 covariates are set as homogeneous. The resulting coefficient vector is $\mathit{\beta }={({\mathit{\beta }}_{1,•}^{\top },{\mathit{\beta }}_{2,•}^{\top },{\beta }_3,\dots ,{\beta }_p)}^{\top }$. Then the corresponding design matrix X can be written as

$$\mathit{X}={\left(\begin{array}{ccccccccc}{\mathit{X}}_{1,1}& & & {\mathit{X}}_{2,1}& & & {\mathit{X}}_{3,1}& \dots & {\mathit{X}}_{p,1}\\ & \ddots & & & \ddots & & ⋮& \ddots & ⋮\\ & & {\mathit{X}}_{1,K}& & & {\mathit{X}}_{2,K}& {\mathit{X}}_{3,K}& \dots & {\mathit{X}}_{p,K}\end{array}\right)}_{N\times (2K+p-2)}$$

where ${\mathit{X}}_{j,k}={(X_{j,k}^{(1)},\dots ,X_{j,k}^{(n)})}^{\top }$, j = 1, …, p, k = 1, …, K. The specification of c is can be dependent on the study interest. For example, in a multi-center clinical trial where we believe that the differences between the services provided across centers are non-negligible, but the study participants are similar, we can specify the clinic-related variables (e.g., treatment and cost) to be heterogeneous and the patient-related variables (e.g., age and gender) to be homogeneous. In addition, the specification of c can be dependent on preliminary marginal analysis of the homogeneousness of each variable, such as tests for random effects. When the homogeneousness of a covariate is unclear, we suggest specifying it as heterogeneous rather than homogeneous.

Under the assumption that both within-study and between-study samples are independent, for any c = (c₁, …, c_p)^⊤ with c_j ∈ {0, 1}, j = 1, …, p, the initial estimate of β, which gives the starting level of clustering (i.e., λ = 0), can be consistently estimated by the maximum likelihood estimator

$$\widehat{\mathit{\beta }}=\underset{\mathit{\beta }\in {ℝ}^{(K\times p)}}{\text{argmax}}\frac{1}{K}\sum _{k=1}^K\frac{1}{n_k}log{L}_k(\mathit{\beta }),$$ (1)

where $L_k(\mathit{\beta })={\prod }_{i=1}^{n_k}{L}_k^{(i)}(\mathit{\beta })$, k = 1, …, K are the study-specific likelihoods from the given GLMs. For the purpose of parameter grouping and fusion, we propose the regularized maximum likelihood estimation for β by minimizing the following objective function:

$$\underset{\mathit{\beta }\in {ℝ}^{(K\times p)}}{min}\left(-\frac{1}{K}\sum _{k=1}^K\frac{1}{n_k}log{L}_k(\mathit{\beta })+P(\mathit{\beta })\right),$$ (2)

where P(β) is a penalty function of certain form. Here we adopt weighting $\frac{1}{n_k}$ to balance the contribution from each study so to avoid the dominance of large studies. Other types of weighting schemes may be considered to serve for different purposes, such as the inverse of estimated variances of initial estimates, which helps to achieve better estimation precision.

To achieve parameter fusion, Shen and Huang (2010) proposed the grouping pursuit algorithm, which specifies the sum of ℓ₁-norm differences of all study-specific coefficient pairs among individual heterogeneous coefficient vectors β_j,·, where c_j = 1, as the penalty:

$$P_{\lambda }(\mathit{\beta })=\lambda \sum _{j=1}^p{c}_j\sum _{k=1}^{K-1}\sum _{k^{\prime }>k}^K\mid {\beta }_{j,k}-{\beta }_{j,k^{\prime }}\mid ,$$

with λ ≥ 0. In this penalty, there are $\left(\begin{array}{c}K\\ 2\end{array}\right)$ terms of pairwise differences for each heterogeneous covariate and the total number of terms increases by an order of O(K²), given p fixed. This penalty contains many redundant constraints and imposes great computational challenges as pointed out in Shen and Huang (2010) and Ke et al. (2015).

Following arguments in Wang et al. (2016) and Ke et al. (2015), we develop the method of FLARCC by a simplified penalty function that uses the information on the ordering of coefficients. For the jth covariate, let U_j = (U_j,1, …, U_j,K)^⊤ be the ranking with no ties of β_j,· = (β_j,1, …, β_j,K)^⊤, from the smallest to the largest. Specifically, $U_{j,k}={\sum }_{k^{\prime }=1}^K\mathbf{1}\{{\beta }_{j,k^{\prime }}\le {\beta }_{j,k}\}$ if there are no ties in β_j,·; otherwise, the ties in U_j are resolved by the first-occurrence-wins rule according to k to ensure rank uniqueness. Then, the fusion penalty in FLARCC with parameter orderings U_j, j = 1, …, p, takes the form:

$$P_{\lambda }(\mathit{\beta })=\lambda \sum _{j=1}^p{c}_j{\nu }_j\sum _{k=1}^{K-1}\sum _{k^{\prime }>k}^K{\mu }_{j,k,k^{\prime }}\mathbf{1}\{\mid U_{j,k}-U_{j,k^{\prime }}\mid =1\}\mid {\beta }_{j,k}-{\beta }_{j,k^{\prime }}\mid ,$$ (3)

where the constraints occur effectively only on adjacent ordered pairs. Clearly, the penalty in (3) only involves K − 1 terms for each case of c_j = 1, which is of an order O(K), given p fixed. The ν_j’s and μ_j,k,k′’s in (3) are weights. Following Zou (2006), we choose adaptive weights μ̂_j,k,k′ = 1/|β̂_j,k − β̂_j,k′|^r, r > 0, so that parameters with smaller difference will be penalized more than those with larger differences. Similarly, for a group of parameters β_j,· = (β_j,1, …, β_j,K)^⊤, ν_j is an adaptive weight to characterize the degree of heterogeneousness of β_j,·. Specifically, in this paper we let ν̂_j = 1/|β̂_j,(K)− β̂_j,(1)|^s, the inverse of the range of the estimates, with s ≥ 0; when a covariate is homogeneous, the differences of study-specific coefficients will be penalized more than those that are heterogeneous. In this way, we can “harmonize” solution paths so to greatly improve the performance by a single tuning parameter. We compare s = 0 and s = 1 in the simulation experiments and show in Section 5 that the introduction of such group-wise weights ν_j, j = 1, …, p, gives rise to improvement on the performance of identifying homogeneous covariates when K and p are large.

A sparse version of FLARCC can also be achieved by including the traditional lasso penalty in (3) for covariate selection. In order to minimize the interference between fusion and sparsity penalties, we only encourage sparsity for the coefficient closest to zero in each β_j,· = (β_j,1, …, β_j,K)^⊤, for j = 1, …, p. Similar to the definition of U_j, let V_j = (V_j,1, …, V_j,K)^⊤ be the ranking with no ties, from the smallest to the largest, of the absolute values of β_j,·, i.e., (|β_j,1|, …, |β_j,K|)^⊤. First we calculate V_j by $V_{j,k}={\sum }_{k^{\prime }=1}^K\mathbf{1}\{\mid {\beta }_{j,k^{\prime }}\mid \le \mid {\beta }_{j,k}\mid \}$, then we resolve the ties in V_j by the first-occurrence-wins rule according to k. Thus we can extend (3) to achieve variable selection by the following penalty function:

$$P_{\lambda ,\alpha }(\mathit{\beta })=\lambda \sum _{j=1}^p{c}_j{\nu }_j\sum _{k=1}^{K-1}\sum _{k^{\prime }>k}^K{\mu }_{j,k,k^{\prime }}\mathbf{1}\{\mid U_{j,k}-U_{j,k^{\prime }}\mid =1\}\mid {\beta }_{j,k}-{\beta }_{j,k^{\prime }}\mid +\alpha \lambda \sum _{j=1}^p\sum _{k=1}^K{\mu }_{j,k}\mathbf{1}\{V_{j,k}=1\}\mid {\beta }_{j,k}\mid ,$$ (4)

where α ≥ 0 is another tuning parameter that controls the relative ratio between fusion and sparsity penalties, and μ̂_j,k = 1/|β̂_j,k|^r. The sparsity penalty, although only enforced on the smallest coefficient in absolute value of β_j,·, is capable of shrinking a group of coefficients to zero when combined with the fusion penalty.

In practice, the weights (ν_j, μ_j,k,k′ and μ_j,k) and the parameter orderings (U_j and V_j) are unknown, for j = 1, …, p. We replace them with their estimates based on root-n consistent estimates $\widehat{\mathit{\beta }}={({\widehat{\mathit{\beta }}}_{1,•}^{\top },\dots ,{\widehat{\mathit{\beta }}}_{p,•}^{\top })}^{\top }$, such as those from (1). In the simulation experiments and the real data application of this paper, we set r = 1 in μ̂_j,k,k′ and μ̂_j,k.

2.2 Algorithm

Optimization problem (2) with P(β) = P_λ,α(β) given in (4) can be carried out by a lasso regression through suitable reparameterization. Let the ordered coefficients of β_j,· in an ascending order based on ranking U_j be (β_j,(1), …, β_j,(K))^⊤, j = 1, …, p. For the jth covariate, consider a set of transformed parameters θ_j,· = (θ_j,1, …, θ_j,K)^⊤ defined by

$$\begin{array}{lll}{\theta }_{j,1}\hfill & ={\beta }_{j,k},\hfill & \text{for}k\text{s.t.}{V}_{j,k}=1;\hfill \\ {\theta }_{j,k}\hfill & ={\beta }_{j,(k)}-{\beta }_{j,(k-1)},\hfill & \text{for}k=2,\dots ,K.\hfill \end{array}$$

Then the P_λ,α(β) in (4) can be rewritten as

$$P_{\lambda ,\alpha }(\mathit{\theta })=\lambda \sum _{j=1}^p\sum _{k=1}^K{\omega }_{j,k}\mid {\theta }_{j,k}\mid ,$$ (5)

where

$${\widehat{\omega }}_{j,k}=\{\begin{array}{ll}\alpha \frac{1}{{\mid {\widehat{\theta }}_{j,1}\mid }^r},\hfill & \text{if}k=1\hfill \\ c_j\frac{1}{{\mid {\sum }_{k^{\prime }=2}^K{\widehat{\theta }}_{j,k^{\prime }}\mid }^s}\frac{1}{{\mid {\widehat{\theta }}_{j,k}\mid }^r},\hfill & \text{if}k=2,\dots ,K,\hfill \end{array}$$ (6)

for j = 1, …, p. Since no ties are allowed in the parameter ordering of FLARCC, one-to-one transformation exists between $\mathit{\beta }={({\mathit{\beta }}_{1,•}^{\top },{\mathit{\beta }}_{2,•}^{\top },\dots ,{\mathit{\beta }}_{p,•}^{\top })}^{\top }$ and $\mathit{\theta }={({\mathit{\theta }}_{1,•}^{\top },{\mathit{\theta }}_{2,•}^{\top },\dots ,{\mathit{\theta }}_{p,•}^{\top })}^{\top }$ by suitable sorting matrix S and reparameterization matrix R; that is, θ = RSβ and β = (RS)⁻¹θ with both S and R being full-rank square matrices. Thus, a solution to the fused lasso problem can be obtained equivalently by solving a routine lasso problem with respect to coefficient vector θ and a transformed design matrix X(RS)⁻¹. As aforementioned, the estimated parameter ordering is used to construct S. It is obvious that the constraint in (5) is convex, thus FLARCC does not suffer from multiple local minimal issue. The optimization is done using R package glmnet (version 2.0–2) (Friedman et al., 2010), which accommodates GLMs with Gaussian, binomial and Poisson distributions.

3. Large-sample Properties

First we present the oracle property of our method when the parameter ordering is known, then we prove that the same large-sample properties are preserved when consistently estimated parameter ordering is used. Here we assume K is fixed. Theorems will be stated under the setting of all coefficients being heterogeneous, i.e., c = (1, …, 1)^⊤. The large-sample theories for other specification of c can be established as a special case.

Denote the true parameter values as β^* and θ^*. Let the collection of true parameter orderings of all covariates and their absolute values be $\mathit{W}={\{{\mathit{U}}_j,{\mathit{V}}_j\}}_{j=1}^p$, and the estimated orderings based on the root-n consistent estimator β̂ from (1) as $\widehat{\mathit{W}}={\{{\widehat{\mathit{U}}}_j,{\widehat{\mathit{V}}}_j\}}_{j=1}^p$. Denote the FLARCC estimator of θ^* as θ̂^W when W is known, and θ̂^Ŵ when the estimated parameter ordering Ŵ is used. Let $\mathcal{A}={\cup }_{j=1}^p\{{\mathcal{A}}_j\}$ be the index set of nonzero values in θ^*, where ${\mathcal{A}}_j=\{(j,k):{\theta }_{j,k}^{\ast }\ne 0\}$, and 𝒜^c be the complement of 𝒜. Thus, θ^* can be partitioned into two subsets, the true-zero set ${\mathit{\theta }}_{{\mathcal{A}}^c}^{\ast }$ and the nonzero set ${\mathit{\theta }}_{\mathcal{A}}^{\ast }$. Similarly, let 𝒜̂^W and 𝒜̂^Ŵ be the index sets of nonzero elements in θ̂^W and θ̂^Ŵ, respectively. Let $n=\underset{1\le k\le K}{min}{n}_k,N={\sum }_{k=1}^K{n}_k$, and λ_N = Nλ.

Theorem 1

Suppose that tuning parameter λ_N satisfies ${\lambda }_N/\sqrt{N}\to 0$ and λ_NN^(r−1)/2 → ∞. Then under some mild regularity conditions (see Appendix A), the FLARCC estimator θ̂^W based on the true parameter ordering W satisfies

1. (Selection Consistency) lim_n P(𝒜̂^W = 𝒜) = 1;

2. (Asymptotic Normality) $\sqrt{N}({\widehat{\mathit{\theta }}}_{\mathcal{A}}^{\mathit{W}}-{\mathit{\theta }}_{\mathcal{A}}^{\ast })\stackrel{d}{\to }\mathcal{N}(0,{\mathit{I}}_{11}^{-1})$ as n → ∞, where I₁₁ is the submatrix of Fisher information matrix I corresponding to set 𝒜.

Theorem 1 states that when the coefficient orderings W of β is known, under mild regularity conditions, the FLARCC estimator θ̂^W enjoys selection consistency and asymptotic normality. The proof of Theorem 1 follows Zou (2006) and is given in Appendix A. Now we present Theorem 3, which states that the same properties of Theorem 1 hold for θ̂^Ŵ, the FLARCC estimator of θ^* based on the estimated parameter ordering Ŵ. In effect, Theorem 3 is a consequence of the following lemma.

Lemma 2

If β̂ is a root-n consistent estimator of β, then lim_n P(Û_j = U_j) = 1 and lim_n P(V̂_j = V_j) = 1 for j = 1, …, p.

The proof of Lemma 2 is given in Appendix A. Lemma 2 implies that the parameter ordering can be consistently estimated. Using Lemma 2, we are able to extend the properties of θ̂^W in Theorem 1 to the proposed FLARCC estimator θ̂^Ŵ.

Theorem 3

Suppose that ${\lambda }_N/\sqrt{N}\to 0$ and λ_NN^(r−1)/2 →∞. Let the estimated parameter ordering Ŵ be the ranks from a root-n initial consistent estimator β̂. Under the same regularity conditions of Theorem 1, the FLARCC estimator θ̂^Ŵ satisfies

1. (Selection Consistency) lim_n P(𝒜̂^Ŵ = 𝒜) = 1;

2. (Asymptotic Normality) $\sqrt{N}({\widehat{\mathit{\theta }}}_{\mathcal{A}}^{\widehat{\mathit{W}}}-{\mathit{\theta }}_{\mathcal{A}}^{\ast })\stackrel{d}{\to }\mathcal{N}(0,{\mathit{I}}_{11}^{-1})$ as n → ∞, where I₁₁ is the submatrix of Fisher information matrix I corresponding to set 𝒜.

The proof of Theorem 3 is given in Appendix A. The asymptotic normality for β̂ can also be derived by a simple linear transformation.

4. Tuning Parameter

In this section, we provide interpretation of the tuning parameter λ and discuss the selection criteria used for selecting λ.

4.1 Interpretation of ν_j’s

Intuitively speaking, the study-specific coefficients of a homogeneous covariate tend to be fused at a small λ value, say λ₁, but the fusion of a heterogeneous covariate requires another λ value, λ₂, assuming λ₂ > λ₁. The region to draw correct clustering conclusion is [λ₁, λ₂], that is, any λ within this region will produce the correct clustering result. However, when the number of covariates p is large, the region that λ can take value from to ensure the correct clustering of all p coefficient vectors simultaneously becomes narrower and may even be empty. For example, when λ₂ < λ₁ in the above case, no single λ is able to correctly cluster both sets of parameters. The introduction of ν_j’s in (4) creates larger separation between homogeneous and heterogeneous groups, so that the range for λ to identify the correct clustering pattern for all covariates is better established than the case with s = 0, namely no use of weighting ν_j’s. When the number of covariates p is large, ν_j plays a more important role in harmonizing solution paths across covariates, and the performance will be greatly improved by simultaneous tuning via a single λ.

4.2 Model Selection

In the current literature, the tuning parameter λ may be selected by multiple model selection criteria, such as Bayesian information criterion (BIC) (Schwarz, 1978) and generalized cross-validation (GCV) (Golub et al., 1979). In this paper, we consider the widely used BIC and its modification, extended BIC, i.e., EBIC (Chen and Chen, 2008; Gao and Song, 2010), which has showed the benefit of achieving sparse solutions.

Following the derivation of BIC for weighted likelihoods in Lumley and Scott (2015), the conventional BIC for FLARCC is defined as follows:

$${\mathit{BIC}}_{\lambda }=-2\sum _{k=1}^K\frac{\overline{n}}{n_k}log{L}_k(\widehat{\mathit{\beta }}(\lambda ))+\text{df}(\widehat{\mathit{\beta }}(\lambda ))log(N),$$ (7)

where n̄ = N/K is the average sample size per study, L_k(β) is the study-specific likelihood, β̂(λ) is the estimation of β at tuning parameter value λ, and $\text{df}(\widehat{\mathit{\beta }}(\lambda ))={\sum }_{j=1}^p\text{df}({\widehat{\mathit{\beta }}}_{j,•}(\lambda ))$ is the total number of distinct parameters in β̂(λ). The study-specific log-likelihoods for three most common models are listed below:

$$\begin{array}{lll}\text{Normal:}\hfill & log{L}_k(\widehat{\mathit{\beta }}(\lambda ))\hfill & \propto -\frac{n_k}{2}log\left\{\sum _{i=1}^{n_k}{\left(Y_k^{(i)}-{\mathit{X}}_k^{(i)\top }\widehat{\mathit{\beta }}(\lambda )\right)}^2/n_k\right\};\hfill \\ \text{Logistic:}\hfill & log{L}_k(\widehat{\mathit{\beta }}(\lambda ))\hfill & \propto \sum _{i=1}^{n_k}\left\{Y_k^{(i)}{\mathit{X}}_k^{(i)\top }\widehat{\mathit{\beta }}(\lambda )-log\left(1+e^{{\mathit{X}}_k^{(i)\top }\widehat{\mathit{\beta }}(\lambda )}\right)\right\};\hfill \\ \text{Poisson:}\hfill & log{L}_k(\widehat{\mathit{\beta }}(\lambda ))\hfill & \propto \sum _{i=1}^{n_k}\left\{Y_k^{(i)}{\mathit{X}}_k^{(i)\top }\widehat{\mathit{\beta }}(\lambda )-e^{{\mathit{X}}_k^{(i)\top }\widehat{\mathit{\beta }}(\lambda )}\right\}.\hfill \end{array}$$

To improve the BIC by further controlling model size and encouraging sparer models, we adapt the EBIC for FLARCC, which takes the following form:

$${\mathit{EBIC}}_{\lambda }=-2\sum _{k=1}^K\frac{\overline{n}}{n_k}log{L}_k(\widehat{\mathit{\beta }}(\lambda ))+\text{df}(\widehat{\mathit{\beta }}(\lambda ))log(N)+2\gamma log\sum _{j=1}^p\left(\begin{array}{c}K\\ \text{df}({\widehat{\mathit{\beta }}}_{j,•}(\lambda ))\end{array}\right),$$ (8)

where γ ∈ [0, 1] is a tuning parameter that is typically fixed at 1 as done in our numerical experiments. Note that EBIC reduces to BIC when γ = 0. The last term in (8) encourages a sparser solution in comparison to the conventional BIC. Simulation studies in Section 5 provide numerical evidence to elucidate the difference between BIC and EBIC in terms of their performance on achieving sparsity.

In a view of hierarchical clustering, the solution path of each covariate can be thought of as a hierarchical clustering tree. For the jth covariate, λ = 0 corresponds to the bottom of the clustering tree; and λ = λ_Fuse,j, the smallest λ value to achieve complete parameter fusion, corresponds to the top of the clustering tree. The completely heterogeneous model corresponds to the position on the solution path at λ = 0 and the completely homogeneous model corresponds to the model at $\lambda ={\lambda }_{\mathit{Fuse}}:=\underset{1\le j\le p}{max}{\lambda }_{\mathit{Fuse},j}$.

5. Simulation Studies

This section presents results from two simulation experiments. The first simulation compares the performance of FLARCC under different GLM regression models. The second simulation is a more complicated scenario with large K and more non-important covariates, where covariate selection is also of interest.

5.1 Simulation Experiment 1

The first simulation study aims to assess the performance of our method for different GLM regression models. For this, we consider combining data sets from K = 10 different studies with, for simplicity, equal sample size n₁ = ⋯ = n₁₀ = 100. Data are simulated from the following mean regression model:

$$h\{E(Y_k^{(i)})\}={\beta }_{1,k}{X}_{1,k}^{(i)}+{\beta }_{2,k}{X}_{2,k}^{(i)}+{\beta }_{3,k}{X}_{3,k}^{(i)},i=1,\dots ,100,k=1,\dots ,10,$$

where the true coefficient vectors have the following clustering structures:

$$\begin{array}{ll}{\mathit{\beta }}_{1,•}\hfill & ={(\underset{10}{\underbrace{0,\dots ,0}})}^{\top };\hfill \\ {\mathit{\beta }}_{2,•}\hfill & ={(\underset{5}{\underbrace{0,\dots ,0}},\underset{5}{\underbrace{1,\dots ,1}})}^{\top };\hfill \\ {\mathit{\beta }}_{3,•}\hfill & ={(\underset{3}{\underbrace{-1,\dots ,-1}},\underset{4}{\underbrace{0,\dots ,0}},\underset{3}{\underbrace{1,\dots ,1}})}^{\top }.\hfill \end{array}$$

The true values in β₂ and β₃ are heterogeneous, while the true values in β₁ are homogeneous across studies. The three covariates are correlated with exchangeable correlation of 0.3 and marginally distributed according to the standard normal distributions, 𝒩(0, 1). Three types of GLM regression models are considered: linear model for continuous normal outcomes (with errors simulated from 𝒩(0, 1)), logistic model for binary outcomes and Poisson model for count outcomes.

To evaluate the performance of FLARCC to correctly detect patterns of all covariates, we assume all covariates are heterogeneous across studies with no prior knowledge on clustering structure of any covariate. Intercept is fitted and assumed to be homogeneous. No sparsity penalty is applied on the covariates (i.e., α = 0) in this simulation experiment. Coefficients of all three covariates are fused simultaneously, and the optimal tuning parameter λ_opt is selected by EBIC. We report sensitivity and specificity as metrics of the performance of FLARCC to identify similar and distinct coefficient pairs. Sensitivity measures the proportion of equal coefficient pairs that are correctly identified. Similarly, specificity measures the proportion of unequal coefficients pairs that are correctly identified; however, specificity is not defined for homogeneous covariates which have no unequal coefficient pairs. In addition, we calculate the mean squared error (MSE) for each β̂_{j, ·} across all K studies, defined as ${\text{MSE}}_j={\sum }_{k=1}^K{({\widehat{\beta }}_{j,k}-{\beta }_{j,k})}^2/K$, j = 1, …, p, and compare with the MSE of each estimate based on homogeneous model (λ = λ_Fuse) and heterogeneous model (λ = 0).

Table 1 shows the results of simulation experiment 1 from 1,000 simulation replicates. The MSE of all estimated covariates based on FLARCC (λ = λ_opt) are consistently and significantly smaller than those based on the homogeneous (λ = λ_Fuse) and heterogeneous (λ = 0) models, regardless of the model type. FLARCC performs very well in the linear and Poisson regressions in terms of identifying the correct clustering, with the sensitivity and specificity both above 95% for all covariates (specificity is not reported for β₁ since there is no unequal pair within β_{1, ·}). Sensitivity and specificity of FLARCC drop in the logistic regression, especially as the level of heterogeneity increases. One reason for the reduced performance of FLARCC in the logistic regression is that the estimated variances of regression coefficients in the logistic model are larger than in the linear and Poisson models, given the same coefficient setting. Therefore, the estimated parameter ordering for which our method is based on may be less accurate. For the logistic regression, increasing sample sizes is one of the possible ways to improve the performance. The performance difference between scaling weight parameter s = 0 and s = 1 in (4) is small in this case because of the relatively small number of covariates p = 3. Additionally, since K is small in this case, the optimal λ selected by BIC and EBIC are very close, thus we only display results based on EBIC. As p and K become larger, FLARCC will increasingly benefit from the additional weights ν_j (i.e., s = 1) and EBIC, as will be shown in Section 5.2. A sensitivity analysis to investigate how the initial ordering affect the performance of FLARCC is conducted, with results shown in Appendix B. We show that when the initial parameter ordering is slightly distorted, our method still achieves satisfactory performance.

Table 1.

Results of simulation experiment 1 for FLARCC when scaling weight parameter s = 0 and s = 1 with λ selected by EBIC, for the linear, logistic and Poisson models. Tuning parameters are reported in log scale, i.e., λ̃ = log₁₀(λ+1). Results are summarized from 1,000 replications.

Method (λ̃opt)	β	β̂ size	λ̃Fuse,j	Sensitivity	Specificity	MSE when λ =
						λopt	λFuse	0
Linear: continuous response
s = 0 (0.154)	β1	1.067	0.111	0.974	–	0.001	0.002	0.012
	β2	2.075	1.275	0.982	1.000	0.003	0.253	0.012
	β3	3.081	1.368	0.982	1.000	0.004	0.603	0.012
s = 1 (0.349)	β1	1.006	0.080	0.998	–	0.001	0.002	0.012
	β2	2.058	1.584	0.986	1.000	0.003	0.253	0.012
	β3	3.123	1.972	0.974	1.000	0.004	0.603	0.012
Logistic: binary response
s = 0 (0.066)	β1	1.270	0.064	0.898	–	0.010	0.005	0.070
	β2	2.572	0.318	0.819	0.963	0.047	0.268	0.087
	β3	3.682	0.437	0.784	0.964	0.069	0.607	0.091
s = 1 (0.112)	β1	1.075	0.050	0.972	–	0.007	0.005	0.069
	β2	2.478	0.414	0.837	0.952	0.052	0.268	0.088
	β3	3.912	0.711	0.749	0.971	0.064	0.607	0.091
Poisson: count response
s = 0 (0.187)	β1	1.087	0.129	0.976	–	0.001	0.005	0.008
	β2	2.084	1.751	0.984	1.000	0.001	0.271	0.008
	β3	3.076	1.885	0.986	1.000	0.002	0.659	0.008
s = 1 (0.433)	β1	1.047	0.087	0.992	–	0.001	0.005	0.008
	β2	2.088	2.060	0.984	1.000	0.002	0.271	0.008
	β3	3.111	2.536	0.978	1.000	0.002	0.657	0.008

5.2 Simulation Experiment 2

The second simulation study aims to evaluate the performance of FLARCC in a more challenging setting. More specifically, we consider data sets from K = 100 studies, each with a sample size 100, totaling 10,000 subject-level observations. Comparing to the previous setting, we increase the number of covariates and reduce the gaps between heterogeneous coefficients. For each study, we simulate data from the following linear regression model:

$$E(Y_k^{(i)})=\sum _{j=1}^8{\beta }_{j,k}{X}_{j,k}^{(i)},i=1,\dots ,100,k=1,\dots ,100.$$

The signals are set sparse; only the first four covariates with coefficient vectors, β₁ to β₄, are influential to Y with the true clustered effect patterns given as follows:

$$\begin{array}{ll}{\beta }_{1,•}\hfill & ={(\underset{50}{\underbrace{0,\dots ,0}},\underset{50}{\underbrace{0.5,\dots ,0.5}})}^{\top },\hfill \\ {\beta }_{2,•}\hfill & ={(\underset{30}{\underbrace{-0.5,\dots ,-0.5}},\underset{40}{\underbrace{0,\dots ,0}},\underset{30}{\underbrace{0.5,\dots ,0.5}})}^{\top },\hfill \\ {\beta }_{3,•}\hfill & ={(\underset{25}{\underbrace{-0.5,\dots ,-0.5}},\underset{25}{\underbrace{0,\dots ,0}},\underset{25}{\underbrace{0.5,\dots ,0.5}},\underset{25}{\underbrace{1,\dots ,1}})}^{\top },\hfill \\ {\beta }_{4,•}\hfill & ={(\underset{20}{\underbrace{-1,\dots ,-1}},\underset{20}{\underbrace{-0.5,\dots ,-0.5}},\underset{20}{\underbrace{0,\dots ,0}},\underset{20}{\underbrace{0.5,\dots ,0.5}},\underset{20}{\underbrace{1,\dots ,1}})}^{\top },\hfill \end{array}$$

whereas β₅ to β₈ are all zero, i.e., β_{j, ·} = (0, …, 0)^⊤, for j = 5, 6, 7, 8. All covariates are equally correlated with an exchangeable correlation of 0.3 and marginally distributed according to 𝒩(0, 1). We set β₁ to β₈ as being heterogeneous from the start and fuse all of them simultaneously. We apply the additional sparsity penalty to all covariates by setting α = 1. The intercept is assumed to be homogeneous in the analysis.

Since K is large, we also present results from individual covariate K-means clustering. This is a two-step method where we first estimate regression coefficients within each study, and then separately for each covariate, we perform the K-means clustering on the estimated study-specific coefficients of each covariate. The number of clusters is selected by the generalized cross-validation criterion ${\sum }_{k=1}^K{({\widehat{\beta }}_k-{\widehat{\beta }}_{c(k)})}^2/{(K-\text{GDF})}^2$, with β̂_c(k) being the cluster center of β̂_k and GDF is the generalized degrees of freedom estimated according to Ye (1998), where purturbations are generated independently from 𝒩(0, 0.01). The cluster centroids are then used as the estimates of the group-level parameters.

Table 2 summarizes the simulation results for linear model where the errors are generated independently from 𝒩(0, 1). Similar to simulation 1, FLARCC gives the smallest MSE for heterogeneous covariates, β₁ to β₄, among all three models, and has comparable MSE as the homogeneous model for homogeneous covariates, β₅ to β₈. More interestingly, when K is large, BIC does not provide satisfactory model selection, erring on the lack of parsimony, while EBIC encourages stronger fusion and improves the ability to detect equal coefficient pairs in all eight covariates, regardless of their levels of heterogeneity. In addition, EBIC improves the sparsity detection among both the important and nonimportant covariates. It is interesting to note that the choice between BIC and EBIC does not alter solution paths, but only model selection. FLARCC with scaling weight parameter s = 1 has the best clustering performance among all compared methods. The difference between the choices of s = 0 and s = 1 is substantial in simulation 2, in contrast to the results from simulation 1. This indicates that the covariate-specific weights for heterogeneity ${\{{\nu }_j\}}_{j=1}^p$ are very effective to improve the performance of the proposed fusion learning, especially when K and p are large. Sensitivity and specificity of the two-step K-means clustering method are higher than those of FLARCC with s = 0, but lower than those of FLARCC with s = 1. The two-step K-means has larger MSE than FLARCC because it does not consider the correlation between covariates. More importantly, the K-means clustering is a model-free method, so the results obtained from this method cannot be plugged in back to the model for prediction. As suggested from the empirical results of both simulation experiments, EBIC tends to provide better model selection for FLARCC than the conventional BIC.

Table 2.

Result of simulation experiment 2 under the linear model. Scaling weight parameter is set at s = 0 and s = 1. Tuning parameters are reported in log scale, i.e., λ̃ = log₁₀(λ+1). Sparsity denotes the proportion of zero in estimation. Results are summarized from 1,000 replications.

Method (λ̃opt)	β	β̂ size	λ̃Fuse,j	Sensitivity	Specificity	Sparsity	MSE when λ =
							λopt	λFuse	0
s = 0 BIC (0.143)	β1	8.115	1.517	0.373	0.995	0.199	0.006	0.063	0.014
	β2	10.689	1.551	0.401	0.996	0.166	0.008	0.150	0.014
	β3	13.107	1.962	0.443	0.997	0.113	0.008	0.313	0.014
	β4	15.178	1.984	0.461	0.997	0.091	0.009	0.500	0.014
	β5	4.818	0.301	0.322	–	0.338	0.003	0.000	0.014
	β6	4.860	0.305	0.322	–	0.339	0.003	0.000	0.014
	β7	4.860	0.302	0.321	–	0.330	0.003	0.000	0.014
	β8	4.820	0.301	0.319	–	0.336	0.003	0.000	0.014
s = 0 EBIC (0.159)	β1	7.538	1.509	0.417	0.994	0.224	0.006	0.063	0.014
	β2	9.975	1.546	0.441	0.995	0.182	0.007	0.150	0.014
	β3	12.212	1.953	0.483	0.996	0.124	0.008	0.313	0.014
	β4	14.096	1.978	0.503	0.997	0.101	0.008	0.500	0.014
	β5	4.388	0.298	0.377	–	0.394	0.003	0.000	0.014
	β6	4.413	0.303	0.379	–	0.397	0.003	0.000	0.014
	β7	4.408	0.299	0.374	–	0.385	0.003	0.000	0.014
	β8	4.385	0.298	0.374	–	0.392	0.003	0.000	0.014
s = 1 EBIC (0.492)	β1	3.563	1.589	0.800	0.981	0.422	0.006	0.063	0.014
	β2	6.111	1.810	0.708	0.989	0.291	0.007	0.150	0.014
	β3	8.843	2.388	0.667	0.994	0.168	0.007	0.313	0.014
	β4	11.358	2.521	0.635	0.995	0.128	0.008	0.500	0.014
	β5	1.329	0.275	0.928	–	0.932	0.000	0.000	0.014
	β6	1.321	0.280	0.933	–	0.937	0.000	0.000	0.014
	β7	1.311	0.274	0.934	–	0.935	0.000	0.000	0.014
	β8	1.321	0.273	0.929	–	0.936	0.000	0.000	0.014
MSE from K-means
K-means GCV (GDF)	β1	7.196	–	0.753	0.971	0.000			0.008
	β2	11.236	–	0.671	0.983	0.000			0.009
	β3	13.721	–	0.639	0.984	0.000			0.011
	β4	18.308	–	0.527	0.985	0.000			0.014
	β5	6.415	–	0.759	–	0.000			0.004
	β6	5.271	–	0.769	–	0.000			0.004
	β7	5.629	–	0.767	–	0.000			0.004
	β8	5.080	–	0.794	–	0.000			0.004

6. Application: Clustering of Cohort Effects

In this data analysis example, we like to demonstrate the use of our method to derive clusters of cohort effects. Here we consider the Panel Study of Income Dynamics (PSID), which is a household survey study following thousands of families across different states in the US. PSID collects information of employment, income, health, and so on. In this data analysis, we focus on the association of household income with body mass index (BMI) on school-aged children between age of 11 and 19, adjusted for age, gender and birth weight. Data of 1880 children were gathered from four census regions (1-Northeast, 2-Midwest, 3-South and 4-West), as defined by U.S. Census Bureau (2015). All variables are standardized before model fitting. We are interested in investigating if regional heterogeneity exists and if the effects of interest differ across regions with region-dependent patterns.

Table 3 shows the results of coefficient estimates obtained from three different models: (A) homogeneous model (λ = λ_Fuse), coefficients estimated by combining data sets from four regions, (B) heterogeneous model (λ = 0), coefficients estimated separately by region-specific data, and (C) FLARCC (λ = λ_EBIC). Model A suggests that age and birth weight are positively associated with BMI for the subjects, but income was negatively associated with BMI. The estimates from Model B suggest that heterogeneous coefficient patterns exist among these associations since conclusions differ between regions. Model C appears more sensible when regression coefficients are heterogeneous across these regions. Since K and p are small in this data application, we apply FLARCC with s = 0 on the PSID data, assuming effects of income, age, gender and birth weight are heterogeneous across regions, and set sparsity parameter α = 1 for variable selection.

Table 3.

Coefficient estimates of the homogeneous model (λ = λ_Fuse), the heterogeneous model (λ = 0) and the fused model using FLARCC with λ selected by EBIC, respectively.

Region	n	Intercept β0	Age β1	Sex β2	Birth Wt. β3	Income β4
(A) Homogeneous model – combine all regions
All regions	1880	0.000	0.206	0.016	0.063	−0.096
(B) Heterogeneous model – region specific estimates
1-Northeast	239	−0.133	0.228	−0.079	−0.003	0.004
2-Midwest	493	−0.054	0.229	0.017	0.124	−0.132
3-South	805	0.128	0.158	0.095	0.068	−0.071
4-West	343	−0.155	0.236	−0.083	0.057	−0.074
(C) Fused model using FLARCC
1-Northeast	239	−0.093	0.201	−0.036	0.000	0.000
2-Midwest	493	−0.093	0.201	0.000	0.021	−0.047
3-South	805	0.075	0.201	0.000	0.021	−0.047
4-West	343	−0.093	0.201	−0.036	0.021	−0.047

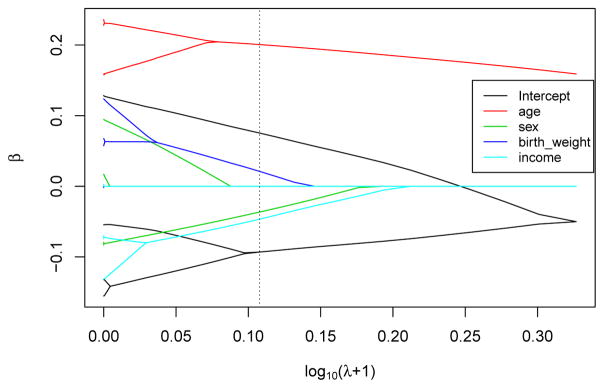
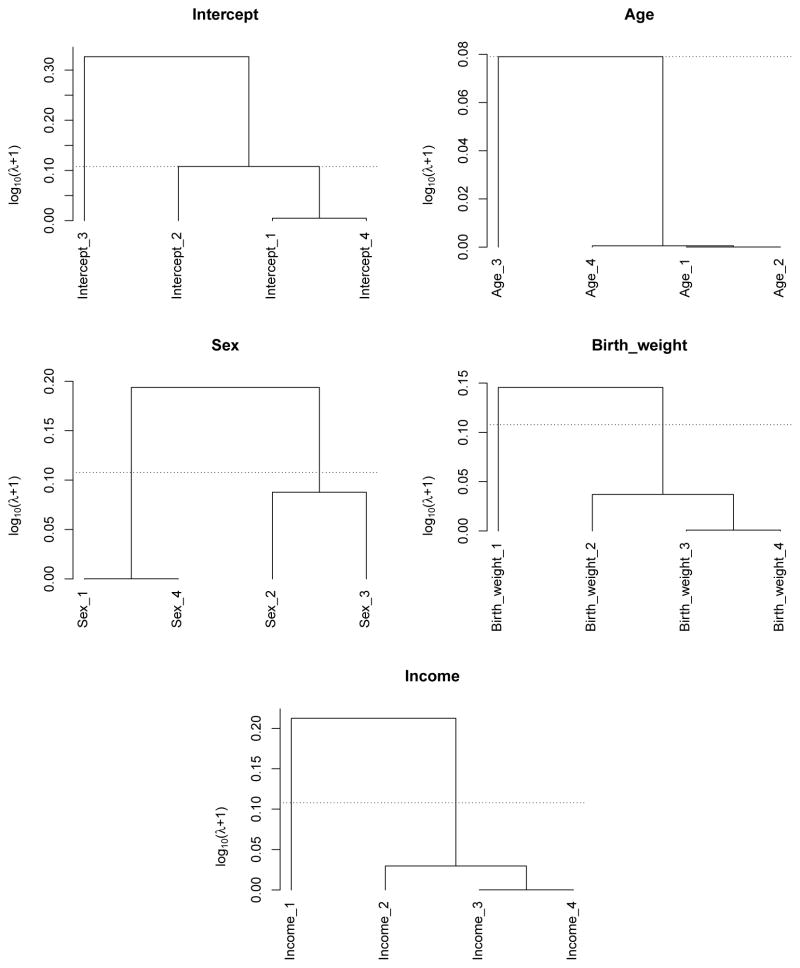
Based on the results from FLARCC, the estimated mean of standardized BMI in the South is 0.168 higher (or 0.97 higher in original scale of BMI) than that of the other three regions, which share the same mean. The effects of age are consistent across four regions. The effects of gender are classified into two clusters. The mean of standardized BMI of females is 0.036 lower (or 0.42 lower in original scale) than that of males in the Northeast and the West, but males and females have the same mean BMI in the Midwest and the South. Standardized BMI increases by 0.021 for every standard deviation increase of birth weight (or BMI increases by 0.19 for every unit increase of birth weight) in all regions except the Northeast. Similarly, standardized BMI decreases by 0.047 for every standard deviation increase of log income (or BMI decreases by 0.27 for every unit increase of income) in all regions except the Northeast where BMI is not affected by income. The leave-one-out mean squared prediction errors for model A, B and C are 0.953, 0.945 and 0.950, respectively. The differences between the prediction errors are small because of the relatively small effect sizes of the heterogeneous covariates identified by FLARCC, i.e., sex, birth weight and income. The most significant covariate, age, is homogeneous thus it does not differentiate the prediction power among the three models. Solution paths and fusograms of all covariates are shown in Figure 2 and Figure 3, respectively, for illustration. In summary, FLARCC ensures parsimony where necessary to maximize the prediction power of the final model; and it provides more informative interpretation and better visualization than the other two traditional models.

Figure 2.

FLARCC solution paths of all covariates over the transformed tuning parameter λ̃ = log₁₀(λ+1), with s = 0. The vertical dotted line denotes the optimal tuning parameter value λ̃_EBIC.

Figure 3.

Fusograms of all covariates based on FLARCC solution paths. The horizontal dotted lines denote the optimal regression coefficient clustering determined by EBIC.

7. Concluding Remarks

The proposed method brings a new perspective to model fitting when combining multiple data sets from different sources is of primary interest. As data volumes and data sources grow fast, more and more opportunities and demands emerge in practice to borrow strengths of combined data sets. In such case, traditional methods are challenged by the complex data structures and do not provide desirable treatments and meaningful interpretations to data heterogeneity, especially when the number of data sets is very large. FLARCC allows the flexibility to explore the heterogeneity pattern of parameters among large number of data sets by tuning the shrinkage parameter.

When K and p are small, weights ${\{{\nu }_j\}}_{j=1}^p$ do not contribute to much difference in terms of clustering and estimation. However, since only one tuning parameter is used to regularize the fusion of all covariates, when both K and p are large, we suggest letting s > 0 to allow covariate-specific weights adapting to the heterogeneousness of coefficients from individual covariates to achieve better results. In addition, the estimation consistency of rank estimator is a critical component needed to determine adjacent pairs. The current consistency is established under the case of K being fixed, and the validity of its property is unknown when K increases along the total sample size.

FLARCC can be applied to various scientific problems, such as the detection of outlying studies by singling out outlying coefficients; it can also be applied to the clustering of patient trajectories by viewing the time series data of patients as individual studies. Essentially, all study that are interested in the group-specific effects may be analyzed from the perspective of parameter fusion using the proposed method.

Appendix A. Theorem Proofs

Proof of Theorem 1

The proof of Theorem 1 closely follows arguments given in Zou (2006). Without loss of generality, we assume n₁ = ··· = n_K = n and N = Kn. As K is fixed, n → ∞ implies N → ∞ in the same order. We assume the following regularity conditions:

1. The Fisher information matrix is finite and positive definite,

   $$\mathit{I}({\mathit{\theta }}^{\ast })=E\left[{\varphi }^{″}\left({\mathit{X}}^{\top }{\mathit{\theta }}^{\ast }\right)\mathit{X}{\mathit{X}}^{\top }\right].$$
   Here, ${\mathit{\theta }}_{(Kp\times 1)}^{\ast }$ is the true parameters, X_(N×Kp) is the design matrix corresponding to θ and ϕ is the link function (i.e., ϕ′ = h⁻¹) defined in the following optimization problem

   $${\widehat{\mathit{\theta }}}^{\mathit{W}}=\underset{\mathit{\theta }}{\text{argmin}}\left\{-\frac{1}{K}\sum _{k=1}^K\frac{1}{n_k}\sum _{i=1}^{n_k}\left(Y_k^{(i)}{\mathit{X}}_k^{(i)\top }\mathit{\theta }(\lambda )-\varphi \left({\mathit{X}}_k^{(i)\top }\mathit{\theta }(\lambda )\right)\right)+P_{\lambda ,\alpha }(\mathit{\theta })\right\}$$

   with P_λ,α(θ) as defined in (4), and θ̂^W is the estimator with true ordering W given.

2. There is a sufficiently large open set 𝒪 that contains θ^* such that ∀θ ∈ 𝒪,

   $$\begin{array}{c}\mid {\varphi }^{‴}({\mathit{X}}^{\top }\mathit{\theta })\mid \le M({\mathit{X}}^{\top })<\infty ,\text{and}\\ E[M(\mathit{X})\mid x_j{x}_k{x}_l\mid ]<\infty \end{array}$$

   for a suitable function M and all 1 ≤ j, k, l ≤ Kp.

   First we prove asymptotic normality. For ∀s ≥ 0 and r > 0, let $\mathit{\theta }={\mathit{\theta }}^{\ast }+\mathit{u}/\sqrt{N}$. Define

   $$\begin{array}{r}{\mathrm{\Gamma }}_N(\mathit{u})=-\sum _{k=1}^K\sum _{i=1}^n\left(Y_k^{(i)}{\mathit{X}}_k^{(i)\top }\left({\mathit{\theta }}^{\ast }+\frac{\mathit{u}}{\sqrt{N}}\right)-\varphi \left({\mathit{X}}_k^{(i)\top }\left({\mathit{\theta }}^{\ast }+\frac{\mathit{u}}{\sqrt{N}}\right)\right)\right)\\ +{\lambda }_N\sum _{j=1}^p\sum _{k=1}^K{\widehat{\omega }}_{j,k}\left|{\mathit{\theta }}_{j,k}^{\ast }+\frac{u_{j,k}}{\sqrt{N}}\right|\end{array}$$

where ω̂_j,k is specified in (6). Let û^(N) = argmin_u Γ_N(u); then ${\widehat{\mathit{u}}}^{(N)}=\sqrt{N}({\widehat{\mathit{\theta }}}^{\mathit{W}}-{\mathit{\theta }}^{\ast })$. By Taylor expansion, we have Γ_N(u) − Γ_N(0) = H^(N)(u), where

$$H^{(N)}(\mathit{u})\equiv A_1^{(N)}+A_2^{(N)}+A_3^{(N)}+A_4^{(N)},$$

with

$$\begin{array}{ll}\hfill A_1^{(N)}& =-\sum _{k=1}^K\sum _{i=1}^n\left[Y_k^{(i)}-{\varphi }^{\prime }({\mathit{X}}_k^{(i)\top }{\mathit{\theta }}^{\ast })\right]\frac{{\mathit{X}}_k^{(i)\top }\mathit{u}}{\sqrt{N}},\hfill \\ \hfill A_2^{(N)}& =\sum _{k=1}^K\sum _{i=1}^n\frac{1}{2}{\varphi }^{″}({\mathit{X}}_k^{(i)\top }{\mathit{\theta }}^{\ast }){\mathit{u}}^{\top }\frac{{\mathit{X}}_k^{(i)}{\mathit{X}}_k^{(i)\top }}{\sqrt{N}}\mathit{u},\hfill \\ \hfill A_3^{(N)}& =\frac{{\lambda }_N}{\sqrt{N}}\sum _{j=1}^p\sum _{k=1}^K{\widehat{\omega }}_{j,k}\sqrt{N}\left(\left|{\theta }_{j,k}^{\ast }+\frac{u_{j,k}}{\sqrt{N}}\right|-\left|{\theta }_{j,k}^{\ast }\right|\right),\hfill \\ \hfill \text{and}{A}_4^{(N)}& =N^{-3/2}\sum _{k=1}^K\sum _{i=1}^n\frac{1}{6}{\varphi }^{‴}\left({\mathit{X}}_k^{(i)\top }{\stackrel{\sim }{\mathit{\theta }}}_{\ast }\right){\left({\mathit{X}}_k^{(k)\top }\mathit{u}\right)}^3,\hfill \end{array}$$

where θ̃_* is between θ^* and ${\mathit{\theta }}^{\ast }+\mathit{u}/\sqrt{N}$. The asymptotic limits of $A_1^{(N)},A_2^{(N)}$ and $A_4^{(N)}$ is exactly the same as those in the proof of Theorem 4 in Zou (2006). It suffice to show that $A_3^{(N)}$ has the same asymptotic limit. If ${\theta }_{j,k}^{\ast }\ne 0,{\widehat{\omega }}_{j,1}{\to }_p\alpha {\mid {\theta }_{j,1}^{\ast }\mid }^{-r},{\widehat{\omega }}_{j,k}{\to }_p{\mid {\sum }_{k^{\prime }=2}^K{\theta }_{j,k^{\prime }}^{\ast }\mid }^{-s}{\mid {\theta }_{j,k}^{\ast }\mid }^{-r}$ for k = 2, …, K, and $\sqrt{N}\left(\left|{\theta }_{j,k}^{\ast }+\frac{u_{j,k}}{\sqrt{N}}\right|-\left|{\theta }_{j,k}^{\ast }\right|\right)\to u_{j,k}sgn({\theta }_{j,k}^{\ast })$. Thus by Slutsky’s theorem, $A_3^{(N)}\to 0$. If ${\theta }_{j,k}^{\ast }=0$, for k = 1, since $\sqrt{N}{\widehat{\theta }}_{j,1}=O_p(1),\frac{{\lambda }_N}{\sqrt{N}}{N}^{r-2}\alpha {(\mid \sqrt{N}{\widehat{\theta }}_{j,1}\mid )}^{-r}\to \infty$; for k = 2, …, K, if ${\sum }_{k^{\prime }=2}^K{\theta }_{j,k^{\prime }}^{\ast }=0$ (i.e., homogeneous), $\sqrt{N}{\sum }_{k^{\prime }=2}^K{\widehat{\theta }}_{j,k^{\prime }}=O_p(1)$, thus $\frac{{\lambda }_N}{\sqrt{N}}{N}^{\frac{s+r}{2}}{(\mid \sqrt{N}{\sum }_{k^{\prime }=2}^K{\widehat{\theta }}_{j,k^{\prime }}\mid )}^{-s}{(\mid \sqrt{N}{\widehat{\theta }}_{j,k}\mid )}^{-r}\to \infty$; similarly, if ${\sum }_{k^{\prime }=2}^K{\theta }_{j,k^{\prime }}^{\ast }\ne 0$ (i.e., heterogeneous), ${\sum }_{k^{\prime }=2}^K{\widehat{\theta }}_{j,k^{\prime }}{\to }_p{\sum }_{k^{\prime }=2}^K{\theta }_{j,k^{\prime }}^{{\theta }^{\ast }},\frac{{\lambda }_N}{\sqrt{N}}{\widehat{\omega }}_{j,k}\to \infty$ still holds. And since $\sqrt{N}\left(\left|{\theta }_{j,k}^{\ast }+\frac{u_{j,k}}{\sqrt{N}}\right|-\left|{\theta }_{j,k}^{\ast }\right|\right)\to \mid u_{j,k}\mid$, we have the following result summary:

$$\frac{{\lambda }_N}{\sqrt{N}}{\widehat{\omega }}_{j,k}\sqrt{N}\left(\left|{\theta }_{j,k}^{\ast }+\frac{u_{j,k}}{\sqrt{N}}\right|-\left|{\theta }_{j,k}^{\ast }\right|\right){\to }_p\{\begin{array}{ll}0\hfill & \text{if}{\theta }_{j,k}^{\ast }\ne 0\hfill \\ 0\hfill & \text{if}{\theta }_{j,k}^{\ast }=0\text{and}{u}_{j,k}=0\hfill \\ \infty \hfill & \text{if}{\theta }_{j,k}^{\ast }=0\text{and}{u}_{j,k}\ne 0.\hfill \end{array}$$

Following same arguments in Zou (2006)’s proof of Theorem 4, we have ${\widehat{\mathit{u}}}_{\mathcal{A}}^{(N)}{\to }_d\mathcal{N}(0,{\mathit{I}}_{11}^{-1})$ and ${\widehat{\mathit{u}}}_{{\mathcal{A}}^c}^{(N)}{\to }_d\mathbf{0}$. The proof of the consistency part is similar and thus omitted.

Proof of Lemma 2

The estimated ordering Û_j of ${\mathit{\beta }}_{j,•}^{\ast }$ is only determined by the differences between distinct parameter groups within ${\mathit{\beta }}_{j,•}^{\ast }$. First note that for any 0 < ε < 1, if two parameters ${\beta }_{j,k}^{\ast }$ and ${\beta }_{j,k^{\prime }}^{\ast }$ are in the same parameter group (i.e., ${\beta }_{j,k}^{\ast }={\beta }_{j,k^{\prime }}^{\ast }$), assigning arbitrary ordering between them will not affect the estimated ordering of the parameters between groups, because the ordering within the same parameter group is exchangeable. On the other hand, when two parameters ${\beta }_{j,k}^{\ast }$ and ${\beta }_{j,k^{\prime }}^{\ast }$ are from different parameter groups, without loss of generality, let ${\beta }_{j,k}^{\ast }>{\beta }_{j,k^{\prime }}^{\ast }$, the probability of estimating a wrong ordering

$$\begin{array}{l}P\left(\mathbf{1}\{{\widehat{\beta }}_{j,k^{\prime }}\ge {\widehat{\beta }}_{j,k}\}>\epsilon \right)=P\left({\widehat{\beta }}_{j,k^{\prime }}\ge {\widehat{\beta }}_{j,k}\right)\\ =P\left({\widehat{\beta }}_{j,k^{\prime }}-{\widehat{\beta }}_{j,k}+{\beta }_{j,k}^{\ast }-{\beta }_{j,k^{\prime }}^{\ast }\ge {\beta }_{j,k}^{\ast }-{\beta }_{j,k^{\prime }}^{\ast }\right)\\ \le P\left(\mid {\widehat{\beta }}_{j,k^{\prime }}-{\beta }_{j,k^{\prime }}^{\ast }\mid +\mid {\widehat{\beta }}_{j,k}-{\beta }_{j,k}^{\ast }\mid >0\right)\\ =1-P\left({\widehat{\beta }}_{j,k^{\prime }}={\beta }_{j,k^{\prime }}^{\ast }\right)P\left({\widehat{\beta }}_{j,k}={\beta }_{j,k}^{\ast }\right)\to 0\end{array}$$

as n → ∞ since β̂_j,k′ and β̂_j,k are independent and consistent estimators. Similarly, the consistency of the estimated ordering V̂_j of the absolute values in vector ${\mathit{\beta }}_{j,•}^{\ast }$ can be derived by taking the square of the absolute values and following the same argument as for Û_j.

Proof of Theorem 3

Here we assume the same regularity condition as in Theorem 1. To complete this proof, we first define the event 𝒲 when the orderings of all p covariates are correctly assigned as

$$\mathcal{W}=\underset{j=1}{\overset{p}{\cap }}\left(\{{\widehat{\mathit{U}}}_j={\mathit{U}}_j\}\cap \{{\widehat{\mathit{V}}}_j={\mathit{V}}_j\}\right).$$

Let θ̂^Ŵ be θ̂_𝒲 when 𝒲 occurs; otherwise, denote it as θ̂_𝒲^c. Then, the estimator can be rewritten as

$${\widehat{\mathit{\theta }}}^{\widehat{\mathit{W}}}={\widehat{\mathit{\theta }}}_{\mathcal{W}}\mathbf{1}\{\mathcal{W}\}+{\widehat{\mathit{\theta }}}_{{\mathcal{W}}^c}\mathbf{1}\{{\mathcal{W}}^c\}$$

and therefore

$$\sqrt{N}\left({\widehat{\mathit{\theta }}}^{\widehat{\mathit{W}}}-{\mathit{\theta }}^{\ast }\right)=\sqrt{N}\left({\widehat{\mathit{\theta }}}_{\mathcal{W}}-{\mathit{\theta }}^{\ast }\right)\mathbf{1}\{\mathcal{W}\}+\sqrt{N}\left({\widehat{\mathit{\theta }}}_{{\mathcal{W}}^c}-{\mathit{\theta }}^{\ast }\right)\mathbf{1}\{{\mathcal{W}}^c\}.$$ (9)

By Theorem 1, we have $\sqrt{N}\left({\widehat{\mathit{\theta }}}_{\mathcal{W}}-{\mathit{\theta }}^{\ast }\right)=O(1)$ and $\sqrt{N}\left({\widehat{\mathit{\theta }}}_{{\mathcal{W}}^c}-{\mathit{\theta }}^{\ast }\right)=O(1)$ as n → ∞. By Lemma 2, we have P(𝒲) → 1 and P(𝒲^c) → 0 as n → ∞. Therefore, by Slutsky’s Theorem, (9) converge to the same distribution as $\sqrt{N}\left({\widehat{\mathit{\theta }}}_{\mathcal{W}}-{\mathit{\theta }}^{\ast }\right)$. Similarly, by results from Theorem 1 and Lemma 2, we have selection consistency

$$P({\widehat{\mathcal{A}}}^{\widehat{\mathit{W}}}=\mathcal{A})=P({\widehat{\mathcal{A}}}^{\widehat{\mathit{W}}}=\mathcal{A}\mid \mathcal{W})P(\mathcal{W})+P({\widehat{\mathcal{A}}}^{\widehat{\mathit{W}}}=\mathcal{A}\mid {\mathcal{W}}^c)P({\mathcal{W}}^c)\to 1$$

as n → ∞. This completes the proof of the Theorem 3.

Appendix B. Performance with Distorted Parameter Ordering

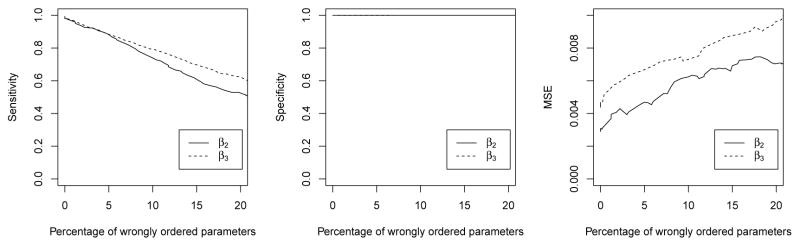
Under the same setting as simulation experiment 1 in Section 5.1 with α = 0 and s = 0, we conduct a sensitivity analysis to evaluate the performance of FLARCC when parameter ordering is incorrectly specified. Specifically, we report results of sensitivity, specificity and MSE for the linear regression model when the coefficient ordering is determined from the initial estimate with distortion through an added disturbance ε, β̂ + ε, where β̂ from (1) and ε ~ 𝒩(0, v²). As v² increases, the percent of order switching in initial estimates increases. Sensitivity, specificity and MSE in relation to the percentage of wrongly ordered parameters are displayed in Figure 4 for the two heterogeneous effects β₂ and β₃, and the homogeneous parameter β₁ is not included in the comparison because of no effect from the distortion on its performance. As the percentage of wrongly ordered parameters increases, as expected, sensitivity becomes lower and MSE becomes larger. However, specificity remains unaffected. When the distortion of ordering is mild (≤ 10%), the performance of FLARCC appears satisfactory in this simulation setting.

Figure 4.

Clustering sensitivity and mean squared error of two heterogeneous slope parameters β₂ and β₃ based on FLARCC with λ selected by EBIC, as the percent of distorted ordering increases. Results are summarized from 100 replications.