Approaches for calculating solvation free energies and enthalpies demonstrated with an update of the FreeSolv database

Abstract

Solvation free energies can now be calculated precisely from molecular simulations, providing a valuable test of the energy functions underlying these simulations. Here, we briefly review “alchemical” approaches for calculating the solvation free energies of small, neutral organic molecules from molecular simulations, and illustrate by applying them to calculate aqueous solvation free energies (hydration free energies). These approaches use a non-physical pathway to compute free energy differences from a simulation or set of simulations and appear to be a particularly robust and general-purpose approach for this task. We also present an update (version 0.5) to our FreeSolv database of experimental and calculated hydration free energies of neutral compounds and provide input files in formats for several simulation packages. This revision to FreeSolv provides calculated values generated with a single protocol and software version, rather than the heterogeneous protocols used in the prior version of the database. We also further update the database to provide calculated enthalpies and entropies of hydration and some experimental enthalpies and entropies, as well as electrostatic and nonpolar components of solvation free energies.

Graphical abstract

Introduction

Solvation free energies give the free energy change associated with the transfer of a molecule between ideal gas and solvent at a certain temperature and pressure. While solvation free energies (ΔG^solv) in general, and hydration free energies (ΔG^hyd, solvation in water) in particular might not seem to have far reaching implications, in fact, researchers in diverse areas can benefit from their prediction, because such solvation free energies are related to a broad range of physical properties such as infinite dilution activity coefficients, Henry’s law constants, solubilities, and distribution of chemical species between immiscible solvents or different phases.

Solvation free energies are differences in thermodynamic potentials which describe the relative populations of a chemical species in solution and gas phase at equilibrium.^1,2 In the thermodynamic limit in the solvated phase and the ideal gas limit in the gas phase, ΔG^solv of component i is equal to μ_i,solv − μ_i,gas, the difference in chemical potentials in the two phases. In the additional limit of one molecule of component i at infinite dilution, these become the infinite dilution excess chemical potentials in the respective solvents.

Solvation free energies not only tell us how much a molecule prefers one phase over another, but they also can provide insight into how solvent behaves in different environments. For example, water solvates molecules of opposite polarity differently, due to its inherent asymmetry,³ surfaces also have asymmetric effects on ion pairing which depend on the curvature of the surface,⁴ and molecular geometry and chemical environment affects hydrophobic solvation.⁵ Although they can be difficult to measure experimentally, ΔG^solv and ΔG^hyd can be calculated to a precision better than 0.4 kJ·mol⁻¹, even with a relatively modest investment of simulation time, for relatively diverse small neutral molecules⁶ such as those seen in the FreeSolv database of hydration free energies⁷ and in recent blind challenges such as the Statistical Assessment of the Modeling of Protein and Ligands (SAMPL) challenges. These challenges aim to improve the quality of predictive computational tools in drug design,^1,6,8–21 and have leveraged solvation free energies to help drive improvements in modeling.

Since the solvation free energy of neutral compounds is an aggregate measure of many competing interactions and entropic effects that can span many kJ/mol, comparison of computed solvation free energies to experiment has proven to be an exacting test of force field quality that has been useful in revealing deficiencies in small molecule force fields.^3,22,23 The relative ease by which solvation free energies can be calculated – as opposed to protein-ligand binding free energies, which are fraught with a variety of sampling issues – also makes them attractive for this purpose^a. For instance, SAMPL has frequently (in SAMPL1 through SAMPL4) included blind predictions of hydration free energies in particular.^1,8–14 However, to our knowledge, no laboratories are currently measuring hydration free energies, leading the field to search for other simple physical properties that can be rapidly computed – such as relative solubilities,²⁴ distribution coefficients,²⁵ and solvation free energies in organic solvents²⁶ – as a tool to assess and improve small molecule force fields. In computational chemistry, hydration free energies are of particular importance because they are frequently used in force field parameterization^26–29 and in the testing of free energy methods and force fields.^{1,8–14,30–37} Furthermore, computed free energies are in some cases found to be accurate enough to highlight problems with experiments and assist in curation of experimental data.^13,38

Solvation free energies are often calculated by alchemical free energy methods,³⁹ which simulate a series of non-physical intermediates to compute the free energy of transferring a solute from solution to gas phase (as here) or vise versa. This alchemical path provides an efficient way to move the solute from solution to the gas phase by perturbing its interactions in a non-physical way. Since free energy is path-independent, this non-physical process still yields the free energy change for transfer of the solute from solvent to gas.^39,40 The path is formed by constructing intermediate states with interactions that modulate between the end states of interest, with the variable λ parameterizing progress along the path. A particularly efficient set of intermediate states uses a two step process, first turning off the van der Waals interactions using one parameter λ_v, and another turning off the electrostatic interactions using a second λ_e. Here, we compute the free energy change to transition between each pair of λ values, and the overall free energy change is the sum of these pairwise differences.

While other approaches have been used to calculate solvation free energies,⁴¹ alchemical free energy calculations using explicit solvent have become a mainstream approach,^42,43 in part because of their formal rigor. Alternative approaches include implicit solvent models,^34–37,44 which yield ΔG^hyd but do not take into consideration solvent configuration around the solute, and Monte Carlo based approaches using the Gibbs ensemble^45–51 and expanded ensemble,⁵² though these are most commonly used for molecules that are particularly small and/or rigid.

Hydration and solvation free energies have a range of applications

The activity coefficient γ_i of a solute species i can be calculated from ΔG^solv:

$${\gamma }_i=exp\left(\frac{{\mu }_i^{\mathit{excess}}}{RT}\right)=exp\left(\frac{\mathrm{\Delta }{G}_i^{\mathit{solv}}}{RT}\right)$$ (1)

where ${\mu }_i^{\mathit{excess}}$ is the excess chemical potential of i and is equal to $\mathrm{\Delta }{G}_i^{\mathit{solv}}$ in the ideal gas limit of the vapor phase, R is the universal gas constant and T, the absolute temperature. For instance, solvation free energies are used to estimate infinite dilution activity coefficients ( ${\gamma }_i^{\infty }$) in many solvents by using a single molecule of solute i.^53–59 Experimental results obtained from gas chromatography^60,61 can be compared to ${\gamma }_i^{\infty }$ obtained from ΔG^solv to further test models and methodologies that use these free energy calculations.

Solubility prediction is another field where ΔG^solv/hyd prediction can have great value. One methodology computes the solubility free energy by computing both the sublimation free energy (from solid to gas) and hydration free energy (from gas to water).⁶² Another way to predict molecular solid solubilities depends on excess chemical potential calculations. The chemical potential, μ, of a species is calculated at different concentrations to build the concentration-dependent chemical potential curve of solutions^63–66 in order to discover phase equilibrium conditions. Free energies of solvation in pure melts and pure amorphous matter have been used to find upper bounds for solubilities given that most drug-like compounds have crystal polymorphs.^67–70 Relative solubilities of a given chemical species between different solvents can also be assessed with these calculations.^24,71 Henry’s law solubility constants^72,73 and solubilities in supercritical fluids⁷⁴ can also be predicted using solvation free energies.

The latest SAMPL challenge, SAMPL5, included blind prediction of distribution coef-ficients between cyclohexane and water for 53 solutes.^32,33,75,76 Distribution and partition coefficients are important properties for toxicology and pharmacology because they play a major part in predicting absorption and distribution of a substance in different tissues.⁷⁷ Partition coefficients – which are the distribution coefficients of the neutral form of a compound – can be estimated from the difference between solvation free energies of the neutral form of the chemical species in two different solvents,²¹ as shown in equation 2:

$${log}_{10}{P}_{A\to B}=\frac{\mathrm{\Delta }{G}^{\mathit{solv},A}-\mathrm{\Delta }{G}^{\mathit{solv},B}}{\mathit{RT}ln(10)}$$ (2)

where ΔG^solv,A and ΔG^solv,B are the solvation free energies of a molecule in solvents A and B, respectively. While in principle, the calculation could be done by transferring the solute between phases, in many software implementations it is more straightforward to simply compute the solvation free energy in each phase separately, or the free energy of removing the solute from each phase. Thus, solvation free energy calculations have found relatively widespread application in calculating partition coefficients, including in SAMPL5.^15–21 Hydration free energies themselves are valuable quantities in drug design^43,78 and can be used to understand the impact of ligand desolvation on the binding process^79,80 or can be utilized as QSAR descriptors.⁸¹

Theory and practical aspects of alchemical calculations

Solvation free energies can be calculated in various ways. In this paper we focus on alchemical free energy calculations, which have been one of the most consistently reliable methods in recent applications such as the SAMPL series of challenges.^1,8–14,25 Consider a pair of end states A and B, and their respective Hamiltonians ℋ_A(q, p; λ) and ℋ_B(q, p; λ).

$$\mathcal{H}(\mathbf{q},\mathbf{p};\lambda )=f(\lambda ){\mathcal{H}}_A(\mathbf{q},\mathbf{p};\lambda )+g(\lambda ){\mathcal{H}}_B(\mathbf{q},\mathbf{p};\lambda )$$ (3)

where f(λ) and g(λ) are functions of λ used to mix the Hamiltonians, typically set such that ℋ = ℋ_A at λ = 0 and ℋ = ℋ_B at λ = 1; q and p represent all the positions and momenta of the system. With ℋ(q, p; λ) we can calculate the free energy difference between A and B:

$$\mathrm{\Delta }G={\int }_{\lambda =0}^{\lambda =1}{\langle \frac{\partial \mathcal{H}}{\partial \lambda }\rangle }_{\lambda }\mathrm{d}\lambda$$ (4)

This method, called thermodynamic integration (TI),⁸² is implemented in practice via a numerical quadrature approach after simulations are done at a discrete set of λ values. It performs similarly to more efficient methods when the integrand is smooth.^83–85 However, it can break down when the integrand is not smooth, and it can be difficult to capture numerical integration errors in resulting uncertainty estimates.

Exponential averaging (EXP), also known as Free Energy Perturbation (FEP), was introduced by Zwanzig.⁸⁶ In this method, the free energy difference between two states A and B is given by:

$$\mathrm{\Delta }G=-\frac{1}{\beta }ln{\langle {\mathrm{e}}^{-\beta [{\mathcal{H}}_B(\mathbf{q},\mathbf{p};\lambda )-{\mathcal{H}}_A(\mathbf{q},\mathbf{p};\lambda )]}\rangle }_A$$ (5)

where β = (k_BT)⁻¹. Although equation 5 is exact in the limit of large numbers of samples, EXP is inefficient and particularly sensitive to the tails of the relevant distributions, leading to unstable free energy estimates and other large biases when configurations sampled in one state are very unlikely to be found in the other state, and vice-versa. The probability that describes this likelihood is called the phase-space overlap between the two states. EXP convergence is far from ideal, requiring states to have sizable phase-space overlap with one another.^39,84,87 Thus, addition of intermediate states (with values of λ between 0 and 1) can improve overlap dramatically and thus the quality of the final result.⁸⁸ Another issue is an asymmetric bias depending on which direction the free energy difference extrapolation is performed,^89,90 so other analysis methods are now preferred.³⁹ In the limit of adequate sampling, EXP converges to the same free energy value in both directions, but there are other ways to calculate free energies more efficiently.

An alternate method, the Bennett’s acceptance ratio (BAR), uses the information from both directions to derive the following relationship (which can and has been written in numerous ways):

$${\langle \frac{1}{1+\frac{N_A}{N_B}{e}^{\beta \mathrm{\Delta }{\mathcal{H}}_{BA}(\mathbf{q},\mathbf{p})-\beta \mathrm{\Delta }G}}\rangle }_A={\langle \frac{1}{1+\frac{N_B}{N_A}{e}^{\beta \mathrm{\Delta }{\mathcal{H}}_{AB}(\mathbf{q},\mathbf{p})+\beta \mathrm{\Delta }G}}\rangle }_B$$ (6)

where N_A and N_B are the number of statistically independent samples gathered from states A and B, and Δℋ_BA(q, p) = ℋ_B(q, p) − ℋ_A(q, p) = − Δℋ_AB(q, p) are the Hamiltonian differences between the states at a given point in phase space.

This expression minimizes the free energy variance⁹¹ and makes BAR much more ef-ficient than EXP.^89,90 The Multistate Bennett acceptance ratio (MBAR) is an extension of BAR that considers the overlap between a given state and all the others in the path between the end states.⁹² BAR and MBAR perform similarly when the spacing between intermediate states is moderate⁸⁵ and therefore only neighboring states have phase-space overlap. Weighted histogram analysis method (WHAM)^93,94 is essentially an approximation to MBAR, and thus also gives very similar results when carefully done with appropriately small bins. MBAR performs consistently well, and indeed is perhaps the most consistently well-performing free energy estimator, ⁸⁵ thus we recommend it as the analysis method of choice whenever possible. TI usually is more sensitive to the choice and number of intermediate states than BAR,⁹⁵ but it can perform as well as BAR and MBAR if the integrand is smooth.^83,84 EXP should generally be avoided due to its asymmetric bias and sensitivity to the tails of the distribution.⁸⁹

Choice of alchemical pathway

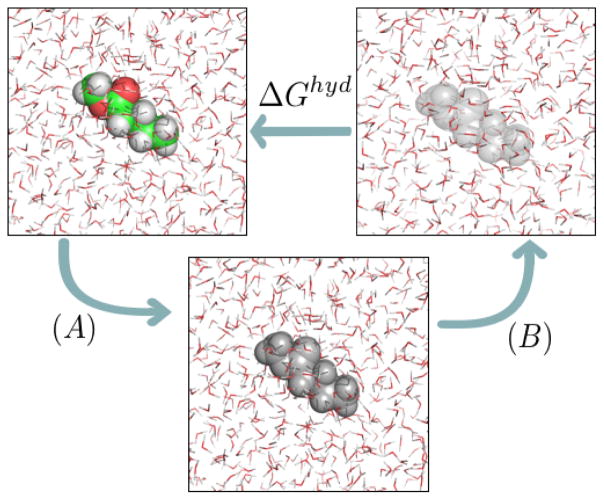
Alchemical free energy calculations were given this name because the pathway involves unphysical changes to the atomic identities, such as to the interactions between components.^43,96,97 Solvation free energy calculations can use several different approaches to modulating interactions. One approach, called decoupling, modulates only the interactions between the solute and its surroundings, retaining internal interactions (the approach we use here). An alternative approach, called annihilation, removes internal non-bonded interactions within the solute as well as those with the surroundings. Mixtures of the two approaches are also possible, such as annihilating internal electrostatic interactions while decoupling non-polar interactions. Here, three main thermodynamic states are considered: a single, non-interacting molecule of the solute in a box of solvent; the solute molecule that interacts with its surroundings through nonpolar (dispersion and repulsion) forces; and a fully interacting system, in which solvent molecules interact with the solute molecule through both electrostatic and nonpolar (dispersion and exclusion) forces. Simulations are then conducted over a series of intermediates connecting these states: going through a phase which changes electrostatic interactions only, and another phase which modifies van der Waals interactions only (figure 1). Each of these intermediates has high configuration space overlap with at least neighboring states, allowing precise calculation of free energy differences.^98–101

Figure 1.

Thermodynamic cycle used to calculate hydration free energies (or, more generally, solvation free energies). In (A), we have states in which charge-charge interactions between the solute and its environment are progressively turned off. In (B) dispersion interactions between solute and water are progressively turned off. Colored atoms (green for carbon, red for oxygen, white for hydrogen) have electrostatic and nonpolar interactions with the environment; gray atoms retain only nonpolar interactions; and transparent atoms have no interactions with their environment (and thus represent the solute in vacuum).

The most straightforward way to switch between states is the linear pathway

$$\mathcal{H}(\mathbf{q},\mathbf{p};\lambda )=(1-\lambda ){\mathcal{H}}_A(\mathbf{q},\mathbf{p})+\lambda {\mathcal{H}}_B(\mathbf{q},\mathbf{p})$$ (7)

but this pathway is in general problematic for solvation of all but the smallest molecules. This is because repulsive forces are often handled by a 1/r¹² term (such as in the Lennard-Jones functional form) which leads to non-integrable singularities in 〈∂H/∂λ〉 at terminal λ values due to sudden changes in the potential at small r. This is a not a problem which is specific to TI; rather, this issue can still result in numerical instabilities or large errors in calculated free energies even with other analysis approaches.^43,102,103 Thus, more complicated λ pathways are required, such as soft-core potentials, which should in general be used to avoid such numerical problems.^98,102,103 A common soft-core form for Lennard-Jones potential between two particles i and j is:

$$U_{ij}^{LJ}(r_{ij},\lambda )={\lambda }^{n}4{\epsilon }_{ij}\left(\frac{1}{{[\alpha {(1-\lambda )}^m+{(r_{ij}/{\sigma }_{ij})}^6]}^2}-\frac{1}{\alpha {(1-\lambda )}^m+{(r_{ij}/{\sigma }_{ij})}^6}\right)$$ (8)

where ε_ij and σ_ij are the Lennard-Jones well-depth and lengthscale parameters, respectively, and α is a positive constant which should typically be set to 0.5.^103,104 The exponents m and n are most efficient at n = 1 and m = 1, but other values have been used too.^{100,103–105} Improvements have been achieved by new soft-core functions that ease the problem with additional minima within the formulation of the original soft-core potential,¹⁰⁶ and alternate potentials that construct near optimal paths for alchemical simulations.¹⁰⁷ Linear basis functions can be used as an alternative to soft-core potentials that approaches the minimum variance possible over all pair potentials;^101,108 these can also enhance the efficiency of alchemical calculations.

The use of soft-core potentials promotes better convergence in many circumstances, and provides much lower variance free energy estimates given a fixed amount of simulation time,^{98,100,102,104,107} thus their use is highly recommended for successful free energy calculations. Without soft-core potentials, convergence is much more difficult or nearly impossible to achieve in many types of solvation free energy calculations.

Considerations for successful alchemical calculations

The accuracy of these calculations is affected by at least three factors:^109,110 Is our sampling representative and adequate? Is the free energy estimator good enough? Is the force field adequate for the system? Are there critical chemical effects omitted from the simulation, such as protonation state or tautomer effects? For solvation free energies of small molecules in solvents with relatively fast dynamics, such as water, sampling is typically adequate with a few nanoseconds of dynamics per λ window (at least for relatively rigid solutes), and the free energy estimators above are robust when applied carefully.

However, when designing new studies, it is still important to choose robustly performing estimators and ensure adequate sampling. As discussed above, we recommend MBAR as the best and most reliable general-purpose estimator.⁸⁵ Sampling remains a critical issue,^109,111 both as the solute size and flexibility grows and as solvent dynamics or environment become heterogeneous, for example, for solvation free energies in octanol which can form local clusters of hydrophilic and hydrophobic sites,²¹ or in mixed solvents.²⁵

We updated FreeSolv, the free community solvation free energy database

About FreeSolv

FreeSolv⁷ is a hydration free energy database for neutral^b compounds that contains experimental and calculated hydration free energy values, SMILES strings, PubChem compound IDs, IUPAC names, and now (as of version 0.5, presented in this work) calculated enthalpies and entropies of hydration of 643 small organic molecules. The molecular weights for compounds in FreeSolv range from 16.06 Daltons (methane) to 498.88 Daltons (decachloro-biphenyl). The number of rotatable bonds runs as high as 12, but most compounds are largely rigid. Since experimental and calculated hydration free energies, ΔG^hyd, can be computed quite precisely for quantitative comparison, FreeSolv can provide information for force field development,^26–29 and can assist the testing of new solvation free energy methods.^112,113 One example of the use of hydration free energies as target physical properties to fit in force field development is the Automated Force Field Topology Builder and Repository (ATB).^114–116 ATB is an online platform based in large part on FreeSolv and provides similar information, though with force field parameters of the GROMOS family. However, the database is not available in an easily downloadable public format and is only accessible via web queries. ATB partly relies on data taken from previous works from Mobley and collaborators,¹¹⁷ which are included in FreeSolv.⁷

While calculated hydration free energies for all compounds have been available in FreeSolv since the database was constructed,⁷ previous values had been calculated with somewhat heterogeneous protocols in a variety of different studies spread over roughly 10 years.^{2,6,11,13,23,42,117,118} In this work, we have updated FreeSolv by repeating all of the calculations using a single protocol, now also computing enthalpies and entropies of hydration.

Method details

We obtained FreeSolv’s calculated hydration free energies using alchemical free energy calculations, connecting the end states (corresponding to the solute in vacuum and in solution) via a λ path with 20 intermediate states (full details in SI). The first five states corresponded to changes in electrostatic interactions, while the last 15 modified the Lennard-Jones terms in the potential. This separation allows electrostatic interactions to be changed linearly, and soft-core potentials to be used only when changing non-polar interactions.¹⁰¹ Box size does not affect the result of solvation free energy calculations as long as good practices, which recommend that box edges be at least twice the Lennard-Jones cutoff distance, are followed.¹¹⁹ We ran 5 nanoseconds of Langevin dynamics per state with 2 femtosecond time steps in GROMACS 4.6.7^120–125 at 298.15K. Van der Waals interactions were neglected beyond a smoothly switched cutoff of 1.2 nm. Different cut-off radii are commonly used, but one should be aware the choice of cut-off can affect calculated solvation free energies. However, long range dispersion corrections can be employed (as here) to remove the cutoff-dependence of calculated free energies.¹²⁶ (However, it is worth noting that in the case of heterogeneous systems, such as for binding free energy calculations, it may be necessary to use reweighting techniques instead).¹²⁶ Our choice of soft-core is the so called 1-1-6 (m and n equal to 1 in equation 8) which leads to statistical uncertainties approximately of the same size as uncertainties from simulations using optimized path soft-cores.¹⁰⁴ Pressure was maintained at 1 atm by the Parrinello-Rahman barostat.¹²⁷ Enthalpy and entropy decomposition required 60 nanosecond Langevin dynamics simulations, with two femtosecond timesteps at 298.15 K and 1 atm in water and in vacuo for each molecule in the database. These long simulations were necessary to reduce error bars on the computed enthalpies to levels around 2.9 kJ · mol⁻¹, roughly the level of typical thermal energy (1 k_BT) as done in, for example, host-guest binding calculations.¹²⁸ We used the default Langevin dynamics’ friction coefficients implemented in GROMACS (see SI). The size of friction coefficient only affects equilibration and correlation times, but should not affect the calculated hydration free energies and enthalpies. In order to obtain consistent results, we used simulation boxes with 1, 309 water molecules and one solute molecule. The same system parameters and water model were used as in the free energy calculations. Full details can be found in the supporting materials.

Input files for version 0.5 of FreeSolv were constructed from scratch from the isomeric SMILES strings for the compounds which are deposited in the database. From these SMILES strings, we used the OpenEye Python toolkits^129–131 to generate molecular structures and assign AM1-BCC partial charges,^132,133 then charged mol2 files were written out. The AMBER Antechamber package (as distributed with AMBER14) was then used to to assign parameters from the GAFF²⁰ small molecule force field (version 1.7), and these were then converted to GROMACS format and solvated with the TIP3P water model.¹³⁴ The script which performs the setup and re-generates all input and molecular structure files in the database is available in the scripts directory of FreeSolv and provides full details. Following the calculations, MBAR hydration free energies were obtained using alchemical-analysis.py (github.com/mobleylab/alchemical-analysis).⁹⁷ Here we also introduce FreeSolv v0.51, which extends v0.5 by making the small molecule parameter sets available additionally in CHARMM, DESMOND, and LAMMPS formats. Additional details can be found in the supporting material and in the FreeSolv README files.

FreeSolv hydration free energy results

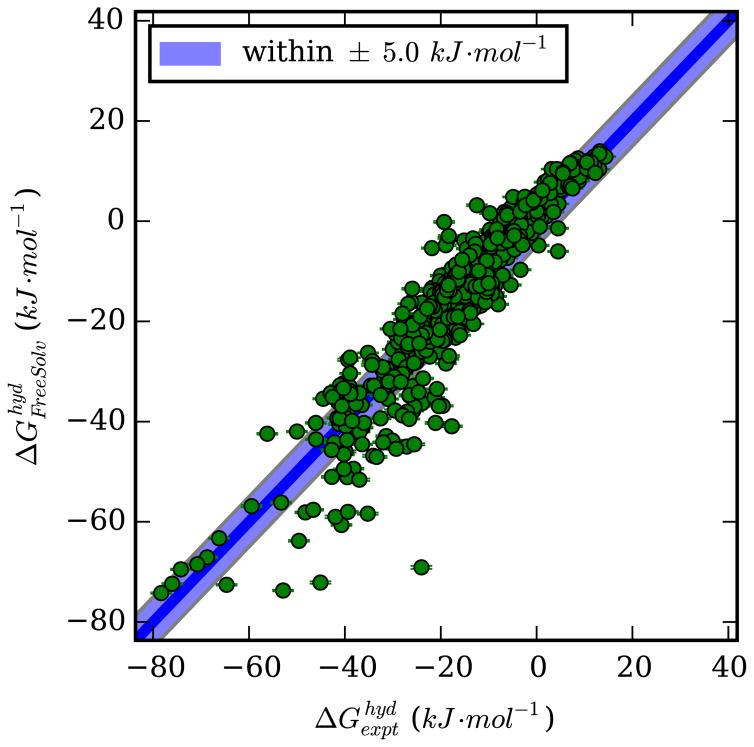
Computed hydration free energies are compared with experiment in figure 2.

Figure 2.

Calculated versus experimental hydration free energies for the compounds in Free-Solv version 0.5. Calculated values are on the vertical axis and experimental on the horizontal.

In the calculations described in this study, we found an average error of 1.3±0.3 kJ·mol⁻¹, RMS error of 6.4 ± 0.3 kJ·mol⁻¹, average absolute error of 4.7 ± 0.2 kJ·mol⁻¹, Kendall τ of 0.80±0.01, and Pearson R of 0.933±0.008, comparable to those in the original FreeSolv set,⁷ though some individual compounds have reasonably significant discrepancies (see SI). This level of accuracy is consistent with what is often seen from classical fixed-charge force fields, which typically yield RMS errors around 4–8 kJ/mol in computed hydration free energies.⁴³ We have previously used this data to address force field issues on hydroxyl groups,²⁸ and also to highlight functional groups in the set which pose particular challenges.⁴² Full details about which compounds have systematic errors, along with the functional groups represented in each compound, are present in the FreeSolv database itself.

In addition to experimental and calculated values, FreeSolv now includes the free energy of decoupling the solute-solvent electrostatic interactions (ΔG^q) and the free energy of decoupling the nonpolar interactions in water (ΔG^vdW) (available at github.com/mobleylab/FreeSolv). These quantities have been used for various purposes, including to assist in the study, development, and testing of implicit solvent models.^135,136 However, it is important to remember that these components come from our particular decomposition of the free energy,^137–140 and are not state functions; other decompositions are possible, so considerable care needs to be taken in interpreting these components. For example, annihilation rather than decoupling of Coulomb interactions would result in somewhat different decompositions due to electrostatics-induced conformational differences while van der Waals interactions are being decoupled.

Hydration enthalpy calculations

In addition to hydration free energies, we have also computed enthalpies (ΔH^hyd) and entropies of hydration (ΔS^hyd), and have added these to the database. Enthalpies of transfer, due to their larger dynamic range and lack of compensating entropic effects, are generally more sensitive to force field parameters than free energies,^128,141,142 and thus can be sensitive probes of force field accuracy, providing an additional point of comparison to experiments. While only a few hydration enthalpies are available experimentally, there are a sufficient number to note that significant discrepancies between experiment and computed values exist for some compounds (Figure S2 and Table S1). We find that compounds which have accurate hydration free energies do not necessarily have accurate hydration enthalpies and vise versa; for example, the calculated hydration free energy of benzene is within error of the experimental value, but the enthalpy is off by approximately 12 kJ/mol. In contrast, the hydration free energy of cyclohexanol is off by more than 5 kJ/mol but the enthalpy is within error of the experimental value. Thus, clearly these quantities yield different information.

To compute hydration enthalpies, we used a difference in potential energies between a water box solvating the compound and a neat water box with the compound removed to vacuum:

$$\mathrm{\Delta }{H}^{\mathit{hyd}}=\langle U_{\mathit{solution}}\rangle -(\langle U_{\mathit{water}}\rangle +\langle U_{\mathit{vacuo}}\rangle )$$ (9)

Here, 〈U_solution〉 is the internal energy of the solution (containing the solute); 〈U_water〉 is the internal energy of a box of the same number of water molecules (under the same conditions) without the solute; and 〈U_vacuo〉 is the internal energy of the solute molecule alone in vacuum. We have neglected the pressure-volume contribution to the enthalpies, PΔV, since for solutes of this size, the contribution is much smaller than our typical uncertainties of ≈ 2.9 kJ · mol^−1;141 at larger pressures or for larger solutes than in this set, this term could become significant. Notably, this scheme also omits other contributions that may be relevant in making direct comparison with experimental enthalpies of hydration, including contributions from the cost of polarizing the molecule from vacuum to solvated phase charges (relevant to fixed-charge force fields), corrections to the vibrational modes due to the quantum chemical nature of real solutes, nonideality of the gas phase, and the fact that the simulation of the liquid is carried out at atmospheric pressure rather than at the vapor pressure of the gas phase; for a review of these contributions, see.¹⁴³ We note that other groups have also omitted these contributions, which still await a thorough assessment of relative magnitude for small molecule hydration enthalpies.¹⁴¹

Hydration entropies are calculated via the equation:

$$\mathrm{\Delta }S=\frac{\mathrm{\Delta }H-\mathrm{\Delta }G}{T}$$ (10)

with ΔG and ΔH calculated as described previously. Calculated hydration enthalpies exhibit some correlation with calculated hydration free energies, but the correlation is not perfect, indicating that enthalpies can indeed provide additional constraints on the force field.¹²⁸ The Kendall τ and the Pearson R between the calculated ΔH^hyd and ΔG^hyd respectively were 0.76 ± 0.02 and 0.943 ± 0.005 (see supplementary information).

Our conclusion that enthalpies can provide an additional constraint on the force field is further supported by comparison to experimental data. Specifically, 11 experimental hydration enthalpies and entropies from ORCHYD, a database of experimental hydration properties,¹⁴⁴ were added to FreeSolv. Calculated and experimental enthalpies have a Kendall τ of 0.77±0.05, and a Pearson R of 0.87±0.03 (see SI). These values indicate that the computed hydration free energies are relatively predictive of experimental values, though there is also clear room for improvement. Calculated hydration enthalpies and their experimental counterparts show significant differences that are not observed in the plot of experimental versus calculated free energies of the same 11 compounds, suggesting (as in previous studies¹⁴¹) that enthalpies provide additional information on the thermodynamics and constraints on the force field (though as noted above, additional enthalpy corrections may be needed¹⁴³). While ΔH^hyd and ΔS^hyd can act as additional constraints for force field parameters, one of them can always be calculated from the other and the corresponding ΔG^hyd, meaning that it is not worthwhile to use all three values as constraints simultaneously. That is, ΔH^hyd and ΔS^hyd are always highly anti-correlated because of how they are calculated. More details can be found in the supporting information.

Components of hydration enthalpies

We also partitioned the hydration enthalpy, ΔH, into two components: a solvent interaction term and a conformational change term, $\mathrm{\Delta }{H}_{\mathit{int}}^{\mathit{hyd}}$ and $\mathrm{\Delta }{H}_{\mathit{conf}}^{\mathit{hyd}}$, respectively, in order to understand how much the solvation enthalpy is influenced by the solute conformation, and how much solute conformation is modulated by solvation. We obtained the solvent interaction component by taking the average energy of the solute in water and subtracting off the solute internal energy and the energy of a corresponding box of pure water, leaving only the enthalpy change due to changing solute-solvent interactions and solvent reorganization:

$$\mathrm{\Delta }{H}_{\mathit{int}}^{\mathit{hyd}}={\langle U_{\mathit{solv}}\rangle }_s-{\langle U_{\mathit{vac}}\rangle }_s-{\langle U_{\mathit{water}}\rangle }_w$$ (11)

where 〈U_solv〉_s is the average potential energy over the original solvated trajectory, 〈U_vac〉_s is the average potential energy of the solute molecule in the solvated trajectory after removing its water molecules, and 〈U_water〉_w is the average potential of a box of pure water containing the same number of water molecules under the same conditions. $\mathrm{\Delta }{H}_{\mathit{int}}^{\mathit{hyd}}$ thus corresponds to the change in solvation enthalpy due to transferring a solute molecule from vacuum to water with a fixed set of configurations (as given by the solvated trajectory) – i.e., it treats the solute as if there is no conformational change going from gas to water, so it includes only changes in solvent structure and solute-solvent interactions.

The conformational change component of the enthalpy is obtained by taking the change in solute internal energy on going from gas to water, which we can evaluate as follows:

$$\mathrm{\Delta }{H}_{\mathit{conf}}^{\mathit{hyd}}={\langle U_{\mathit{vac}}\rangle }_s-{\langle U_{\mathit{vac}}\rangle }_v$$ (12)

where 〈U_vac〉_v is the potential energy of the solute molecule in vacuum evaluated from the trajectory run in vacuum, and 〈U_vac〉_s is the potential energy of the solute molecule in vacuum evaluated from the trajectory run in solvent (after stripping the solvent molecules). $\mathrm{\Delta }{H}_{\mathit{conf}}^{\mathit{hyd}}$ thus gives the enthalpy change due to solute conformational changes on solvation; these occur because interactions with water can stabilize configurations that are not common in vacuum. If a compound’s distribution of configurations is unchanged on transfer to solvent, $\mathrm{\Delta }{H}_{\mathit{conf}}^{\mathit{hyd}}$ will be zero. It can trivially be verified that these components still sum to the total enthalpy change:

$$\mathrm{\Delta }{H}^{\mathit{hyd}}=\mathrm{\Delta }{H}_{\mathit{solv}}^{\mathit{hyd}}+\mathrm{\Delta }{H}_{\mathit{conf}}^{\mathit{hyd}}$$ (13)

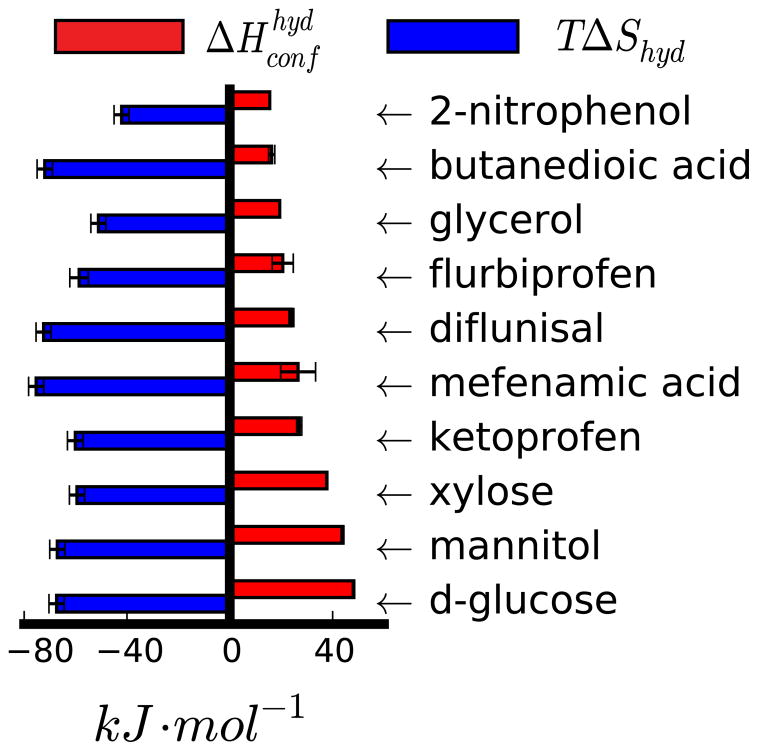
These components, while certainly not a unique decomposition of the total enthalpy, do provide a way to intuitively understand one important set of contributions to the enthalpy of hydration in a way which provides some insight into changes undergone by the solute and environment. For example, solutes which undergo significant conformational changes on solvation may tend to have a large change in the conformational component of the hydration enthalpy (fig. 3). This happens because solutes that make hydrogen bonds with water or have strong internal electrostatic interactions in the gas phase can assume conformations that were energetically unfavorable in vacuo when solvated.

Figure 3.

Conformational enthalpies and associated entropies of compounds with highest $\mathrm{\Delta }{H}_{\mathit{conf}}^{\mathit{hyd}}$. Error bars represent the standard error.

Conclusions

Solvation free energies have been the subject of considerable scientific interest for many years because they are related to a large number of physical properties. Here, we have provided a short review of alchemical methods for computing solvation free energies of small organic molecules, and discussed their application to hydration free energies. Solvation free energies for such molecules can be calculated precisely and effectively using alchemical free energy calculations, as described here. In our experience, BAR and MBAR require less tuning to work well, while TI requires special care to get the gradients right in rapidly varying regions and introduces unknown integration error, thus we recommend MBAR as our preferred general-purpose method, even though TI can in principle also work well. EXP should be avoided, in general, in partly because of the large bias introduced.

We also introduced an update to FreeSolv⁷ (v0.5), a database of calculated and experimental hydration free energies, enthalpies and entropies. The database was designed to be easily incorporated into automated workflows: we provide IUPAC names, PubChem compound IDs and SMILES strings, as well as topology and coordinate files, but additional data is welcome. Additionally, we provide calculated and experimental free energy values that can be used to assist method and force field development. Unfortunately, experimental hydration enthalpies and entropies are not available for every compound.

Calculated free energies show reasonable agreement with experimental values (fig. 2) with an RMS error around 6 kJ· mol⁻¹ and an average error close to 1 kJ· mol⁻¹. With the aid of ORCHYD,¹⁴⁴ we were able to extend FreeSolv to contain experimental hydration enthalpies for a few (11) compounds for the first time. We observe significant errors for hydration enthalpies that are much larger than those for hydration free energies, so further investigation will be needed. This result also suggests that enthalpies can be used as additional constraints in force field development.

Our intention is that FreeSolv serve as an updateable, extensible community resource. While it already covers a large number of molecules, we would be delighted to include input files and calculated values from other force fields and/or methods so it can further serve as a benchmark of methods, simulation packages, and so on. Additionally, while hydration free energy data is not abundant, certainly at least some data is available that is not presently included in FreeSolv, so community contributions of experimental data with references will be appreciated. Additional curation of the experimental data already present is likely needed –for example, much of the experimental data still needs to be tracked back to its original source material rather than literature compilations of data which are currently cited. FreeSolv is available on GitHub at http://github.com/mobleylab/FreeSolv and contributions are welcomed there.

We believe that this update of FreeSolv will assist future efforts in force field development and development and testing of new methods. We also hope that FreeSolv’s new features help serve the scientific community, and provide a valuable resource the community will help extend.