Measuring vocal motor skill with a virtual voice-controlled slingshot

Abstract

Successful voice training (e.g., singing lessons) and vocal rehabilitation (e.g., therapy for a voice disorder) involve learning complex, vocal behaviors. However, there are no metrics describing how humans learn new vocal skills or predicting how long the improved behavior will persist post-therapy. To develop measures capable of describing and predicting vocal motor learning, a theory-based paradigm from limb motor control inspired the development of a virtual task where subjects throw projectiles at a target via modifications in vocal pitch and loudness. Ten subjects with healthy voices practiced this complex vocal task for five days. The many-to-one mapping between the execution variables pitch and loudness and resulting target error was evaluated using an analysis that quantified distributional properties of variability: Tolerance, noise, covariation costs (TNC costs). Lag-1 autocorrelation (AC1) and detrended-fluctuation-analysis scaling index (SCI) analyzed temporal aspects of variability. Vocal data replicated limb-based findings: TNC costs were positively correlated with error; AC1 and SCI were modulated in relation to the task's solution manifold. The data suggests that vocal and limb motor learning are similar in how the learner navigates the solution space. Future work calls for investigating the game's potential to improve voice disorder diagnosis and treatment.

I. INTRODUCTION

Successful voice therapy depends upon patients with voice disorders learning or re-learning vocal motor behaviors—e.g., vocal loudness (Ramig et al., 1995; Schalling et al., 2013; Van Stan et al., 2017), vocal efficiency (Titze, 1992; Titze, 2006), vocal endurance (Buekers, 1998; Schneider and Bigenzahn, 2005; Schneider et al., 2006; Stemple et al., 1994), and voice quality (Kempster et al., 2009; Kreiman et al., 1993; Verdolini-Marston et al., 1995)—to reduce voice-related impairments in daily life (Hogikyan and Sethuraman, 1999; Jacobson et al., 1997). Therefore, “learning” new motor patterns—defined as a relatively permanent change in motor behavior (Schmidt and Lee, 2011)—is a critical part of the voice therapy process. In the same way, singing lessons depend upon vocalists establishing new complex behaviors such as improved voice quality on high notes or improved transitions across register changes (e.g., chest voice into head voice). However, little is known regarding how humans learn new vocal motor skills as research into properties of the cortico-bulbar sensorimotor system typically use well-learned (i.e., habituated) vocal behaviors—e.g., sustained vowels or glissandos (Burnett et al., 1998; Larson et al., 2000; Zarate et al., 2010) and syllables or speech (Chen et al., 2007; Guenther et al., 2006; Tourville et al., 2008; Xu et al., 2004). Also, clinical voice treatment designs focus on average differences between isolated time points—e.g., before versus after surgery/voice therapy (Holmberg et al., 2003; Ramig and Verdolini, 1998; Roy et al., 2003; Roy et al., 2002)—which do not take into account how behavior change occurred. While these clinical investigations improve the field's diagnostic capabilities and provide empirical support for the effectiveness of voice treatments, they rarely offer theoretical insights into how patients learn improved behaviors or how long the measured improvements will last after discontinuing therapy—i.e., carryover or retention. However, there is a growing number of studies in the voice field that apply motor learning principles in the hopes of maximizing carryover or retention through fine-tuning practice and feedback variables (Schalling et al., 2013; Steinhauer and Grayhack, 2000; Van Stan et al., 2015; Wong et al., 2011). These approaches typically measure a patient's overall performance (e.g., accuracy or error), and not how the vocal motor system improved performance (e.g., how did the subject modify various aspects of phonation to minimize error?). Additionally, motor learning studies have asked subjects to pay attention solely to the results of performance (external focus) or the execution of performance (internal focus) (Wulf et al., 1998); these studies neglect to quantify the relationship between how changes in execution are related to improvements in skill. If a method was developed that could examine how humans learn new vocal motor skills, this could produce clinically important measures capable of estimating or predicting a patient's likelihood of improvement, long-term retention, or disorder recurrence after discharge from therapy. However, it is important to note that retention of newly learned motor skills is reliant upon many variables in addition to motor performance (e.g., attention, motivation, cognition, medical history, and baseline skill level) (Marinelli et al., 2017; Studenka et al., 2017).

Theories from the field of motor control and learning frequently attempt to quantify how the central nervous system (CNS) controls and learns new movements. Therefore, these theories may guide the development of assessment approaches that can describe how a patient improved his/her vocal motor behavior and estimate the new behavior's degree of permanence. For example, a model of redundant motor tasks—tasks with infinitely many ways to achieve success—has potential to offer insights into how people establish new movements (Cusumano and Cesari, 2006; Kudo et al., 2000; Martin et al., 2001; Müller and Sternad, 2003; Müller and Sternad, 2009; Scholz et al., 2000). Redundant motor tasks can be described by how execution variables relate to result variables: if there are more execution variables that map into fewer result variables, the task has redundancy. Such redundancy produces an infinite number of combinations of execution variables that can achieve a desired result. It is important to note that redundancy in motor performance can arise from two sources: (1) that of motor equivalence, where multiple bodily configurations map onto a singular outcome, i.e., finger position in space (Kelso et al., 1998) and (2) that of task equivalence, where multiple task-specific variables map onto a singular result in task performance, i.e., getting a perfect score in darts, where the bull's eye is an area and the dart can hit it with many different orientations (Müller and Sternad, 2003). Therefore, the term “execution variable” can refer to many types of variables, from biomechanical (joint angle positions, velocities, etc.) to physics-based (release velocity, release angle, etc.). The most frequently cited example of redundant motor performance is Nicolai Bernstein's observation that even expert blacksmiths exhibited slightly different arm kinematics (multiple execution variables represented by joint angles) during each swing of the hammer, yet consistently hit their desired end point on the anvil (singular result) (Bernstein, 1967). This example of motor equivalence also has task equivalence, since the anvil is not a single point and can be hit with many different orientations. In order to systematically study such motor tasks, virtual environments have been developed where the physics of the task is mathematically modeled so that multiple execution variables fully determine the result or error (John and Cusumano, 2007; Müller and Sternad, 2004). For example, in a virtual throwing task, the result (minimum ball distance from a target) can be fully determined by the user's angle and velocity when releasing the ball (Müller and Sternad, 2009). Therefore, the relationship between execution variables and the result creates a mathematical null space or solution manifold—defining those executions that all lead to the desired result. Using this approach, investigators can quantify how subjects learn new motor skills by relating practice-based performance improvements (reduction in error) to changes in variability of the execution variables.

All vocal behaviors targeted in voice therapy are redundant by nature. In other words, patients must learn how to co-vary multiple execution aspects of phonation on one level—e.g., variables such as pitch, loudness, or vocal fold ab/adduction—to achieve a desired result defined at another level—e.g., improved messa di voce (increasing and subsequently decreasing loudness whilst maintaining the same pitch), vocal efficiency (decreased input for the same or more output) (Titze, 1992), modification of resonance or timbre. However, current approaches to developing virtual environments for voice-related actions have been confined to one descriptive level. For example, the software program visi-pitch (KayPENTAX, Montvale, NJ) allows users to manipulate objects by modifying either pitch, loudness, or both simultaneously; i.e., changes in pitch and/or loudness are results totally determined by themselves. Another example is the prosodic marionette (Patel et al., 2012), which displays multiple voiced features in real-time (e.g., loudness, pitch, word duration) to improve prosody, but the mathematical relationship between all features and overall prosody is not quantified. In general, most quantitative voice therapy tools (i.e., biofeedback tools) have simply displayed a number representing the desired target behavior (e.g., jitter, shimmer, cepstral peak prominence, electromyography) and asked a patient to modify this number as directed (e.g., increase, decrease, or stay in a desired range) (Ferrand, 1995; Ma et al., 2013; van Leer et al., 2016; Wong et al., 2011). Therefore, the resulting data provide minimal insight into how vocal performance is achieved and what accounts for any improvements.

An area of extensive research in motor control is dedicated to characterizing the structure of the ever-present variability in movements—“structure” refers to the distributional (e.g., Gaussian, anisotropy) or temporal (e.g., Brownian motion, pink noise) characteristics of variability. The human sensorimotor system exhibits variability—sometimes referred to as noise—at multiple time scales, at all levels of function (e.g., the cellular physiology of neuronal activation or the accuracy of throwing a ball) and at all levels of skill (e.g., even expert performance produces trial-to-trial fluctuations) (Ajemian et al., 2013; Faisal et al., 2008; Sternad et al., 2014). Therefore, it is believed that investigations into distributional and temporal variability of motor performance will provide unique insights into a subject's sensorimotor function, as well as how the sensorimotor system establishes new skills. More specifically, variability of measured execution and result variables are hypothesized to shed light on control strategies of the CNS.

Analyses of temporal variability in execution variables during well-learned movements—e.g., walking (Dingwell et al., 2010) or grasping (Rácz and Valero-Cuevas, 2013)—have revealed selective control by the CNS in error-relevant or error-irrelevant directions on the task's solution manifold. Furthermore, when applying this approach to learning novel movements—e.g., throwing tasks (Abe and Sternad, 2013), two-arm pointing (Domkin et al., 2005), or posture/balance (Asaka et al., 2008)—temporal variability amongst execution variables in the early stages of practice appears to have minimal directional preference. However, later in practice, the CNS starts to selectively channel temporal variability/noise into error-irrelevant directions (parallel to the solution manifold, where variability does not affect error) and variability in error-relevant directions (orthogonal to the solution manifold where variability can obviously affect error) is lowered.

Studying the structure of vocal motor variability has the potential to provide new diagnostic and therapeutic insights in the field of voice disorders. Vocal biomarkers derived from variability analyses are hypothesized to detect degradation in the complexity or quality of an individual's motor coordination. Many areas outside the field of voice disorders have attained useful biomarkers of neurological and psychological dysfunction from variability-based measures in the voice signal using cross-correlation and/or detrended fluctuation analyses (Helfer et al., 2014; Horwitz et al., 2013; Williamson et al., 2014; Williamson et al., 2015). Other studies have demonstrated potential to discriminate pathological and normal voices when applying stability-based measures (closely related to variability) to sustained vowels (Herzel et al., 1994; Little et al., 2007; Zhang and Jiang, 2008; Zhang et al., 2004). However, none of these studies addressed the question of learning and therefore cannot offer insights as to how vocal skills improve with practice.

Sternad and colleagues (Cohen and Sternad, 2009) developed three costs that assess how variability amongst execution variables directly affects resulting performance. Tolerance cost (T-cost) evaluates sensitivity of the result space to the distribution of execution variables, noise cost (N-cost) evaluates cost to performance per stochastic variability, and covariation cost (C-cost) evaluates the cost to performance per suboptimal covariation between execution variables. Across a range of studies (Abe and Sternad, 2013; Chu et al., 2016; Cohen and Sternad, 2009; Müller and Sternad, 2004), the lowest to highest cost to performance has been T-cost, C-cost, and N-cost, respectively. Also, using pairwise correlations between each cost and mean error, the greatest to least contributor to reduced error has been T-cost, C-cost, and N-cost, respectively. Finally, these three costs have been shown to evolve over different time scales; i.e., T-cost reached asymptote at a significantly faster rate compared to N-cost and C-cost. In summary, it appears that subjects first improve performance exponentially through finding an error-tolerant space in the solution manifold (T-cost). Further improvement proceeds at a slower time scale by exploiting the covariation between execution variables in the result space (C-cost) and, to a lesser extent, reducing stochastic dispersion (N-cost) (Abe and Sternad, 2013; Chu et al., 2016; Cohen and Sternad, 2009; Müller and Sternad, 2004).

To the authors' knowledge, there are no studies to date that have used a vocal motor task to analyze how execution changes over time to produce practice-based improvements. Since the cortico-bulbar (head/neck control) and cortico-spinal (core and limb control) sensorimotor systems differ with regard to several anatomical/physiological factors (e.g., bilateral/unilateral cortical input, prevalence of a gamma neural system, and interconnection with respiration) (Brandon et al., 2003; Kandel et al., 2000; Simonyan and Horwitz, 2011), generalization of limb-based findings to vocal motor learning is a non-trivial endeavor and requires empirical study.

Overall, the specific purpose of the following study is to investigate how changes in execution variability relate to improvements in skilled vocal performance. This study has two aims: In aim 1, we develop a voice-controlled virtual environment mimicking the motor learning approach used with redundant limb-based movements. More specifically, a video game was developed where the user controls a virtual slingshot with two vocal execution variables (related to fundamental frequency and vocal intensity) to hit a target with a projectile. In aim 2, we assess if variability in this vocal task evolves by the same changes in distributional and temporal variability empirically demonstrated in limb-based motor learning. Aim 2 has multiple hypotheses based on replicating empirical findings from limb movements. For distributional variability, it is expected that (a) the TNC-costs will be rank-ordered with T-cost the lowest, then C-cost, and the highest values for N-cost; (b) T-cost will be the strongest contributor to reducing error, with C-cost second, and N-cost last; (c) T-cost will decrease at a faster time scale than C-cost and N-cost (i.e., T-cost will reach asymptotic performance in the shortest time). For temporal variability, it is expected that during asymptotic performance (i.e., when the vocal skill is well learned), the subjects will display directional sensitivity to the solution manifold. More specifically, autocorrelation and detrended fluctuation analysis will reveal tight control in the direction orthogonal to the solution manifold (error-relevant direction) and lack of control in the direction parallel to the solution manifold (error-irrelevant direction).

The long-term goal of this line of research is to investigate if objective measures of variability derived from a virtual environment will provide theoretical and empirical insights into vocal motor control/learning—ultimately for improved assessment/treatment of behaviorally based (e.g., muscle tension dysphonia, vocal fold nodules, polyps) or neurologically based voice disorders.

II. METHODS

A. Participants

The goal of this study was to acquire data from ten adult subjects (five male and five female) to obtain adequate power for repeated-measure group-based statistics. Fourteen subjects (nine male and five female, mean age = 25 years, range = 19–37 years) performed the experimental task after providing written informed consent in accordance with the Institutional Review Board of the Massachusetts General Hospital. Four male subjects did not complete the entire voice video game protocol due to a technical problem during practice (signal saturation, two subjects), allergies associated with vocal deterioration (one subject), and early termination due to multiple cancellations (one subject). The study enrolled only professional singers to maximize the likelihood of all subjects attaining asymptotic performance within 5 days of practice. Professional singers were considered any student enrolled in a vocal performance degree at music conservatories in the Boston area, or any person who reported their primary income was from singing. The singers reported no history of voice disorders and were judged to have normal voice quality by a speech-language pathologist with specialization in voice.

B. Experimental setup

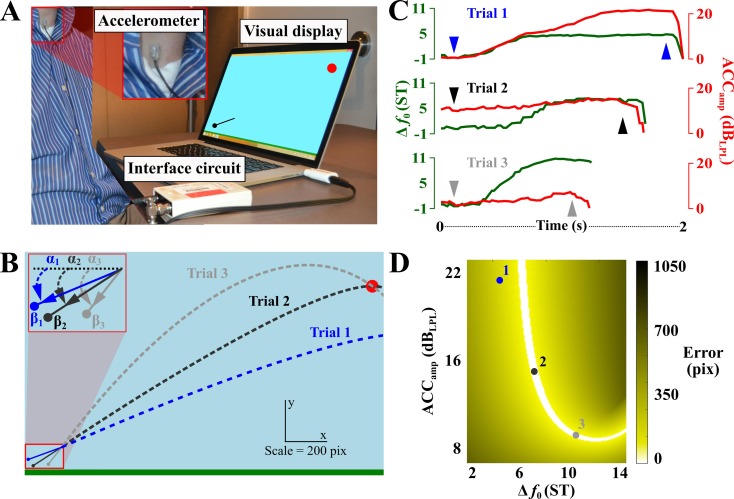
Figure 1(A) shows an illustration of the experimental set-up. Each subject's voice was recorded using a miniature accelerometer (model BU-27135; Knowles Corp., Itasca, IL) placed on the anterior neck using double-sided tape [model 2181, 3 M, Maplewood, MN, see Fig. 1(A) inset]. An interface circuit supplies power to the accelerometer and delivers the neck-skin acceleration signal to custom c# software running on a MacBook Pro (Apple, Cupertino, CA) with windows 8.1 (Microsoft, Seattle, WA). Each day, subjects were seated in front of the computer screen and the accelerometer was affixed to approximately the same spot between their thyroid cartilage and the superior aspect of the sternum. Measurements (in millimeters) were taken from anatomical landmarks (e.g., wrinkles on the neck or superior border of the sternum) to the top or bottom of the accelerometer to minimize placement variability.

FIG. 1.

(Color online) (A) The virtual vocal throwing task. Subjects threw a ball at a target using neck-skin acceleration amplitude above their lowest phonation level (ACC_amp, in dB_LPL) and changes in fundamental frequency [Δf₀, in semitones (st)]. Though the sling is pictured, it was not visible during practice. (B) Visual display showing the sling and ball trajectories for three exemplary trials. α and β represent angle (in radians) and stretch (in pixels). (C) The three plots show frame-based values of Δf₀ and ACC_amp for the three trials. Also, arrows pointing down and up show the start and release values for the slingshot, respectively. Notice that in all three throws, there are moments where one variable is stationary and another is changing. (D) The execution space indicates the amount of error in pixels (pix) for combinations of slingshot release values of Δf₀ and ACC_amp (values shown for three trials).

Since the game was played via recording neck skin acceleration, it is important to note that the amplitude of neck-skin acceleration (ACC_amp) is not exactly the same as the acoustic sound pressure level (SPL); e.g., full lip occlusion with the voiced nasal /m/ can elicit the same ACC_amp as the vowel /a/, but the SPL will be significantly different between the two degrees of mouth opening. Therefore, all subjects played the game using an /m/ to minimize perceptual discrepancies in loudness between auditory input (SPL) and measured ACC_amp. It has been established that SPL and ACC_amp demonstrate a strong, significant linear correlation within a subject when the supraglottal track is not time varying (i.e., in a static position) (Cheyne et al., 2003; Fryd et al., 2016; Švec et al., 2005). Therefore, due to the experimental constraints (closed lips and no variation in accelerometer placement each day), it is reasonable to assume that changes in ACC_amp closely represent the changes in SPL. Also, the fundamental frequency (f₀), which is obtained from the acceleration signal and used for the virtual environment, is an execution variable known to be highly correlated between neck-skin acceleration and acoustics (Coleman, 1988; Mehta et al., 2016; Sugimoto and Hiki, 1960).

The software processed the acceleration signal (recorded with a 10 kHz low-pass filter, 22 050 Hz sampling rate, and 16-bit quantization) every 30 ms to produce estimates of f₀ and ACC_amp. The software computed ACC_amp in decibels (dB) with the reference intensity at full scale of the sound card. A fast Fourier transform was used to obtain f₀ estimates from the first peak that is ≥30% of the highest peak in the spectrum. Frequency detection errors occurred in less than one percent of all trials. For each trial, a simple voice activity detection algorithm was implemented to determine when voicing began and ended, as well as to provide the exact starting/ending values of f₀ and ACC_amp.

C. Voice-controlled virtual environment

Figure 1(B) illustrates the vocal task—displayed on the laptop screen (resolution 2560 × 1440 pixels; pix)—which consists of throwing a ball using a slingshot to hit a target circle. In this two-dimensional (2D) virtual environment, the slingshot's release angle α (in radians) and stretch β (in pixels) fully determine the trajectory of the ball and whether the ball hits or misses the target. The ball follows a simple, frictionless trajectory as defined by Newton's laws of motion, where the initial ball velocities in the horizontal (v_ix) and vertical (v_iy) directions are determined by α and β, respectively, according to the following relations:

$$v_{\mathit{i}\mathit{x}}=\beta \hspace{0.17em}\text{cos}\hspace{0.17em}\alpha ,$$ (1)

$$v_{\mathit{i}\mathit{y}}=\beta \hspace{0.17em}\text{sin}\hspace{0.17em}\alpha .$$ (2)

The 2D position of the ball (x, y) is determined by the following functions of time (t), initial velocities (v_ix, v_iy), and gravity (g):

$$x\left(t\right)=v_{\mathit{i}\mathit{x}}t,$$ (3)

$$y\left(t\right)=v_{\mathit{i}\mathit{y}}t+\frac{g{t}^2}{2}.$$ (4)

Table I lists all the modifiable parameters related to the 2D virtual environment.

TABLE I.

Parameters of the virtual environment and specific values used for all subjects.

Parameter	Value used	Description
Field
Width	1600 px	Virtual environment width (horizontal dimension)
Height	900 px	Virtual environment height (vertical dimension)
Slingshot position
X	150 px	X and Y coordinates (from the left and bottom of the screen, respectively) of the center of the sling.
Y	75 px
Targeta
X	1150 px	X and Y coordinates of the center of the target circle. Ø represents the diameter of the target circle.
Y	600 px
Ø	60 px
Obstacleb
X	1000 px	X coordinate represents the location of an obstacle (i.e., a wall) from the left of the screen. Yt represents the height (i.e. the “top”) of the obstacle minus Yb (i.e., the “bottom”).
Yt	20 px
Yb	20 px
Gravity
	−0.0175 px/s2	Force of gravity on the ball

^aDuring exploratory testing, the target was placed at X = 500 px and Y = 700 px.

^bThe virtual environment can contain a wall, but this was not used for the current study.

The angle α of the slingshot is controlled via the change in f₀ (Δf₀), in semitones (ST), between the starting and ending f₀ values. The stretch β of the slingshot is controlled via ACC_amp during voicing and measured in dB above the lowest phonation level, denoted dB_LPL.

The slingshot and ball appear on the screen once the subject begins voicing. At this initial f₀, the slingshot is parallel to the ground (i.e., at 0°) and the subject must increase his/her f₀ to pull the slingshot downward, which aims the ball trajectory upward. The slingshot can also be angled upward to aim the ball trajectory downward with a decrease in f₀ from the initial f₀. A 90° range (−45° to 45°) for Δf₀ was set at 18 ST for all subjects. The range of slingshot stretch was fixed for all subjects between their lowest phonation level (0 dB_LPL) at minimal stretch and 22.5 dB_LPL at maximal stretch.

To begin a trial, the voice signal must have had six consecutive frames (180-ms of voicing) above a f₀ cut-off of 65-Hz and a subject-specific minimum ACC_amp threshold. The minimum ACC_amp threshold was based on each subject's average vocal intensity over ten trials during which s/he was asked to phonate as softly as possible without voice breaks or whispering; i.e., their lowest phonation level (dB_LPL). The ACC_amp and f₀ values contained in the sixth voiced frame were used as the start values for each trial. The ball is released once the subject stops voicing; the voiced signal needs to decrease below the ACC_amp and/or the f₀ minimum thresholds, at which time the tenth-to-last voiced frame supplies the release ACC_amp and f₀ values. Figure 1(C) shows example Δf₀ and ACC_amp trajectories of the three throws in Fig. 1(B), with downward pointing triangles indicating slingshot “start” times and upward pointing triangles indicating slingshot “release” times. A video illustrating the vocal slingshot task in action during five trials in the voice-controlled 2D virtual environment is given in Mm. 1.

Mm. 1.

Download video file ^{(1.6MB, mp4)}

DOI: 10.1121/1.5000233.1

Video showing a subject performing five test trials of the vocal slingshot task in the virtual environment. The first four throws miss the target, and the fifth throw hits the middle of the target. When the ball hits the target's center, the ball sticks until the subject begins another practice trial. Note the volume (ACC_amp) and pitch (Δf₀) bars on the top of the screen (as well as the slingshot) are not seen by the study subjects during their five days of practice in the study. This is a file of type “mpg” (1.6 MB).

To evaluate trial error, the minimum distance between the ball's trajectory and the center of the target is calculated. The target is a circle with a 60-pixel diameter; i.e., a “hit” occurs when the projectile passes within ± 30 pixels of the circle's center [Fig. 1(B)]. An explicit example of the vocal task's many-to-one mapping or redundancy can be seen in Fig. 1(B), where two exemplary trajectories (trials 2 and 3) show different strategies for hitting the target. The trajectory of trial 2 can be described as a “direct shot,” where the user released the ball at approximately a 35° angle (Δf₀ = 7.02 ST) with a relatively large slingshot stretch of 198 pixels (ACC_amp = 14.85 dB_LPL). The trajectory of trial 3 can be described as a “finesse shot,” where the user released the ball at a steeper angle of approximately 52° (Δf₀ = 10.35 ST) with a relatively small slingshot stretch of 125 pixels (ACC_amp = 9.28 dB_LPL). The trajectory of trial 1 missed the target and the user released the ball at an angle of approximately 24° (4.72 ST) with a very large slingshot stretch of 276 pixels [ACC_amp = 20.57 dB_LPL; stretch for trial 1 is not to scale in Fig. 1(B)].

Since the virtual environment allows a direct mathematical mapping between the two execution variables (Δf₀ and ACC_amp) and the resulting error, this error (minimum distance between trajectory and center of the target) can be portrayed with a color code on a 2D execution space [Fig. 1(D)]. Note that the solution manifold, the set of all zero-error solutions, is depicted by white. Despite the simplicity of the task, the solution manifold has a highly nonlinear U-shape. The task is to arrive at this manifold with minimal error. The three dots represent the user's Δf₀ and ACC_amp at ball release for the three trials shown in Figs. 1(B) and 1(C). Most importantly, dots 2 and 3 land on the white solution manifold, signifying that both trials hit the target despite being significantly different in execution space. Dot 1 lands on a non-white part of the execution space signifying non-zero error for that trial.

D. Experimental protocol

The overall design of the study called for five days of practice with the voice-controlled virtual environment. The first day began with a verbal description of how to control the virtual slingshot with user-controlled pitch and loudness. Then, the subjects completed 100 trials of exploratory testing with the virtual environment, in which they could see the slingshot moving in real time with pitch and loudness changes (see Mm. 1). Throughout the five days of subsequent practice the slingshot was made invisible so that subjects only could see the ball trajectory after release. This was done to mimic the natural conditions of vocal learning, where vision is not routinely considered part of the real-time feedback loop; feedback constituents are traditionally auditory and proprioceptive/somatosensory (Tourville and Guenther, 2011). Furthermore, three blocks of 100 practice trials were completed each day, for all five days of practice (1500 practice trials total). The target was in a different location for the exploratory testing phase from the one used in the five days of experimental practice. During exploratory testing, the target was higher to the left of the screen (closer to the slingshot) compared to the target placement used for practice [shown in Fig. 1(B)]. Subjects were permitted to have one to three days between practice sessions.

E. Analysis of distributional variability

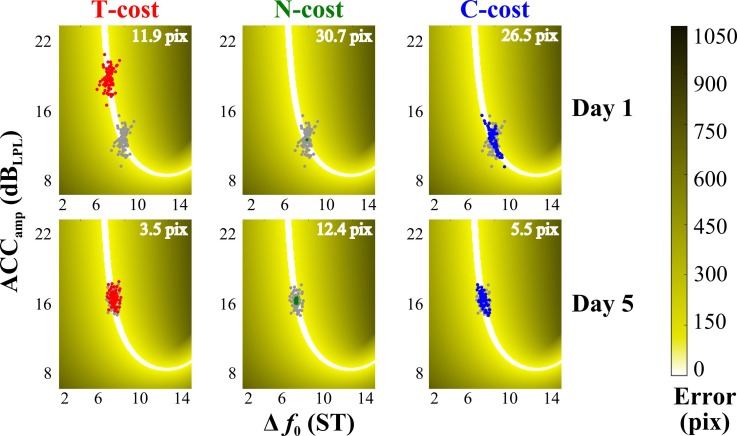
Figure 2 illustrates the tolerance, noise, and covariation cost (TNC costs) calculations for a given data set of 100 trials by one subject in the execution space (Cohen and Sternad, 2009); day 1 of practice is on the top row and day 5 of practice is on the bottom row. In each panel, the gray data points represent the veridical distributions and the darker (color online) data show the transformed data that optimize each cost.

FIG. 2.

(Color online) Exemplary and corresponding virtual sets of two practice blocks from one subject, used to illustrate the tolerance noise covariation cost analysis method (T-cost, N-cost, and C-cost, respectively). The left column shows data optimized in terms of T-cost; the middle column shows data optimized in terms of N-cost, and the right column shows data optimized in terms of C-cost. Gray circles represent actual throws made by the subject's phonatory gesture, and red, green, or blue circles represent surrogate data with one component idealized (tolerance, noise, or covariation, respectively). The panels in the top and bottom rows show data from the first block of practice on day 1 and the last block of practice on day 5, respectively.

T-cost is the cost to overall performance for not finding the most error-tolerant area of the execution space. T-cost is estimated by generating an optimized data set in which the mean release angle (i.e., Δf₀) and the mean release stretch (i.e., ACC_amp) were shifted in execution space to the location yielding the best overall result. The dispersion in execution space is preserved during this process. More specifically, the data set was shifted on a grid of 1500 × 1500 possible center points and the boundaries of this grid were determined by the limits of the task. The angles tested as centers were limited to those between 0° and 90° (which was equivalent to 0–18 ST). The velocity/stretch values tested as centers were limited to those between 0 and 300 pixels of stretch (which was equivalent to 0–22.5 dB_LPL). This range was determined by the settings established for all subjects individually and there were no other options outside of these ranges. The optimization procedure shifted the dataset through every possible center point and evaluated its mean result at each location. When data points extended beyond the grid limits, the values were calculated on the extrapolated execution space. The location that produced the best (lowest) overall mean error was compared to the actual data set and the algebraic difference between the two mean error values defined T-cost.

N-cost is the cost to overall performance due to non-optimal stochastic variability in execution space. N-cost is estimated by generating an optimized data set in which variability is reduced in a step-wise manner to achieve the least possible mean error, while leaving overall mean Δf₀ and ACC_amp unchanged. Though one would initially expect all data sets to be optimally reduced to a single point (the mean Δf₀ and ACC_amp), note that each data set is evaluated in terms of its result (minimum distance from the target). Therefore, the mean of a data set may not always fall directly on the solution manifold and a small distribution might achieve better results on average. In the numerical procedure, the data set was shrunk in 100 steps to converge onto the mean, where the radial distance for every data point was divided into 100 steps. Subsequently, all data points were scaled towards the mean at 1% intervals and the mean error was evaluated at each interval. The algebraic difference between the means of the interval that produced the lowest mean error (optimized data set) and the original data set defined N-cost.

C-cost is the overall cost to performance due to insufficient alignment with the direction of the solution manifold; i.e., not exploiting the redundancy in the execution space. C-cost is estimated by generating an optimized data set where the Δf₀ and ACC_amp values were not modified, but the individual Δf₀–ACC_amp trial-by-trial pairings were recombined to achieve the lowest possible mean error via a greedy hill climbing algorithm using a pairwise matching procedure (Russell and Norvig, 2002). Specifically, all Δf₀–ACC_amp pairs were rank-ordered from lowest error (best) to highest error (worst); i = 1, 2, 3,…, 100 since all data sets were of 100 trials. Subsequently, the worst performing Δf_{0 (i = 100)} was paired with ACC_{amp (i = 99)} and ACC_{amp (i = 100)} was paired with Δf_{0 (i = 99)}; the mean result of the new error_{(i = 100)} and the error_(i = 99) were compared to the original mean error of the two trials. If the error improved over the original, the swap was accepted. As a next step, ACC_{amp (i = 100)} was swapped with ACC_{amp (i = 98)} and the resulting mean error of the two trials was evaluated. If the mean result improved, the swap was accepted. This continued until Δf_{0 (i = 100)} was compared with ACC_{amp (i = 1)}; i.e., ACC_{amp (i = 100)} was swapped with ACC_{amp (i = 1)}. After this sequence of 99 comparisons, the same sequence was repeated with ACC_{amp (i = 99)}; therefore the batch consisted of 4950 comparisons. The batch of procedures was repeated on the improved set until no further swaps could be made. The algebraic difference between the mean error of this optimized data set and the original data set defined C-cost.

An example of data from a single subject in Fig. 2 shows representative changes in all three cost measures due to improved vocal performance. For example, the optimal data transformation shown for T-cost in the upper left panel of Fig. 2 expresses that the subject could have improved her performance by 11.9 pix, if tolerance were optimized. Similarly, for N-cost, the result could be improved by 30.7 pix if the noise were reduced optimally. Finally, for C-cost, the result could be improved by 26.5 pix if the covariation between execution variables was optimal. The subject's data set exhibits decreased costs to performance in all three metrics late in practice (day 5) compared to early in practice (Day 1).

F. Analysis of directionality in execution space

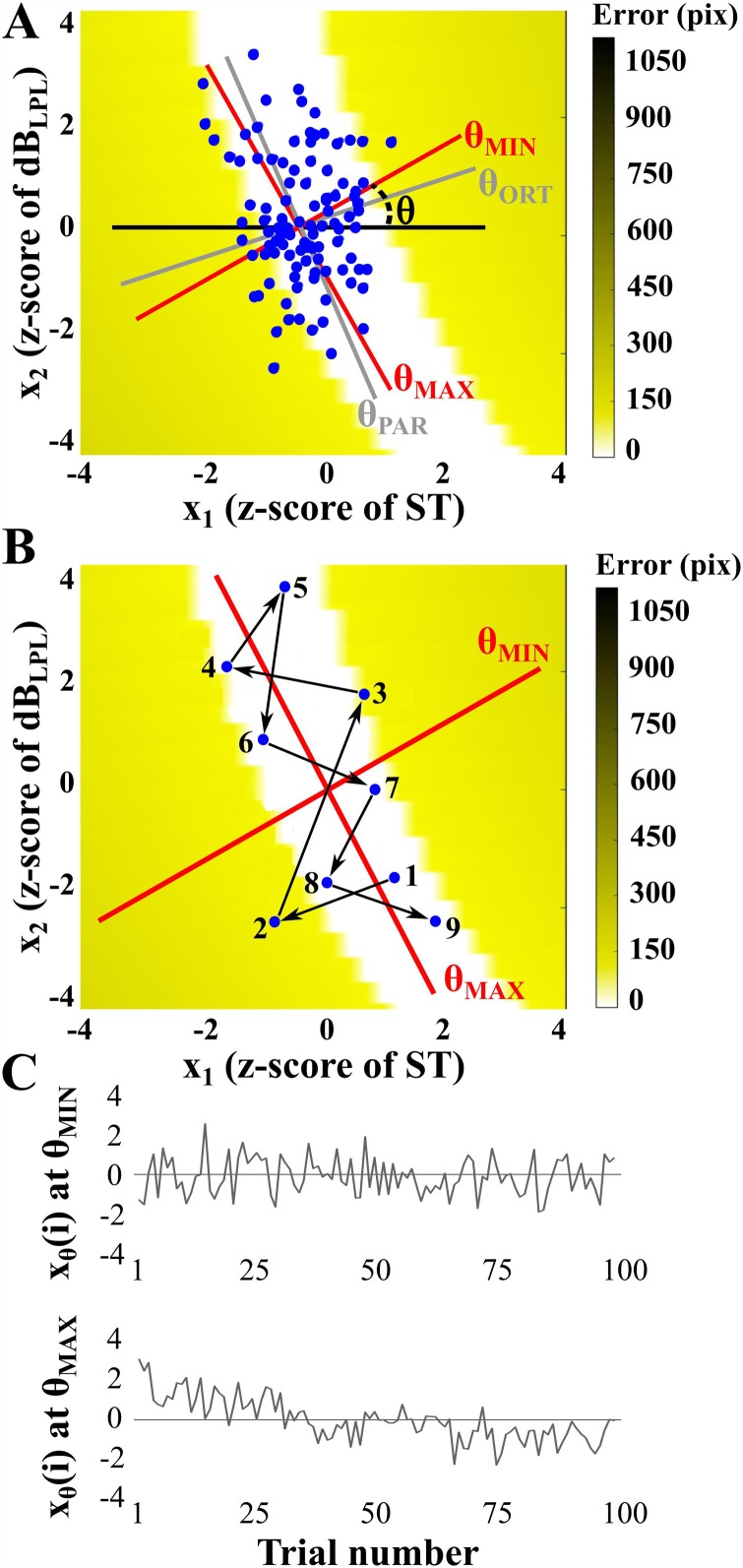
The analysis of directional variability in the execution space was replicated from (Abe and Sternad, 2013) and is illustrated in Fig. 3. To investigate the temporal structure in Δf₀ and ACC_amp, the two axes of the execution space had to be normalized since they are in terms of two different units. To this end, the data for each (nonoverlapping) 100-trial block per subject were transformed into z-scores according to the mean and standard deviation of Δf₀ and ACC_amp for that block.

FIG. 3.

(Color online) (A) Execution space and rotation axis used to analyze temporal structure in various directions. The execution space was normalized using the individual subject's mean and standard deviation. The gray lines show the directions/rotations parallel (θ_PAR) or orthogonal (θ_ORT) to the solution manifold and the red lines show the directions/rotations where the lag-1 autocorrelation coefficient (AC1) was lowest (θ_MIN) and highest (θ_MAX). Number of trials = 100. (B) Example using nine consecutive trials to illustrate trial-by-trial dynamics in the two-dimensional execution space. (C) The upper time series shows x_θ(i) for the rotation angle θ with the minimum AC1 value and the lower time series shows x_θ(i) for the rotation angle θ with the maximum AC1 value.

To evaluate whether trial-to-trial variability was channeled into preferential directions on the solution manifold, the two-dimensional data of each block were projected onto a single line through the center of the dataset using the following equation:

$$x_{\theta }\left(i\right)=x_1\left(i\right)\hspace{0.17em}\text{cos}\hspace{0.17em}\theta +x_2\left(i\right)\hspace{0.17em}\text{sin}\hspace{0.17em}\theta ,$$ (5)

where i is the trial index, x_θ(i) denotes the new time series after projection onto the line, and x₁ and x₂ denote the z-score of Δf₀ and ACC_amp, respectively. It has been shown that variability analysis is highly sensitive to the coordinate system and without normalization, the execution space has no metric (Sternad et al., 2010). The angle θ of this line was zero when parallel to the x axis [Δf₀ direction, black line in Fig. 3(A)] and 0.5π rad when parallel to the y-axis (ACC_amp direction). The center of the data was defined by the mean of Δf₀ and ACC_amp for each block of 100 trials for each individual. This line was then rotated through 0 < θ < π rad, in 180 steps. At each rotation angle (θ), the data were projected onto the line and the time series of the projected data was evaluated using autocorrelation and detrended fluctuation analysis. The angle of the direction parallel (error-irrelevant) to the solution manifold was defined as θ_PAR and the direction orthogonal (error-relevant) to the solution manifold was defined as θ_ORT [gray lines in Fig. 3(A)].

G. Analysis of temporal variability

The temporal structure of x_θ(i) obtained for all rotation angles θ was evaluated by autocorrelation and detrended fluctuation analysis (DFA). These two analysis methods have been chosen because they provide statistical quantifications of temporal persistence/anti-persistence on short-term (autocorrelation) and long-term (DFA) time scales. More specifically, persistence is statistically defined when future fluctuations are likely to be in the same direction as current fluctuations; anti-persistence is defined when currently observed fluctuation are in the opposite direction of future fluctuations (Brenner et al., 2013; Collins and De Luca, 1993; Collins and De Luca, 1994; John et al., 2016). From the autocorrelation analysis, the lag-1 autocorrelation coefficient (AC1) was reported to evaluate trial-to-trial variability since AC1 provides a correlation between the signal and the signal shifted by 1 trial. Temporal structure beyond lag-1 was evaluated using DFA. The DFA method was chosen since it is a modification of the root-mean square analysis of a random walk that is relatively insensitive to non-stationarities and noise in the data (Peng et al., 1995). Specifically, the time series was cumulatively summed to obtain an integrated signal and was then detrended with linear regression within windows of a number of trials n. The root mean square of the detrended time series F(n) was then calculated for windows of n trials. Plotting F(n) versus n in log-log coordinates, the DFA scaling index (SCI) was obtained from the slope of a linear regression (Peng et al., 1995). This SCI has traditionally been used to estimate the fractal dimensions of a time series, which provides an indication of the statistical properties of the fluctuations contained in the time series (Duarte and Sternad, 2008; Feder, 1988). Sets of 100 trials were used in the analysis of directionality in execution space.

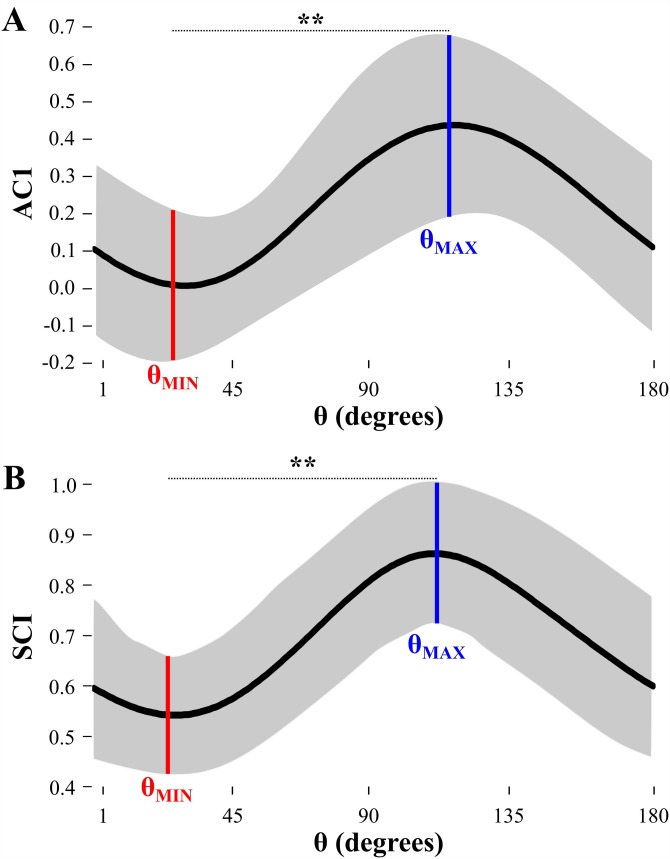
Temporal variability is classified as either uncorrelated white noise (AC1 = 0 and SCI = 0.5); anti-persistence denoting stable dynamic behavior and error correction (AC1 < 0 and SCI < 0.5), or persistence denoting unstable dynamic behavior and lack of error correction (AC1 > 0 and SCI > 0.5) (Collins and De Luca, 1993; Collins and De Luca, 1994; Dingwell and Cusumano, 2010; Dingwell et al., 2010). It was hypothesized that the lowest value of AC1 or SCI (labeled θ_MIN) would be coincident with the direction orthogonal to the solution manifold (θ_ORT), as this is the most error-relevant direction. The rotation angle in execution space with the highest values of AC1 or SCI (labeled θ_MAX) will be coincident with the direction parallel to the solution manifold (θ_PAR), which is the least error-relevant direction. Figure 3(A) represents the angles θ_MIN and θ_MAX in execution space, and Fig. 3(B) shows hypothetical data (nine consecutive trials) to clearly show trial-by-trial fluctuations that produce negative AC1 along the θ_MIN axis (trial-to-trial changes alternate left/right) and positive AC1 along the θ_MAX axis (trial-to-trial changes persist up/down). Figure 3(C) shows time series of execution variables, x_θ(i), at two different rotation angles—specifically, the signals at those angles with minimum AC1 (θ_MIN) and maximum AC1 (θ_MAX).

H. Statistical analysis

Performance improvement across practice was evaluated by fitting exponential functions to the error (minimum distance between the ball trajectory and target), where y = ae^−bx + c. Fits were performed for each participant and for the entire group's mean error, calculated from absolute values of 50 trials. Similarly, exponential functions were fitted to T-cost, N-cost, and C-cost over time, evaluated for blocks of 50 trials. The exponential functions assessed the different time scales of change between the costs and error via the time constant 1/b. To further demonstrate significant improvement over practice, the first 50 trials from all practice days were analyzed with repeated measure analyses of variance (RM-ANOVA) with respect to mean error, T-cost, N-cost, and C-cost. Significant main effects were followed up with one-tailed paired t-tests (post hoc) since the hypothesized direction of change was in one direction (reduction of all metrics over time). All post hoc comparisons were in reference to day 1 (i.e., four total comparisons per metric) since human performance improvement is exponential (most reduction in error metrics occur very early in practice). Bonferroni p-value corrections were not done because this is a preliminary study where the focus was on finding statistically robust (p < 0.05) medium-to-large effect sizes (as determined via Cohen's d). The individual contribution of each cost towards error reduction was evaluated through Spearman's rank correlation coefficient ρ (T-cost, N-cost, or C-cost versus mean error) and resulting ρ values were tested for significant differences using three paired t-tests (T-cost versus N-cost, T-cost versus C-cost, and C-cost versus N-cost).

The subjects' sensitivity to directions in the execution space was assessed using all data from the last day (day 5) of practice. This data set consisted of 3 blocks (100 practice trials per block) from all ten subjects, where θ_MIN and θ_MAX were calculated for each block using AC1 or SCI (total practice blocks = 30). Two paired t-tests (one with data from AC1 and the other from SCI) were used to assess the difference between the 30-paired values of θ_MIN and θ_MAX. If subjects developed a sensitivity to how trial-to-trial fluctuations in the execution space related to performance error, the direction with minimum AC1 and SCI (θ_MIN) will be significantly lower than the direction with maximum AC1 and SCI (θ_MAX). This will be interpreted as increased CNS control in the θ_ORT compared to θ_PAR.

Cohen's d was used as an effect size metric for all statistically significant pairwise comparisons such that effect sizes less than 0.20 were interpreted as small, between 0.20 and 0.80 as medium, and greater than 0.80 as large (Cohen, 1988). All statistics were calculated using spss software (version 22.0, IBM, Armonk, NY). All variables were confirmed to have normal distributions via one-sample Kolmogorov-Smirnov tests.

III. RESULTS

A. Performance improvement

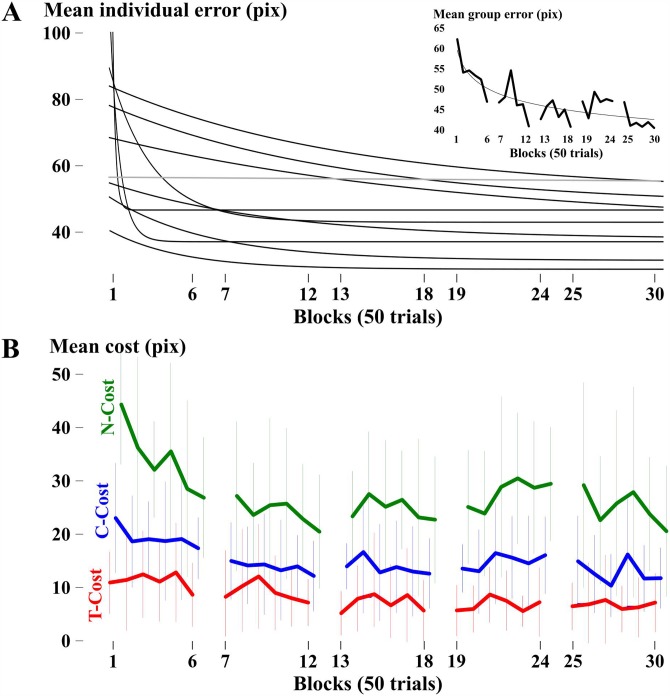
Before analyzing variability as it relates to practice, one must first demonstrate that the group of subjects significantly improved their performance. Figure 4(A) shows the progression of error across practice for all ten individuals who completed 5 days of practice. Only the exponential fits are shown for visual clarity. The fit across all subjects and the mean error per 50 trial block is shown in the inset of Fig. 4(A). One subject (in gray) started out with small error and maintained his relatively high performance throughout all days of practice. Even though this subject did not demonstrate a learning trend, he was included in all analyses. All other subjects had statistically significant exponential fits with r-values (the nonlinear correlation coefficient between the exponential fit and data) ranging from 0.45 to 0.77. An exponential function was also fitted across the group using overall mean error, which resulted in a significant r-value of 0.83 [see inset of Fig. 4(A)]. The subjects began practice at a mean error of 58.57 (15.23) pixels during their first block of trials (n = 100) and decreased it to 44.30 (12.46) pixels during their first block of trials on their last practice day (recall that a “hit” is defined as an error of 30 pixels or less). Therefore, even after 5 days of practice (1500 trials), the group of singers was not hitting the target on average; i.e., the task was challenging to learn. The time scale 1/b was 4.878, indicating that the time constant was approximately 244 individual trials (i.e., slightly less than one day of practice). Furthermore, the results of a RM-ANOVA indicated a significant change in error across practice days—Greenhouse-Geisser F(2.07, 18.61) = 5.708, ŋ² = 0.39, p = 0.011—and post hoc t-tests demonstrated a statistically significant decrease in error for practice days 2–5 compared to day 1 (p = 0.020, p < 0.001, p = 0.005, p = 0.001, respectively) with large effect sizes (mean d = 1.24 across the four comparisons).

FIG. 4.

(Color online) (A) Exponential fits to each individual's mean error computed for blocks of 50 trials, where the gray line represents the subject who did not show improvement across practice. The inset shows the mean error across all ten subjects with spacing between lines representing new days (six trial blocks per day for five days). (B) Means and standard deviations of T-cost (red), C-cost (blue), and N-cost (green) per trial block for all subjects.

B. Distributional variability—TNC-costs

Figure 2 showed exemplary data early in practice (day 1) and late in practice (day 5) from one subject. Comparing days 1 and 5, it can be seen that the distribution of execution variables moves towards a more error-tolerant location on the solution manifold (T-cost), the dispersion of the data cloud decreased (N-cost), and the anisotropy of the data changed to align with the solution manifold (C-cost). Figure 4(B) shows how the group averages of these TNC-costs decreased with practice. As hypothesized, N-cost was the highest cost to performance followed by C-cost, and finally T-cost. The results of the RM-ANOVA using N-cost and C-cost demonstrated a significantly decreased cost to performance across all practice days. More specifically, N-cost decreased across all practice days—Greenhouse-Geisser F(2.64, 23.75) = 6.215, ŋ² = 0.41, p = 0.001—and post hoc paired t-tests demonstrated a significant decrease in N-cost for practice days 2–5 compared to day 1 (p = 0.003, p < 0.001, p = 0.001, p = 0.007, respectively) with large effect sizes (mean d = 1.55 across the four comparisons). C-cost decreased across all practice days—Greenhouse-Geisser F(2.48, 22.35) = 3.83, ŋ² = 0.30, p = 0.03—and post hoc paired t-test demonstrated a significant decrease in C-cost for practice days 2–5 compared to day 1 (p = 0.014, p = 0.003, p = 0.013, p = 0.037, respectively) with large effect sizes (mean d = 0.85 across the four comparisons). T-cost changes, on the other hand, did not attain a significant main effect in the RM-ANOVA—Greenhouse-Geisser F(1.94, 17.47) = 2.48, ŋ² = 0.22, p = 0.11—but post hoc paired t-tests demonstrated a significant decrease in T-cost for practice days 3–5 compared to day 1 (p = 0.008, 0.028, 0.023, respectively). The lack of a significant main effect is likely due to insufficient statistical power since the associated mean effect size across all four comparisons indicated a moderate-to-large decrease in T-cost (d = 0.66).

Exponential fit functions demonstrated significant r-values of 0.80 for T-cost, 0.84 for N-cost, and 0.82 for C-cost. N-cost and C-cost evolved at a faster time scale than T-cost. More specifically, the b-coefficients were 0.095 for T-cost, corresponding to a time constant of 526 trials, or slightly less than 2 days of practice. The time scale for C-cost was 0.246, corresponding to 203 trials, or slightly less than 1 day of practice. The time scale for N-cost was 0.428, equivalent to 117 trials, or approximately a half day of practice. These profiles were correlated with the error profiles. Table II displays the resulting rho values from Spearman's correlations between error and T-, N-, or C-cost, respectively. Qualitatively, the ranking from highest to lowest correlation across participants was different than hypothesized. However, paired t-tests demonstrated no significant difference between mean rho values when comparing between costs at a group level.

TABLE II.

Spearman correlations (ρ) between error and each of the TNC costs. Subject ID denotes sex of each individual: Male (M) and female (F).

Subject	T-cost	N-cost	C-cost
F3	0.825a	0.453b	0.348
F4	0.655a	0.079	0.025
F5	0.839a	0.388b	0.299
F6	0.679a	0.632a	0.608a
F7	0.485c	0.828a	0.583a
M2	0.586a	0.593a	0.747a
M3	0.382b	0.315	0.479c
M6	0.528c	0.697a	0.558a
M8	0.531c	0.624a	0.306
M9	0.457b	0.560a	0.453b
Mean (SD)	0.60 (0.15)	0.52 (0.22)	0.44 (0.21)

^ap < 0.001.

^bp < 0.05.

^cp < 0.01.

C. Temporal variability—AC1 and SCI at θ_MIN or θ_MAX

Figure 3(A) shows that, for the exemplary data set, θ_MAX aligns at an angle approximately parallel to the solution manifold (error-irrelevant direction θ), and θ_MIN forms an angle approximately orthogonal to the solution manifold (error-relevant direction θ). Additionally, Fig. 3(C) displays exemplary time series for the signal at minimum and maximum AC1 to illustrate how the two time series can be different. The signal at θ_MIN shows anti-persistent temporal structure fluctuating around the mean. In contrast, the signal at θ_MAX shows persistent temporal structure with a noticeable drift in the first half of the trials.

Figure 5 summarizes the results of the temporal analyses with respect to direction θ. According to paired t-tests, θ_MIN was significantly lower than θ_MAX in both AC1 and SCI analyses with very large effect sizes; AC1: t(29) = 13.65, p < 0.001, d = 2.92; SCI: t(29) = 12.06, p < 0.001, d = 2.62. Therefore, both temporal correlation measures demonstrated significantly different trial-by-trial dynamics between θ_MIN and θ_MAX; i.e., uncorrelated, stable dynamics at θ_MIN and persistent dynamics at θ_MAX, indicative of selective control depending on the direction in solution space.

FIG. 5.

(Color online) Analysis of temporal variability and directionality in execution space. (A) Lag-1 autocorrelation coefficient (AC1) and (B) detrended fluctuation analysis scaling index (SCI) of x_θ(i) as a function of rotation angle θ across all subjects' last day of practice (three blocks of 100 trials each). Solid horizontal black curves show the mean measure across all 30 practice blocks in each group, and shaded areas represent ±1 standard deviation around the mean. θ is indicated for which AC1 and SCI are minimum (θ_MIN) and maximum (θ_MAX), with their difference statistically significant (**p < 0.01).

IV. DISCUSSION

A voice-controlled video game has been described and was used to investigate whether theoretically based findings from limb motor learning were applicable to vocal motor learning. The relationship between motor performance and distributional variability were quantitatively examined, as well as the time scales over which error and TNC-costs evolved. Finally, temporal variability in the two-dimensional execution space was evaluated to determine if subjects' trial-to-trial behavior were sensitive to error-relevant directions in the solution manifold.

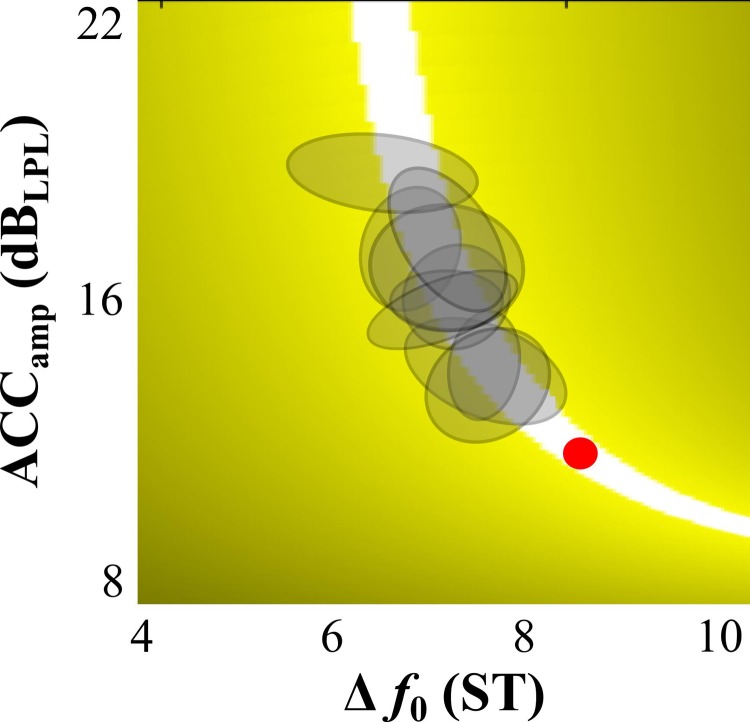
Before interpreting the variability results, it will be helpful to first examine the final skilled vocal behavior exhibited by the group of ten professional singers. Figure 6 provides a visualization of how each subject performed in the execution space during his/her final block of 100 trials on practice day 5. A gray ellipse represents each subject's final block of practice and was centered at the final practice block's mean ACC_amp and Δf₀. Overall, it qualitatively appears that they all performed a relatively similar vocal gesture. On average, the subjects produced most harmonic intervals between a diminished and augmented fifth (mean ± 1 standard deviation; 6.98 ± 0.49 ST) at over two times louder than their lowest phonation level (14.57 dB_LPL ± 1.74 dB).

FIG. 6.

(Color online) Summary of each subject's error in the execution space for their final block (100 trials) of practice on day 5, represented by gray ellipses. The aspect ratio of the execution space was scaled according to the estimated controllable limits such that a Δf₀ of 0.2 ST and ACC_amp of 0.5 dB_LPL represent the same length in the execution space (the red circle below the ellipses is a scale marker).

In order to interpret how difficult the task was (and how skilled the final behavior became), published perturbation studies were consulted for estimates of minimal controllable limits. These limits were approximately 0.20–0.25 ST for f₀ (Burnett and Larson, 2002; Hain et al., 2000; Liu and Larson, 2007) and 0.5–0.75 dB for sound pressure level (Bauer et al., 2006; Larson et al., 2007). Studies on just noticeable differences provided even lower estimated limits, but they were not used since the derivations were based on perceptual judgments not connected to motor performance (Braida et al., 1984; Fletcher and Munson, 1933; Klatt, 1973; Nikjeh et al., 2008; Tervaniemi et al., 2005). To show how these estimated minimal controllable limits related to game play, a circle (axes diameters = 0.2 ST and 0.5 dB) was placed on Fig. 6 (below the gray ellipses) where it could fit inside the solution manifold; i.e., trial-to-trial variability would be present, but the ball would still hit the target for every throw. First, the proximity of the standard deviation of Δf₀ and ACC_amp across all individual subjects (0.37 ST and 0.73 dB, respectively) to the estimated controllable limits (0.2 ST and 0.5 dB, respectively) speaks to the resulting elite vocal performance of the group as a whole and the high difficulty of the virtual task. Second, it is realistic to assume that trial-by-trial variations reflect volitional vocal control (or lack of control) in relation to error correction, since the standard deviation of Δf₀ and ACC_amp exhibited by the study subjects are above these estimated controllable limits. And finally, the subjects found a location on the solution manifold (gray ellipses in Fig. 6) that was reasonably tolerant to variability, i.e., the subjects could realistically reduce their variability and stay on the zero error, or white, solution manifold.

A. Distributional variability—TNC-costs

In general, the relationship between costs and error is similar to findings in limb movement studies. However, two results were different than what was expected based on previous limb work. T-cost exhibited the slowest time scale (which it typically demonstrates the fastest time scale of all cost metrics in limb studies) and C-cost and N-cost exhibited higher positive correlations with error than observed in limb research. These two results may be due to the baseline skill level of the ten subjects; i.e., they were all professional singers highly competent at manipulating pitch and loudness before practicing the game. Thus, the expert singers may have been able to find an error-tolerant space on the solution manifold very early in practice. Therefore, T-cost appeared to evolve at longer temporal periods than C-cost and N-cost. Also, the large group-based correlation coefficients between N-cost or C-cost and error indicated that subjects were past the stage of establishing a new vocal skill, and instead, were in the later stages of skill learning where they fine-tuned their motor performance. It has been noted in previous limb-based experiments that correlations between C-cost or N-cost and error increased during improvement of expert performance. Strong positive N-cost correlations with error have been noted in subjects who performed well during early practice (Abe and Sternad, 2013) and in subjects who had professional sports experience (Cohen and Sternad, 2009).

B. Temporal variability—Directionality in execution space

As seen in Fig. 5 (and supported via statistical results), trial-by-trial dynamics demonstrated clear modulations across different directions in the execution space, suggesting that the subjects were sensitive to the direction of the solution manifold. Furthermore, θ_MIN for AC1 was around zero instead of negative and θ_MIN for SCI was around 0.5 instead of <0.5; i.e., both minima should be characterized as white noise instead of anti-persistence/error correction. One would have expected to find negative AC1 values or SCI values <0.5 at θ_MIN since, theoretically, low values would represent error-correction—and anti-persistent structure has been found at θ_MIN in studies using well-learned behaviors (e.g., walking or pointing) (Dingwell et al., 2010; van Beers et al., 2013). This apparent deviation was also reported in a previous study using a similar task and explained through a computational learning model. This model suggested that additive noise sources (e.g., perceptual and motor noise) could obscure corrective errors from feedback and result in positive AC1 and SCI at θ_MIN (Abe and Sternad, 2013). Furthermore, the mapping from execution to error is highly nonlinear; therefore, perceiving the direct relation between error and execution is difficult and the resulting time series of execution variables may not demonstrate strong anti-persistent/error-correction patterns. Last, the significantly lower AC1 and SCI at θ_MIN compared to θ_MAX support the hypothesis that subjects became sensitive to the directionality of the underlying non-linear solution manifold and compensated on a trial-by-trial basis in only those directions that were closely related to a change the error.

V. CONCLUSION AND FUTURE DIRECTIONS

The results of this investigation suggest that vocal motor learning shares similar features to limb motor learning—especially how variability is modified over time to reduce the overall error. This is particularly significant as replicating findings from motor control/learning studies based on limb movements (outside of perturbation and adaptation paradigms) are not often successful when applied to bulbar movements/skills (e.g., speech, swallowing, voice); for reviews see Bislick et al., 2012; Maas et al., 2008. To date, the study of variability in vocal motor behavior has focused primarily on decreases or increases in relation to performance improvement or normal versus pathological. In contrast, the present study demonstrates that the vocal motor system may not be primarily concerned with simply decreasing variability, but selectively channeling temporal and distributional variability according to the task demands. Furthermore, selective control of variability may even be indicative of late-stage skill learning or habituation.

This paradigm warrants future work to investigate the potential for quantification of improvements in voice training and novel clinical capabilities in the field of voice disorder rehabilitation—the ultimate goal being to improve assessment and treatment of patients with voice disorders. For example, the TNC-costs approach enabled novel characterizations of upper-limb control and learning in children with dystonia (Chu et al., 2016) and a virtual throwing task has been used in a group of patients with Parkinson's disease (Pendt et al., 2012). Consequently, it seems feasible that this approach may be applied to patients with neurologic disorders associated with vocal deterioration (e.g., Parkinson's disease, multiple sclerosis, amyotrophic lateral sclerosis). New voice-specific diagnostic features (i.e., vocal biomarkers) could be derived from the game through analysis of the Δf₀–ACC_amp trajectory, TNC-costs, or directional variability in execution space. These features could also become therapeutically important if they correlated with behavioral retention or longer-term learning. For example, the degree of correlation between N- or C-cost and error, or directional variability analysis could help quantify if a patient is implicitly aligning his/her performance with the underlying solution manifold. Also, since the current investigation included only subjects with high/expert baseline levels of vocal skill (i.e., professional singers), future investigations should test this paradigm in those with novice levels of baseline skill.

The voice-controlled slingshot task may help patients improve their specific pathological vocal features that are subtle and otherwise difficult to volitionally vary. Also, just as singers practice vocalises and pianists practice scales, the slingshot task could be a platform for patients to improve basic vocal skills or for experts to improve vocal technique. Patients who demonstrate minimal kinesthetic/proprioceptive awareness may find indirect benefits (i.e., learning to learn) through using the visual feedback to help establish a complex two-dimensional pitch-loudness vocal skill. Additionally, patients with Parkinson's disease may benefit from playing the game in its current state, since the vocal execution variables are related to known targets for therapy (pitch and loudness) (Ramig et al., 2001). This is also true of vocal function exercises since they hypothetically focus on rebalancing and strengthening the phonatory system through prolonged soft voicing at specific pitches (Stemple et al., 1994). It could additionally be hypothesized that adherence to therapy or therapeutic outcomes would be improved with the addition of a “game” to treatment regimens. The features used to control the virtual slingshot could vary according to patient diagnosis; e.g., for patients with vocal hyperfunction, vocal intensity could be replaced with a measure of aerodynamic importance such as subglottal pressure or glottal airflow (Fryd et al., 2016; Zañartu et al., 2014) or a ratio of aerodynamics to acoustics (i.e., a vocal efficiency type measure). Even more specifically, future work that has potential for clinical adoption (i.e., voice therapy) should include the addition of voice quality measures (e.g., cepstral peak prominence, spectral tilt, noise-to-harmonics ratio) or laryngeal biomechanics (e.g., open/closed quotient, maximum flow declination rate, AC Flow). Finally, the acquisition/retention paradigm in motor learning may be applied to this video game to study the effects of varying feedback and practice variables (e.g., concurrent/terminal feedback, frequency of feedback, massed/distributed practice) (Schmidt and Lee, 2011).