Inspired by black butterfly scales, self-assembled phase-separated nanostructures form efficient photovoltaic absorbers.
Abstract
The wings of the black butterfly, Pachliopta aristolochiae, are covered by micro- and nanostructured scales that harvest sunlight over a wide spectral and angular range. Considering that these properties are particularly attractive for photovoltaic applications, we analyze the contribution of these micro- and nanostructures, focusing on the structural disorder observed in the wing scales. In addition to microspectroscopy experiments, we conduct three-dimensional optical simulations of the exact scale structure. On the basis of these results, we design nanostructured thin photovoltaic absorbers of disordered nanoholes, which combine efficient light in-coupling and light-trapping properties together with a high angular robustness. Finally, inspired by the phase separation mechanism of self-assembled biophotonic nanostructures, we fabricate these bioinspired absorbers using a scalable, self-assembly patterning technique based on the phase separation of binary polymer mixture. The nanopatterned absorbers achieve a relative integrated absorption increase of 90% at a normal incident angle of light to as high as 200% at large incident angles, demonstrating the potential of black butterfly structures for light-harvesting purposes in thin-film solar cells.
INTRODUCTION
Evolution-driven photonic structures in nature, such as those found in butterflies (1–3), beetles (4, 5), birds (6, 7), reptiles and spiders (8–10), fishes (11, 12), or plants (13, 14), can effectively manipulate the flow of light for camouflage, inter- or intraspecies communication, signaling, heat regulation, and many other biological processes. Mimicking these optimized photonic prototypes plays an unprecedented important role in the design and function of optoelectronic devices and technologies (15–18). In thin-film solar cells, where efficiencies are limited by severe optical losses, using photonic structures was shown to improve light collection and to assist light trapping of low-energy photons (19–24). In particular, randomly textured surfaces and periodic structures have been extensively investigated because of their ease of implementation via wet etching (25) or low-pressure deposition (26), and interference or nanoimprint lithography techniques (27), respectively. More recently, photonic structures featuring a tailored degree of disorder were shown to operate over a broader spectral and angular range than their periodic counterparts while preserving controllable optical properties (28–33). In this context, understanding the contribution of disordered structures observed in black butterfly wings, known for their thermoregulation and light management properties (34–36), can provide valuable insights into designing and fabricating efficient light-harvesting nanostructures for thin-film photovoltaic (PV) devices.
The scales of black butterflies’ wings exhibit a wide variety of hierarchical micro- and nanostructures with specific functionalities such as visual appearance and thermoregulation (37–42). The blackness of these butterfly wings was attributed to strongly absorbing pigmentation alone until Vukusic et al. (37) demonstrated that the micro- and nanostructured scales play an important role in harvesting incoming light in addition to the pigmentation. The nanostructures on black butterfly scales were mostly simulated as periodic structures (38, 39). However, Wang et al. (42) numerically demonstrated that disordered arrangements of nanostructures in black butterfly wing scales can improve the absorption with enhanced angular and polarization robustness. This is an important requirement for efficient solar energy conversion because diffuse illumination can also be captured, which further improves the overall efficiency of the devices.
Here, we present experimental and numerical analyses of the structural inhomogeneity observed in the scales of the black butterfly, Pachliopta aristolochiae (Lepidoptera: Papilionidae) (Fig. 1A). We retrieve design rules for the fabrication of highly absorbing PV active layers. The absorption is first examined experimentally by microspectroscopy. Unlike previous studies (37–39), this analysis enables probing of wings locally and relates the structural variations, particularly the air-filling fraction (denoted ff in the following), to the observed optical properties. We construct a full-wave three-dimensional (3D) optical model to understand the light-harvesting properties of micro- and nanostructures by extracting the exact structure from top-view and cross-sectional scanning electron microscopy (SEM) images. Using the finite element method (FEM), we analyze the respective influence of the micro- and nanostructures on the resulting absorption properties together with the wavelength-dependent light propagation mechanisms. Finally, we exploit our experimental and numerical results for the design and fabrication of bioinspired thin PV absorbers made of hydrogenated amorphous silicon (a-Si:H). For that purpose, we use a scalable, wet-processable method based on the lateral phase separation of binary polymer mixture to mimic the exact mesoscale nanostructural pattern.
Fig. 1. Structure and absorption spectra of the P. aristolochiae butterfly wing scales.
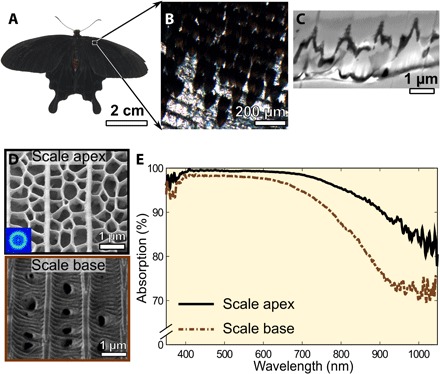
(A) Image of a P. aristolochiae butterfly. (B) Microscopic image of the matt black region. A gradient of blackness is observed along each scale. (C) Cross-sectional SEM image of a matt black scale. (D) SEM images of a scale from the matt black region reveal that the air-filling fraction at the apex is higher (by about +59%) than at the base. The inset in the lower left corner shows the 2D Fourier power spectrum of the corresponding nanohole array. (E) Absorption spectra measured in the apex and base of a single scale from the matt black region of P. aristolochiae. The scale apex of a single scale exhibits higher absorption than the base.
RESULTS
Analysis and characterization of the black butterfly scales
The male black butterfly P. aristolochiae shown in Fig. 1A is a well-studied species because of its efficient behavioral thermoregulation (36). Similar to other black butterflies (37–42), the scales of P. aristolochiae contain intricate micro- and nanostructures. Periodic ridges are distributed along the longitudinal length of the scales and are connected by cross-ribs. The latter creates a 2D network of disordered nanoholes above the scale interior made of a chitin and melanin composite. The basal region near the thorax is matt black on both forewing and hindwing, and is darker than any other black regions of the wing of P. aristolochiae (see Fig. 1, A and B). These nanoholes are suspended from the ridges and cross-ribs and hang down around 800 ± 35 nm into the interior scales measured from cross-sectional SEM images of the scales (Fig. 1C). The matt black and dull black regions of the wings were compared by SEM, and their air-filling fractions (that is, ff = 0 indicates no holes) were evaluated (see fig. S1). For both matt black and dull black regions of the wings, the hole diameters follow a random distribution with a mean of 300 ± 85 nm. The hole distribution has a short-range order as can be concluded from the ring-shaped fast Fourier transform (FFT) pattern of the matt black scale apex SEM image (inset in Fig. 1D). A statistically significant difference in the density of holes, and hence in ff, is observed between the two regions. The mean ff in the matt black region is about 59%, whereas the dull black region has a lower ff of only 37%. This ff difference in different regions was also qualitatively reported previously (37). However, we noted that the ff is even lower (less than 23%) near the scale base, as shown in Fig. 1D. The corresponding difference in the visual appearance caused by this structural variation can be observed in Fig. 1B.
As illustrated in Fig. 1 (B to D), the scales display different colors when the ff changes, suggesting that the absorption properties strongly correlate to this morphological feature. There is a substantial relative difference of more than 60% in the ff between the regions near the base and apex of the scale. To quantify this effect, we performed single-scale microspectroscopy on the scale apex and base of a single matt black scale. Figure 1E reveals the quantitative absorption difference between those two sections. The region with the highest ff, that is, with the lowest material volume, shows around 98% absorption in the visible range. This is 6% higher than the base of the scale. This absorption difference increases even more for wavelengths above 800 nm and reaches up to 18% at 900 nm. The following results suggest that the higher the ff, the lower the reflection and consequently the better the absorption. Although the low nanohole density in the basal region supports the mechanical stability, the light harvesting is optimized by maximizing ff toward the scale tip, resulting in a low-weight yet efficient absorber. The impact of the longitudinal ridges and the disordered nanohole array should be distinguished from the influence of the nanohole ff. This point is addressed by analyzing the micro- and nanostructures with 3D wave optics simulations.
To gain insight into how the incident light is affected by the micro- and nanostructures of P. aristolochiae, we performed FEM-based simulations. The “3D model” parameters for these simulations were taken from surface and cross-sectional SEM images (Fig. 1, C and D) of the matt black region with an ff of 59% (Fig. 2A). To evaluate the influence of these structures, an unpatterned slab with an equivalent absorbing material volume was used as a reference (“slab model”). The optical index data of the melanin-chitin composite were adopted from the wavelength-dependent complex permittivity used by Herman et al. (39) for Troides magellanus, which was calculated using a multi-oscillator Lorentz dispersion law (fig. S2A). The overall agreement between the simulated and experimental data (Fig. 2B) confirms the validity of our model.
Fig. 2. 3D FEM optical simulations of the micro- and nanostructures of the P. aristolochiae butterfly.
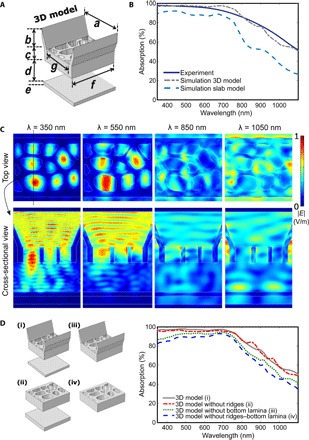
(A) 3D model of the butterfly scale and corresponding parameters extracted from SEM images. The dimensions of this model are as follows: a = 2.0 μm, b = 1.2 μm, c = 0.8 μm, d = 1.2 μm, e = 0.22 μm, f = 5.0 μm, and g = 1.5 μm. (B) Comparison of experimental and simulated absorption spectra under normal incidence. The experimental data are measured with an integrating sphere in the matt black region (solid line). The dashed line corresponds to the simulated 3D model with an air-filling fraction of 59%. For comparison, we also constructed an unpatterned slab model by squeezing the 3D original model into a slab with the same bottom area and volume (long dashed line). (C) Normalized electric field intensity distribution calculated for normal incidence and wavelengths of 350, 550, 850, and 1050 nm. (D) Influence of different structural components of the scale architecture of P. aristolochiae on the absorption properties. The schematics represent different 3D models. The corresponding simulated absorption spectra are shown in the plot on the right. The nanohole array is found to be the primary contributing element for the absorption in the UV-vis–NIR region.
For an equivalent volume of material, Fig. 2B shows that structuring the absorbing medium, as found in the scales of the black butterfly, leads to a marked increase in the absorption over the whole spectral range considered. Quantitatively, this translates into an integrated absorption (IA) increase of 18% with respect to the unpatterned slab of equivalent volume. The absorption enhancement is more prominent in the near-infrared (NIR) region (20 to 35%) than in the visible range (15 to 20%) because of the lower absorption coefficient of the melanin in the NIR range (39).
To understand how these micro- and nanostructures assist the light absorption process, light propagation through the architecture was investigated by using field mapping at four different wavelengths in Fig. 2C. Figure 2D singles out the individual role of different components of butterfly scale morphology in the total light absorption. The selected wavelengths correspond to a value slightly higher than the mean nanohole diameter (350 nm), above the maximum nanohole diameter (850 nm), and covering several nanoholes (1050 nm). Additionally, the field distribution was simulated for an intermediate wavelength of 550 nm, which is close to the solar spectral irradiance maximum. At 350 nm, simulated field maps show that the light does not pass through the ridges. Instead, it propagates along their sidewalls toward the nanohole array. Subsequently, light is channeled inside the nanoholes and partially absorbed at their surface. This mechanism is efficient enough for sustaining a high absorption at short wavelengths, as highlighted by the low absorption difference between the configurations with and without the bottom slab (see Fig. 2D). This propagation regime was numerically and experimentally shown in thin PV absorbers drilled by periodically arranged nanoholes and is referred to as “vertical channeling” (43). The channeled modes, mostly concentrated in the low–refractive index region (air), lead to a lowering of the mean refractive index. Consequently, reflection losses are decreased because of an improved impedance matching between air and the wing. The situation differs as the wavelength increases (see 850 nm), and the light then is efficiently scattered within the whole hole-rib architecture. Both effects—vertical channeling and “in-plane scattering”—act together at 550 nm. The ridges start playing a noticeable role on the light propagation mechanism in the NIR, as observed in Fig. 2C (λ = 1050 nm). However, they do not have a significant impact on the overall broadband absorption (Fig. 2D).
Thus, the outstanding absorption properties originate from a multilevel system where the light is first collected and partly absorbed by the 2D disordered nanohole network (and, to a lower extent, by the grating-like ridges). Then, the photons that emerge out of those structures have a second chance of absorption because of the bottom lamina. As mentioned earlier, the nanohole array is found to be the main contributing element for the absorption in the ultraviolet-visible (UV-vis)–NIR region. Therefore, further analysis is needed to understand the influence of the nanohole size and position disorder on the absorption to design improved thin-film absorbers inspired by black butterfly scales.
Designing thin-film absorbers inspired by black butterfly scales
Several models (38, 39, 44) described the scales of the black butterfly by a periodic distribution of nanoholes. Only recently, Wang et al. (42) showed that the inherent disordered 2D structure found in black butterflies primarily leads to an improved omnidirectionality and polarization tolerance of the absorption compared to periodic designs. However, the correlation between this effect and the degree of disorder was not analyzed and quantified. We therefore numerically investigated this dependence to engineer efficient, bioinspired thin-film absorbers.
For our analysis, we considered photonic structures with three different hole arrangements, as shown in Fig. 3. The latter were drilled into a thin layer made of a-Si:H (see fig. S2B for its optical indices), a commonly used thin-film PV absorber. More precisely, we introduced an “ordered” periodic arrangement of holes with a single diameter, a “perturbed” periodic arrangement of holes with varying diameters, and finally a “correlated” combination of position and diameter size disorder inspired by the black butterfly scales. An unpatterned slab with a thickness of 100 nm served as a reference. All layers were simulated with air as a surrounding medium.
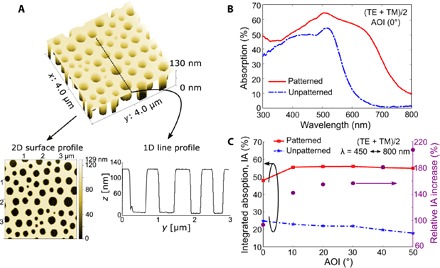
Fig. 3. Simulated optical properties of thin and patterned absorbers made of a-Si:H with increasing disorder magnitudes.

(A) Schematic view of the four considered geometries: “unpatterned” bare slab, ordered periodically arranged holes with a single diameter, perturbed structure of holes with periodic arrangement but varying diameters, and correlated structure with disordered hole positions and varying diameters. The ordered structure has a hole diameter of 240 nm and a period of 300 nm. The ff of all patterned configurations is set to 50.26%. The insets in the lower right corners show the 2D Fourier power spectra of the corresponding structures. (B) A Gaussian distribution with a mean hole diameter of 240 nm and a variance of 20 nm is introduced into the ordered configuration to investigate the effect of size dispersion. (C) Absorption spectra of the four simulated geometries under normal incidence for unpolarized light [(TE + TM)/2]. The IA of each geometry is reported in the legend. (D) IA of the three patterned geometries versus the AOI. The resulting IA varies from 67 to 45% for angles up to 80°.
To establish a meaningful comparison between these three structures, we started with the ordered arrangement comprising a periodic square array of circular holes. The period of the structure (300 nm) and the uniform hole diameter (240 nm) were adopted from Gomard et al. (45), where 2D patterned a-Si:H absorbers were already optimized with respect to their IA. To generate the perturbed configuration, we considered a Gaussian distribution of hole diameters (average, 240 nm; variance, 20 nm) with no overlap of the holes. The resulting distribution is shown in Fig. 3B (eight other different perturbed configurations are considered for calculation, as provided in fig. S3; no significant difference in IA is noticed among them). We chose a Gaussian distribution because it reflects what is obtained experimentally, as discussed in the following sections. To obtain the correlated hole configuration, we shifted the position of the holes by the application of the Lubachevsky-Stillinger (LS) algorithm (46). The generated configurations using the LS algorithm are called correlated disordered structures and exhibit only a short-range order (see the ring-shaped feature on the 2D Fourier spectrum in Fig. 3A). The correlated disorder is controlled by imposing a minimum distance between the centers of the holes. For the three configurations discussed above, the same volume of a-Si:H was considered, but because of patterning, it was lower than that of the unpatterned reference.
The IA was calculated to assess the light-harvesting capability of the four different photonic structures under consideration. The resulting simulated absorption spectra of the four configurations and their corresponding IA were compared in Fig. 3C for a plane wave with a normal angle of incidence (AOI). In the case of the unpatterned reference slab, the IA is only 31.6% [in accordance with the study of Gomard et al. (45)]. On the other hand, the photonic slab with ordered hole array exhibits 63.8% of the average optical absorptivity weighted by solar spectral irradiance in the wavelength range between 305 and 720 nm. This outcome is already two times larger than the bare slab. However, the perturbed structure has an increased IA of 64.5%. Introducing correlation on the position of the holes together with size dispersion, similar to the black butterfly, leads to an IA of 63.9%. All three photonic structures double the IA by a factor of more than 2 compared to unstructured layer.
The absorption peaks of the periodic structure in Fig. 3C can be attributed to the coupling of the incident plane wave with pseudo-guided modes, which is enabled by the periodic patterning (47). The core principle of these designs is a collection of discrete and narrowband resonances based on the coherent scattering of photons (30). The main advantage of ordered structures is the tunability of diffraction (47), which allows a marked increase in the absorption in a targeted, though restricted, spectral range. On the other hand, a great number of resonances are required to cover a large bandwidth and hence to produce a significant IA enhancement (30, 32, 48). For the perturbed configuration, the overlapping absorption peaks broaden, which increases the absorption at around 550 nm, close to the solar spectral irradiance maximum. Consequently, the IA is enhanced by 0.8% (absolute gain). The perturbation of the periodic hole array and the resulting peak broadening is even more pronounced for the correlated configuration. However, the important absorption reduction at short wavelengths (below 450 nm) and around 650 nm limits the IA gain.
The ordered and correlated structures have almost comparable performance for a normal AOI. At high oblique angles, we observed that the ordered configuration is able to maintain a relatively high IA because of the flat photonic bands exploited (49). Nevertheless, the correlated structure enables further improvement of this angular robustness, as demonstrated in Fig. 3D. The drop in the IA of the correlated structure is limited to 22.8% between 0° and 80°, whereas the ordered (perturbed) structure exhibits a drop in IA as high as 27.3% (respectively 26.8%). The IA in periodic or slightly perturbed structures relies on a limited number of absorption peaks with a moderate bandwidth. In contrast, the bioinspired correlated designs have a richer collection of absorption peaks (see also the Fourier spectrum in Fig. 3A) and are therefore less sensitive to angular effects.
We also investigated the polarization dependence of the absorption for all three configurations (fig. S4). The spectra show that the absorption is globally higher for transverse magnetic (TM)–polarized light than for transverse electric (TE)–polarized light under non-normal incidence. The reduction in the absorption for all the configurations at higher AOI is primarily due to increased front-side reflection of the TE-polarized light. The spectra computed for the TM polarization exhibit either an increase or a decrease in the absorption for the ordered and perturbed cases, depending on the spectral region considered. Conversely, the correlated configuration displays a broadband and gradual enhancement of its absorption with increasing AOI (up to 70°) and only a limited absorption decrease at an incidence angle of 80°. This qualitative analysis is consistent with the IA values reported in Fig. 3D and enables us to stress the advantage of bioinspired disordered nanohole distribution over the periodic ones because it optimizes the absorption over a broad spectral and angular range.
Fabrication of thin-film absorbers inspired by black butterfly scales
Motivated by the positive outcome of the simulations, we fabricated bioinspired thin-film absorbers using lateral phase separation of polymer blends and reactive ion etching (RIE). Figure 4A illustrates the fabrication process flow. The lithography technique relies on the phase separation of two nonmiscible polymers in a blend solution during a spin-coating process (see Materials and Methods for details). Multisize nanohole patterns with controllable size distribution and ff were thus obtained (50, 51). Afterward, the nanoholes were transferred into a 130-nm-thick a-Si:H layer by RIE using the patterned resist layer as an etching mask. The optical images in Fig. 4B show the darkish appearance of the patterned and completely etched sample (Fig. 4B, right), in comparison to the unpatterned absorber (Fig. 4B, left) at moderate (30°) and large (80°) viewing angles. SEM images of the resulting correlated disordered nanoholes in the PV absorber are shown in Fig. 4C. A corresponding 2D Fourier power spectrum in the inset of the overview SEM image demonstrates the correlated disorder nature of the nanoholes, confirming the similarity with the previously discussed black butterfly structures. The statistical histogram of the nanohole distribution is provided in Fig. 4D. The hole diameters follow a Gaussian distribution and range between 100 and 600 nm with a mean diameter of 238 nm, which is close to the optimized mean value of 240 nm previously considered in the optical simulations. The resulting ff of approximately 41% is lower than that observed in the matt black wing scales of P. aristolochiae because of the comparably thick “walls” between the holes. Therefore, we analyzed the ff variation of the bioinspired design (results are provided in fig. S5). As expected, we noticed sequential IA increase with increasing ff. The IA significantly drops if the ff goes below 30% because absorption strongly decreases around the solar irradiance peak of 550 nm, but the IA is quite stable for sufficiently high ff (above 40%). Figure 5A shows an atomic force microscopy (AFM) image of the nanoholes etched into the a-Si:H layer. A 1D line profile extracted from this image allows us to confirm that the etching is achieved throughout the whole absorber thickness.
Fig. 4. Fabrication of the bioinspired patterned thin PV absorbers.

(A) Schematic view of the three main fabrication steps including the spin coating of a blend solution of poly(methyl methacrylate) (PMMA) and polystyrene (PS) in methyl ethyl ketone (MEK) on a thin a-Si:H layer deposited on a glass substrate, followed by a selective development of the PS, and finally the transfer of the pattern into a-Si:H by dry etching (RIE). (B) Image of a patterned 130-nm-thin a-Si:H layer on a glass substrate with completely etched disordered nanoholes (right) demonstrates the high omnidirectional absorption properties with respect to the unpatterned sample (left). All images are taken under diffusive white light with observation angles of 30° (top) and 80° (bottom). (C) SEM top-view image of the nanostructured a-Si:H thin film shows the distribution of nanoholes with both size and position disorders. The ring-shaped pattern in the 2D Fourier power spectrum corresponding to this SEM image (inset) confirms the correlated disordered nature of the nanoholes introduced in the thin absorber. (D) Statistical analysis of the nanohole diameters of this sample. The histogram depicting the distribution of nanohole diameters can be approximated by a Gaussian profile with a mean diameter of 238 ± 105 nm.
Fig. 5. Characterization of the bioinspired patterned thin PV absorbers.
(A) 3D AFM image of the bioinspired a-Si:H thin film. 2D surface profile shows a short-range ordered hole distribution that is used for bioinspired solar cell simulation (fig. S7). 1D line profile shows uniform surface patterning with height (etching) profile. (B) Impact of the etched disordered nanoholes on the absorption spectrum measured at normal AOI with unpolarized light. (C) Angular dependence of the IA of the patterned and unpatterned samples. The relative increase in IA raises up to +200% for an AOI of 50°.
The resulting absorption spectrum of the patterned a-Si:H layer at a normal AOI is shown in Fig. 5B. The benefits of patterning become clear by comparing this sample with the unpatterned one (blue dash-dotted line in Fig. 5B). The latter features a low absorption for wavelengths above 500 nm, where the absorption coefficient of a-Si:H is low (see fig. S2B), and exhibits an IA of only 24.8%. In contrast, the bioinspired disordered nanoholes enable the enhancement of the absorption over the whole spectral range. This originates from the previously described light in-coupling (coupling to vertical channeling modes) and light-trapping (coupling to pseudo-guided modes) mechanisms, leading to an IA of 48%. We nevertheless note that the absorption enhancement is limited at around 350 nm. The etching through the whole a-Si:H layer thickness leads to high transmission losses. Because the absorber was thin compared to the simulated black butterfly structure, the channeled light cannot be fully absorbed in a single pass. However, this issue is circumvented in a complete solar cell stack including a rear reflector. Besides, we emphasize that the relative IA increase of 93% measured under normal incidence (and between 450 and 800 nm; see Materials and Methods for details) is even higher at larger AOI and reaches +207% at an incident angle of 50°. Figure 5C highlights this upward trend in the relative IA enhancement with the increase in AOI.
To assess the potential impact of these bioinspired structures of disordered nanoholes on the absorption of complete a-Si:H–based solar cells (21), we performed additional simulations (fig. S6). To this end, we considered a layout consisting of bioinspired holes drilled into the front transparent conductive oxide layer and into the a-Si:H absorbing layer. To be as close as possible to the fabricated samples, we directly imported the measured 3D patterning profile shown in Fig. 5A in the simulated model. The simulated spectra indicate that, under normal incidence, relative IA increases of 16 and 5% are achieved with respect to unpatterned and ordered nanohole patterned solar cells, respectively. Although substantial, this absorption enhancement in a-Si:H does not reach that obtained in the single-patterned slab because of the suppressed transmission losses (back reflector) and the parasitic absorption taking place in all the other layers. Nevertheless, our fabricated patterned a-Si:H thin film demonstrates ideal utilization of bioinspired design principles, optimizing the absorption over a broad spectral and angular range.
DISCUSSION
The wings of P. aristolochiae have a hierarchical design based on ridges and nanoholes to simultaneously provide good mechanical stability and efficient light harvesting. This is notably enabled by an air filling fraction gradient along the wing scales, with a high-ff nanohole array found toward their apex, where the mechanical constraints are more relaxed. Using microspectroscopy, we experimentally correlated the absorption enhancement along the scale with an increase in ff.
To gain further insight into the optical properties of this photonic biostructure, we set up a 3D model based on SEM images and calculated its absorption using FEM simulations. This enabled us to study the respective contribution of the main elements involved, including the disordered nanohole array, the regularly arranged microridges, and the bottom lamina. We conclude that most of the absorption takes place in the hierarchical structure in the upper lamina, with a weak contribution from the ridges especially below 800 nm. Conversely, the nanohole array plays a major role in the visible range with respect to the light in-coupling properties. The incoming light is mostly propagating within the nanoholes, whereby the channeled photons can be efficiently absorbed at their sidewalls. Hole diameters on the order of optical wavelengths further assist in efficient light scattering, in contrast to micrometer-sized holes in other butterflies’ scales (1, 52). In both our simulations and experiments, the wings’ absorption thus plateaued above 95% between 300 and 800 nm. We note that light propagation within the black butterfly biostructures could be further analyzed using artificial, scaled-up samples produced by, for example, 3D printing stereolithography (53).
For these reasons, we implemented the bioinspired structure of nanoholes to enhance absorption in thin a-Si:H active layers that also operate over the visible range. By using simulations, we demonstrated that the IA obtained by patterning the a-Si:H layer with an optimized periodic array of monodisperse holes could be overcome by introducing a controlled amount of disorder in the diameter size distribution, eventually combined with long-range disorder of the hole position (given a fixed volume of absorbing material). This gain is attributed to the broadening of absorption peaks at larger wavelengths. We note that, unlike (ultra)thin crystalline silicon layers, whose optical properties are ruled by a rich collection of absorption peaks, the present a-Si:H absorber only involves a few resonances such that the resulting increase in IA is limited under normal incidence. However, this IA gain becomes more important when the AOI increases, which denotes an ameliorated angular robustness compared to the ordered pattern (54).
In contrast to original butterfly scales, we considered a circular shape of holes in our study, because we can obtain that shape in our fabrication approach. In the horizontal plane, the exact geometry of the holes is likely to modify the absorption (light-coupling) properties of the patterned slab by breaking the symmetry elements of the periodic hole array (55). However, here, the symmetry elements of the array are already broken by the size and position disorder such that the in-plane geometry (shape) of the holes should have a limited impact on the overall absorption properties of the patterned a-Si:H slab. We additionally simulated the absorption of a 100-nm-thick a-Si:H layer drilled with the exact hole geometry of the black butterfly wing matt scales extracted from Fig. 1D (see fig. S7). We observed broad absorption spectrum akin to the correlated one with no specific resonances.
Furthermore, we simulated the original black butterfly 3D model with a correlated circular nanohole geometry, as shown in fig. S8. A hole diameter distribution of 300 ± 85 nm with ff of 59%, similar to matt black butterfly scales, was considered. The simulated absorption spectrum is plotted along with the experimental outcome and with the spectrum simulated using the actual and complete 3D model introduced in Fig. 2A, which are all in good agreement. Consequently, the black butterfly scales optimize the size and position disorder of the nanoholes in the correlated manner, and the shape of the nanoholes has a negligible contribution on their absorption.
To produce a disordered structure of nanoholes inspired by the black butterfly scales, we used a self-assembly technique with controllable ff and hole diameter distribution. Our method has several advantages over conventional lithography because of its simplicity and scalability. In comparison to other bottom-up techniques, for example, colloidal lithography for similar nanostructures, phase separation of binary polymer blends via spin coating offers great flexibility because the hole distribution can be easily tailored by adjusting the processing parameters. For example, by regulating the mass ratio between PS and PMMA, their molecular chain length, the spin-coating parameters with solvent concentration and humidity during spin coating, the hole distribution, and the ff can be tuned in a wide range (50, 51, 56). Moreover, the proposed technique does not require the evaporation of a metal film as an etching mask to transfer the pattern into the a-Si:H slab (33, 57, 58). These advantages make the fabrication process very competitive.
The microphase separation of lipid bilayer membranes of living cells and intracellular organelles in arthropods is believed to self-organize into a rich collection of complex, nano- to mesoscale biostructures (59–62). For example, the coherently blue scattering 2D hexagonally periodic air nanoholes in chitin found in a digger bee (Amegilla cingulata) are possibly formed within the scale cells from the introversion of the plasma membrane into a lyotropic template, followed by extracellular chitin deposition and the maturation of the cell (62). This possible morphological arrangement is found to be analogous to the microphase separation of common amphiphilic macromolecules, such as block copolymers, surfactants, and lipids (62). However, synthetic realization of these structures by phase separation of macromolecules was challenging at the optical length scale so far. In our case, the phase separation of polymer blends in a solvent gives rise to similar structural morphology of chitin/air nanostructures in a black butterfly scale. It leads to an interesting hypothesis of forming these biostructures in black butterfly scales. The self-assembly by phase separation of lipid bilayer membrane in an aqueous medium forms the initial precursor template of disordered nanostructures. The formation pathway follows extracellular chitin deposition onto that preshaped template. Once the cell dies, the cellular cytoplasm could be replaced with air, leaving behind a disordered nanohole chitin/air structure. However, the development of cellular mechanisms tracking the phase separation of chitin in black butterfly scales requires further experiments and observations to test this hypothesis.
Last, we verified experimentally that, by integrating the short-range ordered ensemble of cylindrical holes into a 130-nm-thin a-Si:H slab standing on glass, its IA could be enhanced by up to 93% under normal incidence compared to a flat slab. In addition, by imposing a short-range order, the absorption could be further enhanced for a broad angular range. We thus report more than 200% increase in the IA after patterning the sample with bioinspired nanoholes at large view angles of 50°. The remarkably improved optical performance and scalability of these structures over large areas makes this fabrication route a promising candidate for the integration of bioinspired disordered ensembles of nanoholes as a light in-coupling and light-trapping nanostructures in future PV applications. We note that the in-coupling properties of our design, and hence its absorption capability, can be further enhanced by optimizing the etching profile. Thus, an improved collection of the incoming light is expected by considering an inverted pyramid profile rather than a cylindrical one (54).
Summing up, this study uniquely ventures into the territory of combining bioinspired nanostructures with thin-film PV absorbers, improving their functionality by a factor of 2. They also provide a pathway for further systematic study of nature-inspired nanostructures for optimal design and function of PV devices.
MATERIALS AND METHODS
Patterning of thin-film PV absorbers
a-Si:H (130 nm thick) was deposited on Corning glass substrates using plasma-enhanced chemical vapor deposition at a plasma excitation frequency of 13.56 MHz and a substrate temperature of 180°C. A high discharge power of 0.3 W/cm2 and a SiH4/H2 flow of 41/339 SCCM (standard cubic centimeter per minute) were used for the deposition of the a-Si:H films. More details regarding the deposition parameters are provided by Merdzhanova et al. (63). The a-Si:H layer on glass was used as a substrate to spin coat the polymer blend. PMMA (Mw = 9590; Polymer Standards Service GmbH) and PS (Mw = 19,100; Polymer Standards Service GmbH) were dissolved in MEK (Sigma-Aldrich Co. LLC) with a mass ratio of 60 and 40%, respectively. The concentration of the solutions was kept fixed at 20 mg/ml. Solutions were spin-coated on the glass substrates with a speed of 1500 rpm and an acceleration of 2000 rpm/s for 30 s. Relative humidity was maintained between 40 and 50% during the spin coating. The demixing of the blend components out of the smooth surface occurred during spin coating itself because of the difference in relative solubilities of PS and PMMA in MEK. From the values of the Hildebrand solubility parameter (64), MEK is a better solvent for PMMA. PMMA collapses earlier into solidification that forms the surface covering layer, whereas PS forms island-like structures in PS/PMMA blends with this particular solvent.
The samples were then rinsed in cyclohexane for 6 min and dried in a stream of N2 to remove the PS islands. Afterward, the pattern was transferred into the a-Si:H layer by RIE (Oxford 80 Plasmalab Etcher) using the PMMA layer as an etching mask. a-Si:H was etched using a SF6/Ar-based plasma at an operational pressure of 25 mT and a power of 50 W. The SF6/Ar flow rate was fixed at 5/20 SCCM. The remaining PMMA was finally removed under oxygen plasma.
Optical simulations
All optical simulations were performed using the FEM with the software COMSOL Multiphysics. Periodic boundary conditions in the lateral directions (x and y) were applied in all calculations. An incoming plane wave impinging the structures under normal incidence was used, and all the calculations were performed with a spatial resolution of 5 nm. In the simulation process, the boundary conditions of the electromagnetic fields in the vertical (z) direction were set on the perfect matching layer for the model. The mesh resolution was set to have at least 10 grid points per wavelength in the chitin-melanin composite material of the butterfly scales and in the a-Si:H thin films.
The IA was calculated for individual geometries for unpolarized light [(TE + TM)/2] at normal and oblique incident angles. The IA of the structures is defined as the integration of the absorption, taking into account the spectral irradiance of the sun (http://rredc.nrel.gov/solar/spectra/am1.5/; American Society for Testing and Materials, AM1.5 standard curve) from λmin to λg, and is given by (21)
| (1) |
where is the incident solar radiation intensity per unit wavelength and A(λ) is the absorption
| (2) |
Pincident(λ) is the incident power in watts, and = 1/2ωε|||E(λ)|2 is the power absorbed per unit volume (65) calculated from the divergence of the Poynting vector. |E(λ)|2 is the magnitude of the electric field intensity, ω = 2πc/λ is the angular frequency of the light, where c is the speed of light in vacuum, and ε|| is the imaginary part of the dielectric permittivity.
P. aristolochiae wing micro- and nanostructures
The parameters of the 3D FEM model of the P. aristolochiae wing nano- and microstructures were obtained from SEM images. The IA was calculated from 350 nm (λmin) to 1100 nm (λg).
Bioinspired thin films
The correlated thin-film configuration was generated using a freely available source code (http://chemists.princeton.edu/torquato/links-and-codes/) based on the LS algorithm (46). The method is a hard-particle molecular dynamics algorithm for producing dense disordered and ordered systems. Adjusting a few available parameters, different kinds of structures, ranging from random to nearly periodic, can be generated with this method, imposing hard or periodic boundary conditions. The final structure was then obtained by recording the position of the center of the discs and using these coordinates. The FEM model was constructed with MATLAB and COMSOL software packages. We considered 25 nanoholes in the simulation domain because this value has been reported to be sufficient to mimic the infinite structural optical absorption (66). A thickness of 100 nm for the a-Si:H layer was considered, which is lower than the mean free path of the minority carriers in this material (21). The IA was calculated from 305 nm (λmin) to 720 nm (λg).
Characterization
Macrospectroscopic analysis
We macroscopically measured the overall reflection (at 8° AOI) and transmission spectra of the P. aristolochiae wings and the fabricated bioinspired a-Si:H absorbers. This was performed in the visible range (300 to 800 nm) using a UV-vis spectrometer (Lambda 1050, PerkinElmer Inc.) with an InGaAs 150-mm integrating sphere. A spot diameter of ≈3 mm was used. All measurements were recorded with unpolarized light. The absorption (A) was derived out of the reflection (R) and transmission (T) measurements by using A = 1 − R − T.
Angle-dependent reflectance (R), transmittance (T), and hence absorption (1 − R − T) measurements were performed with a custom-built motorized integrating sphere apparatus, similar to previous work (67, 68) with a monochromator-coupled tunable (λ = 450 to 800 nm) supercontinuum laser (Fianium) and a Si photodetector. Again, all measurements were recorded with unpolarized light. The sample was placed in the middle of the integrating sphere using a vise-type center mount, and the sample holder was rotated around the vertical axis for angle-resolved measurements. Transmission measurements were normalized to the uncovered area of the underlying glass slide, whereas reflection measurements were normalized to a reflectance standard (Labsphere) within the sphere.
Microspectroscopic analysis
A customized Zeiss Axio microscope with a spot diameter of ≈25 μm in bright-field reflection and transmission mode with a halogen lamp in Koehler illumination was used for the microspectroscopic analysis of individual scales. Unpolarized light from the halogen lamp was illuminated via a 10× objective (EC Epiplan-Apochromat, Zeiss) with a numerical aperture (NA) of 0.3 for reflection measurement. A condenser with a NA of 0.25 was used for transmitted light. The transmitted and reflected light was collected with a spectrometer (AvaSpec-HS2048, Avantes) through a 200-μm core optical fiber (Avantes) mounted in confocal configuration. Absorption was then derived by applying A = 1 − R − T of the integrating sphere measurements.
High-resolution imaging
Dried wings of P. aristolochiae were coated with 15-nm-thin gold layer (K575X sputter coater, Quorum Technologies Ltd.) before examination by SEM (SUPRA 60 VP, Carl Zeiss Microscopy GmbH) operated at 5 kV.
Cross-sectional imaging was performed to design the 3D model for FEM simulation. For that, small pieces of wings were embedded in epoxide resin. First, the pieces were dipped in a combination of 70% acetone and 30% epoxide mix (42.4 g of glycidether, 29.6 g of dodecenyl succinic anhydride, and 18.4 g of methyl nadic anhydride; all chemicals were from SERVA Electrophoresis GmbH). Subsequently, they were exposed to vacuum for a few minutes to remove air bubbles. Afterward, the mixture was shaken for an hour. This step was first repeated with a combination of 30% acetone and 70% epoxide mix and then twice with 100% epoxide mix to ensure that the viscous resin penetrated into all the tiny cavities of the butterfly scales. The resin-infiltrated wing pieces were placed into a silicone mold, covered with an epoxide mix plus accelerator (10 g of epoxide mix and 0.265 g of benzyldimethylamine), and baked at 65°C for 2 days. The polymerized block was removed from the mold and trimmed to expose the wing piece. Thin (≈70 nm) sections from the block face were prepared using an ultramicrotome (Leica Microsystems) and transferred to small pieces of silicon wafer for SEM imaging. The cross section shown in Fig. 1C was imaged at 1.5 kV in a SEM (Ultra, Carl Zeiss Microscopy GmbH).
Topographical analysis
ImageJ, a public domain and Java-based image processing program tool, was used to perform the statistical analysis of the nanohole size on the wing membrane (69). The image analysis requires a “binary” black and white image. A threshold range was set in our case to recognize the objects of interest (holes) apart from the background. All pixels with values below the threshold were converted to black (holes), whereas all pixels with values above the threshold were converted to white (background). Subsequently, their centers and areas were computed. The 2D Fourier power spectra were obtained from the presented SEM images and calculated with the FFT algorithm of MATLAB.
Supplementary Material
Acknowledgments
We thank A. Gerstner (Stadtpark Mannheim GmbH) for supplying the P. aristolochiae butterfly sample and P. Abaffy [Karlsruhe Institute of Technology (KIT)], C. Bartels (University of Heidelberg), and I. Wacker (University of Heidelberg) for performing the surface and cross-sectional imaging of the butterfly scales with SEM. Furthermore, we are indebted to S. Vignolini (University of Cambridge) for allowing us to use their microspectroscopy setup. We also acknowledge fruitful discussions with all members of the Biomimetics group at the Institute of Microstructure Technology (KIT). Last, we acknowledge support from the state of Baden-Württemberg through bwHPC. Funding: R.H.S. acknowledges funding by the Karlsruhe House of Young Scientists for a research stay at the University of Cambridge. G.G. acknowledges funding by the Helmholtz Postdoctoral Program. This work was supported, in part, by the Deutsche Forschungsgemeinschaft (DFG) through program DFG-SPP 1839 “Tailored Disorder,” the Karlsruhe School of Optics and Photonics (KSOP; www.ksop.kit.edu), and the Karlsruhe Nano Micro Facility (KNMF; www.ksop.kit.edu), a Helmholtz Research Infrastructure at KIT (www.kit.edu). Author contributions: R.H.S., G.G., and H.H. conceived the study. R.H.S., Y.J.D., and G.G. designed the analyses. R.H.S. conducted the microscopy and spectroscopy of the black butterfly. Y.J.D. conducted the simulations and numerical analysis. R.H.S., Y.J.D., T.M., and G.G. fabricated and characterized the samples. R.H.S., Y.J.D., G.G., and S.Y. performed the optical characterization. H.H. and U.L. supervised the project. R.H.S., G.G., and H.H. wrote the initial manuscript. All authors discussed the results and commented on the manuscript. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/10/e1700232/DC1
fig. S1. Matt black and dull black scales of the P. aristolochiae butterfly wings.
fig. S2. Optical indices of the materials considered for the simulations.
fig. S3. Simulated absorption spectra of different perturbed patterned PV absorbers.
fig. S4. Polarization and angle-resolved simulated absorption spectra of the different patterned thin PV absorbers considered in Fig. 3.
fig. S5. Air-filling fraction influence on absorption properties of PV absorber patterned with correlated disorder design.
fig. S6. Comparison of simulated absorption spectra of unpatterned, ordered, and bioinspired nanohole patterned solar cells.
fig. S7. Simulated absorption spectrum of a 100-nm-thick a-Si:H film patterned with exact high absorbing nanohole geometry of P. aristolochiae butterfly wings.
fig. S8. Simulated absorption spectra of the P. aristolochiae butterfly wings obtained with a nanohole array made of the “actual” and correlated arrangement.
REFERENCES AND NOTES
- 1.Ghiradella H., Light and color on the wing: Structural colors in butterflies and moths. Appl. Opt. 30, 3492–3500 (1991). [DOI] [PubMed] [Google Scholar]
- 2.Siddique R. H., Diewald S., Leuthold J., Hölscher H., Theoretical and experimental analysis of the structural pattern responsible for the iridescence of Morpho butterflies. Opt. Express 21, 14351–14361 (2013). [DOI] [PubMed] [Google Scholar]
- 3.Siddique R. H., Gomard G., Hölscher H., The role of random nanostructures for the omnidirectional anti-reflection properties of the glasswing butterfly. Nat. Commun. 6, 6909 (2015). [DOI] [PubMed] [Google Scholar]
- 4.Sharma V., Crne M., Park J. O., Srinivasarao M., Structural origin of circularly polarized iridescence in jeweled beetles. Science 325, 449–451 (2009). [DOI] [PubMed] [Google Scholar]
- 5.Syurik J., Siddique R. H., Dollmann A., Gomard G., Schneider M., Worgull M., Wiegand G., Hölscher H., Bio-inspired, large scale, highly-scattering films for nanoparticle-alternative white surfaces. Sci. Rep. 7, 46637 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Prum R. O., Torres R., Structural colouration of avian skin: Convergent evolution of coherently scattering dermal collagen arrays. J. Exp. Biol. 206, 2409–2429 (2003). [DOI] [PubMed] [Google Scholar]
- 7.Stavenga D. G., Leertouwer H. L., Marshall N. J., Osorio D., Dramatic colour changes in a bird of paradise caused by uniquely structured breast feather barbules. Proc. R. Soc. B 278, 2098–2104 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Spinner M., Kovalev A., Gorb S. N., Westhoff G., Snake velvet black: Hierarchical micro and nanostructure enhances dark colouration in Bitis rhinoceros. Sci. Rep. 3, 1846 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Teyssier J., Saenko S. V., van der Marel D., Milinkovitch M. C., Photonic crystals cause active colour change in chameleons. Nat. Commun. 6, 6368 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Hsiung B.-K., Siddique R. H., Jiang L., Liu Y., Lu Y., Shawkey M. D., Blackledge T. A., Tarantula-inspired noniridescent photonics with long-range order. Adv. Opt. Mater. 5, 1600599 (2017). [Google Scholar]
- 11.Mäthger L. M., Denton E. J., Marshall N. J., Hanlon R. T., Mechanisms and behavioural functions of structural coloration in cephalopods. J. R. Soc. Interface 6 (suppl. 2), S149–S163 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Gur D., Palmer B. A., Leshem B., Oron D., Fratzl P., Weiner S., Addadi L., The mechanism of color change in the neon tetra fish: A light-induced tunable photonic crystal array. Angew. Chem. Int. Ed. 54, 12426–12430 (2015). [DOI] [PubMed] [Google Scholar]
- 13.Vignolini S., Moyroud E., Glover B. J., Steiner U., Analysing photonic structures in plants. J. R. Soc. Interface 10, 20130394 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Vignolini S., Rudall P. J., Rowland A. V., Reed A., Moyroud E., Faden R. B., Baumberg J. J., Glover B. J., Steiner U., Pointillist structural color in Pollia fruit. Proc. Natl. Acad. Sci. U.S.A. 109, 15712–15715 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Huang Z., Yang S., Zhang H., Zhang M., Cao W., Replication of leaf surface structures for light harvesting. Sci. Rep. 5, 14281 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hünig R., Mertens A., Stephan M., Schulz A., Richter B., Hetterich M., Powalla M., Lemmer U., Colsmann A., Gomard G., Flower power: Exploiting plants’ epidermal structures for enhanced light harvesting in thin-film solar cells. Adv. Opt. Mater. 4, 1487–1493 (2016). [Google Scholar]
- 17.Kim J.-J., Lee J., Yang S.-P., Kim H. G., Kweon H.-S., Yoo S., Jeong K.-H., Biologically inspired organic light-emitting diodes. Nano Lett. 16, 2994–3000 (2016). [DOI] [PubMed] [Google Scholar]
- 18.Li X., Yuan X., Shang W., Guan Y., Deng L., Chen S., Lifetime improvement of organic light-emitting diodes with a butterfly wing’s scale-like nanostructure as a flexible encapsulation layer. Org. Electron. 37, 453–457 (2016). [Google Scholar]
- 19.Zhou D., Biswas R., Photonic crystal enhanced light-trapping in thin film solar cells. J. Appl. Phys. 103, 093102 (2008). [Google Scholar]
- 20.Wang W., Wu S., Reinhardt K., Lu Y., Chen S., Broadband light absorption enhancement in thin-film silicon solar cells. Nano Lett. 10, 2012–2018 (2010). [DOI] [PubMed] [Google Scholar]
- 21.Gomard G., Meng X., Drouard E., El Hajjam K., Gerelli E., Peretti R., Fave A., Orobtchouk R., Lemiti M., Seassal C., Light harvesting by planar photonic crystals in solar cells: The case of amorphous silicon. J. Opt. 14, 024011 (2012). [Google Scholar]
- 22.Narasimhan V. K., Cui Y., Nanostructures for photon management in solar cells. Nanophotonics 2, 187–210 (2013). [Google Scholar]
- 23.Brongersma M. L., Cui Y., Fan S., Light management for photovoltaics using high-index nanostructures. Nat. Mater. 13, 451–460 (2014). [DOI] [PubMed] [Google Scholar]
- 24.Haug F.-J., Ballif C., Light management in thin film silicon solar cells. Energy Environ. Sci. 8, 824–837 (2015). [Google Scholar]
- 25.Palanchoke U., Jovanov V., Kurz H., Dewan R., Magnus P., Stiebig H., Knipp D., Influence of back contact roughness on light trapping and plasmonic losses of randomly textured amorphous silicon thin film solar cells. Appl. Phys. Lett. 102, 083501 (2013). [Google Scholar]
- 26.Hongsingthong A., Krajangsang T., Yunaz I. A., Miyajima S., Konagai M., ZnO films with very high haze value for use as front transparent conductive oxide films in thin-film silicon solar cells. Appl. Phys. Express 3, 051102 (2010). [Google Scholar]
- 27.Hauser H., Tucher N., Tokai K., Schneider P., Wellens C., Volk A. K., Seitz S., Benick J., Barke S., Dimroth F., Müller C., Glinsner T., Bläsi B., Development of nanoimprint processes for photovoltaic applications. J. Micro Nanolithogr. MEMS MOEMS 14, 031210 (2015). [Google Scholar]
- 28.Martins E. R., Li J., Liu Y. K., Depauw V., Chen Z., Zhou J., Krauss T. F., Deterministic quasi-random nanostructures for photon control. Nat. Commun. 4, 2665 (2013). [DOI] [PubMed] [Google Scholar]
- 29.Smith A. J., Wang C., Guo D., Sun C., Huang J., Repurposing blue-ray movie discs as quasi-random nanoimprinting templates for photon management. Nat. Commun. 5, 5517 (2014). [DOI] [PubMed] [Google Scholar]
- 30.Oskooi A., Favuzzi P. A., Tanaka Y., Shigeta H., Kawakami Y., Noda S., Partially disordered photonic-crystal thin films for enhanced and robust photovoltaics. Appl. Phys. Lett. 100, 181110 (2012). [Google Scholar]
- 31.Pratesi F., Burresi M., Riboli F., Vynck K., Wiersma D. S., Disordered photonic structures for light harvesting in solar cells. Opt. Express 21 (suppl. 3), A460–A468 (2013). [DOI] [PubMed] [Google Scholar]
- 32.Vynck K., Burresi M., Riboli F., Wiersma D. S., Photon management in two-dimensional disordered media. Nat. Mater. 11, 1017–1022 (2012). [DOI] [PubMed] [Google Scholar]
- 33.Trompoukis C., Massiot I., Depauw V., El Daif O., Lee K., Dmitriev A., Gordon I., Mertens R., Poortmans J., Disordered nanostructures by hole-mask colloidal lithography for advanced light trapping in silicon solar cells. Opt. Express 24, A191–A201 (2016). [DOI] [PubMed] [Google Scholar]
- 34.Rawlins J. E., Thermoregulation by the black swallowtail butterfly, papilio polyxenes (Lepidoptera: Papilionidae). Ecology 61, 345–357 (1980). [Google Scholar]
- 35.Kingsolver J. G., Butterfly thermoregulation: Organismic mechanisms and population consequences. J. Res. Lep. 24, 1–20 (1985). [Google Scholar]
- 36.Schmitz H., Thermal characterization of butterfly wings—1. Absorption in relation to different color, surface structure and basking type. J. Therm. Biol. 19, 403–412 (1994). [Google Scholar]
- 37.Vukusic P., Sambles J. R., Lawrence C. R., Structurally assisted blackness in butterfly scales. Proc. R. Soc. B 271 (suppl. 4), S237–S239 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Zhao Q., Guo X., Fan T., Ding J., Zhanga D., Guo Q., Art of blackness in butterfly wings as natural solar collector. Soft Matter 7, 11433–11439 (2011). [Google Scholar]
- 39.Herman A., Vandenbem C., Deparis O., Simonis P., Vigneron J. P., Nanoarchitecture in the black wings of Troides magellanus: A natural case of absorption enhancement in photonic materials. Proc. SPIE 8094, 80940H1–80940H12 (2011). [Google Scholar]
- 40.Zhang W., Zhang D., Fan T., Gu J., Ding J., Wang H., Guo Q., Ogawa H., Novel photoanode structure templated from butterfly wing scales. Chem. Mater. 21, 33–40 (2009). [Google Scholar]
- 41.Zhao Q., Fan T., Ding J., Zhang D., Guo Q., Kamada M., Super black and ultrathin amorphous carbon film inspired by anti-reflection architecture in butterfly wing. Carbon 49, 877–883 (2011). [Google Scholar]
- 42.Wang W., Zhang W., Fang X., Huang Y., Liu Q., Bai M., Zhang D., Omnidirectional light absorption of disordered nano-hole structure inspired from Papilio ulysses. Opt. Lett. 39, 4208–4211 (2014). [DOI] [PubMed] [Google Scholar]
- 43.Gomard G., Peretti R., Callard S., Meng X., Artinyan R., Deschamps T., Roca i Cabarrocas P., Drouard E., Seassal C., Blue light absorption enhancement based on vertically channeling modes in nano-holes arrays. Appl. Phys. Lett. 104, 051119 (2014). [Google Scholar]
- 44.Lou S., Guo X., Fan T., Zhang D., Butterflies: Inspiration for solar cells and sunlight water splitting catalysts. Energy Environ. Sci. 5, 9195–9216 (2012). [Google Scholar]
- 45.Gomard G., Drouard E., Letartre X., Meng X., Kaminski A., Fave A., Lemiti M., Garcia-Caurel E., Seassal C., Two-dimensional photonic crystal for absorption enhancement in hydrogenated amorphous silicon thin film solar cells. J. Appl. Phys. 108, 123102 (2010). [Google Scholar]
- 46.Skoge M., Donev A., Stillinger F. H., Torquato S., Packing hyperspheres in high-dimensional Euclidean spaces. Phys. Rev. E 74, 041127 (2006). [DOI] [PubMed] [Google Scholar]
- 47.M. Lou, H. Bao, C. Zhao, Light trapping in thin film disordered nanohole patterns: Effects of oblique incidence and intrinsic absorption. arXiv:1312.1425 (2013).
- 48.Lin C., Martínez L. J., Povinelli M. L., Experimental broadband absorption enhancement in silicon nanohole structures with optimized complex unit cells. Opt. Express 21 (suppl. 5), A872–A882 (2013). [DOI] [PubMed] [Google Scholar]
- 49.Park Y., Drouard E., El Daif O., Letartre X., Viktorovitch P., Fave A., Kaminski A., Lemiti M., Seassal C., Absorption enhancement using photonic crystals for silicon thin film solar cells. Opt. Express 17, 14312–14321 (2009). [DOI] [PubMed] [Google Scholar]
- 50.Huang C., Moosmann M., Jin J., Heiler T., Walheim S., Schimmel T., Polymer blend lithography: A versatile method to fabricate nanopatterned self-assembled monolayers. Beilstein J. Nanotechnol. 3, 620–628 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Guo X., Liu L., Zhuang Z., Chen X., Ni M., Li Y., Cui Y., Zhan P., Yuan C., Ge H., Wang Z., Chen Y., A new strategy of lithography based on phase separation of polymer blends. Sci. Rep. 5, 15947 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Siddique R. H., Vignolini S., Bartels C., Wacker I., Hölscher H., Colour formation on the wings of the butterfly Hypolimnas salmacis by scale stacking. Sci. Rep. 6, 36204 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Man W., Florescu M., Matsuyama K., Yadak P., Nahal G., Hashemizad S., Williamson E., Steinhardt P., Torquato S., Chaikin P., Photonic band gap in isotropic hyperuniform disordered solids with low dielectric contrast. Opt. Express 21, 19972–19981 (2013). [DOI] [PubMed] [Google Scholar]
- 54.Trompoukis C., El Daif O., Pratim Sharma P., Sivaramakrishnan Radhakrishnan H., Debucquoy M., Depauw V., Van Nieuwenhuysen K., Gordon I., Mertens R., Poortmans J., Passivation of photonic nanostructures for crystalline silicon solar cells. Prog. Photovoltaics 23, 734–742 (2015). [Google Scholar]
- 55.Xia Z., Qin X., Wu Y., Pan Y., Zhou J., Zhang Z., Efficient broadband light absorption in elliptical nanohole arrays for photovoltaic application. Opt. Lett. 40, 5814–5817 (2015). [DOI] [PubMed] [Google Scholar]
- 56.Siddique R. H., Mertens J., Hölscher H., Vignolini S., Scalable and controlled self-assembly of aluminum-based random plasmonic metasurfaces. Light Sci. Appl. 6, e17015 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Yeo C. I., Song Y. M., Jang S. J., Lee Y. T., Wafer-scale broadband antireflective silicon fabricated by metal-assisted chemical etching using spin-coating Ag ink. Opt. Express 19, A1109–A1116 (2011). [DOI] [PubMed] [Google Scholar]
- 58.Wang F., Yu H. Y., Wang X., Li J., Sun X., Yang M., Wong S. M., Zheng H., Maskless fabrication of large scale Si nanohole array via laser annealed metal nanoparticles catalytic etching for photovoltaic application. J. Appl. Phys. 108, 024301 (2010). [Google Scholar]
- 59.Ghiradella H. T., Butler M. W., Many variations on a few themes: A broader look at development of iridescent scales (and feathers). J. R. Soc. Interface 6 (suppl. 2), S243–S251 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Dufresne E. R., Noh H., Saranathan V., Mochrie S. G. J., Cao H., Prum R. O., Self-assembly of amorphous biophotonic nanostructures by phase separation. Soft Matter 5, 1792–1795 (2009). [Google Scholar]
- 61.Saranathan V., Osuji C. O., Mochrie S. G. J., Noh H., Narayanan S., Sandy A., Dufresne E. R., Prum R. O., Structure, function, and self-assembly of single network gyroid (I4132) photonic crystals in butterfly wing scales. Proc. Natl. Acad. Sci. U.S.A. 107, 11676–11681 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Saranathan V., Seago A. E., Sandy A., Narayanan S., Mochrie S. G. J., Dufresne E. R., Cao H., Osuji C. O., Prum R. O., Structural diversity of arthropod biophotonic nanostructures spans amphiphilic phase-space. Nano Lett. 15, 3735–3742 (2015). [DOI] [PubMed] [Google Scholar]
- 63.Merdzhanova T., Woerdenweber J., Zimmermann T., Zastrow U., Flikweert A. J., Stiebig H., Beyer W., Gordijn A., Single-chamber processes for a-Si:H solar cell deposition. Sol. Energy Mater. Sol. Cells 98, 146–153 (2012). [Google Scholar]
- 64.Cui L., Ding Y., Li X., Wang Z., Han Y., Solvent and polymer concentration effects on the surface morphology evolution of immiscible polystyrene/poly (methyl methacrylate) blends. Thin Solid Films 515, 2038–2048 (2006). [Google Scholar]
- 65.Grandidier J., Deceglie M. G., Callahan D. M., Atwater H. A., Simulations of solar cell absorption enhancement using resonant modes of a nanosphere array. J. Photonics Energy 2, 024502-1–024502-11 (2012). [Google Scholar]
- 66.Fang X., Lou M., Bao H., Zhao C. Y., Thin films with disordered nanohole patterns for solar radiation absorbers. J. Quant. Spectrosc. Radiat. Transfer 158, 145–153 (2015). [Google Scholar]
- 67.Kelzenberg M. D., Boettcher S. W., Petykiewicz J. A., Turner-Evans D. B., Putnam M. C., Warren E. L., Spurgeon J. M., Briggs R. M., Lewis N. S., Atwater H. A., Enhanced absorption and carrier collection in Si wire arrays for photovoltaic applications. Nat. Mater. 9, 239–244 (2010). [DOI] [PubMed] [Google Scholar]
- 68.Yalamanchili S., Emmer H. S., Fountaine K. T., Chen C. T., Lewis N. S., Atwater H. A., Enhanced absorption and <1% spectrum-and-angle-averaged reflection in tapered microwire arrays. ACS Photonics 3, 1854–1861 (2016). [Google Scholar]
- 69.Schneider C. A., Rasband W. S., Eliceiri K. W., NIH Image to ImageJ: 25 years of image analysis. Nat. Methods 9, 671–675 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/10/e1700232/DC1
fig. S1. Matt black and dull black scales of the P. aristolochiae butterfly wings.
fig. S2. Optical indices of the materials considered for the simulations.
fig. S3. Simulated absorption spectra of different perturbed patterned PV absorbers.
fig. S4. Polarization and angle-resolved simulated absorption spectra of the different patterned thin PV absorbers considered in Fig. 3.
fig. S5. Air-filling fraction influence on absorption properties of PV absorber patterned with correlated disorder design.
fig. S6. Comparison of simulated absorption spectra of unpatterned, ordered, and bioinspired nanohole patterned solar cells.
fig. S7. Simulated absorption spectrum of a 100-nm-thick a-Si:H film patterned with exact high absorbing nanohole geometry of P. aristolochiae butterfly wings.
fig. S8. Simulated absorption spectra of the P. aristolochiae butterfly wings obtained with a nanohole array made of the “actual” and correlated arrangement.


