Time-to-Seizure Modeling of Lacosamide Used in Monotherapy in Patients with Newly Diagnosed Epilepsy

Abstract

Objectives

To quantify the relationship between exposure to lacosamide monotherapy and seizure probability, and to simulate the effect of changing the dose regimen.

Methods

Structural time-to-event models for dropouts (not because of a lack of efficacy) and seizures were developed using data from 883 adult patients newly diagnosed with epilepsy and experiencing focal or generalized tonic–clonic seizures, participating in a trial (SP0993; ClinicalTrials.gov identifier: NCT01243177) comparing the efficacy of lacosamide and carbamazepine controlled-release monotherapy. Lacosamide dropout and seizure models were used for simulating the effect of changing the initial target dose on seizure freedom.

Results

Repeated time-to-seizure data were described by a Weibull distribution with parameters estimated separately for the first and subsequent seizures. Daily area under the plasma concentration–time curve was related linearly to the log-hazard. Disease severity, expressed as the number of seizures during the 3 months before the trial (baseline), was a strong predictor of seizure probability: patients with 7–50 seizures at baseline had a 2.6-fold (90% confidence interval 2.01–3.31) higher risk of seizures compared with the reference two to six seizures. Simulations suggested that a 400-mg/day, rather than a 200-mg/day initial target dose for patients with seven or more seizures at baseline could potentially result in an additional 8% of seizure-free patients for 6 months at the last evaluated dose level. Patients receiving lacosamide had a slightly lower dropout risk compared with those receiving carbamazepine.

Conclusion

Baseline disease severity was the most important predictor of seizure probability. Simulations suggest that an initial target dose >200 mg/day could potentially benefit patients with greater disease severity.

Electronic supplementary material

The online version of this article (doi:10.1007/s40262-017-0530-8) contains supplementary material, which is available to authorized users.

Key Points

The present work applied time-to-event modeling to quantify the dropout risk as well as the exposure–response relationship between lacosamide plasma concentration and seizure probability, in newly diagnosed patients with focal or generalized tonic–clonic seizures without signs of focal onset (provided they had no history or findings suggestive of idiopathic generalized epilepsy).

Baseline disease severity expressed as the number of seizures in the previous 3 months was identified as a key predictor of seizure risk in addition to the area under the plasma concentration–time curve of lacosamide.

Simulations suggested that an initial target dose >200 mg/day could potentially benefit patients with greater disease severity.

Introduction

Lacosamide (LCM) is an anti-epileptic drug (AED) that exerts its therapeutic activity by selectively enhancing the slow inactivation of voltage-gated sodium channels [1]. Like that of all newer AEDs, the clinical trial program of LCM began in the adjunctive setting, as treatment for adult patients with focal epilepsy. Following demonstration of efficacy and safety as adjunctive therapy [2–4], clinical trials in the monotherapy setting were initiated. Lacosamide was approved as monotherapy for patients with newly diagnosed epilepsy in USA in 2014 based on the results of a historical-controlled, double-blind, conversion-to-monotherapy trial [5]. However, for approval in Europe, an active-controlled trial is required. Therefore, according to European Medicines Agency guidelines [6], a non-inferiority trial (SP0993; ClinicalTrials.gov identifier: NCT01243177) [7] was conducted with the aim of demonstrating at least a similar benefit-risk balance for LCM compared with an acknowledged standard AED at individually optimized dosages using clinically relevant endpoints. The choice of carbamazepine controlled release (CBZ-CR) as the standard AED was based on the 2006 treatment guidelines of the International League Against Epilepsy [8]. Over 800 patients with newly diagnosed epilepsy were randomized and results indicated that LCM met the primary endpoint, based on the proportion of patients remaining seizure free for 6 consecutive months following stabilization at the last evaluated dose, LCM was non-inferior to CBZ-CR [7]. LCM was also generally well tolerated in this patient population [7].

The aim of the present work was to identify an exposure–response relationship under the challenging setting of a trial design where patients move to a higher dose level if their response is insufficient (i.e., seizures occurring despite treatment). Given that patients could have more than one seizure during the course of the trial, data were analyzed using a repeated time-to-event modeling approach. Step-wise model building was carried out using data from a previous clinical trial comparing levetiracetam and CBZ-CR in a similar patient population using a similar design [9]. The structural and covariate model from this first analysis was then applied to the new study involving LCM. The report presented here focuses on the description and discussion of the modeling results from that latter study. We also used simulations to evaluate the impact of varying the dose, according to baseline disease severity, on seizure freedom.

Patients and Methods

Study Design

SP0993 (ClinicalTrials.gov identifier: NCT01243177) was a multicenter, double-blind, double-dummy, randomized, positive-controlled, non-inferiority trial comparing the efficacy and safety of LCM and CBZ-CR as monotherapy in patients with epilepsy [7]. Target dose levels were 200, 400, or 600 mg/day for LCM, and 400, 800, or 1200 mg/day for CBZ-CR, respectively (twice-daily administration). Patients were ≥16 years of age and newly diagnosed with focal or generalized tonic–clonic seizures without signs of focal onset, provided they had no history or clinical or electroencephalographic findings suggestive of idiopathic generalized epilepsy. Patients with a history or a clinical or electroencephalographic finding suggestive of genetic generalized epilepsy were excluded [7].

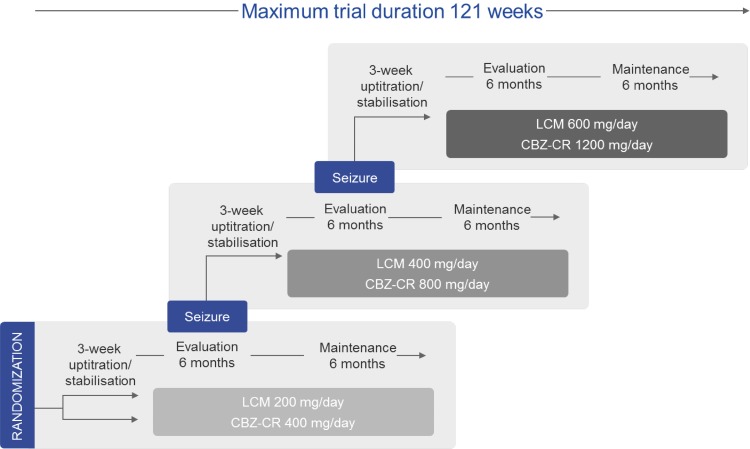
The dose-escalation procedure is depicted in Fig. 1. Patients entered a 2-week up-titration period to the first target dose, followed by a 1-week stabilization period, a 26-week evaluation period, and a maintenance period of 26 additional weeks. If a seizure occurred during the evaluation period, the dose was escalated over a 2-week period to the next level, followed once again by a 1-week stabilization period, a 26-week evaluation period, and a 26-week maintenance period. The same process was followed in the event of a second seizure. If patients still experienced seizures at the third dose level, they were withdrawn from the trial.

Fig. 1.

Design of lacosamide (LCM) SP0993 clinical trial. The randomization starting dose was LCM 100 mg/day or carbamazepine controlled release (CBZ-CR) 200 mg/day

Blood samples were collected for the determination of LCM and CBZ plasma concentrations at the end of the up-titration/stabilization period and at evaluation and maintenance visits, as well as the early termination visit. LCM and CBZ plasma concentrations were determined by SGS Cephac Europe (Saint Benoit, France) using validated liquid chromatography methods with tandem mass spectrometry detection. The lower limits of quantification were 0.05 and 0.25 µg/mL, respectively. The mean imprecision (coefficient of variation) and inaccuracy (% relative error) on quality control samples were <8 and <3% for LCM, and <7 and <4% for CBZ, respectively.

Modeling Strategy and Software

As stated previously, step-wise model building, including the evaluation of covariates, of the dropout and the seizure model was carried out on a historic data set comparing CBZ-CR with levetiracetam (N01061; ClinicalTrials.gov identifier: NCT00150735). In a subsequent step, the resulting final models were applied to the new dataset from clinical trial SP0993. Finally, all model parameters were re-estimated on the SP0993 dataset. The turnaround time of the SP0993 analysis was critical to meet the project timelines, hence this two-step approach avoiding a full model development on SP0993 data. The parameter estimates of the dropout and seizure model developed on N01061 data are provided in Online Resource 1.

The analyses and simulations were performed using NONMEM version 7.2.0 (ICON Development Solutions, Ellicott City, Maryland, USA) [10], supplemented with the PsN toolkit version 4.2.0 (https://uupharmacometrics.github.io/PsN/) [11], and were further processed using R Version 3.2.0 (https://www.r-project.org/) [12]. In the pharmacokinetic analysis, the first-order conditional estimation method with interaction was used, while the Laplace’s method was used for the time-to-event analysis.

Pharmacokinetic Modeling

Because the available individual plasma concentration data were rather sparse (one measurement per occasion, usually at trough), a previously published [13] population pharmacokinetic model for CBZ-CR was used to obtain individual estimates of plasma clearance. Likewise, a previously developed population pharmacokinetic model for LCM was used for this purpose. Typical pharmacokinetic parameters were fixed to the historical values and only the inter-individual variability of F and the residual variability were estimated. The daily area under the plasma concentration–time curve (AUC) at steady state was derived from the empirical Bayes estimate of plasma clearance for each patient and used as a measure of exposure in the seizure model. A description of the pharmacokinetic models is provided in Online Resource 2.

Dropout Modeling

Only dropout occurrences for any reason other than lack of efficacy were taken into account for the modeling. The probability of not having an event (i.e., no dropout) by time t is described by the survivor function S(t), which is determined by the hazard. A flexible empirical function was applied as described in Frobel et al. [14], where the hazard changes in a step-wise fashion at given breakpoints. To avoid discontinuities in the hazard when passing a breakpoint, often leading to numerical problems during estimation, several sigmoidal functions were connected to achieve some smoothness. A model with four breakpoints was found to give the best model fit in terms of objective function value (OFV):

$$\text{FLG5}=\frac{t^{\text{GAM}}}{{\text{BP4}}^{\text{GAM}}+t^{\text{GAM}}};1\text{if}t>\text{BP4},0\text{otherwise}$$

$$\text{FLG4}=\frac{t^{\text{GAM}}}{{\text{BP3}}^{\text{GAM}}+t^{\text{GAM}}}-\frac{t^{\text{GAM}}}{{\text{BP4}}^{\text{GAM}}+t^{\text{GAM}}};1\text{if}t\text{between BP3 and BP4},0\text{otherwise}$$

$$\text{FLG3}=\frac{t^{\text{GAM}}}{{\text{BP2}}^{\text{GAM}}+t^{\text{GAM}}}-\frac{t^{\text{GAM}}}{{\text{BP3}}^{\text{GAM}}+t^{\text{GAM}}};1\text{if}t\text{between BP2 and BP3},0\text{otherwise}$$

$$\text{FLG2}=\frac{t^{\text{GAM}}}{\text{BP1GAM}+t^{\text{GAM}}}-\frac{t^{\text{GAM}}}{{\text{BP2}}^{\text{GAM}}+t^{\text{GAM}}};1\text{if}t\text{between BP1 and BP2},0\text{otherwise}$$

$$\text{FLG1}=1-\frac{t^{\text{GAM}}}{{\text{BP1}}^{\text{GAM}}+t^{\text{GAM}}};1\text{if}t<\text{BP1},0\text{otherwise}$$

$$h_0\left(t\right)=\left(\mathit{\lambda }1\times \text{FLG}1+\mathit{\lambda }2\times \text{FLG}2+\mathit{\lambda }3\times \text{FLG}3+\mathit{\lambda }4\times \text{FLG}4+\mathit{\lambda }5\times \text{FLG}5\right)$$

where FLG1–5 are indicator variables changing their values from 0 to 1 depending on the value of time t; a high value of 50 was chosen for the GAM variable, to mimic a very steep change but avoiding discontinuity. The hazard h ₀(t) starts with a value of λ1 until breakpoint 1 (BP1), where it switches to λ2, until time reaches BP2.

Automated stepwise covariate modeling using a forward addition/backward deletion procedure as implemented in PsN was applied on the N01061 dataset. The covariate effect was added to the hazard as:

$$h\left(t\right)=h_0\left(t\right)\times exp(\text{COVAR})$$

where COVAR describes the hazard-covariate relationship. Because this function assumes proportionality of the hazard with respect to the covariate effect, a hazard ratio of the covariate effect is simply: exp(COVAR). For example:

$$\text{COVAR}=\mathit{\theta }\times \text{SEX};\text{where SEX}=1\text{if}\text{female},0\text{if male}$$

In this case, exp(θ) is the hazard ratio of female vs. male, with values >1 indicating a higher risk of dropout for women.

For a continuous covariate COVAR, the relationship was as follows (e.g., age):

$$\text{COVAR}=\mathit{\theta }\times (\text{AGE}-\text{median}[\text{AGE}])$$

The covariate effect relationship was considered statistically significant when p < 0.005 (ΔOFV = 7.88, for 1 degree of freedom difference) for forward selection and p < 0.001 (ΔOFV = 10.83) for backward deletion. The following covariates were tested: treatment (CBZ-CR, levetiracetam, or LCM), duration of epilepsy, number of AEDs taken before the trial, number of seizures in the previous 3 months (NSP3M), race, geographical region, sex, age, and body weight. The forward–backward covariate search was performed on the N01061 dataset but was not repeated on the SP0993 dataset in full. Any relationship found on the N01061 dataset was maintained for the SP0993 modeling with the coefficient re-estimated. Only relationships pertinent to the LCM treatment were revisited when analyzing the SP0993 data (treatment effect on dropout).

Seizure Modeling

For the purpose of modeling, if a patient experienced multiple seizures on one day, this was counted as a single event and is referred to here as a seizure or seizure event. Although roughly 30% of the patients had multiple seizure events during the trial, a standard repeated-time-to-event model did not satisfactorily account for the low seizure rate overall in the population (more than 50% of the patients had no seizure at all). Instead, an approach first presented by Abrantes et al. [15] was successfully employed, using two sub-models of the hazard: one for the time to the first seizure and one for the time to the second and subsequent seizures (time counted from the first dose):

$$h^{1\text{st}}(t)=h_0^{1\text{st}}(t);\text{if SCOUNT}<1(\text{hazard for 1st seizure})$$

$$h^{2\text{nd}+}(t)=h_0^{2\text{nd}+}(t)\times exp(\mathit{\eta });\text{if SCOUNT}\ge 1(\text{hazard for 2nd and subsequent seizures})$$

where SCOUNT is a counter variable included in the NONMEM code that starts at 0 for every new patient and increases by one with every seizure that occurs in a patient as the estimation proceeds through the individual data records. The random-effect parameter η is only included in the second hazard equation. A Weibull model was used to describe the base hazard for $h_0^{1\text{st}}(t)$ and $h_0^{2\text{nd}+}(t)$ with different scale (λ) and shape (p) parameters (see equation below) for each sub-model. Drug or covariate effect as described below was explored on both hazard terms.

The effect of drug exposure (daily AUC at steady state) on the scale parameter λ was described with an exponential function [i.e., linear with respect to ln(λ)], with the AUC centered on the typical AUC value at the first dose level for each drug:

$$\text{DE}=\mathit{\theta }\times (\text{AUC}-104);\text{for LCM}$$

$$\text{DE}=\mathit{\theta }\times (\text{AUC}-132);\text{for CBZ-CR}$$

Then, the drug effect term was included in the Weibull model:

$$h(t)={\mathit{\lambda }}^{\prime }\times p\times {({\mathit{\lambda }}^{\prime }\times t)}^{p-1},\text{with}{\mathit{\lambda }}^{{}^{\prime }}=\mathit{\lambda }\times exp(\text{DE})$$

Because exploratory plots indicated a very strong relationship between the NSP3M and seizure probability, this covariate was already included in the model during development of the base structural model. Owing to the skewed distribution of this variable (median 2, range 0–450), NSP3M was split into four categories: <2, 2–6, 7–50, and >50, with 2–6 being the reference category. The process for covariate modeling was similar to that described for the dropout model, i.e., significant relationships found on the N01061 dataset were maintained and coefficients re-estimated. Only the age-relationship was revisited specifically because of the potential clinical interested. The same covariates tested in the dropout model were also tested in the seizure model.

Model Qualification

To evaluate the predictive performance of the models, visual predictive checks (VPCs) [16] and posterior predictive checks [17] were performed using the final model parameter estimates. A simulation dataset was generated using a patient population with the same covariates as in the dataset used for model building. Every patient in the simulation dataset had dummy observation records to allow for seizure or dropout events being simulated at every day from 1 to 800.

As the simulations should mimic the original trial design with dose escalation based on seizure events, the individual dose and AUC were assigned to patients ‘on-the-fly’ during the simulation. This means that the simulation code in NONMEM (see Online Resource 4) included flag and counter variables changing their value if a seizure (or dropout) event was simulated at a given point in time for a patient. If, for example, a seizure event was simulated and the current time was within the evaluation period (days 21–203 since the start of a new dosing step), the flag for the dose escalation was changed and at the next iteration for this patient (next record in the simulation dataset) a higher dose was assigned and the AUC for this patient (based on individual pharmacokinetic parameters) was re-calculated. If a dropout event was simulated this was also flagged accordingly, thus records after the dropout day were filtered out in the post-processing step. The simulations were repeated 500 times and Kaplan–Meier curves comparing observed and predicted probabilities (95% prediction interval) were generated.

The positive predictive check focused on two trial endpoints: percentage and the Kaplan–Meier estimated proportion of patients being seizure free for 6 months at the last evaluated dose. To derive these parameters from the simulated time-to-event data, only the seizure-free patients in the evaluation period (i.e., excluding the 3-week up-titration/stabilization period at the beginning of each dose step) were counted in the post-processing step, just as in the real trial.

Simulations

Simulations were conducted to explore the potential benefit of a higher first target dose for those patients with a high seizure frequency at baseline. The simulation procedure was similar to the one applied for VPCs and positive predictive checks described in the previous section. The population characteristics for the simulations were the same as in SP0993 (n = 443 receiving LCM). Uncertainty was taken into account by taking the parameter vector for each of 500 trial replicates from a bootstrap distribution.

Two scenarios were compared: scenario (A) was essentially the same as the original design of SP0993 (‘default’ regimen): first target dose: 200 mg/day, second target dose: 400 mg/day, third target dose: 600 mg/day. In scenario (B), patients were stratified based on disease severity. Patients with seven or more seizures in the previous 3 months received a first target dose of 400 mg/day, then 600 mg/day at the second and third step (i.e., no dose increase beyond 600 mg/day). Patients with fewer than seven seizures received the ‘default’ regimen. Up-titration to the target dose level during the first 3 weeks in each dose step was taken into account in both scenarios.

Results

Data

In trial SP0993, 888 patients were randomized of whom five (LCM: 2; CBZ-CR: 3) were excluded from the analysis as they withdrew their consent before receiving a dose (n = 2), or no dosing history was available (n = 3). Valid plasma concentration vs. time records were available from 807 patients (LCM: 407; CBZ-CR: 400) providing 3748 plasma concentrations (LCM: 1909; CBZ-CR: 1839). About 55% of the patients in the trial did not experience any seizures, 15% had one seizure and about 30% had two or more seizures. A summary of the seizure events in the trial by treatment group is provided in Online Resource 1.

In the trial, 205 of 883 (23.2%) patients discontinued prematurely (dropout) for reasons other than lack of efficacy. Of the patients who dropped out, 111 received LCM and 94 CBZ-CR.

Summary statistics of important patient demographic variables and the seizure count at baseline (NSP3M) are shown in Table 1. A more complete overview of patient-specific variables is provided in Online Resource 1.

Table 1.

Demographics and seizure counts at baseline

	LCM	CBZ-CR	Total
N (%)	443 (50.2)	440 (49.8)	883 (100.0)
Age (years)
Mean (CV %)	42.0 (42.6)	41.8 (41.3)	41.9 (41.9)
Median (range)	40 (16–87)	41 (16–85)	40 (16–87)
IQR	25.5–55	26–55	26–55
Sex, n (%)
Female	200 (45.1)	209 (47.5)	409 (46.3)
Male	243 (54.9)	231 (52.5)	474 (53.7)
Number of seizures in the previous 3 months
Mean (CV %)	12.4 (319.8)	10.2 (279.1)	11.3 (305.3)
Median (range)	3 (1–450)	2 (0–300)	2 (0–450)
IQR	1–6	2–5	1–6
Number of seizures in the previous 3 months (categorical), n (%)
<2	122 (27.5)	105 (23.9)	227 (25.7)
2–6	216 (48.8)	238 (54.1)	454 (51.4)
7–50	80 (18.1)	80 (18.2)	160 (18.1)
>50	25 (5.6)	17 (3.9)	42 (4.8)

IQR interquartile range, CBZ-CR carbamazepine controlled release, CI confidence interval, CV coefficient of variation, LCM lacosamide

Pharmacokinetic Modeling

Parameter estimates and goodness-of-fit plots for LCM and CBZ are provided in Online Resource 2.

Dropout Modeling

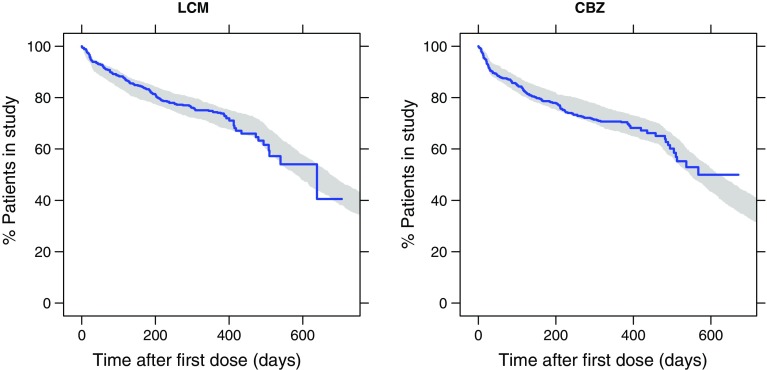
The final dropout model consisted of four breakpoints. The VPC shown in Fig. 2 demonstrates excellent agreement between observed and predicted probability of dropout not because of a lack of efficacy. Patients in the LCM group had a slightly lower risk to drop out than those receiving CBZ-CR; hazard ratio LCM vs. CBZ-CR was 0.871 [90% confidence interval (CI) 0.714–1.06]. Sex was identified as a significant covariate with a 1.27-fold (90% CI 1.04–1.55) higher risk of dropout for women than for men across treatments. Parameter estimates of the dropout model are given in Table 2.

Fig. 2.

Visual predictive check of dropout probability. Blue line observed Kaplan–Meier curve of dropout not because of a lack of efficacy in SP0993; shaded area represents the 95% prediction interval based on 500 simulations with the updated dropout model using SP0993 data. The drop of the curve after 400 days is owing to most patients (the responders) exiting the trial as planned after 385 days (21 days up-titration/stabilization + 364 days on treatment without escalation). After this point, only a few patients remained in the trial such that the Kaplan–Meier curve declined appreciably on any subsequent event. CBZ carbamazepine, LCM lacosamide

Table 2.

Parameter estimates for the dropout model

Parameter	Description	Estimate	90% CIa
BP1 (day)	Breakpoint 1	20	18.2–20.9
BP2 (day)	Δ(BP2–BP1)	9.76	5.29–11.5
BP3 (day)	Δ(BP3–BP2)	105	95.7–140
BP4 (day)	Δ(BP4–BP3)	340	251–357
λ1 (1/day)b	Hazard from t = 0 to BP1	0.00205	0.0014–0.00267
λ2 (1/day)b	Hazard from BP1 to BP2	0.00358	0.00254–0.00601
λ3 (1/day)b	Hazard from BP2 to BP3	0.000946	0.000759–0.00123
λ4 (1/day)b	Hazard from BP3 to BP4	0.000613	0.000456–0.00074
λ5 (1/day)b	Hazard from BP4 to end	0.00221	0.00134–0.00358
Coeff_SEX	Effect of sex = female on hazard	0.238	0.0346–0.437
HR_SEXb	Hazard ratio female vs. male	1.27	1.04–1.55
Coeff_TYPE	Effect of LCM on hazard	−0.138	−0.333–0.0399
HR_TYPEb	Hazard ratio LCM vs. CBZ-CR	0.871	0.717–1.04

BP breakpoint, CBZ-CR carbamazepine controlled release, CI confidence interval, HR hazard ratio, LCM lacosamide

^a5th–95th percentiles of 500 bootstrap replicates

^bDerived from the corresponding coefficient as: exp(x)

Seizure Modeling

A significant effect of exposure on seizure probability was identified, as indicated by the negative slope estimates for the AUC effects of CBZ and LCM, meaning a lower hazard for higher AUC values (Table 3). The estimates of λ1 and λ2 and the shape parameters p1 and p2 refer to a typical patient aged 41 years having experienced two to six seizures in the previous 3 months and with a typical CBZ AUC of 132 mg·h/L (calculated based on the population pharmacokinetic parameters for a 70-kg patient receiving CBZ-CR 400 mg/day). To facilitate interpretation of the covariate effect coefficients, hazard ratios were derived assuming proportional hazards as shown in Table 4.

Table 3.

Parameter estimates of the final seizure model

Parameter	Description	Estimate	90% CIa
λ1 (1/day)b	λ for the time to 1st event	0.000733	0.000534	0.000957
p1	Weibull shape parameter 1st event	0.493	0.464	0.531
λ2 (1/day)b	λ for the 2nd + event	0.00889	0.00606	0.013
p2	Weibull shape parameter 2nd + event	0.713	0.675	0.75
NSP3M (<2) ~ λ1	Effect of NSP3M <2 on ln(λ1)	−1.12	−1.65	−0.648
NSP3M (7–50) ~ λ1	Effect of NSP3M 7–50 on ln(λ1)	1.94	1.43	2.43
NSP3M (>50) ~ λ1	Effect of NSP3M >50 on ln(λ1)	3.3	2.08	5.07
NSP3M (<2) ~ λ2	Effect of NSP3M <2 on ln(λ2)	−1.37	−2.06	−0.659
NSP3M (7–50) ~ λ2	Effect of NSP3M 7–50 on ln(λ2)	1.36	0.898	1.82
NSP3M (>50) ~ λ2	Effect of NSP3M >50 on ln(λ2)	2.53	1.98	3.1
AUC_LCM ~ λ1c	Slope of AUC-ln(λ1) for LCM 1st event	−0.00917	−0.0164	−0.000334
AUC_CBZ ~ λ1c	Slope of AUC-ln(λ1) for CBZ 1st event	−0.00658	−0.015	0.00325
AUC_LCM ~ λ2c	Slope of AUC-ln(λ1) for LCM 2nd + event	−0.00751	−0.00985	−0.006
AUC_CBZ ~ λ2c	Slope of AUC-ln(λ1) for CBZ 2nd + event	−0.0153	−0.0183	−0.0122
AGE ~ λ1d	Slope of AGE-ln(λ1) for LCM only	−0.0256	−0.0449	−0.0112
IIV ln(λ2) (SD)	Inter-individual variability ln(λ2)	2.03	1.85	2.2

AUC area under the plasma concentration–time curve over one dosing interval, CI confidence interval, CBZ carbamazepine, LCM lacosamide, NSP3M number of seizures in the 3 months before the trial, SD standard deviation

^a5th–95th percentiles of 500 bootstrap replicates

^bParameter back-transformed to normal scale as exp(x)

^cAUC centered on typical value at the first dose level (LCM 104 mg·h/L; CBZ 132 mg·h/L)

^dAGE centered on 41 years

Table 4.

Derived hazard ratios for covariate effects

Covariate	Hazard ratioa	90% CIb
1st seizure
NSP3M ≤1 vs. 2–6	0.58	0.44	0.73
NSP3M 7–50 vs. 2–6	2.60	2.02	3.31
NSP3M >50 vs. 2–6	5.09	2.79	12.20
AGE 65 vs. 41	0.74	0.59	0.88
AUCc LCM 300 vs. 100	0.40	0.20	0.97
AUC CBZ 130 vs. 210	0.77	0.55	1.14
2nd + seizures
NSP3M ≤1 vs. 2–6	0.38	0.23	0.62
NSP3M 7–50 vs. 2–6	2.63	1.90	3.67
NSP3M >50 vs. 2–6	6.09	4.12	9.10
AUC LCM 300 vs. 100	0.34	0.25	0.42
AUC CBZ 130 vs. 210	0.42	0.35	0.50

AUC area under the plasma concentration–time curve in h × mg/L, CBZ carbamazepine, CI confidence interval, CR controlled release, LCM lacosamide, NSP3M number of seizures in the 3 months before the trial

^aHazard ratios were derived as exp(coefficient × p), where coefficient is the estimate of the covariate effect as in Table 3 and p is the estimate of p1 or p2. For the age and AUC effect the coefficient was multiplied by the difference in the contrast (e.g., 65 − 41 = 24)

^b5th–95th percentiles of 500 bootstrap replicates

^cComparisons are based on the typical daily AUC values for a patient receiving a high or low dose of LCM (200 vs. 600 mg/day) or CBZ-CR (400 vs. 1200 mg/day)

A higher NSP3M before the trial largely increased the risk of having a seizure during the trial. A significant effect of age was only identified for the LCM group (and for the first seizure event), as a log-linear relationship on λ1. Testing the age effect on all patients or the CBZ group only did not result in a significant decrease in the OFV, indicating a treatment–age interaction. Older patients receiving LCM had a somewhat lower risk of experiencing a first seizure than younger patients.

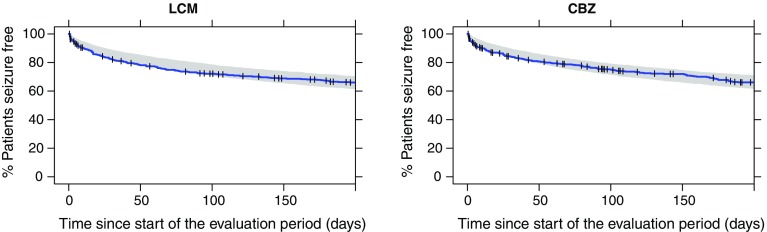
Visual predictive checks of the Kaplan–Meier curves for time to the first four events are presented in Fig. 2 in Online Resource 3. While the predicted survival curves are close to those derived from the observed data for the CBZ-CR group, the model under-predicts the hazard in the first 2 weeks after treatment initiation (the stabilization/up-titration phase) in the LCM group. Attempts to improve the model fit for LCM in this early phase, by including a drug effect or NSP3M on the shape parameter or inclusion of a higher hazard for the first 21 days, were not successful. This early phase, however, is not essential for predicting the clinical endpoint of interest (percentage of patients seizure free for 6 months) because, per protocol, only events happening during the evaluation period (i.e., after the stabilization/up-titration) are taken into account. The Kaplan–Meier VPC for the time to the first event in the evaluation phase shown in Fig. 3 demonstrates that the model was able to predict seizure probability in this relevant period.

Fig. 3.

Visual predictive check of time to first seizure in the evaluation period. Blue line observed Kaplan–Meier curve; shaded area represents the 95% PI based on 500 simulations. The vertical ticks indicate dropouts in the observed data (right censoring). CBZ carbamazepine, LCM lacosamide

The posterior predictive check on the percentage of patients seizure free for 6 months is shown in Fig. 4. The predictions correspond closely to the observations in SP0993. Additionally, the small difference between the percentages observed in the LCM group compared with the CBZ-CR group at the third dose step (73.6 vs. 69.7%, Δ +4%) could be reproduced with the model (68.6 vs. 65.5%, Δ +3.1%). However, the difference between the two treatments is too small to be considered of clinical relevance.

Fig. 4.

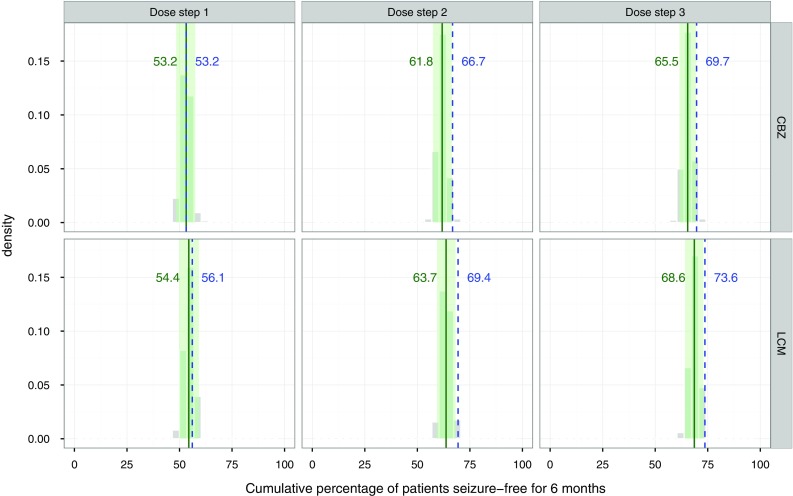
Posterior predictive check for the cumulative percentage of patients seizure free for 6 months. Gray histograms outcome of 500 replicate simulations; solid green line median of the 500 simulations; dotted blue line observed percentages in SP0993; green area encompasses the 95% prediction interval. CBZ carbamazepine, LCM lacosamide

An alternative endpoint in epilepsy studies is the Kaplan–Meier estimated proportion of patients being seizure free for 6 months at the last evaluated dose. In this approach, only the number of patients at risk (i.e., not dropped out/censored) is taken into account in the calculation of the seizure probability at each event in time. Visual and posterior predictive checks for this endpoint are presented in Figs. 3 and 4 in Online Resource 3 and indicate a slight over-prediction of the Kaplan–Meier proportion at 6 months by about 3–5%. Overall, although the model may not be suitable for predicting seizure probability in the first 3 weeks after the start of treatment with LCM, it is nevertheless adequate for predicting the clinical endpoints that by definition exclude the initial up-titration/stabilization period.

Simulations

As shown in Table 5, in the overall LCM population, dose individualization increased the proportion of patients responding to treatment by about 2% at the last dose step compared with the default dosing scheme. However, the additional benefit was low, only about 25% of the patients in SP0993 reported seven or fewer seizures in the previous 3 months. Focusing on this specific subset in the simulations, the proportion of patients who were seizure free was 10% higher at the first dose step and 8% at the last dose step for patients with a higher initial target dose (>200 mg/day).

Table 5.

Simulated cumulative percentage of seizure-free patients at each dose step

Subset	Dosing scenarioa	Percentage seizure free (90% CI)b
		Dose step 1	Dose step 2	Dose step 3
All patients	(A) As in SP0993	54.4 (49.4–59.1)	63.7 (59.4–68.4)	68.4 (64.1–73.4)
	(B) NSP3M-based	56.7 (51.7–61.4)	66.1 (61.6–70.9)	70.2 (65.7–74.7)
Subset with NSP3M ≥7	(A) As in SP0993	30.5 (21.9–39.0)	41 (31.4–49.5)	49.5 (40.0–59.0)
	(B) NSP3M-based	40 (28.6–52.4)	52.4 (41.0–61.9)	57.1 (46.7–65.7)

CI confidence interval, LCM lacosamide, NSP3M number of seizures in the 3 months before the trial

^aDefault dosing scheme of LCM as in SP0993 is compared with a regimen with a higher initial target dose for patients with NSP3M ≥7

^b5th–95th percentiles of 500 bootstrap replicates

Discussion

Dropout Modeling

The dropout risk (not because of a lack of efficacy) was slightly lower for patients taking LCM compared with those taking CBZ-CR with a hazard ratio of 0.871 (90% CI 0.714–1.06; LCM vs. CBZ-CR). This may be linked to tolerability differences between the two drugs because fewer patients taking LCM (10.6%) than CBZ-CR (15.6%) discontinued because of adverse events (see Baulac et al. [7] for a detailed overview of reasons for discontinuation). Although the CI of the hazard ratio just included 1, indicating no statistical significance at the p < 0.05 level, it was decided to not remove the relationship from the model because graphical diagnostics (Fig. 6 in Online Resource 3) did indicate that the relationship, albeit weak, is supported by the data.

Certainly, a model that could describe the probability of dropout for each of the different reasons (adverse events, protocol violation, withdrawal of consent, lost to follow-up, other reasons) would have provided a more granular description of the data. However, it was considered that the overall low number of dropout events did not allow for a split into smaller categories and separate modeling, as this would have compromised the precision of the parameter estimates. For this reason, the potential relationship between exposure and dropout was not investigated because such a relationship would only be plausible for dropout because of adverse events.

The risk of discontinuation (not because of a lack of efficacy) was 1.27-fold higher (90% CI 1.04–1.55) among female compared with male patients. Of note, Kaplan–Meier plots grouped by treatments indicated a weaker association between sex and dropout in the LCM group compared with the CBZ-CR group (Fig. 1 in Online Resource 3).

Seizure Modeling

The seizure model aimed at demonstrating and quantifying the impact of drug exposure on the probability of seizure events. The trial design did not allow for a straightforward comparison of e.g., median time-to-seizure per dose group. In fact, the response-dependent dose escalation inevitably led to confounding of dose (or exposure) and pharmacodynamic effect (i.e., sensitivity to the drug, responsiveness), meaning that patients who responded poorly or not at all received the highest dose. Although the design limitations are recognized [18, 19], they do reflect clinical practice. Non-linear mixed-effects modeling can, to some extent, overcome this issue. In a seminal article about the design of dose-ranging studies [20], Sheiner et al. used the example of a blood pressure-lowering drug to explain how unbiased estimates of the dose–response relationship can be obtained in a dose-escalation trial by analyzing the data with a parametric pharmacokinetic/pharmacodynamic model. Alternative analysis methods (analysis of variance, analysis of covariance) based on group comparisons, however, fail in this context.

Nevertheless, the absence of a placebo group (for ethical reasons) and the relatively narrow dose range in the current trial prevented exploration of more pharmacologically plausible models, such as the (sigmoid) Emax model [attempts resulted in unstable models, sensitive to changes in initial estimates]. An assessment of the relative potency of the drugs investigated is also very limited for similar reasons (absence of a common anchor point). Despite these shortcomings, it could be shown that AUC is an important predictor of efficacy.

To appropriately handle the AUC-hazard relationship across the different dose-escalation steps as described before, it was necessary to account for the fact that many patients had more than one seizure event during the course of the trial. Therefore, a repeated-time-to-event framework was used. However, owing to the low overall seizure rate—approximately 50% of the patients reported no seizure—there was a severe imbalance in the distribution of the between patient variability on the hazard [those with no event share the same (low) hazard, the rest of the patients are more normally distributed]. To account for this data feature, the hazards for the first and subsequent seizures were handled separately by two sub-models (Fig. 5 in Online Resource 3 illustrates the hazard curves for the two sub-models). Considering that only the subset of patients with more than one seizure informed the parameters of the second sub-model, the covariate relationships can differ between the two terms. This has also been observed by Abrantes et al., who applied this approach for patients with epilepsy during a short-term hospital stay [15]. A downside of this approach is that model parameters are not directly interpretable in terms of their impact on the clinical endpoint in a quantitative manner and simulations need to be performed to assess the influence of, for example, covariates on the percentages of patients seizure free for 6 months.

Simulations

During development of the seizure model, the NS3PM was identified as having important predictive value. Therefore, potential clinical implications in terms of an optimized dosing strategy for LCM based on baseline disease severity was explored further. A simulation scenario was set up where a higher dose was given to patients with a more severe disease state (seven or more seizures in the previous 3 months). In fact, the overall percentage of patients seizure free for 6 months at the last evaluated dose would be slightly higher (by approximately 2%) if such a treatment schedule with a priori dose individualization would be applied to a patient population similar to the one studied in SP0993 (Table 5). The benefit may appear rather small overall. However, focusing on the subset of patients with seven or more seizures in the previous 3 months, it becomes clear that indeed this subgroup could benefit from a higher initial LCM target dose. For example, the difference in response rate between patients receiving a higher initial target dose (400 mg/day) and those receiving a lower initial target dose (200 mg/day) was simulated to be about 10% at the first dose step and 8% at the last dose step. A limitation of this simulation is that it is based only on an efficacy model, while in clinical practice, tolerability is also taken into account when selecting titration schedule and initial target dose. Nevertheless, the simulations provide a basis for exploring such a priori individualization strategies in a clinical context where an appropriate benefit-risk assessment can be made.

Currently, it is common practice in the treatment of patients with epilepsy to adapt the dose of the drug based on response and tolerability (i.e., dose increase if seizures occur, dose reduction in the case of adverse events). Targeting a maintenance dose (following up-titration) that is closer to the individual optimal dose may have the potential to save the patient some iterations in this empirical dose-finding process. Additional studies to validate this approach should specifically investigate potential tolerability issues associated with higher doses.

Conclusions

A repeated time-to-event model was successfully applied to quantify the exposure–response relationship of LCM (and CBZ-CR) on the probability of seizures in patients aged ≥16 years newly diagnosed with focal or generalized tonic–clonic seizures without signs of focal onset (provided they had no history or findings suggestive of idiopathic generalized epilepsy). Baseline disease severity expressed as NSP3M was found to be the most important predictor of seizure probability. Simulations suggest that patients with seven or more seizures in the previous 3 months would benefit from a dosing regimen aiming at a higher target maintenance dose. Further clinical research is needed to confirm these findings and to ensure that tolerability is not compromised.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Compliance with Ethical Standards

Funding

This study was funded by UCB Pharma (Brussels, Belgium).

Conflict of interest

Andreas Lindauer is an employee of SGS Exprimo. Christian Laveille was an employee of SGS Exprimo when the study was performed. Armel Stockis is an employee of UCB Pharma.