Abstract
Pristine graphene encapsulated in hexagonal boron nitride has transport properties rivalling suspended graphene, while being protected from contamination and mechanical damage. For high quality devices, it is important to avoid and monitor accidental doping and charge fluctuations. The 2D Raman double peak in intrinsic graphene can be used to optically determine charge density, with decreasing peak split corresponding to increasing charge density. We find strong correlations between the 2D 1 and 2D 2 split vs 2D line widths, intensities, and peak positions. Charge density fluctuations can be measured with orders of magnitude higher precision than previously accomplished using the G-band shift with charge. The two 2D intrinsic peaks can be associated with the “inner” and “outer” Raman scattering processes, with the counterintuitive assignment of the phonon closer to the K point in the KM direction (outer process) as the higher energy peak. Even low charge screening lifts the phonon Kohn anomaly near the K point for graphene encapsulated in hBN, and shifts the dominant intensity from the lower to the higher energy peak.
Introduction
Raman spectroscopy is a versatile experimental technique for exploring fundamental properties of graphene and characterizing properties such as layer thickness, defect density, charge and strain1. The 2D Raman mode is of particular interest, as it involves two D band phonons with opposite, non-zero momenta. Despite the higher order process and non-zero momentum phonons, the 2D mode is the strongest Raman mode in single layer graphene. The double resonance (DR) mechanism2 explains why this higher order phonon mode is so strong; resonant virtual electron and hole scattering picks phonon q vectors that satisfy momentum and energy conservation. The DR process together with the strong K-point Kohn anomaly is why the 2D line provides so much information about the electronic and phonon dispersions around the K and K ’ points. The phonon Kohn anomaly near K softens the D band phonon energies conically near K, resulting in a discontinuity of the derivative of the dispersion at K 3. The slope of the phonon dispersion is a direct measure of the electron-phonon coupling (EPC) strength3. The DR and phonon dispersion are responsible for the shift in the 2D band energy with changing laser excitation energy4. Similarly, the strong dependence of the 2D mode on dielectric screening is readily observable by the shift in the 2D position for different environments, e.g., suspended graphene, graphene on SiO2, graphene on top of hexagonal boron nitride (hBN) or encapsulated in hBN, etc5. Larger dielectric screening6 will reduce the Fermi velocity, v F, so that the DR conditions will select larger phonon energy. The screening affects v F since electron energies are much higher than expected from a single particle picture, with a significant self-energy correction in a 2D material, in particular for free standing graphene near the charge neutrality point (CNP)7–9. The self-energy is decreasing as ε−1, where ε is the effective dielectric constant of the environment6. Charging the graphene layer will also renormalize and reduce the self-energy and therefore v F. For example, a study of gated graphene on hexagonal boron nitride (hBN) examined with scanning tunnelling spectroscopy demonstrated a change of v F from 1.3 to 1.05 × 106 m/s as the doping increased one order of magnitude from 2 × 1011 cm−2 to 2 × 1012 cm−2 9. Ultraclean suspended graphene with mobility reaching 106 cm2/Vs have shown v F reaching 3 × 106 m/s, measured by Shubnikov-de Haas oscillations7. Screening will also have an effect on the phonon dispersion, as it may decrease the strength of the EPC, and thereby weakening the Kohn anomaly at K, resulting in higher phonon energies with increased screening5,10,11. The reduced v F and reduced Kohn anomaly with screening are both expected to lead to a higher energy 2D peak. Hence, changes to the dispersion of the Dirac cone and the phonon branch can be experimentally deduced from the 2D peaks.
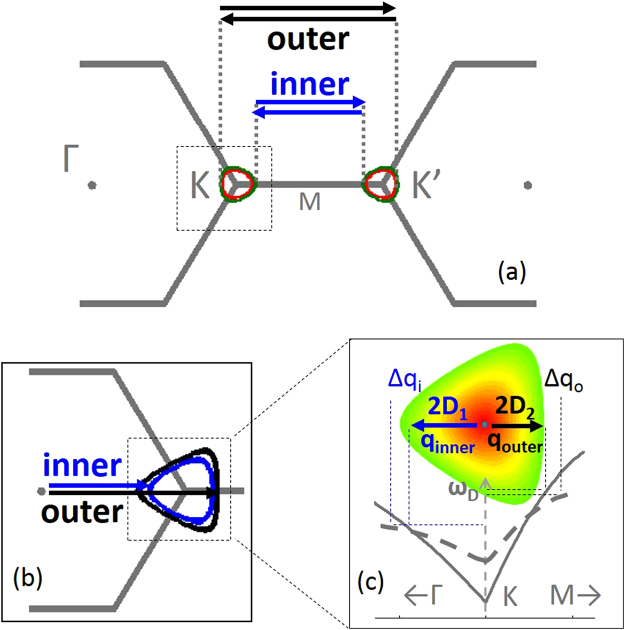
The DR method can be used for mapping out a contour of participating phonon wave-vectors12,13. The vectors are found by translating the iso-electronic energy contour determined by half the laser energy at K, with a vector that puts the K iso-electronic energy contour tangentially in contact with the slightly smaller iso-energy contour (E L /2 − hcω D) at K’, shown in Fig. 1(a). From this argument, it is clear that the trigonal warping of the Dirac cone determines the q vectors associated with the 2D Raman peak. While the DR Raman scattering is a two-dimensional process, the strongest contributions come from the high symmetry direction ΓK and KM, so that we can consider the one-dimensional case where electron (hole) scattering from ΓK to K’Γ followed by hole (electron) scattering back from K’Γ to ΓK are referred to as the outer process and the similar process between KM and MK’ as the inner process 11–13, as shown in Fig. 1(a). Because of the trigonal warping of the Dirac cone, there is a difference between the length of the selected inner and outer vectors, shown in Fig. 1(a–c). If the phonon dispersion around K was cylindrically symmetric, the 2D peak would yield two very different phonon frequencies from the inner and outer process since q i > q o where q is measured from the K point with cylindrical coordinates, shown in Fig. 1(c). However, the phonon dispersion has an opposite trigonal warping so as to almost perfectly compensate for the electronic distortion12. Indeed, early in the study of graphene, a symmetric 2D peak for graphene on SiO2/Si was identified as a signature of a single layer14. Later studies showed that the intrinsic 2D line shape of single layer suspended graphene is asymmetric15–17, but reverts to a symmetric line shape when charge is added by field doping to 2 × 1011 cm−2, indistinguishable in shape from graphene on SiO2 18. Hence, we can deduce that there is not a perfect compensation of the phonon trigonal warping at low doping condition, and that the two peaks can reveal the behaviour of the inner and outer scattering processes, respectively. In addition, the energy upshift of the 2D peak is indicative of screening due to changes in the Fermi velocity, which has been pointed out previously19,20, but also due to changes in the phonon velocities12, addressed here.
Figure 1.
Schematic of the double resonance mechanism. (a) Top view of the K and K’ electron dispersion iso-energy contours for the selected k vectors. Red and green circles in (a) are the iso-energy contours E L /2 and (E L /2 − hcω D) at K and K’, respectively for the red (633 nm) and green laser (532 nm) excitation wavelengths. The black and blue arrows show the resonant k-vectors for the outer and inner processes, respectively. These vectors pick out the phonon iso-energy contours shown in (b) and the phonon q vectors in (c) shown both in a top view (top) and a crosscut (bottom). If the phonon dispersion does not fully match the electronic dispersion, there will be an energy difference between the inner and outer phonon, here shown as the outer resonance having higher energy. The dashed line in the cross cut qualitatively depicts the change in phonon dispersion with increased screening. The Δq addition to the q vectors represents the added length with increased screening due to the change in Fermi velocity and therefor the electronic iso-energy contours.
Here we are considering the effect of very low doping levels in ultra-clean graphene, dielectrically screened by encapsulation in hBN. Encapsulated graphene possesses many of the superior transport properties of suspended graphene with the added advantage of being mechanically more robust and easier to fabricate21. The accidental doping in these samples is approximately ~1011 cm−2 or less as deduced from transport measurements22, more than an order of magnitude lower than for graphene on SiO2. We find strong correlations between the 2D peak splitting and the relative peak intensities and linewidths. The decrease of the 2D 2 peak energy with charge screening is opposite to expectations. It follows from a crossover, shown in Fig. 1(c) bottom, of the phonon dispersions for unscreened and screened graphene, as have been predicted10,11. This is a consequence of screening the Kohn anomaly at K. One has to carefully consider the ratio of the inner and outer Fermi velocities with the ratio of the inner and outer phonon velocities before determining if 2D 1 is an inner or outer process. Here we present evidence to suggest that the lower energy 2D 1 peak originates from the inner process, based on the calculated stronger intensity from the inner process in the low doping regime12, and linewidth behaviour. The analysis below is based on the assumption that increasing the charge also increases the screening. This assumption is supported by the reduction in Fermi velocity with increasing charge level, especially close to the charge neutrality point, attributed to screening the self-energy correction of the electronic energy dispersion7,9.
On a practical level, the peak split between 2D 1 and 2D 2 can be used as a measure of charge doping two orders of magnitude lower than is possible to measure using the G band response to doping23,24.
Results
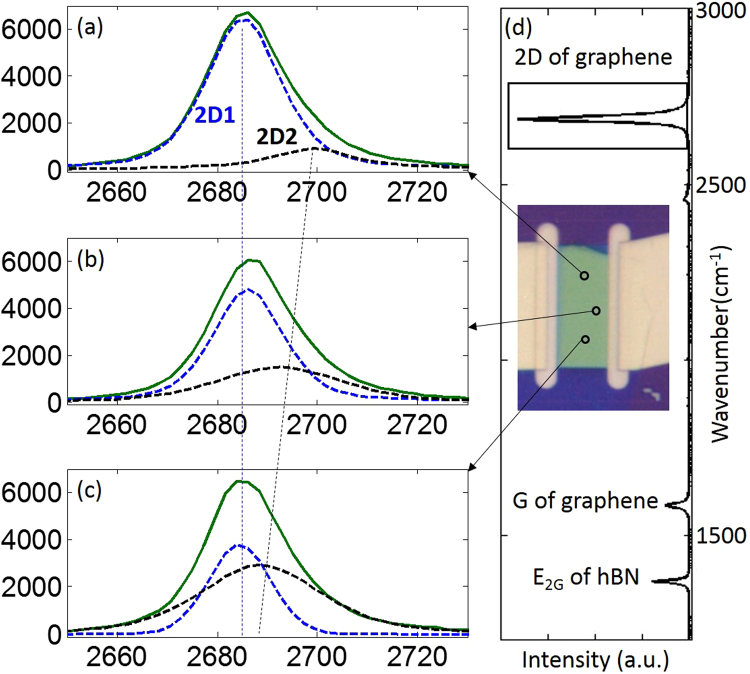
Raman data is collected from a graphene sample encapsulated in hBN. Examples of 2D spectra (λ = 532 nm) are shown in Fig. 2. The 2D peak is asymmetric and is fitted with two Voigt peaks where the lower energy peak is denoted 2D 1 (blue), and the higher energy peak is denoted 2D 2 (black). The 2D peaks measured at different locations have different 2D 1 and 2D 2 peak separations, linewidths, energies and intensities as shown in Fig. 2(a–c). We find similar variability in the 2D peaks across the sample. A full spectrum is shown in Fig. 2(d) with an insert of an optical image of the sample.
Figure 2.
Examples of the variation of the 2D band at different spatial locations. (a–c) illustrates from top to bottom decreasing 2D 1 and 2D 2 peak separation, change in relative intensity and varying peak energies. (d) shows a full spectrum with an inset of an optical image of the sample.
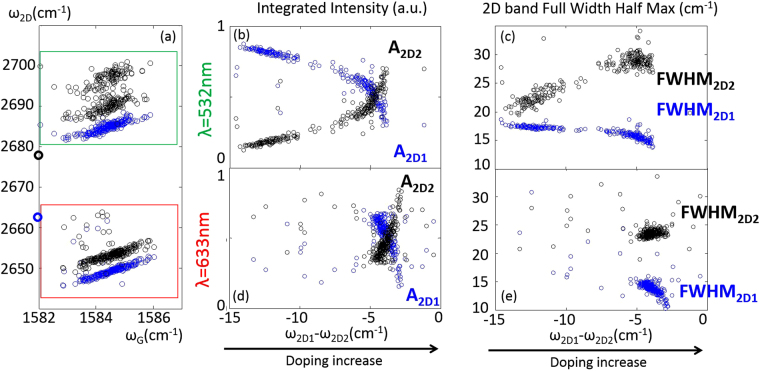
In order to evaluate the range of 2D spectra across the sample, we plot all the data measured on the same sample for two laser lines, λ = 532 nm and λ = 633 nm, in a 2D versus G diagram which reveals the contribution to the peak position due to strain or charge density25. Figure 3(a) shows 2D 1 (blue symbols) and 2D 2 (black symbols) versus the corresponding G peak position where the different data sets are boxed with their respective laser colour. The red laser selects shorter q vectors through the DR mechanism and therefore has a significantly lower 2D energy than the green laser, as expected. Both data sets exhibit strain lines, indicating some compression25,26. We first consider Fig. 3(a) for λ = 532 nm. The lower energy 2D 1 peak has a well-defined strain-induced slope of 1.7 ± 0.13, very close to the calculated value for uniaxial strain/compression in a random lattice direction25,26. The strain variation across the sample is on the order of ±0.1% which is small enough not to cause strain-induced peak-splitting27. The presence of the small strain variation will increase the linewidth only marginally26. The higher energy peak 2D 2 does not fall along a single, well defined line. Instead, the data falls mainly in two groups: a lower 2D 2− vs G, and a higher 2D 2+ vs G. Despite there being two 2D 2 groups, there is only one 2D 1 line. (Supplementary Information (SI) Fig. S1). The slopes measured for 2D 2− vs G and 2D 2+ vs G are 2.2 ± 0.3 and 3.0 ± 0.4 respectively. The variation and range of the strain slopes matches earlier studies of graphene/hBN sandwiches28. For reference, 2D1 and 2D2 values for λ = 532 nm for freely suspended graphene has been included in Fig. 3(a) 18.
Figure 3.
2D peak behaviour. (a) 2D 1-G correlation (blue) and 2D 2-G correlation (black) for λ = 532 nm and λ = 633 nm for the hBN encapsulated graphene. For λ = 532 nm, the 2D 1-G slope is 1.72, the 2D 2 is clustered with two different linear correlations with slope of 2.2 ± 0.3 (2D 2−) and 3.0 ± 0.4 (2D 2+)). For λ = 633 nm 2D 1-G has slope of 2.3 and 2D 2-G has a slope of 2.2. For comparison with free-standing graphene we have included in bold symbols values for λ = 532 nm extrapolated from reference 18. (b–e) Scaled 2D 1 (blue) and 2D 2 (black) normalized integrated intensities (A2D2 and A2D1) and their linewidths (FWHM2D2 and FWHM2D1) plotted against 2D 1 and 2D 2 peak separation.
Here we are not interested in the strain per se, but rather the effect of low charge doping on the graphene Raman peaks. The charge present is much lower than can be evaluated with help of a 2D versus G plot25, or by the G band linewidth or peak position23,24 (SI Fig. S2 (a)). Instead of attempting to remove the strain component from the 2D peak behaviour (requiring exact knowledge of the strain slope and position) we analyse the 2D characteristics versus the 2D peak splitting, since the split is a direct measure of doping and vanishes as doping increases18. Figure 3 (b–e) shows the normalized intensity and line width evolution as a function of 2D peak splitting for λ = 532 nm, top, and λ = 633 nm, bottom panels. Here we have chosen the x-axis to increase with increasing doping, as , with large 2D peak split to the left defined as “pristine”, here meaning close to the CNP18, and higher charge density (small peak split) to the right. Figure 3(b) and (d) show the relative integrated intensity of 2D 1 and 2D 2 band versus peak splitting, and Fig. 3(c) and (e) show how the linewidths of 2D 1 and 2D 2 evolve as the splitting decreases. Figure 3(b–e) demonstrate that the normalized integrated intensity and the linewidth for each peak are strongly correlated with the peak splitting. The behaviours are qualitatively similar for both laser lines. The largest difference is that the 2D peak split range is much larger for λ = 532 nm, and the similar behaviour for λ = 633 nm is reproducibly compressed to a much smaller peak split variation for the identical sample scan area.
We establish a quantitative relationship between 2D peak splitting and doping by assuming a linear relationship between split and charge, and comparing means and standard deviations between the two. Transport measurements on a similarly prepared sample show that the mean doping level is 1.4 × 1011 cm−2 based on the back-gate voltage at the CNP. The charge variation is 0.4 × 1011 cm−2 given the residual conductivity at the CNP (see supporting information section 2). Comparing with our Raman data, which has a mean and standard deviation of −8.1 and 3.6 cm−1 for the 2D peak splitting, we find that for each cm−1 of 2D peak splitting, the doping changes by 0.11 × 1011 cm−2 making the 2D peak splitting a very sensitive probe of local charge density. Extrapolating linearly, we also find from this relationship that the CNP corresponds to a 2D peak splitting of 20.4 cm−1 (see supporting information section 3). While we know the mean and standard deviations for the doping in the sample used for transport measurements with high precision, and we know the mean and standard deviations for the 2D peak splitting for the sample used for Raman measurements, there is sample-to-sample variation which introduces uncertainty in our values for the slope of the linear correspondence and 2D peak splitting at CNP. We estimate a roughly 5% sample-to-sample variation, which translates into uncertainty in charge per wavenumber of 0.11 × 1011 ± 0.02 × 1011 cm−2 per cm−1, and 20.4 ± 1.1 cm−1 for the 2D peak splitting at the CNP.
While it would be advantageous to use electrostatic field gating to confirm, attempts to control the charge level via back-gating samples for optical measurements are complicated due to light-induced charge screening of the gate voltage for graphene on hBN. This is because light illumination on a gated graphene/hBN sample on SiO2/Si produces optical excitations of defect transitions in hBN and charge transfer to the graphene. In fact, light exposure during gating quickly returns the graphene to the charge neutrality point, undoing the gate doping29. The sign of the charge is also undetermined, but recent measurements30 on ultraclean samples have shown a symmetric electron and hole blue-shift of the 2D peak (single peak fitting) for charge density up to 2 × 1012 cm−2. Hence, the 2D peak response for holes and electron doping is indistinguishable on the Raman spectra at such low charge density. Early gated Raman measurements31 on graphene on SiO2 showed a weak difference between electron vs hole doping below 1012 cm−2 in contrast to the newer easurements30. This illustrates the need for excellent charge homogeneity to observe the low charge density effects achieved on suspended or hBN encapsulated graphene.
Intensity, and the inner and outer processes
Generally, a high density of vector nesting creates a stronger Raman peak. This would indicate that the outer process, with flatter parts of the trigonal warping of the iso-energy contour matched by the phonon contour, has a stronger contribution to the Raman spectra than the inner process15, see Fig. 1(c). However, calculations including quantum interference and the q-dependent scattering matrix elements of the phonon intensity have shown that the inner process dominates despite the stronger vector nesting for the outer process11–13. Our results show the 2D 1 peak with the strongest intensity at the lowest doping level. A higher 2D 1 intensity has also been observed experimentally previously on both suspended15,16,18 and hBN encapsulated17 graphene. Based on the observed and predicted higher intensity for the inner process for pristine graphene, we tentatively assign the 2D 1 peak as originating from the inner process, and show below how this assignment is supported by the results. Figure 1(c) illustrates this assignment with the inner phonon having the lowest phonon energy. From previous work we know that the inner phonon vector q i is larger than the outer vector q o, but the inner KΓ phonon dispersion is flatter than the steeper outer KM phonon branch10,11,32, as illustrated schematically in Fig. 1(c). In the schematic of Fig. 1(c), the outer phonon branch has a high enough slope to result in a higher phonon energy, consistent with the assignment of 2D 1 as the inner process.
Intensity behaviour as a function of charge has not yet been explored theoretically. We suggest that the observed switch in intensity from 2D 1 to 2D 2 with increased charge screening may be an effect of changing wave vectors and phonon energies that will affect both the scattering matrix terms in the numerator, as well as the denominator of the Raman intensity scattering expression12, which will change the relative strengths of the 2D 1 and 2D 2 peak due to quantum interference. Regardless of the cause for the intensity behaviour of the two 2D peaks, it is clear that added charge to graphene in hBN changes the dominant intensity from the 2D 1 peak (inner) to the 2D 2 peak (outer) with increasing charge.
Linear dispersion model
The key to the split of the 2D peak into 2D 1 and 2D 2 components and their linewidths is the ratio of the phonon velocity v ph to the Fermi velocity v F for the inner and outer process. Using the DR mechanism and the simplifying assumption of perfectly linear electronic and phonon dispersions around the K and K’ points (but with different slopes for the inner and outer directions)10–13, and using v ph ≪ v F, we have
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
where is the D phonon energy (cm−1) at the K point (q = 0), γ is the imaginary part of the electronic self energy (eV), h is Planck’s constant, and c is the speed of light. The subscripts i and o refer to the inner and outer phonons, respectively. Equations 2–5 illustrate that the phonon energies, Eqn. (2); the dispersion with laser energy, Eqn. (3); the peak split, Eqn. (4); and the full width at half maximum (FWHM) linewidths, Eqn. (5), all depend on the ratio of the phonon to electron velocity in the inner and outer scattering processes. We use the results from the two laser lines to find the shift with laser energy33, ∂ω/∂E L, of the 2D 1 and 2D 2 band for “pristine” and charged graphene and use Eqn. (3) to determine the velocity ratio. For 2D 2+, the low intensity peak at CNP, the slope is 120 cm−1/eV, while the other ratios fall in the range of the values reported for graphene and carbon nanotubes ~88–110 cm−1/eV22,33,34. Using these ratios, we can also calculate , which in turn can be used to determine how the phonon velocity changes with screening along the KΓ and KM directions. The results are tabulated in Table 1. The linear approximation gives the “local” slope between the phonon wave-vectors selected by the green and red laser. Hence, the different values of are a reflection of the local slopes. The phonon dispersion near K has a negative second derivative, so the actual , which is the same for both the inner and outer process, will be below or equal to the smallest tabulated value, 1214 cm−1.
Table 1.
Extracted values for the lower and higher 2D energy peaks.
| Correlations | ||||
|---|---|---|---|---|
| variables | 2D 1(+) | 2D 1(−) | 2D 2(+) | 2D 2(−) |
| 97 | 97 | 120 | 103 | |
| 6.5 | 6.0 | 6.8 | 6.1 | |
| ωD 0(cm −1) | 1233 | 1233 | 1214 | 1230 |
| 1343 | 1342 | 1349 | 1345 | |
| Δω(cm −1) | 110 | 110 | 135 | 115 |
The ± signs denote the “pristine” and charged Raman response, where “pristine” results are denoted with (+). Δω denotes the difference of the measured ½ω 2D and the extracted value of at the K point (q = 0). Note that 2D 1 has overlapping values for 2D 1 pristine and charged graphene, but that the increased charge causes an increase in the q vector, q 1 + Δq 1, which indicate a lower phonon velocity.
We can also fit the data with a linear model, detailed in SI, section 2, that forces a common as shown in Fig. 4. Here we are using a scaled x-axis, where instead of q, we are plotting the phonon dispersion versus x = q i v F,i/2πc, which is directly measurable without knowing v F. This gives the exact scaled q values for i = 1 ~ 4, i representing red and green laser for uncharged and charged graphene, respectively. Note that by this construction, the laser energy sets the scaled q value x, see SI. The best fit values for are 1228 and 1233 cm−1 for uncharged and charged graphene, respectively, tabulated in SI Table S3.
Figure 4.
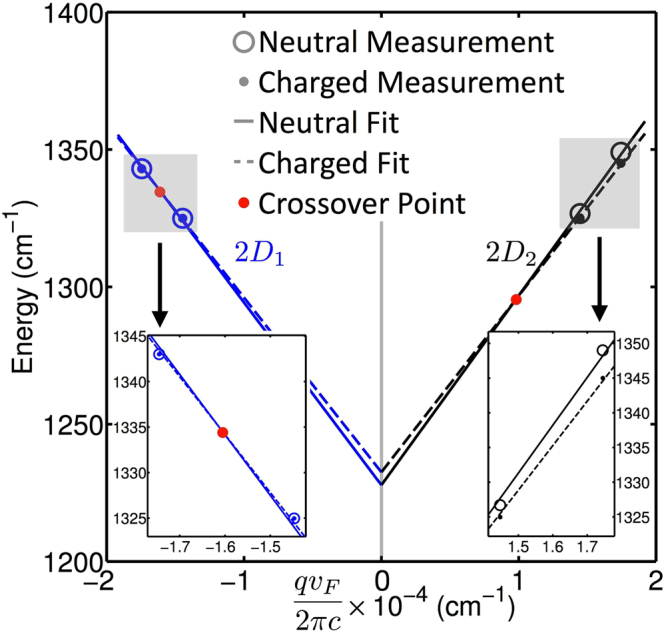
Scaled phonon dispersion. The figures shows the experimental data from Table 1 and the best fit linear model forcing a common for 2D 1 and 2D 2 phonons. The phonon momentum on the x-axis is scaled so that all scaled q values are given directly by measurements. Note that the Fermi velocity scaling q is that of the particular case, i.e., inner or outer process, and uncharged or charged.
Both linear models (local slope versus common ) exhibit the crossover in dispersion attributed to screening of the phonon dispersion, illustrated both in Fig. 1(c), bottom, and Fig. 4. The change in the local phonon dispersion with increased screening has been predicted by comparisons between the phonon dispersion using the GW approach for screened interactions, and density-functional theory that represents unscreened interactions10,11. The increase in and decrease in phonon velocities with increased charge is a direct indication of lifting of the K-point Kohn anomaly due to screening10,11 and a weakening of EPC3.
Split peak phonon energy versus charge density
It is counterintuitive that the 2D 2 phonons decrease with increased charge (Fig. 3a), since increased screening lowers the Fermi velocity and increases the DR-selected q vector from q to q + Δq, which typically corresponds to a higher ω D 17,19,20. The linear models above demonstrate that the decrease in 2D 2 with increased charge is due to a crossover of the unscreened and screened phonon dispersion, as seen in calculations10,11. The dispersion crossover under different charge screening conditions enables the decrease in phonon energy on the outer branch, while the slope and crossover of the inner branch conspires to yield a basically unchanged 2D 1 phonon energy as indicated by the two q values, q i and q i + Δq i (Fig. 1c). The reduction of the phonon velocities is commensurate with lifting the Kohn anomaly at K with charge screening. The significant decrease in peak splitting for λ = 633 nm compared to λ = 532 nm from 15 to 4 cm−1 for graphene near the CNP is indicative of a sub-linear dispersion (negative second derivative) of the inner branch, as expected10,11.
Linewidths
As indicated in Eqn. (5), the linewidths of 2D 1 and 2D 2 are not indicative of the phonon lifetime, but rather determined by the electronic lifetime (imaginary part of the self-energy) and ratio of the phonon to electron velocity. However equation 2 provides a convenient mapping between scattered photon energy and phonon energy, and from this perspective the linewidth is pictured as a blurring of the DR phonon contour to a width, δq i,o. Phonons that fall within the blurred contour make a significant contribution to the 2D peak, and we will regard them as participatory phonons, and the blurred line as the participatory contour. The middle of the participatory contour is mapped almost perfectly to the triangularly warped iso-energy phonon contour with the “corners” pointing towards Γ rather than M. The width of the participatory contour in the KΓ direction (inner), δq i, has been calculated12 to be broader than the width in KM direction (outer), δq o, which provides a method for assigning 2D peaks to inner and outer processes. Using equations (1) and (5) and our measurements we relate the ratio of inner to outer participatory contour widths to the ratio of inner to outer linewidths, outer to inner phonon to Fermi velocity ratios, and outer to inner electron velocities . To make a proper comparison with theory computed assuming zero doping, we use our data in Table 1 and electron transport data to estimate the ratio of contour widths at the CNP (see supporting information section 3 for details). Assuming the 2D1 peak corresponds with the inner process and the 2D2 peak corresponds with the outer process we find this ratio to be 1.3, but if the correspondence between peaks and inner/outer is reversed, this ratio is only 0.8. Since theory predicts the ratio of contour widths to be greater than one12, our data supports the assignment of 2D 1 as originating from the inner process.
Charge affects the 2D linewidth through two primary mechanisms: scattering and phonon velocity renormalization. Eqn. (5) shows that the linewidth is proportional to the imaginary part of the electronic self-energy and the phonon velocity. Experimentally we can only measure the phonon to electron velocity ratio, which we will use as a proxy for the phonon velocity keeping in mind that the electron velocity slightly decreases with charge9. For λ = 532 nm, the “pristine” linewidths of the 2D 1 and 2D 2 peaks are almost equal, but as charge increases the 2D 2 linewidth steadily rises while the 2D 1 linewidth remains level until the peak split nearly reaches its minimum, at which point the linewidth surprisingly decreases (Fig. 3(c)). It is generally expected that the linewidth should increase with charge because the electronic self-energy increases12, which makes the nearly constant 2D1 linewidth surprising. However, taking into account the change to the phonon velocity we’ll see that our observations are consistent with increased electronic self-energy. Our data shows that the phonon to electron velocity ratio for the 2D 1 peak decreases with charge (Table 1), which, given that charge reduces the electron velocity, implies that the phonon velocity must decrease as well. Our observation of a nearly flat 2D1 linewidth versus charge is then consistent with a self-energy that increases with charge, but compensated for by a reduced phonon velocity. For the 2D 2 peak, the phonon to electron velocity ratio also decreases with charge, but in this case the linewidth increases. We offer two explanations for this difference: 1) The electronic self-energy is momentum dependent, and the momenta that contribute to the 2D 1 and 2D 2 peaks are different. Our observations are then consistent with an electronic self-energy that increases more greatly with charge for momenta that contribute to the 2D 2 peak than momenta that contribute to the 2D 1 peak. 2) The Fermi velocity decreases with charge less dramatically along the direction of the 2D 2 process than the 2D1 process. If this is the case, then the 2D 2 phonon velocity reduces by smaller amount than the 2D 1 phonon velocity, and will result in a 2D 2 linewidth that increases more rapidly with charge.
Discussion
The results presented here on hBN encapsulated graphene have both similarities and differences to suspended graphene. Both types of samples exhibit a decrease in the 2D double peak split with increased charge, and the lower energy peak, 2D 1, has the highest intensity. The screening of the K-point Kohn anomaly with increasing charge has not yet been addressed experimentally on suspended graphene. A significant difference is the substantial decrease in the peak split at the CNP for λ = 633 nm, not observed for suspended graphene where the 2D peak-split stays nearly constant (~13 ± 3 cm−1) over a laser energy range from 1.5–2.7 eV15,18. This indicates that the dielectrically screened graphene is less well fit with a linear model than suspended graphene: The peak split between inner and outer phonon energies is proportional to the difference between the inner and outer velocity ratio, Eqn. (4), which is constant in a linear model. Based on the linewidth as a function of E L, Berciaud et al.18 dismissed the theory of the peak split originating from the difference in the inner and outer 2D phonons. The phonon linewidth is expected to decrease with lower laser energy, since γ eh ∝ E L, and Berciaud et al.18 observed an increasing linewidth for laser line energies below ~1.7 eV for suspended graphene. We note that it is possible that the predicted increase in phonon dispersion slope closer to the K point10,11, probed with lower laser energies, dominates over the decrease in electronic linewidth, γ eh.
The lifting of the K-point Kohn anomaly with screening observed here is a sign of the weakened EPC3. Excitation of D band phonons by electrons is a fundamental bottleneck for ballistic transport at high fields35. Hence, it is possible that encapsulated graphene with low and uniform charge screening could have better transport properties at high fields than suspended graphene if the screening sufficiently reduces the strength of the EPC of the D phonons, without introducing other scattering mechanisms.
Summary
In conclusion, we have used Raman spectroscopy of graphene encapsulated in hBN to explore the intrinsic double peaked 2D phonon behaviour under low charge screening. The analysis of the 2D data as a function of 2D 1 and 2D 2 peak separation removes influence of strain, and reveals strong correlations between charge, peak intensities, peak positions and linewidths. The peak split can be used to estimate the charge density with sensitivity ~ 1010 cm−2 per cm−1 2D peak split, an improvement of two orders of magnitude compared to use of the G band Kohn anomaly at the Γ point. Hence, the 2D peak split could be very informative for detecting low amounts of charge, with the caveat that the peak split with charge behaviour is known for the particular substrate screening and laser line used. The method also reveals information about the origin of the double peak and the effect of increased charge, for example the intensity shifts from the inner to the outer phonon with increased charge. We associate the lower energy 2D 1 peak with the so called inner process, and the higher energy 2D 2 peak with the outer process. Even the low amount of charge puddling found in these samples is enough to significantly alter the strength of the D band Kohn anomaly at the K point.
Methods
The encapsulated graphene sample was fabricated at Columbia University by Carlos Forsythe with their pick-and-place method that avoids direct contact between the pick-up polymer and graphene layer or the accompanying hBN surfaces that contact the graphene21. This particular sample did not have functioning edge contacts, but similar samples have a room temperature mobility of ~3.2 × 104 cm2/Vs.
The collected 2D Raman spectral map is fitted with two Voigt peak functions at all different locations on the hBN encapsulated graphene. Different incident laser photon energies, green laser with wavelength of 532 nm (E L = 2.33 eV) and red laser with wavelength of 633 nm (E L = 1.96 eV), are applied at 1 µm by 1 µm spacing with a laser spot of approximately 1µm2 with typical spectra shown in Fig. 2. The incident laser power was limited to 1.2 mW to avoid heating.
Data Availability
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
Electronic supplementary material
Acknowledgements
This work was supported by the United States National Science Foundation (DMR 1411008, DMR 1308659). J.C. thanks the Department of Defence (DoD), Air Force Office of Scientific Research for its support through the National Defence Science and Engineering Graduate (NDSEG) Fellowship, 32 CFR 168a. The authors would like to thank Cory Dean and Carlos Forsythe for the graphene encapsulated hBN sample.
Author Contributions
A.K.S. conceived of the study, and X.W. carried out experimental measurements J.W.C. carried out the statistical analysis. All authors contributed to analysis and writing the paper.
Competing Interests
The authors declare that they have no competing interests.
Footnotes
Electronic supplementary material
Supplementary information accompanies this paper at 10.1038/s41598-017-13769-3.
Publisher's note: Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Ferrari AC, Basko DM. Raman spectroscopy as a versatile tool for studying the properties of graphene. Nat. Publ. Gr. 2013;8:235–246. doi: 10.1038/nnano.2013.46. [DOI] [PubMed] [Google Scholar]
- 2.Thomsen C, Reich S, Maultzsch J. Resonant Raman spectroscopy of nanotubes. Philos. Trans. A. Math. Phys. Eng. Sci. 2004;362:2337–2359. doi: 10.1098/rsta.2004.1444. [DOI] [PubMed] [Google Scholar]
- 3.Piscanec S, Lazzeri M, Mauri F, Ferrari AC, Robertson J. Kohn anomalies and electron-phonon interactions in graphite. Phys. Rev. Lett. 2004;93:185503. doi: 10.1103/PhysRevLett.93.185503. [DOI] [PubMed] [Google Scholar]
- 4.Matthews MJ, Pimenta MA, Dresselhaus G, Dresselhaus MS, Endo M. Origin of dispersive effects of the Raman D band in carbon materials. Phys. Rev. B. 1999;59:R6585. doi: 10.1103/PhysRevB.59.R6585. [DOI] [Google Scholar]
- 5.Forster F, et al. Dielectric screening of the Kohn anomaly of graphene on hexagonal boron nitride. Phys. Rev. B. 2013;88:85419. doi: 10.1103/PhysRevB.88.085419. [DOI] [Google Scholar]
- 6.Hwang C, et al. Fermi velocity engineering in graphene by substrate modification. Sci. Rep. 2012;2:590. doi: 10.1038/srep00590. [DOI] [Google Scholar]
- 7.Elias DC, et al. Dirac cones reshaped by interaction effects in suspended graphene. Nat. Phys. 2011;7:701–704. doi: 10.1038/nphys2049. [DOI] [Google Scholar]
- 8.Siegel DA, et al. Many-body interactions in quasi-freestanding graphene. Proc. Natl. Acad. Sci. 2011;108:11365–11369. doi: 10.1073/pnas.1100242108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chae J, et al. Renormalization of the graphene dispersion velocity determined from scanning tunnelling spectroscopy. Phys. Rev. Lett. 2012;109:116802. doi: 10.1103/PhysRevLett.109.116802. [DOI] [PubMed] [Google Scholar]
- 10.Lazzeri M, Attaccalite C, Wirtz L, Mauri F. Impact of the electron-electron correlation on phonon dispersion: Failure of LDA and GGA DFT functionals in graphene and graphite. Phys. Rev. B. 2008;78:81406. doi: 10.1103/PhysRevB.78.081406. [DOI] [Google Scholar]
- 11.Narula R, Reich S. Graphene band structure and its 2 D Raman mode. Phys. Rev. B. 2014;90:85407. doi: 10.1103/PhysRevB.90.085407. [DOI] [Google Scholar]
- 12.Venezuela P, Lazzeri M, Mauri F. Theory of double-resonant Raman spectra in graphene: Intensity and line shape of defect-induced and two-phonon bands. Phys. Rev. B. 2011;84:35433. doi: 10.1103/PhysRevB.84.035433. [DOI] [Google Scholar]
- 13.May P, et al. Signature of the two-dimensional phonon dispersion in graphene probed by double-resonant Raman scattering. Phys. Rev. B. 2013;87:75402. doi: 10.1103/PhysRevB.87.075402. [DOI] [Google Scholar]
- 14.Ferrari AC, et al. Raman spectrum of graphene and graphene layers. Phys. Rev. Lett. 2006;97:187401. doi: 10.1103/PhysRevLett.97.187401. [DOI] [PubMed] [Google Scholar]
- 15.Luo Z, Cong C, Zhang J, Xiong Q, Yu T. Direct observation of inner and outer G′ band double-resonance Raman scattering in free standing graphene. Appl. Phys. Lett. 2012;100:243107. doi: 10.1063/1.4729407. [DOI] [Google Scholar]
- 16.Berciaud S, Ryu S, Brus LE, Heinz TF. Probing the intrinsic properties of exfoliated graphene: Raman spectroscopy of free-standing monolayers. Nano Lett. 2009;9:346–352. doi: 10.1021/nl8031444. [DOI] [PubMed] [Google Scholar]
- 17.Neumann C, et al. Line shape of the Raman 2D peak of graphene in van der Waals heterostructures. Phys. Status Solidi Basic Res. 2016;253:2326–2330. doi: 10.1002/pssb.201600283. [DOI] [Google Scholar]
- 18.Berciaud S, et al. Intrinsic line shape of the Raman 2D-mode in freestanding graphene monolayers. Nano Lett. 2013;13:3517–3523. doi: 10.1021/nl400917e. [DOI] [PubMed] [Google Scholar]
- 19.Ahn G, et al. Optical probing of the electronic interaction between graphene and hexagonal boron nitride. ACS Nano. 2013;7:1533–1541. doi: 10.1021/nn305306n. [DOI] [PubMed] [Google Scholar]
- 20.Ni Z, Wang Y, Yu T, You Y, Shen Z. Reduction of Fermi velocity in folded graphene observed by resonance Raman spectroscopy. Phys. Rev. B. 2008;77:235403. doi: 10.1103/PhysRevB.77.235403. [DOI] [Google Scholar]
- 21.Wang L, et al. One-dimensional electrical contact to a two-dimensional material. Science. 2013;342:614–617. doi: 10.1126/science.1244358. [DOI] [PubMed] [Google Scholar]
- 22.Burson KM, et al. Direct imaging of charged impurity density in common graphene substrates. Nano Lett. 2013;13:3576–3580. doi: 10.1021/nl4012529. [DOI] [PubMed] [Google Scholar]
- 23.Ferrari AC. Raman spectroscopy of graphene and graphite: Disorder, electron-phonon coupling, doping and nonadiabatic effects. Solid State Commun. 2007;143:47–57. doi: 10.1016/j.ssc.2007.03.052. [DOI] [Google Scholar]
- 24.Yan J, Zhang Y, Kim P, Pinczuk A. Electric field effect tuning of electron-phonon coupling in graphene. Phys. Rev. Lett. 2007;98:166802. doi: 10.1103/PhysRevLett.98.166802. [DOI] [PubMed] [Google Scholar]
- 25.Lee JE, Ahn G, Shim J, Lee YS, Ryu S. Optical separation of mechanical strain from charge doping in graphene. Nat. Commun. 2012;3:1024. doi: 10.1038/ncomms2022. [DOI] [PubMed] [Google Scholar]
- 26.Wang X, Tantiwanichapan K, Christopher JW, Paiella R, Swan AK. Uniaxial Strain Redistribution in Corrugated Graphene: Clamping, Sliding, Friction, and 2D Band Splitting. Nano Lett. 2015;15:5969–5975. doi: 10.1021/acs.nanolett.5b02107. [DOI] [PubMed] [Google Scholar]
- 27.Huang M, Yan H, Heinz TF, Hone J. Probing strain-induced electronic structure change in graphene by Raman spectroscopy. Nano Lett. 2010;10:4074–4079. doi: 10.1021/nl102123c. [DOI] [PubMed] [Google Scholar]
- 28.Neumann C, et al. Raman spectroscopy as probe of nanometre-scale strain variations in graphene. Nat. Commun. 2015;6:8429. doi: 10.1038/ncomms9429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Ju L, et al. Photoinduced doping in heterostructures of graphene and boron nitride. Nat. Nanotechnol. 2014;9:348–352. doi: 10.1038/nnano.2014.60. [DOI] [PubMed] [Google Scholar]
- 30.Li, Y. Probing the response of two-dimensional crystals by optical spectroscopy. (Springer, 2015).
- 31.Das A, et al. Monitoring dopants by Raman scattering in an electrochemically top-gated graphene transistor. Nat. Nanotechnol. 2008;3:210–215. doi: 10.1038/nnano.2008.67. [DOI] [PubMed] [Google Scholar]
- 32.Hasdeo EH, Nugraha ART, Dresselhaus MS, Saito R. Fermi energy dependence of first-and second-order Raman spectra in graphene: Kohn anomaly and quantum interference effect. Phys. Rev. B. 2016;94:75104. doi: 10.1103/PhysRevB.94.075104. [DOI] [Google Scholar]
- 33.Dresselhaus MS, Dresselhaus G, Jorio A, Souza Filho AG, Saito R. Raman spectroscopy on isolated single wall carbon nanotubes. Carbon N. Y. 2002;40:2043–2061. doi: 10.1016/S0008-6223(02)00066-0. [DOI] [Google Scholar]
- 34.Malard LM, Pimenta MA, Dresselhaus G, Dresselhaus MS. Raman spectroscopy in graphene. Phys. Rep. 2009;473:51–87. doi: 10.1016/j.physrep.2009.02.003. [DOI] [Google Scholar]
- 35.Perebeinos V, Tersoff J, Avouris P. Electron-phonon interaction and transport in semiconducting carbon nanotubes. Phys. Rev. Lett. 2005;94:86802. doi: 10.1103/PhysRevLett.94.086802. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.