Abstract
Molecular Dynamics (MD) simulations based on the implicit solvent generalized Born (GB) models can provide significant computational advantages over the traditional explicit solvent simulations. However, the standard GB becomes prohibitively expensive for all-atom simulations of large structures; the model scales poorly, ~ n2, with the number of solute atoms. Here we combine our recently developed Optimal Point Charge Approximation (OPCA) with the Hierarchical Charge Partitioning (HCP) approximation to present an ~ n log n multi-scale, yet fully atomistic, GB model (GB-HCPO). The HCP approximation exploits the natural organization of biomolecules (atoms, groups, chains, and complexes) to partition the structure into multiple hierarchical levels of components. OPCA approximates the charge distribution for each of these components by a small number of point charges so that the low order multipole moments of these components are optimally reproduced. The approximate charges are then used for computing electrostatic interactions with distant components, while the full set of atomic charges are used for nearby components. We show that GB-HCPO can deliver up to two orders of magnitude speedup compared to the standard GB, with minimal impact on its accuracy. For large structures, GB-HCPO can approach the same nominal speed, as in nanoseconds per day, as the highly optimized explicit-solvent simulation based on particle mesh Ewald (PME). The increase in the nominal simulation speed, relative to the standard GB, coupled with substantially faster sampling of conformational space, relative to the explicit solvent, makes GB-HCPO a suitable candidate for MD simulation of large atomistic systems in implicit solvent. As a practical demonstration, we use GB-HCPO simulation to refine a ~1.16 million atom structure of 30-nm chromatin fiber (40 nucleosomes). The refined structure suggests important details about spatial organization of the linker DNA and the histone tails in the fiber: (1) the linker DNA fills the core region, allowing the H3 histone tails to interact with the linker DNA, which is consistent with experiment; (2) H3 and H4 tails are found mostly in the core of the structure, closer to the helical axis of the fiber, while H2A and H2B are mostly solvent exposed. Potential functional consequences of these findings are discussed. GB-HCPO is implemented in the open source MD software, NAB in Amber 2016.
Graphical Abstract
1 INTRODUCTION
Atomistic simulation is one of the most widely used theoretical tools in bio-medical research;1–3 high accuracy of solvent representation in these simulations is of paramount concern. Arguably the most accurate among classical models of solvation is the one in which individual water molecules are treated explicitly on the same footing with the target biomolecule.4–8 Yet, accuracy of this explicit solvent representation comes at extremely high price, computationally. 9,10 In particular, even straightforward atomistic simulations of very large structures in explicit solvation4–8 can be extremely challenging. For example, a recent study of a 64 million atom structure of the complete HIV-1 capsid model required one of the most powerful supercomputers in the world11 to produce a 100ns long trajectory. Structure sizes and/or time scales affordable to a typical computational lab with much more limited resources are considerably smaller. At the same time, there are many situations when a fully atomistic simulation of a large structure may yield meaningful results: for example, parts of the structure may be moving on time-scales that can still fall within reach of atomistic simulations, but these motions may be significantly affected by the rest of the “scaffold”, making their study in isolation uninformative.
An alternative that can significantly reduce the cost of conformational sampling in atomistic simulations is the implicit (or continuum) solvation model that treats solvent implicitly as a continuum with dielectric and non-polar properties of water.15–24 A particularly computationally efficient version of the approach, the so-called generalized Born (GB) model, 25,26 is the current “workhorse” in Molecular Dynamics (MD)27–34 including QM/MM35,36 and REMD simulations.37 GB provides significant computational advantage over explicit solvent MD simulations in two main ways: First, GB approximates the discrete solvent as a continuum, thus drastically reducing the number of particles to keep track of in the system,20,25,38–61 which significantly increases the nominal speed (nanoseconds per day of simulation time). Second, the GB model can sample conformational space substantially faster than explicit solvent model due to the reduction of solvent viscosity. For instance, it has been shown that the conformational sampling in implicit solvent simulations can be ~100 times faster compared to common explicit solvent PME simulations.62–66 The combination of these two benefits makes the GB model particularly well suited for all-atom MD simulations in several areas, notably the protein folding process,27–34,67 and protein design.68,69
Despite these advantages, GB is rarely used for simulating very large structures, in part because of its poor algorithmic complexity: the functional form for the most widely used practical GB models scales as ~ n2, where n is the number of solute atoms. Therefore, GB-based simulations can become too slow for large and especially very large (100,000 atoms and more) structures, essentially negating all of the potential benefits of the implicit solvation. In contrast, the most common explicit-solvent simulations based on the “industry standard” particle mesh Ewald (PME),70–73 or the fast multipole,74–76 scale as ~ N log N, where N is the total number of solvent and solute atoms combined. Thus, even though n ≪ N in a typical simulation, the nominal computational speed of the GB model can become much lower than that of the corresponding explicit-solvent simulation for large systems, with the “break-even” point being around n of several thousand atoms, depending on the specifics of the structure and implementation details.26 In cases where large-scale atomistic level modeling is desired, practitioners currently have no choice but to resort to the traditional, explicit solvent approach which leads to inordinate computational costs, or resort to further drastic approximations within the GB.
A common approach for reducing the computational cost of GB models is to apply the concept of spherical cutoff, i.e. ignore interactions and computations involving atoms beyond a cutoff distance, referred to as cutoff-GB here. The cutoff-GB reduces the computational cost of traditional GB-based MD simulations from ~ n2 to ~ n log n. However, it was known for a long time that the use of spherical cutoffs in explicit solvent simulations could lead to unacceptable errors and severe artifacts, such as spurious forces and artificial structures around the cutoff distance,77–79 especially when the structures were highly charged, such as nucleic acids.80 It was the possibility of unpredictable artifacts, and the availability of the considerably more accurate yet efficient PME implementations, 70–73,80 that made the community eventually abandon the use of spherical cutoffs in routine explicit solvent simulations. However, the absence of a clear alternative to the cutoffs for the GB simulations extended the “life” of this once indispensable approach to reducing computational costs. In what follows we revisit the issue of cutoff artifacts specifically in the context of the GB model, then describe in detail the proposed alternative.
Namely, in this study, we combine our recently developed Optimal Point Charge Approximation (OPCA)81 with the Hierarchical Charge Partitioning (HCP) approximation82,83 to present an ~ n log n multi-scale, yet fully atomistic, approach based on the generalized Born model (GB-HCPO). We evaluate the accuracy, speed, and stability of the GB-HCPO on a set of representative biomolecular structures. We show that GB-HCPO can deliver up to two orders of magnitude speedup compared to the standard GB, depending on structure size.
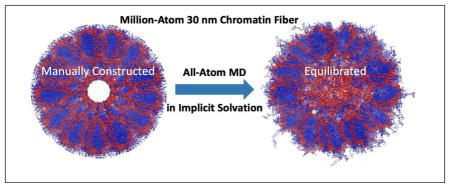
We then apply GB-HCPO to gain insight into the structure of ~1.16 million atom 30-nm chromatin fiber. Chromatin fiber is the next hierarchical level of chromatin compaction beyond the nucleosome (Figure 1), its organization is believed to be important for regulation of gene expression.84 Specifically, modifications to N-terminal tails of the histone proteins that make up the fiber core are known to regulate DNA accessibility, and affect vital cellular processes such as transcription.85 However, due to the large size of the fiber –millions of atoms–only low-resolution (e.g. cryo-EM) experimental structures of the fiber are currently available;86,87 its atomistic details, including relative location of the histone tails, are not known experimentally. Atomic-level studies of the histone tails and linker DNA dynamics of the nucleosome have so far relied on single nucleosome particle,88,89 a detailed characterization of the histone tails in the presence of many other nucleosomes within the chromatin fiber remains elusive. Computational studies investigating the organization of chromatin fiber have so far used coarse-grain simulations,90,91 in which small groups of atoms are treated as single particles. However, such simulations can not elicit finer atomistic details. In addition, force fields utilized by these studies do not have the accuracy of fully atomistic potentials that have been refined for decades.92
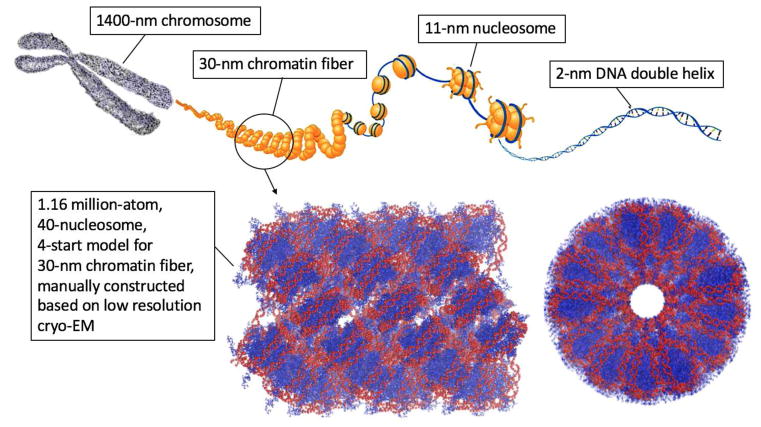
Figure 1.
Top: The hierarchy of DNA compaction in eukaryotic nuclei. The 2-nm wide DNA helices (blue) wrap around histone proteins to form 11-nm nuclesomes (yellow. Protruding histone tails are shown for the first two nucleosomes). The nulceosomes are believed to be further compacted to form 30-nm-diameter chromatin fibers. The chromatin fibers are further packed to make up the chromosomes (grey). Some elements of the top figure are taken from Ref.12 Reprinted with permission from AAAS. Bottom: A 30-nm chromatin fiber model (1.16 million atoms).13 The images were rendered using VMD.14
Here we start with a ~1.16 million atom model of the 30-nm chromatin fiber, “manually” constructed from 40 nucleosomes based on a model13 consistent with low resolution cryo-EM data (Figure 1). We perform multi-scale, all-atom GB-HCPO simulations of 30-nm chromatin fiber to investigate the atomistic detail of the tails (H3, H4, H2A and H2B) in solvent exposure and position relative to the core of the fiber and the linker DNA. Based on these findings, we discuss potential functional roles of different histone tails in compaction of chromatin components and post-translational modifications.
2 METHODS
2.1 The Reference GB (Without Further Approximation)
The GB models available in most widely used MD software packages, such as Amber, 93,94 approximate the electrostatic energy Eelec of a solvated system as below,25,95
| (1) |
| (2) |
| (3) |
where Evac and Esolv are the electrostatic vacuum and solvation energy, εw is the dielectric constant of the solvent, qi and qj are the charges of atoms i and j, and rij is the distance between the atoms. Here we employ the most widely used functional form25 of , where Bi and Bj are the so-called effective Born radii. For the most prevalent case where the atoms i and j do not overlap the effective Born radii, Bi, can be calculated as:
| (4) |
where Ri is the intrinsic radius of atom i, rij is the distance from i to any point j in the solute volume.
As seen from eq 2 and eq 3, the calculations of Evac and Esolv scale as ~ n2, the computational implementation of analytical pairwise approximation to the effective Born radii Bi, eq 4, also scales as ~ n2. Therefore, without further approximation, the computational cost of the GB model described above scales as ~ n2, where n is the number of solute atoms.
2.2 The ~ n log n Multi-scale All-atom GB Approximation
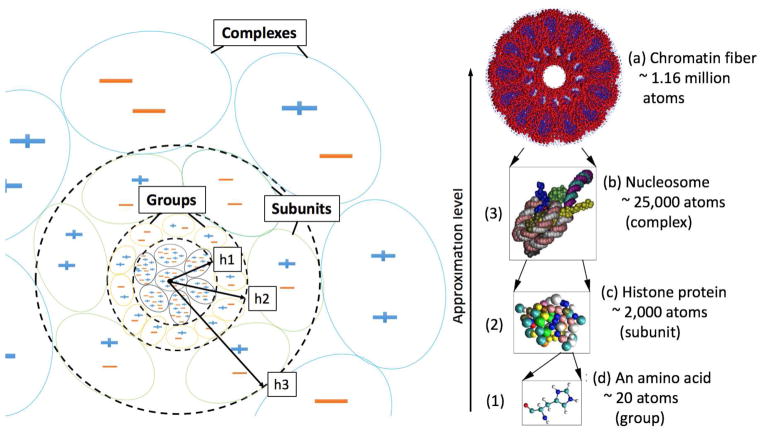
Previously,83 we showed that an ~ n log n approximation of the GB model can be achieved by resorting to the concepts of the Hierarchical Charge Partitioning (HCP).82 Based on the HCP approximation, the biomolecular structures are partitioned into multi-level hierarchical components using the natural organization of biomolecules, as illustrated in Figure 2 – atoms (level 0), nucleic and amino acid groups (level 1), protein, DNA and RNA subunits (level 2), complexes of multiple subunits (level 3), and higher level structures such as fibers and virus capsids. To apply the HCP approximation to the GB model (i.e. GB-HCP83), the charge distribution for each component c beyond level 0 (groups, subunits and complexes) is approximated by two point charges (qc1, rc1 and qc2, rc2), which are used in place of qj charges to approximate the electrostatic interactions of the corresponding component c with charge qi (eq 2 and eq 3). Accordingly, two equivalents of the effective Born radii, Bc1 and Bc2, are assigned to the approximate point charges.83 These equivalent effective Born radii are used to approximate the contribution of distant components to the solvation energy of atom i, instead of the effective Born radii (Bj) of the individual atoms within these components. Also, an equivalent radius for each component, Rc, is calculated and used in place of the intrinsic radius of atoms j (Rj) (eq 4).83 The HCP method then uses the approximate point charges and their corresponding parameters (qc1, qc2, rc1, rc2, Bc1, Bc2 and Rc) for computations involving distant components, while the full set of atomic point (partial) charges and their corresponding parameters (qj, rj, Bj, Rj) are used for computations involving nearby components (Figure 2). The level of approximation used is determined by the distance of a component from the point of interest: the greater the distance from the point of interest, the larger (higher level) is the component used in the approximation. As a result, the computational cost of the GB model (eqs 2, 3, and 4) is reduced from n2 to ~ n log n.83
Figure 2.
Left: Illustration of hierarchical charge partitioning (HCP) for three levels of approximation. The greater the distance from the point of interest, the larger (higher level) is the component used in the approximation. Here, h1, h2 and h3 are the level 1 (group), level 2 (subunit) and level 3 (complexes) threshold distances, respectively. The charge distribution for each component at level 1 and beyond is represented by two approximate point charges,83 which are used for computations involving distant components. Right: Multi-level hierarchical partitioning of 40-nucleosome 30-nm chromatin fiber (see Figure 1) based on its natural structural organization: (a) The fiber is made up of 40 nucleosome complexes excluding the DNA, (b) each complex (level 3) is made up of 9 subunits (histones), (c) each subunit (level 2) is made up of 68–135 groups, and (d) each group (level 1) is made up of 7–32 atoms (level 0). The DNA is partitioned into segments of 32 nucleotides with each segment being treated as a complex with a single subunit. The images were rendered using VMD.14
The accuracy of the ~ n log n approximation described above is strongly influenced by the magnitudes and positions of the approximate point charges, and their corresponding effective Born radii. The original GB-HCP83 simply places the approximate charges at the center of charge (for the 1-charge approximation), or at the center of the positive and negative charges (for the 2-charge approximation) for each component. Although straightforward in technical implementations, such simple charge placement does not guarantee an optimal representation of the electrostatic potential around the original charge distributions of the components, 81 and can translate into inaccurate representation of electrostatic forces and energies. As will be seen in the results section, such inaccuracies can lead to unacceptable instabilities in MD simulations of biomolecules (e.g., see Figure 9).
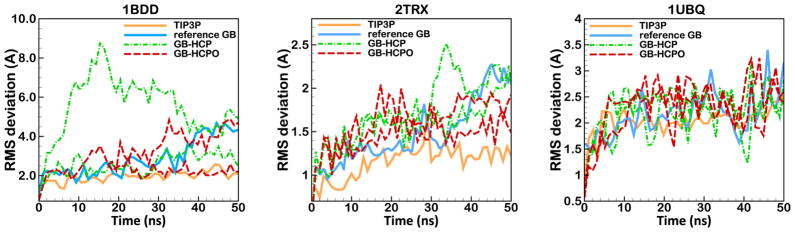
Figure 9.
Backbone RMS deviation from the experimental reference structure for 50 ns MD simulation based on GB-HCPO (red dashed line) compared to the reference explicit-solvent method (TIP3P), reference GB (without approximation), and GB-HCP. The test structures are, from left to right: immunoglobulin binding domain (1BDD, residues 10–55), thioredoxin (2TRX, all residues), and Ubiquitin (1UBQ, all residues). Two independent trajectories were produced for each of GB-HCPO and GB-HCP approximations. Each trajectory is sampled every 1 ns. Connecting lines are shown to guide the eye.
In our new ~ n log n GB model presented here, GB-HCPO, we significantly improve the accuracy of the HCP approximation of GB by rigorously optimizing the placement of the approximate charges. The optimization is performed based on the concept of Optimal Point Charge Approximation (OPCA):81 the approximate charges (qc1, rc1 and qc2, rc2) are calculated such that the lowest order multipole moments of the original charge distribution for each component is optimally reproduced, ensuring that the error in electrostatic potential far from the distribution is minimized. Furthermore, to fully take advantage of the improved accuracy in the computations of electrostatic interactions in GB-HCPO achieved by the implementation of OPCA, here we also present a new expression for computing the “equivalent” effective Born radii (Bc1 and Bc2), as described below.
2.2.1 Calculation of Approximate Charges (qc1, rc1 and qc2, rc2) Based on OPCA
To best represent the electrostatic potential around a given component, OPCA places a small number of approximate point charges so that the lowest order multipole moments of the corresponding charge distribution are optimally reproduced.81 A general framework for numerically computing OPCA, for any given number of approximate charges was described previously.81 Briefly, for any input charge distribution, and a desired number of approximating charges, OPCA finds their location such that maximum possible number M of the lowest multipole moments of the original distribution are reproduced exactly, while the error in the next multipole order is minimized. The resulting error in the electrostatic potential computed using OPCA is guaranteed to fall off at least as fast as 1/RM+1, where R is the distance from the charge distribution.
The two approximate charges for HCP components (qc1, rc1 and qc2, rc2) can be calculated via closed-form analytical expressions developed based on OPCA,81 which provide computational efficiency and algorithmic simplicity for MD simulations. The analytical expressions for 2-charge OPCA exactly reproduces the monopole (for charged structures) and the dipole, and optimally approximates the quadrupole moments of the original charge distribution (minimum rms error). Due to important differences in the characteristics of charged and uncharged components,81 the analytical expression for these components are different, as described below (Figure 3).
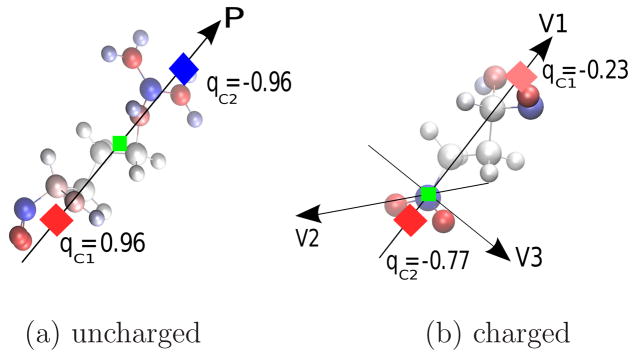
Figure 3.
Illustration of a 2-charge optimal point charge approximation. (a) A sample charge distribution- a neutral amino acid (C-terminal arginine at physiological pH.). The 2 optimal point charges (red and blue diamonds) are placed in equal distances (drn) from the center of dipole (green square) of the original charge distribution, along the dipole moment direction of the original charge distribution. (b) A sample charge distribution with non-zero net charge (a glumatic acid group within a protein with net charge = −1 e). The 2-charge optimal point charges (red diamonds) are placed so that their center of charge matches the center of charge of the original charge distribution (the green square), along the eigenvector of the quadrupole moment of the original charge distribution with the largest eigenvalue.81
OPCA for Uncharged Components
For uncharged components, the monopole and dipole moments are exactly reproduced when a pair of charges of equal magnitude but opposite sign are aligned with the direction of the dipole moment of the original charge distribution.81 The quadrupole moment for uncharged charge distributions is optimally reproduced if the geometrical center of the optimal point charges coincides with the center of dipole for the original charge distribution (green square in Figure 3(a)). This leaves only one unknown parameter, the separation between the charges drn = |rc2 − rc1|, where rc1 and rc2 are the position vectors of the approximate charges. The drn value is chosen so that the octupole moment is optimally reproduced. Depending on whether or not there exists an analytical solution to the equation that relates the OPCA charges to the octupole moment of the original charge distribution, drn can vary from a very small value (drn ≪ R0) to a value close to R0 (drn ~ R0),81 where R0 is the distance of the furthest charge from the center of geometry. 81 For practical applications it is computationally more efficient to use an empirically determined value for drn.81 For each test case described in the Results section below, we varied the value of drn so that the RMS error in force (explained below) is minimized. Our testing suggests that drn in the range of 0.1R0 and 0.4R0 is optimal for the force calculations for the test cases studied here (results not shown). Given the diversity of the structures sizes studied here (Table 1), we suggest that the same range of drn values can be applied for structures other than those studied here. For practical applications, the recommended procedure for setting drn is to test accuracy of force calculations for the starting configuration of the structure in the above range (0.1R0 < drn < 0.4R0) in increments of 0.05R0. An illustration of 2-charge OPCA for a sample uncharged distribution is given in Figure 3(a).
Table 1.
List of representative structures used for testing. Unless stated otherwise, the cutoff and threshold distances listed here were used for all testing.
| Structure | PDB ID | Size (atoms) | |Charge| (e) | Cutoff dist (Å) | drn (Å) for OPCA | Threshold dist (Å) | ||
|---|---|---|---|---|---|---|---|---|
| h1 | h2 | h3 | ||||||
| 10 bp B-DNA fragment | 2BNA | 632 | 18 | 21 | 21 | n/a | n/a | 0.35 |
| Immunoglobulin binding domain | 1BDD | 726 | 2 | 15 | 15 | n/a | n/a | 0.25 |
| Ubiquitin | 1UBQ | 1231 | 1 | 15 | 15 | n/a | n/a | 0.25 |
| Thioredoxin | 2TRX | 1654 | 5 | 15 | 15 | n/a | n/a | 0.35 |
| Nucleosome core particle | 1KX5 | 25101 | 133 | 21 | 21 | 90 | n/a | 0.1 |
| Microtubule sheet | * | 158016 | 360 | 15 | 15 | 48 | n/a | 0.25 |
| Virus capsid | 1A6C | 475500 | 120 | 15 | 15 | 66 | n/a | 0.25 |
| Chromatin fiber | ** | 1159998 | 8238 | 21 | 21 | 90 | 169 | 0.35 |
OPCA for Charged Components
For charged components, the monopole and the dipole of the original charge distributions are exactly reproduced if two approximate charges with total net charge equal to the net charge of the original charge distribution are positioned so that their center of charge coincides with the center of charge of the original distribution81 (green square in Figure 3(b)). The quadurpole moment is optimally reproduced if point charges are placed along the eigenvector with largest corresponding eigenvalue obtained from the quadrupole moment of the original charge distribution. 81 The distance between the two approximate charges from the center of charge is determined empirically. It was previously shown that fixing the distance of one of the two approximate charges to 1.5R0 from the center of geometry of the component, which automatically fixes the position of the other charge, is the best fit to optimally approximate charge distribution of amino acids.81 Our testing shows the same value of 1.5R0 can be applied for GB-HCPO (results not shown). The eigenvalues and eigenvectors of the quadrupole moment are computed using the analytical solutions previously introduced by Sigalov et al96 for calculating the the principal moments of inertia of a mass distribution. An illustration of 2-charge OPCA for a sample charged distribution is given in Figure 3(b).
Removing Overlaps Between Charge Distributions
For both charged and uncharged components, it is possible that the calculated approximate point charges fall outside the interior region of the corresponding charge distribution. In such case, accidental overlaps between approximate charges and their neighboring charge distributions can introduce instabilities in MD simulations. To avoid such instabilities, we define a smooth function that restricts the calculated approximate point charges within a certain threshold from the center of geometry of components. Consider d to be the calculated (based on OPCA) distance of the approximate point charges from the center of geometry of the original charge distribution, the corrected distance from the center of geometry (dc) is obtained from the smooth function below,
| (5) |
where R1 is the radius of an inner spherical threshold, and R2 is radius of an outer spherical threshold. R2 should be smaller than the size of the charge distribution (R0) defined as the distance from its center of geometry to the outermost charge, and R1 should be smaller than R2. Here we use R1 = 0.8R0 and R2 = R0 for approximations at level 1, and R1 = 0.8R0 and R2 = 0.9R0 for approximations beyond level 1.
2.2.2 Equivalent of Effective Born Radii (B c1 and B c2)
To calculate the equivalent of effective Born radii to be assigned to the approximate charges, we use the following equation
| (6) |
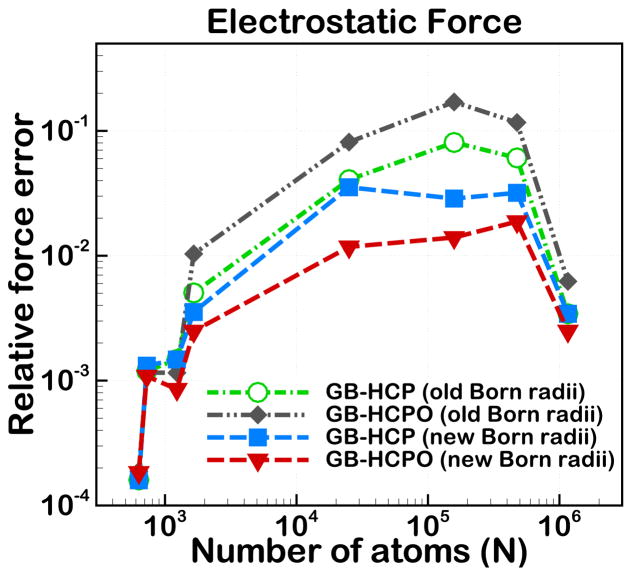
where is the effective Born radii for components at level k+1, is the effective Born radii for components at level k, qk is the point charges associate with , and rkc is the distance between qk and qk+1 (the charge associated with ). For k = 0, and qk represent atomic Born radii and atomic charges. For k ≥ 1, and qk represent the equivalent effective Born radii and approximate charges calculated at level k. is a harmonic average of weighted by qk and 1/rkc. Note that effective Born radius of a point charge represents its degree of burial within the component, and therefore it is best approximated by the charges in close proximity of that point, thus in this expression (eq 6) is weighted by 1/rkc. For the two-charge approximation, two separate component effective radii are computed, one for each of the two approximate charges (Bc1 and Bc2). In this case, the sum in eq 6 is performed over the positive and negative point charges, and the component effective Born radius obtained from the sum over positive charges is assigned to the larger approximate charge (with sign), and the effective Born radii obtained from the sum over negative charges is assigned to the smaller approximate charge. We found that, when applied to GB-HCPO, the approximation described by eq 6 is significantly more accurate than the expression previously developed for GB-HCP83 (results included in Appendix A.1). We have therefore chosen to base all further analysis on eq 6.
2.2.3 Component Radius (Rc)
The component radius Rc is used in place of the intrinsic radius of atom j (Rj) (eq 4). Rc is the radius of a sphere with the same volume as the sum of volumes of its constituent atoms, that can be estimated as below,83
| (7) |
2.3 Test Structures
We used a set of eight representative biomolecular structures ranging in size from 632 atoms to 1159998 atoms with absolute total charge ranging from 1 to 8238 e to test the accuracy and speed for GB-HCPO (Table 1). The test structures were taken from Ref.,83 except for the largest structure, the ~1.16 million atom chromatin fiber which is manually constructed in this work, see Figure 1 and Section 3.1.
2.4 Simulation Protocols
We compare the performance of GB-HCPO to two other GB models that also scale as ~ n log n: its predecessor model without OPCA (GB-HCP83), and the commonly used spherical cutoff method with GB (cutoff-GB). Both GB-HCP and GB-HCPO are now available in NAB, the open source molecular dynamics (MD) software in Amber 2016.94 In some sense, NAB is a minimal version of the production Amber MD software and is particularly suitable for experimentation unlike the highly optimized but also more complex production version. NAB uses the same force fields and implements the same GB implicit solvent methods and options as the production Amber code.
The following parameters and protocol were used for the simulations, unless otherwise stated. For the purpose of this study, we employed the commonly used OBC GB model (igb = 5, gbsa = 1 in Amber) for reference GB, and as the basis for all GB approximations tested here. The HCP threshold distances (for both GB-HCPO and GB-HCP) were chosen such that, for a given atom within a given test structure, the exact atomic computation (level 0) is used for interactions with other atoms within its own and nearest neighboring groups (level 1) as illustrated in Figure 2. To satisfy this condition, threshold distances hl are calculated as where l is the HCP level, is the maximum component radius at level l, and is the maximum group (level 1) radius, for a given structure. The HCP threshold distances thus calculated for each of the test structures are shown in Table 1. These are the suggested conservative defaults for these and other similar structures, and unless stated otherwise, were used for all of the testing described in the Results section.
The spherical cutoff-GB method ignores all interactions beyond a cutoff distance for the computation of electrostatic energy and effective Born radii in eqs 1, 2 and 3. The atom-based cutoff, parameter cut in Amber, is used to truncate nonbonded pair-wise charge-charge interactions, without any switching/shifting function. The rgbmax parameter for the cutoff-GB computations is set equal to the cutoff distance. The rgbmax parameter in Amber controls the maximum distance between atom pairs that will be considered in carrying out the pairwise summation involved in calculating the effective Born radii;94 i.e. atoms that are further away than rgbmax from a given atom will not contribute to that atom’s effective Born radius. The setting cut=rgbmax makes the entire calculation (including the cost of building the pair list) scale as n log n, as opposed to n2 of the reference GB.
When comparing HCP and cutoff-GB, the level 1 threshold distance for a given structure is used as the cutoff distance for the corresponding cutoff-GB computations.
12-6 van der Waals interactions for GB-HCPO and GB-HCP were computed using only the atoms that are within the level 1 threshold distance, i.e., atoms that are treated exactly. The simulations used the Amber ff99SB force field.99 Langevin dynamics with a collision frequency of 50 ps−1 (appropriate for comparison to explicit water results) was used for temperature control, a surface-area dependent energy of 0.005 kcal/mol/Å2 was added, and an inverse Debye-Hückel length of 0.125 Å−1 was used to represent a 0.145 M salt concentration. To remove center of mass drift and rotation during the course of molecular dynamics, a velocity correction algorithm (the NSCM option in Amber) was used to remove center-of-mass motion every 100 steps. A 1 fs time step was used for the simulation with the nonbonded neighbor list being updated after every step.
For explicit solvent simulations, the structures were solvated in a truncated cuboid box of TIP3P water model, extending 10 Å from the solute. The system was neutralized by adding counterions. The Joung/Cheatham monovalent ion parameters100 optimized for TIP3P were used to model ion-water interactions. SHAKE algorithm101 was used to constrain covalently bound hydrogen atoms (its analytical variant102 was used to constrain the geometry of the water model). We used the particle mesh Ewald (PME) method70 with constant-volume periodic boundary condition. The explicit solvent simulations were run using the GPU-accelerated pmemd.cuda available in the Amber 2015 suite of programs.103,104
The simulation protocol consisted of five stages. First, the starting structures were minimized using the conjugate gradient method with a restraint weight of 5.0 kcal/mol/Å2. Next, the system was heated to 300 K over 10 ps (600 ps for explicit solvent) with a restraint weight of 1.0 kcal/mol/Å2. The system was then equilibrated for 10 ps (500 ps for explicit solvent) at 300 K with a restraint weight of 0.1 kcal/mol/Å2, and then for another 10 ps (1 ns for explicit solvent) with a restraint weight of 0.01 kcal/mol/Å2. Finally, all restraints were removed for the production stage. Default values were used for all other simulation parameters.
The protocols used for GB-HCPO simulation of chromatin fiber is slightly different from the protocols explained above. The collision frequency was reduced to γ = 0.01ps−1 to enhance sampling of conformational space. Also, the nscm and gbsa options were turned off to reduce the run time. After the starting structure of chromatin was minimized using the conjugate gradient method with a restraint weight of 5.0 kcal/mol/Å2, the structure was heated to 300 K over 5 ps with a restraint weight of 1.0 kcal/mol/Å2. For the production stage, we ran 95 ps unrestrained simulation. The chromatin fiber simulation was performed on a regular compute cluster (Virginia Tech’s Blueridge computer cluster, see http://www.arc.vt.edu) using 192 cores, which took about 30 days of wall clock time.
2.5 Accuracy and Speed Evaluation
The accuracy of the approximate methods were evaluated using relative error in electrostatic solvation energy (relative energy error), ErrE, and relative RMS error in electrostatic force (relative force error), ErrF, calculated as
| (8) |
| (9) |
| (10) |
| (11) |
where Eapprox is the electrostatic solvation energy calculated using an approximation, Eref the electrostatic solvation energy calculated using the reference GB computation (without cutoff or any further approximations), is the average force, and and are the total force on atom i calculated using the approximate and reference GB computations, respectively. Errrms is the root-mean-square (RMS) error in force for the atoms in a given structure.
ErrE and ErrF are calculated for GB-HCPO, GB-HPC and cutoff-GB for the starting configuration of the test structures (Table 1). As another accuracy test, we also evaluate GB-HCPO in dynamics: the backbone RMS deviation from the crystal structure for 50 ns simulation predicted by GB-HCPO is compared to the predictions by GB-HCP, reference GB and explicit solvent (TIP3P) simulations.
Speedup was measured as CPU time for the reference GB computation divided by the CPU time for the approximation tested. Testing was conducted on Virginia Tech’s Blueridge computer cluster (http://www.arc.vt.edu) consisting of 408-node Cray CS-300 cluster, each node is outfitted with two octa-core Intel Sandy Bridge CPUs and 64 GB of memory. Where possible, testing was performed using a single CPU (a single core of the octa-core processor) to reduce the potential variability due to interprocessor communication. For the 475 500 atom virus capsid and the 1 159 998 atom chromatin fiber we used 16 and 64 cores, respectively. To limit the run time for the reference GB computation to a few days, speedup was calculated for 1000 iterations of MD for structures with < 10000 atoms, 100 iterations for structures with 10000 − 1000000 atoms and 10 iterations for the structure with > 1000000 atoms. To make the results representative of typical simulations involving much larger numbers of iterations, the CPU time excludes the time for loading the data and initialization prior to starting the simulation.
2.6 Calculation of Electrostatic Binding Free Energies
To illustrate the artifacts of spherical cut-offs within the GB model, we calculated the electrostatic binding free energies (ΔΔGpol) for a set of 15 small protein-ligand complexes provided in Ref.,105 using the reference GB without cutoff, cutoff-GB (cut=15Å) and GB-HCPO (h1=15Å). The set of complexes is diverse with respect to values of electrostatic binding free energies. The ligands are neutral and the proteins are either neutral or are forced to be neutral.105
The electrostatic component of binding free energies (ΔΔGpol) were computed as below
| (12) |
where and are electrostatic solvation free energy of the complex, the protein and the ligand, respectively. ΔECoulombic is the difference in Coulombic energies in vaccum ( ).
The accuracy of the GB models in estimating the ΔΔGpol was evaluated in terms of their ability in reproducing the values from Possion-Boltzman (PB) calculations. The PB values were computed using the Adaptive Poisson-Boltzmann Solver (APBS) software package.106 The solute dielectric constant was set to 1 and the solvent dielectric constant was 80. The grid spacing was set to 0.3 Å and the grid dimension size was set to 449 in x, y and z directions for all of the structures. The solvent probe radius is 1.4 Å. We use APBS default values for the remaining parameters, see Ref.105 for further details.
3 RESULTS AND DISCUSSION
In this section, we first demonstrate a practical application of GB-HCPO by using it to simulate the structure of ~ 1.16 million atoms (40 nucleosome) chromatin fiber. Next, a detailed technical analysis of GB-HCPO’s performance (accuracy, speed and dynamics) as compared to cutoff-GB and GB-HCP will be presented.
3.1 Insights into the Structure of Chromatin Fiber
It is now well established that details of DNA packing inside the cell nucleus are critical for many cellular processes including cell differentiation and transcription.85,109 The primary level of DNA compaction in eukaryotes is the nucleosome – a protein-DNA complex of about 25,000 atoms.109,110 While the next level of the genome compaction, Figure 1, is still debated,111,112 one widely discussed option is the so-called 30 nm chromatin fiber, which is a well-defined helical arrangement of the nucleosomes.86 And while the structural features of individual nucleosomes have been known to atomistic detail109 for almost 20 years, the same level of structural detail is not available for the 30-nm chromatin fiber. Histone N-terminal tails have been shown to regulate DNA accessibility, gene transcription and chromatin structure.85 These tails are highly positively charged and the above regulation may be partly through the modulation of this charge by post translational modifications. However, due to the large size of the chromatin fiber, only low-resolution (e.g. cryo-EM) experimental structures of the fiber are available,86 its atomistic details including the tails, are unknown.
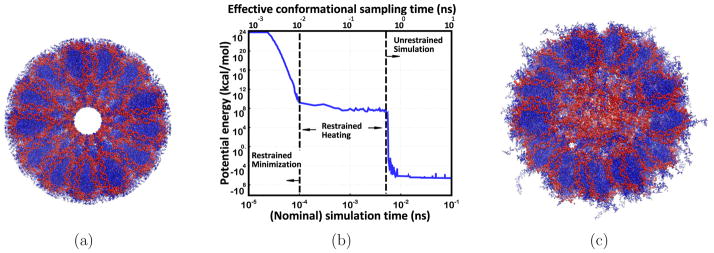
Here we start with a “manually” constructed 40-nucleosome (~1.16 million atom) model of the 30-nm chromatin fiber, consistent with low resolution cryo-EM data. The model is constructed by repeatedly combining 40 crystal structure of nucleosomes (1KX5), linker DNA and linker histone (187 bp nucleosome repeat length) using a set of coordinate transformations described by Wong et. al.,98 consistent with low resolution cryo-EM data86 (see Figures 1 and 4). The model fiber is “4-start”, meaning that (N + 4)th nulceosome is stacked on the Nth one. The original, unrelaxed model98 was a significant step beyond the low resolution representations of the fiber, but inevitably contained various structural artifacts (evident from the energy analysis, Figure 4(a)). These are likely consequences of the coordinate transformations applied, during construction of the fiber, to the entire nucleosomes, linker DNA and linker histone; in effect, a coarse-grained approach was used to build an atomically detailed model. As a result, an artificial hollow in the core of the structure is observed (Figure 4(a)), which appears inconsistent with the expected tight packing of the fiber atoms and experimental observations regarding tail-linker contacts, see below. Similar hollow regions of various dimensions in the fiber center are present in several other fiber models not considered here.13,113
Figure 4.
(a) The manually constructed model13 of ~ 1.16 million atom chromatin fiber (consistent with low resolution cryo-EM data86) is energetically unrealistic; no atomically detailed experimental structures are available. (b) A 0.1 ns GB-HCPO simulation of the fiber significantly reduces the steric clashes, as seen by the large reduction in the potential energy. Data points represent averages over 100 time step intervals (1 fs each). In terms of sampling the conformational transitions involved, the 100 ps simulation performed here is effectively equivalent to ~10 ns explicit-solvent TIP3P PME simulation (the conformational sampling is ~100 folds faster66), denoted as effective conformational sampling time. (c) Equilibrated structure (all-atom MD, GB-HCPO) suggests important structural details consistent with experimental results: the linker DNA fills the core region, the H3 histone tails interact with the linker DNA.107,108
To make the fiber model self-consistent at atomic level, we have relaxed the structure via an all-atom, muti-scale GB-HCPO simulation at room temperature. The GB-HCPO simulation significantly reduces the steric clashes of the starting structure, as seen by the large reduction in the potential energy (Figure 4(b)), and provides a much more energetically realistic model of the fiber (Figure 4(c)). The re-distribution of density and charge in the fiber structure upon equilibration is noticeable, especially near the fiber axis, Figure 5.
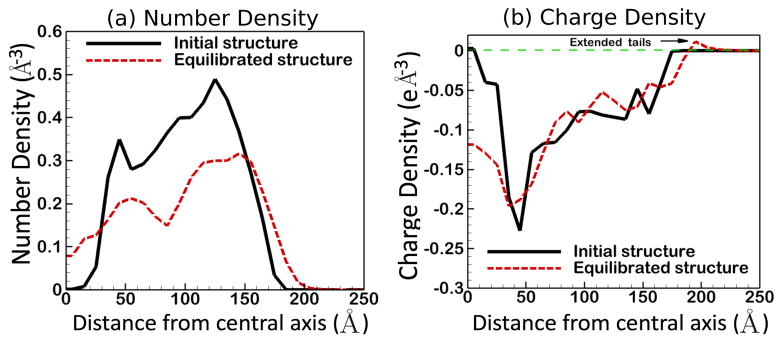
Figure 5.
Density (number of atoms per unit volume) and charge density along the radius of the equilibrated chromatin fiber: (a) Linker DNA fills the core and H2A and H2B N-terminal histone tails extend out of the fiber surface, leading to a wider distribution of atoms along the radial axis, compared to the initial structure. (b) After equilibration, the core becomes more negatively charged, due to the presence of linker DNA in the core, and the outer region becomes positively charged due to the presence of histone tails.
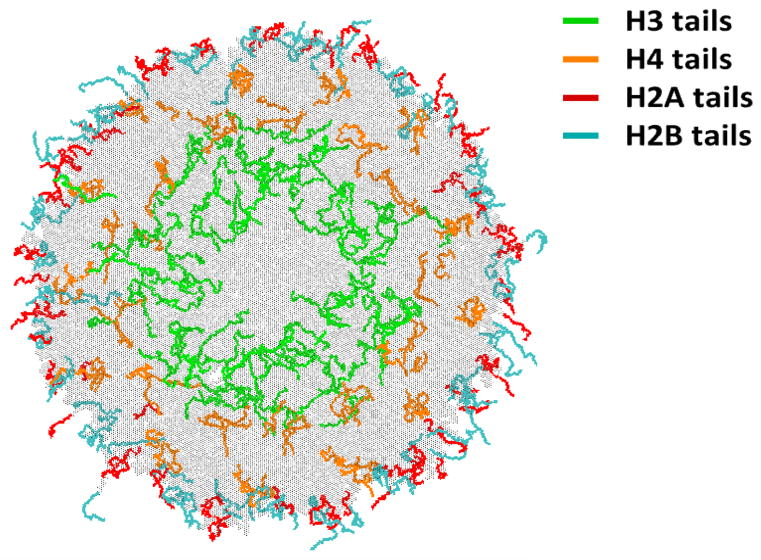
Importantly, the linker DNA fills the artificial hollow in the core region (Figure 4(c)), allowing H3 histone tail to interact with the linker DNA, as expected from experiment. 107,108 Among all four tails, H3 is most shielded from the solvent, Figure 6, consistent with a recent experimental funding that the majority of the amide protons of the H3 are protected from solvent exchange in 12-nucleosome arrays.114
Figure 6.
The atomistic details of the histone tail positioning within the 30-nm chromatin fiber, revealed by simulation. A “top” view. H3 and H4 N-terminal histone tails are buried within the fiber, participating in multiple inter-nucleosomal and tail–DNA interactions, which may explain why these two tails play a prominent role in condensation/de-condensation of nucleosomal arrays associated with charge-altering post-translational modifications. In contrast, H2A and H2B N-terminal histone tails extend out of the fiber surface and are therefore better accessible to chromatin binding factors, which may be important for other regulatory functions.
Further analysis of the equilibrated fiber model reveals several important details that may be of functional importance. Specifically, H3 and H4 tails positions relative to the vertical axis of the fiber is clearly different from those of H2A and H2B tails, Figure 6. Namely, while H3 and H4 N-terminal tails are buried within the fiber, H2A and H2B are mostly solvent exposed. This difference in tail positions may explain the experimentally observed tendency115,116 of H3 and H4 tails to have stronger relative effect on condensation/decondensation of nucleosomal arrays. It may also explain why charge-altering post-translation modifications (PTMs) of H3 and H4 tails, such as acetylations of several lysines in H4, affect chromatin compaction.117 Indeed, being in the “bulk” of the fiber offers these positively charged tails multiple opportunities to participate in internucleosomal and DNA-tail electrostatic interactions, strengthened by the relatively low dielectric environment. One can draw an analogy here with the nucleosome itself – it was shown that altering the charge of the globular histone core has a strong effect on the histone-DNA association, leading to a suggestion that charge-altering PTMs in the globular core are important for selective accessibility control of nucleosomal DNA.118
In contrast to H3 and H4, H2A and H2B histones are more solvent exposed within the fiber, lowering the strength of potential fiber stabilizing interactions that these tails may be part of. On the other hand, being solvent exposed offers greater accessibility to histone binding proteins that may regulate chromatin compaction indirectly.
The above suggestions are just an example of the kind of structural analysis made possible by the availability of an experimentally consistent atomistic model of the 30-nm fiber. We stress again that how ubiquitous the 30-nm fiber is in in-vivo systems remains an open question. Where it exists, it may take on many different forms,119 possibly dependent on cell type and cell-cycle stage.113 Our approach can help construct consistent atomistic models of any of these structures from available low resolution data.
3.2 Accuracy limitations of spherical cut-offs within the GB models
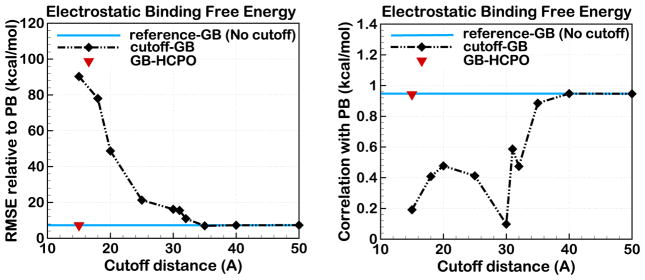
In contrast to modern PME-based treatment of long-range electrostatics, where the use of even relatively short, e.g. 9 Å, direct sum cutoff makes negligible impact on the accuracy, the use of even much longer cutoff distances within the GB formalism can significantly impact the accuracy of the computed electrostatic energies, Fig. 7. As an example, we have evaluated the accuracy of the GB model with different cutoff distances in estimating the electrostatic binding free energies for a set of small neutral protein-ligand complexes, Fig. 7. A detailed description of these complexes is provided elsewhere.105 The average size of these complexes is 47.7 Å. Fig. 7 demonstrates that setting the cutoff distances to values smaller than 40Å can cause large deviations from electrostatic binding free energies calculated within the standard numerical Poisson-Boltzmann approach. In particular, for the cutoff distance equal to 15Å, commonly used in the GB MD simulations, the accuracy completely deteriorates both relative to the PB and, perhaps more importantly, to the reference GB without the cutoff. Even with a computationally very demanding 30 Å cutoff, the correlation with the PB reference (or no cutoff GB) is virtually absent. It is also noteworthy that in each complex, both the protein and the ligand are net neutral – even these systems are not immune to the cutoff errors. Note that the use of switching or shifting functions,92 with any practically reasonable buffer region, will have little effect on the errors shown in Fig. 7. In contrast to the use of the spherical cutoff, the proposed GB-HCPO can provide virtually the same accuracy as the reference GB model without the any cutoffs, at the fraction of the computational cost.
Figure 7.
Error in the electrostatic binding free energies computed by GB model using different cutoff distances, GB-HCPO, and reference GB without any cutoffs. The error is estimated relative to the standard numerical PB treatment for 15 small, neutral proteinligand complexes specified in Ref.105
The relationship between the cutoff errors seen in Figs. 7, and artifacts that these errors may lead to in long MD simulations is complex. What the size of the above errors demonstrate is that the possibility of such artifacts can not be ignored.
3.3 Technical Analysis GB-HCPO’s Performance
In this section, we provide a detailed technical analysis of some characteristics of GB-HCPO that are important for Molecular Dynamics, including accuracy, speed and dynamics, which are described below.
3.3.1 Accuracy
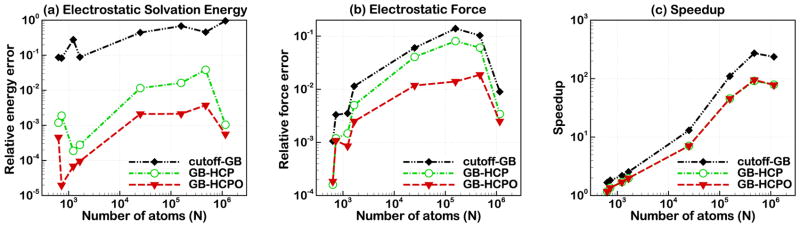
Figures 8(a) and (b) show the accuracy of GB-HCPO in calculating electrostatic force and electrostatic solvation energy for the set of test structures shown in Table 1. The accuracy of GB-HCPO is tested by computing the relative errors in electrostatic solvation energy and electrostatic force for the starting configuration of the test structures, relative to the values obtained from reference GB (without approximation). The accuracy of GB-HCPO is compared to that of GB-HCP (2-charge) and cutoff-GB. For the test structures considered here, the electrostatic force and solvation energy obtained with GB-HCPO is in closer agreement with those obtained with reference GB. The smaller deviation of GB-HCPO from reference GB compared to GB-HCP and cutoff-GB is uniform across the broad range of test structure sizes. In particular, the relative error in electrostatic solvation energy computed using GB-HCPO can be up to two orders of magnitude smaller than that of cutoff-GB, and up to one order of magnitude smaller than that of GB-HCP (Figure 8(a)). The relative RMS error in electrostatic force calculated by GB-HCPO can be up to one order of magnitude smaller than that by GB-HCP and cutoff-GB (Figure 8(b)).
Figure 8.
Accuracy ((a) and (b)) and speed (c) of GB-HCPO compared to cutoff-GB and GB-HCP, where standard GB (without cutoffs) is used as reference. Accuracy is computed as relative error in electrostatic solvation energy (a) and relative RMS error in electrostatic force (b). A logarithmic scale is used to better demonstrate distribution of errors in both energy and force over the broad range of test structure sizes. Threshold and cutoff distances used for the different structures are listed in Table 1. Connecting lines are shown to guide the eye.
For large structures where we expect GB-HCPO to be most useful, the associated relative force error is expected to be similar to that of the equivalent “industry standard” PME-based calculation. Specifically, for an ~104 atom structure GB-HCPO gives 10−2 relative force error, comparable to our previous estimate for the PME,82 and an order of magnitude smaller compared to the cut-off scheme.
3.3.2 Speedup
Figure 8(c) shows that GB-HCPO can be up to two orders of magnitude faster than the reference GB, depending on structure size. The speedup for GB-HCPO and GB-HCP are nearly the same indicating that the higher accuracy of GB-HCPO compared to GB-HCP is achieved without sacrificing its speed. However, both GB-HCPO and GB-HCP are, expectedly, slower than cutoff-GB: the average speedup for the 8 structures tested here was ~78× for the cutoff-GB, while it is ~30× for the GB-HCP and GB-HCPO methods. The higher speed of cutoff-GB is expected as cutoff-GB totally ignores the electrostatic interaction beyond a certain threshold, in contrast to GB-HCPO and GB-HCP that take into account distant electrostatic interactions. Generally the speedup is higher when the number of atoms increases. However, for the largest structure considered here; the ~1.16 million atom chromatin fiber; the speedup is slightly smaller than that for 475500 atom virus capsid (1A6C) for all of the approximations, which is because the threshold and cutoff distances used to simulate the chromatin fiber are larger than those used for virus capsid (see Table 1).
Note that an equivalent simulation of chromatin fiber (Section 3.1) using the regular GB without additional approximation on the same compute cluster is ~100-fold slower in terms of nominal speed (Figure 8(c)).
3.3.3 Stability in MD simulations
The primary purpose for the development of computationally efficient GB approximations is application in dynamics; we test GB-HCPO by conducting 50 ns MD simulations of the immunoglobulin binding domain (1BDD), thioredoxin (2TRX), and ubiquitin (1UBQ). Note that a comprehensive analysis of the conformational stability of GB-HCP in dynamics (such as RMS difference in distribution of χ1, χ2 angles and RMS residue fluctuations) was previously conducted, and the method was compared extensively to cutoff-GB and reference (no cut off) GB simulations.83 Severe artifacts of cut-off GB for highly charged systems were also discussed previously.83 Overall, it was shown that GB-HCP simulations are in better agreement with the reference GB simulation than the cutoff-GB simulations. Given the significant improvement of GB-HCPO in electrostatic forces and energies relative to GB-HCP (see Section 3.3.1), we assume that GB-HCPO is no worse than GB-HCP in conformational stability of trajectories. Therefore, here we focus on testing the ability of GB-HCPO to maintain over-all structural of proteins on 50 ns time scale (Figure 9). Since the intended use for GB-HCPO is MD simulations of very large structures, in which case the affordable time-scales are necessarily limited and fine details are less important, this is a reasonable testing strategy.
The results shown in Figure 9 suggest that MD trajectories generated by GB-HCPO method are generally in good agreement with the reference GB and explicit solvent simulation. For 1BDD the GB-HCP trajectories show RMS deviations that are substantially larger than the GB-HCPO or the reference explicit-solvent trajectories. This example emphasizes how subtle errors in charge-charge interactions, as reflected in electrostatic forces and energies (Figure 8) can result in qualitatively different conformational dynamics. On a practical level, small inaccuracies in the energy or force calculations in the simulations of small flexible structures such as 1BDD can lead to large structural deviations over the course of the trajectory. Similarly, for 2TRX the trajectories obtained from GB-HCPO are in better agreement with the reference GB and explicit solvent simulation that those from GB-HCP. Due to the high stability of the structure of 1UBQ, the trajectories for 1UBQ from all of the simulations (GB-HCPO, GB-HCP, reference GB and explicit solvent simulation) are in close agreement.
3.4 The computational speed of GB-HCPO relative to explicit solvent simulations
On the basis of the run times for a GB-HCPO simulation of the ~ 150, 000 atom microtubule structure (tub46), compared to an equivalent PME simulation in TIP3P explicit solvent using sander module of Amber 2015 (default simulation parameters), the nominal speeds (nanoseconds per day) of GB-HCPO is only about 20% times slower than the PME simulations in TIP3P explicit solvent, on Virginia Tech’s HokieSpeed computer cluster using single node (8 cores). Note that unlike the production PME module of Amber 2015 used here to generate the explicit solvent trajectories, NAB (where GB-HCPO is now implemented) is not as highly optimized.
It has been shown that the speed of conformational sampling in implicit-solvent simulations can be ~ 10 to 100 times faster than common explicit-solvent PME simulations.66 Therefore, even for the case where explicit solvent (TIP3P) PME is slightly faster than GB-HCPO, when combined with the speedup due to conformational sampling, the overall speed of conformational sampling for GB-HCPO can be substantially faster.
4 CONCLUSION
GB models can increase the computational speed of MD simulations significantly by approximating the discrete solvent as a continuum, and by providing much faster sampling of conformational space due to reduced solvent viscosity. However, currently these benefits of standard GB are effectively limited to small and medium size structures, because standard GB models scale as ~ n2, where n is the number of solute atoms. The use of cut-off schemes to speed-up these calculations, while computationally effective, is problematic due to the possibility of severe artifacts. This is not to say that every GB-based calculation that relies on a cutoff will necessarily fail, but that the possibility of significant artifacts is always there, even with large cutoffs that may be deemed “safe”. For instance, we showed that using the typical cutoff distance of 15Å in the standard GB model completely deteriorates its accuracy in estimating the electrostatic binding free energies of small protein-ligand complexes. Even with a computationally very demanding 30Å spherical cutoff, the correlation with the numerical PB reference (or the no cutoff GB) is close to zero.
The GB-HCPO multi-scale approximation presented in this work significantly speeds up the GB computations as it scales as ~ n log n, but without the cut-off artifacts. The reasonable speedup-accuracy balance is achieved by combining the previously developed Hierarchical Charge Partitioning approximation with optimal placement of few point charges to represent complex charge distributions. Specifically, the natural organization of the biomolecules are used to partition the structure into hierarchical components; each being approximated by two point charges. The electrostatic interactions between distant components are computed using approximate charges, while the original atomic partial charges are used for nearby interactions. The approximate charges are placed so that the low order multipole moments (up to the quadrupole) of the corresponding components are best reproduced.
We have shown that GB-HCPO estimates the electrostatic forces and energies substantially more accurately, in some case up to an order of magnitude, than its predecessor model (GB-HCP), which also relied on HCP, but simply placed the approximate charges at the center of negative and positive charges. The accuracy gain of GB-HCPO relative to the cutoff-GB approach, which totally ignores the effects of electrostatic interactions beyond a certain distance, is even more appreciable. For instance, unlike the cutoff-GB approach that leads to large deviations from PB results, GB-HCPO is virtually as accurate as the reference GB model without any cutoffs in reproducing the electrostatic binding free energies obtained from PB, at the fraction of the computational cost. The extra accuracy is achieved at a moderate cost: GB-HCPO is about a factor of two slower than the cut-off GB. At the same time, GB-HCPO can be up to two orders of magnitude faster the standard (no cut-off) GB computation, with the speed-up being larger for larger structures.
The latter property makes GB-HCPO particularly attractive for atomistic simulation of very large systems where the computational costs of standard GB or explicit solvent simulations becomes inordinate. By exploring the low effective solvent viscosity regime one can achieve an effective speed-up of conformational sampling of up to two orders of magnitude relative to standard explicit solvent MD.
As a practical demonstration, we have used GB-HCPO to equilibrate a ~1.16 million atom “manually constructed” structure of 30-nm chromatin fiber (40 nucleosomes plus linker DNA, 187 bp nucleosome repeat length). The goal was to obtain a realistic model of this potentially very important structure, consistent with experiment. With just 192 processor cores, effective time-scales of ~ 10 ns were reached, which was enough to observe substantial and meaningful structural re-arrangements in the fiber. The GB-HCPO simulations successfully resolved numerous severe steric clashes, significantly improving the quality of the starting structure. We have demonstrated that the linker DNA fills the core region of the chromatin fiber, and the H3 histone tails interact with the linker DNA, reproducing experimental findings. Upon equilibration, the obvious hollow region in the center of the fiber disappears; we conjecture that the closing of the central hollow region might be relevant to other fiber models not considered here. The tail regions of H3, H4, H2A and H2B are in distinctively different locations relative to the core of the fiber: H3 and H4 are mostly buried within the core, while H2A and H2B are mostly solvent exposed. Positively charged histone tails are known to be important for compaction of (negatively charged) chromatin components beyond the nucleosome, often regulated by charge-altering post-translational modifications (PTMs). In particular, acetylation of certain lysine residues in the histone tails is known to cause de-condensation of nucleosomal arrays. However, H3 and H4 tails have more prominent effect compared to H2A and H2B. In this respect, the difference in solvent exposure and position relative to the core of the fiber may provide an explanation: the burial of H3 and H4 tails in the fiber core create multiple opportunities to participate in inter-nucleosomal and DNA-tail electrostatic interactions, strengthened by the relatively low dielectric environment of the core. In contrast, charge-charge interactions are weakened by solvent exposure of H2A and H2B, while providing easier access for histone binding complexes. It appears very likely now that many different structural forms of the 30-nm fiber exist; it should be possible to construct and investigate their atomistic models in the same manner to identify commonalities and differences with respect to the conclusions drawn above.
GB-HCPO is implemented in the open sourceMD software, NAB in Amber 2016,94 for general use. The equilibrated structure of the 30-nm fiber, along with several files needed to reproduce the simulation results, are available at http://www.cs.vt.edu/~onufriev/software.
Acknowledgments
This work was supported by the NIH GM076121. The authors acknowledge Advanced Research Computing at Virginia Tech for providing computational resources and technical support that have contributed to the results reported within this paper. URL: http://www.arc.vt.edu
A APPENDIX
A.1 Accuracy evaluation of component effective Born radii
As described in the Methods section, we examined two different approaches to compute the component effective Born radii: the new approximation (new Born) presented in this work (eq 6), and the approximation previously presented in Ref.83 (old Born), defined as
| (13) |
where qj and Bj are the charges and effective Born radii, respectively, for the atom j belonging to component c. Both approximations were applied to GB-HCP and GB-HCPO. As shown in Figure 10, the new Born approximation (eq 6) is more accurate than the old Born approximation (eq 13) in calculating the electrostatic forces, when applied to each of the GB-HCP and GB-HCPO methods. One can also see that the old Born approximation does not properly lend itself to the GB-HCPO model.
Figure 10.
Comparison of two alternative methods for computing component effective Born radii showing relative RMS error in electrostatic force GB-HCP and GB-HCPO, with the GB model without any cutoffs used as reference. Connecting lines are shown to guide the eye.
References
- 1.Adcock S, McCammon J. Chem Rev. 2006;106:1589–1615. doi: 10.1021/cr040426m. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Karplus M, Kuriyan J. Proc Natl Acad Sci U S Ȧ. 2005;102:6679–6685. doi: 10.1073/pnas.0408930102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Karplus M, McCammon JA. Nat Struct Biol. 2002;9:646–652. doi: 10.1038/nsb0902-646. [DOI] [PubMed] [Google Scholar]
- 4.Jorgensen W, Chandrasekhar J, Madura J, Impley R, Klein M. J Chem Phys. 1983;79:926–935. [Google Scholar]
- 5.Berendsen HJC, Grigera JR, Straatsma TP. J Phys Chem. 1987;91:6269–6271. [Google Scholar]
- 6.Horn HW, Swope WC, Pitera JW, Madura JD, Dick TJ, Hura GL, Head-Gordon T. J Chem Phys. 2004;120:9665–9678. doi: 10.1063/1.1683075. [DOI] [PubMed] [Google Scholar]
- 7.Izadi S, Anandakrishnan R, Onufriev AV. J Phys Chem Lett. 2014;5:3863–3871. doi: 10.1021/jz501780a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Izadi S, Onufriev AV. J Chem Phys. 2016;145 doi: 10.1063/1.4960175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lindorff-Larsen K, Piana S, Dror RO, Shaw DE. Science. 2011;334:517–520. doi: 10.1126/science.1208351. [DOI] [PubMed] [Google Scholar]
- 10.Aguilar B, Onufriev AV. J Chem Theory Comput. 2012;8:2404–2411. doi: 10.1021/ct200786m. [DOI] [PubMed] [Google Scholar]
- 11.Zhao G, Perilla JR, Yufenyuy EL, Meng X, Chen B, Ning J, Ahn J, Gronenborn AM, Schulten K, Aiken C, Zhang P. Nature. 2013;497:643–646. doi: 10.1038/nature12162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Science. 2004;306:636–640. doi: 10.1126/science.1105136. [DOI] [PubMed] [Google Scholar]
- 13.Wong H, Victor JM, Mozziconacci J. PLOS One. 2007;436:e877. doi: 10.1371/journal.pone.0000877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Humphrey W, Dalke A, Schulten K. J Molec Graphics. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 15.Cramer CJ, Truhlar DG. Chem Rev. 1999;99:2161–2200. doi: 10.1021/cr960149m. [DOI] [PubMed] [Google Scholar]
- 16.Honig B, Nicholls A. Science. 1995;268:1144–1149. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- 17.Beroza P, Case DA. Methods Enzymol. 1998;295:170–189. doi: 10.1016/s0076-6879(98)95040-6. [DOI] [PubMed] [Google Scholar]
- 18.Madura JD, Davis ME, Gilson MK, Wade RC, Luty BA, McCammon JA. Rev Comput Chem. 1994;5:229–267. [Google Scholar]
- 19.Gilson MK. Curr Opin Struct Biol. 1995;5:216–223. doi: 10.1016/0959-440x(95)80079-4. [DOI] [PubMed] [Google Scholar]
- 20.Scarsi M, Apostolakis J, Caflisch A. J Phys Chem A. 1997;101:8098–8106. [Google Scholar]
- 21.Luo R, David L, Gilson MK. J Comput Chem. 2002;23:1244–1253. doi: 10.1002/jcc.10120. [DOI] [PubMed] [Google Scholar]
- 22.Simonson T. Rep Prog Phys. 2003;66:737–787. [Google Scholar]
- 23.Baker N, Bashford D, Case D. Implicit Solvent Electrostatics in Biomolecular Simulation. New Algorithms for Macromolecular Simulation. 2006:263–295. [Google Scholar]
- 24.Li L, Li C, Zhang Z, Alexov E. J Chem Theory Comput. 2013;9:2126–2136. doi: 10.1021/ct400065j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Still WC, Tempczyk A, Hawley RC, Hendrickson T. J Am Chem Soc. 1990;112:6127–6129. [Google Scholar]
- 26.Onufriev A. Modeling Solvent Environments. Wiley-VCH Verlag GmbH & Co. KGaA; 2010. pp. 127–165. [Google Scholar]
- 27.Simmerling C, Strockbine B, Roitberg AE. J Am Chem Soc. 2002;124:11258–11259. doi: 10.1021/ja0273851. [DOI] [PubMed] [Google Scholar]
- 28.Chen J, Im W, Brooks CL. J Am Chem Soc. 2006;128:3728–3736. doi: 10.1021/ja057216r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Jang S, Kim E, Pak Y. J Chem Phys. 2008;128:105102. doi: 10.1063/1.2837655. [DOI] [PubMed] [Google Scholar]
- 30.Zagrovic B, Snow CD, Shirts MR, Pande VS. J Mol Biol. 2002;323:927–937. doi: 10.1016/s0022-2836(02)00997-x. [DOI] [PubMed] [Google Scholar]
- 31.Jang S, Kim E, Shin S, Pak Y. J Am Chem Soc. 2003;125:14841–14846. doi: 10.1021/ja034701i. [DOI] [PubMed] [Google Scholar]
- 32.Lei H, Duan Y. J Phys Chem B. 2007;111:5458–5463. doi: 10.1021/jp0704867. [DOI] [PubMed] [Google Scholar]
- 33.Pitera JW, Swope W. Proc Natl Acad Sci U S Ȧ. 2003;100:7587–7592. doi: 10.1073/pnas.1330954100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jagielska A, Scheraga HA. J Comput Chem. 2007;28:1068–1082. doi: 10.1002/jcc.20631. [DOI] [PubMed] [Google Scholar]
- 35.Pellegrini E, Field MJ. J Phys Chem A. 2002;106:1316–1326. [Google Scholar]
- 36.Walker RC, Crowley MF, Case DA. J Comput Chem. 2007;29:1019–1031. doi: 10.1002/jcc.20857. [DOI] [PubMed] [Google Scholar]
- 37.Okur A, Wickstrom L, Layten M, Geney R, Song K, Hornak V, Simmerling C. J Chem Theory Comput. 2006;2:420–433. doi: 10.1021/ct050196z. [DOI] [PubMed] [Google Scholar]
- 38.Bashford D, Case DA. Annu Rev Phys Chem. 2000;51:129–152. doi: 10.1146/annurev.physchem.51.1.129. [DOI] [PubMed] [Google Scholar]
- 39.Hawkins GD, Cramer CJ, Truhlar DG. Chem Phys Lett. 1995;246:122–129. [Google Scholar]
- 40.Hawkins GD, Cramer CJ, Truhlar DG. J Phys Chem. 1996;100:19824–19836. [Google Scholar]
- 41.Ghosh A, Rapp CS, Friesner RA. J Phys Chem B. 1998;102:10983–10990. [Google Scholar]
- 42.Lee MS, FR, Salsbury J, Brooks CL., III J Chem Phys. 2002;116:10606–10614. [Google Scholar]
- 43.Onufriev A, Bashford D, Case DA. Proteins. 2004;55:383–394. doi: 10.1002/prot.20033. [DOI] [PubMed] [Google Scholar]
- 44.Tsui V, Case D. J Am Chem Soc. 2000;122:2489–2498. [Google Scholar]
- 45.Cramer C, Truhlar D. Chem Rev. 1999;99:2161–2200. doi: 10.1021/cr960149m. [DOI] [PubMed] [Google Scholar]
- 46.David L, Luo R, Gilson MK. J Comput Chem. 2000;21:295–309. doi: 10.1002/jcc.10120. [DOI] [PubMed] [Google Scholar]
- 47.Im W, Lee MS, Brooks CL. J Comput Chem. 2003;24:1691–1702. doi: 10.1002/jcc.10321. [DOI] [PubMed] [Google Scholar]
- 48.Schaefer M, Karplus M. J Phys Chem. 1996;100:1578–1599. [Google Scholar]
- 49.Calimet N, Schaefer M, Simonson T. Proteins. 2001;45:144–158. doi: 10.1002/prot.1134. [DOI] [PubMed] [Google Scholar]
- 50.Feig M, Im W, Brooks CL. J Chem Phys. 2004;120:903–911. doi: 10.1063/1.1631258. [DOI] [PubMed] [Google Scholar]
- 51.Archontis G, Simonson T. J Phys Chem B. 2005;109:22667–22673. doi: 10.1021/jp055282+. [DOI] [PubMed] [Google Scholar]
- 52.Feig M, Brooks CL. Curr Opin Struct Biol. 2004;14:217–224. doi: 10.1016/j.sbi.2004.03.009. [DOI] [PubMed] [Google Scholar]
- 53.Nymeyer H, Garcia AE. Proc Natl Acad Sci U S Ȧ. 2003;100:13934–13939. doi: 10.1073/pnas.2232868100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Dominy BN, Brooks CL. J Phys Chem B. 1999;103:3765–3773. [Google Scholar]
- 55.Gallicchio E, Levy RM. J Comput Chem. 2004;25:479–499. doi: 10.1002/jcc.10400. [DOI] [PubMed] [Google Scholar]
- 56.Grant JA, Pickup BT, Sykes MJ, Kitchen CA, Nicholls A. Phys Chem Chem Phys. 2007;9:4913–4922. doi: 10.1039/b707574j. [DOI] [PubMed] [Google Scholar]
- 57.Haberthür U, Caflisch A. J Comput Chem. 2007;29:701–715. doi: 10.1002/jcc.20832. [DOI] [PubMed] [Google Scholar]
- 58.Spassov VZ, Yan L, Szalma S. J Phys Chem B. 2002;106:8726–8738. [Google Scholar]
- 59.Ulmschneider MB, Ulmschneider JP, Sansom MS, Di Nola A. Biophys J. 2007;92:2338–2349. doi: 10.1529/biophysj.106.081810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Tanizaki S, Feig M. J Chem Phys. 2005;122:124706. doi: 10.1063/1.1865992. [DOI] [PubMed] [Google Scholar]
- 61.Zhang LY, Gallicchio E, Friesner RA, Levy RM. J Comput Chem. 2001;22:591–607. [Google Scholar]
- 62.Feig M. J Chem Theory Comput. 2007;3:1734–1748. doi: 10.1021/ct7000705. [DOI] [PubMed] [Google Scholar]
- 63.Amaro R. private communication.
- 64.Tsui V, Case D. J Am Chem Soc. 2000;122:2489–2498. [Google Scholar]
- 65.Zagrovic B, Pande V. J Comput Chem. 2003;24:1432–1436. doi: 10.1002/jcc.10297. [DOI] [PubMed] [Google Scholar]
- 66.Anandakrishnan R, Drozdetski A, Walker RC, Onufriev AV. Biophys J. 2015;108:1153–1164. doi: 10.1016/j.bpj.2014.12.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Nguyen H, Maier J, Huang H, Perrone V, Simmerling C. J Am Chem Soc. 2014;136:13959–13962. doi: 10.1021/ja5032776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Lopes A, Alexandrov A, Bathelt C, Archontis G, Simonson T. Proteins. 2007;67:853–867. doi: 10.1002/prot.21379. [DOI] [PubMed] [Google Scholar]
- 69.Felts AK, Gallicchio E, Chekmarev D, Paris KA, Friesner RA, Levy RM. J Chem Theory Comput. 2008;4:855–868. doi: 10.1021/ct800051k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Darden T, York D, Pedersen L. J Chem Phys. 1993;98:10089–10092. [Google Scholar]
- 71.Essmann U, Perera L, Berkowitz ML, Darden T, Lee H, Pedersen LG. J Chem Phys. 1995;103:8577–8593. [Google Scholar]
- 72.Toukmaji AY, Board JA. Comput Phys Commun. 1996;95:73–92. [Google Scholar]
- 73.York D, Yang W. J Chem Phys. 1994;101:3298–3300. [Google Scholar]
- 74.Carrier J, Greengard L, Rokhlin V. SIAM J Sci Stat Comput. 1988;9:669–686. [Google Scholar]
- 75.Cai W, Deng S, Jacobs D. J Chem Phys. 2007;223:846–864. [Google Scholar]
- 76.Lambert CG, Darden TA, Board JA., Jr J Chem Phys. 1996;126:274–285. [Google Scholar]
- 77.Mark P, Nilsson L. J Comput Chem. 2002;23:1211–1219. doi: 10.1002/jcc.10117. [DOI] [PubMed] [Google Scholar]
- 78.Loncharich RJ, Brooks BR. Proteins. 1989;6:32–45. doi: 10.1002/prot.340060104. [DOI] [PubMed] [Google Scholar]
- 79.Schreiber H, Steinhauser O. Chem Phys. 1992;168:75–89. [Google Scholar]
- 80.Cheatham TE, Miller JL, Fox T, Darden TA, Kollman PA. J Am Chem Soc. 1995;117:4193–4194. [Google Scholar]
- 81.Anandakrishnan R, Baker C, Izadi S, Onufriev AV. PloS one. 2013;8:e67715. doi: 10.1371/journal.pone.0067715. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Anandakrishnan R, Onufriev AV. J Comput Chem. 2010;31:691–706. doi: 10.1002/jcc.21357. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Anandakrishnan R, Daga M, Onufriev AV. J Chem Theory Comput. 2011;7:544–559. doi: 10.1021/ct100390b. [DOI] [PubMed] [Google Scholar]
- 84.Luger K, Dechassa ML, Tremethick DJ. Nat Rev Mol Cell Biol. 2012;13:436–447. doi: 10.1038/nrm3382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Henikoff S. Nat Rev Genet. 2008;9:15–26. doi: 10.1038/nrg2206. [DOI] [PubMed] [Google Scholar]
- 86.Robinson PJJ, Fairall L, Huynh VAT, Rhodes D. Proc Natl Acad Sci U S Ȧ. 2006;103:6506–6511. doi: 10.1073/pnas.0601212103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Song F, Chen P, Sun D, Wang M, Dong L, Liang D, Xu RMM, Zhu P, Li G. Science (New York, NY) 2014;344:376–380. doi: 10.1126/science.1251413. [DOI] [PubMed] [Google Scholar]
- 88.Shaytan AK, Armeev GA, Goncearenco A, Zhurkin VB, Landsman D, Panchenko AR. J Mol Biol. 2016;428:221–237. doi: 10.1016/j.jmb.2015.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Öztürk MA, Pachov GV, Wade RC, Cojocaru V. Nucleic Acids Res. 2016 doi: 10.1093/nar/gkw514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 90.Korolev N, Fan Y, Lyubartsev AP, Nordenskiöld L. Curr Opin Struct Biol. 2012;22:151–159. doi: 10.1016/j.sbi.2012.01.006. [DOI] [PubMed] [Google Scholar]
- 91.Schlick T, Hayes J, Grigoryev S. J Biol Chem. 2012;287:5183–5191. doi: 10.1074/jbc.R111.305763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 92.Schlick T. Molecular modeling and simulation, an interdisciplinary guide. Springer-Verlag; New York: 2002. [Google Scholar]
- 93.Case DA, Cheatham TE, Darden T, Gohlke H, Luo R, Merz KM, Onufriev A, Simmerling C, Wang B, Woods RJ. J Comput Chem. 2005;26:1668–1688. doi: 10.1002/jcc.20290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Case D, Betz R, Botello-Smith W, Cerutti D, Cheatham T, III, Darden T, Duke R, Giese T, Gohlke H, Goetz A, Homeyer N, Izadi S, Janowski P, Kaus J, Kovalenko T, amd Lee A, LeGrand S, Li P, Lin C, Luchko T, Luo R, Madej B, Mermelstein D, Merz K, Monard G, Nguyen H, Nguyen H, Omelyan I, Onufriev A, Roe D, Roitberg A, Sagui C, Simmerling C, Swails J, Walker R, Wang J, Wolf R, Wu X, Xiao D, York L, Kollman P. AMBER 2016. University of California; San Francisco: 2016. [Google Scholar]
- 95.Mongan J, Simmerling C, McCammon JA, Case DA, Onufriev A. J Chem Theory Comput. 2007;3:156–169. doi: 10.1021/ct600085e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Sigalov G, Fenley A, Onufriev A. J Chem Phys. 2006;124:124902. doi: 10.1063/1.2177251. [DOI] [PubMed] [Google Scholar]
- 97.Wang HWW, Nogales E. Nature. 2005;435:911–915. doi: 10.1038/nature03606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Wong H, Victor JM, Mozziconacci J. PLOS One. 2007;436:e877. doi: 10.1371/journal.pone.0000877. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Hornak V, Abel R, Okur A, Strockbine B, Roitberg A, Simmerling C. Proteins. 2006;65:712–725. doi: 10.1002/prot.21123. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Joung IS, Cheatham TE. 2008;112:9020–9041. doi: 10.1021/jp8001614. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Ryckaert JP, Ciccotti G, Berendsen HJC. J Chem Phys. 1977;23:327–341. [Google Scholar]
- 102.Miyamoto S, Kollman PA. J Comput Chem. 1992;13:952–962. [Google Scholar]
- 103.Case D, Berryman J, Betz R, Cerutti D, Cheatham T, III, Darden T, Duke R, Giese T, Gohlke H, Goetz A, Homeyer N, Izadi S, Janowski P, Kaus J, Kovalenko T, amd Lee A, LeGrand S, Li P, Luchko T, Luo R, Madej B, Merz K, Monard G, Needham P, Nguyen H, Nguyen H, Omelyan I, Onufriev A, Roe D, Roitberg A, Salomon-Ferrer R, Simmerling C, Smith W, Swails J, Walker R, Wang J, Wolf R, Wu X, York D, Kollman P. AMBER 2015. University of California; San Francisco: 2015. [Google Scholar]
- 104.Grand S, Goetz A, Walker R. Comput Phys Commun. 2013;184:374–380. [Google Scholar]
- 105.Izadi S, Aguilar B, Onufriev AV. J Chem Theory Comput. 2015;11:4450–4459. doi: 10.1021/acs.jctc.5b00483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Baker NA, Sept D, Joseph S, Holst MJ, McCammon JA. Proc Natl Acad Sci U S Ȧ. 2001;98:10037–10041. doi: 10.1073/pnas.181342398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Rhee HS, Bataille AR, Zhang L, Pugh BF. Cell. 2014;159:1377–1388. doi: 10.1016/j.cell.2014.10.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Smith MF, Athey BD, Williams SP, Langmore JP. J Cell Biol. 1990;110:245–254. doi: 10.1083/jcb.110.2.245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Luger K, Mäder AW, Richmond RK, Sargent DF, Richmond TJ. Nature. 1997;389:251–260. doi: 10.1038/38444. [DOI] [PubMed] [Google Scholar]
- 110.Richmond TJ, Davey CA. Nature. 2003;423:145–150. doi: 10.1038/nature01595. [DOI] [PubMed] [Google Scholar]
- 111.Nishino Y, Eltsov M, Joti Y, Ito K, Takata H, Takahashi Y, Hihara S, Frangakis AS, Imamoto N, Ishikawa T, Maeshima K. EMBO J. 2012;31:1644–1653. doi: 10.1038/emboj.2012.35. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.van Holde K, Zlatanova J. Semin Cell Dev Biol. 2007;18:651–658. doi: 10.1016/j.semcdb.2007.08.005. [DOI] [PubMed] [Google Scholar]
- 113.McGinty RK, Tan S. Chem Rev. 2015;115:2255–2273. doi: 10.1021/cr500373h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Kato H, Gruschus J, Ghirlando R, Tjandra N, Bai Y. J Am Chem Soc. 2009;131:15104–15105. doi: 10.1021/ja9070078. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Tse C, Hansen JC. Biochemistry. 1997;36:11381–11388. doi: 10.1021/bi970801n. [DOI] [PubMed] [Google Scholar]
- 116.Gordon F, Luger K, Hansen JC. J Biol Chem. 2005;280:33701–33706. doi: 10.1074/jbc.M507048200. [DOI] [PubMed] [Google Scholar]
- 117.Shogren-Knaak M, Ishii H, Sun JMM, Pazin MJ, Davie JR, Peterson CL. Science (New York, NY) 2006;311:844–847. doi: 10.1126/science.1124000. [DOI] [PubMed] [Google Scholar]
- 118.Fenley A, Adams D, Onufriev A. Biophys J. 2010;99:1577–1585. doi: 10.1016/j.bpj.2010.06.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Boulé JB, Mozziconacci J, Lavelle C. J Phys Condens Matter. 2015;27:033101. doi: 10.1088/0953-8984/27/3/033101. [DOI] [PubMed] [Google Scholar]