Skip to main content
PMC home page
The ISME Journal logoLink to The ISME Journal
. 2017 Jul 21;11(11):2426–2438. doi: 10.1038/ismej.2017.91

Cohesion: a method for quantifying the connectivity of microbial communities

Cristina M Herren 1,*, Katherine D McMahon 2,3
PMCID: PMC5649174  PMID: 28731477

Abstract

The ability to predict microbial community dynamics lags behind the quantity of data available in these systems. Most predictive models use only environmental parameters, although a long history of ecological literature suggests that community complexity should also be an informative parameter. Thus, we hypothesize that incorporating information about a community’s complexity might improve predictive power in microbial models. Here, we present a new metric, called community ‘cohesion,’ that quantifies the degree of connectivity of a microbial community. We analyze six long-term (10+ years) microbial data sets using the cohesion metrics and validate our approach using data sets where absolute abundances of taxa are available. As a case study of our metrics’ utility, we show that community cohesion is a strong predictor of Bray–Curtis dissimilarity (R2=0.47) between phytoplankton communities in Lake Mendota, WI, USA. Our cohesion metrics outperform a model built using all available environmental data collected during a long-term sampling program. The result that cohesion corresponds strongly to Bray–Curtis dissimilarity is consistent across the six long-term time series, including five phytoplankton data sets and one bacterial 16S rRNA gene sequencing data set. We explain here the calculation of our cohesion metrics and their potential uses in microbial ecology.

Introduction

Most efforts to model microbial communities primarily use environmental drivers as predictors of community dynamics (Patterson, 2009; Hambright et al., 2015). However, despite the vast quantities of data becoming available about microbial communities, predictive power in microbial models is often surprisingly poor (Blaser et al., 2016). Even in one of most well-studied microbial systems, the San Pedro Ocean Time Series, there are sampling sites where none of the 33 environmental variables measured are highly significant (P<0.01) predictors of community similarity (Cram et al., 2015). Thus, there may be room to improve predictive models by adding new parameters; ecological literature has long suggested that the degree of complexity in a community should inform community dynamics (MacArthur, 1955; Cohen and Newman., 1985; Wootton and Stouffer, 2016). We use the term ‘complexity’ as defined in the theoretical ecology literature, which refers to the number and strength of connections in a food web (May, 1974). We hypothesize that incorporating information about the complexity of microbial communities could improve predictive power in these communities.

Here, we present a workflow to generate metrics quantifying the connectivity of a microbial community, which we call ‘cohesion’. We demonstrate how our cohesion metrics can be used to predict community dynamics by showing that cohesion is significantly related to the rate of compositional turnover (Bray–Curtis dissimilarity) in microbial communities. As an application of our metrics, we present a case study using our newly developed cohesion variables as predictors of the compositional turnover rate (a common response variable in microbial ecology) in phytoplankton communities. Prior modeling efforts have indicated that incorporating taxon traits and interactions improved models of phytoplankton community assembly (Litchman and Klausmeier, 2008; Thomas et al., 2012). However, even basic traits such as taxonomy are still often unknown for other microbial taxa, such as bacteria (Newton et al., 2011). Thus, taxon interactions and community connectivity must be inferred statistically.

Our cohesion metrics overcome two barriers that often preclude using information about community complexity in microbial analyses. First, the large number of taxa in microbial data sets makes it difficult to use information about all taxa in statistical analyses. Although methods exist to analyze microbial community interconnectedness (for example, local similarity analysis, artificial neural networks), this often involves constructing networks with many parameters that are difficult to interpret. Second, microbial community data are often ‘relativized’ or ‘compositional’ data sets, where the abundance of each taxon represents the fraction of the community it comprises. This creates several problems in downstream analysis (Weiss et al., 2016). For example, taxon correlation values are different in absolute versus relative data sets (Faust and Raes, 2012; Friedman and Alm, 2012), and it is unclear how using relative abundances influences the apparent population dynamics of individual taxa (Lovell et al., 2015). Thus, these two features (many taxa and relative abundance) have previously proven problematic when analyzing microbial community connectivity. The methods used to account for these biases influence the results of the analyses. For instance, the proportion of positive versus negative pairwise interactions identified in a single data set varied widely when using different correlation detection methods (Weiss et al., 2016). In addition, the power to detect significant relationships between taxa declines steeply when taxa are less persistent and as relationships become nonlinear (Weiss et al., 2016). In contrast to existing correlation detection methods, which aim to identify significant pairwise interactions, our cohesion metrics evaluate connectivity at the community level.

Here, we describe and test a method to quantify one aspect of microbial community complexity. Our resulting ‘cohesion’ metrics quantify the connectivity of each sampled community. Thus, our cohesion metrics integrate easily with other statistical analyses and can be used by any microbial ecologist interested in asking whether community interconnectedness is important in their study system. We demonstrate how to obtain these cohesion metrics from time series data and, as a case study, show how cohesion relates to rates of compositional turnover in long-term microbial data sets. We develop this workflow with data sets where raw abundance data are available and use these raw abundances to validate our methods when working with relativized data sets. Thus, our approach was designed to overcome known challenges of analyzing microbial data sets.

Materials and methods

Description of data sets

The North Temperate Lakes Long-Term Ecological Research database hosts many long-term time ecological series. We used five long-term phytoplankton data sets (two from the North Temperate Lakes Long-Term Ecological Research and three from the Cascade research group) to validate the cohesion workflow. These data sets met a number of criteria that made them good candidates for the validation: the samples were collected regularly, sampling spanned multiple years and many environmental gradients, and taxa were counted in absolute abundance. The term ‘phytoplankton’ refers to the polyphyletic assemblage of photosynthetic aquatic microbes (Litchman and Klausmeier, 2008). The data sets are from the following lakes in Wisconsin, USA: Lake Mendota (293 samples with 410 taxa over 19 years), Lake Monona (264 samples with 382 taxa over 19 years), Paul Lake (197 samples with 209 taxa over 12 years), Peter Lake (197 samples with 237 taxa over 12 years) and Tuesday Lake (115 samples with 121 taxa over 12 years). These lakes vary in size, productivity and food web structure. Lake Mendota and Lake Monona are large (39.4 km2 and 13.8 km2), urban, eutrophic lakes (Brock, 2012). Peter, Paul and Tuesday lakes are small (each <0.03 km2) lakes surrounded by forest (Carpenter and Kitchell, 1996). Peter Lake and Tuesday Lake were also subjected to whole-lake food web manipulations during the sampling timeframe (detailed in Elser and Carpenter, 1988 and Cottingham et al., 1998). After validating our workflow using the phytoplankton data sets, we tested the cohesion metrics on a bacterial data set obtained using 16S rRNA gene amplicon sequencing. These types of data sets often contain thousands of taxa, most of them rare, which may influence the results of correlation-based analyses (Faust and Raes, 2012). We used the Lake Mendota bacterial 16S rRNA gene sequencing time series (91 samples with 7081 taxa over 11 years) for this analysis (Hall et al., in review). Sample processing, sequencing and core amplicon data analysis were performed by the Earth Microbiome Project (www.earthmicrobiome.org; Gilbert et al., 2014), and all amplicon sequence data and metadata have been made public through the data portal (qiita.microbio.me/emp). Briefly, community DNA (Kara et al., 2013) was used to amplify partial 16S rRNA genes using the 515F-806R primer pair (Caporaso et al., 2011) and an Illumina MiSeq, with standard Earth Microbiome Project protocols.

We present the workflow using results from the Lake Mendota phytoplankton data set, as it is the largest (longest duration and most taxa) data set available in absolute abundance. The dominant taxa in the Lake Mendota phytoplankton data set change throughout the year, with diatoms most abundant during the spring bloom and cyanobacteria most abundant in summer. Details about phytoplankton data sets can be found at https://lter.limnology.wisc.edu/. Further details about the Lake Mendota 16S rRNA gene data set are included in the Supplementary Online Material.

Data curation

Phytoplankton densities in Lake Mendota varied by more than two orders of magnitude between sample dates. The densities of cells in these samples ranged from 956 cells ml−1 to 272 281 cells ml−1. We removed individuals that were not identified at any level (for example, categorized as Miscellaneous). For each sample date, we converted the raw abundances to relative abundances by dividing each taxon abundance by the total number of individuals in the community, such that all rows summed to 1. Relative abundances indicate the fraction of a community comprised by the taxon. We removed taxa that were not present in at least 5% of samples, as we were not confident that we could recover robust connectedness estimates for very rare taxa. This cutoff retained an average of 98.9% of the identified cells in each sample. The results of our analyses using other cutoff values can be found in the Supplementary Online Material.

Results

Overview

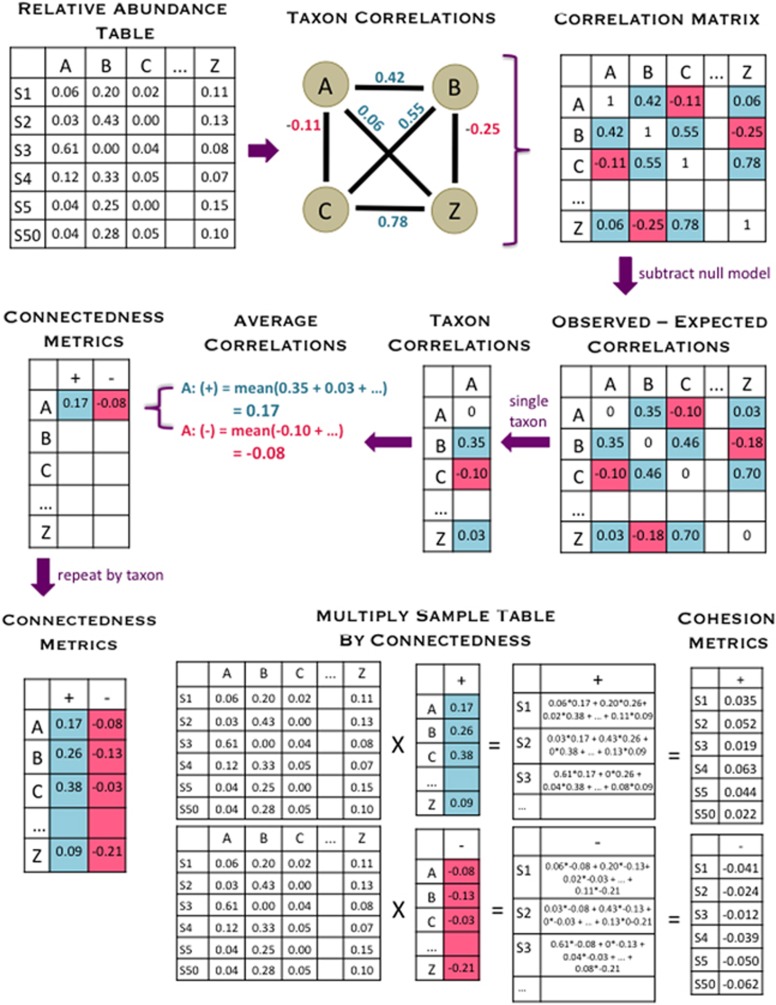
The input of our workflow is the taxon relative abundance table, and the outputs are measurements of the connectivity of each sampled community, which we call community ‘cohesion’ (Figure 1). In the process, our workflow also produces metrics of the connectedness of each taxon. Briefly, our workflow begins by calculating the pairwise correlation matrix between taxa, using all samples. We use a null model to account for bias in these correlations due to the skewed distribution of taxon abundances (that is, many small values and a few large values) and relativized nature of the data set (that is, all rows sum to 1). We subtract off these ‘expected’ correlations generated from the null model to obtain a matrix of corrected correlations. For each taxon, the average positive corrected correlation and average negative corrected correlation are recorded as the connectedness values. As previously noted, our goal was to create a metric of connectivity for each community; thus, the next step in the workflow calculates cohesion values for each sample. Cohesion is calculated by multiplying the abundance of each taxon in a sample by its associated connectedness values, then summing the products of all taxa in a sample. There are two metrics of cohesion, because we separately calculate metrics based on the positive and negative relationships between taxa. Within each section given below, we alternate between presenting an analysis step and showing a validation of these techniques.

Figure 1.

Figure 1

Open in a new tab

This diagram shows an overview of how our cohesion metrics are calculated, beginning with the relative abundance table and ending with the cohesion values. The relative abundance table shows six samples (S1 indicating ‘Sample 1’ and so on) and a subset of taxa (A, B, C and Z). First, pairwise correlations are calculated between all taxa, which are entered into the correlation matrix. We then used a null model to account for how the features of microbial data sets might affect correlations, and we subtracted off these values (null model detailed in Figure 2). For each taxon, we averaged the positive and negative corrected correlations separately and recorded these values as the positive and negative connectedness values. Cohesion values were obtained by multiplying the relative abundance table by the connectedness values. Thus, there are two metrics of cohesion, corresponding to positive and negative values.

Connectedness metric

Analysis

Null models: It is difficult to directly observe interactions within microbial communities, so correlations are often used to infer relationships between taxa or between a taxon and the environment. Thus, we used a correlation-based approach for determining the connectedness of taxa. However, when using correlation-based approaches with relativized microbial data sets, it is necessary to use a null model to evaluate how the features of the data set (skewed abundances and the fact that all rows sum to 1) contribute to correlations between taxa (Weiss et al., 2016). The purpose of a null model is to assess the expected strengths of correlations when there are no true relationships between taxa (Ulrich and Gotelli, 2010).

The null model was used to calculate how strongly the features common to microbial data sets contribute to taxon connectedness estimates, so that this structural effect could be subtracted from the connectedness metrics. Of the several dozen null models tested, we have selected two for inclusion in the cohesion R script. We discuss both null models here and in the Supplementary Online Material. The Supplementary Online Material and readme document should assist in choosing the null model appropriate for a given data set. While testing various null models, it became clear that a taxon’s pairwise correlation values were strongly related to its persistence (fraction of samples when present) across the data set. Thus, taxon persistence was preserved in both the null models.

The objective of the null model was to calculate the strength of pairwise correlations that would be observed if there were no true relationship between taxa. This paragraph describes the ‘taxon/column shuffling’ null model used for the phytoplankton data set analyses. During each iteration, one taxon was designated as the ‘focal taxon’ (Figure 2). For each taxon besides the focal taxon, abundances in the null matrix were permuted (that is, randomly sampled without replacement) from their abundance distribution across all the samples. Then, we calculated Pearson correlations between the focal taxon and the randomized other taxa. We iterated through this process of calculating pairwise correlations between the focal taxon and all other taxa 200 times. The median correlations from these 200 randomizations were called the ‘expected’ correlations for the focal taxon. We recorded the median value as the ‘expected’ correlation, rather than the mean value, because distributions were skewed toward larger values. Thus, a greater proportion of the distribution fell within one standard deviation of the median, as compared with within one standard deviation of the mean. We repeated this process for each taxon as the focal taxon, which resulted in a matrix of expected taxon correlations. Finally, we subtracted the expected taxon correlations from their paired observed taxon correlations, thereby producing a matrix where each value was an observed minus expected correlation for the given pair of taxa.

Figure 2.

Figure 2

Open in a new tab

Microbial data are in the form of relative abundance, and some taxa are much more abundant than others, which are factors that may cause taxa to be spuriously correlated. Thus, we devised a null model to account for the bias that these data features introduce into our metrics. We repeated this process with each taxon as the ‘focal taxon’, which is A in this figure. For each of the 200 iterations, we randomized all taxon abundances besides the focal taxon. We then calculated correlations between the focal taxon and all other taxa. We recorded the median value of the 200 correlations calculated for each pair of taxa in the median correlation matrix.

The second null model uses the same workflow as described above, where the data set is iteratively randomized and median correlations are used as the ‘expected’ pairwise correlations. However, the method of randomization is different; instead, the abundances of all taxa present within one sample were randomized. We refer to this null model as the ‘row shuffling’ model. The benefit of this null model is that row sums are maintained. Thus, negative dependencies between taxa within the same sample are accounted for in this model. The drawback of this null model is that a taxon might be assigned an abundance value that is implausible (that is, larger than its maximum observed abundance). In the online script to calculate cohesion, we have included the option to choose between these two null models (taxon shuffle and row shuffle).

We have included an additional option to input a pre-determined correlation matrix, thereby bypassing the null model. Using a pre-determined correlation matrix allows researchers to use a different correlation detection strategy to generate the correlation matrix. This option to import a custom correlation matrix makes our cohesion workflow compatible with other software packages designed for detecting pairwise relationships in microbial communities.

Calculating connectedness: We calculated taxon connectedness values from the corrected (observed minus expected) correlation matrix. For each taxon, we separately averaged its positive and negative correlations with other taxa to produce a value of positive connectedness and a value of negative connectedness. We kept positive and negative values separate for both mathematical and biological reasons. First, we had hypothesized that positive and negative correlations may capture different ecological relationships between taxa. Furthermore, positive correlations were stronger (an average of 2.5 times larger in magnitude) than negative correlations. And, correlation distributions were generally skewed toward positive values. Thus, a small number of positive correlations could mute the signal of negative correlations, if positive and negative correlations were averaged together.

The averaging step in this workflow was intended to overcome the issue that individual correlations between taxa can be influenced by many factors and may be spurious (Fisher and Mehta, 2014). However, assuming that correlations often (but not always) reflect complexity in a community, the average of many correlations should be a more robust metric of complexity than any single correlation. In other words, we assume only that highly connected taxa have stronger correlations on average. Invoking the law of large numbers, these average correlations should be increasingly accurate measures of a taxon’s connectedness as the number of pairwise correlations increases (that is, as the number of taxa in the data set increases). Similarly, applying the central limit theorem, each mean correlation should be normally distributed with low variance due to the large number of pairwise correlations.

Validation

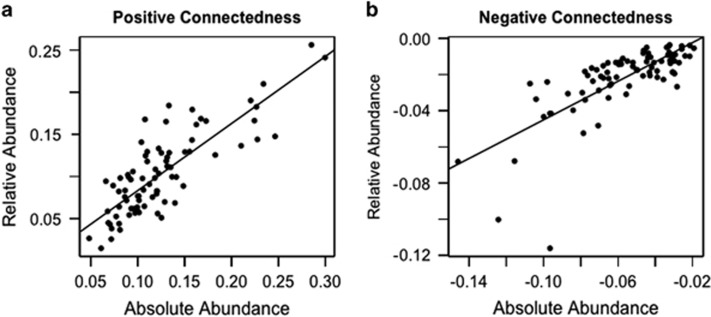
As discussed previously, there are inherent limitations of using correlation-based methods with relative abundance data instead of absolute counts (Fisher and Mehta, 2014). Thus, we examined whether a measure of connectedness based on absolute abundance would show the same pattern observed using the relativized data. However, we needed a different approach for calculating correlations to account for the following properties of count data: (1) variance-mean scaling, which results in very large population variances of abundant taxa (Taylor, 1961) and (2) the fact that individual population sizes are strongly related to overall community densities, which causes positive correlations among all taxa (Doak et al., 1998). As noted previously, phytoplankton densities in Lake Mendota samples varied by more than two orders of magnitude among sample dates. Therefore, using correlations between raw abundances would inflate the positive relationships between taxa as a result of changing overall community density. Thus, we first detrended the count data to account for changing community density (on different sampling dates) and drastically different variances of taxon populations (which are expected as a result of mean-variance scaling).

We used a hierarchical linear model to estimate the effects of overall community density and mean taxon abundance on individual taxon observations (sensu Jackson et al., 2012), so that these effects could be removed when calculating correlations. We modeled the abundance of each taxon at each time point as a function of sample date and taxon, assuming a quasipoisson distribution (which accounts for increases in population variances when population means increase). The model estimates a mean abundance effect for each sample, based on the abundances of each taxon in the sample. Similarly, the model estimates mean abundances for each taxon, based on the distribution of taxon abundances across all the samples. Thus, the residuals of this analysis represent the normalized (transformed) deviations of taxon abundances after accounting for overall community density on the sample date and taxon abundance/variance. We created a pairwise correlation matrix for the phytoplankton taxa using the correlations between these residuals. We calculated connectedness metrics from the pairwise correlation matrix using the same technique that we applied to the corrected correlation matrix from the relativized data: we used the average positive and negative taxon correlations as their connectedness values.

We validated our workflow for the relative abundance data set using the estimates of taxon connectedness obtained from the absolute abundance data set. Comparing the connectedness values from these two methods shows strong agreement between the two sets of connectedness metrics (correlation for positive connectedness metrics= 0.820; correlation for negative connectedness metrics= 0.741, Figure 3). Although two taxa deviate from the linear relationship between the negative connectedness metrics (appearing as outliers in Figure 3b), both metrics rate these taxa as having strong connectedness arising from negative correlations. Thus, the two methods are qualitatively consistent for these two anomalous points. Furthermore, using the null model improved the correspondence between absolute and relative connectedness metrics, as measured by their proportionality. The variance in the proportions (relative metric/absolute metric) decreased after the null model correction was implemented (variance in proportions for positive metrics: uncorrected=0.25, corrected= 0.065; variance in proportions for negative metrics: uncorrected=0.047, corrected= 0.035).

Figure 3.

Figure 3

Open in a new tab

Comparing the metrics of connectedness obtained from the absolute abundance data set (x axes) and the relative abundance data set (y axes) shows agreement between the two methods of generating these metrics. Correlations between the metrics are 0.810 (a) and 0.741 (b). We used separate variables for positive and negative metrics because relativizing the data set is expected to differentially affect positive and negative correlations. Solid lines show the fit of linear models.

Cohesion metric

Analysis

Many researchers seek to detect differences in community connectivity across time, space or treatments. Thus, it would be useful to have a metric that quantifies, for each community, the degree to which its component taxa are connected. The aim of our cohesion metric is to quantify the instantaneous connectivity of a community, where connectivity increases when highly connected taxa become more abundant in the community. We used a simple algorithm to collapse the connectedness values of individual taxa into two parameters representing the connectivity of the entire sampled community, termed ‘cohesion’. Again, one metric of cohesion stems from positive correlations, and one metric stems from negative correlations. To calculate each cohesion metric, we multiplied the relative abundance of taxa in a sample by their associated connectedness values and summed these products. This cohesion index can be represented mathematically as the sum of the contribution of each of the n taxa in the community, after removing rare taxa (Equation 1). Thus, communities with high relative abundances of strongly connected taxa would have a high score of community cohesion. We note that this index is bounded by −1 to 0 for negative cohesion or from 0 to 1 for positive cohesion.

graphic file with name ismej201791e1.jpg

Validation

We had hypothesized that our cohesion metrics could be significant predictors of microbial community dynamics. Thus, a natural question to ask was whether our metrics of cohesion outperform environmental variables when analyzing the Lake Mendota phytoplankton data. Fortunately, the North Temperate Lakes Long-Term Ecological Research program has collected paired environmental data for the Lake Mendota phytoplankton samples. We obtained these environmental data sets to use as alternative predictors of phytoplankton community dynamics in Lake Mendota. The environmental data sets available (11 variables) were: water temperature, air temperature, dissolved oxygen concentration, dissolved oxygen saturation, Secchi depth, combined NO3 + NO2 concentrations, NH4 concentration, total nitrogen concentration, dissolved reactive phosphorus concentration, total phosphorus concentration and dissolved silica concentrations. Protocols, data and associated metadata can be found at https://lter.limnology.wisc.edu/. We use these environmental data to build an alternate model in our case study below.

Case study of utility

Analysis

To demonstrate their utility, we applied our new metrics to the Lake Mendota phytoplankton data set. We tested whether community cohesion could predict compositional turnover, a common response variable in microbial ecology. We used multiple regression to model compositional turnover (Bray–Curtis dissimilarity between time points) as a function of community cohesion at the initial time point. That is, Bray–Curis dissimilarity was the dependent variable, whereas positive and negative cohesion were the independent variables. Because time between samples influences Bray–Curtis dissimilarity (Nekola and White, 1999; Shade et al., 2013), we only included pairs of samples taken within 36 to 48 days of each other. These criteria included 186 paired communities across the 19 years. Cohesion values (both positive and negative) were calculated at the first time point for each sample pair. We chose this timeframe because it was sufficiently long for multiple phytoplankton generations to have occurred, and because this timeframe was compatible with the sampling frequency.

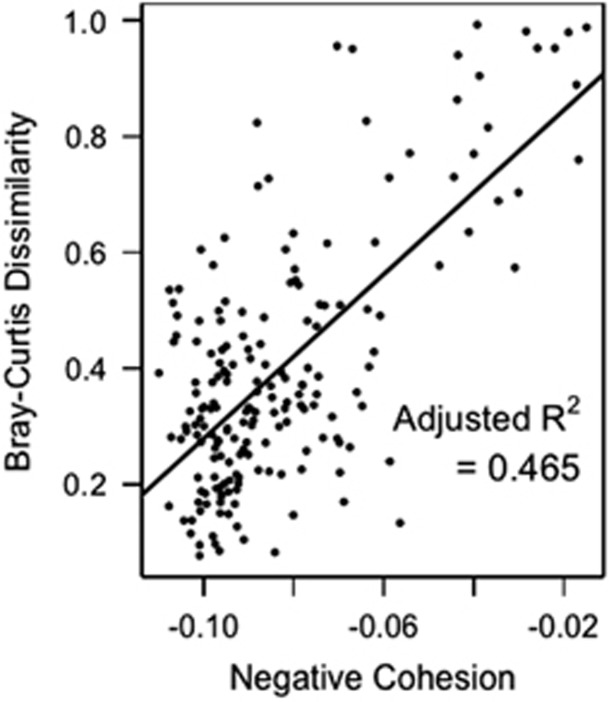
Community cohesion was a strong predictor of compositional turnover (Figure 4). The regression using our cohesion metrics explained 46.5% of variability (adjusted R2=0.465) in Bray–Curtis dissimilarity. Cohesion arising from negative correlations was a highly significant predictor, whereas cohesion arising from positive correlations was not significant (negative cohesion: F1,183=6.81, P<1 × 10−20; positive cohesion: F1,183=0.735, P=0.405).

Figure 4.

Figure 4

Open in a new tab

We used our metrics of community cohesion as predictors of the rate of compositional turnover (Bray–Curtis dissimilarity) in the Mendota phytoplankton communities. Negative cohesion was a significant predictor (P<1 × 10−20) of Bray–Curtis dissimilarity, and the regression explained 46.5% of variation in compositional turnover.

For the purpose of model comparison, we used the associated environmental data to model Bray–Curtis dissimilarity as a function of environmental drivers. We included as predictors the 11 variables previously mentioned, as well as 11 additional predictors that measured the change in each of these variables between the two sample dates. Finally, because many chemical and biological processes are dependent on temperature (Brown et al., 2004), we included first-order interactions between water temperature and the 21 other variables. We first included all 43 terms in the model, then used backward selection (which iteratively removes the least-significant term in the model, beginning with interaction terms) until all the remaining terms in the model were significant at P<0.1, as to maximize the adjusted R2 value. Although this analysis does not represent an exhaustive list of possible environmental drivers, it includes all available paired environmental data from the long-term monitoring program. Twenty-nine values of Bray–Curtis dissimilarity were excluded from this analysis (leaving 157 of the 186 values), because they lacked one or more associated environmental variables. Additional details about this analysis can be found in the Supplementary Online Material.

In the final model after backward selection, 16 variables were retained as significant predictors (see the Supplementary Online Material). Significance was determined using type III sums of squares. Using the guideline that each variable should have approximately 10 additional data points to prevent overparameterization (Peduzzi et al., 1995), we were not concerned about overfitting. The adjusted R2 of this model was 0.229. The non-adjusted R2 value of the full model (all 43 variables) was 0.393. When adding negative cohesion as a parameter into the final environmental model, negative cohesion was highly significant (P<1 × 10−13) and 12 environmental variables remained significant at P<0.1.

To address the generality of the relationship between cohesion and community turnover, we calculated cohesion metrics and Bray–Curtis dissimilarity for the four other phytoplankton data sets (Monona, Peter, Paul and Tuesday lakes) and for the Lake Mendota bacterial 16S rRNA gene sequencing data set. Community cohesion was a significant predictor of Bray–Curtis dissimilarity in all the data sets. In each instance, stronger cohesion resulting from negative correlations was related to lower compositional turnover. Table 1 presents the results of these analyses and associated workflow parameters. Additional information about the sensitivity of model performance to varying parameters can be found in the Supplementary Online Material.

Table 1. Cohesion predicts community turnover in six long-term time series.
Lake Taxon pers. cutoff a Adjusted R2 Positive cohesion P-value Negative cohesion P-value Positive cohesion direction b Negative cohesion direction b Days between samples Number of samples
Mendota (phyto) 5% 0.465 0.405 <1 × 10−20 NS Stronger is stabilizing 36–48 186
Monona 5% 0.355 0.413 <1 × 10−15 NS Stronger is stabilizing 36–48 166
Peter 10% 0.357 0.062 <1 × 10−3 NS Stronger is stabilizing 39–45 121
Paul 10% 0.500 <1 × 10−11 <1 × 10−19 Weaker is stabilizing Stronger is stabilizing 39–45 125
Tuesday 10% 0.374 0.355 <1 × 10−8 NS Stronger is stabilizing 39–45 72
Mendota (16S) 5% 0.378 0.0039 <1 × 10−5 Weaker is stabilizing Stronger is stabilizing 25–41 54
Open in a new tab
a

Stands for ‘taxon persistence cutoff’, which was the minimum proportion of presences across the data set that we used as a cutoff for including taxa in the connectedness and cohesion metrics. Other cutoffs may give higher model-adjusted R2 values (see the Supplementary Online Material), but we wanted to use the same cutoff for data sets collected within the same sampling program. We also applied a mean abundance cutoff to the Lake Mendota 16S rRNA gene data set, where we removed taxa with a mean abundance <1 × 10−7.

b

These columns indicate the direction of a significant relationship between cohesion and Bray–Curtis dissimilarity. For example, ‘stronger is stabilizing’ means that greater cohesion is related to lower Bray–Curtis dissimilarity. Nonsignificant relationships are denoted ‘NS’.

Validation

Strong correlations between predictor variables are known to influence the results of statistical analyses (Neter et al., 1996). Thus, we wondered whether strong correlations between taxa would necessarily generate the observed relationship where greater cohesion is related to lower compositional turnover. We conducted simulation studies to investigate whether our significant results might be simply an artifact of strong inter-taxon correlations. We generated data sets where taxa were highly correlated in abundance, as if they were synchronously responding to exogenous forces. We calculated cohesion metrics and Bray–Curtis dissimilarities for the simulated data sets to analyze whether strong taxon correlations was sufficient to produce results similar to those we observed in the real data.

Here, we briefly describe the process used to simulate data sets, while additional details can be found in the Supplementary Online Material. First, we generated four autocorrelated vectors to represent exogenous forces, such as environmental drivers. Taxa were artificially correlated to these external vectors, thereby also producing strong correlations between taxa. We manipulated the taxon abundances to mimic other important features of the microbial data sets, including skewed taxon mean abundances and a large proportion of zeroes in the data set. We calculated cohesion metrics and Bray–Curtis dissimilarities for the simulated data sets, and we used a multiple regression to model Bray–Curtis dissimilarity as a function of positive cohesion and negative cohesion. We recorded the R2 value and parameter estimates of this multiple regression. We repeated this simulation process 500 times to generate distributions of these results.

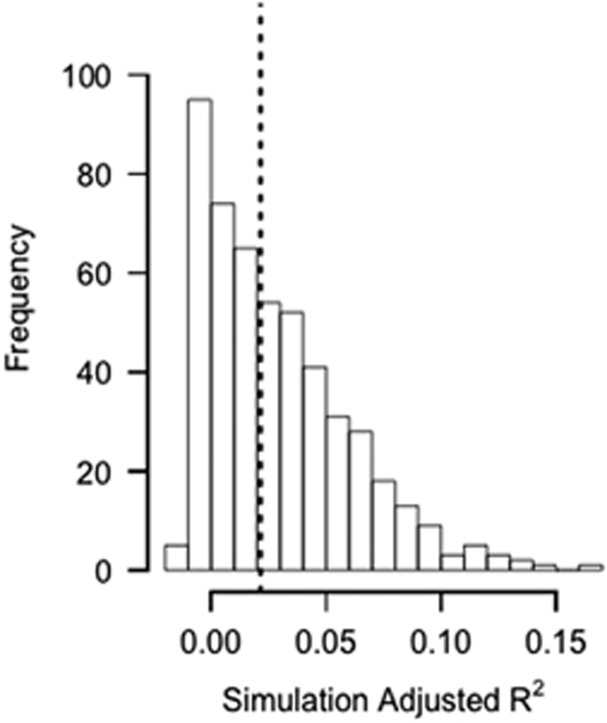
Our cohesion metrics had a very low ability to explain compositional turnover (Bray–Curtis dissimilarity) in the simulated data sets. The median model-adjusted R2 value was 0.022, with 95% of adjusted R2 values below 0.088 (Figure 5). Although the community cohesion metrics were highly significant predictors (P<0.001) of community turnover more commonly than would be expected by chance (1.0% of simulations for positive cohesion and 8.6% for negative cohesion), the proportion of variance explained by these metrics was comparatively very low. For comparison, across the six long-term data sets from Wisconsin lakes, model-adjusted R2 values ranged from 0.36 to 0.50. Thus, there was comparatively little ability to explain compositional turnover in the simulated data sets using our cohesion metrics.

Figure 5.

Figure 5

Open in a new tab

We simulated data sets where correlations between taxa were artificially produced by forced correlation to external factors. We calculated cohesion values for the simulated communities to test whether cohesion and Bray–Curtis dissimilarity were strongly related in simulated data sets. The histogram of model-adjusted R2 values from our simulations shows that the median-adjusted R2 was 0.022 (dashed line), with 95% of values falling below 0.088. For comparison, observed adjusted R2 values ranged from 0.36 to 0.50.

Discussion

The ability to predict microbial community dynamics lags behind the amount of data collected in these systems (Blaser et al., 2016). Here, we present new metrics, called ‘cohesion’, which can be used as additional predictor variables in microbial models. The cohesion metrics contain information about the connectivity of microbial communities, which has been previously hypothesized to influence community dynamics (MacArthur, 1955; May, 1972; Nilsson and McCann, 2016). Our cohesion metrics are easily calculated from a relative abundance table (R script provided online) and might be of interest to a variety of microbial ecologists and modelers.

In the Lake Mendota phytoplankton example, our two cohesion parameters outperformed the available environmental data at predicting phytoplankton community changes. The two cohesion parameters explained 46.5% of variability (adjusted R2=0.465) in community turnover over 19 years of phytoplankton sampling, in comparison with the final environmental model using 16 predictors, which explained 22.9% of community turnover (adjusted R2=0.229). The simultaneous significance of negative cohesion and 12 environmental variables when all predictors were included in a single model indicates that environmental variables and negative cohesion explained different sources of variability in Bray–Curtis dissimilarity. Although there are almost certainly important predictors missing from the environmental model (for example, photosynthetically active radiation, three-way interactions), the environmental model represents a commonly applied approach to explaining microbial compositional turnover (Tripathi et al., 2012; Chow et al., 2013) that uses all associated environmental data from a long-term sampling program. Although we still strongly advocate for the collection of environmental data, we note that cohesion was a much better predictor of compositional turnover than any available environmental variable.

Our workflow overcomes many challenges associated with using correlation-based techniques in microbial data sets. The validations we conducted indicated that our connectedness metrics are appropriate for relativized data sets, because connectedness metrics from relative and absolute data sets showed strong correspondence. Most DNA-sequencing data sets are only available in relative abundance. Previous methods for analyzing relative abundance data sets have identified potential pitfalls of calculating correlations for these data (Friedman and Alm, 2012; Weiss et al., 2016); however, the extent to which these biases influence analysis results is often unknown, because paired absolute abundance data sets do not exist. The validations of our cohesion workflow with absolute abundance data indicate that the steps taken to account for biases (using a null model and averaging pairwise correlations) make the cohesion metrics robust for relative abundance data sets.

Our cohesion metrics address a common problem of techniques describing community complexity (such as network analyses), which is that they do not quantify the connectivity of individual communities. For instance, the ‘hairball’ generated from a network analysis is generated from many samples; there are no parameters specific to each sample, and therefore the network cannot be used as a predictor variable. Thus, existing methods to quantify connectivity do not pair easily with other analyses. Furthermore, in contrast to many other network analyses, we did not attempt to calculate significance values for pairwise correlations as a part of the cohesion workflow. Based on our a priori hypothesis that weak interactions are ecologically important (McCann et al., 1998), we included all pairwise correlations in the connectedness metrics. Our cohesion metrics quantify sample connectivity using only two parameters, which can be used as predictors in a variety of further analyses (linear regression, ordinations, time series and so on). Finally, our simulations showed that strong inter-taxon correlations were not sufficient to reproduce the observed result that cohesion was a strong predictor of Bray–Curtis dissimilarity. In the simulations, cohesion had low explanatory power, even though taxa were highly correlated. From this result, we infer that correlations between taxa in real communities are an important aspect of complexity that is captured by our cohesion metrics.

Our cohesion metrics explain a significant amount of compositional change in all six data sets (five phytoplankton and one bacterial 16S rRNA gene data set). Yet, it is not immediately clear what cohesion is measuring. There are two broad factors that could cause correlations between taxa: biotic interactions and environmental drivers. Thus, at least one of these two factors must underlie our connectedness and cohesion metrics. Here, we discuss the evidence supporting either of these interpretations:

Cohesion as a measure of biotic interactions

Even if shared responses to environmental drivers underlie most pairwise taxon correlations, cohesion could still indicate biotic interaction strength in a community. This would occur if taxa were influenced to the same degree by environmental drivers, but differentially influenced by species interactions. In this case, averaging over all correlations would give larger connectedness values for strong interactors and smaller connectedness values for weak interactors. Many studies have indicated that microbial taxa have differential interaction strengths. For example, some microbial communities contain keystone taxa, which have disproportionate effects on community dynamics through their strong taxon interactions (Trosvik and de Muinck, 2015; Banerjee et al., 2016). Similarly, recent work suggests that many taxa within candidate phyla are obligate symbionts, meaning they must interact strongly with other taxa for their survival and reproduction (Kantor et al., 2013; Hug et al., 2016). Conversely, there are many taxa that can be modeled adequately as a function of environmental drivers; this is true for some bloom forming cyanobacteria, which are known to respond strongly to nutrient concentrations and temperature (McQueen and Lean, 1987; Beaulieu et al., 2013). Taken together, these studies suggest that there is a wide spectrum of how strongly taxa interact with one another. These differences in interaction strength would be detected by our connectedness metric due to averaging over the large number of pairwise correlations. Thus, it is plausible that connectedness and cohesion are reflecting biotic interactions in communities.

We now examine results from the long-term data set analyses under the assumption that cohesion measures biotic interactions. The Bray–Curtis dissimilarity regression results would mean that communities with many strong interactors have lower rates of change, especially when the interactions create negative correlations between taxon abundances. This finding is in line with prior work showing that biotic interactions affect microbial community stability (Coyte et al., 2015). Thus, the interpretation that stronger biotic interactions lead to lower compositional turnover is a plausible explanation for our observed results. However, we specifically refrain from interpreting positive or negative connectedness values as indications of specific biotic interactions, such as predation, competition or mutualism. For example, a positive correlation between two taxa could be the result of a mutualism between the taxa, or it could be the result of a shared predator declining in abundance. Further work, both empirical and theoretical, is necessary to identify what these positive and negative correlations signify in the context of the ecology of these organisms.

Cohesion as a measure of environmental synchrony

We now consider the possibility that connectedness and cohesion are simply detecting environmental synchrony. If a subset of taxa respond to a changing environmental driver, then these taxa will have strong pairwise correlations. For example, correlations between phytoplankton species of the same genus (and, therefore, with similar niches) can be upwards of 0.9, indicating strong similarity in abundance patterns. In this case, connectedness would measure the degree of environmentally driven population synchrony that a taxon has with other taxa. A high cohesion value would indicate that a community has many taxa that respond simultaneously to external forces; then, cohesion would quantify overall community responsiveness to one or more environmental drivers. Under this assumption, cohesion should correlate with environmental drivers (for example, cohesion is high because many taxa are positively correlated to warm temperatures, but cohesion drops when it gets colder and these taxa senesce). We tested this prediction with 22 variables from the environmental model (11 for the environmental variables and 11 for the changes in environmental variables) and found that negative cohesion in the Lake Mendota phytoplankton data set generally had weak correlations with these predictors (absolute correlations <0.25, Supplementary Online Material). We also looked for a seasonal trend in cohesion, but found no significant correlation between cohesion (positive or negative) and Julian Day, or a quadratic term for Julian Day. Thus, we do not find any evidence that cohesion is simply reproducing the information contained in environmental data. Finally, our simulations show one example where taxon abundances could be driven exclusively by external factors (such as the environment), but this does not necessarily lead to strong predictive power of compositional turnover. However, our simulations omitted many features of real ecological communities, and so we cannot completely rule out the possibility that environmental drivers contributed to our cohesion metrics in the phytoplankton data sets.

Under the assumption that cohesion measures environmentally driven population synchrony, we examine our result that stronger negative cohesion was related to lower Bray–Curtis dissimilarity. In this scenario, communities that have strong cohesion contain high abundances of taxa that respond simultaneously to environmental forces. Then, communities with many synchronous taxa would turn over more slowly than communities with taxa whose abundances are independent of the environment. This conclusion is counterintuitive, but possible. This pattern could occur if taxa that are strongly influenced by the environment have lower variability than taxa that are weakly influenced by the environment; in that case, highly correlated taxa would have their abundances more tightly regulated than other taxa. Although possible, this explanation disagrees with many studies that have found that environmental gradients regulate which taxa can persist in communities (Fierer and Jackson, 2006; Walter and Ley, 2011; Freedman and Zak, 2015).

Comparing the two possible signals that cohesion might be detecting, we believe the evidence points to biotic interaction as the larger contributor. However, we expect that environmental synchrony is captured to some extent, with the relative importance of environmental factors depending on the particular communities and ecosystem. In instances where synchronous responses to environmental drivers cause positive correlations between taxa, we would expect this environmentally driven signal to affect positive cohesion values more than negative cohesion values. Regardless of the ecological force measured by cohesion, there is a clear result in the six data sets analyzed that stronger negative cohesion is related to lower compositional turnover. This result suggests that negative correlations between taxa are arranged non-randomly to counteract one another, thereby stabilizing community composition. In other words, relationships between taxa appear to buffer, rather than amplify, changes to community composition. This result agrees with prior theoretical models that propose that feedback loops originating from taxon interactions are integral to modulating food web stability (Neutel et al., 2007; Brose, 2008). Although stronger negative cohesion was related to lower compositional turnover, negative pairwise correlations were, on average, weak. The negative connectedness values ranged from −0.004 to −0.12, and the mean negative correlation was −0.022. Thus, our results are not inconsistent with the hypothesis that weak interactions are stabilizing to communities (McCann et al., 1998). The finding that negative cohesion was stabilizing was not easily replicated in our simulations, where positive and negative correlations were interspersed with random magnitude throughout the data set. Thus, the arrangement of correlations between taxa in the data set appears to be an important feature of real communities that may contribute to their stability (Worm and Duffy, 2003).

Guidelines for using our metrics

Although we used long-term time series data sets for the analyses presented here, our cohesion metrics can be used to predict community dynamics in a variety of data sets. For example, cohesion could be used with a spatially explicit data set, where samples were collected from different locations across a landscape. In the context of phytoplankton samples, this could be a data set consisting of samples from different locations in a lake or watershed. Then, the cohesion metrics could be used to predict community composition change at one location over time, or to predict differences in community composition between locations. It would also be interesting to investigate how cohesion is affected by experimental perturbations. Finally, cohesion could be used as a predictor for many response variables. Additional applications of the cohesion metrics could include identifying communities susceptible to major compositional change (for example, cyanobacterial blooms, infection in the human microbiome), relating community cohesion to spatial structure (for example, how taxon connectedness relates to the dispersal abilities of different microbial taxa), and investigating how disturbance influences cohesion (for example, how illness influences the cohesion of communities in a host-associated microbiome, how oil spills affect cohesion of marine microbial communities). The consistent results between the phytoplankton data sets and the bacterial 16S rRNA gene data set indicates that our cohesion metrics are robust for DNA-sequencing data sets.

The critical step in the cohesion workflow is calculating reliable correlations between taxa. Thus, some data sets will be more suitable for our cohesion metric than others. For example, a data set consisting of 20 samples from five lakes over multiple years might be a poor candidate for the cohesion metrics. In this case, correlations between taxa might be driven mainly by environmental differences or location, and the sample number would be too low to calculate robust correlations. Based on the phytoplankton data sets analyzed here, we suggest a lower limit of 40–50 samples when calculating cohesion metrics, with more samples necessary for more heterogeneous data sets. We also suggest including environmental variables as covariates when analyzing heterogeneous data sets. Finally, the persistence cutoff for including taxa should be adjusted based on the data set being analyzed. For example, in data sets obtained by DNA sequencing, the sequencing depth affects taxon persistence (Smith and Peay, 2014). Thus, for DNA-sequencing data sets, we also recommend implementing a cutoff by mean abundance, where very rare taxa are omitted from the cohesion metrics.

Conclusion

Our cohesion metrics provide a method to incorporate information about microbial community complexity into predictive models. These metrics are easy to calculate, needing only a relative abundance table. Furthermore, across all data sets analyzed in this study, negative cohesion was strongly related to compositional turnover. In systems where cohesion is a significant predictor of community properties (for example, nutrient flux, rates of photosynthesis), this result could guide further investigation into the effects of microbial interactions in mediating community function. In this case, researchers might focus their efforts on understanding the role of highly connected taxa, which are identified in our workflow. We aim to eventually determine the features that distinguish systems in which cohesion is important versus systems in which cohesion does not predict community properties.

Acknowledgments

We thank the North Temperate Lakes LTER program for the use of their publicly available data on Lake Mendota and Lake Monona. We also thank the Cascade research group for the use of their data from Peter, Paul and Tuesday lakes, which is hosted on the LTER website. This manuscript has been much improved as a result of comments from the McMahon lab. Mark McPeek provided helpful comments on this work. This work was funded by a United States National Science Foundation (NSF) GRFP award to CMH (DGE- 1256259). KDM acknowledges funding from the NSF Long-Term Ecological Research program (NTL-LTER DEB-1440297) and an INSPIRE award (DEB-1344254).

Footnotes

Supplementary Information accompanies this paper on The ISME Journal website (http://www.nature.com/ismej)

The authors declare no conflict of interest.

Supplementary Material

Supplementary Dataset 1
Click here for additional data file. (3.2MB, csv)
Supplementary Dataset 2
Click here for additional data file. (25.7KB, csv)
Supplementary Dataset 3
Click here for additional data file. (279.6KB, csv)
Supplementary Information 1
Click here for additional data file. (158.4KB, docx)
Supplementary Information 2
Click here for additional data file. (108.6KB, docx)
Supplementary Information 3
Click here for additional data file. (121.8KB, docx)
Supplementary Information 4
Click here for additional data file. (164.2KB, docx)
Supplementary Information 5
Click here for additional data file. (8.4KB, txt)
Supplementary Information 6
Click here for additional data file. (10.3KB, txt)

References

  1. Banerjee S, Kirkby CA, Schmutter D, Bissett A, Kirkegaard JA, Richardson AE. (2016). Network analysis reveals functional redundancy and keystone taxa amongst bacterial and fungal communities during organic matter decomposition in an arable soil. Soil Biol Biochem 97: 188–198. [Google Scholar]
  2. Beaulieu M, Pick F, Gregory-Eaves I. (2013). Nutrients and water temperature are significant predictors of cyanobacterial biomass in a 1147 lakes data set. Limnol Oceanogr 58: 1736–1746. [Google Scholar]
  3. Blaser MJ, Cardon ZG, Cho MK, Dangl JL, Donohue TJ, Green JL et al. (2016). Toward a predictive understanding of Earth’s microbiomes to address 21st century challenges. Mbio 7: e00714–e00716. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Brock TD. (2012) A Eutrophic Lake: Lake Mendota, Wisconsin. Springer Science & Business Media: New York, NY, USA. [Google Scholar]
  5. Brose U. (2008). Complex food webs prevent competitive exclusion among producer species. Proc R Soc Lond B Biol Sci 275: 2507–2514. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Brown JH, Gillooly JF, Allen AP, Savage VM, West GB. (2004). Toward a metabolic theory of ecology. Ecology 85: 1771–1789. [Google Scholar]
  7. Caporaso JG, Lauber CL, Walters WA, Berg-Lyons D, Lozupone CA, Turnbaugh PJ et al. (2011). Global patterns of 16S rRNA diversity at a depth of millions of sequences per sample. Proc Natl Acad Sci USA 108: 4516–4522. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Carpenter SR, Kitchell JF. (1996) The Trophic Cascade in Lakes. Cambridge University Press: New York, NY, USA. [Google Scholar]
  9. Chow C-ET, Sachdeva R, Cram JA, Steele JA, Needham DM, Patel A et al. (2013). Temporal variability and coherence of euphotic zone bacterial communities over a decade in the Southern California Bight. ISME J 7: 2259–2273. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Cohen JE, Newman CM. (1985). When will a large complex system be stable? J Theor Biol 113: 153–156. [Google Scholar]
  11. Cottingham KL, Carpenter SR, Amand ALS. (1998). Responses of epilimnetic phytoplankton to experimental nutrient enrichment in three small seepage lakes. J Plankton Res 20: 1889–1914. [Google Scholar]
  12. Coyte KZ, Schluter J, Foster KR. (2015). The ecology of the microbiome: networks, competition, and stability. Science 350: 663–666. [DOI] [PubMed] [Google Scholar]
  13. Cram JA, Chow C-ET, Sachdeva R, Needham DM, Parada AE, Steele JA et al. (2015). Seasonal and interannual variability of the marine bacterioplankton community throughout the water column over ten years. ISME J 9: 563–580. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Hambright KD, Beyer JE, Easton JD, Zamor RM, Easton AC, Hallidayschult TC. (2015). The niche of an invasive marine microbe in a subtropical freshwater impoundment. ISME J 9: 256–264. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Doak DF, Bigger D, Harding EK, Marvier MA, O’Malley RE, Thomson D. (1998). The statistical inevitability of stability‐diversity relationships in community ecology. Am Nat 151: 264–276. [DOI] [PubMed] [Google Scholar]
  16. Elser JJ, Carpenter SR. (1988). Predation-driven dynamics of zooplankton and phytoplankton communities in a whole-lake experiment. Oecologia 76: 148–154. [DOI] [PubMed] [Google Scholar]
  17. Faust K, Raes J. (2012). Microbial interactions: from networks to models. Nat Rev Micro 10: 538–550. [DOI] [PubMed] [Google Scholar]
  18. Fierer N, Jackson RB. (2006). The diversity and biogeography of soil bacterial communities. Proc Natl Acad Sci USA 103: 626–631. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Fisher CK, Mehta P. (2014). Identifying keystone species in the human gut microbiome from metagenomic timeseries using sparse linear regression. PLoS One 9: e102451. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Freedman Z, Zak DR. (2015). Soil bacterial communities are shaped by temporal and environmental filtering: evidence from a long-term chronosequence. Environ Microbiol 17: 3208–3218. [DOI] [PubMed] [Google Scholar]
  21. Friedman J, Alm EJ. (2012). Inferring correlation networks from genomic survey data. PLoS Comput Biol 8: 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Gilbert JA, Jansson JK, Knight R. (2014). The Earth Microbiome project: successes and aspirations. BMC Biol 12: 69. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Hall MW, Rohwer RR, Perrie J, McMahon KD, Beiko RG. (in review). Ananke: temporal clustering reveals ecological dynamics of microbial communities. Preprint available at https://peerj.com/preprints/2879/. [DOI] [PMC free article] [PubMed]
  24. Hug LA, Baker BJ, Anantharaman K, Brown CT, Probst AJ, Castelle CJ et al. (2016). A new view of the tree of life. Nat Microbiol 1: 16048. [DOI] [PubMed] [Google Scholar]
  25. Jackson MM, Turner MG, Pearson SM, Ives AR. (2012). Seeing the forest and the trees: multilevel models reveal both species and community patterns. Ecosphere 3: 1–16. [Google Scholar]
  26. Kantor RS, Wrighton KC, Handley KM, Sharon I, Hug LA, Castelle CJ et al. (2013). Small genomes and sparse metabolisms of sediment-associated bacteria from four candidate phyla. Mbio 4: e00708–e00713. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Kara EL, Hanson PC, Hu YH, Winslow L, McMahon KD. (2013). A decade of seasonal dynamics and co-occurrences within freshwater bacterioplankton communities from eutrophic Lake Mendota, WI, USA. ISME J 7: 680–684. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Litchman E, Klausmeier CA. (2008). Trait-based community ecology of phytoplankton. Annu Rev Ecol Evol Syst 39: 615–639. [Google Scholar]
  29. Lovell D, Pawlowsky-Glahn V, Egozcue JJ, Marguerat S, Bähler J. (2015). Proportionality: a valid alternative to correlation for relative data. PLOS Comput Biol 11: e1004075. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. MacArthur R. (1955). Fluctuations of animal populations and a measure of community stability. Ecology 36: 533–536. [Google Scholar]
  31. May RM. (1972). Will a large complex system be stable? Nature 238: 413–414. [DOI] [PubMed] [Google Scholar]
  32. May RM. (1974) Stability and Complexity in Model Ecosystems. Princeton University Press: Princeton, NJ, USA. [Google Scholar]
  33. McCann K, Hastings A, Huxel GR. (1998). Weak trophic interactions and the balance of nature. Nature 395: 794–798. [Google Scholar]
  34. McQueen DJ, Lean DRS. (1987). Influence of water temperature and nitrogen to phosphorus ratios on the dominance of blue-green algae in Lake St. George, Ontario. Can J Fish Aquat Sci 44: 598–604. [Google Scholar]
  35. Nekola JC, White PS. (1999). The distance decay of similarity in biogeography and ecology. J Biogeogr 26: 867–878. [Google Scholar]
  36. Neter J, Kutner MH, Nachtsheim CJ, Wasserman W. (1996) Applied lInear Statistical Models vol. 4. Irwin: Chicago, IL, USA. [Google Scholar]
  37. Neutel A-M, Heesterbeek JAP, van de Koppel J, Hoenderboom G, Vos A, Kaldeway C et al. (2007). Reconciling complexity with stability in naturally assembling food webs. Nature 449: 599–602. [DOI] [PubMed] [Google Scholar]
  38. Newton RJ, Jones SE, Eiler A, McMahon KD, Bertilsson S. (2011). A guide to the natural history of freshwater Lake Bacteria. Microbiol Mol Biol Rev 75: 14–49. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Nilsson KA, McCann KS. (2016). Interaction strength revisited—clarifying the role of energy flux for food web stability. Theor Ecol 9: 59–71. [Google Scholar]
  40. Patterson DJ. (2009). Seeing the big picture on microbe distribution. Science 325: 1506–1507. [DOI] [PubMed] [Google Scholar]
  41. Peduzzi P, Concato J, Feinstein AR, Holford TR. (1995). Importance of events per independent variable in proportional hazards regression analysis II. Accuracy and precision of regression estimates. J Clin Epidemiol 48: 1503–1510. [DOI] [PubMed] [Google Scholar]
  42. Shade A, Gregory Caporaso J, Handelsman J, Knight R, Fierer N. (2013). A meta-analysis of changes in bacterial and archaeal communities with time. ISME J 7: 1493–1506. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Smith DP, Peay KG. (2014). Sequence depth, not PCR replication, improves ecological inference from next generation DNA sequencing. PLoS ONE 9: e90234. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Taylor LR. (1961). Aggregation, variance and the mean. Nature 189: 732–735. [Google Scholar]
  45. Thomas MK, Kremer CT, Klausmeier CA, Litchman E. (2012). A global pattern of thermal adaptation in marine phytoplankton. Science 338: 1085–1088. [DOI] [PubMed] [Google Scholar]
  46. Tripathi BM, Kim M, Singh D, Lee-Cruz L, Lai-Hoe A, Ainuddin AN et al. (2012). Tropical soil bacterial communities in Malaysia: pH dominates in the Equatorial Tropics too. Microb Ecol 64: 474–484. [DOI] [PubMed] [Google Scholar]
  47. Trosvik P, de Muinck EJ. (2015). Ecology of bacteria in the human gastrointestinal tract—identification of keystone and foundation taxa. Microbiome 3: 44. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Ulrich W, Gotelli NJ. (2010). Null model analysis of species associations using abundance data. Ecology 91: 3384–3397. [DOI] [PubMed] [Google Scholar]
  49. Walter J, Ley R. (2011). The human gut microbiome: ecology and recent evolutionary changes. Annu Rev Microbiol 65: 411–429. [DOI] [PubMed] [Google Scholar]
  50. Weiss S, Van Treuren W, Lozupone C, Faust K, Friedman J, Deng Y et al. (2016). Correlation detection strategies in microbial data sets vary widely in sensitivity and precision. ISME J 10: 1669–1681. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Wootton KL, Stouffer DB. (2016). Many weak interactions and few strong; food-web feasibility depends on the combination of the strength of species’ interactions and their correct arrangement. Theor Ecol 9: 185–195. [Google Scholar]
  52. Worm B, Duffy JE. (2003). Biodiversity, productivity and stability in real food webs. Trends Ecol Evol 18: 628–632. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Dataset 1
Click here for additional data file. (3.2MB, csv)
Supplementary Dataset 2
Click here for additional data file. (25.7KB, csv)
Supplementary Dataset 3
Click here for additional data file. (279.6KB, csv)
Supplementary Information 1
Click here for additional data file. (158.4KB, docx)
Supplementary Information 2
Click here for additional data file. (108.6KB, docx)
Supplementary Information 3
Click here for additional data file. (121.8KB, docx)
Supplementary Information 4
Click here for additional data file. (164.2KB, docx)
Supplementary Information 5
Click here for additional data file. (8.4KB, txt)
Supplementary Information 6
Click here for additional data file. (10.3KB, txt)

Articles from The ISME Journal are provided here courtesy of Oxford University Press

RESOURCES