Tumor Control Probability Modeling for Stereotactic Body Radiation Therapy of Early-Stage Lung Cancer Using Multiple Bio-physical Models

Abstract

Purpose

To analyze pooled clinical data using different radiobiological models and to understand the relationship between biologically effective dose (BED) and tumor control probability (TCP) for stereotactic body radiotherapy (SBRT) of early-stage non-small cell lung cancer (NSCLC).

Method and Materials

The clinical data of 1-, 2-, 3-, and 5-year actuarial or Kaplan-Meier TCP from 46 selected studies were collected for SBRT of NSCLC in the literature. The TCP data were separated for Stage T1 and T2 tumors if possible, otherwise collected for combined stages. BED was calculated at isocenters using six radiobiological models. For each model, the independent model parameters were determined from a fit to the TCP data using the least chi-square (χ²) method with either one set of parameters regardless of tumor stages or two sets for T1 and T2 tumors separately.

Results

The fits to the clinic data yield consistent results of large α/β ratios of about 20 Gy for all models investigated. The regrowth model that accounts for the tumor repopulation and heterogeneity leads to a better fit to the data, compared to other 5 models where the fits were indistinguishable between the models. The models based on the fitting parameters predict that the T2 tumors require about additional 1 Gy physical dose at isocenters per fraction (≤5 fractions) to achieve the optimal TCP when compared to the T1 tumors.

Conclusion

This systematic analysis of a large set of published clinical data using different radiobiological models shows that local TCP for SBRT of early-stage NSCLC has strong dependence on BED with large α/β ratios of about 20 Gy. The six models predict that a BED (calculated with α/β of 20) of 90 Gy is sufficient to achieve TCP ≥ 95%. Among the models considered, the regrowth model leads to a better fit to the clinical data.

INTRODUCTION

Surgery has been the preferred modality for operable early stage non-small cell lung cancer (NSCLC) patients with a 5-year overall survival rates of 50–80% (1, 2). For medically inoperable early stage NSCLC, conventional fractionated radiotherapy resulted in disappointing long-term local control and overall survival rates of 30–70% and 15–30%, respectively (3). Stereotactic body radiotherapy (SBRT) appears to provide outcomes that are comparable with surgery (4). With improvement in technology including image guidance and respiratory motion management, SBRT is increasingly becoming a standard of care for inoperable early stage lung cancer, and possibly an option for medically resectable patients as well. Hypo-fractionated RT of 3–5 Gy per fraction may also be a reasonable option for some patients inappropriate for SBRT (5).

A wide variety of doses and dose fractionation schemes have been used for SBRT. A method to compare different schemes is to use radiobiologic/physical modeling, as the fraction size and overall treatment time have an impact on treatment outcomes and a simple comparison based on physical dose is not adequate. A variety of models have been suggested to express the biological effects of different radiation fractionation schemes. These models typically consider the dose per fraction, number of fractions, total dose, and overall elapsed treatment time. A commonly used overall figure of merit to express cell killing is the biologically effective dose (BED). The linear quadratic (LQ) model has been the most widely applied within the context of conventional doses per fraction. However, the continuously bending survival curve predicted by this model raises concerns of potential overestimation of tumor cell killing at the larger doses per fraction often employed with SBRT. Guerrero and Li (6) proposed a modification of the LQ model that could better handle higher dose ranges with a survival curve that features linear quadratic and linear (LQL) relation between the logarithm of the cell survival and dose in low and high fraction dose ranges, respectively. Park et al. (7) proposed the universal survival curve (USC) model by combining the LQ model in the low dose range and the single hit multi-target model (SHMT) of linear behavior in the high dose range with a smooth transition from the LQ to SHMT model for SBRT. Tai et al. (8) proposed a LQ-inspired regrowth model (hereafter regrowth model) by introducing inter-tumor heterogeneity and tumor regrowth after radiation treatment to describe the survival rate dependence of follow up time. McKenna and Ahmad proposed a modification of the LQ model (mLQ) for SBRT (9). Guckenberger et al. applied a modified linear quadratic and linear (mLQL) model (10,11) to a multi-institution dataset. However, the utility and suitability of these bio-physical models for SBRT are still under debate (12, 13). In addition, dose and fractionation schemes for SBRT remain to be optimized.

This work is to model radiation dose responses in SBRT for early stage NSCLC by analyzing the available published clinical local-control data using various bio-physical models proposed for SBRT or hypofractionation schemes. The model parameters are determined by fitting the clinical data. The results from this modeling study may be informative in guiding clinicians to optimize dose and/or dose fractionation for SBRT of early stage lung cancers.

METHODS

A. Clinical data

A total of 160 reported studies, identified by a thorough literature search of medical journals through May 2014 on SBRT and hypofractionation RT for NSCLC, were reviewed. Among these reports, 46 were identified (14–59) to contain the necessary information based on the selection criteria including tumor control probability (TCP) of primary tumors, detailed radiation dose specification, and the number of patients greater than 10. From each of the reports identified, the 1-, 2-, 3-, and 5-year actuarial or Kaplan-Meier TCP data, obtained directly from the paper or indirectly by extracting from the graphs in the paper, were collected for stages T1 and T2 NSCLC. The data from patients with metastatic disease to the lung were excluded. Among all the patients analyzed, 90% were staged as T1/2N0M0 and 10% were unspecified. Tumor controls were evaluated based on follow-up diagnostic quality CT with very limited aid of positron emission tomography (PET). The TCP data consists of 77% of patient population following the guidelines by Response Evaluation Criteria in Solid Tumors (RECIST) (60), 11% similar to, but slight different from RECIST or the World Health Organization (WHO) (61), 10% unspecified, and 2% neither RECIST nor WHO. It is well known that the pencil beam dose calculation algorithm used in some identified reports is inaccurate at the lung-tissue interface, resulting in erroneous periphery doses (62). In this analysis, all prescribed radiation doses were converted to the isocenter doses based on the specified isodose lines (either from the papers or via private communications with authors) or 80% if unspecified in the paper (6% of the studies analyzed did not specify the prescribed isodose lines). The isocenter doses were preferred in other studies (10, 63). The hypo-fractionated data of at least 3 Gy per fraction were also included to increase the data points at low doses. The dose rates of 1/5 to 1/2 Gy per minute with the same or similar delivery techniques from available data are used to calculate the beam-on time if unavailable for the LQL model (see details below). For studies not reporting TCP data specifically for tumor stage, dose or fractionation, the patient population averaged or median values of prescribed doses, fractionations, or treatment times were used. For studies not reporting the percentage of patient/tumor in a particular stage (T1 or T2), the T1 portion of 50% was assumed if unavailable, since the average of T1 portion was 52% in all selected studies that reported tumor stage details. The selected 46 studies contain 3479 early stage NSCLC patients with prescription doses ranging from 15 to 70 Gy in 1 to 20 fractions, out of which, 211 patients received hypo-fractionated RT with doses from 50 to 60 Gy at 3–4 Gy per fraction, and 3268 patients received RT of at least 6 Gy per fraction.

B. Radiobiological models

The following six models expressed in BED formula were used in this analysis.

1. LQ model:

   $${\mathit{BED}}^{LQ}=D(1+\frac{d}{\alpha /\beta }),$$ (1)

   where α and β characterize intrinsic radiosensitivity of cells, D and d are the total and fractional doses, respectively.

2. The LQL model (6): relating the BED and constant dose-rate exposure with the dose protraction factor G for dose-rate effects as

   $${\mathit{BED}}^{\mathit{LQL}}=D\left[1+G(\lambda T+\mathit{\Delta }d)\frac{d}{\alpha /\beta }\right],$$ (2)

   where G(x) = 2(x + e^−x −1)/x², λ=ln2/T_r is the repair rate (T_r repair half-time) and T the treatment delivery time, Δ is calculated by adjusting the low-dose and the high-dose regions of the model to reproduce lethal–potentially lethal behavior for infinite dose rates.

3. The USC model (7):

   $${\mathit{BED}}^{\mathit{USC}}=\{\begin{array}{ll}D\left(1+\frac{d}{\alpha /\beta }\right),\hfill & d<d_T\hfill \\ \frac{1}{\alpha D_0}(D-n{D}_q),\hfill & d\ge d_T\hfill \end{array}$$ (3)

   where −1/D₀ and D_q are the slope and x-intercept of the logarithm survival curve, n the number of fraction. The smooth transition at dose d_T from the LQ to SHMT yields $\beta =\frac{{(1-\alpha D_0)}^2}{4D_0{D}_q}$ and $d_T=\frac{2D_q}{1-\alpha D_0}$.

4. The mLQ model (9):

   $${\mathit{BED}}^{\mathit{mLQ}}=D\left(1+\frac{d}{\frac{\alpha }{\beta }(1+\frac{\beta }{\gamma }d)}\right),$$ (4)

   where γ is a model parameter to take high fractionation dose effects into account. The model reduces to the LQ model at low fractional doses.

5. The mLQL model (10, 11):

   $${\mathit{BED}}^{\mathit{mLQL}}=\{\begin{array}{ll}D\left(1+\frac{d}{\alpha /\beta }\right),\hfill & d<d_T\hfill \\ n{d}_T\left(1+\frac{d_T}{\alpha /\beta }\right)+n\left(1+2\frac{d_T}{\alpha /\beta }\right)(d-d_T),\hfill & d\ge d_T\hfill \end{array}$$ (5)

   where d_T is the transition dose between the LQ model at low doses and linear behavior at high doses.

   For the above five models, the TCP has the form

   $$\mathit{TCP}=e^{-K_0\ast e^{-\alpha \ast \mathit{BED}}},$$ (6)

   where K₀ is the number of tumor cells at the beginning of radiotherapy.

6. The regrowth model (8):

   $${\mathit{BED}}^{\mathit{Regrowth}}=D\left(1+\frac{d}{\alpha /\beta }\right)-\frac{ln2}{T_p}\frac{\mathit{\Gamma }}{\alpha }$$ (7)

For this model, TCP has the form:

$$\mathit{TCP}=1-\frac{1}{\sqrt{2\pi }}{\int }_{-\infty }^t{e}^{-\frac{x^2}{2}}dx,$$ (8)

with

$$t=\frac{e^{-{\left[\alpha \ast \mathit{BED}-{\left(\frac{ln2}{T_p}\tau \right)}^{\delta }\right]}_{-K_{cr}/K_0}}}{{\sigma }_k/K_0},$$ (9)

Γ is elapsed treatment time; T_p potential effective tumor doubling time; τ the follow-up time after treatment; δ a parameter characterizing the speed of tumor cell regrowth after radiation treatment, T_p is the conventional doubling time when δ→1; K_cr the critical tumor number that defines the control of an individual tumor; σ_k the Gaussian width for the distribution of tumor cell numbers. The six independent model parameters are: α, α/β, $\frac{K_{cr}}{K_0},\frac{{\sigma }_k}{K_0}$, T_p, and δ.

The key formula and model parameters of these 6 models are summarized in a table in the supplementary material.

C. Model fitting to the clinical data

To model the regrowth of the residual tumor cells after treatment, the term ${\left(\frac{ln2}{T_p}\tau \right)}^{\delta }$ in Eq. (9) is used. The regrowth model takes the follow-up time into account, and it was used to fit the TCP data as a function of serial follow-up times. Other models were used to fit the data only at a given follow up time. For each of the models considered, the independent model parameters were determined from a simultaneous fit to the TCP data using the least chi-square (χ²) fitting method. The parameter sets were obtained for tumor stage T1 and T2 separately or combined for the regrowth model. For all other models, one set of the model parameters was obtained with stages T1 and T2 tumor combined due to limited statistics on the TCP at the individual follow-up time. The TCP predicted by the models (Eqs. 6 or 8) is TCP^model = f_T1 * TCP_T1^model + f_T2 * TCP_T2^model, where f_T1 and f_T2are the T1 and T2 portions and f_T1 + f_T2 =1. The χ² has the form:

$${\chi }^2-\sum _{i=1}^n\frac{{[{{\mathit{TCP}}_i}^{\mathit{data}}(D_i,d_i,{\tau }_i)-{{\mathit{TCP}}_i}^{\mathit{model}}(D_i,d_i,{\tau }_i)]}^2}{{\sigma }_i^2}$$

with the TCP uncertainty ${\sigma }_i={{\mathit{TCP}}_i}^{\mathit{data}}\sqrt{\frac{1-{{\mathit{TCP}}_i}^{\mathit{data}}}{N_i\ast {{\mathit{TCP}}_i}^{\mathit{data}}}}$. N_i is the number of patients for the i^th data point. The uncertainty for TCP→1 is calculated using the maximum TCP value other than 1 in the clinic data. The fit is weighted by $1/{\sigma }_i^2$ of each data point, so that high-quality data points were considered preferably. Given large statistics of the TCP data, χ² is expected to be Gaussian-distributed. The goodness of the fitting was justified by χ²/ndf, here ndf is the number of degree of freedom (ndf) defined as the total number of data points minus the number of free parameters in the fit. During the fitting process, BED, model predicted TCP, and χ² are recalculated if model parameters change until the least χ² is found. The fitting procedures have been described in details elsewhere using the regrowth model (64) and had been validated in Ref. (8). The regrowth model takes into account the correlations of TCP at different follow-up time automatically as shown in Eq. 8 and it can be used to fit the 1, 2, 3, and 5 year TCP data simultaneously, while all other models are used to fit the TCP data at different follow-up time separately since those correlations are not taken into account.

RESULTS

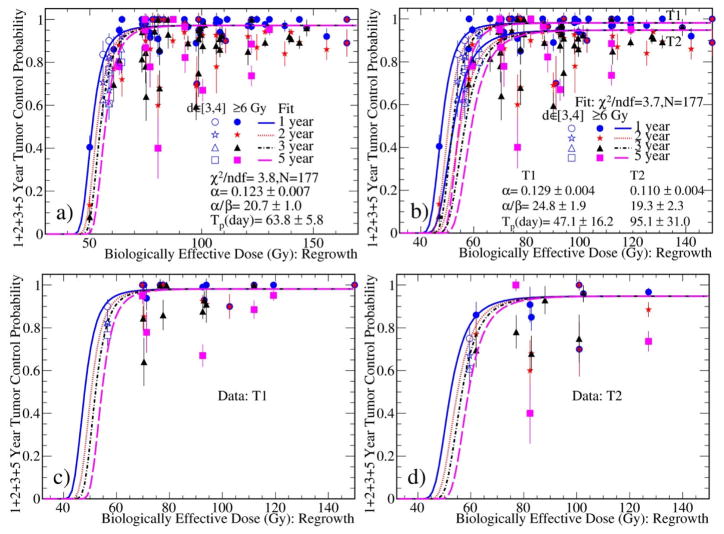
Figure 1a presents the fit to all TCP data with one set of parameters regardless of the tumor stages using the regrowth model. The data points are presented with error bars of one standard deviation. Unless otherwise specified, BED is calculated with the corresponding α/β ratio. Fig. 1b shows the fit to all TCP data with two different sets of parameters for the T1 and T2 tumors separately. It is seen that TCP reached an asymptotic plateau at a BED of about 90 Gy and 110 Gy for T1 and T2 tumors, respectively. Figures 1c and 1d depict the fit curves superimposed over the T1 and T2 sub-datasets. The model parameters determined from the fits with the regrowth model are summarized in Table 1 along with other data.

Fig. 1.

Simultaneous fits to the 1, 2, 3, and 5 year TCP data with a) one set of parameters regardless of the tumor stages, and b) two sets for the stage T1 and T2 tumors, respectively. The data points are shown with error bars of one standard deviation. The BED was calculated using the α/β obtained during the fitting. In Fig. 1b, the BED is calculated using the parameters for the T1 tumors. The fit curves from Fig. 1b are overlaid with the c) T1 and d) T2 sub-datasets.

Table 1.

Model parameters determined from simultaneous fits to 1-, 2-, 3-, and 5-year TCP data with one set of parameters regardless of tumor stages and two sets for Stage T1 and T2 tumors separately using the regrowth model and from the fits to the 1-, 2-, and 3-year TCP using the remaining five models.

Fit			regrowth	Fit	LQ	USC	mLQ	LQL	mLQL
Fits to the data with the same model parameters for the T1 and T2 tumors		χ2/ndf	3.8	1 year	1.5	1.6	1.6	1.6	1.6
		α (Gy−1)	0.123±0.007		0.215±0.022	0.215±0.006	0.215±0.017	0.215±0.017	0.215±0.002
		α/β (Gy)	20.7±1.0		17.9±0.9	D0=1.1±0.1 Gy	β =0.0120±0.003 Gy−2	17.9±1.1	17.9±0.6
		Tp(days)/Dx/γ	Tp=63.8±5.8 days, δ=0.253±0.025, Kcr/K0=0.008±0.003, σK/K0=0.004±0.002		-	Dq=11.3±0.5 Gy	γ=873±2932 Gy−1	Δ≈0, Tr=40.5±16.9 days	dT=90.2±9.1 Gy
Fits to the data with T1 two sets parameters for the T1 and T2 tumors separately		χ2/ndf	3.7	2 year	4.8	4.9	4.9	5.0	4.9
	T1	α (Gy−1)	0.129±0.004		0.185±0.013	0.185±0.022	0.185±0.010	0.184±0.012	0.185±0.001
		α/β (Gy)	24.8±1.9		26.0±2.5	D0=1.5±0.1 Gy	β=0.007±0.0007 Gy−2	24.4±1.6	26.0±0.7
		Tp(days)/Dx/γ	Tp=47.1±16.2 days, δ=0.267±0.041, Kcr/K0=0.010±0.002, σK/K0=0.005±0.001		-	Dq=12.2±2.5 Gy	γ=1623±3938 Gy−1	Δ≈0, Tr=0.3±0.3	dT=84.0±8.1 Gy
		χ2/ndf	-	3 year	7.1	7.2	7.2	7.4	7.2
	T2	α (Gy−1)	0.110±0.004		0.163±0.010	0.163±0.005	0.163±0.007	0.160±0.010	0.163±0.010
		α/β (Gy)	19.3±2.3		32.5±3.5	D0=1.7±0.1 Gy	β=0.0050±0.0005 Gy−2	29.1±4.1	32.5±3.7
		Tp(days)/Dx/γ	Tp=95.1±31.0 days, δ=0.278±0.035, Kcr/K0=0.012±0.001, σK/K0=0.007±0.001		-	Dq=16.1±1.2 Gy	γ=884±2781 Gy−1	Δ≈0, Tr=0.1±0.2 days	dT =57.3±16.8 Gy

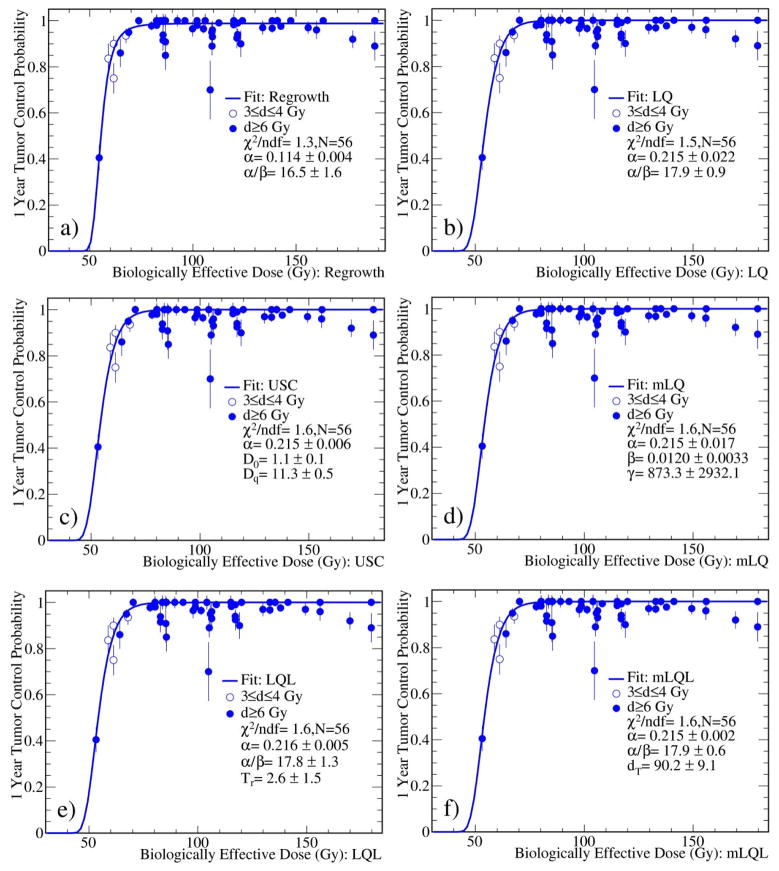
Figure 2 shows the fits to the 1 year TCP data with all six models. The fit with the regrowth model is presented for comparison. All model fits consistently yield large α/β ratios of about 20 Gy. The results are summarized in Table 1. The numbers of cells K₀ at the beginning of radiotherapy were found to vary from 10⁴ to 10⁶ for the models considered. It is clear that the fit with the regrowth model yields the lowest χ²/ndf value, indicating the best fit among the six models considered. All other models give indistinguishable fits to the clinical data and consistent radiobiological parameters. For LQL model, the fit results were insensitive to the delivery time since it is a higher order correction.

Fig. 2.

Fits to the 1 year TCP data with different models. The fit with the regrowth model is also shown for comparison.

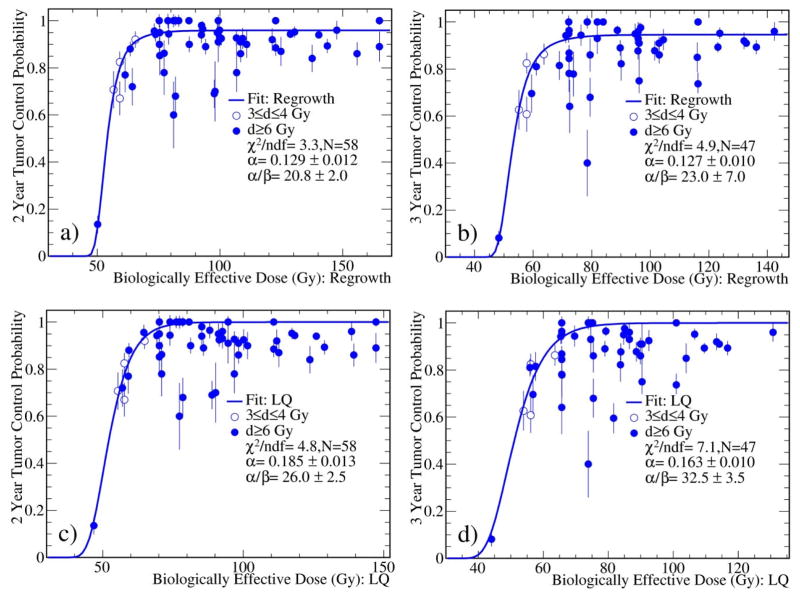
The 2 and 3 year TCP data were also fitted using the six models. The regrowth model again yields the best fits to the data as indicated by the smaller χ²/ndf values. As an example, the fits to the 2 and 3 year TCP data using the regrowth and LQ models were shown in Fig. 3. The fit results are summarized in Table 1. From the table, the α values tend to decrease and α/β ratios tend to increase as the follow-up time increases, reflecting the fact that the tumor control rate decreases as a function of the follow up time.

Fig. 3.

Fits to the 2 (left) and 3 (right) year TCP data with the regrowth and LQ models. The fits to other four models (not shown) are similar to the fits with the LQ model. The fits with the regrowth model are also shown for comparison. The BED was calculated using the α/β obtained during the fitting.

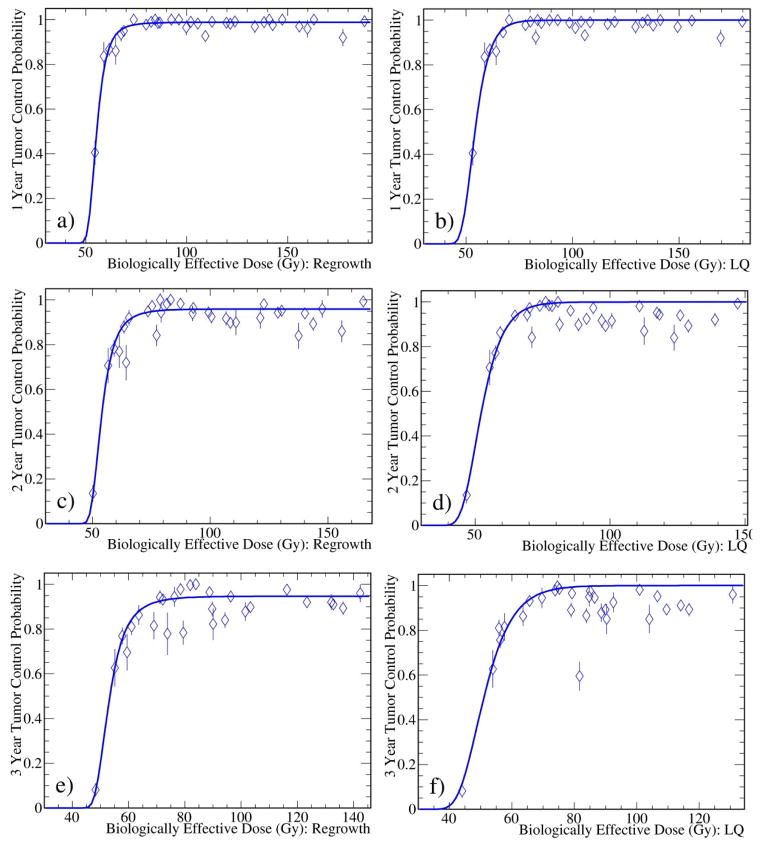
Due to limited statistics of some data points, there exist large fluctuations of the TCP data for a given BED. In Fig. 4, the weighted averages of 1, 2, and 3 year TCP data in BED bins are overlaid with the fit curves of the regrowth and LQ models shown in Figs. 2 and 3. The LQ model is indistinguishable with the remaining four models (not shown). It clearly shows that the regrowth model describes the data better.

Fig. 4.

Weighted averages of 1, 2, and 3 year TCP data in BED bins overlaid with the fit curves in Figs. 2 and 3 for the regrowth (left) and LQ (right) models. The remaining four models show similar patterns (not shown) as the LQ model.

DISCUSSION

We have fitted the selected clinic data using six models by assigning high weights to high-quality data points (studies with large patient numbers) and adjusting a number of fitting parameters including α/β ratio. The fit lead to steep TCP-BED relationships for SBRT of NSCLC, showing that TCP increases drastically with BEDs of 50–60 Gy and reaches an asymptotic plateau around a BED of 90 Gy (see Fig. 1a). This implies that a BED (calculated with the fitted value of α/β = 20) of larger than 90 Gy may lead to a TCP ≥ 95% for T1 tumors based on these 6 models investigated. The regrowth model yields a better fit compared to other models. This is not attributed to a few more model parameters, the reason is that it allows TCP<1 for high BED, permitting the model crosses the data points by their weights, but all other models always have asymptotic plateau of TCP=1 for large BED, while most (~80%) clinical TCP data are <1.

To achieve the optimal TCP, the T2 tumors require approximately additional 1 Gy dose per fraction (up to 5 fractions) compared to the T1 tumors based on the regrowth model. This finding is similar to that for oropharyngeal tumors where additional 3 Gy is required for each increase in T stage (65) for a given TCP.

The maximum likelihood method (ML) is another well-known fitting method. However, when ML was used to fit the TCP data, it run into a divergence problem when a model predicts a TCP=1.0 at high BED. In addition, the ML fitting method does not weight each clinical TCP data based on its statistical error. It was found that the ML fitting yielded a result similar to the χ² fitting with equal weighting to all TCP data for the growth model. To fit TCP data collected from studies of various number of patients, the least chi-square (χ²) fitting method was therefore chosen to determine the best model parameters.

Various attempts were made to ensure that the steep dose response obtained is not due to the modeling process used. For example, we tested the fitting with empirical formulism, TCP=1/[1+(BED₅₀/BED)^κ] and 1/[1+exp[−(BED−BED₅₀)/κ], where BED₅₀ is the BED required to achieve 50% TCP and κ a fitting parameter. Those tests yielded the consistent α/β ratio and the steep TCP-BED relationship as those obtained with the six models. To test whether the steep dose response is attributed mainly by several low BED data points (Fig. 1a), we re-fitted the data with those low BED data points removed and still found the consistent steep dose response (e.g., α=0.110±0.004 Gy⁻¹ and α/β=20.6±3.1 Gy). These fits are different from an analysis (66) where a monotonic relationship between TCP and BED with nearly no asymptotic plateau was reported with empirical α=0.33 Gy⁻¹ and α/β=8.6 Gy for early stage NSCLC. It might be attributed to the different radiobiological parameters used. We also varied the prescribed isodose from 75% to 85% if unspecified in the paper, we found consistent results since only 6% papers did not specify the prescribed isodoses.

The fits to the TCP data with the regrowth model give K_cr/K₀≈0 and σ_K/K₀≈0 due to large K₀ of 10⁴ to 10⁶, while K_cr/σ_K is of order of 2 as expected. The fits to the TCP data using the LQL model (6) yield Δ≈0 (Eq. 2), suggesting that the high fractional dose term Δ may be omitted in the LQL model with the large α/β ratio for SBRT of NSCLC. The fits to the data using the USC and mLQL models give high thresholds (d_T >30 Gy), implying that the LQ-based BED (see Eqs. 3 and 5) with large α/β ratios can lead to a reasonably fit to the data. The fits using the mLQ model result in large γ values (Eq. 4) indicate that the higher order correction term β/γ is negligible. Amongst all models considered, the regrowth model fits the data with the lowest χ²/ndf and can provide extra information on the potential tumor doubling time (47±16 and 95±31 days for the T1 and T2 tumors, respectively, and 64±6 days regardless of tumor stages), consistent with those in Ref. (67). The T1 tumors grow much faster than the T2 tumors. The regrowth model, accounting for the tumor repopulation, can also predict TCP dependence on the follow-up time as a function of BED and as well as the TCP difference on tumor stage as seen in the clinic data even at higher BED in the plateau region (the term ${(\frac{ln2}{T_d}\tau )}^{\delta }$ in Eq. 9), while all other models have an asymptotic value of 1 in the plateau region. All fits to the clinical data with different models yield consistently a large α/β ratio of about 20 Gy. The values of α and α/β for the T1 tumors are systematically larger than those for the T2 tumors, meaning that the T1 tumors are more sensitive to radiation. A slightly higher dose is needed to achieve the optimal TCP for T2 tumors when compared to T1 tumors as shown in Table 2. As shown in Table 2, the fits of different models to the TCP data at individual follow up time also yield consistent large α/β ratios.

Table 2.

Fractionation regimens of least doses at isocenters to reach asymptotic plateau for the regrowth model. The 1, 3, 4, and 5 fractions are assumed to be delivered in 1 day, 7 days, 10 days, and 14 days, respectively.

Regrowth	asymptotic plateau (optimal)
Isocenter Dose (Gy)	1 fx	3 fx	4 fx	5 fx
T1	36.4±1.0	53.0±1.0	57.6±0.9	61.3±0.7
T2	37.4±1.1	56.1±1.0	61.6±0.9	65.9±0.9

It has been debated whether the widely used LQ model in the conventional dose fractionation schemes be applicable to the SBRT regimens. It is well-known that the LQ model of continuous bending behavior overestimates the cell-killing in the high dose region. However, Fowler (68) pointed out that an α/β ratio greater than 10 Gy could make the LQ model work better in the high dose region. Maciejewski et al (65) reported a good biological evidence of α/β ratios greater than 20 Gy in rapidly proliferating and hypoxic oropharyngeal tumors from the best fits to their clinical data. It was found (69) that NSCLC repopulates approximately as fast as oropharyngeal tumors and therefore was likely to have α/β ratios higher than 10 Gy. The α/β values from our study are of about 20 Gy, agreed in general with the qualitative findings in Refs. 69 and 70 which were not able to provide quantitative α/β ratios for SBRT of NSCLC. The current results demonstrate that the LQ formulism with an α/β value of 20 Gy including tumor heterogeneity and tumor regrowth can describe the tumor dose response after SBRT. Our study shows that the alternative USC, mLQ, LQL, and mLQL models become indistinguishable with the LQ model for the SBRT regimens for NSCLC. Mehta et al (66) also found that the clinical data could not distinguish the LQ and USC models. Brown et al (72) showed in their Figure 1 that, in an idealized case, the LQ model with large α/β ratio can be comparable to the LQL and USC models.

Out of six models considered, the regrowth model specifically takes the population heterogeneity into account. Carlone et al. (73) showed that the population-based TCP model in case of dominant heterogeneity in radio-sensitivity has the form: ${\text{TCP}}_{\text{pop}}=\frac{1}{2}\text{erfc}\left(\frac{\mathrm{\xi }-\alpha \ast \text{BED}+{\text{lnK}}_{\mathrm{o}}}{\sqrt{2}{\sigma }_{\mathrm{h}}}\right)$, where erfc is the complementary error function $\text{erfc}(\mathrm{x})=\frac{1}{\sqrt{\pi }}{\int }_{\mathrm{x}}^{\infty }{\mathrm{e}}^{-{\mathrm{y}}^2}\text{dy}$, σ_h the combination of the standard deviations of radiobiological parameters, ξ the Euler’s gamma constant with ξ ≈ 0.577. The fits to the clinical data with the population-based TCP using the models other than the regrowth model yield smaller α when compared to those without heterogeneity. The standard deviations σ_h of different models vary from 0.4 to 1.0. The α/β ratios remain stable and consistent with those from the fits to the data without population heterogeneity as discussed in Ref. 73.

The potential role of hypoxia and reoxygenation were not explicitly incorporated in the models used in this study. It is possible that the extracted value of α/β may be different when hypoxia and reoxygenation are included (74). Therefore, the presently determined α/β value should be considered as an effective radiobiological parameter that is associated with the formulism of a model.

The major sources of inaccuracy in this analysis include the lack of sufficient information and the wide variations in patient selection, dose prescription and fractionations, treatment techniques, radiation dose actually delivered, and outcome assessment in the selected studies. The models used may not be capable of fully considering these data heterogeneities. Therefore the relation between TCP and BED from this meta-data-based analysis may not be the same as the relation between individual patient TCP and BED. Standardization in data report for clinical SBRT study is critically needed. In addition, normal tissue toxicity is not taken into account in this study, although low or mild normal tissue toxicity was reported. Due to the limited information on tumor size or volume from the selected studies, the tumor size-corrected model (75) was not considered in this study.

CONCLUSION

We performed a systematic study to analyze the pooled TCP data for SBRT of early stage NSCLC using six different radiobiological models. The fit to the pooled TCP data with these models yield steep relationships between TCP with BED with a large α/β value of about 20 Gy. The models predict that a BED of 90 Gy, as calculated with α/β of 20 Gy, is sufficient to achieve a TCP of greater than 95% for T1 tumors. The regrowth model leads a better fit than other five models, while the LQ model was the simplest. However, caution should be excised when using the data generated by the models, as insufficient information and/or incomplete models might be used.