Coarse-grained Directed Simulation

Abstract

Many free-energy sampling and quantum mechanics/molecular mechanics (QM/MM) computations on protein complexes have been performed where, by necessity, a single component is studied isolated in solution while its overall configuration is kept in the complex-like state by either rigid restraints or harmonic constraints. A drawback in these studies is that the system’s native fluctuations are lost, both due to the change of environment and the imposition of the extra potential. Yet, we know that having both accurate structure and fluctuations is likely crucial to achieving correct simulation estimates for the subsystem within its native larger protein complex context. In this work, we provide a new approach to this problem by drawing on ideas developed to incorporate experimental information into a molecular simulation by relative entropy minimization to a target system. We show that by using linear biases on coarse-grained (CG) observables (such as distances or angles between large subdomains within a protein), we can maintain the protein in a particular target conformation while also preserving the correct equilibrium fluctuations of the subsystem within its larger biomolecular complex. As an application, we demonstrate this algorithm by training a bias that causes an actin monomer (and trimer) in solution to sample the same average structure and fluctuations as if it were embedded within a much larger actin filament. Additionally, we have developed a number of algorithmic improvements that accelerate convergence of the on-the-fly relative entropy minimization algorithms for this type of application. Finally, we have contributed these methods to the PLUMED open source free energy sampling software library.

TOC image

Introduction

It is a fundamental challenge of molecular dynamics (MD) simulation that the accessible time and length scales are limited by the level of detail at which a system is described.¹ As a consequence, computational studies generally compromise on the size of the system under consideration in order to achieve a desired level of detail. A prime example arises in the study of enzymes where reactivity must be incorporated into the simulation, but it is thus far impractical to treat the entire system quantum mechanically. Hence, in order to do a quantum calculation on the active site while including the important role of the protein environment, hybrid methods have been developed to couple the protein’s fluctuations into the reactive subsystem. These ideas led to the commonly used practice of QM/MM simulation, and contributed to the 2013 Nobel Prize in Chemistry.²

The continued development of enhanced sampling techniques, as well as advances in computational power, have made it possible to compute complex free energy surfaces for quantum mechanical reactions or conformational transitions taking place in biomolecular systems (see, e.g., Refs. 3–4). However, many problems of current focus do not occur isolated in solution, but rather in a much larger macromolecular context. For example, we might be interested in a process occurring for a particular protein embedded in a membrane or one within a much larger many-protein complex. In these cases, free energy sampling methods, which aim to enhance sampling along “slow” degrees of freedom in a low dimensional set of collective variables (CVs), are constrained by our ability to sample the many other degrees of freedom in the system. In the past, such simulations have been made to be more computationally tractable by extracting the key subcomponent of the system and adding restraints or harmonic biases to keep this subsystem in approximately the same configuration as it would sample in its native (much larger) context. Unfortunately, doing so neglects both the effect of long range forces coming from the other molecules in the complex, and alters the fluctuations sampled by the subsystem, which in many cases are strongly coupled with dynamics in the larger system. In this work, we focus on the latter problem, namely, we wish to have a protein of interest isolated in solution sample configurations as if it were embedded within a larger multi-protein complex, thus greatly reducing the computational cost and hence enabling studies where extensive free energy sampling is possible. In many cases, the larger complex can also first be simulated for some limited amount of MD sampling time in order to obtain information about the conformational ensemble of the subsystem of interest (alternatively, one could imagine approximating this information from normal mode or elastic network model analysis performed on experimental structures⁵).

In an ideal world with perfect sampling, one could simulate the subsystem by first finding an exact potential of mean force, by integrating over all the other configurations of the larger system. In the canonical ensemble, for a subsystem with N particles having the coordinates q = (q₁, q₂, …, q_3N) and a supersystem with N+M particles with coordinates r = (q₁, q₂, …, q_3N, q_3N+1, …, q_3N+3M) and overall potential energy function U(r), this corresponds to first calculating:

$$F(X)=-k_{B}T\text{ln}\left(\frac{{\displaystyle \int dr\delta (q-X)e^{-\frac{U(r)}{k_{B}T}}}}{{\displaystyle \int dr{e}^{-\frac{U(r)}{k_{B}T}}}}\right)$$ (1)

This many-body potential of mean force (PMF), F(X), captures the effects of the exact coupling to the larger supersystem on the subsystem variables X = q, and could be used to measure the average of any desired observable function of the subsystem variables, 〈f〉, as if we had performed the computation on the supersystem:

$$\langle f\rangle =\frac{{\displaystyle \int drf(q)e^{-\frac{U(r)}{k_{B}T}}}}{{\displaystyle \int dr{e}^{-\frac{U(r)}{k_{B}T}}}}=\frac{{\displaystyle \int dXf(X)e^{-\frac{F(X)}{k_{B}T}}}}{{\displaystyle \int dX{e}^{-\frac{F(X)}{k_{B}T}}}}$$ (2)

However, we know in practice this cannot be done for anything but the simplest cases, both because the amount of sampling required would be enormous and because the amount of information required to express the many-body PMF F(X) is too large.

In this work, we suggest an alternative approach and show that some key information about the supersystem can be imparted to the subsystem in a different and computationally practical way. Here, we will modify the potential energy function that would normally be used for the subsystem alone, by “learning” a bias function on coarse-grained (CG) observables of interest, f_i, via a relative entropy based approach. The bias is such that when those observables are sampled by the biased subsystem they will match what would be observed by sampling from F(X).

The idea of adding a bias to incorporate additional information into a system’s Hamiltonian comes from work where experimental data is included into an MD simulation via either adding a set of linear biases to the system’s Hamiltonian or, alternatively, using many copies of the system biased to have an ensemble averaged target observable.^6–7 These techniques have been shown to minimally bias the system such that it samples the target values of the observables.⁶ Several techniques now exist to determine a bias to match experimental data on-the-fly,^8–9 starting with a method called Experiment Directed Simulation (EDS), where the linear restraints are learned through a stochastic gradient descent procedure.⁸ Later work¹⁰ demonstrated that this type of EDS bias always decreases (or at least, does not increase) the relative entropy with respect to an ideal target distribution that gives the same desired properties, and so this method can be used to systematically improve multiscale CG (MS-CG) models that may utilize an imperfect molecular force field. This method of adaptive linear biases is also beginning to demonstrate its utility in other applications, including providing a significant improvement of the static and dynamic properties of an ab initio MD (AIMD) water system which is based on a rather inaccurate level of electronic density functional theory, biasing the oxygen-oxygen radial distribution function.¹¹ A similar method was used to incorporate experimental data (and additionally, experimental errors) to improve the quality of force fields for RNA.⁹ The empirical evidence in all cases is that the biasing of one observable tends to improve (or at least not decrease) the quality of others which were not biased, as would be expected for this class of minimal bias techniques.

In this work, we test whether the methods developed in EDS can learn biasing parameters that constrain a subsystem to behave as if it is embedded in its native (much larger) supersystem environment, recapitulating some of the desired properties from Eqs. 1 and 2 above. We apply these ideas to the protein actin, because it is a challenging biopolymer target with complex structural transitions that have nevertheless been relatively well characterized in MD simulation and experiment by our group and others. In solution, actin exists as a globular domain (G-actin) with a bound ATP molecule (Figure 1A)^12–13 and adopts a twisted conformation characterized by a dihedral angle of its four sub-domains ~ − 20°.¹⁴ Monomers can assemble to form a non-covalent semi-flexible biopolymer (F-actin), within which each subunit is flattened, adopting a dihedral angle > −10°. This flattening is associated with an increase in rate of actin catalyzed hydrolysis of the bound ATP molecule by a factor of > 10⁴,^{3, 15} such that the hydrolysis rate is on the order of ~1 sec⁻¹. The release of the free inorganic phosphate is very slow, occurring on a time scale of ~5 min,¹⁶ and makes the actin filament softer and more prone to depolymerization.^17–20 The hydrolysis and phosphate release are crucial processes governing the lifetime and structural properties of actin filaments and cytoskeletal networks in cells, and the molecular mechanisms have been studied using simulations. While it is now relatively standard to simulate with MD a semi-periodic actin filament consisting of 13 subunits (~500,000 atoms when solvated with water), the extensive simulation time needed to study phosphate release by free energy methods and the QM/MM methods required to study the explicit hydrolysis reaction preclude simulating such a large system; instead, only a single actin monomer has been used while being restrained in the filamentous or globular form.^3–4

Figure 1.

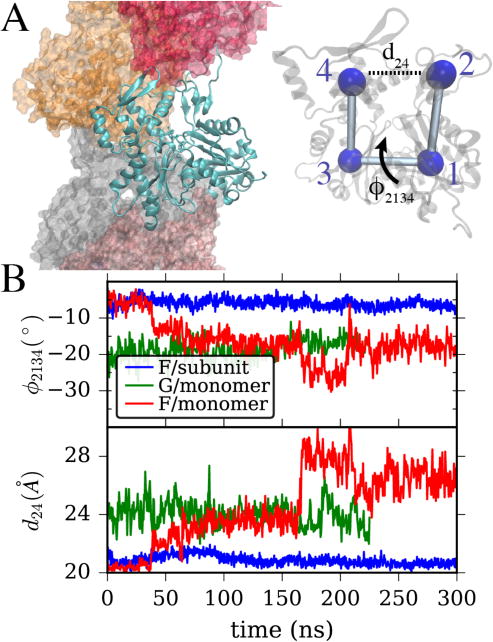
(A) Left, a snapshot from an actin filament simulation shows one actin subunit in ribbon style with a bound ATP molecule, surrounded by adjacent subunits. Right, a single actin subunit is overlaid with CG beads at the center of mass of its four major subdomains. Important CVs describing the transition from globular to filamentous conformation are the “cleft distance” from bead 2 to 4, and the “twist” dihedral angle formed by the four subdomains, a rotation around the central “bond” as shown. (B) The values of twist angle and cleft distance are shown for three systems. In blue is a single actin subunit within a filament, in green, a single G-actin in solution starting from its crystal structure, and in red, a single actin in solution starting from the filamentous structure.

Below, we will show that using the EDS approach on a set of CG observables (a combination we call Coarse-grained Directed Simulation, or CGDS) can be used to minimally bias an actin monomer to be in a filamentous-like configuration while maintaining correct fluctuations for the two collective variables that characterize the transition from globular to filamentous actin structure.^{13, 21–22}. However, given the large and complex system size compared to what has been studied previously, we found that the previous algorithms did not learn EDS biasing parameters fast enough to achieve these goals. Hence a major part of the present work is devoted to improving the algorithms for this type of problem so they can be practicable for similar future applications. These enhancements are first developed on a CG model of actin for speed of testing and development, then demonstrated on fully atomistic systems. All of these algorithms have been implemented and are available for use in the open source sampling library PLUMED2,²³ and the major components are already included in the main release of the PLUMED2 software as an optional module.

The remaining sections of this paper is organized as follows:

1. Methods: The construction both of atomistic systems and CG systems are described. The CGDS relative entropy minimization algorithm is written in a general framework that encompasses both prior work and our changes to the algorithms.

2. Results: A CG model is used to show how the prior methods can be optimized, and the performance of a first order guess for bias parameters. We then show how the optimization algorithm can be further improved for multiple CVs by transitioning to a simultaneous update of the bias parameters rather than a stochastic one, in this case. These improved algorithms are then demonstrated to work for a monomeric as well as trimeric actin system which would be appropriate for future free energy simulations.

3. Discussion and Conclusions: Future outlook and ramifications, as well as the challenges encountered are discussed.

Methods

Molecular dynamics simulations of actin filaments and monomers

G-actin with a bound ATP and a periodic 13 subunit F-actin structure with bound ATP were built and equilibrated at 310 K as described previously^{21–22, 24} (~94,000 atoms and ~485,000 atoms respectively), with the structure of ATP-bound actin derived from the crystal structure PDB ID 1NWK²⁵ and for F-actin from the electron microscopy structure in PDB ID 2ZWH.¹⁴ For the filament, the actin subunit had its nucleotide replaced by an ATP, bound magnesium, and waters within 5 angstroms of the nucleotide from a previously equilibrated monomer simulation. MD simulation of these structures was then performed using GROMACS²⁶ for ~5 ns to relax the configurations before the data shown below. A third and fourth system were then created by solvating a single actin monomer (~94,000 atoms) and a trimer of actin monomers (~138,000 atoms) from the equilibrated filament structure and relaxing those structures for ~5 ns.

Construction of an elastic network model for an actin monomer

An MD trajectory of the G-actin monomer bound to ATP was used to generate a CG elastic network model of an actin monomer as follows: after equilibrating the structure for 20 ns, the next 50 ns of simulation data were mapped onto a previously characterized 12-bead representation of an actin monomer, with beads 1–4 representing the four major subdomains of actin, seven others comprised by other important sub-regions, and a final bead for the nucleotide (Figure 2A);^21–22 a heterogeneous elastic network model (hENM) was then built from this trajectory using the method of Ref. 27. In brief, all pairs of beads closer than 100Å were connected by an effective spring whose rest length was given by the average separation in the MD trajectory and whose spring constants are all identical at first. An iterative procedure was then performed that updates the values of the spring constants by an amount proportional to the difference between the normal mode fluctuations along that bond in a given iteration and the fluctuations of that pair distance in the mapped MD simulation (summed over 3N_beads normal modes). MD simulations of this CG model then reproduce approximately the structural ensemble observed in the original all-atom trajectory.²⁷ This hENM model was then used to quickly test improvements in the methods described next.

Figure 2.

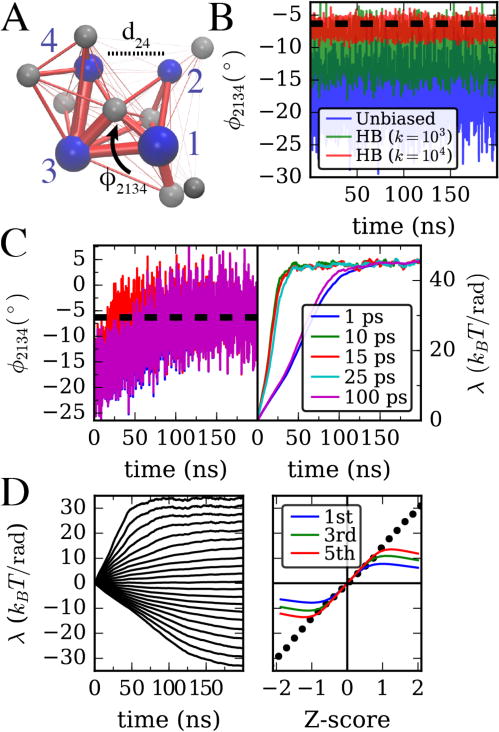
(A) Twelve-site hENM of an ATP-bound actin monomer parameterized as described in the main text. The four major subdomains of actin are labeled, and cleft distance and twist angle CVs are defined as in Figure 1A. (B) Twist angle for an unbiased hENM, as well as with a harmonic bias with force constants 10³ and 10⁴ kJ/mol/rad² centered at $\overline{\varphi }=-6.3°$ (dashed line). (C) Twist angle evolution as well as biasing parameter using gradient descent algorithm of Ref. 8 is shown for different τ^avg. (D) Left, bias parameter as in C (τ^avg = 10ps) with target values for ϕ from −25.2° to −9.16°. Right, comparison of final bias parameters on left (dots) with first, third, and fifth order predictions given in the main text. The horizontal axis shows difference of target ϕ from ϕ_unbiased scaled by the unbiased standard deviation as computed from data in (B).

Relative entropy minimization

In this work, the objective is for our system to evolve under minimally biased dynamics such that average value of particular CG observables of a subsystem of interest match target values obtained via simulations of a larger encompassing supersystem (or alternatively values obtained from experiment). In principle, as in previous work, we can derive the necessary change to the system Hamiltonian (H₀) by minimizing the relative entropy between the distribution normally sampled by that system, P₀(X), and the distribution, P(X), arising from an unknown Hamiltonian (H). The latter unknown Hamiltonian system is subject to constraints on a mean of a set of observables, {f_i(X)}, which are scalar functions of the configuration of the system and are known properties of the system described by the unknown Hamiltonian.^{8, 10} In other words, we want to minimize the functional

$$S[P(X)]={\displaystyle \int \mathit{dXP}(X)}\text{ln}\left(\frac{P(X)}{P_0(X)}\right)$$ (3)

with the constraints ʃ dX P (X) = 1, and ${\displaystyle \int dX{f}_i}(X)P(X)={\overline{f}}_i$. This is formally solved by introducing Lagrange multipliers, {λ_i}:

$$P(X)=P_0(X)e^{\beta ({\lambda }_0+{\displaystyle {\sum }_i{\lambda }_i{f}_i(X)})}$$ (4)

with β =1/k_B^T. Using the first normalization constraint to set λ₀, and taking P₀ from the canonical ensemble gives the result:

$$P(X)=\frac{e^{-\beta (H_0(X)+{\displaystyle {\sum }_i{\lambda }_i{f}_i}(X))}}{{\displaystyle \int dX{e}^{-\beta (H_0(X)+{\displaystyle {\sum }_i{\lambda }_i{f}_i(X)})}}}$$ (5)

By comparison with the usual canonical ensemble distribution function, we see here that in order to simulate our system and have it maintain particular target values of our observables, $\left\{{\overline{f}}_i\right\}$, i.e., that are manifest in a simulation (or experiment) for the full and larger encompassing supersystem, we must modify the Hamiltonian H₀ of our system to include a linear term for each observable with (at this point) unknown proportionality constants {λ_i} (these are the same as the {α_i} in Ref. 10 and {λ_i} in Ref. 9, but differ by a constant factor $\left\{{\overline{f}}_i\right\}$ from {α_i} in the EDS formulation in Refs. 8 and 11).

Several papers have offered suggestions for how to determine these parameters in a molecular simulation context.^{6–9, 28} In each case, the idea is to iteratively update the values of {λ_i} proportional to the difference ${\Delta }_i({\mathit{\lambda }}^t)={\langle f_i(X)\rangle }_t-{\overline{f}}_i$, where the average is taken by sampling for a time τ^avg using the Lagrange multipliers from the t^th iteration. The rule for updating λ = {λ_i} (bold font indicating vectors, double-bar indicating matrices, dots indicating vector matrix multiplication, other vector arithmetic is element-wise) then takes a form similar to:

$${\mathit{\lambda }}^{t+1}={\mathit{\lambda }}^t-{\mathit{\eta }}^t\left(\mathit{\Delta }({\lambda }^t)\cdot {\left(\frac{\partial \mathit{\Delta }}{\partial {\mathit{\lambda }}^t}\right)}^n\right)\equiv {\mathit{\lambda }}^t-{\mathit{\eta }}^t{\mathit{\delta }}^t,$$ (6)

where n = 1 corresponds to gradient descent,⁸ n = 0 a scheme that only depends on the current distance from the average observables,⁹ and n = −1 to Newton’s method, and the error function being function being minimized is the total squared difference from observed to target CV values, i.e. ε_t = Σ_iΔ_i(λ^t)².⁷ The way that the pre-factor η^t is adjusted corresponds to a learning rate rule, that is, how much trust to ascribe to the step size coming from the other λ-dependent terms. For example, Bussi and coworkers use⁹:

$${\eta }_i^t=\frac{A_i}{1+\frac{t}{{\tau }_i}}$$ (7)

while White and Voth use^{8, 10–11}:

$${\eta }_i^t=\frac{A_i}{\sqrt{{\displaystyle {\sum }_{j=1}^t{\left({\delta }_i^t\right)}^2}}}$$ (8)

For the linear bias, the gradient term is a matrix with entries given by:

$${\left(\frac{\partial \mathit{\Delta }}{\partial {\mathit{\lambda }}^t}\right)}_{ij}=-{\langle f_i{f}_j\rangle }_t+{\langle f_i\rangle }_t{\langle f_j\rangle }_t,$$ (9)

so, the gradient is proportional to the covariance of the two observables on iteration t:

$$\left(\frac{\partial \mathit{\Delta }}{\partial {\mathit{\lambda }}^t}\right)=-{\text{Cov}}^t(f_i,f_j)\equiv \overline{\overline{J}}$$ (10)

In all cases where these methods have been applied in a molecular context, a stochastic procedure was used where one Lagrange multiplier was chosen randomly and adjusted based on this recipe (using only the diagonal elements in Eq. 9). Below, we will use the learning rate rule of White and Voth, but show that for the type of problems we are interested in, rather than the stochastic gradient descent (SGD) a simultaneous adjustment of all the parameters using the full covariance, either with gradient descent (Covar) or a Levenberg-Marquardt-type algorithm (LM) as suggested previously (see below)²⁸ can be superior, and prevent the need for tuning of the constant factor A_i for each observable. (Note that in the work of White and Voth and in this implementation, the constant A_i is scaled by the target observable value, so the A_i in this general formulation is replaced by $A_i=2A_i^{\prime }/{\overline{f}}_i$, with $A_i^{\prime }$ the value set as a RANGE parameter in the current Plumed2 implementation. The bias parameters λ_i always have units [Energy]/[CV], so in this way, $A_i^{\prime }$ has units of [Energy]. These are the values reported simply as A below.)

In the LM algorithm, the step size in Eq. 6 is replaced by

$${\mathit{\delta }}^{\mathit{t}}=\left({\left[{\overline{\overline{J}}}^T\overline{\overline{J}}+{\gamma }^t\text{diag}\left({\overline{\overline{J}}}^T\overline{\overline{J}}\right)\right]}^{-1}{\overline{\overline{J}}}^T\right)\cdot \mathit{\Delta }({\mathit{\lambda }}^t)$$ (11)

where $\text{diag}\left({\overline{\overline{J}}}^T\overline{\overline{J}}\right)$ is the purely diagonal matrix having the same diagonal elements as ${\overline{\overline{J}}}^T\overline{\overline{J}}$, and γ^t is a mixing parameter (which in general could be made adaptive as in Ref. 28), and causes the method to behave with some character of Newton’s method (γ = 0) and steepest-descent (γ ≫ 1).²⁸ We have implemented an adaptive version of the algorithm where we average the total squared error ε_t for all CVs over LM_stride iterations of the algorithm. This quantity is retained over m windows of length LM_stride*τ^avg. If the error decreases monotonically for these m stages, γ is increased by a multiplicative factor l >1, i.e. γ^t+1 = lγ^t. If it decreases in each stage, γ^t+1 = γ^t/l. If it is not monotonic over m stages, then γ is not changed.

All algorithmic parameters for each figure are listed in Table 1. We make a practical note here, that in order to reduce the overhead of biasing via PLUMED, CVs are defined using only two atoms per protein residue (C_α, C_β) and for all-atom simulations we use the built-in multiple time stepping procedure of Bussi and coworkers,²⁹ with the bias algorithm performed every-other MD time step (STRIDE=2).

Table 1.

Algorithmic parameters

Fig/System	Algorithm	Parameters
Fig. 2B/hENM	HB	$k_{\varphi }={10}^3$, ${10}^4\frac{\text{kJ}}{\text{mol}{\text{rad}}^2}$, $\overline{\varphi }=-6.32°$
Fig. 2C/hENM	SGD	$A=10k_{B}T$, $\overline{\varphi }=-6.32$τ̅avg = from 1–100 ps
Fig. 2D/hENM	SGD	$A=10k_{B}T$, ${\tau }^{\text{avg}}=10\text{ps}$. $\overline{\varphi }:-9.16°\text{to}-25.2°(\langle \varphi \rangle \approx -17°,{\sigma }_{\varphi }\approx 4°$
Fig. 3A (top)/hENM	SGD	τavg = 10 ps, A = 10kBT, $\overline{\varphi }=-6.32°$, $\overline{d}=20.62\text{Å}$
Fig. 3A (top)/hENM	Covar	See above, but A = 1kBT
Fig. 3A (bottom)/hENM	SGD	τavg = 100 ps, A = 10kBT, $\overline{\varphi }=-6.32°$, $\overline{{\varphi }^2}={40.86}^{{(\circ )}^2}$, $\overline{d}=20.62\text{Å}$, $\overline{d^2}=425.03{\text{Å}}^2$
Fig. 3A (top)/hENM	Covar	See above, but A = 1kBT
Fig. 3B/hENM	Covar	τavg = 100 ps, A = 1kBT, $\overline{\varphi }=-6.32°$, $\overline{{\varphi }^2}={40.86}^{{(\circ )}^2}$, $\overline{d}=20.62\text{Å}$, $\overline{d^2}=425.03{\text{Å}}^2$
	LM	See above, with γ = 0.1,0.01
	Adaptive LM	See above, with γ0 = 0.1, m = 3, l = 1.2, LM_stride = 10
Fig. 4A (top), 4B/G-monomer	HB	$k_d=k_{\varphi }=5000\frac{\text{kcal}}{\text{mol}{\text{red}}^2}$, $\overline{\varphi }=-6.32°$, $\overline{d}=20.62\text{Å}$
	Adaptive LM	τavg = 100 ps, A = 10kBT, γ0 = 0.1 $\overline{\varphi }=-6.32°$, $\overline{{\varphi }^2}={40.86}^{{(\circ )}^2}$, $\overline{d}=20.62\text{Å}$, $\overline{d^2}=425.03{\text{Å}}^2$, m = 3, l = 1.2, LM_stride = 100
Fig. 4A (bottom)/F-monomer	Adaptive LM	See above, except γ0 = 0.1
	Frozen bias (after 80 ns of above)	${\lambda }_{\varphi }=-10.2\frac{\text{kcal}}{\text{mol}\text{rad}}$, ${\lambda }_{{\varphi }^2}=484.0\frac{\text{kcal}}{\text{mol}{\text{rad}}^2}$, ${\lambda }_d=2.2\frac{\text{kcal}}{\text{mol}\text{Å}}$, ${\lambda }_{d^2}=6.63\frac{\text{kcal}}{\text{mol}{\text{Å}}^2}$
Fig. 5B,C	LM	τavg = 100ps, A = 1kBT, γ0 = 0.01 $\overline{{\varphi }_{A1}}=\overline{{\varphi }_{A2}}=\overline{{\varphi }_{A3}}=-6.32°$, $\overline{d_{A1}}=\overline{d_{A2}}=\overline{d_{A3}}=20.6\text{Å}$

Results

Actin monomers in solution are more twisted and open, with larger fluctuations than subunits in a filament

As described in the methods section, MD simulations of an actin filament and actin monomers from two different starting configurations were performed. The difference between the G-actin and F-actin structure can be well characterized (as in previous works^{13, 21}) by defining the cleft distance (d) and twist angle (ϕ) as shown in Figure 1A. In this study, CG bead positions used for analysis and for biasing are defined by computing the center of mass of the C_α and C_β in each actin subdomain. Using these definitions, we computed the value of actin monomer twist angle and cleft distances in our MD simulations. In Figure 1B, we show that, as in previous simulations and experimental studies, an actin subunit in a filament is flat (ϕ ≥ −10°) and closed (d ⪅ 21Å)^13–14 while a G-actin with bound ATP is twisted, (ϕ ⪅ −20°) and more open (d ⪆ 25Å).^{22, 25} Interestingly, in our simulation of an ATP-bound monomer starting from a filamentous configuration, the monomer readily adopts a G-actin like structure over the course of a relatively short MD simulation, suggesting that the twisted/open structure has a lower free-energy outside of a filamentous context, as expected based on known actin biology.¹³ Finally, we observe that the fluctuations of these two CVs for an actin monomer in solution are larger than in a filament, where allosteric coupling to adjacent actin subunits constrains the range of conformations (see Table 2).

Table 2. Observed values for collective variables parameters.

Quantities are computed for the final 50ns shown in each figure. Percentages are comparison with respect to a single actin monomer, data on the first line of the table (bold). Biased parameters are underlined.

$\text{Fig}/\text{System}+\text{method}$	$\langle d_{24}\rangle (\text{Å})$	$\langle d_{24}^2\rangle ({\text{Å}}^2)$	$\langle {\varphi }_{2134}\rangle (\circ )$	$\langle {\varphi }_{2134}^2\rangle ({\circ }^2)$
Fig. 1B/F-actin (1 subunit)	20.62 (0.0%)	425.03 (0.0%)	−6.32 (−0.0%)	40.86 (0.0%)
Fig. 1B/G-monomer	23.82 (15.5%)	568.15 (33.7%)	−16.93 (168.0%)	290.70 (611.4%)
Fig. 1B/F-monomer	26.52 (28.6%)	704.00 (65.6%)	−17.37 (175.0%)	307.00 (651.3%)
Fig. 2B/hENM (no bias)	23.95 (16.2%)	574.24 (35.1%)	−17.44 (176.1%)	317.18 (676.2%)
Fig. 2B/hENM HB K=1000	23.79 (15.4%)	566.72 (33.3%)	−10.54 (66.8%)	116.27 (184.5%)
Fig. 2B/hENM HB K=10000	23.82 (15.5%)	568.04 (33.6%)	−6.95 (9.9%)	49.07 (20.1%)
Fig. 2C/hENM SGD τavg = 15 ps	23.88 (15.8%)	570.98 (34.3%)	−6.30 (−0.2%)	54.97 (34.5%)
Fig. 3A/hENM SGD 2 CV	20.62 (−0.0%)	425.72 (0.2%)	−6.48 (2.6%)	52.02 (27.3%)
Fig. 3A/hENM Covar 2 CV	20.65 (0.2%)	427.28 (0.5%)	−6.53 (3.4%)	52.65 (28.8%)
Fig. 3A/hENM SGD 4 CV	20.60 (−0.1%)	425.03 (−0.0%)	−6.50 (2.8%)	50.99 (24.8%)
Fig. 3A&B/hENM Covar 4 CV	20.60 (−0.1%)	424.88 (−0.0%)	−5.99 (−5.2%)	40.03 (−2.0%)
Fig. 3B/hENM LM γ = 0.1	20.62 (0.0%)	425.95 (0.2%)	−6.04 (−4.3%)	44.52 (8.9%)
Fig. 3B/hENM LM γ = 0.01	20.63 (0.0%)	426.02 (0.2%)	−6.07 (−4.0%)	44.63 (9.2%)
Fig. 3B/hENM LM Adapt γ0 = 0.1	20.62 (0.0%)	425.94 (0.2%)	−6.02 (−4.7%)	43.97 (7.6%)
Fig. 4A/G-monomer HB 2 CV	20.87 (1.3%)	435.78 (2.5%)	−7.37 (16.7%)	55.38 (35.5%)
Fig. 4A/G-monomer LM Adapt 4 CV	20.55 (−0.3%)	422.51 (−0.6%)	−6.04 (−4.4%)	38.03 (−6.9%)
Fig. 4A/F-monomer LM Adapt 4 CV	20.44 (−0.8%)	418.08 (−1.6%)	−5.11 (−19.1%)	28.01 (−31.5%)
Fig. 4A/F-monomer Fixed Bias 4CV	20.32 (−1.4%)	412.95 (−2.8%)	−4.37 (−30.9%)	20.56 (−49.7%)
Fig. 5/Trimer-A1 LM Adapt	20.32 (−1.4%)	412.90 (−2.9%)	−6.21 (−1.7%)	40.78 (−0.2%)
Fig. 5/Trimer-A2 LM Adapt	20.53 (−0.4%)	421.68 (−0.8%)	−7.03 (11.3%)	51.62 (26.3%)
Fig. 5/Trimer-A3 LM Adapt	20.53 (−0.4%)	421.39 (−0.9%)	−6.75 (6.8%)	47.31 (15.8%)

Linear bias method can out-perform harmonic bias for matching target CV value

Unconstrained simulations of our hENM test system show a ϕ angle oscillating around the atomistic G-actin value from Figure 2B. Applying a harmonic bias (HB) to the hENM model of the form $\frac{1}{2}{k}_{\varphi }{\left(\varphi -\overline{\varphi }\right)}^2$ with spring constant k_ϕ =10³ kJ/mol/rad² and even k_ϕ =10⁴ kJ/mol/rad² centered at $\overline{\varphi }=-6.3°$ moves the sampled value of ϕ closer to but not all the way to this target value. As discussed previously, applying this bias also substantially changes the size of fluctuations of this observable (see Table 2).⁶ In contrast, Figure 2C shows that when using the adaptive algorithm of Ref. 8, the target average is achieved exactly, although it takes some time to learn the bias parameter.

Adaptive algorithm has optimal averaging time for 1 CV

The adaptive algorithms discussed in the Methods section sample observable values over a time τ^avg before adjusting the bias parameter based on a learning rule. In Figure 1C we show in simulations of the hENM actin model that the convergence of the gradient descent algorithm can be very sensitive to the value of τ^avg, and appears to have an optimal value, in this case approximately 10–15 ps. Very short averaging windows produce a poor average of the variance of the observable used in the update rule, and very long averaging time produces a better average, but too long is spent on this process. An idea of how to set this can come from computing the autocorrelation function (ACF) for the CV in an unbiased simulation. For the twist angle, we estimate the autocorrelation time (when the ACF decays to 1/e) at ~ 4 ps. Hence to get a good estimate for the average and variance of this CV used in the algorithm, it seems that at least 2 autocorrelation times are needed. The speed of convergence can also be adjusted by changing the constant A in the learning rule (in this case all simulations used A = 10 k_BT), but we have found that having too large of an initial value of A can cause the bias parameters to overshoot, hence it is better to choose good values for τ^avg first, as this has a non-linear effect on the learning time.

Derivation and validity of a linear response approximation to bias parameters

If the target value for a CV is close to the value in an unbiased simulation, then we know that λ_i for that CV will be small. Hence, we can expand the exponential as a Taylor series around λ_i = 0. We will illustrate this derivation first for a single CV. From Eq. 5, we can see that when the correct Lagrange multiplier has converged for a CV f′:

$$\overline{f^{\prime }}={\langle f^{\prime }\rangle }_{\lambda }=\frac{{\displaystyle \int dX{f}^{\prime }(X)e^{-\beta (H_0(X)+\lambda f^{\prime }(X))}}}{{\displaystyle \int dX{e}^{-\beta (H_0(X)+\lambda f^{\prime }(X))}}}$$ (12)

Without loss of generality, we can consider the CV $f\equiv f^{\prime }-\overline{f^{\prime }}$, with target value $\overline{f}=0$. Hence for this new CV, the left-hand side of this equation is zero and the denominator on the right-hand side, as a constant, does not affect the equality. We can then expand the exponential in the numerator and write:

$$0={\displaystyle \int \mathit{dXf}(X)}{e}^{-\beta H_0(X)}\left(1-\beta \lambda f(X)+\frac{{\left(-\beta \lambda \right)}^2}{2}{f}^2(X)+\cdots \right)$$ (13)

Dividing both sides of the equation by the unbiased partition function $Z={\displaystyle \int dX{e}^{-\beta H_0(X)}}$, we can express each term as an average that can be obtained in the unbiased simulation. This gives an equation to be solved for the unknown constant λ.

$$0=\langle f\rangle -\beta \lambda \langle f^2\rangle +\frac{{\left(-\beta \lambda \right)}^2}{2}\langle f^3\rangle +\cdots ={\displaystyle \sum _{j=0}^{\text{∞}}\frac{{\left(-\beta \lambda \right)}^j\langle f^{j+1}\rangle }{j!}}$$ (14)

If the averages 〈f^j〉 can be computed accurately from an unbiased simulation, then this equation can be truncated at some power and solved for λ, using, for example, Mathematica.³⁰ At first order, this equation is trivially solved:

$$\lambda =k_{B}T\frac{\langle f\rangle }{\langle f^2\rangle }=k_{B}T\frac{\langle f-\overline{f^{\prime }}\rangle }{\langle {\left(f^{\prime }-\overline{f^{\prime }}\right)}^2\rangle }$$ (15)

For N CVs {f_i} centered at the target value, we get N equations:

$$0={\displaystyle \int \mathit{dX}{f}_i(X)e^{-\beta H_0(X)}}{\displaystyle \prod _{k=1}^N{\displaystyle \sum _{j=0}^{\text{∞}}\frac{{\left(-\beta {\lambda }_k\right)}^j{f}_k^j}{j!}}}$$ (16)

At first order, we get the multi-dimensional equivalent expression to equation 15:

$$\mathit{\lambda }=k_{B}T\text{Cov}{\left(f_i,f_i\right)}^{-1}.\langle \mathit{f}\rangle$$ (17)

This solution is equivalent to taking a single step of Newton’s method (see, equation 10 and 11).

These results are tested on the hENM model in Figure 2. In Figure 2D we vary the target value for the twist angle in an actin monomer from above to below the average ϕ. Using Mathematica, we compute the moments $\langle {\left(\varphi -\overline{\varphi }\right)}^n\rangle$ and solve Eq. 14 numerically truncating from first to fifth order in λ. We find for the distribution of ϕ generated by our hENM model, the even-ordered solutions can be purely imaginary. However, the odd ordered equations always have a real solution and these are shown on the right as a function of how far the target is from the unbiased mean, scaled by the standard deviation, $Z=(\overline{\varphi }-\langle \varphi \rangle )/\sqrt{\langle {\left(\varphi -\langle \varphi \rangle \right)}^2\rangle }$.

As expected, for target values close to the unbiased average, the bias parameter is very small. We observe that the first order approximation breaks down near Z = ±0.5 and the fifth order solution breaks down around Z = ±1. The linearity of the learned bias parameters in this range is likely a consequence of applying this method to a purely harmonic test system (although the cost of twisting ϕ is not perfectly quadradic).

Given the simplicity of computing the first order solution (even for N CVs), we suggest that future practitioners of these relative entropy minimization algorithms start with this as an initial guess. Since it arises from a linear response approximation, this amount of bias is unlikely to cause an irreversible change in the system when activated. However, in the rest of the data below, this is not done so as to show the full process of the learning algorithm.

Simultaneous update of bias parameters outperforms stochastic gradient descent

To fulfill our goal outlined in the introduction, we need to bias the actin monomer to behave as if it is in a filament. To do this, we will attempt to simultaneously bias four CVs: the twist angle and cleft distance, as well as their second moments (fluctuations). As discussed before, the optimal τ^avg for a CV is related to that CV’s auto-correlation time. The problem that can be encountered when going to multiple CVs is that there can be a large timescale separation. This forces a user of the method to use a τ^avg as big as needed for the slowest-to-average CV. In the stochastic algorithm, only one CV is updated at a time, and so it is possible to have many long averaging periods in a row where only the faster averaging CV’s bias parameter is updated. In Figure 3A(top), we first show in simulations of the hENM model that the SGD algorithm is effective for biasing the average cleft distance and twist angle. However, in order to bias these parameters and their second moments, a longer averaging time is needed, making convergence much slower. We show in Figure 3A(bottom) that in this case, using the full covariance matrix as in Eq. 10 greatly accelerates convergence (note that this is after choosing a 10x lower learning rate parameter A for the covariance calculation).

Figure 3.

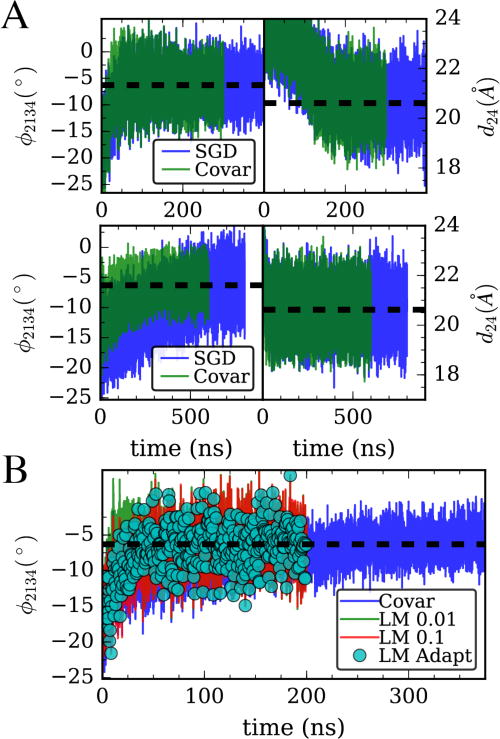
(A) Simulation of hENM model using stochastic gradient descent (blue) and full covariance matrix (green) to bias the two shown CVs as well as their variance, with otherwise identical algorithmic parameters, (B) The full covariance method is compared to the Levenberg-Marquardt (LM) algorithm with γ = 0.1, γ = 0.01, and the adaptive algorithm with starting γ = 0.1.

Levenberg-Marquardt algorithm greatly improves on gradient descent

Since we were no longer using the stochastic version of the optimization algorithm, we modified our learning algorithm to include the LM update rule.²⁸ In Figure 3B, we compare results of LM to the covariance version of our algorithm. We see that the LM algorithm with γ = 0.01 accelerates convergence by another factor of >10x (~50 vs ~500 ns) over the covariance gradient descent. This allows us to easily see the difference in speed between the two algorithms. This also demonstrates that when using the more “intelligent” step sizes of the LM algorithm, we no longer find it necessary to tune A to get fast convergence. We also show one simulation using the adaptive algorithm described above. In this case, we see that the adaptive LM algorithm converges at about the same speed as the algorithm with its fixed initial γ. However, we note that this method may be useful in atomistic contexts (such as discussed in the following sections), where it could be advantageous to for this this confidence parameter γ to change as the atomistic system moves from one state to another.

Linear bias on monomer CVs is effective as a restraint, matches structure in filament

Having now developed and implemented improved learning algorithms, we sought to test these methods on the all-atom MD simulation of G-actin and F-actin monomers. The four CVs, cleft distance and angle, as well as their second moments, were targeted to match the values from a single actin monomer in the 13-mer simulation shown in Figure 1B (see Table 2). The LM algorithm of all various flavors were found to converge in reasonable amounts of simulation time, with the amount of time required to match all CVs depending upon the particular parameters. In the upper panels of Figure 4A, we show a simulation using the adaptive LM that matches the target CVs in ~100ns, with a small error in all 4 CVs (see Table 2). We note that given the moderately large expense of simulating this system, we did not try to optimize the parameters used much beyond what was learned from the simpler hENM, besides increasing τ^avg to account for the slower fluctuations in the atomistic system. Nevertheless, the algorithms showed themselves to be robust, converging eventually in all trials of the LM algorithm with large enough τ^avg. The LM results in Figure 4A are compared to a harmonically biased simulation with a very large spring constant applied to both the twist angle and cleft distance CVs. Despite being ~10x larger than what was used previously in a QM/MM application,^3–4 the harmonic bias (starting from the G-actin structure) fails to match the target twist angle. In Figure 4B, we compare the structure of this biased G-actin monomer to a filament subunit configuration. We see that as the algorithm progresses, the G-actin structure (which is already similar to an F-actin monomer structure) converges to a structure that has a lower RMSD to the target, although RMSD was not an observable explicitly biased. We note that previous simulation studies have shown that actin filaments are heterogeneous,²⁰ and the RMSD of an actin subunit in a filament compared to another or compared to itself later in an MD simulation is typically in this range (for the last 100ns of the simulation in Figure 1B, the subunit-subunit RMSD is 3.35 ± 0.30 Å). Hence, we cannot expect to achieve a closer match than what is seen in Figure 4B without explicitly biasing RMSD.

Figure 4.

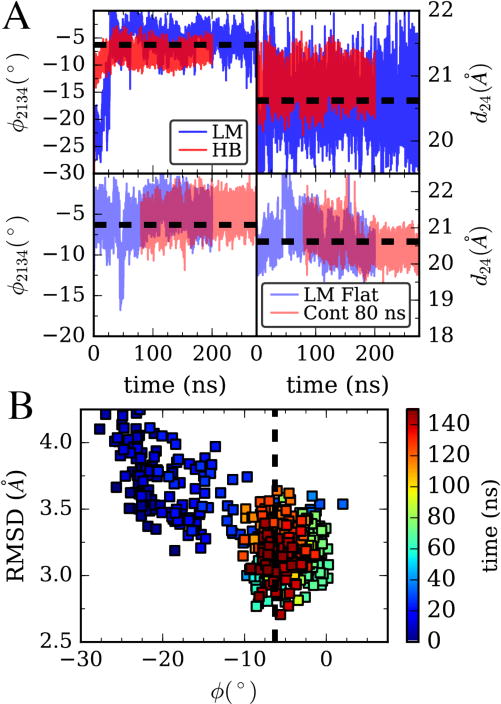
(A) Top, Adaptive Levenberg-Marquardt (LM) algorithm matching 4 CVs: cleft distance, twist angle, and their second moments is compared to harmonic bias on angle and distance with large spring constants on both. Data is for all-atom MD simulations of the G/monomer system in Figure 1. Bottom, in blue, the LM algorithm is performed on an actin monomer starting from a filament structure (F/monomer in Figure 1). In red, the bias parameters at time 80 ns are fixed and a separate simulation is run using this learned bias. (B) Comparison of the structure of the G/monomer in the LM trajectory from (A,top) with a filament subunit by backbone RMSD. Color shows progress along the trajectory in (A).

In the lower panels of Figure 4A, the adaptive LM algorithm is used on a simulation of an actin monomer starting from a flat, filamentous like structure. In this case, it can be seen that around 50 ns, the structure begins to twist and open, as was seen in the unbiased simulation in Figure 1B. Remarkably, the bias algorithm is able to adapt to this change in observable and return the configuration to close to the target value. In other trials using the stochastic gradient descent and covariance gradient descent, the convergence was not fast enough to prevent the structure from twisting, and then it took a much longer time for the system to return to a flattened structure. We note that during this 200ns simulation, convergence is not yet achieved, meaning that there is greater error here/slower convergence to the target CV values than starting from the twisted structure. This seems to be a general trend, and we will consider this idea further in the Discussion section. Finally, in these lower panels we show the result of freezing the bias that has been learned at 80ns from the flat-monomer (before convergence) and show that the simulation approximately maintains the CV values from that starting time.

Biasing CVs in a larger subsystem is an effective alternative constrained moiety

When considering the problem of biasing a subsystem to represent aspects of its behavior within a larger supersystem, in general there will be many possible subsystems of different sizes to consider using. In most cases, it would be advantageous to choose the smallest system size possible, as we have done by choosing a single actin subunit in a filament. However, larger systems afford the advantage of representing a more native-like context; for example, including more protein-protein interfaces. To demonstrate this idea, we tested our algorithms for an actin trimer which was previously used in a metadynamics study¹⁹ of the nucleotide effect on the conformational states of actin (Figure 5A). In Figure 5B, we show data from a simulation where the cleft distance and dihedral angle in all three actin subunits are biased, but in this case only the mean values for these six CVs are set. The algorithm is able to find six parameters for which all the CVs closely match their target values (see Table 2). Interestingly, due to the allosteric coupling between monomers, variances of these six CVs are much closer to the full filament values than in the case of an unbiased monomer. This is reflected in Figure 5C where the dihedral angles of an unbiased trimer simulation are histogrammed and compared to the filament value, with the unbiased dihedral distributions having only ~35% larger standard deviations than an actin subunit in a filament (and the distance distribution being even closer, ~20% different, not shown). When the bias is applied, then, the peak of the distribution shifts as desired while leaving the rest of the distribution approximately the same. The result is only ~10% error in the mean of twist angle and <15% error in the second moment (with distances having <3% error in both). Although a larger system, we believe this kind of tradeoff between size and additional molecular context could be appropriate in some future applications of our GCDS methodology.

Figure 5.

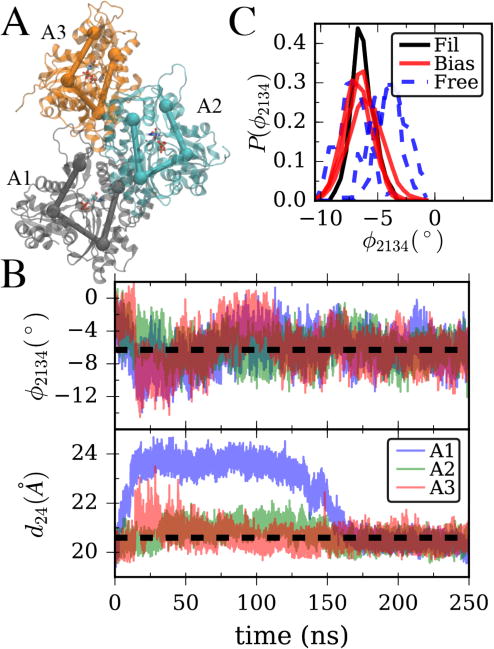
(A) Illustration of all-atom three actin sub-filament with CG subdomains from Figure 1A overlaid. (B) Twist angle and cleft distance for each of the subunits in (A) during LM bias simulation. (C) Observed distribution of twist angles in the final 50ns of an unbiased 100ns simulation of the structure in (A) (dashed line) vs. the final 50ns of the biased simulation with data plotted in (B) and the final 50 ns of filament data from Figure 1B.

Discussion and Conclusions

In this work, we present the idea that linear biases learned by a relative entropy minimization scheme can be used to restrain a molecular system in such a way that it retains some information about its behavior within a larger macromolecular “supersystem” context. In particular, we show that in the case of actin, we can bias two CG observables and their second moments, with the result being that an actin monomer can adopt and maintain a filament-like conformation with native-like fluctuations in these observables. Although the CGDS algorithm takes some time as compared to simply applying a harmonic bias, these methods can achieve a closer match for the distribution of the target observables. We have also made a number of algorithmic improvements which for this application greatly reduce the amount of sampling needed to learn the biasing parameters, down to a very reasonable amount of simulation time (<100ns), and produce systems that would be appropriate for use in subsequent free energy or reactive (QM/MM or otherwise) MD simulations where a small subsystem is required but including the effects of larger scale fluctuations are expected to affect the results.

In previous studies from our group, the stochastic gradient descent algorithm was sufficient to learn biasing parameters in a very short amount of simulation time.^{8, 11} We note that the context we are presenting here is very different, where within the simulation the observables to be biased depend on the positions of a few CG observables. In the previous studies, the systems of interest were isotropic liquids, and the CVs of interest (averages over radial distribution functions) depend on the pairwise distance between each molecule. This produces a self-averaging such that the effect of changing the biasing parameter can be sampled over many environments simultaneously. In the protein context, the relaxation time of the observable is much longer and moreover it is likely to be sampled only over a single copy of the system. We suggest that (1) starting from a linear response approximation to the bias parameters, (2) optimizing sampling time, and (3) using methods such as the Levenberg-Marquardt algorithm that take advantage of covariance and try to make “smart” step sizes based on that information, are all important steps that should be applied in this (CGDS) context. Although we suspect these three steps are likely useful in the prior cases, in practice the learning time for previous applications was not a bottleneck.

Previously, there was some concern in the literature that using the full covariance matrix with correlated observables might result in an optimization problem that was non-convex and might not converge.⁶ Although in this work we have biased both the first and second moment of our CVs, which are correlated, we have not found this to be a problem in practice (as also discussed in Ref. 9). Another concern with using the full covariance matrix and a Newton-like method with correlated observables is that it might be singular and hence produce divergent step sizes in the iterative algorithm. As noted previously, the Levenberg-Marquardt term proportional to γ (Eq. 10) is specifically designed to avoid this problem.²⁸

Finally, we return to one challenge encountered during our CGDS studies, which is that these adaptive algorithms are not well tailored to biasing a system that starts close to a target configuration in a state that is metastable on simulation time scales. An idealized free energy surface in such a case is likely to look something like the illustration in Figure 6. We in fact know this for an actin monomer from previous and ongoing umbrella sampling and metadynamics simulations using these CVs to obtain the free energy landscape for actin flattening.^{21, 31} If the starting state of the system is a local free energy minimum, such as for an ATP-bound actin monomer in a flattened configuration, then the initial estimate for the Lagrange multiplier on that CV will be close to zero until fluctuations begin to cause the system to drift towards a deeper minimum. This is exactly what is observed in Figure 4A. On the other-hand, starting in another state is less desirable for two reasons: (1) starting from the lower free energy minimum, the Lagrange multiplier estimate may be very large at first, and then it may take some time once the system is near the target state for the Lagrange multiplier to return to its fixed point, and (2) during this process, there is no guarantee that the simulation will find the target structure as the values of the CVs are improved (although we demonstrate in Figure 4B that this was not an issue for the case of G-actin). This is a challenge for which we do not yet have a complete solution. Yet, we have found in our experience that biasing the second moment of the target CV in addition to the mean when starting from the higher free-energy state goes a long way towards solving this problem. We believe that this is because, as illustrated in Figure 6, even if the minimum for the subsystem has the same mean as the target system, it is likely to be much less constrained, and hence will have a much wider basin in any CG CV such as the ones considered in this work.

Figure 6.

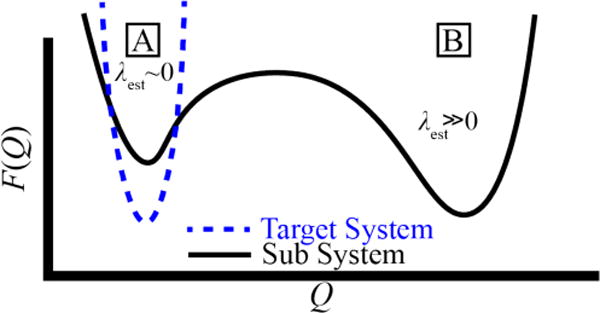
A structure of a target system (in this study, an actin filament) is likely to be known from experiment, and as such is in a relatively deep local free-energy minimum. Hence, the observed values for a CV (Q) are likely to be normally distributed around a single value (with a roughly harmonic potential of mean force F(Q)). When a sub-structure such as an actin monomer is removed to solution, the starting structure (A) will likely still be near a local free energy minimum, however there may be alternative lower free-energy configurations (B). The initially-estimated Lagrange multipliers needed to have the subsystem stay in state A will depend on whether the system starts in state A or B.

The present paper does not claim to provide the final word in the development of CG “guided” or “directed” methods to bias an all-atom MD simulation of a subsystem within a larger supramolecular complex, so that it “feels” certain key effects of being in the macromolecular supersystem, such as a structural bias and altered fluctuations. However, we suggest that the CGDS method developed herein is an important step in that direction. We will certainly improve and extend this approach in the future, and we encourage other researchers to contribute to this effort.