Recent progress and open challenges in modeling p53 dynamics in single cells

Abstract

In mammalian cells, the tumor suppressor p53 is activated upon a variety of cellular stresses and ensures an appropriate response ranging from arrest and repair to the induction of senescence and apoptosis. Quantitative measurements in individual living cells showed stimulus-dependent dynamics of p53 accumulation upon stress induction. Due to the complexity of the underlying biochemical interactions, mathematical models were indispensable for understanding the topology of the network regulating p53 dynamics. Recent work provides furhter insights into the causes of heterogeneous responses in individual cells, the rewiring of the network in response to different inputs and the role of the downstream processes in determining the cellular fate upon stress.

p53 – a versatile and highly dynamic stress response pathway

Mammalian cells are constantly under stress: metabolism generates reactive by-products that attack biomolecules; malfunctions during replication and rearrangement of the genome induce lesions in the DNA; imbalances in production and secretion of proteins need to be compensated [1]. In addition to these cell-intrinsic stressors, environmental stresses such as toxic substances and radiation further challenge the integrity of our cells. One of the main defense mechanisms to counteract cellular stress is activation of the tumor suppressor p53 [2]. Upon activation, p53 initiates transcription of hundreds of target genes involved in response pathways ranging from transient cell cycle arrest and repair to terminal cell fates such as senescence and apoptosis (Figure 1A). Alterations in the structure and function of the p53 network cause severe human diseases such as cancer [3]. While many cellular stressors are known to activate p53, most research focused on its role in coordinating the cellular response to DNA damage [4].

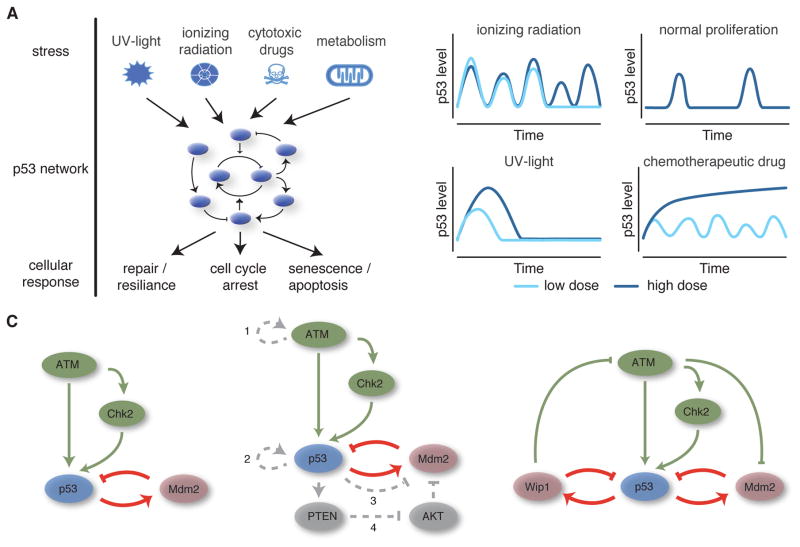
Figure 1. p53 is a versatile dynamic signaling system.

A) p53 is activated by various stresses and controls cellular responses by inducing expression of target genes involved in damage control and repair, apoptosis, and cell cycle arrest and senescence. B) The dynamics of p53 accumulation are stimulus dependent. In response to DNA double strand breaks caused by ionizing radiation, p53 accumulates in pulses of uniform amplitude and duration, the number of which depends on the extent of damage. Similar pulses are observed during normal proliferation due to spontaneously occurring endogenous damage. In contrast, the amplitude and duration of p53 accumulation upon UV radiation increases gradually with the damage dose. High doses of chemotherapeutic drugs like etoposide or cisplatin lead to monotonic increases in p53 levels, while low doses induce oscillatory dynamics. C) Mathematical models were used to explore network topologies that could reproduce the observed p53 dynamics: single negative feedback loop (left), combined negative – positive feedbacks (middle) and two negative feedback loops affecting upstream activators as well. Postulated positive feedbacks: 1 – switch-like activation of ATM through autophosphorylation; 2 – auto-activation of p53; 3 – p53-mediated inhibition of MDM2; 4 – transcriptional feedback via PTEN and AKT.

To enable versatile signaling, the p53 network shows intricate dynamic changes during the stress response. Initial studies in single living cells showed that p53 accumulated in regular pulses with uniform amplitude and duration in response to DNA double strand breaks (DSBs) [5]. Features of these pulses were independent of the damage dose; information about the strength of the stimulus were mainly encoded in the pulse pattern [5,6]. Single cell analysis also revealed considerable heterogeneity of p53 dynamics even in genetically identical cells. Sources of heterogeneity include intrinsic and extrinsic biochemical noise [6] as well as variability in the amount of DNA damage and its repair [7]. Interestingly, no distinct damage threshold for induction of a p53 pulse could be observed. Instead, the probability of a p53 response was linearly correlated to the number of DSBs [7]. Even in normally cycling cells, endogenous breaks caused by replication or division induced spontaneous pulses of p53 accumulation [8].

When other forms of DNA damage were considered, it became evident that p53 dynamics in single cells are stimulus-dependent (Figure 1B). In response to UV radiation, p53 showed a single pulse of accumulation with amplitude and duration that increased with the strength of the damage [9]. Continuously recurring damage by topoisomerase inhibitors led to a bi-modal response, where in addition to periodic pulses of p53 accumulation, monotonic increases in p53 levels were observed that correlated with the induction of cell death [10]. Similar p53 dynamics were observed upon induction of DNA cross-links by the chemotherapeutic drug cisplatin [11].

Quantitative studies in single cells showed that the dynamics of p53 accumulation influence the cellular response to stress. Targeted genetic perturbations altering the interaction of p53 and its negative regulators led to decreased duration of p53 accumulation while preserving pulse amplitude. Despite increased pulse frequency, these alteration led to attenuated target gene expression and compromised cell cycle arrest [12]. In contrast, pharmacological perturbation showed that converting p53 pulses to sustained accumulation of similar amplitude leads to preferential expression of target genes mediating senescence or apoptosis [13,14]. While p53 dynamics are important for cell fate decisions, other processes such as post-translational modifications and availability of co-factors contribute as well [15].

The sheer numbers of biomolecules that have been reported to interact with p53 as well as the plethora of proposed feedback interactions that govern its dynamics are prohibitive of a meaningful intuitive understanding of the signaling pathway. Given this complexity, a computational framework provides a useful tool for synthesizing what is known about network topology, aids in the generation of new hypotheses regarding its regulation and function, and reveals areas in which our understanding is currently lacking. The challenges are to select an appropriate level of abstraction, to sufficiently constrain models by quantitative time-resolved data and to generate novel, experimentally tesTABLE predictions.

Mathematical models of p53 constrain network topology

Most efforts to model p53 focused on revealing the network interactions controlling its dynamic response. In the absence of stress, p53 is maintained at low levels to prevent unnecessary expression of its target genes. Several negative feedback loops maintain low p53 levels during homeostasis and restore basal levels following alleviation of stress. These include the E3 ubiquitin ligases MDM2, COP1 and PIRH2 as well as the phosphatase PPM1D/WIP1 [16–20]. A particular focus was set on the interactions between p53 and MDM2 due to their mutual interactions in mouse knock-out models [21,22],. First models of this negative feedback loop demonstrated the potential to show oscillatory dynamics in response to DNA damage [23–25]. However, the predicted oscillations were always damped, which is, in single cells, only observed when an isolated p53-MDM2 feedback is activated in the absence of cellular stress [26]. Which network structure could then explain the occurrence of uniform p53 pulses upon induction of DSBs?

Several dynamic modeling frameworks were developed to describe p53 dynamics in single cells (Figure 1C). One approach was to augment a time-delayed feedback loop between p53 and Mdm2 with ATM-mediated degradation of MDM2 [27,28]. Alon and colleagues then proposed a series of phenomenological models to explore general network architectures capable of recapitulating the experimentally observed dynamics [6]. While a single time-delayed negative feedback loop alone could not generate sustained oscillations for feasible biochemical parameters as mentioned above, several other classes of core network architecture could recapitulate the observed dynamics, including relaxation oscillators consisting of positive feedback coupled to the core negative feedback loop. As relaxation oscillators are well known in systems theory, this approach has been frequently used to model single cell data, implementing for example auto-activation of p53, p53-mediated inhibition of Mdm2, cooperative activation of upstream kinases or transcriptionally activated positive feedbacks such as PTEN/AKT [29,30]. However, several of these feedbacks are absent in cell lines showing uniform p53 pulses upon damage, arguing against important contributions to regulating p53 dynamics. In this context, it is interesting to note that rapid and switch like-activation of ATM is a universal feature of the response to DSBs. Mathematical modeling suggests that autophosphorylation of ATM mediated by the MRN complex and MDC1 constitute a corresponding positive feedback loop [31].

Another noteworthy architecture proposed by the Alon group was a coupling of the p53-Mdm2 loop with additional feedback impinging on a putative upstream regulator of p53 [6]. Based on this computational prediction, Batchelor et al identified the phosphatase PPM1D/WIP1 as important in generating p53 dynamics in response to DBSs [32]. A subsequent systems identification approach and Fourier analysis showed that the experimentally observed oscillations were better described by a linear third-order model with white noise than a second-order model, providing further support for the critical role of an additional negative feedback loop [33].

Excitability and variation in damage strength can explain heterogeneity of p53 responses

The observation of spontaneous p53 pulses during normal cell cycle progression further constrained possible network structures [8]. Experimental evidence suggested that p53 has properties of an exciTABLE system showing uniform responses upon stimulation above a given threshold [8,9,32]. This behavior could be reproduced to a large extend by models implementing stochastic delay in feedback activation combined with stochastic induction of DSBs [34,35]. However, depending on the network topologies used, different predictions for sensitivity thresholds were made, which remain to be experimentally validated.

Excitability in the p53 network suggests that variation in input is an important contributor to heterogeneity in the response of individual cells. Indeed, measurements of DSBs by time-resolved microscopy showed that their number and repair kinetics vary in genetically identical cells, depending, for example, on cell cycle phase and repair pathways used [7,36]. Moreover, models of DSB induction by ionizing radiation suggest the existence of both simple and complex breaks that are repaired with differential kinetics [37,38]. Complex breaks are generated when DSBs cluster in chromatin loops. Another important determinant of repair kinetics is the epigenetic state of the affected chromatin region. This insight could now be used to refine existing stochastic models of DSB repair [39,40] and couple them to p53 models. Similar approaches with simpler stochastic DSB models have already succeeded in reproducing the observed heterogeneity to a certain extent [27]. A recent study combining stochastic DSB repair, positive feedback on ATM and negative feedback between p53, MDM2 and WIP1 shows that the resulting exciTABLE network reproduces all features of measured signaling responses including their heterogeneity in individual cells (Moenke et al, unpublished). Model predictions and experiments suggest that WIP1 levels set cell-specific thresholds for p53 activation, providing means to modulate its response through interacting signaling pathways.

Stimulus-dependent p53 dynamics are generated by alternate network wiring

Since the first observation of p53 pulses in living cells, combining computational models with quantitative data has yielded a refined understand of the underlying network topology. However, other cellular stresses induce different dynamic patterns of p53 activation, suggesting a stimulus-dependent wiring of the signaling pathway. Interestingly, early experiments showed that eliminating the PPM1D/WIP1-mediated feedback switched undamped oscillatory dynamics in response to DSBs to a single, longer duration pulse [32]. Analysis of computation models that differed only in the presence or absence of feedback from p53 to upstream activators showed that this change in network wiring was indeed sufficient to switch the system from uniform dose-independent pulses to a p53 response that gradually increased in amplitude and duration with the strength of the insult as observed in response to UV radiation [9]. Similarly, a model of the bi-modal response of p53 to etoposide treatment suggested that the change in dynamics is driven by a stimulus-dependent interaction of phosphorylated Mdm2 with p53 mRNA [41]. However, this hypothesis needs to be validated in future experiments.

The downstream network and the impact on cell fate

The identification of complex p53 dynamics raised questions regarding its impact on the expression of the hundreds of target genes that effect cell fate decisions [42]. Moreover, p53 is heavily post-translationally modified, with different modifications conferring specificity in its transcriptional activity [15]. Due to this complexity, early computational studies of downstream dynamics simplified the system by considering abstract classes of modified p53 with defined properties and focused on the induction of select key effectors of cell cycle arrest and apoptosis [30,43,44]. These efforts delineated a model in which cell cycle arrest (represented by the cyclin-dependent kinase inhibitor p21) can be activated during the initial pulses of p53, while apoptosis (as a function of pro-apoptotic factors including PUMA, p53AIP1, and APAF1) can be delayed until the level of p53 integrated over multiple pulses crosses a threshold. A combined computational and experimental study expanded these models and validated predictions of the impact of p53 dynamics on the activation of distinct cell cycle arrest mechanisms [45], showing that p53 pulses play important roles in sustaining cell cycle arrest upon damage and in preventing improper cell cycle re-entry and endoreduplication. Future efforts connecting detailed models of p53 dynamics with more specific mechanistic models of downstream pathways will likely prove valuable for understanding the regulation of cell fate decisions in individual cells (Figure 2A).

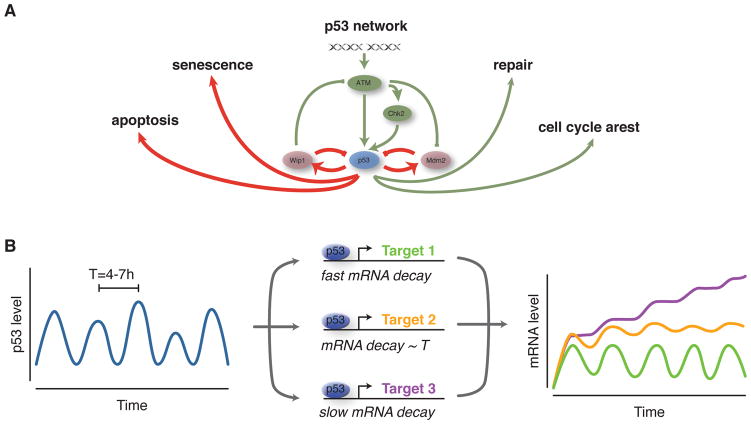
Figure 2. p53 dynamics are interpreted by a network of target genes.

A) p53 signaling influences the cellular response to stress by interacting with regulatory networks controlling, for example, cell cycle progression or induction of apoptosis. Further modeling efforts need to focus on understand this dynamic interplay and the underlying biochemical interactions. B) Depending on mRNA stability and the timing between p53 pulses, p53 target genes may show different extents of oscillatory and rising dynamics. mRNA decay rates can therefore act as a filter for p53 dynamics.

Recent work has developed a broader-scale perspective of the impact of p53 dynamics on target gene expression dynamics. Through quantification of expression dynamics for the majority of well-characterized p53 target genes, Porter et al. identified clusters of target genes that are expressed in a strongly pulsatile, weakly pulsatile, or sustained manner in response to DSBs (Figure 2B) [46]. Using a mathematical model and experimental validation, it was determined that mRNA stability is a key factor in determining the expression pattern of any particular target. Determining the extent to which mRNA expression dynamics translate into target protein dynamics and the impact on specific cell fate pathways remain open questions.

Future challenges

Despite decades of intensive research, our understanding of p53 function still remains limited. In the future, we will need to refine and validate models of the p53 network to gain a deeper understanding of its cell-type and stimulus-specific wiring. This may include investigating the role of additional feedbacks or modulators of the core p53-MDM2 feedback such as TRIM25 [18,19,47]. Recently, miRNAs have emerged as potential feedback modulators that provide robustness to the p53 response [48]. Moreover, it will be interesting to explore how interacting pathways modulate the dynamics of p53 to cellular stress and how this translates into altered cell fate decisions. Combined models of p53 and cell regulatory networks may shed light on these critical processes. Finally, we are challenged both from an experimental and theoretical perspective to unite our understanding of dynamics and post-translational modifications to complete our picture of p53’s fascinating role in protecting our cells from stress.

Highlights.

• p53 is a versatile signaling system with stimulus-dependent dynamics in single cells

• Mathematical modeling constrains feasible network topologies

• Excitability and stochastic damage repair lead to heterogeneous responses

• Stimulus-dependent dynamics are generated by alternative network wiring

• Decay rates of target gene mRNAs serve as filters for p53 dynamics