We show the fault-tolerant encoding, measurement, and operation of a logical qubit via quantum error detection.
Abstract
Quantum computers will eventually reach a size at which quantum error correction becomes imperative. Quantum information can be protected from qubit imperfections and flawed control operations by encoding a single logical qubit in multiple physical qubits. This redundancy allows the extraction of error syndromes and the subsequent detection or correction of errors without destroying the logical state itself through direct measurement. We show the encoding and syndrome measurement of a fault-tolerantly prepared logical qubit via an error detection protocol on four physical qubits, represented by trapped atomic ions. This demonstrates the robustness of a logical qubit to imperfections in the very operations used to encode it. The advantage persists in the face of large added error rates and experimental calibration errors.
INTRODUCTION
The discovery of quantum error correction codes gave credibility to the idea of scaling up physical quantum systems to arbitrary sizes (1–3). Showing that all elements of error correction can be realized in a fault-tolerant way is therefore of fundamental interest. Fault tolerance removes the assumption of perfect encoding and decoding of logical qubits (4), because the logical error probability scales as a convex function of the physical error probability for small errors (5). Although several experiments have shown a reduction of high intrinsic or artificially introduced errors in logical qubits (6–14), fault-tolerant encoding of a logical qubit has never been demonstrated. We note that there are subtle issues with respect to the definition of fault tolerance that are beyond the scope of this paper.
Here, we implement a four-qubit error detection code with two stabilizers (see Fig. 1). This leaves two possible encoded qubits, La and Lb, for which errors can be detected: a [[4, 2, 2]] code (15, 16). The preparation and error detection procedures considered here are fault-tolerant on only a single encoded qubit. From a fault tolerance perspective, this is a [[4, 1, 2]] subsystem code where the logical qubit La is protected and the gauge qubit Lb is not. As such, the code was used in experiments with photonic qubits (17, 18). By instead considering errors on both encoded qubits, we highlight the importance of fault tolerance for reducing intrinsic errors and managing error propagation. The non–fault-tolerant procedures that generate Lb still succeed in reducing added errors.
Fig. 1. Graphical representation of the logical operators and stabilizers defining the [[4, 2, 2]] code on physical qubits 1 to 4.
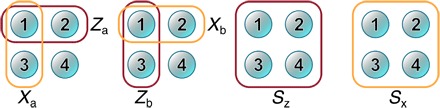
The structure of the logical operators X and Z for the two encoded qubits La and Lb, and for the two stabilizers Sx and Sz, is defined in Eqs. 3 and 4.
The code implements La and Lb on only four physical qubits and hence violates the quantum Hamming bound (5), which means that detected errors cannot be uniquely identified and corrected. We must therefore rely on postselection to find and discard cases where an error occurred. The code does have the advantage of requiring only five physical qubits for the fault-tolerant encoding of La: four data qubits and one ancilla qubit.
The logical codewords |LaLb〉L in the computational or Z-basis are
| (1A) |
| (1B) |
| (1C) |
| (1D) |
and with , we can write them down along X as follows
| (2A) |
| (2B) |
| (2C) |
| (2D) |
The encoding of different initial states is shown in Fig. 2 (A to D). The fault tolerance arises because the circuits for encoding and syndrome extraction are carefully constructed such that a single physical qubit error occurring anywhere cannot lead to an undetectable error on logical qubit La. It comes at the cost of the logical gauge qubit Lb, for which there is such an undetectable error channel. An example of this is shown in Fig. 2G.
Fig. 2. Circuit diagrams.
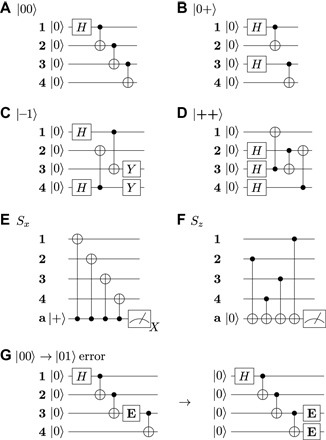
(A to D) Circuits for the encoding of four different logical states constructed such that logical qubit La is prepared fault-tolerantly. Any logical state can be achieved by applying single logical qubit operators to states encoded as shown here. (E and F) Circuits for the two stabilizers Sx and Sz, which project Z- and X-type errors, respectively, onto an ancilla qubit a. Note that a controlled Z-gate is realized by an inverted CNOT with the ancilla in the Z-basis as the target. (G) Example of fault-tolerant construction of circuits for logical qubit La: The encoding circuit for |00〉L has a single nondetectable error channel. A bit-flip error E occurring as shown can change the state to |01〉L, which is an error on the logical gauge qubit Lb. Logical qubit La is prepared fault-tolerantly. This property holds for all circuits (A to F).
With the Pauli operators X, Y, and Z and the identity I, the logical operators are
| (3A) |
| (3B) |
| (3C) |
| (3D) |
With these operators and the circuits given in Fig. 2 (A to D), any state |LaLb〉L can be generated maintaining the fault tolerance of La.
The [[4, 2, 2]] code has the additional advantage that, in contrast to other codes (19), fault-tolerant syndrome extraction for the logical qubit La can be achieved using a bare ancilla, that is, an ancilla qubit that is not itself a logical qubit. The stabilizers to extract logical phase-flip (Z) and bit-flip (X) errors are Sx and Sz, respectively
| (4A) |
| (4B) |
As in a Bacon-Shor code block (20, 21), the code space together with the logical operators and stabilizers form a subsystem that allows local syndrome extraction similar to that of Napp and Preskill (22), as depicted in Fig. 1. The difference is that the stabilizers have weight 4 because we simultaneously extract information about the gauge qubit Lb. Applying these stabilizers conditional on the state of an ancilla qubit extracts the parity of the data qubits along X or Z (see Fig. 2, E and F). Measuring the ancilla yields either |0〉, indicating no error, or |1〉, meaning an error has occurred and the run is to be discarded. With only one ancilla qubit available, we measure the two stabilizers in separate experiments. Because we prepare eigenstates of logical Pauli operators, only logical Pauli operations that change the ideal state result in errors. Both stabilizer measurements serve to determine the overall yield, that is, the fraction of runs for which no error was indicated. In addition to the error checks provided by stabilizer measurements, only even-parity outcomes are accepted when the data qubits are measured at the end of the circuit. Note that similar weight 4 stabilizers have recently been implemented in superconducting qubits (23).
We implement the [[4, 2, 2]] code on a fully connected quantum computer comprising a chain of five single 171Yb+ ions confined in a Paul trap (see Materials and Methods). The state-detection fidelity for a single qubit is 99.7(1)% for state |0〉 and 99.1(1)% for state |1〉. A general five-qubit state is detected with 95.7(1)% fidelity. Single- and two-qubit gate fidelities are typically 99.1(5) and 97(1)%, respectively. Typical gate times are 20 and 250 μs for single- and two-qubit gates, respectively. The computational gates H and CNOT are generated by combining several physical-level single- and two-qubit gates in a modular fashion (24).
RESULTS
We start by preparing state |00〉L using the circuit shown in Fig. 2A. The results of measuring this state directly after preparation are shown in Fig. 3A. The target states 0 (|00000〉) and 30 (|11110〉) show that we succeed in preparing and measuring this state with ≃90% probability. The data yield 91.1(4)% even-parity outcomes from the four data qubits. Breaking these results down by logical state gives 98.0(2)% population in the target state |00〉L. The error falls almost entirely on |01〉L, which corresponds to a 1.7(2)% error on the non–fault-tolerantly prepared gauge qubit Lb. The 0.11(6)% error exclusively on La is an order of magnitude lower than this, and at a similar level to the 0.18(7)% logical two-qubit error resulting in |11〉L. For the logical state preparation step, both of these small erroneous state populations are dominated by physical readout errors.
Fig. 3. Results achieved with logical state |00〉L.
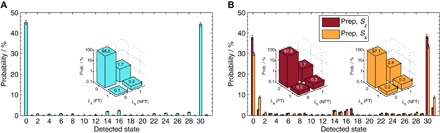
(A) Results from the preparation of state |00〉L. The abscissa represents the five-qubit states in decimal. We succeed in preparing (prep) and measuring the state with ~90% probability. The inset shows the result after postselection on the state being in the logical basis, that is, even parity. It is broken down by the logical state of the fault-tolerantly (FT) prepared qubit La and the non–fault-tolerantly (NFT) prepared qubit Lb. (B) Results of the stabilizer measurements after preparation of |00〉L. The yields are 77.8(6) and 65.2(7)% for Sz and Sx, respectively. The insets show that the error probability on the fault-tolerantly prepared and stabilized logical qubit La is an order of magnitude below the non–fault-tolerantly prepared and stabilized qubit Lb.
With |00〉L thus prepared, we apply in turn the two stabilizers Sz and Sx, shown in Fig. 2 (E and F), for nondemolition syndrome extraction. The results are shown in Fig. 3B. Populations in the odd-numbered states reflect events where an error is detected by a stabilizer. The results of the logical states are similar, with |00〉L populations of 97.8(2) and 97.1(3)%, respectively, and the errors occur predominantly in the non–fault-tolerantly prepared gauge qubit Lb. The errors on La are 0.2(1)%, similar to the error floor given by the |11〉L population, which is slightly higher than after mere state preparation due to the additional gates introduced by the stabilizers. Sx introduces X-type errors in the system, which can be seen from a higher Lb error. Sz introduces Z-type errors, which do not affect |00〉L. The opposite is true when applying the stabilizers to |++〉 instead. Table 1 (see Materials and Methods) summarizes results for different logical states prepared with the circuits shown in Fig. 2 (A to D). The circuit elements that dominate the intrinsic errors in our system are the two-qubit gates. Note that after a circuit with seven CNOT gates, each of which introduces 3 to 4% infidelity, we obtain the correct answer |00〉L with 97 to 98% probability. The gauge qubit Lb circuit failures occur at approximately the error rate of one two-qubit gate, whereas La errors are suppressed substantially below that level to <1%. These results show the power of fault-tolerant preparation and stabilizer measurement. The circuits succeed in discarding nearly all errors, but we pay a price because the yield is in the 65 to 75% range. We must expect to discard around half of the runs when measuring both stabilizers. The yield is higher for preparation of logical states without syndrome measurements because there are fewer gates to introduce error and there is only a single selection step.
Table 1. Probability distributions (in percentage) of measured logical states |LaLb〉 for various prepared logical states in each row, with and without stabilizers Sx or Sz applied.
The measurement basis is shown in the last column. The logical states are |00 > L … |11 > L, measured in the Z-basis, and | + + 〉L … | − − 〉L, measured in the X-basis. The very low error probability on the first logical qubit La compared to Lb shows the action of its fault-tolerant construction. We run every circuit 5000 to 6000 times. The results without stabilizer show the number of rejected runs from the parity check on the data qubits (typically ~8%) whereas the additional discard on the results with stabilizer (typically ~20%) is due to the ancilla result. The physical errors for state preparation and measurement are 0.3(1)% for states |0〉 and | + 〉, and 1.2(1)% for states |1〉 and | − 〉.
| Yield | Measured logical state |LaLb〉 | Measurement basis | ||||
| |00〉 | |01〉 | |10〉 | |11〉 | Z | ||
| | + + 〉 | | + − 〉 | | − + 〉 | | − − 〉 | X | ||
| |00〉L | 91.1(4) | 98.0(2) | 1.7(2) | 0.11(6) | 0.18(7) | Z |
| |00〉LSz | 77.8(6) | 97.8(2) | 1.7(2) | 0.18(8) | 0.3(1) | Z |
| |00〉LSx | 65.2(7) | 97.1(3) | 2.4(3) | 0.2(1) | 0.3(1) | Z |
| | + + 〉L | 91.1(4) | 95.7(3) | 3.9(3) | 0.24(8) | 0.22(8) | X |
| | + + 〉LSz | 68.2(7) | 93.0(5) | 4.2(4) | 1.3(2) | 1.5(2) | X |
| | + + 〉LSx | 72.1(6) | 94.3(4) | 4.5(4) | 0.5(1) | 0.7(2) | X |
| | − 1〉L | 90.1(4) | 0.22(8) | 50.5(8) | 0.09(6) | 49.2(8) | Z |
| | − 1〉L | 87.0(5) | 0.3(1) | 0.3(1) | 50.4(8) | 48.9(8) | X |
| | − 1〉LSz | 79.9(6) | 0.15(7) | 50.0(8) | 0.10(6) | 49.8(8) | Z |
| | − 1〉LSz | 75.5(6) | 0.4(1) | 0.3(1) | 50.1(8) | 49.2(8) | X |
| | − 1〉LSx | 72.1(6) | 0.6(1) | 50.2(8) | 0.5(1) | 48.7(8) | Z |
| | − 1〉LSx | 76.2(5) | 0.4(1) | 0.4(1) | 50.0(7) | 49.2(7) | X |
| |0 + 〉L | 93.2(3) | 47.4(5) | 52.5(5) | 0.06(3) | 0.05(3) | Z |
| |0 + 〉L | 92.4(4) | 50.0(8) | 0.04(4) | 49.8(8) | 0.09(5) | X |
| |0 + 〉LSz | 81.6(6) | 48.3(8) | 51.4(8) | 0.17(8) | 0.17(8) | Z |
| |0 + 〉LSz | 68.5(7) | 47.1(9) | 2.4(3) | 47.4(9) | 3.1(3) | X |
| |0 + 〉LSx | 72.0(6) | 48.3(8) | 51.5(8) | 0.16(7) | 0.12(7) | Z |
| |0 + 〉LSx | 70.9(7) | 49.4(9) | 0.4(1) | 49.7(9) | 0.5(1) | X |
| |11〉LSz | 73.3(6) | 0.4(1) | 0.3(1) | 2.8(3) | 96.5(3) | Z |
The [[4, 2, 2]] code allows transversal operations, that is, single-qubit logical gates that are generated by applying single-qubit physical gates. To show an example of this, we prepare |00〉L followed by the logical XaXb operation consisting of X-gates on physical qubits 2 and 3. This gives |11〉L, on which we apply the Sx stabilizer followed by readout. The yield is 77.3(6)%, and the logical state populations are as follows: |00〉L, 0.4(1)%; |01〉L, 0.3(1)%; |10〉L, 2.8(3)%; and |11〉L, 96.5(3)%. Apart from surpassing Lb as before, the La error of 0.7% also outperforms the physical qubit. We find that after an X-gate, the correct state of a physical qubit is measured with 98.8(2)% fidelity, nearly a factor of 2 worse than La. The infidelity in this case is dominated by the single-qubit detection error of 0.9(1)% for |1〉, which the code successfully suppresses in La.
To further investigate the robustness of the code, we add two kinds of error to the system. First, we deliberately introduce single- and two-qubit Pauli errors and study how errors on La and Lb scale with increasing physical qubit errors. Instead of trying to reproduce a stochastic error channel, which can be tedious for low error rates (25), we sample the various error configurations and then multiply them by their respective statistical importance to obtain a logical error probability (see Materials and Methods). We further compare our experimental results to an exact simulation with optimized error parameters (see Materials and Methods). The results are shown in Fig. 4A. The clear separation between the two logical qubits is persistent until they converge above 20% introduced error and approach the curve for the theoretical case without intrinsic errors. In this example, a physical qubit prepared in state |0〉 is outperformed by logical qubit La over the entire range, although our measurement uncertainty limits the significance of this to above p ~ 0.07%. Lb outperforms the physical qubit above 4% added error (solid black line in Fig. 4A). For state preparations |−〉 and |1〉, La also outperforms the physical error based on circuits of preparation and measurement, whereas for |+〉, the errors are consistent within statistical uncertainty (see Table 1).
Fig. 4. Performance of the code under different kinds of artificial errors.
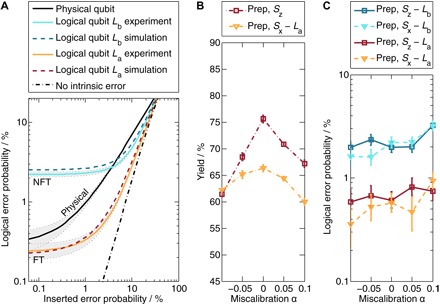
(A) Logical error probability under artificially introduced stochastic Pauli errors. Uncertainties shown in gray with dashed outlines. We prepare state |00〉L, introduce a specific error, and apply Sz before readout. The parameter values for the curves (see Materials and Methods) corresponding to the two logical qubits are determined either experimentally (solid lines) or from simulation (dashed lines). The black curve shows the limiting theoretical case without intrinsic errors (see Materials and Methods). At low added error rates, the intrinsic errors dominate, and the fault-tolerantly constructed qubit La starts about an order of magnitude below the non–fault-tolerantly constructed qubit Lb. With increasing inserted error probability, the added Pauli errors become dominant, and the La/b curves converge and approach the theory curve without intrinsic error. The solid black line shows the error rate for a single physical qubit. La results in a lower error across the entire range relative to the physical qubit, although our measurement uncertainty means that this is no longer significant below p ~ 0.07%. The Lb error is lower than the physical qubit for added errors >4%. (B and C) Preparing |00〉L and measuring Sx/z with purposefully miscalibrated two-qubit gates, known as XX-gates. A miscalibration of α means that the Bell state produced by the gate is imbalanced: . The yields diminishing with miscalibration for the stabilizer measurements are shown in (B), whereas the errors on the logical qubits presented in (C) remain similar, with La errors about an order of magnitude lower than Lb errors.
Second, we run the |00〉L data with purposefully miscalibrated two-qubit gates. The results for the logical errors are shown in Fig. 4C. The error gap of nearly an order of magnitude between La and Lb persists over a wide range of calibration errors, which are absorbed into a reduced yield as shown in Fig. 4B. This proves that the code succeeds in protecting qubit La against intrinsic systematic errors.
DISCUSSION
Note that the [[4, 2, 2]] code is relevant beyond its limited immediate application as an error detection code. It forms the base encoding layer of the high-threshold Knill C4/C6 code (26) and of a recent proposal for a topological code (27), and it is equivalent to one face of the distance 3 color code (28) or the Steane code (2). The code is robust to the high levels of intrinsic errors present in current realizations of quantum computers. We find no evidence of unexpected two-qubit correlated errors, which are always assumed absent when constructing error correction procedures. Therefore, our results both serve as a demonstration that this underlying model is correct and pave the way toward error-corrected quantum computations on a larger scale.
MATERIALS AND METHODS
Experimental system
The experiment was performed on a quantum computer consisting of a chain of five single 171Yb+ ions confined in a Paul trap and laser-cooled near the motional ground state. Each ion provided one physical qubit in the form of a pair of states in the hyperfine-split 2S1/2 ground level with an energy difference of 12.642821 GHz, which is magnetic field–independent to first order. This so-called “atomic clock” qubit has a typical coherence time of 0.5 s, which could be straightforwardly extended by suppressing magnetic field noise. All qubits were collectively initialized by optical pumping and measured via state-dependent fluorescence detection (29). Each ion was mapped to a distinct channel of a photomultiplier tube array. Its state could be detected with 99.4(1)% average fidelity, although a five-qubit state was read out with 95.7(1)% average fidelity, limited by channel-to-channel cross-talk. Qubit manipulation was achieved by applying two Raman beams from a single 355-nm mode-locked laser, which formed beat notes near the qubit frequency. The first Raman beam was a global beam applied to the entire chain, whereas the second was split into individual addressing beams, each of which could be switched independently to target any single qubit (24). Single qubit gates were generated by driving resonant Rabi rotations of defined phase, amplitude, and duration. Two-qubit gates (so-called XX-gates) were realized by illuminating two ions with beat-note frequencies near the motional sidebands and creating an effective spin-spin (Ising) interaction via transient entanglement between the state of two ions and all modes of motion (30–32). To ensure that the motion was left disentangled from the qubit states at the end of the interaction, we used a pulse shaping scheme by modulating the amplitude of the global beam (33, 34).
Artificial stochastic errors
To analyze how the code copes with artificially introduced stochastic errors, we prepared logical state |00〉L and added a specific Pauli error, for example, I ⊗ X ⊗ Y ⊗ I. We then applied the Sz stabilizer and measured the state. We repeated this for different error configurations ε. The error probability p on a physical qubit corresponds to an X, Y, or Z error, each occurring with probability p/3. The number of errors that appear in a particular error configuration is given by its weight w, and its probability of occurrence or statistical importance is po = (p/3)w(1 − p)4−w. The probability of a logical error is given by
| (5) |
The sum runs over all error configurations. pa is the yield, that is, the probability that a run is accepted, and pf is the probability of failure after postselection, that is, the probability that an accepted run suffers a logical error. The dividend is the number of accepted runs with a logical error, whereas the divisor is the number of accepted runs (both divided by the total number of runs). The parameters pa and pf were found from either experiment or simulation (see Fig. 4A). Out of the total number of error configurations, . We covered the error configurations of weight 0 and 1 exhaustively. For the w = 2 subset, we only sampled 27 representative configurations out of the total 54 and doubled their weight. The weight 3 and weight 4 subsets were not sampled, and their logical error rates were set to zero, because their statistical importance is significant only at very high added error rates. In the limit of no intrinsic errors, that is, perfect gates, preparation, and measurement, both logical qubits had the same error rate under this model (dash-dotted line in Fig. 4A). We found this error rate from Eq. 5 by counting accepted error configurations with w ≤ 2 (denominator) and checking which of those caused an error (numerator).
| (6) |
The dashed curves in Fig. 4A were obtained by performing a full density matrix simulation of the five-qubit circuits. We used a simplified error model to emulate experimental errors. The model had three independent parameters corresponding to errors associated with over- or underrotations after (i) single-qubit and (ii) two-qubit gates and (iii) phase errors caused by Stark shifts. An experimentally found state-transfer matrix was used to take state preparation and detection errors, including cross-talk, into account. We then optimized the model over the parameter space to minimize the difference between the final state populations of the experimental and simulated circuits. The resulting values for the error rates were 0.50, 1.0, and 1.4%, respectively.
The physical error curve in Fig. 4A is the straight line pp = r + (2/3 Fx)p, where r = 0.003 is the readout error for a physical qubit in state |0〉. The slope is 2/3 Fx because one in three added errors is a Z-type error, which does not affect |0〉, and Fx = 0.997 is the success probability of a physical spin flip operation.
Acknowledgments
We thank J. Kim and D. Maslov for helpful discussions and D. Gottesman for useful comments. Funding: This work was supported by the Army Research Office with funds from the Intelligence Advanced Research Projects Activity LogiQ program (grant 3130638), the Air Force Office of Scientific Research Multidisciplinary University Research Initiative program on Quantum Measurement and Verification (grant 5710003628), and the NSF Physics Frontier Center at the Joint Quantum Institute (grant PHY0822671). Author contributions: N.M.L., M.G., K.A.L., C.F., S.D., K.R.B., and C.M. all contributed to the experimental design, construction, data collection, and analysis of this experiment. All authors contributed to this manuscript. Competing interests: C.M. is a founding scientist of IonQ Inc. All other authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper. Additional data related to this paper may be requested from the authors.
REFERENCES AND NOTES
- 1.Calderbank A. R., Shor P. W., Good quantum error-correcting codes exist. Phys. Rev. A 54, 1098–1105 (1996). [DOI] [PubMed] [Google Scholar]
- 2.Steane A. M., Multiple-particle interference and quantum error correction. Proc. R. Soc. A 452, 2551–2577 (1996). [Google Scholar]
- 3.Preskill J., Reliable quantum computers. Proc. R. Soc. A 454, 385 (1998). [Google Scholar]
- 4.M. A. Nielsen, I. L. Chuang, Quantum Computation and Quantum Information: 10th Anniversary Edition (Cambridge Univ. Press, ed. 10, 2011). [Google Scholar]
- 5.D. Gottesman, An introduction to quantum error correction and fault-tolerant quantum computation, in Quantum Information Science and Its Contributions to Mathematics, S. J. Lomonaco Jr., Ed. (American Mathematical Society, 2009), vol. 68, pp. 13–59. [Google Scholar]
- 6.Chiaverini J., Leibfried D., Schaetz T., Barrett M. D., Blakestad R. B., Britton J., Itano W. M., Jost J. D., Knill E., Langer C., Ozeri R., Wineland D. J., Realization of quantum error correction. Nature 432, 602–605 (2004). [DOI] [PubMed] [Google Scholar]
- 7.Schindler P., Barreiro J. T., Monz T., Nebendahl V., Nigg D., Chwalla M., Hennrich M., Blatt R., Experimental repetitive quantum error correction. Science 332, 1059–1061 (2011). [DOI] [PubMed] [Google Scholar]
- 8.Lanyon B. P., Jurcevic P., Zwerger M., Hempel C., Martinez E. A., Dür W., Briegel H. J., Blatt R., Roos C. F., Measurement-based quantum computation with trapped ions. Phys. Rev. Lett. 111, 210501 (2013). [DOI] [PubMed] [Google Scholar]
- 9.Waldherr G., Wang Y., Zaiser S., Jamali M., Schulte-Herbrüggen T., Abe H., Ohshima T., Isoya J., Du J. F., Neumann P., Wrachtrup J., Quantum error correction in a solid-state hybrid spin register. Nature 506, 204–207 (2014). [DOI] [PubMed] [Google Scholar]
- 10.Nigg D., Müller M., Martinez E. A., Schindler P., Hennrich M., Monz T., Martin-Delgado M. A., Blatt R., Quantum computations on a topologically encoded qubit. Science 345, 302–305 (2014). [DOI] [PubMed] [Google Scholar]
- 11.Kelly J., Barends R., Fowler A. G., Megrant A., Jeffrey E., White T. C., Sank D., Mutus J. Y., Campbell B., Chen Y., Chen Z., Chiaro B., Dunsworth A., Hoi I.-C., Neill C., O’Malley P. J. J., Quintana C., Roushan P., Vainsencher A., Wenner J., Cleland A. N., Martinis J. M., State preservation by repetitive error detection in a superconducting quantum circuit. Nature 519, 66–69 (2015). [DOI] [PubMed] [Google Scholar]
- 12.Córcoles A. D., Magesan E., Srinivasan S. J., Cross Andrew W., Steffen M., Gambetta Jay M., Chow Jerry M., Demonstration of a quantum error detection code using a square lattice of four superconducting qubits. Nat. Commun. 6, 6979 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Cramer J., Kalb N., Rol M. A., Hensen B., Blok M. S., Markham M., Twitchen D. J., Hanson R., Taminiau T. H., Repeated quantum error correction on a continuously encoded qubit by real-time feedback. Nat. Commun. 7, 11526 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Ofek N., Petrenko A., Heeres R., Reinhold P., Leghtas Z., Vlastakis B., Liu Y., Frunzio L., Girvin S. M., Jiang L., Mirrahimi M., Devoret M. H., Schoelkopf R. J., Extending the lifetime of a quantum bit with error correction in superconducting circuits. Nature 536, 441–445 (2016). [DOI] [PubMed] [Google Scholar]
- 15.Grassl M., Beth T., Pellizzari T., Codes for the quantum erasure channel. Phys. Rev. A 56, 33–38 (1997). [Google Scholar]
- 16.Gottesman D., Quantum fault tolerance in small experiments. arXiv:1610.03507 (2016). [DOI] [PubMed] [Google Scholar]
- 17.Lu C.-Y., Gao W.-B., Zhang J., Zhou X.-Q., Yang T., Pan J.-W., Experimental quantum coding against qubit loss error. Proc. Natl. Acad. Sci. U.S.A. 105, 11050–11054 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bell B. A., Herrera-Martí D. A., Tame M. S., Markham D., Wadsworth W. J., Rarity J. G., Experimental demonstration of a graph state quantum error-correction code. Nat. Commun. 5, 3658 (2014). [DOI] [PubMed] [Google Scholar]
- 19.Cross A. W., DiVincenzo D. P., Terhal B. M., A comparative code study for quantum fault tolerance. Quantum Inf. Comput. 9, 0541–0572 (2009). [Google Scholar]
- 20.Bacon D., Operator quantum error-correcting subsystems for self-correcting quantum memories. Phys. Rev. A 73, 012340 (2006). [Google Scholar]
- 21.Shor P. W., Scheme for reducing decoherence in quantum computer memory. Phys. Rev. A 52, R2493 (1995). [DOI] [PubMed] [Google Scholar]
- 22.Napp J., Preskill J., Optimal Bacon-Shor codes. Quantum Inf. Comput. 13, 490–510 (2013). [Google Scholar]
- 23.Takita M., Córcoles A. D., Magesan E., Abdo B., Brink M., Cross A., Chow J. M., Gambetta J. M., Demonstration of weight-four parity measurements in the surface code architecture. Phys. Rev. Lett. 117, 210505 (2016). [DOI] [PubMed] [Google Scholar]
- 24.Debnath S., Linke N. M., Figgatt C., Landsman K. A., Wright K., Monroe C., Demonstration of a small programmable quantum computer with atomic qubits. Nature 536, 63–66 (2016). [DOI] [PubMed] [Google Scholar]
- 25.Bravyi S., Vargo A., Simulation of rare events in quantum error correction. Phys. Rev. A 88, 062308 (2013). [Google Scholar]
- 26.Knill E., Quantum computing with realistically noisy devices. Nature 434, 39–44 (2005). [DOI] [PubMed] [Google Scholar]
- 27.Criger B., Terhal B., Noise thresholds for the [[4, 2, 2]]-concatenated toric code. QIC 16, 1261–1281 (2016). [Google Scholar]
- 28.Bombin H., Martin-Delgado M. A., Topological quantum distillation. Phys. Rev. Lett. 97, 180501 (2006). [DOI] [PubMed] [Google Scholar]
- 29.Olmschenk S., Younge K. C., Moehring D. L., Matsukevich D. N., Maunz P., Monroe C., Manipulation and detection of a trapped Yb+ hyperfine qubit. Phys. Rev. A 76, 052314 (2007). [Google Scholar]
- 30.Mølmer K., Sørensen A., Multiparticle entanglement of hot trapped ions. Phys. Rev. Lett. 82, 1835 (1999). [Google Scholar]
- 31.Solano E., de Matos Filho R. L., Zagury N., Deterministic Bell states and measurement of the motional state of two trapped ions. Phys. Rev. A 59, R2539 (1999). [Google Scholar]
- 32.Milburn G. J., Schneider S., James D. F. V., Ion trap quantum computing with warm ions. Fortschritte der Physik 48, 801–810 (2000). [Google Scholar]
- 33.Zhu S.-L., Monroe C., Duan L.-M., Arbitrary-speed quantum gates within large ion crystals through minimum control of laser beams. Europhys. Lett. 73, 485 (2006). [Google Scholar]
- 34.Choi T., Debnath S., Manning T. A., Figgatt C., Gong Z.-X., Duan L.-M., Monroe C., Optimal quantum control of multimode couplings between trapped ion qubits for scalable entanglement. Phys. Rev. Lett. 112, 190502 (2014). [DOI] [PubMed] [Google Scholar]


