From flamingo dance to (desirable) drug discovery: a nature-inspired approach

Abstract

The therapeutic effects of drugs are well known to result from their interaction with multiple intracellular targets. Accordingly, the pharma industry is currently moving from a reductionist approach based on a ‘ one-target fixation ’ to a holistic multitarget approach. However, many drug discovery practices are still procedural abstractions resulting from the attempt to understand and address the action of biologically active compounds while preventing adverse effects. Here, we discuss how drug discovery can benefit from the principles of evolutionary biology and report two real-life case studies. We do so by focusing on the desirability principle, and its many features and applications, such as machine learning-based multicriteria virtual screening.

Graphical abstract

Introduction

For years, the drug discovery pipeline has been outlined by a well-established series of rationally connected steps aimed at (i) defining a biological target; (ii) screening large collections of compounds to identify hits; (iii) hit-to-lead generation implying chemical modifications; (iv) lead optimization for developing drug candidates; and (v) performing preclinical trials validating a new potential drug, among others. The success rate along the drug discovery pipeline depends on the chance of crossing filters that are used to discard compounds whose features do not match those typical of drugs [1]. However, approaching drug discovery in such an ‘inverted cone-shaped’ fashion constitutes a simplified procedural abstraction often detached from the intimate nature of drug biology encompassing the occurrence of simultaneous and multilevel complex interactions, that is, the mode of action of the drug.

It is now widely accepted that drugs are inherently poly-pharmacological because they can act on multiple targets or disease pathways [2]. Even drugs with relatively high target specificity are known to engage a multitude of proteins via a structured network of hydrogen, hydrophobic, and ionic interactions, thus inducing their 3D structures and modulating their functioning [3]. In this complex scenario, we should reconsider the way we search for new drugs and move beyond the reductionist ‘one-target fixation’ paradigm [4].

To bridge drug discovery and biology, we should first acknowledge the multifaceted nature of drugs and then readdress the drug discovery approach [5]. Instead of analyzing thousands of candidate compounds by using sequential filters, each accounting for one property at a time, we should attempt to optimize more properties simultaneously. Such an approach would also be more akin to that which occurs in nature. In fact, most known natural drugs are likely to have been molded by the process of evolution indirectly via the enzymatic systems responsible for their synthesis [6], thus optimizing all the possible ‘facets’ to balance their on/off-target profile [7,8].

Thus, we suggest that the concept of evolution should be applied to drug discovery. The process of drug discovery can be directly paralleled to that of evolution, whose success depends on natural selection, among other driving forces. In nature, evolutionary improvement occurs via the continuous selection of well-established features enabling organisms to adapt, survive, and reproduce. In drug discovery, scientists are committed to adjusting several physicochemical and biological properties in the search for drugs. However, potent ligands against a therapeutic target are abandoned along the drug discovery pathway [1] if they do not show an acceptable spectrum of physicochemical, absorption, distribution, metabolism, and elimination (ADME) properties along with a minimal risk of toxic effects.

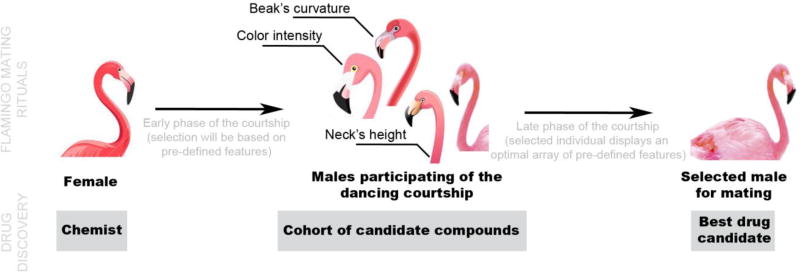
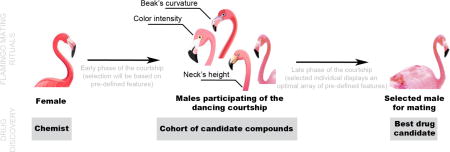
The parallelism between this new way of approaching drug discovery and the courtship rituals of the flamingo is exemplified in Figure 1. When flamingos are approximately 6 years of age, they are ready to start mating. To find a partner, flamingos engage in a variety of courtship rituals, mostly initiated by the males. If these are impressive enough, the female will likely pair up. By studying hundreds of mating couples, it was realized that females judge dancing males by several key factors: color intensity of the feathers; movement coordination; height of the neck; and curvature of the beak. Similar to an experienced chemist looking for an appropriate drug candidate, a female flamingo will choose the partner that has the most suitable features for mating [9,10].

Figure 1.

From flamingo mating rituals to drug discovery.

Therefore, we argue that evolution and drug discovery are both meaningful examples of an optimization process. Thus, if we wanted to approach drug discovery by mimicking evolution, which strategy should we use? We suggest that multicriteria optimization (MCO) methods are well suited to guide the simultaneous optimization of multiple factors. Many recent developments have focused on methods to aid the simultaneous optimization of multiple factors required in a successful drug, targeting compounds with the highest chance of downstream success early during the discovery process [1]. However, formalized MCO approaches are not widely used in drug design [11]. Thus, here provide the ‘anatomy’ and potential scope of methods for MCO in drug discovery. In particular, we focus on MCO methods based on desirability functions.

Digging in the brain of a female flamingo: MCO

Similar to the female flamingo in our parallel story, a chemist at the start of a drug discovery project already has in mind the type of compound(s) that is being looked for. In both cases, the aim is to reach an objective (being that a male to mate with, or a drug candidate) by walking a viable route. In this scenario, a potential solution is a multidimensional search space (i.e., a complete combinatorial library or all the males in the flamingo colony) that is highly scored across all dimensions. The idea of scoring compounds based on multicriteria functions is not new in drug discovery: the Rule of Five (Ro5) for the design of oral drugs initially proposed by Lipinski et al. [12] was one of the earliest and perhaps the most popular example of such an approach. The Ro5 inspired many others and encouraged the implementation of other rules for assessing the ‘drug-likeness’ of compounds [13].

Despite their applicability, the Lipinski Ro5 as well as other related approaches reflect a static view of drug discovery [11] that is based on a compound-centric perspective typical of lead optimization projects [14]. However, to quantify the progression of lead optimization projects through process-centric analysis, statistical frameworks are needed. Such process-centric statistical frameworks operate as compound prioritization systems that are flexible and easily adaptable to issues, such as druggability and safety concerns, binding potency, and even conflicting properties, that emerge from the early stages of the drug discovery process. In this context, MCO methods are useful because they accelerate the identification of candidates at each stage of the drug discovery process.

There are numerous examples of MCO methods applied to drug discovery: to derive multiobjective quantitative structure-activity relationship (QSAR) models [15,16]; to trade-off scoring and posing in molecular docking [17,18]; to build maximally diverse and drug-like molecular libraries; and to carry out de novo design programs [19,20]. In this respect, the variety of mathematical implementations of MCO methods is vast, including the simple application of multiple property filters and complex data integration and classification schemes (e.g., support vector machines), all with arguable pros and cons. However, it can be difficult for inexperienced chemists to navigate this rainbow of possible MCO approaches. The lack of a specific knowledge background and the intrinsic complexity of such methods are the main reasons why these approach have gained little practical use and are not appealing to nonstatistician practitioners. Here, we highlight the ‘real-life’ potential of MCO methods and introduce these concepts to nonexperts. Emphasis is given to the implementation of the desirability functions that, just as in evolution, exert a kind of natural selection process to address the choice of the best possible option.

For the sake of clarity, we exemplify this concept once more. If we are to perform a MCO on a compound series based in a standard (less natural) fashion, we would apply several serial filters, each one stepwise, controlling a given property, such as molecular weight, solubility, and so on. However, the optimization of a property at a given stage can sometimes be to the detriment of another one at a different level. In our proposed strategy, the optimization process aims to find an optimal balance between all the properties so that deviations in even one property will affect the overall solution [21]. Coming back to our flamingo example, even when the female looks for the best demonstration of male attributes, such as feather color intensity and curvature of the beak, natural selection imposes boundaries along which such characters might manifest. For instance, intense feather color is disadvantageous because it makes the male an easy target for predators, whereas a beak that is too curved beak its ability to find food [9,10]. Applied to drug discovery, the desirability function aims to achieve the optimal trade-off between different compound properties.

First introduced by Harrington in 1965 [22], the desirability function approach is one of the most widely used methods in industry for the optimization of multiple response processes. It is based on the idea that the quality of a product or process that has multiple quality characteristics but where one is outside some desired limit is completely unacceptable. The method finds operating conditions (i.e., the properties) that provide the most desirable response values (i.e., the endpoints). The desirability principle is especially useful for solving problems that involve incommensurate and conflicting responses that require simultaneous optimization to some extent, because separate analyses can result in incompatible solutions [23].

In this respect, a widely pursued MCO strategy comprises combining multiple individual endpoints into a single composite optimization function: the desirability function. It offers some advantages over other MCO approaches, including: (i) desirability-based methods are easy to understand, easy to use, and highly flexible when incorporating decision-maker preferences (weights or priorities assigned to responses); and (ii) the most popular desirability-based method, the Derringer and Suich’s method [24] or its modifications [25], are available in many data analysis software packages.

Most reviews on MCO, including surveys of desirability-based approaches, focus on examples of successful applications of MCO to drug discovery. However, this can be hard to follow for unfamiliar readers, in particular nonstatisticians. Here, we take an anatomical tour through the desirability principle because we believe that drug discovery will benefit from four advantages to its use: (i) avoiding hard filters; (ii) its adaptability; (iii) its ability to deal with missing values and data uncertainty; and (iv) solution ranking and virtual screening (VS). Therefore, here we review those studies that best describe each of these features (Table 1).

Table 1.

Examples of formalized MCO applications in drug discovery that maximally exploit different features of the desirability principle

Application	Endpoints being co-optimized	Desirability function feature(s) that is (are) most exploited	Refs
Central nervous system marketed drugs	Lipophilicity; distribution coefficient; topological polar surface area; molecular weight; number of hydrogen bond donors; most basic center	Solution ranking and VS	[33]
Non-nucleoside HIV reverse transcriptase (RT) inhibitors	RT inhibitory efficacy; toxicity over MT4 blood cells	Solution ranking and VS	[54]
Antidepressant drugs	Binding to a targeted receptor (tR); functional assay on a receptor different to tR; binding to other four receptors; probability of non-mutagenicity; metabolization rate	Adaptability	[28]
Inflammatory/immune process (P2X7 inhibitors)	Potency; solubility; safety	Ability to deal with missing values and data uncertainty; avoiding hard filters	[26]
Antibacterial activity (fluoroquinolones)	Potency; safety; bioavailability	Solution ranking and VS	[35]
Central nervous system marketed drugs	Aqueous solubility; human intestinal absorption; calculated logP; P-gp transport; plasma protein binding; CYP2D6 affinity; CYP2C9 affinity; blood–brain barrier penetration; hERG inhibition	Ability to deal with missing values and data uncertainty; avoiding hard filters	[29]
Antialzheimer agents	Affinity; selectivity	Solution ranking and VS	[55]
Extended-release formulations for propranolol	Set of 20 pharmacokinetics parameters	Adaptability; avoiding hard filters; solution ranking and VS	[27]
Optimization of oral drugs	MOLECULAR weight; ALOGP; number of HBDs; number of HBAs; molecular PSA; number of ROTBs; number of AROMs	Solution ranking and VS	[56]
Inhibitors of serotonin 5-hydroxytryptamine (5-HT1A) receptor	Set of 11 pharmacokinetics parameters	Ability to deal with missing values and data uncertainty	[57]

Seeing through the eyes of a female flamingo: what is desired?

A desirability function is a mathematically simplified description of a decision-maker preference. It transforms an objective function to a scale-free desirability value, which measures the decision-maker satisfaction against the objective value [11]. In the context of drug design, the decision maker is the chemist and the objective functions, as shown in Table 1, refer to the endpoint values, which can be experimentally measured or theoretically predicted. Here, we highlight four features that make desirability functions appropriate for drug discovery projects.

Feature 1: avoiding hard filters

By using a desirability function, one can avoid the artificial harshness of using dichotomic filters. The desirability function enables the translation of the value of an endpoint into a number ranging from 0 to 1, where a desirability equal to 1 indicates an ideal endpoint value, whereas a desirability equal to 0 indicates a completely unacceptable outcome. In contrast to the binary pass/fail outcome of hard filters, this approach provides a continuous desirability scale accounting for even slight changes in the value of the endpoint. This enables in-depth and more informative compound analysis and quality assessment [11].

Desirability functions can take many forms (see [1,26] for graphical representations), which mostly depend on the so-called ‘shape factors’ flagged by the user. For instance, the desirability function can take a single input (an assay response that is a potency measure in nM units) and transform it according to the linear decay between given thresholds for modeling. This approach can be easily extrapolated to the usual practice in medicinal chemistry, where a drug designer intuitively works with thresholds and acceptable ranges for endpoint values [26]. Suppose an acceptable potency ranges from 500 nM to 50 nM, the desirability function will return a score of 1 for compounds with potency <50 nM and a score of 0 for compounds with potency >500 nM. A score in the interval [0,1] is given to all the other compounds completing the piecewise linear desirability function. Irrespective of whether the piecewise desirability function is linear, sigmoidal, or of another form, the use of the desirability function has the benefit of smoothing endpoint values compared with to hard filters [11]. Once each endpoint has been assigned a [0, 1] desirability score, all the endpoints can be combined into an overall weighted desirability.

There are still two open questions. First, how can we assign weights to the desirability scores of individual endpoints? Second, how can we choose the aggregation scheme to integrate information relative to all endpoints being optimized to provide a unique desirability score per compound? Regarding the first question, weights should reflect the current priorities in a project ,which can change from the very early stages. This means that equally weighted desirabilities can be set, whereas priorities are not well established, and that the weights can change if some issues become critically important to solve during the course of the project. For the second question, there are several possible ways to convert the multiple individual endpoint desirability values into a single comprehensive measure of overall desirability. This includes the simple summation of all individual desirability scores, the weighted geometric mean, among others (reviewed in [26,27]).

At the end, the overall desirability value is always maximized so that the optimal settings of the ingredient amounts can ensure the best balance among the multiple characteristics of interest. By doing so, drug design becomes a more natural process that is comparable with human nature in the sense that one is not able to grasp a complex set of values until the impact of them is seen in a concrete way.

Feature 2: adaptability

Unlike those based on sequential hard filters, modern drug design projects need to be flexible and easily adaptable to unforeseen changes. The desirability principle implements such flexibility into drug design projects by enabling us to optimize what is needed at any stage. By applying the steps described in ‘Feature 1’ of the desirability principle, a designer can automatically create custom functions to optimize any number of endpoints (or properties) at any point during the process. For instance, we have mentioned that weights assigned to the desirability scores of individual endpoints can change from one stage to another, when the project goals change, or when our understanding of the chemical and biological systems sharpens.

Work by Le Bailly de Tilleghem et al. [28] is an excellent example of how we can maximally benefit from the adaptability and flexibility of the desirability principle. In this research, the authors aimed to generate new potential drugs by using combinatorial chemistry, implying the selection and combination of R-groups and reagents for decorating a lead compound to generate novel candidates. Such an approach leads to the creation of chemical libraries usually containing a very large number of virtual compounds, far too large to permit their chemical synthesis. Here is where the desirability principle comes in handy to select a smaller subset of ‘good’ reagents for each R-group and synthesize all their possible combinations. However, the number of possible sublibraries is huge, making the task unfeasible in a reasonable time. Le Bailly de Tilleghem et al. found a way to explore each possible sublibrary in a parallel fashion by applying custom desirability functions, each one tailored to the specificity of the sublibrary in question [28]. The tailoring process is guided by a weighting of the endpoints that is recursively adapted as the solution space is explored.

Another striking example of adaptability is reported in the case of the optimization of a pharmaceutical formulation [27]. When applying the weighted overall desirability value (calculated as mentioned above) for the optimization of a pharmaceutical formulation, the results are not always those expected. Instead, they are sensitive to the weights, whose values are highly subjective. Moreover, traditional desirability function-based methods only take into account the means of the compound characteristics. To overcome these limitations, Li et al. [27] implemented additional parameters accounting for the response variance and covariance into the desirability function, thus obtaining more reliable outcomes.

Feature 3: ability to deal with missing values and data uncertainty

The ability of desirability functions to deal with missing values (and with data uncertainty) is perhaps their most important feature. When experimental data are used in the framework of a MCO project, often there are molecules devoid of experimental values. At this point, any MCO approach that applies ties between optimization and data completeness will leave us stranded midway. Once more, the desirability principle comes in handy. In this respect, the designer can take two possible decisions: (i) to implement a mathematical expression for the overall desirability score (aggregation scheme) that explicitly accounts for gaps in the data; or (ii) to make use of an imputation system to fill in those missing values. There are several examples in the literature for both strategies (refer to Table 1 for selected examples).

Nissink et al. [26] transparently dealt with missing values by adopting the approach of so-called ‘dimensionality reduction’. Depending on the number of available data points (properties with experimentally measured values), the dimension of the property space for each compound is defined. Thus, it is possible that, for compound A, the overall desirability score is calculated on the basis of four values, whereas that for compound B is done on the basis of only three values. By contrast, Segall et al. [29] took advantage of in silico models, such as SAR models, specifically of their ability to predict properties of virtual structures. In silico tools have the potential to derive a meaningful properties space in terms of both the number of processed molecules and the property spectrum.

However, when choosing the path for data imputation, we acknowledge that not all the predicted values have the same reliability. Even for experimentally determined values, their reliability could vary substantially. An experimental value from an assay with a high signal:noise ratio has higher reliability than a measure from a different assay with a low signal:noise ratio [11]. Greater attention is now paid to assessing the uncertainty of the data used for the selection and optimization of compounds [1]. Unless the selected MCO approach explicitly reflects the impact of combining multiple uncertain data points into an overall assessment of compound quality, there is a high risk of incorrectly rejecting good compounds because of uncertain predictions. The probabilistic nature of the desirability functions makes them suitable for explicitly approaching data uncertainty. Nissink et al. [26] considered the potential for errors in the overall desirability of a compound resulting from the uncertainty in the underlying predicted or experimental compound data. They examined the probability that the desirability of each compound property is greater or less than the value assigned and combined these into an overall confidence parameter for the compound score. This strategy provides an indication of cases where a compound score should be treated with caution. In general terms, the weighting of various measures (i.e., desirability functions) can reflect their importance with respect to not only the goals of the project, but also the reliability of the measures.

Feature 4: solution ranking and virtual screening

The ultimate goal of a MCO approach is to end up with a narrowed-down pool of optimal compounds that will survive for further applications (i.e,, a male to pair with in our parallel flamingo story). As in the flamingo courtship ritual, where the female has to rank all the male candidates, a chemist can find the optimal compound by ranking a plethora of compounds based on an objective function. However, a question arises here: should we prefer to perform simple ranking based on the overall combined desirability score or should we prefer to explicitly model compound optimality among our solutions space? The latter can be addressed by the Pareto optimization. This optimization scheme is based on the assumption that there might not be a single optimal solution to an optimization problem, but a family of possible equivalent trade-off solutions [30]. A Pareto optimal solution (a compound in the context of drug discovery) is one for which there is no other solution that is better in all other properties. In other words, a compound is Pareto optimal if, when examining the aspects being considered (i.e., endpoints), further improvement to one property would come at the detriment of one or more other properties of that molecule.

Pareto optimization is best applied in situations where an ideal compound cannot be found and the acceptable trade-offs between properties are not known a priori [1]. The Pareto algorithm samples different properties combinations, which can be studied further to determine the best compromise (i.e., trade-off). However, a limitation of Pareto optimization is that the number of optimal compounds increases exponentially with the number of properties being optimized. In practice, the number of optimal compounds becomes too large to be useful when considering more than approximately four properties [1]. A further limitation is that data uncertainty cannot be explicitly incorporated into the Pareto optimization scheme. This becomes an important drawback when the MCO approach is used as a strategy to fill in missing data, such as by using in silico SAR models. The uncertainty associated with in silico predictions are traditionally captured in what is called the ‘applicability domain’ [31,32], an especially important concept in QSAR that allows researchers to estimate the reliability in the prediction of a target molecule based on the information used to build that model [33].

Desirability-based optimization can overcome all the limitations above described for Pareto optimization when it is combined with the appropriate classification schemes. As anticipated in the previous paragraph, it is possible to explicitly incorporate data uncertainty during desirability function calculations. Therefore, the desirability functions can, in various ways, account for the domain of applicability when used side-by-side with QSAR studies (which can act as a classification schemes). As shown by Cruz-Monteagudo et al. [34–36], desirability-based MCO strategies enable researchers to conduct global QSAR studies to detect predictor variables that produce the best possible compromise among considered properties (endpoints). The resultant QSAR model can be easily used for downstream applications, such as VS, as discussed below.

To wrap up the discussion on whether it is better to pick the best compound from a ranking list or to perform an optimality search from desirability scores, let us consider the flamingo parallel story once again. At the end of the courtship ritual, the female is compelled to pick a male to reproduce. As selfish as our instinct is, the ultimate goal of the female decision is to pass her genes to the progeny, so she expects the selected male to be as good as possible during the nesting season for their progeny to survive. In the absence of previous experience with this particular male, selection by the female is full of uncertainty but she perceives the male as a plausible best choice, having no evidence this male is an optimum one. In essence: when dealing with data uncertainty (which commonly happens in drug discovery), compound ranking will work better than searching for an overall optimal compound.

The flamingo dancing courtship in action

To show the potential of the desirability principle, we herein first describe how to construct tailored ensembles-derived desirability functions for multicriteria VS. Such a method was challenged on two real-life case studies. The proposed approach incorporates the aforementioned advantages of the desirability functions when applied to multicriteria research programs for drug discovery. In essence, this methodology: (i) avoids the use of hard filters; (ii) is easily adaptable to the current requirements; (iii) can deal with endpoint missing values; and (iv) provides a continuous score to prioritize chemical compounds after screening large databases. In addition, our approach based on ensemble modeling ensures better coverage of the chemical space through the definition of a dynamic applicability domain [37].

To use desirability functions in MCO, it is mandatory to have measurements of all endpoints for every sample in the data set. Unfortunately, this is not usual in most drug discovery problems. The most common scenario in a drug discovery campaign where different properties are to be simultaneously optimized is that data for each endpoint were not always measured for all the compounds. Even worse, these pools of compounds for which the properties under investigation have been measured are often of limited size and, thus, cover only a small region of the chemical space. To address these issues, we propose the use of accurate, robust, and predictive classification ensemble models as predictors for each endpoint. These ensemble models are built from base QSAR models according to good practices for QSAR modeling [38]. In this respect, it is important to define the applicability domain of the model to be able to confidently predict samples not used to train the model. In our proposal, the applicability domain of the base models, as well as of the ensembles, is explicitly considered throughout the modeling process, from the training of the base models to the prediction of the final aggregated multicriteria desirability.

Unlike using regression models, we use desirability functions derived from classification models to minimize the risk of noise in the modeling process [39,40]. This usually happens because endpoint data come from different labs and measurements can significantly deviate from one experiment to other even when the same protocols have been used. As a result, the uncertainty related to the determination of accurate endpoint data is the main reason to develop classification models.

The choice of one ensemble of QSAR models as the predictor for each property is justified by the success of this type of modeling strategy in previous studies [41,42]. QSAR modeling bases on the similarity principle: that is, compounds with similar structures should have similar bioactivities. In brief, QSAR modeling correlates the structure of chemical compounds with their bioactivities [43]. This is done by codifying the chemical structures through molecular descriptors, which results in their transformation into vectors of features containing relevant structural information. This information is then used as input for statistical and machine-learning algorithms leading to models (which can be seen as black boxes) capable of predicting the bioactivity of new compounds.

To ensure a proper QSAR modeling workflow, it is necessary to perform a curation of the data (compounds and bioactivities) used in the modeling process and the thorough validation of the proposed models, and to define the applicability domain of the models [38,44]. The data curation process includes steps such as: ring aromatization; normalization of specific chemotypes, such as nitro, to one unique representation; the curation of tautomeric forms; the removal of duplicate structures; the unambiguous assignment of each compound to a group; and the identification of activity cliffs [45]. In addition, QSAR models need to be properly validated. Besides measuring the accuracy of a model, cross-validation experiments have to be performed to estimate its potential generalization capabilities. Ultimately, a set of compounds with known bioactivities (external test set) has to be reserved to evaluate the real predictive power of a model once it has been trained and validated.

A critical step when using a QSAR model for the prediction of the bioactivity of new chemical compounds is to establish whether the model is suitable for this task. This evaluation is performed based on the definition of an applicability domain for the model [31,38]. This can be established based on the similarity of the compound to be predicted to the compounds used to train it. Also, the range of the values of the descriptors the model is trained from can be used to define the applicability domain of a model. If a chemical compound is within the applicability domain of a model, then the bioactivity prediction it makes for the compound can be considered reliable.

It is a fact well accepted by QSAR practitioners that no model can capture all information related to the SARs. Ensemble modeling has emerged as an effective approach to obtain a more complete description of this relationship [41,42]. The rationale behind ensemble modeling is to develop a set of local models, that is, models that are accurate and predictive in different regions of the chemical space. These models are then aggregated, for example through the averaging of their outputs, to produce a prediction that considers different sources of information. Given that ensemble models comprise the aggregation of a set of diverse models, the applicability domain of this ensemble increases relative to that of the individual models.

Tailored ensemble-derived desirability functions for multicriteria VS

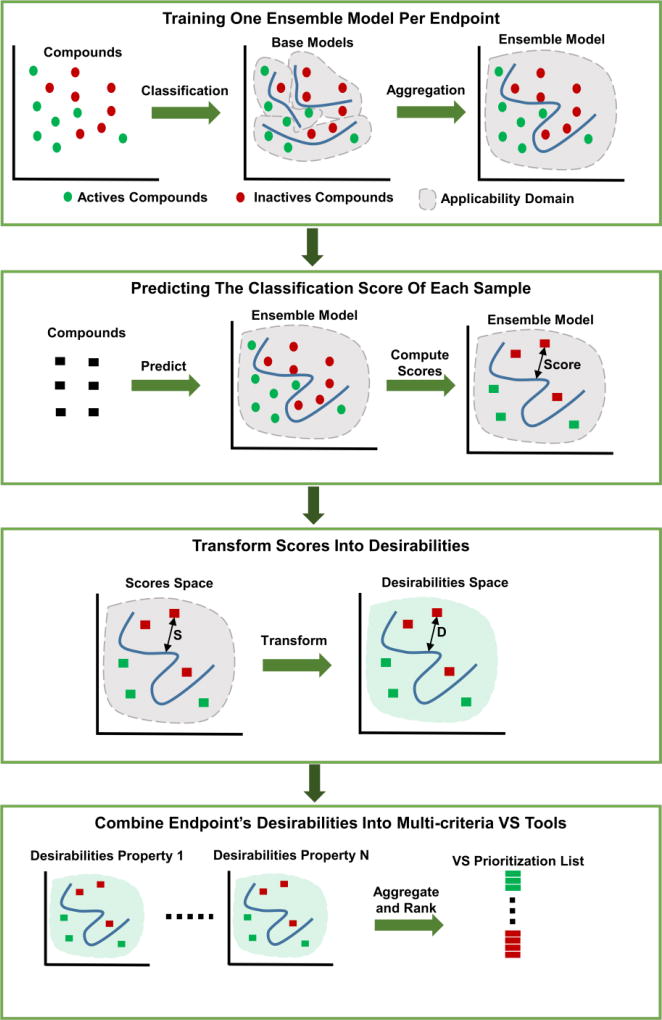
The approach proposed herein is based on three steps. In the first, a predictive ensemble model for each individual endpoint is derived from a pool of base QSAR models. In the second, these ensemble models are used to return the predicted classification scores of a given data set. Afterward, these scores are transformed into individual endpoint desirability values, which are finally combined to obtain a desirability-based multicriteria prioritization VS tool. The overall workflow of our methodology is depicted in Figure 2. The complete methodology was implemented in MATLAB [46].

Figure 2.

Overall workflow of the proposed methodology.

The steps involved in this modeling workflow are summarized below. A complete detailed description of all these steps is provided in the supplemental information online.

(i) Data preparation

As routinely done in chemoinformatics programs, the first step of our approach is to compile, curate, and codify through molecular descriptors a data set of chemical compounds per endpoint. All compounds included in an endpoint data set should have a known reference bioactivity value defining its membership to either the active or inactive group. Molecular descriptors were calculated with the ISIDA Fragmentor software (freely available at http://infochim.u-strasbg.fr/spip.php?rubrique49). The top-250 more informative (i.e., those with higher relevance and lower redundancy) descriptors were selected by using the mRMR algorithm [47].

(ii) Training a pool of base models per endpoint

The next step involves the training of a pool of diverse base classification models per endpoint. To ensure diversity, a random features subset selection strategy was used. Each base model can contain several descriptors ranging from 5 to 25. To be acceptable, a base model should return an accuracy value in predicting the training and test sets, as well as in fivefold cross-validation experiments, no lower than 0.65. Test set compounds are predicted only if they are inside the applicability domain of the model. For the generation of the base QSAR models, the Least Squares Support Vector Machines (LSSVM) classification algorithm was used [48].

The applicability domain of the base models is defined according to the molecular descriptors range method [31]. In this case, each feature included in the model is used to build a hyper-rectangle defined by the maximum and minimum values of the features on the training data. A sample is considered to be inside the model applicability domain if it is included in the defined hyper-rectangle.

(iii) Aggregation of the base models into an ensemble model

Base models were aggregated into ensembles following three different data fusion strategies: Major vote (MV), Borda vote (BV), and Scores vote (SV). For MV aggregation, given a pool of base models, the class of each compound is predicted by each base model. The sample is assigned to the class having the higher number of votes [49]. In BV [37] aggregation, each classifier ranks the candidates. To this end, the base classifiers have to provide a continuous estimator accounting for the support a given to a class prediction. The scores produced by the base LSSVM models were used as ranking criterion. For BV, if there are N candidates, the first-place candidate receives N - 1 votes, the second-place candidate receives N - 2, and so on, with the candidate in last place receiving 0 votes. The last aggregation strategy is based on the combination of the classifier output scores [37]. For this aggregation strategy, the LSSVM scores produced by the base models are first averaged. A given compound is assigned to the active class if its aggregated score is positive, whereas it is assigned to the inactive class if its aggregated score is negative. Irrespective of the aggregation strategies, only those models including a sample within their applicability domains are considered as valid decision makers, thus conferring a dynamic nature to the ensemble-based decision-making process.

One of the factors influencing the performance of ensemble models is the diversity of the base models being aggregated [37]. To ensure a good level of diversity, two different strategies were used for the selection of base models. The first was based on a clustering approach, whereas the second used Genetic Algorithms (GA). In particular, two different distance metrics were considered for clustering and six different fitness functions were challenged for the GA optimization.

For each endpoint, the best ensemble is selected as the one having the highest value of the Balanced Classification Rate (BCR) metric among all modeling methods. The BCR metric is defined by Equation 1:

$$\mathit{\text{BCR}}=\frac{\mathit{\text{Se}}+\mathit{\text{Sp}}}{2}\ast (1-|\mathit{\text{Se}}-\mathit{\text{Sp}}|)$$ [1],

where Se and Sp indicate the sensitivity and specificity of a model, respectively. This metric is a modification of the well-established Correct Classification Rate [50] and gives the highest scores to models with the best balance between Se and Sp.

The applicability domain of the ensemble models was defined as the union of the applicability domain of the members of the ensemble. This approach increases the applicability domain of the ensemble model relative to that of the individual models. When predicting a new sample using an ensemble model, only the models having that sample within their applicability domain are allowed to contribute to the aggregated decision.

(iv) Transformation of classification scores to desirability values

Once one ensemble has been selected as the final classifier for each endpoint, it can be used to predict the classification scores of new compounds considering the applicability domain of the ensemble. A given sample is predicted by considering the arithmetic mean of the scores produced by the base models including it inside their applicability domain.

These scores are transformed into desirability values as reported in the supplemental information online. This transformation is based on the aggregated scores across training, test, and external data sets. For a new sample, its aggregated score has to be predicted by the endpoint ensemble. Then, this score can be translated into a specific desirability value.

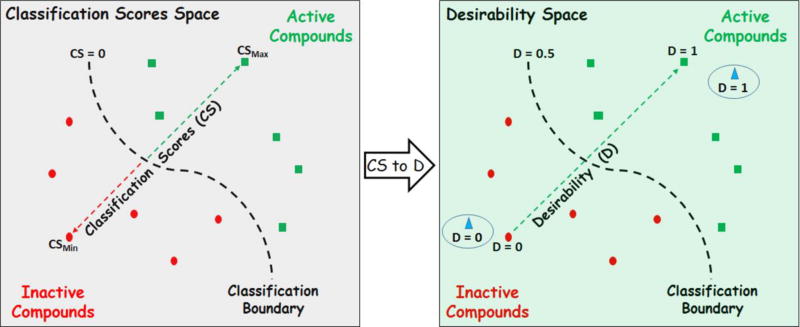
As shown in Figure 3, compounds provided with positive/negative LSSVM scores will be predicted as actives/inactives. The higher the scores are, the larger the distances from the classification boundary and, as consequence, the higher the desirability values. Compounds close to the classification border will have score values close to 0.

Figure 3.

Transforming classification scores into desirability values.

For a pool of compounds with a measured endpoint, the classification scores can be translated to desirability values following a simple rule: the highest scored compound receives a desirability value equal to 1, while the lowest scored compound receives a desirability value equal to 0. In addition, a scale factor is defined (see supplemental information online) so that a score value of 0 is transformed into a desirability value of 0.5. Once the transformation from scores to desirability values is defined, any new predicted sample can be represented in terms of desirability. If the score of the new sample is greater than the highest score for the reference data, it gets a desirability value equals to 1. By contrast, if its score is lower than the lowest score in the reference data, it is assigned a value of desirability equal to 0. A new sample will get a value of desirability in the interval [0, 1] when its score lies between the highest and lowest scores with respect to the reference data.

(v) Aggregation of the desirability values into the final desirability-based multicriteria prioritization VS tool

The last step is needed to aggregate the individual desirability values into one multicriteria decision-making VS tool. This aggregation step involves computing the weighted geometric mean of the desirability values corresponding to the individual endpoints. Two different scenarios were investigated. In the first, all endpoints were assigned the same weight, which, for convenience, was set to one. As a second variant, all the weights were enabled to vary in the interval [0.5, 1] by using a GA engine to find the optimal weights maximizing the enrichment of active compounds in the first 1% of a ranked ad hoc built validation set.

Proof of concept

Two multicriteria drug discovery problems were challenged in our proof of concept. The first involved the identification of nontoxic antimalarial hit compounds requiring the optimization of three separate endpoints: activity against a drug-sensitive Plasmodium falciparum strain (3D7); activity against a multidrug-resistant P. falciparum strain (W2); and compounds toxicity (Huh7). The second problem aimed to identify dual-target compounds acting as A_2A adenosine receptor (A_2AAR) antagonists as well as monoamine oxidase B (MAO-B) inhibitors. In the case of antimalarial hit modeling, there was a large overlap among the compounds assayed for the three different endpoints. Instead, a minimal overlap existed between the data sets used for identifying dual-target compounds, thus making the modeling process more difficult.

The structural overlapping among compounds measured for each property defining the multicriteria problem is a critical factor that can affect both the classification and VS performance of consensus classifiers used for multicriteria VS. For problems where structural overlapping is high, the reliability of predictions is favored because all cases involved in each property to predict share a large chemical space. Consequently, base models will be based on similar structural patterns. Accordingly, when the structural overlapping is low, the reliability of predictions can be affected if the applicability domain is not considered during the selection of the base models constituting the final consensus classifier.

Taking into consideration the above-mentioned issues, we challenged our approach in these extreme scenarios to gain insights into the influence of such a critical factor on the reliability and performance of the proposed multicriteria VS approach. These data sets were subject to a thorough preparation and curation treatment as described in the supplemental information online. For assessing VS performance, two panels of 50 hit compounds each were used in the case the malaria data set and two groups of eight dual-target A_2AAR/MAO-B compounds were used for the dual-target case study.

The SD files, including compound structures and biological annotations of the training, test, external, and VS validation sets, as well as lists of the final subset of 250 ISIDA Fragments per endpoint, are provided in the supplemental information online. Table S1 in supplemental information online also summarizes the composition of all these sets.

A total of 1001 base models satisfying the previously defined acceptability criteria were trained for each endpoint for each data set. The performance metrics of the base classifiers are summarized in Table S2 in the supplemental information online.

In the case of the antimalarial compounds, the models for the toxicity endpoint (Huh7) returned better average performances than those for antimalarial endpoints (3D7 and W2). In the case of the dual A_2AAR/MAO-B ligands, the best performance was obtained for the MAO-B inhibitors. In addition, the performance of the base models was higher in the modeling of the dual A_2AAR/MAO-B ligands. This can be explained based on the diversity of the modeling data sets. In the case of the dual A_2AAR/MAO-B ligands, the data set was less structurally diverse was the antimalarial one. This different structural diversity means that there are fewer rules guiding the bioactivity of dual A_2AAR/MAO-B ligands, making the discovery of these rules easier throughout the machine learning-based modeling process. The drawback of this lower structural diversity is that the applicability domain of the dual A_2AAR/MAO-B ligands ensemble covers a narrower region of the whole chemical space compared with the antimalarial model.

The selection of the best model, not only in the case of the base models but throughout the classification modeling workflow, is based on the maximum value of BCR achieved for the test set. In addition, the external data set is only used for the verification of the predictive capability of the selected models and its prediction does not affect the decision regarding the selection of the best models.

As described above, different strategies were adopted for combining base models into ensembles for each endpoint. Not surprisingly, the best-performing ensemble was obtained by using a GA to select its base models. In addition, for the two endpoints related to antimalarial activity (3D7 and W2), the best-performing ensemble was found when the base models were combined using the SV aggregation strategy and the GA maximized the value of BCR. By contrast, the best ensemble for the toxicity endpoint (Huh7) was found using MV for the aggregation of the base models and the Akaike Index Criterion (AIC) was minimized.

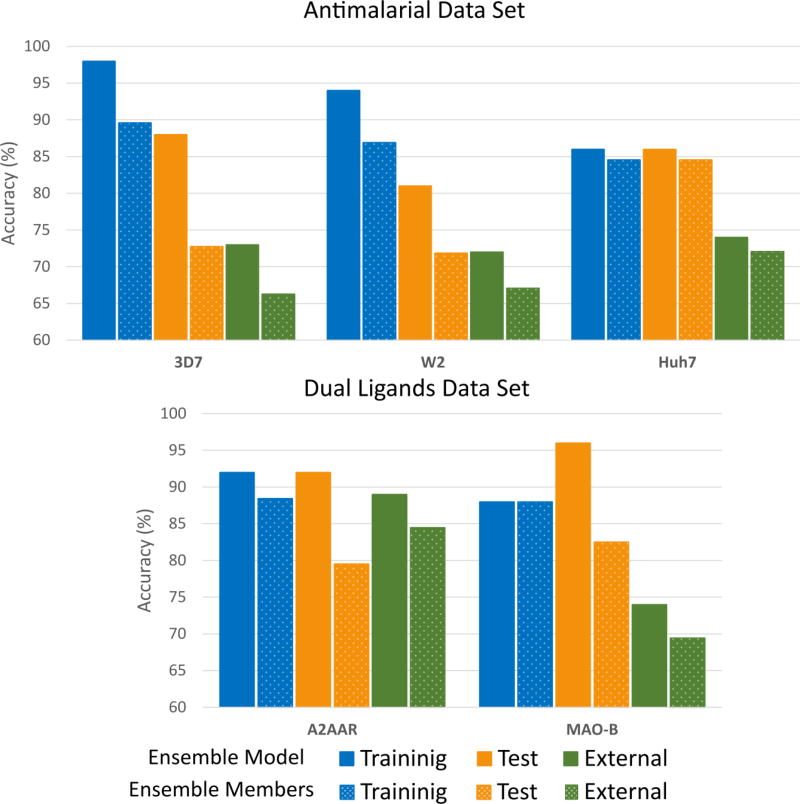
In the case of the dual A_2AAR/MAO-B ligands, the best ensembles were obtained when BV and MV were used for the maximization of BCR during model aggregation for A_2AAR and MAO-B, respectively. The statistics for the best ensemble per endpoint are summarized in Figure 4 and presented in more detail in Table S3 in the supplemental information online.

Figure 4.

Classification performance of the obtained ensembles for the antimalarial (a) and dual ligands (b) data sets. The average performance of the base models each ensemble comprises is shown using dotted bars.

The obtained ensembles improved the average performance of the base models for the five endpoints. From Figure 4, it can be seen that the ensemble models (solid bars) showed better performance than the average of the base models they were composed from (dotted bars) for all endpoints. More importantly, these ensembles also improved the performance of the best base model for all endpoints (see Tables S2 and S3 in the supplemental information online). Although the quality of the ensemble models is granted by optimizing performances on the test set, the improvements are not obtained at the expense of the statistics in predicting the training set. The obtained ensembles also showed a better balance between sensitivity and specificity compared with the base models.

We found that the less complex ensemble comprised five base models, whereas 14 base models were encompassed in the more sophisticated ensemble. These numbers of model represent approximately 1% of the total number of base models. If the performance of the selected ensembles was compared to that obtained when all base models were aggregated, the overall classification accuracy increased by approximately 10% (data not shown). This highlights the importance of combining a tailored subset of base models comprising a certain level of diversity rather than large numbers of base models.

Given that the external data set is used only to assess the predictive potential, we can be confident that the obtained ensembles can generate trustworthy score values in the case of compounds within their applicability domain.

The next step of our approach is the conversion of the ensemble classification scores into endpoint desirability values. This was guided by the highest and lowest scores predicted by the ensemble across all the training, test, and external sets. All these processes were carried out as previously described.

To evaluate the VS performance of our approach, three different VS Validation Sets (VSVS) were designed. The first VSVS (VSVS-1) comprises, in the case of the antimalarial data set, 50 known antimalarial hits and a pool of decoys selected using the DUD-E server [33]. For the dual A_2AAR/MAO-B ligands, the DUD-E decoys were generated for eight known dual-target ligands to form the VSVS-1. These VSVS-1 were used for the optimization of the individual desirability weights used to aggregate them into the final multicriteria VS tool.

Given that VSVS-1 was used for the optimization of the weights, two more VSVS, namely VSVS-2 and VSVS-3, were built for each data set. These sets were built from a second subset of 50 antimalarial hits and eight dual A_2AAR/MAO-B ligands. The decoy molecules for these second sets of positive compounds were generated with the DUD-E server for VSVS-2 and with the DecoyFinder [34] application for VSVS-3. The classification scores were computed for the VSVS and were transformed into desirability values according to the previously established transformations. The SD files with the VSVS structures are provided in the supplemental information online.

The final ensembles for all endpoints, except for MAO-B inhibitors, contained all compounds of the VSVS within their applicability domains. By contrast, no single model in any of the ensembles had all samples in the VSVS within its applicability domain. To illustrate the benefits of using the ensemble modeling strategy over individual models from the applicability domain point of view, the worst-case scenario corresponding to the modeling of MAO-B inhibitors can be analyzed. In this case, the individual models covered, on average, 87% of the samples included in the VSVS. However, the applicability domain of the ensemble covered 99.94% of all samples included in the VSVS. That is, in the worst-case scenario, the applicability domain of the ensemble model can increase the coverage of the chemical space by 13% relative to the individual model average. This fact clearly highlights one of the advantages, in terms of coverage of the chemical space, of using ensemble models instead of individual models.

Going back to our flamingo analogy and having all decision makers properly described (endpoint desirability values), the female flamingo (chemist) is ready to take her decision on which place each candidate (compound) should have in an ordered list. In this final step, the individual endpoint desirability values are combined into the final multicriteria VS model. As previously mentioned, we examined two scenarios: all the endpoints received the same unitary weight for aggregation and the weights were optimized to maximize the initial enrichment of actives in the first 1% of screened data.

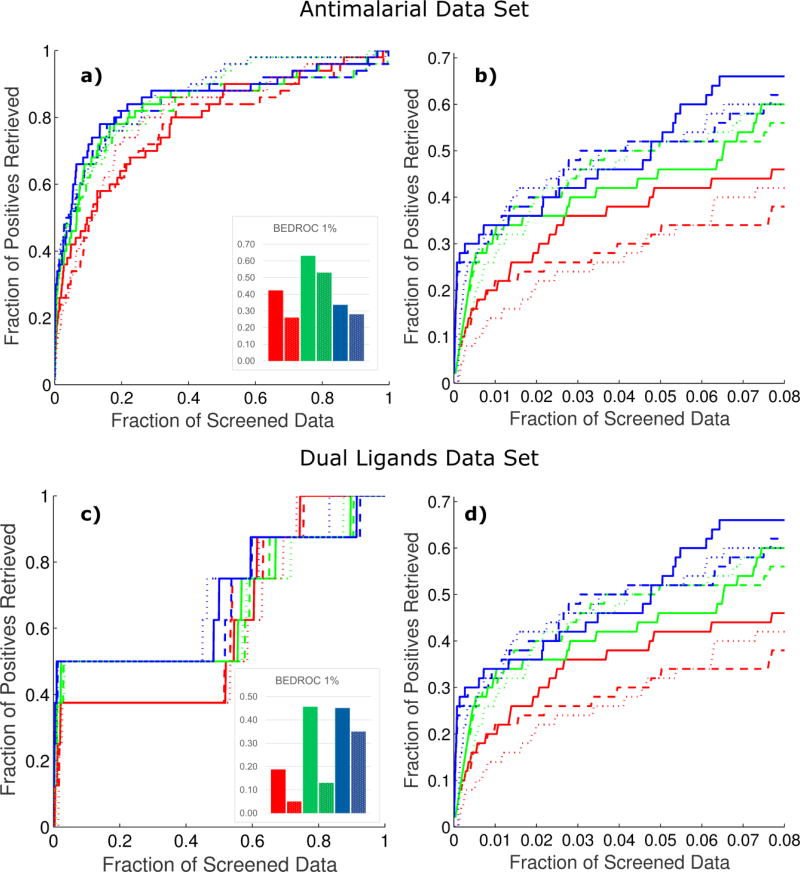
These experiments were performed using the three VSVS previously built. In the worst-case scenario, the VSVS comprised 55 decoys per active ligand. Such an active ratio is well over the minimum of 36 proposed in [51] for an unbiased estimation of the performance of VS methods [52]. The results relative to these two cases are shown in the accumulative curves of Figure 5, whereas other details are provided in Table S4 in the supplemental information online. The values of BEDROC at 1% of screened data for the unweighted aggregation are presented as bars for both modeling problems in Figure 5.

Figure 5.

Accumulative curves for the two case studies. Curves corresponding to Virtual Screening Validation Sets (VSVS)-1, VSVS-2, and VSVS-3 are colored red, green, and blue respectively. Solid lines represent the curves corresponding to the weighted aggregation of the desirability functions; dashed lines correspond to their unweighted aggregation; and dotted lines correspond to the aggregation of the classification scores. The colors of the bars representing BEDROC correspond to the same color used for each VSVS. The bars representing the values of BEDROC obtained from the aggregation of the classification scores are presented with a dotted pattern. (a) Cumulative curve for the antimalarial data set. (b) Magnification of the first 8% of screened data for the antimalarial data set. (c) Cumulative curve for the dual ligand data set. (d) Magnification of the first 8% of screened data for the dual ligand data set.

For comparison purposes, we also studied the VS performance of the aggregation of the classification scores without transforming them to desirabilities. For this comparison, the classification scores of each sample were aggregated across all problem-related endpoints using the arithmetic mean. These aggregated scores were then used as the multicriteria VS ranking criterion. The accumulation curves obtained for these experiments are shown in Figure 5.

The results obtained showed the robustness of the proposed methodology and its suitability for VS campaigns. More importantly, all the experiments showed a significant initial enrichment of active compounds even at very low fractions of screened data. This observation holds true even in the case of the worst-performing VS validation experiments. Furthermore, the optimization of the weights for the aggregation of the individual desirability functions can only provide a slight improvement in the initial enrichment of active compounds. This means that weights optimization is not necessarily mandatory for obtaining effective VS tools. In addition, neither the actives nor the decoys included in the VSVS had ever been previously used at any modeling stage.

In the case of VSVS-2 for the antimalarial compounds, in addition to the ligands and the decoys, the six confirmed inactive compounds, common to the three endpoint external sets, were also present in this set. These inactive compounds had never been used in the modeling process of any of the individual endpoints. None of these confirmed inactive compounds are ranked in the first 1% fraction of screened data. Also, five of these compounds were ranked beyond the 15% of screened data, occupying ranking positions that would make them ineligible for any experimental validation in a real VS campaign. In addition, because four of these compounds were ranked in positions beyond the 20% of screened data, they would be ineligible for experimental validation even when a small database of chemical compounds is screened. When the composition of the first 1% of screened data is analyzed, 59% of the compounds in this data subset correspond to confirmed hits, which represent an outstanding active rate even for a retrospective VS validation [40].

As far as the dual A_2AAR/MAO-B ligand VS validation experiments were concerned, four out of the eight known dual ligands were retrieved at early fractions of screened data in most experiments, whereas the others were ranked at the end of the list. A detailed analysis of the position that the known dual A_2AAR/MAO-B ligands have in these ranked lists shows that the compounds retrieved at the start of the list had potencies around or below 100 nM toward both targets. By contrast, the compounds ranked at the end of the lists were far from this potency cutoff value for both targets. This means that our approach is capable of ranking compounds with an outstanding dual-binding profile at the beginning of the ranked list, whereas those with lower affinity for the targets are positioned far away from the top of the list.

To test the worth of the desirability-based methodology proposed herein, we compared its VS performance to that obtained from the aggregation of the classification scores as described above. The obtained results in Figure 5 might indicate an overall similar performance in both scenarios. However, a closer look at the first 8% of screened data as well as inspection of the values of BEDROC, clearly support the advantages of using a desirability-based methodology for multicriteria VS. In none of the six VS experiments performed was the aggregation of the classification scores able to achieve initial enrichment performances close to those obtained with our desirability-based methodology.

All this evidence strongly supports our hypothesis that desirability functions can be effectively used for the development of high-performance multicriteria VS tools. Finally, comparison of the classification and VS performances showed that, despite better classification performance being achieved for the dual A_2AAR/MAO-B ligands, a better VS performance was obtained for the antimalarial data set. This finding supports our previous observation that good classification performances do not ensure good VS results [35]. Thus, the evaluation of the models in VS conditions using proper data sets is an essential component of any cheminformatics effort for VS.

Concluding remarks

Drug discovery can (and we believe must) be approached by methodologies able to explicitly account for the cascade of events initiated by biologically active compounds because of their mode of action and poly-pharmacological character. We have demonstrated here that it is possible to do so by considering how evolution works. The flamingo story we describe here brought us to a nature-inspired drug-discovery workflow that is centered on the desirability principle. In that sense, we investigated the potential of desirability functions for the multicriteria VS of databases of chemical compounds. For using classification scores to derive endpoint desirability values, it is critical to rely on high-quality classification models for a robust modeling. In our proposal, this was achieved through ensemble modeling, a technique that, in addition to providing trustworthy predictions, ensures larger coverage of the chemical space by the applicability domain of the final predictor. We consider that a key factor determining the success of the proposed strategy herein is the inclusion of the applicability domain, which is dynamically structured throughout the modeling process. The results provided strong evidence supporting our hypothesis that desirability functions can be used for obtaining highly effective and robust tools for the development of high-performance multicriteria VS workflows.

Although ensemble models represent a good solution to the problems under investigation, we further focus here on the development of new methods for improving their generalization. This future direction is motivated by the evidence that each sample in the external set can be correctly classified by at least one base classifier for all endpoints. Thus, using more appropriate ensemble modeling methods could result in a considerably increase in the quality of the ensemble predictions. Although there is room for improving the proposed methodology, we consider that the results obtained are promising. We recently introduced a novel systemic QSAR approach that takes advantage of the integration of chemogenomic data [53]. In further research, we plan to investigate how the present methodology could improve the multicriteria VS performance of the systemic QSAR approach.

Highlights.

• We approach drug discovery as a nature-inspired multi-criteria optimization process

• We propose a desirability-based method for multi-criteria virtual screening

• We highlight the role of ensemble modeling and the applicability domain

• We provide evidences of the suitability of the method through two case studies

Biographies

Maykel Cruz-Monteagudo

Maykel Cruz-Monteagudo is currently a postdoctoral researcher in CIQUP based in the Department of Chemistry and Biochemistry, Faculty of Sciences of the University of Porto. He was awarded his BSc in pharmaceutical sciences from the Central University of Las Villas, Cuba, in 2003; and his PhD (toxicology) in pharmaceutical sciences from the Faculty of Pharmacy, University of Porto, in 2010. His current research is devoted to the development and application of chemoinformatics approaches to drug discovery, focusing on the application of system chemical biology concepts to multitarget and/or multiobjective drug discovery. He has authored more than 40 publications in peer-reviewed journals and two international book chapters.

Yunierkis Perez-Castillo

Yunierkis Perez-Castillo is currently a professor in the Department of Chemistry, Universidad Técnica Particular de Loja, Ecuador. He was awarded his BSc in nuclear physics from the Instituto Superior de Tecnologías y Ciencias Aplicadas, Cuba in 2004 and his PhD from the Vrije Universiteit Brussel, Belgium in 2013. His current research interests include the design, implementation, and application of machine learning-based chemoinformatics approaches as well as the application of structure-based methods to drug discovery. He has authored more than 15 papers in peer-reviewed journals and two international book chapters.

Stephan Schürer

Stephan Schürer is the director of drug discovery at the Center for Computational Science and an associate professor in the Department of Pharmacology at the University of Miami. He was awarded his PhD in synthetic organic chemistry from the Technical University of Berlin and studied chemistry at Humboldt University-Berlin and University of California, Berkeley. The research focus of the Schürer group is on systems drug discovery. The group integrates and models small molecule–protein interactions, systems biology ‘omics’, and chemistry data to improve the translation of disease models into novel functional small molecules. Dr Schürer is a principal investigator in two national Consortia: the Library of Integrated Network-based Cellular Signatures (LINCS), which is also part of the Big Data to Knowledge (BD2K) program, and the Illuminating the Druggable Genome (IDG) project. He has authored more than 80 publications in peer-reviewed journals, six international book chapters and several patents.