Printed optics: phantoms for quantitative deep tissue fluorescence imaging

Abstract

Three-dimensional (3D) printing allows for complex or physiologically realistic phantoms, useful, for example, in developing biomedical imaging methods and for calibrating measured data. However, available 3D printing materials provide a limited range of static optical properties. We overcome this limitation with a new method using stereolithography that allows tuning of the printed phantom’s optical properties to match that of target tissues, accomplished by printing a mixture of polystyrene microspheres and clear photopolymer resin. We show that Mie theory can be used to design the optical properties, and demonstrate the method by fabricating a mouse phantom and imaging it using fluorescence optical diffusion tomography.

Printed optics is an emerging field that allows rapid fabrication of custom optical elements [1]. By depositing materials layer by layer, 3D printing of objects having virtually any desired shape is possible. In optical imaging, printed optics is ideal for the fabrication of tissue-simulating phantoms, or customizable objects for testing, evaluating, and calibrating imaging methods [2]. 3D printing offers precise design of the phantom geometry and exact placement of complex inhomogeneities in a fashion that is not possible using molds. For example, the XFM-2 phantom mouse available from Perkin Elmer was fabricated using a mold, and has concomitant restrictions on the location, shape, and composition of inhomogeneities.

Custom 3D printed phantoms are useful for a myriad of optical imaging methods and biomedical applications, as we and others have demonstrated recently [3–6]. For example, printed phantoms of the human eye allow assessment of optical coherence tomography and related ophthalmic devices [7]. Additionally, printed phantoms formed from images of human vascular networks have allowed development of hyperspectral oximetry [8]. Phantoms have also been printed with cells [9]. Of particular note, printed phantoms allow collection of high-quality calibration data [3,5]. By printing a phantom with the same surface geometry as the target object, component by component calibration of the measured data becomes possible.

Crucial to improving printed optical phantoms is a means to tune the reduced scattering ${\mu }_s^{\prime }({\text{mm}}^{-1})$ and absorption μ_a (mm⁻¹) coefficients of the printed material to match those of a target tissue, which is the focus of the work presented here. Recently, this was accomplished by combining nigrosin absorbers and titanium dioxide (TiO₂) scatterers with acrylonitrile butadiene styrene (ABS), a common printing material [10]. The relation of the mass percentage of TiO₂ and nigrosin to ${\mu }_s^{\prime }$and μ_a was determined empirically. The lowest ${\mu }_s^{\prime }$ and μ_a attainable with this method is limited by the ${\mu }_s^{\prime }$ and μ_a of the base material (ABS), which is higher than some tissues. Additionally, it would be useful to design the material to be printed a priori, circumventing the need to empirically determine the scattering parameters. Finally, phantoms printed with ABS are not watertight and tend to be heterogeneous with a mesh of air gaps that influence light propagation. We present a design method and a material that allows a broader range of parameters and a watertight printed phantom.

We used Mie theory to design the ${\mu }_s^{\prime }$ of a printed phantom, providing a simple and effective method for tuning the optical properties. First, we used Mie theory to calculate the concentration of polystyrene microspheres to be mixed with a clear printing resin in order to achieve a target ${\mu }_s^{\prime }$. Second, we used stereolithography to print phantoms from this bead–resin mixture. We demonstrate the method by designing the optical properties of a printed mouse phantom. We placed a fluorescent inhomogeneity within the mouse phantom (simulating a tumor or organ stained with a targeted fluorescent imaging agent) and imaged it using fluorescence optical diffusion tomography (FODT) [11]. FODT is a whole animal optical imaging method, useful, for example, for finding tumors [12], determining pharmacokinetic rates [13], and imaging the whole brain [14]. We show quantitative imaging of the inhomogeneity, analogous to determining the fluorophore concentration in deep tissue, demonstrating the usefulness of the printed phantoms for developing FODT and other optical imaging methods for biomedical applications.

Experimental data was captured using the setup shown in Fig. 1, which is similar to a setup we have used previously to image live mice [13]. An EXR-20 generates a pulsed super-continuum which is filtered by a VARIA tunable bandpass filter, giving picosecond pulses tunable from 485 to 850 nm with 10–100 nm variable bandwidth. A photodiode allows triggering of the gated camera, constituting a time-domain measurement of the medium response.

Fig. 1.

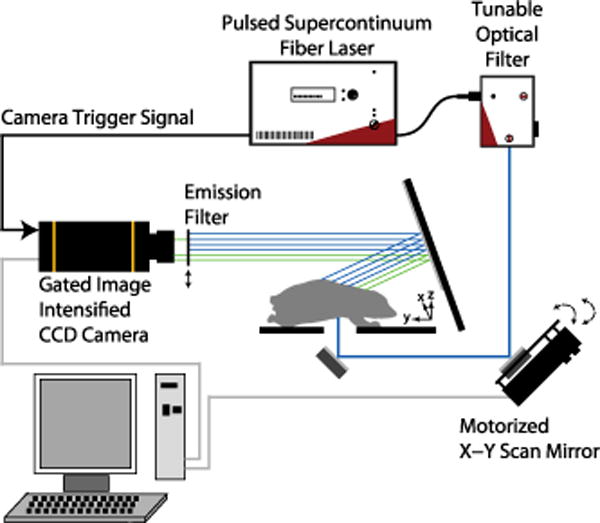
Experiment setup. An EXR-20 and VARIA (NKT Photonics) outputs pulses at 20 MHz (allowing fluorescence decay between pulses). Transmitted highly scattered light is detected by a gated ICCD camera (Roper PIMAX). A bandpass filter allows collection of fluorescence. A motorized mirror (Zaber) changes the source position before each measurement.

Mie’s solution to Maxwell’s equations describes the scattering of a plane wave in a homogeneous medium by a sphere with known diameter and refractive index (RI) [15]. The fields are written as an expansion in vector spherical harmonics, and coefficients describing the amplitudes of the scattered and internal fields can be calculated from the boundary conditions. The sphere’s scattering cross section, σ_s, and anisotropy, g, can be written in terms of these coefficients. Then, assuming that the spheres are far apart, ${\mu }_s^{\prime }={\sigma }_{s}C(1-g)$, where C is the concentration of spheres [16]. We fabricated a 3D printed material with known ${\mu }_s^{\prime }$ by mixing polystyrene microspheres (Bangs Laboratories, diameter 0.76 μm, RI ~ 1.59) with a clear printing photopolymer resin. By varying the concentration of microspheres C, ${\mu }_s^{\prime }$ can be designed to match that of a target tissue. In terms of the sphere volume fraction f_v, C = f_v∕V, where V is the volume of a single sphere. We prepared 100 mL solutions with f_v = 0.005 by mixing 1.67 mL of f_v = 0.3 bead solution in water with 98.33 mL of clear printing resin. The density of the water, microspheres, and clear resin are all close to 1 g/mL.

We used the Formlabs 3D printer shown in Fig. 2(a), where the bead–resin mixture is shown in the resin tank. The Formlabs clear resin is a mixture of methacrylic acid esters and a photo-initiator, and has a RI similar to acrylic glass (~1.49). The printer uses stereolithography to form each layer of the 3D print, where a UV laser cures the photopolymer resin at desired positions. Stereolithography allows the polystyrene microspheres to be “frozen” in place, and is preferred to fused-deposition modeling where the polymer would be fed through a heated nozzle, possibly influencing the diameter distribution of the microspheres such that ${\mu }_s^{\prime }$ could not be reliably designed with Mie theory. To verify the design method, ${\mu }_s^{\prime }$ and μ_a were estimated by using the setup shown in Fig. 1. The temporal response of a 7 × 7 × 0.75 cm slab printed using the bead–resin mixture was measured and fit to an analogous analytical solution to the diffusion equation in an infinite slab geometry [5]. The estimated ${\mu }_s^{\prime }$ from the fit is compared to the theoretical result predicted using Mie theory in Fig. 2(b). The mean experimental error was 6.4%, showing close agreement with the Mie theory prediction. The absorption was found to not vary much with wavelength, and had a mean value of 0.007 mm⁻¹. g was calculated from Mie theory, and was approximately 0.9. Initially, we used a low sphere volume fraction (f_v = 0.005) to ensure we did not disrupt the stereolithography, resulting in a ${\mu }_s^{\prime }$ that is similar to breast tissue (~1 mm⁻¹) [17].

Fig. 2.

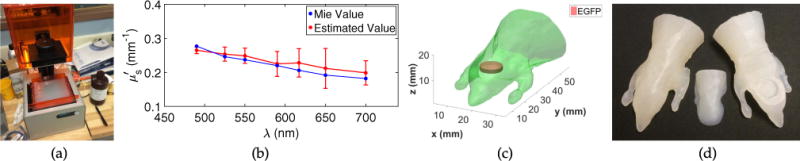
(a) Formlabs Form 1 + used for 3D printing. (b) ${\mu }_s^{\prime }$ spectrum of the printed mixture of polystyrene beads and resin, designed using Mie theory (blue) and estimated from measurements of 3D printed slabs (red). The red points are the mean of 10 datasets, and the red error bars have a total length of two standard deviations. (c) Digimouse mesh used to generate the STL file for 3D printing. A cylindrical cavity for placing chemicals was created in the region of the brain. (d) 3D printed digimice with controlled optical properties. A removable printed piece gives access to the cavity inhomogeneity, allowing chemical solutions to be placed within the phantom. The printed material does not react with most solvents.

The same bead–resin mixture described above was used to print an anatomically realistic mouse phantom using the Digimouse atlas [18], which contains the surface profile of all major mouse organs. Here, we placed a simple cylindrical cavity inhomogeneity in the general location of the brain, as seen in Fig. 2(c). The cylindrical cavity is proof of concept, and could easily be replaced using the brain surface profile, creating a more anatomically realistic inhomogeneity. The printed phantom is shown in Fig. 2(d).

Frozen aliquots of the fluorescent protein EGFP (484 nm excitation, 507 nm emission) were thawed and buffer exchanged into phosphate buffered saline (10 mM phosphate buffer, 2.7 mM KCl, and 137 mM NaCl, pH 7.4) using a 10 kDa spin filter, and the protein concentration was assessed using the bicinchoninic acid assay. Prior to use in imaging analysis, the protein was diluted to 10 μM in a solution of microspheres and water such that f_v = 0.005, to match the background scatter. The diluted protein was injected into the phantom cavity inhomogeneity to be imaged.

In FODT, a forward model describes the propagation of modulated incoherent light through tissue and the μ_a, ${\mu }_s^{\prime }$, and fluorescent parameters are reconstructed as a function of position from boundary measurements using an inverse solver. We use a forward model defined by the coupled diffusion equations [11]:

$$\nabla \cdot \left[D_x\left(\mathit{r}\right)\nabla {\varphi }_x\left(\mathit{r},\omega \right)\right]-\left[{\mu }_{a_x}\left(\mathit{r}\right)+j\omega /c\right]{\varphi }_x\left(\mathit{r},\omega \right)=-S_x\left(\mathit{r};\omega \right),$$ (1)

$$\nabla \cdot \left[D_m\left(\mathit{r}\right)\nabla {\varphi }_m\left(\mathit{r},\omega \right)\right]-\left[{\mu }_{a_m}\left(\mathit{r}\right)+j\omega /c\right]{\varphi }_m\left(\mathit{r},\omega \right)=-{\varphi }_x\left(\mathit{r},\omega \right)S_f\left(\mathit{r};\omega \right),$$ (2)

where r denotes the position; ϕ (W/mm²) is the photon flux density; ω is the angular modulation frequency; $D=1/\left[3\left({\mu }_s^{\prime }+{\mu }_a\right)\right]$ is the diffusion coefficient; c is the speed of light in the medium; the subscripts x and m denote parameters at the fluorophore excitation and emission wavelengths, λ_x and λ_m; S_x is the excitation source term; and S_f = η(1 + jωτ)⁻¹ is the fluorescence source term. The fluorescence parameters are the lifetime τ (ns) and the fluorescence yield $\eta ={\eta }_q{\mu }_{a_f}({\text{mm}}^{-1})$, where η_q and ${\mu }_{a_f}$ are the quantum yield and absorption of the fluorophore, respectively. Equations (1) and (2) were solved on an unstructured finite element method mesh [19].

In an FODT experiment, three boundary measurements are needed [11]. Following this procedure, the EXR-20 was tuned to 490 nm with a 10 nm bandwidth for λ_x (17 mW average power), and to 525 nm with a 10 nm bandwidth for λ_m (9 mW average power). An emission bandpass filter centered at 525 nm with a 25 nm bandwidth (EO 87-801) was placed in front of the camera when collecting the fluorescence emission.

The boundary measurements were repeated for 15 source positions, and 322 CCD camera pixels were selected as detectors. Transmittance measurements only were made, where the sources were on the bottom and the detectors were on the top of the printed phantom. A 3D topography laser line scanner was used to project the CCD pixels to detector positions on the surface, as we have described previously [5]. Pseudo-CW data was captured for the FODT reconstruction using a 200 ms integration time, allowing reconstruction of η but not τ. Calibration is necessary to account for source and detector coupling to the scattering medium, relating synthetic numerical data to experimental data. For calibration the phantom cavity was filled with a mixture of polystyrene microspheres and water such that f_v = 0.005, making the phantom approximately homogeneous. Data was then captured and used for calibration as we have described previously [5,11].

We solved the image reconstruction problem using the iterative coordinate descent algorithm we developed [11,13], which is described by

$${\widehat{x}}_i=\underset{{\stackrel{\sim }{x}}_i}{\text{arg}\text{min}}\left[\Vert \mathit{y}-\mathit{f}({\stackrel{\sim }{\mathit{x}}}_i){\Vert }_{\mathrm{\Lambda }}^2+\frac{1}{\rho {\sigma }^{\rho }}{\displaystyle \sum _{j\in {\mathcal{N}}_i}{b}_{ij}|{\stackrel{\sim }{x}}_i-x_j{|}^{\rho }}\right],$$ (3)

where x is the image to be reconstructed, subscript i represents the voxel being updated, ${\widehat{x}}_i$ is the updated or reconstructed value, ${\stackrel{\sim }{x}}_i$ is the initial or current value to be updated, y is a vector of length N representing the measurements (calibrated experimental data—here N = 4830), f(x) is the solution to the forward model described by Eqs. (1) and (2), for assumed x, and for an arbitrary vector w, $\Vert \mathit{w}{\Vert }_{\mathrm{\Lambda }}^2={\mathit{w}}^H\mathrm{\Lambda }\mathit{w}$, where H denotes Hermitian transpose with Λ⁻¹ = diag[|y₁|,…,|y_p|]. The prior model, the GGMRF, constitutes regularization and is characterized by σ and ρ, which are constants representing scale and shape parameters for the distribution, respectively, and b_ij, which provides a local 26-neighborhood $({\mathcal{N}}_i)$ weight.

The calibrated datasets at λ_x and λ_m were used to reconstruct ${\mu }_{a_x}(\mathit{r})$ and ${\mu }_{a_m}(\mathit{r})$. ${\mu }_s^{\prime }(\mathbf{r})$ was assumed known and homogeneous from Fig. 2(b). The validity of this assumption is apparent in the results. The reconstructed ${\mu }_{a_x}(\mathit{r})$ cross section is shown in Fig. 3(a), and its isosurface is shown in Fig. 3(b). For EGFP, ${\mu }_{a_x}=\text{ln}(10){\epsilon }_x{C}_{\text{EGFP}}=0.129({\text{mm}}^{-1})$, where ε_x is the molar absorptivity (56001/M/mm) and C_EGFP is the concentration (10 μM) of EGFP. From Fig. 3(a), we see that ${\mu }_{a_x}(\mathit{r})$ was quantitatively reconstructed in the region of the inhomogeneity. For brevity the reconstructed ${\mu }_{a_m}(\mathit{r})$ is not shown, but it was lower in the region of the fluorescent inhomogeneity.

Fig. 3.

Image of ${\mu }_{a_x}(\mathit{r})$ and η(r) parameters reconstructed from calibrated data collected from the printed mouse phantom with an EGFP inhomogeneity: (a) μ_a(r) cross section at the peak reconstructed value (z = 9 mm plane); (b) μ_a(r) isosurface; (c) η(r) cross section at the peak reconstructed value (z = 12 mm plane); and (d) η(r) isosurface. Black circles show the target inhomogeneity.

The calibrated fluorescence data excited at λ_x and measured at λ_m was used to reconstruct η(r) using the reconstructed ${\mu }_{a_x}(\mathit{r})$ and ${\mu }_{a_m}(\mathit{r})$ and homogeneous ${\mu }_s^{\prime }(\mathbf{r})$. The reconstructed η(r) cross section is shown in Fig. 3(c), and its isosurface is shown in Fig. 3(d). Comparing to the surface profile used to print the phantom in Fig. 2(c), the size and location of the fluorescent inhomogeneity was accurately reconstructed despite some error in the reconstruction of ${\mu }_{a_x}$. For EGFP, $\eta ={\eta }_{\text{EGFP}}{\mu }_{a_x}=0.0774({\text{mm}}^{-1})$, where η_EGFP is the quantum yield of EGFP (0.6), and we see that this value was reconstructed in the region of the inhomogeneity. The fractional error [11] is $|{\sum }_i^N{\eta }_{\text{target}}({\mathit{r}}_i)-{\sum }_i^N\eta ({\mathit{r}}_i)|/|{\sum }_i^N\eta ({\mathit{r}}_i)|=0.329$, where η_target(r) is the target fluorescence image. The fractional error is relatively small, with contributions from smoothing at the sharp boundary caused by regularization. The reconstruction results support the validity of the ${\mu }_s^{\prime }$ spectrum in Fig. 2(b). Note that the fluorophore concentration was quantitatively determined without calibration with a fluorescent inhomogeneity of known concentration.

Our reconstruction includes the regularization term σ, which acts as a low-pass filter to prevent overfitting when solving the ill-posed inverse problem. As σ is increased, the amount of smoothing is reduced, causing the reconstructed values to change. It is desirable for σ to be large to minimize smoothing, but small enough to ensure that the image does not become distorted due to overfitting. Here, we found that the values of σ which gave quantitatively correct values for ${\mu }_{a_x}$, ${\mu }_{a_m}$, and η corresponded to the most accurate images of the inhomogeneity size and location. These values of σ were not the maximum values that resulted in no distortion of the images due to overfitting, as would otherwise be used if the quantitatively correct values for ${\mu }_{a_x}$, ${\mu }_{a_m}$, and η where unknown. Thus, using known quantitative information allows improved regularization, resulting in better reconstructed images. Alternatively, if the size and location of the inhomogeneity are known or can be estimated, quantitative information can be extracted, useful for biomedical applications.

In Fig. 4 we show a printed slab and its corresponding ${\mu }_s^{\prime }$ spectrum, demonstrating that ${\mu }_s^{\prime }$ can be increased beyond Fig. 2(b), such that it is more pertinent to tissues. We expect that ${\mu }_s^{\prime }$ can be increased significantly beyond Fig. 4(b). Theoretically, the design of ${\mu }_s^{\prime }$ is limited by the settling of beads from the resin mixture during printing, but we did not observe this for any of our prints. The design may also be limited by the power of the 405 nm Form 1 + laser, which may not be able to solidify the resin for very large ${\mu }_s^{\prime }$. We also did not observe this, but the problem could be remedied with a different printer.

Fig. 4.

(a) A 5 × 5 × 0.4 cm slab printed using f_v = 0.015. The removable piece shown in Fig. 2(d) is included for comparison. (b) ${\mu }_s^{\prime }$ spectrum of the slab, designed using Mie theory (blue) and estimated from measurements (red).

The RI of the clear resin is high compared to water, but this did not affect our results using unmodulated light, and other resins may become available with lower RI. Mie theory can describe the absorption of a medium [15], allowing straightforward extension of our method to design both the ${\mu }_s^{\prime }$ and μ_a of printed phantoms with the addition of absorbing agents, such as India ink or nigrosin to the resin. Black photopolymer resins are available, leading us to believe the absorption could be tuned over a wide range on commercial 3D printers without disrupting the printing process. Fluorescent chemicals such as quantum dots could also be added to the resin.

We have demonstrated a new method for fabricating phantoms using 3D printing that allows design of the phantom’s optical properties and geometry, for example, to match a particular subject. We fabricated and imaged a mouse phantom with FODT and obtained quantitative information. Our method can be used to create phantoms with different geometries, for other imaging modalities, and for calibration of data captured from live animals. Fundamentally, with improved printing technology, our method could allow a phantom to be printed from multiple materials with optical properties that match those of the respective tissues.