Computational Fluid Dynamics and Additive Manufacturing to Diagnose and Treat Cardiovascular Disease

Abstract

Non-invasive engineering models are now being used for diagnosing and planning the treatment of cardiovascular disease. Techniques in computational modeling and additive manufacturing have matured concurrently, and results from simulations can inform and enable the design and optimization of therapeutic devices and treatment strategies. The emerging synergy between large-scale simulations and 3D printing is having a two-fold benefit: first, 3D printing can be used to validate the complex simulations, and second, the flow models can be used to improve treatment planning for cardiovascular disease. In this review, we summarize and discuss recent methods and findings for leveraging advances in both additive manufacturing and patient-specific computational modeling, with an emphasis on new directions in these fields and remaining open questions.

New strategies for modeling cardiovascular disease

Engineering modeling advances have played critical roles in the diagnosis and treatment of vascular disease since at least the 1990s when the first image-based modeling technologies were developed for simulating hemodynamics [1]. These models have provided non-invasive techniques for both diagnostics and treatment planning. The models can also be used to drive the development of therapeutic devices. The long-term utility of these models, however, is limited by the available computational power and validation capabilities. Two trends have emerged that warrant an exposition on the synergy between massively parallel hemodynamic simulations and additive manufacturing. First, three-dimensional printing can be used to create phantoms and facilitate in vitro experiments to validate flow models using complex vascular geometries that recapitulate the vascular system in vivo. The construction of patient-specific geometric models from medical imaging data has enabled the precise identification of areas of perturbed blood flow and prediction of how flow patterns will change following possible therapeutic interventions. Second, high-resolution CFD simulations can be used to drive the development or refinement of medical devices by providing much needed information on the anatomic variations, biomechanical forces, and wall properties that can influence the design of stents, flow diverters, stent grafts and conduits, and similar devices. In this review, we concentrate on these two trends after we briefly describe the impact of wall shear stress (WSS, see Glossary) and affiliated computational techniques on the study and treatment of vascular disease, device design, and evaluation.

The Vascular System

The cardiovascular system is a highly integrated closed loop circuit of vessels that circulates blood to deliver oxygen and nutrients to organs and removes byproducts of metabolism. The vascular system exists in an arborized pattern with vessels and daughter branches arranged into vascular beds based on the end organ served. Within the vascular system, the cross-sectional area of the combined capillary beds is approximately 103 times greater than that of the aorta with a concomitant decrease in flow velocity as vessel diameter decreases [2]. Functional differences between vascular beds are attributable to both the structural properties of the vessels (i.e., vessel diameter, length, tortuosity, and stiffness) and the effects of hemodynamic forces on vascular phenotype. Blood vessels are continuously exposed to hemodynamic forces resulting from pulsatile pressure generated by cardiac contraction, the flow characteristics of circulating blood, and modifications to these forces locally by the geometry and mechanical properties of the blood vessels themselves [3].

Tensile stress and WSS are the key mechanical forces that regulate and maintain vascular homeostatic phenotype and function in a spatial and temporal manner. Tensile stress is distributed circumferentially around the vessel wall and is related to blood pressure, lumen radius, and wall thickness. Tensile stress regulates autocrine and paracrine signaling between blood vessel cells, mediates angiogenesis, and maintains the normal vascular phenotype [4, 5]. WSS is determined by the gradient of blood velocity at the vessel wall surface and is influenced by blood viscosity. In normal human arteries with pulsatile flow, WSS ranges from 1–5 Pa, whereas it is between 0.1–0.5 Pa in the venous system, which is characterized by minimal pulsatility [6]. Laminar blood flow with normal WSS protects the vascular endothelium, increases production of nitric oxide and prostacyclin, upregulates expression of the vasculoprotective transcription factors Krüppel-like factor 2 (KLF2) and nuclear factor erythroid 2-related factor 2 (Nrf2), and is important for barrier function, maintaining an antithrombotic surface, and regulating vascular tone [7–9].

The vascular system is adaptive and capable of growth and remodeling (G & R) throughout development, adulthood, and aging. Growth and remodeling in blood vessels are inherently coupled processes that incorporate vascular dynamics and hemodynamic forces, such as WSS. At baseline, the healthy vasculature is at homeostasis with stresses at ambient levels that maintain the vessel wall and render G & R quiescent. A theory to explain G & R based on a constrained mixture model assumes that a blood vessel can respond to hemodynamic stress, undergo G & R, and return to its basal state by modulating the response of vascular smooth muscle cells [10–12]. Based on this theory, G & R has been studied in response to transient and sustained changes in hemodynamic and mechanical loads in models of the arterial system. The study showed that an artery can maintain homeostatic conditions over a range of pressure and flow and with a range of material properties, an effect that was dependent on prestretch of elastin and collagen. This study also determined that prestretch of collagen and elastin played a role in homeostasis, whereas material properties determined response time [13]. Similar work has been performed to study other clinically relevant vascular diseases, including an infrarenal aorta model to study expansion of aneurysms and vein grafts in response to increased pressure [14, 15].

Injury to the vascular system can cause maladaptive vascular remodeling and vascular dysfunction. Vascular abnormalities may also occur following prolonged high blood pressure, diabetes mellitus, hyperlipidemia, inflammation, drugs, or toxins that promote chemical and/or hemodynamic stress and cause architectural changes predicted by G & R that remodel the vessel and form atherosclerotic plaques. These vascular lesions that alter the topography of the vessel wall, in turn, effect changes in local WSS causing luminal narrowing in areas of low WSS or outward remodeling of blood vessels and aneurysm formation in areas of high WSS [9]. In patients with congenital heart disease, the unique hemodynamic and WSS profiles have a propensity to lead to (mal)adaptive vascular remodeling and dysfunction in patterns not observed normally. Patents with coarctation of the aorta have low levels of time-averaged WSS in the descending aorta that correlate with atherosclerotic plaque formation; repair of the coarctation with resection and end-to-end anastomosis was associated with elevated time-averaged WSS in the vicinity of residual narrowings, indicating that these treated patients are at risk for the development of atherosclerosis in unique locations because of the repair [16]. Patients with congenital biscupid aorta valves were also had increased aorta WSS compared with individuals with tricuspid aortic valves, suggesting that the WSS and hemodynamic flow patterns contribute to aortic dilatation in these patients [17].

Cardiovascular disease continues to be an urgent clinical problem affecting 92.1 million adults in the US, with a projected 43.9% having some form of the disease by 2030 (http://www.who.int/mediacentre/factsheets/fs317/en/). Worldwide, cardiovascular disease accounts for 31% of deaths annually and is a significant contributor to cardiovascular morbidity. Current methodologies to diagnose and determine the severity or significance of cardiovascular disease at the level of blood vessels include non-invasive imaging, e.g., computed tomography angiography (CTA) and invasive angiography. Invasive procedures enable a higher resolution visual assessment of the vessel lumen using intravascular ultrasound (IVUS) or optical coherence tomography (OCT) imaging; however, these methods describe only anatomy and provide limited information about local hemodynamic forces. Other invasive techniques that functionally assess luminal narrowing are guidewire-based technologies with high fidelity sensors that provide a low-resolution summed measure of pressure. As standalone technologies, none of the aforementioned imaging or pressure measurement tools can provide complex high-resolution assessments of flow in the vasculature or predict how flow-related parameters will change with a standard therapeutic intervention. Computational and advanced manufacturing tools can bridge this gap, and, to date, they are becoming more widely employed in the diagnosis and treatment of vascular disease.

Computational Fluid Dynamics

The quantification of hemodynamic forces, including velocity and pressure fields on a per-patient basis is poised to play a crucial role in the diagnosis of, and treatment planning for, patients with cardiovascular disease. Understanding the principles that govern vascular disease localization and progression has been a long-established goal of computational biomechanics [18]. Models used to understand these principles have ranged from 0D to 3D numerical methods to represent the human vascular system. The 0D models, or lumped parameter models, include no spatial dimensions and assume physiological variables such as pressure and resistance to be spatially uniform across the system. 1D models can represent wave propagation and reflection and represent the physiological variables in one spatial dimension. Simulations in 2D often assume symmetry of the solution about a central axis. There are several excellent references on the broader spectrum of CFD models [19–22]. This review focuses on massively parallel 3D models of hemodynamics.

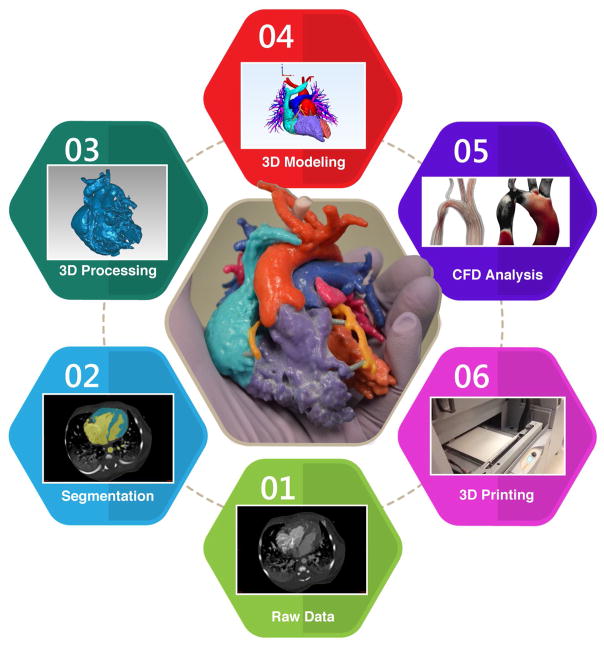
Figure 1 shows the process for deriving fluid and 3D printed models from medical imaging modalities. Methods for quantifying vascular flow start with deriving patient-specific anatomic and physiologic data from imaging modalities such as computed tomography angiography (CTA), magnetic resonance imaging (MRI), ultrasound, IVUS and OCT imaging. The medical images must resolve sufficient anatomical detail for segmentation and geometry extraction. Segmentation software is used to convert the medical images to a triangulated mesh based on the vascular anatomy. Table 1 provides a sample of popular segmentation packages for building the meshes that typically serve as input to the complex numerical solvers used in 3D CFD simulations. Withey and Koles detail an in depth review of the methods and available software for medical image segmentation [23]. Furthermore, PACS systems, such as eRAD Image Medical and Osirix, now offer a range of segmentation capabilities.

Figure 1.

Schematic of the process moving from medical imaging to computational fluid dynamics and 3D printed models.

Table 1.

Popular mesh reconstruction software packages.

Software Package	Open Source	Reference
3D Slicer	Y	https://www.slicer.org
Avizo	N	https://www.fei.com/software/amira-avizo/
Embodi 3D	Y	https://www.embodi3d.com/democratiz3D/
ITK Snap	Y	https://http://www.itksnap.org/
Mimics	N	http://www.materialise.com/en/medical/software/mimics
SCAN IP	N	https://www.simpleware.com/software/
SimVascular	Y	https://simvascular.github.io/
Terarecon	N	https://www.terarecon.com/
Vitrea	N	https://vitalimages.com

Blood flow within the vasculature is then simulated as an incompressible fluid. Flowing blood in the larger arteries can be represented as a Newtonian fluid, whereas the shear rates in smaller vessels necessitate a non-Newtonian description [24]. Table 2 provides an overview of current state-of-the-art computational hemodynamic software packages.

Table 2.

Common computational fluid dynamics software packages for simulating 3D hemodynamics in patient-derived geometries.

Software Package	Method	FSI	Open Source	Reference
ABAQUS	FE	Y	N	https://3ds.com
COMSOL	FE	Y	N	https://www.comsol.com
CRIMSON	FE	Y	N	http://www.crimson.software
FLUENT	FE	Y	N	http://www.ansys.com
HARVEY	LB	Y	N	[96]
HemeLB	LB	N	Y	https://github.com/UCL/hemelb
IBAMR	FE	Y	Y	https://github.com/IBAMR
MUPHY	LB	Y*	N	[97]
NEK5000	FE	Y	Y	https://nek5000.mcs.anl.gov/
NEKTAR	FE	Y	Y	https://nektar.info
OPENFOAM	FV	Y	Y	https://www.openfoam.com
SimVascular	FE	Y	Y	https://simvascular.github.io/
WaLBerla	LB	Y	Y	https://www.walberla.net/

FE: finite element, FV: finite volume, LB: lattice Boltzmann.

^*includes explicit cells but rigid walls.

As modeling the entire vascular system is not tractable, the simulated region will include at least one inlet and one outlet where physiological boundary conditions must be specified. These conditions are typically based on either data measured for a specific patient, average patient data, a physical model, or defined assumptions. The challenge lies in patient-specific tuning of the boundary conditions. These conditions can be specified by setting the pressure or flow at the boundaries or by coupling an additional, lower-order model to the 3D CFD solver to provide more realistic conditions. The coupled models enable detailed analysis in the 3D region while providing efficient models of regions proximal and distal to the area of interest [22]. Furthermore, lumped parameter and coupled models can account for wave propagation phenomena present in the arteries. The proper choice of boundary conditions influences the robustness, stability, computational cost, and accuracy of 3D simulations [25, 26]. To match clinical data, parameter estimation, automated tuning, and uncertainty quantification are often necessary [27–29].

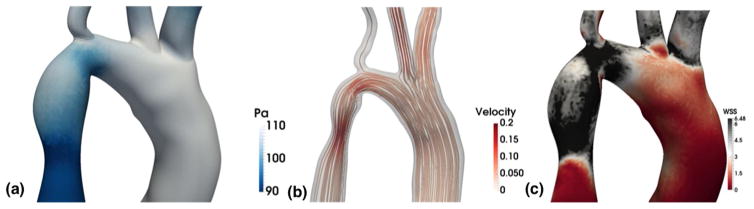
Typically, such large-scale models rely on either a Navier-Stokes [30] or lattice Boltzmann solver [31, 32]. The computational demands of these simulations have historically restricted their size and scope, but advances in parallel algorithms and computer hardware have extended the reach of these simulations to much larger regions [30, 32–34]. High-performance computing (HPC) has extended the time-scale, domains, and fidelity that can be captured with CFD simulations. Efforts to simulate the full arterial network of the human body have started to be undertaken. In 2013, Xiao and colleagues completed a key feasibility study for simulating flow in a full body simulation [35]. The largest 3D simulation to date simulated flow in all arteries of a human greater than 1 mm in diameter [34]. The flow was simulated at a 9 μm resolution, required 509 billion grid points, and was modeled using 1.6 million processors. Example results from a parallel CFD simulation are shown in Figure 2, depicting different types of data that can be extracted: pressure, velocity streamlines, and wall shear stress. Other key challenges to accurately representing patient-specific hemodynamics are capturing the material properties of the vessel walls and, sometimes, explicitly accounting for cells in the blood. Typically for fluid structure interaction (FSI), the fluid domain will be coupled to the solid domain using a momentum coupling in which the wall or cells are models as elastic materials. FSI models are necessary to simulate study of the role of ventricular and valve hemodynamics [36, 37]. As outlined in Table 2, many of the aforementioned CFD software packages have begun building in FSI capabilities. Traditional FSI techniques rely on the arbitrary Lagrangian-Eulerian (ALE) method, and, more recently, alternatives such as the coupled momentum method (CMM) and immersed boundary method (IBM) are becoming popular [21]. In each case, stability concerns must be addressed and vessel-specific properties are needed to parameterize the model.

Figure 2.

Results from CFD software for hemodynamics modeled as a Newtonian fluid in an image-derived vascular geometry of a coarcted human aorta. (a) The left panel shows a pressure map. (b) The middle panel demonstrates velocity flow lines. (c) The right panel shows a wall shear stress map.

A key goal for CFD studies is to provide insight into the relationships between vascular anatomy, local hemodynamics, and the development and progression of vascular disease and, thereby, serve as a diagnostic tool. Understanding the connection between flow patterns and topology is particularly important for simulations using geometries derived from medical imaging data. CFD enables non-invasive capture of critical hemodynamic variables from a study intended to provide anatomical information only. The importance of these hemodynamic variables has been realized over the last few decades, with the identification of parameters such as low or oscillatory WSS [38, 39], pressure gradients [40], and velocity flow fields [41] as risk factors for both different vascular diseases and mechanobiologic drivers of vascular growth, remodeling, and adaptation. Large computational studies investigating the use of such hemodynamic markers in diagnosis have been completed for a range of diseases including but not limited to coarctation of the aorta [16, 42, 43], atherosclerosis [32, 44, 45], aortic aneurysms [46–48], cerebral aneurysms [49–51], coronary artery bypass grafting (CABG) [52], Kawasaki disease [53] (D. Sengupta, PhD thesis, University of California-San Diego, 2013), and congenital heart diseases [54–57].

Three-dimensional hemodynamic simulations are approaching widespread use for the diagnosis of cardiovascular disease. The use of CFD for clinical decision support is increasing [58]. In 2014, the FDA approved the Heartflow FFR-CT software, which enables physicians to non-invasively evaluate hemodynamics in the coronary arteries and determine the functional severity of a blockage based on a quantity known as fractional flow reserve (FFR) [59]. Prior to the availability of this service, FFR could be obtained only through invasive testing.

3D Printing

3D printing is a process of additive manufacturing by which a 3D object is built layer-by-layer. The process is fundamentally different from subtractive manufacturing, wherein a 3D object is formed by progressively cutting material away from a solid block (e.g., computer numerical control, or CNC, cutting). The clear advantage of 3D printing is that the process can be applied to create arbitrarily complex geometries, whereas geometries created through subtractive manufacturing must be compatible with the limited access afforded to cutting tools operating from the outside in. Different 3D printing technologies relevant to the biomedical field include stereolithography, fused deposition modeling, digital light processing, and selective laser sintering, among others.

Studies of flow in 3D printed models necessarily require coupling with a flow measurement system. One option is MRI, which can measure flows within models printed directly by machines including the Objet family (Stratasys, Eden Prairie, MN, USA) [60]. Another option is particle image velocimetry (PIV), which, unlike MRI, requires optical access to the flow test section. Directly printed models for PIV flow experiments have been used for decades [61]. However, the process is challenged by the inherent layering artifacts generated by 3D printing. These artifacts can disturb refractive index uniformity within a model, even when accessed from only a certain direction (e.g., a direction in-plane with respect to the created layers). The artifacts may also disrupt fluid mechanics near the boundary layer in the form of small-scale recirculation. When applying PIV to test sections representing anatomical geometries, the best overall results we observed were generated by more industrial grade PIV systems (e.g., the LaVision Flowmaster system (LaVision, Ypsilanti, MI, USA)) in conjunction with models that were recast using a 3D print as the starting point [62]. Figure 3 shows an example setup. One process for generating these models begins with 3D printing a core model out of wax using a Solidscape MAX2 printer (Solidscape, Merrimack, NH, USA). Investment plaster is then used to form a mold around the core, and the core is dissolved out. Next, a eutectic metal core can be recast inside the mold, and the mold is then removed. Lastly, a transparent material such as urethane or silicone can be poured and set around the metallic core, and the core is subsequently melted out, leaving a transparent lost-core model suitable for PIV. This process enables management of interior surface smoothness during the recasting process. Further, despite the optical requirements of PIV, such models can be used in conjunction with metallic medical devices that tend to disrupt MR imaging.

Figure 3.

Photograph of an in vitro flow loop. Image reproduced with permission from [43].

The aforementioned method is, of course, only one of numerous viable mechanisms for 3D printing vascular models for flow experiments or otherwise. Most popular among these other mechanisms may be the Objet family of devices mentioned earlier in the context of MRI-based experiments. As demonstrated in [63] and [64], this platform can generate highly accurate vascular models at the scale of the human neurovasculature. Compared with the originally segmented and reconstructed (virtual) anatomy in [64], high-resolution CT scans of the 3D printed anatomy provided (virtual) 3D models that differed on the order of only 100 microns based on distance analysis. Table 3 lists other forms of additive manufacturing.

Table 3.

Forms of additive manufacturing, commonly known as 3D printing.

Process*	Example Media**	Technology	Basic Description
Binder Jetting	Gypsum Printing	Inkjet	Liquid agents are applied to powder media selectively, in an inkjet (or inket-like) process
Material Jetting	Photopolymer	Polyjet	Photopolymer liquid is deposited on a build platform and exposed to a light source for curing
Powder Bed Fusion	Nylon	Selective laser sintering, electron beam melting	Powder materials are melted together via a high-energy heat source
Directed Energy Deposition	Metals	Laser engineered net shaping	Media is media onto a build platform while being heated by a high energy heat source
Sheet Lamination	Paper, plastic, metal film	Laminated object manufacturing	Material sheets are selectively cut and laminated together
Vat Photopolymerization	Photopolymer	Stereolithography	A vat of photopolymer liquid is selectively exposed to a light source
Material Extrusion	Plastic (ABS, PLA)	Fused deposition (fused filament fabrication)	Media is heated to a glass transition temperature and selectively deposited on a build platform

^*The nomenclature presented here is developed by ASTM International.

^**These examples of media and technologies are intended to be a representation of the field, but not exhaustive.

Treatment Planning and Device Design

3D Printing vasculature for education

3D printing has been applied extensively in the context of cardiovascular disease for educating students, patients, and families [65, 66], and for treatment planning [67, 68]. 3D prints of relevant cardiovascular anatomy are typically generated based on the same types of medical images used to construct 3D geometries for CFD analyses (e.g., CT, MRI, angiography, IVUS, etc.). For treatment planning, both anatomical and physiological (e.g., blood flow) representations of cardiovascular structures have been targeted as end points. For example, in repair planning, the use of anatomical representations of congenital heart defects or other structural heart disease is growing rapidly. Ryan and colleagues [68] demonstrated models printed with a 3D Systems Zprinter 650 machine (3D Systems, Rock Hill, SC, USA) that communicated cardiovascular anatomy and associated anomalies through specific colorization. Other models such as those produced by Costello and colleagues enable surgical practice of the repair procedure [69]. Such models can be fabricated using the Objet family of printers (Stratasys, Eden Prairie, MN, USA) or similar machines.

Validating patient-specific fluid simulations through comparison with results from in vitro experiments

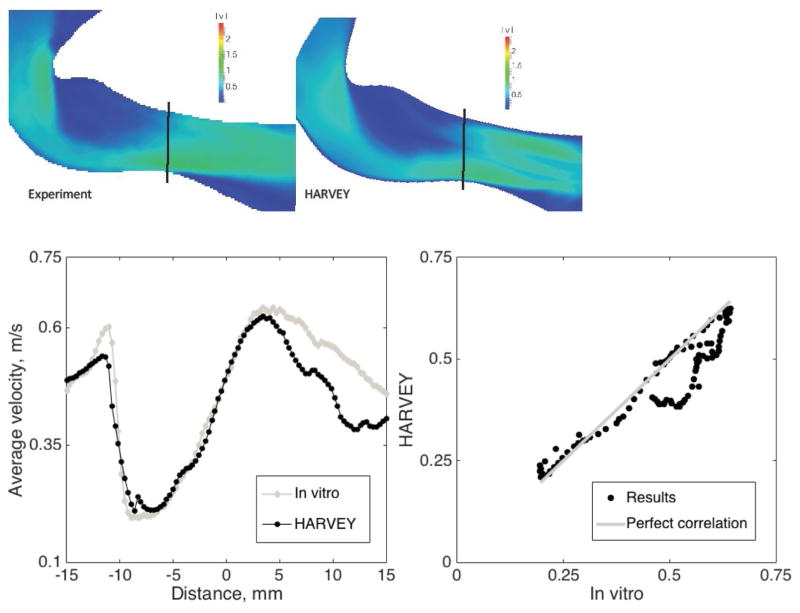
Additive manufacturing in combination with experimental techniques such as PIV is being used to validate CFD simulations in complex geometries. Traditionally, CFD packages were validated through comparison with analytical results [70, 71]. Such comparisons become untenable for complex geometries such as those found in the human vasculature. Some work has compared fluid simulation results with in vivo measurements from 4D-MRI [72, 73]; however, it is nearly impossible to control input parameters in a living biological system. 3D printed models offer a method to perform controlled fluid experiments for simulation validation. Such validation studies have been completed for aortic flow [43], cerebral aneurysms [50, 62], valve/leaflet interaction [74], coronary artery disease [32, 75–79], CABG [52, 80, 81] and in a left ventricular assist device (LVAD) [82]. An iterative feedback loop can be established to optimize the fluid simulations and ensure reproducible, robust, and accurate results. Figure 4 shows an example comparison between fluid simulation and experimental results.

Figure 4.

Magnitude of velocity through coarctation, from in vitro experiment compared to HARVEY (left). In the two graphs on the right, average velocity over vertical slices of the images along the vessel is shown first, followed by a direct comparison of simulation values to in vitro measurements on the right. Image reproduced with permission from [43].

Comparisons of simulation results with experimental results provide a critically valuable mechanism toward ensuring that simulations are, in fact, realistic. However, one persistent challenge in authentically recreating in vivo environments in vitro is building vascular phantoms that behave physiologically with respect to fluid structure interaction. Vascular phantoms with a range of Young’s moduli and Shore hardnesses that overlap with in vivo conditions can be 3D printed (and/or recast after 3D printing), but isolating the vascular geometry in the laboratory, and thereby omitting the many surrounding structures and dynamics present in vivo, necessarily limits the degree to which in vivo conditions can be reproduced. The ability to recapitulate in vivo conditions both anatomically and mechanically remains a relatively unsolved problem.

Leveraging CFD simulations to inform treatment planning and device design

The results of the fluid simulations can also be used to refine the 3D printed model most often for treatment planning and device design. Through fluid simulations, many perturbations of device designs or treatment options can be simulated in silico before either high cost surgery or further in vitro experiments. CFD simulations have been used to evaluate the design of Y-grafts for Fontan operations [83–85], anastomosis design [86], stents [87, 88], and flow-diverters [89, 90]. To enable predictive treatment planning, the mesh representing the vascular geometry is modified to represent different potential surgical outcomes. This approach of using 3D flow simulations to interrogate and optimize treatment plans has been used successfully for cerebral aneurysms [91, 92], coarcted aortas [93, 94], and other congenital disorders [95].

Concluding Remarks

The advancement of both high performance computing and 3D printing has presented a unique opportunity to tackle key questions in vascular biology at unprecedented scale and complexity. The trends toward patient-specific computational simulations and models have necessitated the ability to validate flow in such complex models, enabling high-resolution diagnostic screens, new techniques to predict the outcome of different treatment options, and improved device design. We propose that the synergy between large-scale hemodynamic simulation and 3D printing will transform development and treatment of vascular disease. However, many open challenges remain (see Outstanding Questions). We expect that patient-specific modeling (both experimental and computational) will produce a quantitative method for more accurate diagnostics and treatment on a per-patient basis.

Outstanding Questions.

• What data analyses will be needed to quantitatively assess a wide range of treatment options?

• What are the limits in terms of scale and resolution that we can 3D print biocompatible medical devices? What computational limits must be overcome to facilitate near real-time diagnostics? What computational limits must be overcome to enable patient-specific device design and manufacturing?

• What analytical methods can be used to extend the temporal domain captured by high-resolution CFD models?

• How do we address the need for parameter estimation, automated tuning to match clinical data, and uncertainty quantification in cardiovascular simulations?

• Can we capture flow in large regions of the human vasculature that include cellular components such as erythrocytes and neutrophils in computationally tractable simulations?

• How do we build fully integrated models of cardiac function, ventricular hemodynamics, and valves in a data-driven, computationally efficient manner?

• How can we 3D print vascular phantoms that are not only anatomically accurate but also physiologically accurate?

Trends.

• The improved capabilities of additive manufacturing in terms of material properties and resolution is opening new and exciting possibilities for the use of 3D printing in cardiovascular medicine.

• Methods for using high performance computing to enable high fidelity and patient-specific fluid simulations are rapidly evolving, providing new insights into the role hemodynamic forces play in cardiovascular disease.

• The emerging synergy between large-scale simulations and 3D printing is having a two-fold benefit: 1) 3D printing can be used to validate the complex simulations and 2) the flow models can be used to improve treatment planning for cardiovascular disease.

Glossary

3D printing

a process of additive manufacturing by which a 3D object is built layer-by-layer.

Computational fluid dynamics (CFD)

numerical analysis used to solve fluid dynamics equations and simulate flow in complex geometries.

Computed tomography angiography (CTA)

anon-invasive imaging study that uses an injection of iodinated contrast to visualize blood vessels.

Fractional flow reserve (FFR)

this measurement accounts for the pressure gradient across a narrowed region in an artery. It is typically measured using an invasive, guide-wire based catheter procedure.

High performance computing (HPC)

massively parallel computing has been leveraged in recent years to extend the domain, time- scale, and resolution of CFD simulations. HPC relies on the use of large-scale parallel systems typically with more than one thousand processors.

Lattice Boltzmann method

an alternative approach to solving the standard Navier-Stokes equations governing fluid motion. It is based on kinetic theory and represents the fluid as a probability distribution function of particles that can move at discrete velocities around fixed Cartesian lattice.

Image segmentation

the process of partitioning an image from a medical imaging modality into different segments. Typically, in the case of studying vascular phenomena, the vessel lumen is extracted in a 3D stack of images. The extracted vessel walls are then stitched together to create a 3D triangulated mesh depicting a patient’s vascular topology. The goal of segmentation is to create a representation that can be used as input for 3D printing or simulation.

Intravascular ultrasound (IVUS)

a miniature ultrasound probe attached to the tip of a catheter that is placed inside a blood vessel and provides images of a vessel lumen and vessel wall.

Navier-Stokes equations

physical models used to capture the motion of fluids that are derived from Newton’s second law of motion. They are the common equations underlying computational fluid dynamics simulations.

Optical coherence tomography (OCT)

a catheter-based intravascular imaging technique that uses light scattering to image blood vessels with ultrahigh resolution (10 microns).

Particle-image-velocimetry (PIV)

an experimental technique to optically measure flow patterns.

Magnetic resonance imaging (MRI)

a non-invasive study that creates high-resolution images of structures in the body using a magnetic field, pulse radio wave energy, and field gradients.

Wall shear stress (WSS)

the stress that the fluid applies to the vessel wall, a known pathogenic factor in a range of vascular diseases.