Parvalbumin and Somatostatin Interneurons Control Different Space-Coding Networks in the Medial Entorhinal Cortex

Summary

The medial entorhinal cortex (MEC) contains several discrete classes of GABAergic interneurons, but their specific contributions to spatial pattern formation in this area remain elusive. We employed a pharmacogenetic approach to silence either parvalbumin (PV)- or somatostatin (SOM)-expressing interneurons while MEC cells were recorded in freely moving mice. PV-cell silencing antagonized the hexagonally patterned spatial selectivity of grid cells, especially in layer II of MEC. The impairment was accompanied by reduced speed modulation in colocalized speed cells. Silencing SOM cells, in contrast, had no impact on grid cells or speed cells but instead decreased the spatial selectivity of cells with discrete aperiodic firing fields. Border cells and head direction cells were not affected by either intervention. The findings point to distinct roles for PV and SOM interneurons in the local dynamics underlying periodic and aperiodic firing in spatially modulated cells of the MEC.

Graphical Abstract

Highlights

• •Parvalbumin (PV) interneurons maintain spatially periodic firing in grid cells
• •PV interneurons are necessary for speed tuning in entorhinal speed cells
• •Somatostatin (SOM) interneurons maintain selectivity of aperiodic spatial cells
• •PV and SOM cells regulate discrete subsets of spatially tuned entorhinal cell types

Two distinct sub-classes of inhibitory interneurons modulate different forms of spatial representation in the medial entorhinal cortex.

Introduction

The medial entorhinal cortex (MEC) is a key component of the mammalian circuit for neural representation of space (Moser et al., 2014, Rowland et al., 2016). The first functional cell type to be described in this circuit was the grid cell (Hafting et al., 2005). Grid cells fire action potentials at locations that, for each cell, occupy the vertices of a hexagonal grid spanning the entire space available to an animal in an open environment. Although grid cells are particularly abundant in MEC layer II, they are embedded within a wider MEC-pre- and parasubiculum network of functionally distinct cell types, including head direction cells (Taube et al., 1990, Sargolini et al., 2006, Boccara et al., 2010), border cells (Savelli et al., 2008, Solstad et al., 2008, Boccara et al., 2010), and speed cells (Kropff et al., 2015, Hinman et al., 2016). This wider network, in turn, interacts with specialized cells in neighboring brain regions, such as object and object-trace cells in the lateral entorhinal cortex (Deshmukh and Knierim, 2011, Tsao et al., 2013) and place cells (O’Keefe and Dostrovsky, 1971) and goal-vector cells (Eichenbaum et al., 1987, Sarel et al., 2017) in the hippocampus. Collectively, this assemblage of entorhinal and hippocampal functional cell types is thought to provide animals with a dynamic representation of location that enables them to navigate between places in a purposeful manner.

The surprising abundance of functionally dedicated cell types in MEC has prompted investigators to address the neural mechanisms underlying their differential firing patterns. Particular interest has been devoted to the origin of directionally tuned firing in head direction cells and spatially periodic firing in grid cells. It has been proposed that in these cell types, localized firing reflects continuous attractor dynamics enabled by connectivity between cells with similar directional or spatial tuning profiles (Skaggs et al., 1995, Zhang, 1996, Fuhs and Touretzky, 2006, McNaughton et al., 2006). Such recurrent connectivity is believed to engage consistent neuronal subsets in response to particular instances of external stimulation. External inputs carrying information about the animal’s speed and direction of movement are then thought to displace the locus of active cells in the network in a way that mirrors the animal’s changing position or orientation in the environment. However, for this network activity to remain localized, connectivity between similarly tuned cells must be balanced by inhibition between cells with more dissimilar tuning profiles (Fuhs and Touretzky, 2006, McNaughton et al., 2006, Burak and Fiete, 2009). Recent models have shown that, under certain conditions, such inhibitory connections are sufficient to generate hexagonally patterned firing in excitatory neurons without direct connectivity between the excitatory neurons themselves (Burak and Fiete, 2009, Bonnevie et al., 2013, Couey et al., 2013, Pastoll et al., 2013). This is potentially important because in MEC layer II, stellate cells, the principal cell type of the layer, communicate only via GABAergic interneurons (Dhillon and Jones, 2000, Couey et al., 2013, Pastoll et al., 2013). Considering that a substantial fraction of the grid cells are stellate cells (Domnisoru et al., 2013, Schmidt-Hieber and Häusser, 2013, Sun et al., 2015), it is therefore conceivable that GABAergic networks contribute critically to grid formation. However, the nature of such a contribution, and whether GABAergic cells exert a similar impact on other cell types of the MEC, has not been determined.

The mammalian cortex comprises a multitude of GABAergic cell types. In many regions of cortex, three major classes of immunochemically distinct GABAergic interneurons can be distinguished: one immunoreactive to parvalbumin (PV), one to somatostatin (SOM), and one to 5HT3A receptors (Kubota et al., 1994, Freund and Buzsáki, 1996, Gonchar and Burkhalter, 1997, Kawaguchi and Kubota, 1997, Lee et al., 2010, Rudy et al., 2011, Urban-Ciecko and Barth, 2016). Among these subtypes, PV- and SOM-expressing cells have been best characterized. PV- and SOM-expressing interneurons have unique morphological and electrophysiological properties (Freund and Buzsáki, 1996, Rudy et al., 2011, Urban-Ciecko and Barth, 2016). Most PV cells are fast-spiking basket or chandelier cells with low input resistances, fast membrane time constants, and limited spike frequency adaptation. By targeting the soma and the spike initiation zone, these cells are in a unique position to control whether or not a cell fires, as well as the timing of the cell’s action potentials. SOM cells, in contrast, include non-fast-spiking, facilitating, and more slowly adapting cell types, such as Martinotti cells and bitufted cells, which preferentially form synapses on the dendrites of their target cells. By forming synapses on specific dendritic segments, SOM-immunoreactive cells can effectively gate, and modulate, components of the excitatory input.

A structural and functional separation of PV- and SOM-immunoreactive interneuron populations is likely also present in MEC. In layer II, stellate cells receive strong perisomatic inhibition from PV interneurons (Beed et al., 2013, Couey et al., 2013, Fuchs et al., 2016), as well as more distributed dendritic inhibition from SOM interneurons (Fuchs et al., 2016). PV interneurons directly inhibit firing in grid cells, border cells, and head direction cells (Buetfering et al., 2014). However, whether PV cells are necessary for spatial or directional tuning in any of these cells—as proposed in some network models for grid cells (Couey et al., 2013, Pastoll et al., 2013)—remains to be established. It has also not been determined whether any impact on spatial or directional firing in MEC cells is exclusive for PV cells or whether SOM interneurons modify rates and patterns in a similar or complementary manner.

In the present study, we compared directly the impact of PV and SOM interneuron activity on spatial and directional representations in the MEC. Neural activity was recorded in MEC layers II and III of PV-Cre and SOM-Cre mice. In these mice, we used a Cre-dependent adeno-associated virus (AAV) to express selectively the pharmacologically selective designer Gi-protein-coupled muscarinic receptor hM4D (Armbruster et al., 2007) in conjunction with the fluorescent protein mCitrine in either PV or SOM-immunoreactive of the MEC. Ligand (CNO)-induced activation of hM4D receptors in either PV or SOM interneurons allowed us to selectively inhibit firing in these two major subtypes of MEC interneurons and examine the effects on the spatial and directional firing properties of MEC cells.

Results

Selective Expression of hM4D in PV and SOM Interneurons of MEC

In PV mice, hM4D and mCitrine were expressed selectively in dorsomedial-MEC PV interneurons (Figure 1A and Figures S1A and S1B). Tetrodes were within the infected MEC region (Figures S2 and S3). The estimated total number of hM4D-mCitrine-expressing MEC cells did not differ significantly between PV and SOM groups (Figures S1A, S1B, and S3). Within the infected region, mCitrine was expressed by 79% of PV cells and 73% of SOM cells (Figures S1A, S1B, and S3).

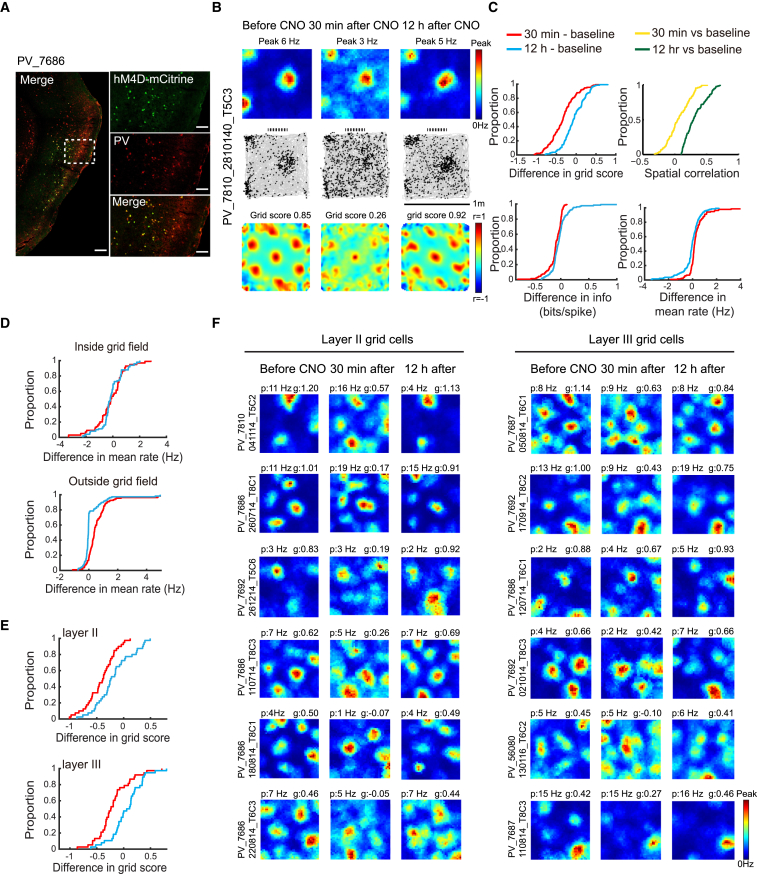
Figure 1.

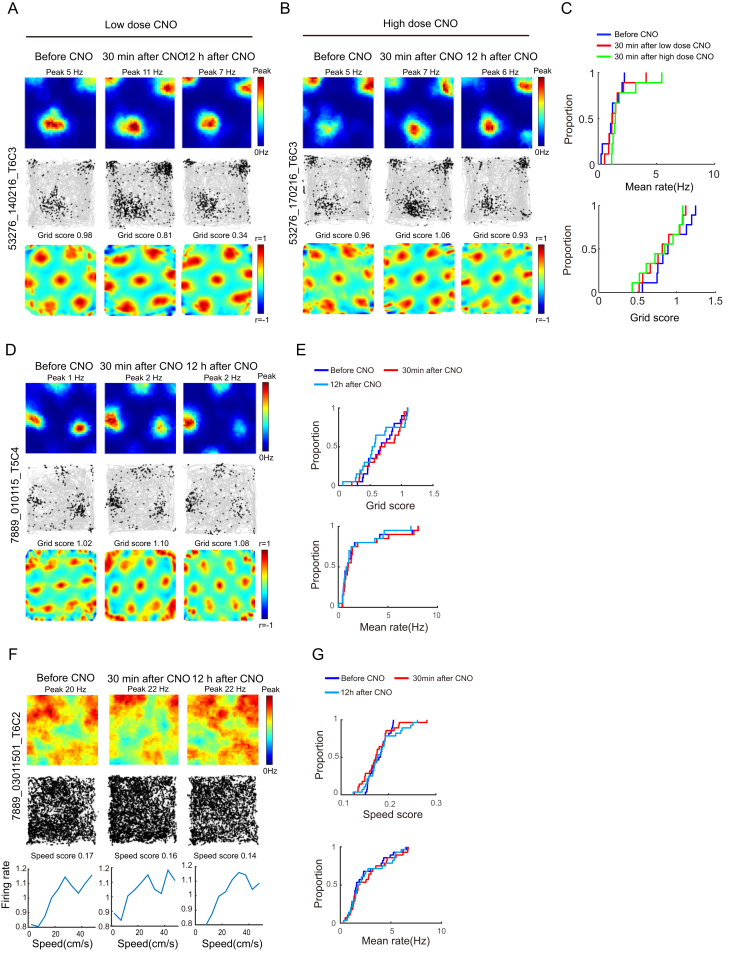
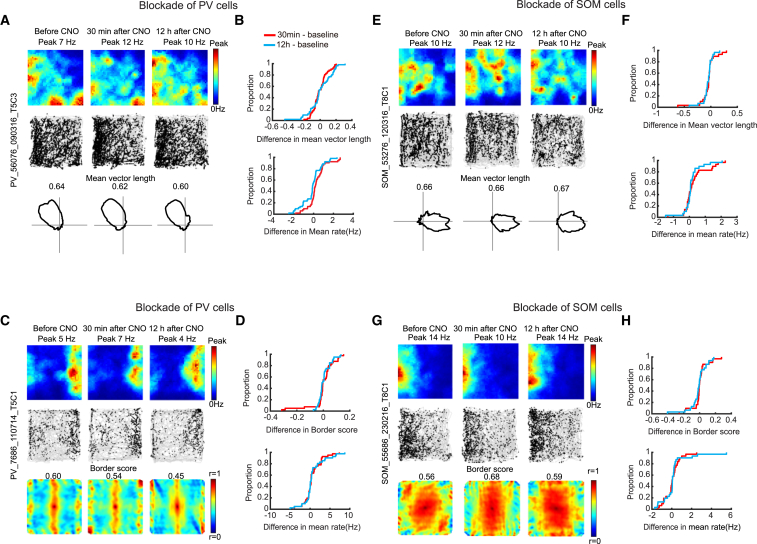
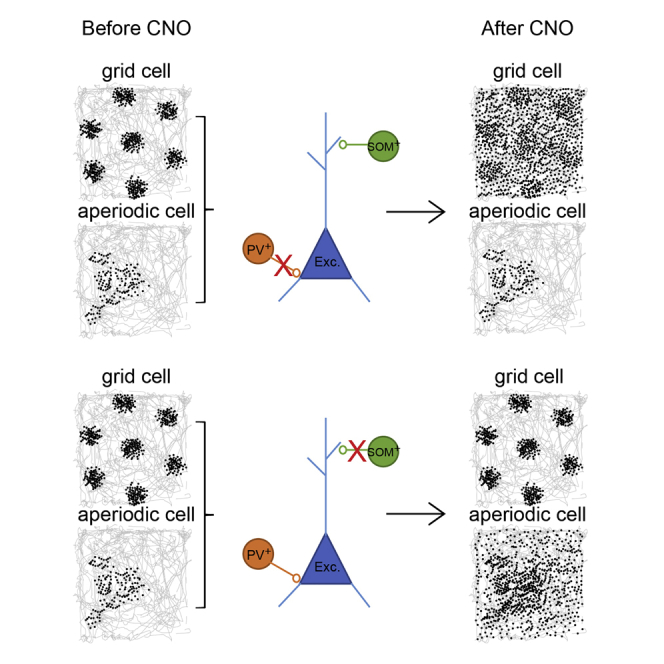
Inactivation of PV Interneurons Impairs Spatial Periodicity in Grid Cells

(A) Expression of hM4D-mCitrine in PV cells of the MEC (sagittal sections). Low-magnification image of entire MEC (left); high-magnification images from white frame in left panel (right). mCitrine-expressing cells in green (top), PV–expressing cells in red (middle), merge of mCitrine and SOM in yellow (bottom). Scale bars in left panel, 200 μm; right panel, 60 μm. Animal number is indicated at the top (for corresponding tetrode trace, see Figure S2). Note co-expression of mCitrine and PV (yellow, bottom frame).

(B) Representative MEC grid cell in a 1 m box from mouse with hM4D expression in PV interneurons (scale bar, 1 m). Location of cue card is indicated (stippled line atop). Subsequent figures all have the same size box and the same location of cue cards. Data were collected before CNO and both 30 min and 12 hr after. Top to bottom: color-coded firing rate maps (top, color bar indicates firing rate), spike locations overlaid on trajectory (middle, black on gray), and color-coded autocorrelograms (color bar, correlation from −1 to 1).

(C) Cumulative frequency diagrams showing significant decrease in grid score, spatial information, and spatial stability of grid cells 30 min after CNO-induced inactivation of PV interneurons, but not 12 hr later. Spatial stability is visualized as spatial correlation between rate maps at baseline and either 30 min or 12 hr after CNO.

(D) Cumulative frequency diagrams showing increase in mean firing rate outside, but not inside, grid fields after inactivation of PV interneurons.

(E) Cumulative frequency diagrams showing stronger decrease of grid scores in layer II than in layer III grid cells after CNO. See Figure S4 for absolute scores.

(F) Color-coded rate maps from grid cells in MEC layers II (left) and III (right) after CNO (six pairs of cells with approximately similar baseline grid scores in layers II and III). Peak rates (p) and grid scores (g) are indicated above each rate map. Animal and cell numbers are shown to the left.

See also Figures S1, S2, S3, S4, and S5.

Figure S1.

Expression of hM4D-mCitrine in PV and SOM Interneurons in MEC in PV-Cre and SOM-Cre Mice, Related to Figures 1, 2, 3, 4, 5, 6, and 7

The study included 12 PV-Cre mice and 8 SOM-Cre mice. Ten and six of these mice, respectively, were infected with hM4D-expressing virus; the remaining mice received control injections of AAV with mCitrine only.

(A and B) Co-expression of hM4D-mCitrine and either PV (A, top panel) or SOM (B, bottom panel) in MEC (same animal). The mice were injected into dorsal MEC with AAV expressing hM4D-mCitrine. First column, mCitrine expression at low magnification (green); second column, high magnification of framed areas in the first column (green); third column, staining for PV (top panel) or SOM (bottom panel), with signal shown in red at low magnification; fourth column, high magnification of the framed areas in the third column; fifth column, merge of first and third column, showing colocalization of mCitrine and either PV or SOM. Scale bars in first, third, and fifth column, 400 μm; second and fourth panel, 60 μm.

(C) Double staining with antibodies for PV and SOM antibody in the same wild-type mouse. Cells were counted across 10 regularly spaced sections of MEC in each of 2 animals. Note lack of co-labeling for PV and SOM. PV and SOM cells were distributed across all MEC layers, although the density for PV cells, but not SOM cells, was somewhat higher in layer II (mean number of cells per section: layer I: 5 ± 3.2, layer II: 30 ± 6.6; layer III and below: 18 ± 4.2), in agreement with previous observations (Wouterlood, 2002).

Figure S2.

Saggital Brain Sections Showing Locations of Tetrodes in MEC, Related to Figures 1, 2, 3, 4, 5, 6, and 7

Sagittal Nissl-stained brain sections showing locations of tetrodes in MEC in 10 PV-Cre and 6 SOM-Cre mice that received injections of AAV8-hSyn-DIO-hM4D-mCitrine as well as 2 PV-Cre mice that received control injections of AAV8-hSyn-DIO-mCitrine. For the remaining 2 SOM-Cre mice that received control injections of AAV8-hSyn-DIO-mCitrine, tetrode traces could not be reconstructed. Tetrode locations are indicated with arrowheads. Four-digit animal numbers are indicated.

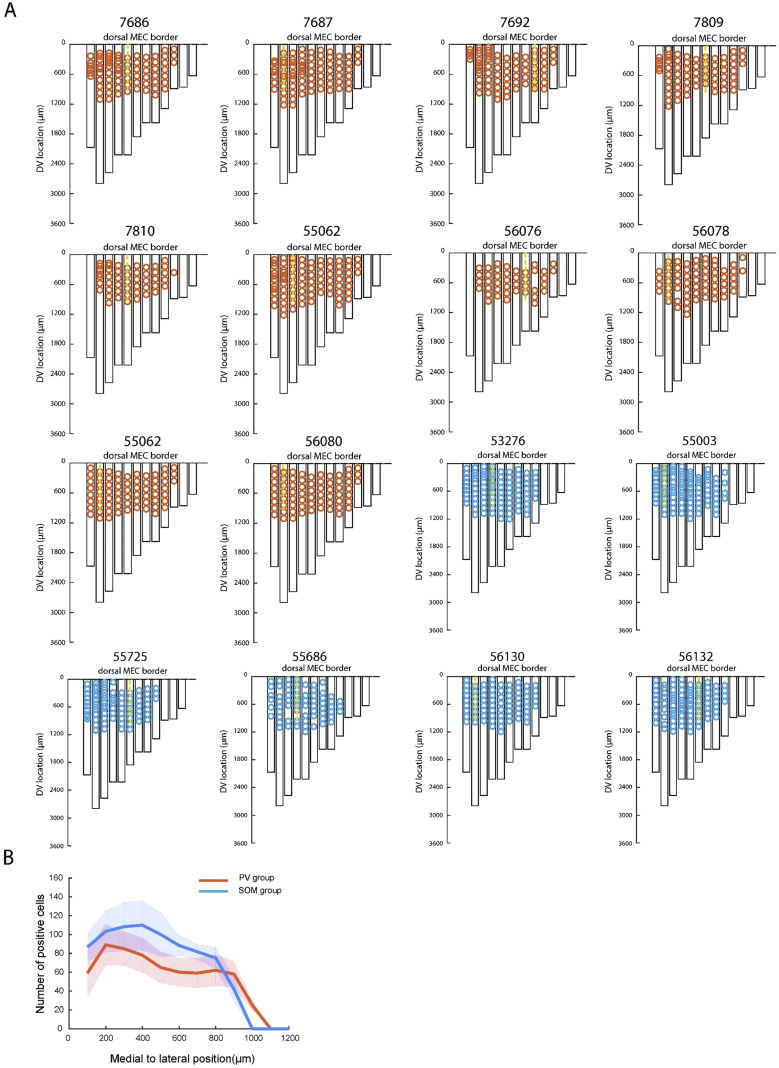
Figure S3.

Flat Maps of MEC Showing Anatomical Distribution of Infected PV and SOM Cells, Related to Figures 1 and 3

Distribution of infected (hM4D-mCitrine-expressing) PV and SOM cells in MEC of PV-Cre and SOM-Cre mice, respectively.

(A) Unfolded MEC maps showing distribution of infected cells. Unfolded maps are aligned to the dorsal border of MEC (x axis, ML, with medial side to the right; y axis, DV). The ML axis was divided into 12 × 100 μm sections, and the number and distribution of infected cells was determined for each section. Black rectangles indicate MEC for each section. For one section in each block (usually the first), we counted infected PV and SOM cells at successive dorsoventral levels. Infected cells were also counted in neighboring parahippocampal regions on the same section. The analysis showed that infected PV and SOM cells were localized mainly in the dorso-medial part of MEC, where the tetrodes were implanted. Every 10th infected MEC PV cell is represented with a red circle in the unfolded MEC maps, whereas every 10th infected SOM cell is displayed with a blue circle. Locations of tetrodes are shown with yellow dotted lines. The estimated total number of infected MEC cells did not differ significantly between the PV and SOM groups (53.2 ± 11.5 and 64.0 ± 10.8 immunopositive cells per section, respectively; two-sample t test, t (22) = 1.05, p = 0.31). Within the infected region (defined as the area where signal of mCitrine exceeded 2 SD of the mean value of the background signal), mCitrine was expressed by 78.6 ± 6.2% of the PV cells and 72.5 ± 5.1% of the SOM cells (means ± S.E.M.; Figure S1). The infected area covered similar percentages of layer II and III area within the MEC of the PV and SOM groups (layer II: 29.6 ± 3.3% in PV group; 35.1 ± 1.4% in SOM group; layer III: 29.6 ± 3.0% in PV group; 34.5 ± 2.2% in SOM group; layer II versus III in PV group: t(7) = 0.044, p = 0.97, and in SOM group: t(5) = 0.53, p = 0.62; layer II PV versus layer II SOM: t(12) = 1.13, p = 0.27; layer III PV versus layer III SOM: t(12) = 1.08, p = 0.29). Within the infected regions, the percentage of infected cells was similar for layers II and III (layer II: 78.2 ± 5.9% in PV group; 83.1 ± 7.3% in SOM group; layer III: 77.2 ± 5.3% in PV group; 71.6 ± 3.8% in SOM group; layer II versus III t(7) = 0.051, p = 0.96 and t(5) = 1.10, p = 0.32; layer II PV versus layer II SOM: t(12) = 0.57, p = 0.58; layer III PV versus layer III SOM: t(12) = 0.55, p = 0.59). On average, only 5.2 ± 1.4% of the mCitrine-infected cells were in neighboring regions, defined as presubiculum, parasubiculum, postrhinal cortex, and subiculum. In the PV mice, 97.2 + 0.7% of the mCitrine-labeled cells were positive for PV. In the SOM mice, 94.7 + 0.5% of the mCitrine-labeled cells were positive for SOM.

(B) Average number of infected cells as a function of position along ML axis of MEC in PV-Cre and SOM-Cre mice. Bin size 100 μm. Shaded areas indicate SEM.

Using antibodies for PV and SOM on the same sections in two wild-type mice, we found that less than 1% of the SOM interneurons in MEC layers II–III coexpressed PV (3.8 ± 0.4 out of 390 ± 15.7 SOM-positive cells per section, Figure S1C). Similarly, only 1.4% of the PV interneurons co-expressed SOM (3.8 ± 0.4 out of 260 ± 12.2 PV-positive cells per section, Figure S1C). The low number of double-stained cells is consistent with the lack of overlap between PV and SOM interneurons reported in previous work in MEC (Fuchs et al., 2016), as well as other cortical regions (Kubota et al., 1994, Gonchar and Burkhalter, 1997, Kawaguchi and Kubota, 1997, Lee et al., 2010).

Inactivation of PV Interneurons Impairs Spatial Tuning of Grid Cells

A total of 125 of the 133 cells identified as grid cells in PV-Cre mice were recorded in MEC and 8 in the parasubiculum; 41 of the MEC grid cells were in layer II (8.9% of layer II cells), 39 in layer III (5.6% of layer III cells), and 45 could not be determined (too near the border between the layers).

We first examined how individual grid cells responded to CNO-induced decreases in inhibition from PV cells (Figure 1). The criterion for grid cells was a minimum grid score of 0.42 on the baseline trial, corresponding to the 99^th percentile of a shuffled distribution (STAR Methods). As expected, if PV interneurons inhibit grid cells (Couey et al., 2013, Buetfering et al., 2014), the mean firing rate of the grid cells increased after the onset of the silencing (before, 1.10 ± 0.12 Hz; 30 min after, 1.52 ± 0.14; paired-sample t test, t (132) = 4.95, p = 2.23 × 10⁻⁶; Figure 1C; Figure S4A). The firing rate returned to baseline 12 hr after CNO (1.10 ± 0.13; paired-sample t test for baseline versus 12 hr, t (132) = 1.17, p = 0.24; Figure 1C; Figure S4A). Peak firing rates did not change (6.43 ± 0.46 versus 6.13 ± 0.45; t (132) = 1.09, p = 0.28). The changes in mean firing rate confirmed that PV interneurons were inhibited as intended.

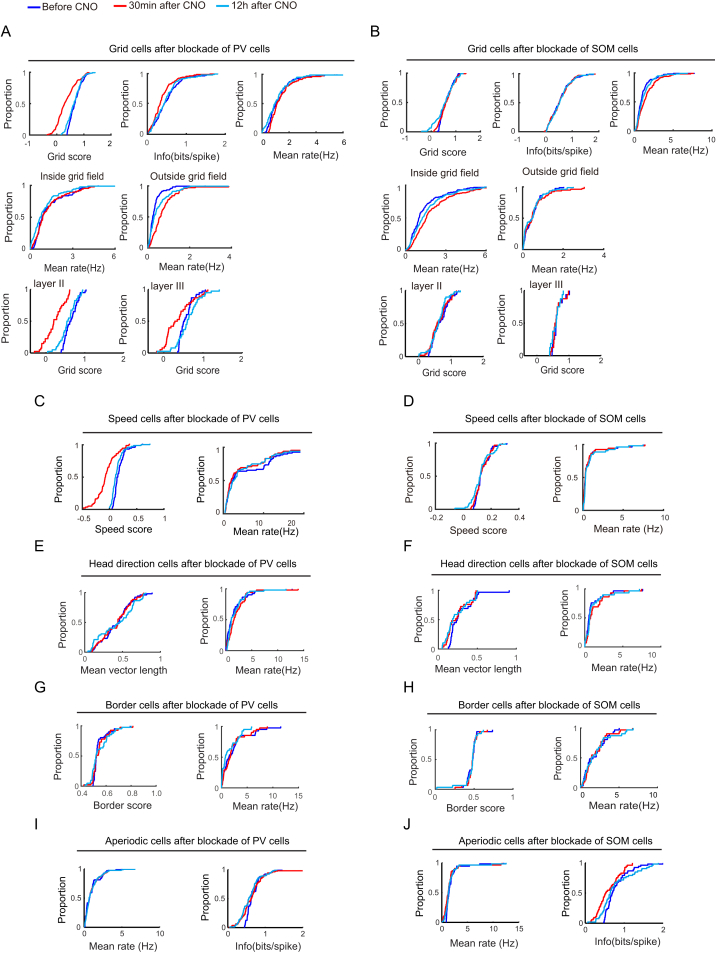
Figure S4.

Absolute Scores for Multiple Properties of Neural Firing during Baseline and 30 min and 12 hr after CNO, Related to Figures 1, 2, 3, 4, 5, and 6

While Figures 1, 2, 3, 4, 5, and 6 show difference scores (30 min–baseline or 12 hr–baseline), the present figure shows absolute scores for each of the three trials involved.

(A) (Upper panel) Cumulative frequency diagrams showing significant decrease in grid score and spatial information of grid cells 30 min after CNO-induced inactivation of PV interneurons but not 12 hr later. Mean firing rate of grid cells exhibits a small but significant increase after the inactivation. (Middle panel) Cumulative frequency diagrams showing increase in mean firing rate outside but not inside grid fields after inactivation of PV interneurons. (Bottom panel) Cumulative frequency diagrams showing stronger decrease of grid scores in layer-II than layer-III grid cells 30 min after CNO.

(B) (Upper panel) Cumulative frequency diagrams showing no change in grid score, or spatial information of grid cells after CNO-induced inactivation of SOM interneurons. The mean firing rate of the grid cells is increased after CNO. (Middle panel) Cumulative frequency diagrams showing significant increase in mean firing rate inside but not outside grid fields after inactivation of SOM interneurons. (Bottom panel) Cumulative frequency diagrams showing no change of grid scores in layer II or layer III 30 min after inactivation of SOM interneurons.

(C and D) Cumulative frequency diagrams showing significant decrease in speed-rate correlation (speed score) of speed cells after inactivation of PV interneurons (C, left panel), but not after inactivation of SOM interneurons (D, left panel). The mean firing rate of the speed cells showed a small but significant decrease after inactivation of PV interneurons (C, right panel) or SOM interneurons (D, right panel).

(E and F) Cumulative frequency diagrams showing no change in mean vector length of head direction tuning after inactivation of PV (E, left panel) or SOM interneurons (F, left panel). The mean firing rate of the head direction cells showed a slight but significant increase after CNO inactivation of PV interneurons (E, right panel) but no significant change in mean firing rate of head direction cells after CNO-induced inactivation in the SOM group (F, right panel).

(G and H) Cumulative frequency diagrams indicating no change in border scores or mean firing rates of border cells after CNO in the PV group (G) and the SOM group (H).

(I and J) Cumulative frequency diagrams showing that mean firing rate (I, left panel) and spatial information (I, right panel) did not change in aperiodic spatial cells after inactivation of PV interneurons, whereas inactivation of SOM interneurons reduced spatial information in these cells (J, right panel). Mean firing rate was not changed (J, left panel).

Inactivation of PV interneurons significantly reduced spatial periodicity in grid cells (Figures 1B and 1C; Figure S4A). Grid scores decreased from 0.69 ± 0.020 to 0.35 ± 0.031 (paired-sample t test, t (132) = 11.56, p = 9.89 × 10⁻²²). Within 12 hr after CNO, the scores had almost recovered (0.63 ± 0.022; baseline versus 12 hr, t (132) = 2.00, p = 0.05). The decrease in grid scores was expressed as an increase in the dispersal of spike locations (Figure 1D; Figure S4A). After CNO, there was a significant increase in spikes outside the original boundaries of the grid fields (before, 0.53 ± 0.12 Hz; 30 min after, 1.20 ± 0.14 Hz; t (132) = 6.62, p = 3.26 × 10⁻⁹; grid fields defined by a local-maximum detection procedure). The increase in spike dispersal had partly recovered 12 hr after CNO (0.83 ± 0.064; t (132) = 3.12, p = 0.03; Figure 1D; Figure S4). Firing rates inside the boundaries of the grid fields on the baseline trial did not change significantly after CNO (before, 2.16 ± 0.20 Hz; 30 min after, 2.10 ± 0.21 Hz; t (132) = 0.021, p = 0.98; Figure 1D; Figure S4). The increased dispersal was accompanied by a significant decrease in spatial information content (from 0.42 ± 0.037 bits per spike to 0.32 ± 0.034 bits per spike; t (132) = 8.42, p = 5.67 × 10⁻¹⁴; Figure 1C; Figure S4A; 12 hr after CNO, 0.40 ± 0.036 bits per spike; t (132) = 1.07, p = 0.28). There was also a substantial reduction in the spatial stability of the grid fields (correlation with baseline rate maps, 30 min after: 0.065 ± 0.016; 12 hr after: 0.37 ± 0.015; paired-sample t test comparing the two sets of correlations, t (132) = 12.0, p = 1.39 × 10⁻²²; Figure 1C). There was no significant change in the running speed of the animals after CNO (before, 28.2 ± 1.36 cm/s; 30 min after, 27.3 ± 1.65 cm/s; t (183) = 0.20, p = 0.84). Coverage of the box was also unaltered (before CNO, 91.8 ± 0.28%; 30 min after, 91.5 ± 0.33%; t (183) = 1.35, p = 0.18).

We next asked if grid patterns were affected more severely in layer II than layer III of MEC, considering that in layer II, a predominant fraction of the principal cell population consists of stellate cells, which are connected exclusively via inhibitory interneurons, many of which express PV (Dhillon and Jones, 2000, Couey et al., 2013, Pastoll et al., 2013). Layer III, in contrast, is dominated by pyramidal cells, which have additional excitatory connections (Dhillon and Jones, 2000). Consistent with the prominent role of inhibitory coupling in layer II, layer II cells were affected more severely than layer III cells after PV-interneuron silencing (Figures 1E and 1F; Figure S4A). In layer II, grid scores decreased from 0.65 ± 0.027 at baseline to 0.23 ± 0.039 after CNO (t (40) = 9.67, p = 6.51 × 10⁻¹²; 12 hr after CNO, 0.57 ± 0.033; t (40) = 1.74, p = 0.09; Figure 1E, top; Figure S4A). In layer III, the grid scores dropped less, from 0.57 ± 0.029 to 0.37 ± 0.056 (t (38) = 3.77, p = 5.64 × 10⁻⁴; 12 hr after CNO, 0.62 ± 0.048; t (38) = 1.22, p = 0.23; Figure 1E, bottom; Figure S4A). While layer II cells had higher grid scores than layer III cells during the baseline trial (independent-samples t test, t (78) = 2.06, p = 0.05), the scores were reversed after CNO (layer II versus layer III grid cells 30 min post CNO, t (78) = 2.10, p = 0.04). The magnitude of the drop in grid scores was significantly larger in layer II than layer III (t (78) = 3.40, p = 0.001). The increase in firing rates outside the grid fields was not significantly different between grid cells in layers II and III (layer II, from 0.75 ± 0.04 Hz to 1.12 ± 0.04 Hz; layer III, from 0.81 ± 0.095 Hz to 1.11 ± 0.092 Hz; independent-samples t test, t (78) = 1.60, p = 0.11). There was no significant change in in-field firing rates in any of the layers (layer II, from 2.14 ± 0.31 Hz to 2.17 ± 0.35 Hz; layer III, from 2.15 ± 0.23 Hz to 2.00 ± 0.22 Hz; independent-samples t test for change in frequency, t (78) = 0.31, p = 0.76). In mCitrine-expressing control mice lacking hM4D receptors, there was no detectable effect on the grid patterns (Figures S5D and S5E).

Figure S5.

Grid Pattern Did Not Change after Higher Doses of CNO in the SOM Group nor in Control Animals Not Expressing hM4D, Related to Figures 1, 2, and 3

Effect on grid pattern after higher doses of CNO in the SOM group (A–C) and in control animals not expressing hM4D (D–G).

(A–C) Grid cells were not affected in the SOM group after doubling of the CNO dose. A possible reason for the lack of effect on grid structure might be that the SOM-expressing interneurons were not sufficiently inhibited. The similarity in the number of infected cells and the pronounced change in firing rate speak against this possibility but to test the idea further, we doubled the dose of CNO to 4 mg/kg in one SOM-Cre mouse with 10 grid cells. (A) and (B) show rate maps, trajectory maps, and autocorrelation maps for representative MEC grid cell after a low and a high dose of CNO in an animal with hM4D-mCitrine expression in SOM interneurons (low dose, 2 mg/kg, to the left; high dose, 4 mg/kg, to the right). Data were collected in a 1 m box before CNO, 30 min after CNO, and 12 hr after CNO. Symbols as in Figure 1B. Inactivation of SOM interneurons with the higher dose did not affect the spatial periodicity of grid cells. (C) Cumulative frequency diagrams showing mean firing rate (top) and grid scores (bottom) for grid cells recorded after inactivation of SOM interneurons with low or high dose of CNO. Increasing the dose did not reduce the periodicity of firing in grid cells (grid score before CNO, 0.91 ± 0.076; 30 min after, 0.87 ± 0.082; paired-sample t test, t(9) = 1.31, p = 0.23; 30 min after low dose of CNO in the same mouse, 0.89 ± 0.072, paired-sample t test, t(9) = 1.04, p = 0.33, Figure S5, B and C). As in the experiments with the lower CNO dose, the mean firing rates of the grid cells were increased after the high dose (before, 1.02 ± 0.20 Hz; 30 min after, 1.71 ± 0.31 Hz, paired-sample t test, t(9) = 2.52, p = 0. 04; Figure S5, A and C).

(D–G) Injection of CNO does not affect spatial periodicity of grid cells or speed coding of speed cells in 2 control mice injected with Cre-dependent AAV expressing mCitrine only. hM4D receptors were thus lacking in these mice. (D) Representative MEC grid cell from animal with mCitrine expression in PV interneurons. Data from 1 m box before CNO, 30 min after CNO, and 12 hr after CNO. Symbols as in Figure 1B. (E) Cumulative frequency diagrams showing no change in grid score or mean firing rate of grid cells in the two control mice lacking hM4D. We did not observe any significant change in grid scores after CNO (before, 0.62 ± 0.055; 30 min after, 0.61 ± 0.065; paired-sample t test, t(19) = 0.41, p = 0.68; mean firing rate: before, 1.85 ± 0.51 Hz; 30 min after, 1.89 ± 0.51 Hz; paired-sample t test, t(19) = 1.64, p = 0.12). (F) Representative MEC speed cell from animal with mCitrine expression in PV interneurons. Symbols as in Figure 2A. (G) Cumulative frequency diagrams showing no change in speed score or mean firing rate of speed cells after CNO in the two control mice with only mCitrine in PV cells. There was no detectable change in speed scores after CNO (before, 0.18 ± 0.0037; 30 min after, 0.18 ± 0.0062, paired-sample t test, t(27) = 0.45, p = 0.66).

Inactivation of PV Interneurons Impairs Speed Tuning of Speed Cells

As animals move through the environment, grid cells are thought to be updated by path integration through cells that monitor the animal’s instantaneous speed (McNaughton et al., 2006, Sargolini et al., 2006, Kropff et al., 2015). The impairment in the spatial selectivity of the grid cells in the PV group might reflect impaired integration of speed information from such speed cells. To address this possibility, we examined tuning to speed in speed cells recorded simultaneously with the grid cells. In the PV-Cre mice, 73 cells were classified as speed cells (speed scores > 0.14, defined by 99^th percentile of a distribution of shuffled data). All speed cells were recorded in MEC (35 in layer II, 11 in layer III, 27 at layer II-III border).

Silencing of hM4D-expressing PV interneurons impaired speed coding in MEC (Figure 2; Figure S4C). Within the speed-cell population, there was a significant decrease in speed-rate correlations (before CNO, 0.21 ± 0.0073; 30 min after, 0.080 ± 0.0012; paired-sample t test, t (72) = 10.99, p = 5.73 × 10⁻¹⁷; Figure 2B; Figure S4C). The drop was almost, but not completely, reversed 12 hr after CNO (0.19 ± 0.0081; t (72) = 2.77, p = 0.01). The drop was expressed in both layers of MEC (layer II, from 0.22 ± 0.011 to 0.082 ± 0.017; layer III, from 0.19 ± 0.010 to 0.098 ± 0.027; independent-samples t test for change in speed scores in layer II versus III, t (44) = 1.28, p = 0.21; Figure 2C).

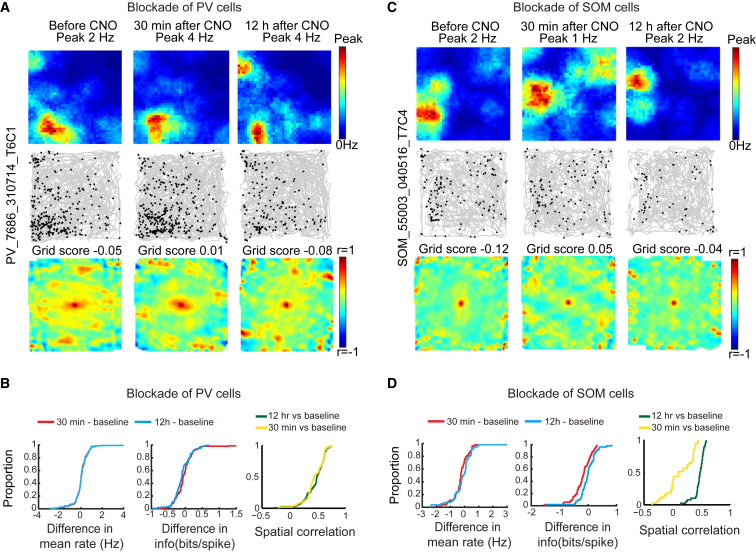
Figure 2.

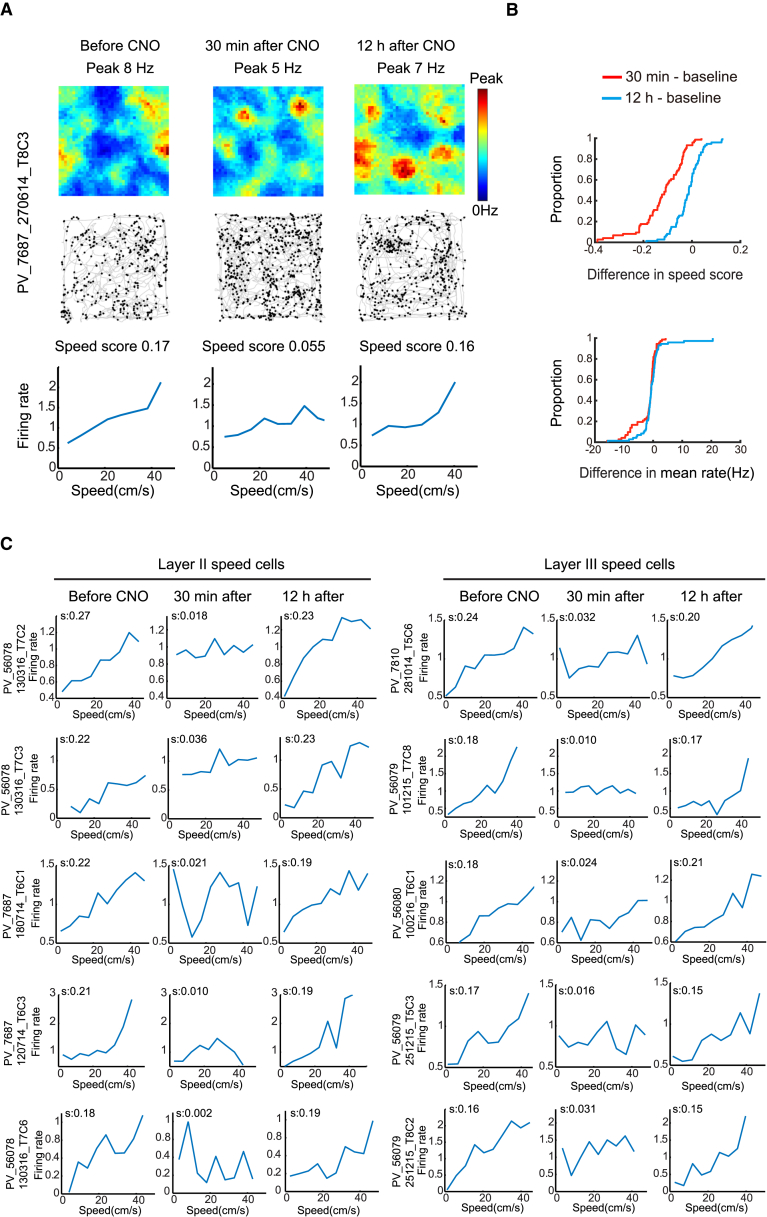
Inactivation of PV Interneurons Impairs Speed Coding in Speed Cells

(A) Firing rate map (top), map of spike locations on trajectory (middle), and normalized firing rate as a function of speed (bottom) for a representative MEC speed cell from a mouse with hM4D-mCitrine in PV interneurons. Left, before CNO; middle, 30 min after; right, 12 hr after.

(B) Cumulative frequency diagrams showing significant decrease in speed-rate correlation (speed score) of speed cells after inactivation of PV interneurons (top). The mean firing rate of the speed cells showed a small but significant decrease (bottom). See Figure S4 for absolute scores.

(C) Speed-rate relationship in layer II (left) and III (right) speed cells from animals with hM4D-mCitrine in MEC-PV interneurons (five representative pairs of layer II and III speed cells with approximately similar baseline speed scores). Symbols as in (A). Speed scores (s) are indicated at the top of each panel. Animal and cell numbers are indicated to the left.

See also Figures S1, S2, S4, and S5.

The decrease in speed scores was accompanied by a small but significant reduction in the mean firing rates of the speed cells (before CNO, 6.54 ± 0.36 Hz; 30 min after CNO, 5.29 ± 0.15 Hz; paired-sample t test, t (72) = 2.56, p = 0.01; Figure 2B; Figure S4C), as would be expected if the majority of MEC speed cells were fast-spiking interneurons (Ye et al., 2016). The drop in firing rates recovered 12 hr after CNO (6.10 ± 1.15 Hz, t (72) = 0.997, p = 0.32). The decrease in speed scores was not caused by lower spike numbers. Downsampling the number of spikes in the baseline trial to the number recorded after CNO did not abolish the drop in speed scores (speed score after downsampling of baseline, 0.18 ± 0.0056; paired-sample t test for downsampled baseline versus CNO, t (72) = 7.64, p = 7.77 × 10⁻¹¹). There was no detectable effect on speed scores in the two control animals expressing mCitrine only (Figures S5F and S5G).

The effect on speed coding was independent of whether the cells had interneuron-like or principal-like firing properties. We used a 5 Hz firing rate threshold to identify a putative uniform subset of fast-spiking interneurons (Frank et al., 2001, Buetfering et al., 2014). Half of the speed-cell population (37 out of 73 cells) passed this threshold. As for the speed-cell population as a whole, the speed scores of the fast-spiking subpopulation decreased when PV interneurons were silenced (before CNO, 0.21 ± 0.070; 30 min after CNO, 0.076 ± 0.11; t (36) = 7.49, p = 7.49 × 10⁻⁹). The speed scores recovered to baseline levels 12 hr after CNO (0.19 ± 0.058, t (36) = 1.67, p = 0.10). The mean firing rates of the fast-spiking speed cells were decreased by CNO (before, 12.4 ± 0.5 Hz; 30 min after, 8.75 ± 0.9 Hz; t (36) = 4.87, p = 2.26 × 10⁻⁵) but returned to pre-CNO levels 12 hr after CNO (11.3 ± 1.0 Hz; t (36) = 1.62, p = 0.11). Decreased speed scores were observed also in the remaining speed cells, where the mean rates were below 5 Hz (before CNO, 0.20 ± 0.040; 30 min after CNO, 0.086 ± 0.056; t (35) = 8.33, p = 1.02 × 10⁻⁹; 12 hr after CNO: 0.18 ± 0.069; t (35) = 1.69, p = 0.10). The mean firing rates of this subpopulation did not change significantly after CNO (from 2.22 ± 0.60 Hz to 2.04 ± 1.31 Hz; t (35) = 1.16, p = 0.26). Taken together, the data suggest that the inactivation of PV cells impairs grid and speed cells in concert.

Inactivation of SOM Interneurons Has No Effect on Grid Structure or Speed Tuning

We next asked if similar changes in grid cells and speed cells were present following inactivation of SOM interneurons. The number of infected SOM cells in the SOM-Cre group was similar to the number of infected PV cells in the PV-Cre group (Figures 3A; Figure S3). We first identified a total of 115 cells as grid cells in the SOM-Cre group (grid scores above 0.38, corresponding to the 99^th percentile of the shuffled data). Among these cells, 109 were from MEC and 6 from parasubiculum (50 in MEC layer II, corresponding to 10.7% of layer II cells; 16 in MEC layer III, or 6.2% of the layer III cells; and 43 at the layer II-III border).

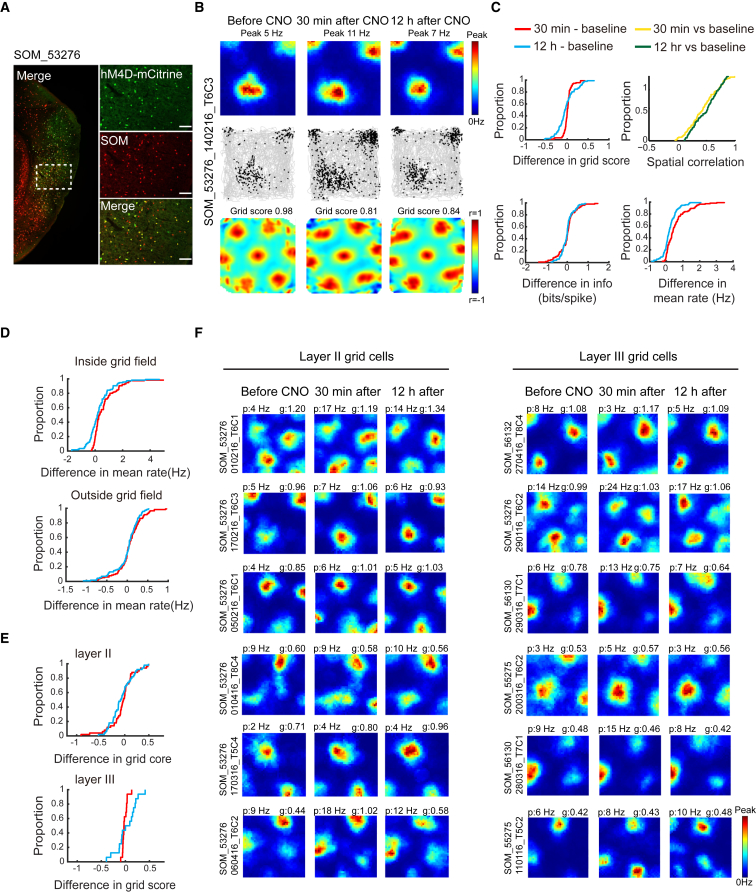
Figure 3.

Inactivation of SOM Interneurons Did Not Change the Spatial Periodicity or Selectivity of Grid Cells

(A) Expression of hM4D-mCitrine in MEC-SOM interneurons (sagittal sections). Low-magnification image of entire MEC (left); high-magnification images from white frame in left panel (right). mCitrine-expressing cells in green (top), SOM-expressing cells in red (middle), merge of mCitrine and SOM in yellow (bottom). Note co-expression of mCitrine and SOM (yellow, bottom).

(B) Example of grid cell from mouse expressing hM4D-mCitrine in SOM interneurons. Symbols as in Figure 1B.

(C) Cumulative frequency diagrams showing no change in grid score, spatial information, or spatial correlation for rate maps of grid cells after CNO. Symbols as in Figure 1C.

(D) Cumulative frequency diagrams showing significant increase in mean firing rate inside, but not outside, grid fields after inactivation of SOM interneurons.

(E) Cumulative frequency diagrams showing no change of grid scores after inactivation of SOM interneurons. See Figure S4 for absolute scores.

(F) Color-coded rate maps for grid cells from MEC layers II (left) and III (right) after inactivation of SOM interneurons (six layer II and six layer III cells with approximately similar baseline grid scores).

See also Figures S1, S2, S3, S4, and S5.

In contrast to inactivation of PV cells, silencing of SOM interneurons caused no detectable reduction in spatial periodicity or selectivity of grid cells (grid scores before CNO, 0.56 ± 0.42; 30 min after, 0.62 ± 0.027; paired-sample t test, t (114) = 1.26, p = 0.21; Figures 3B and 3C; Figure S4B). Grid scores remained stable in both MEC layers (layer II, from 0.67 ± 0.036 to 0.63 ± 0.038; layer III, from 0.64 ± 0.038 to 0.62 ± 0.039; independent-samples t test for layer II versus layer III grid cells, t (64) = 0.46, p = 0.66; Figures 3E and 3F; Figure S4B). As in the PV-Cre mice, the mean firing rates of the grid cells increased after CNO (from 1.30 ± 0.10 Hz to 1.62 ± 0.13 Hz; t (114) = 6.33, p = 4.97 × 10⁻⁹; Figure 3C; Figure S4B), suggesting that the inhibition of SOM cells was effective. The firing rates returned to baseline 12 hr later (1.17 ± 0.11 Hz; t (114) = 1.94, p = 0.06). There was also a significant increase in the peak firing rate of the grid cells after CNO (from 4.92 ± 0.45 to 6.50 ± 0.62; t (114) = 4.63, p = 9.83 × 10⁻⁶). In contrast to the data from the PV group, the increase in firing rates in the SOM mice was confined to the area within the grid fields (mean rate inside fields before CNO, 1.15 ± 0.10 Hz; 30 min after CNO, 1.73 ± 0.13 Hz; paired-sample t test, t (114) = 9.16, p = 3.62 × 10⁻¹⁵; Figure 3D, top; Figure S4B). Firing rates outside the grid fields displayed no significant change (from 0.54 ± 0.052 Hz to 0.61 ± 0.076 Hz; t (114) = 1.65, p = 0.10; Figure 3D, bottom; Figure S4B).

Consistent with the lack of change in grid scores, there was no change in the spatial information content of the grid cells (0.55 ± 0.032 bits per spike versus 0.56 ± 0.031 bits per spike; t (114) = 0.52, p = 0.61; Figure 3C; Figure S4B). CNO also failed to change the spatial correlation with rate maps from the baseline trial (30 min after CNO versus baseline; 0.45 ± 0.025; 12 hr after CNO versus baseline; 0.49 ± 0.021; t (114) = 1.34, p = 0.16; Figure 3C). The spatial correlation between rate maps before CNO and 30 min after was substantially lower in the PV group than in the SOM group (0.065 ± 0.016 and 0.45 ± 0.025, respectively; independent-samples t test, t (233) = 13.42, p = 8.18 × 10⁻³¹). The lack of effect on grid cells after silencing of SOM interneurons was not caused by too-low doses of CNO; doubling the dose failed to affect the grid pattern (Figures S5A–S5C).

SOM-cell inactivation also failed to alter speed-rate relationships (Figure 4; Figure S4D). We identified 63 cells with significant speed-rate relationships in the SOM-Cre mice (speed scores above 0.14, corresponding to the 99^th percentile of a shuffled distribution). All these cells were recorded in MEC (35 in layer II, 5 in layer III, 23 at layer II-III border). Inactivation of SOM interneurons did not change the speed-rate relationship of the recorded speed cells (before CNO, 0.14 ± 0.0064; 30 min after, 0.14 ± 0.0066; t (62) = 0.76, p = 0.45; Figures 4A and 4B; Figure S4D). The speed scores remained stable in both MEC layers (layer II, from 0.18 ± 0.0077 to 0.18 ± 0.0062; layer III, from 0.18 ± 0.014 to 0.18 ± 0.0060; independent-samples t test for layer II versus layer III speed cells, t (38) = 0.0069, p = 0.99; Figure 4C). The mean firing rates of the speed cells decreased weakly but significantly after CNO (before, 1.61 ± 0.15 Hz; 30 min after, 1.54 ± 0.14 Hz; t (62) = 2.51, p = 0.02; Figure 4B; Figure S4D), suggesting that the SOM cells were indeed silenced, despite the lack of effect on speed coding.

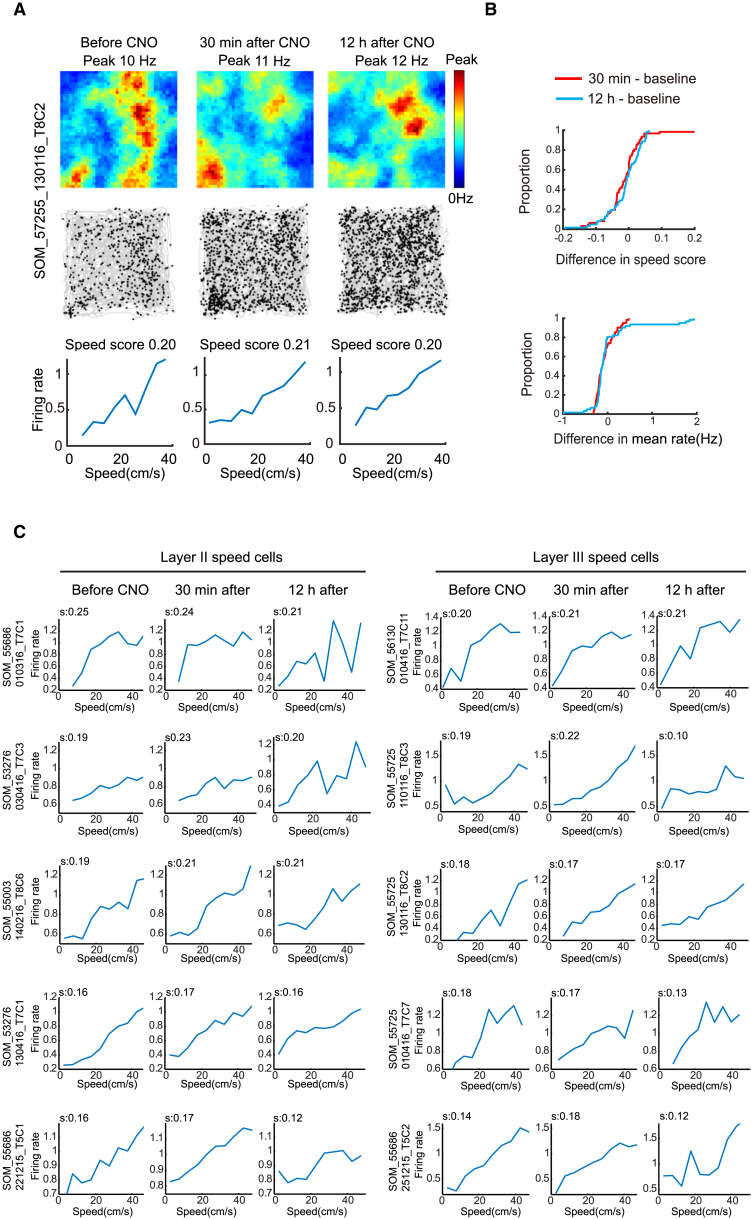
Figure 4.

Inactivation of SOM Interneurons Did Not Change Speed Coding in Speed Cells

(A) Firing rate map, spike locations on trajectory, and normalized firing rate as a function of running speed for a representative MEC speed cell from mouse with hM4D-mCitrine expression in SOM interneurons. Data were collected before CNO, 30 min after, and 12 hr after.

(B) Cumulative frequency diagrams showing no significant change in speed-rate correlation of speed cells after SOM-interneuron inactivation (top). The mean firing rate of the speed cells showed a small decrease (bottom). See Figure S4 for absolute scores.

(C) Speed-rate relationship in layer II and III speed cells from animals with hM4D-mCitrine expression in MEC-SOM interneurons, plotted as in Figure 2C.

See also Figures S1, S2, and S4.

Border Cells and Head Direction Cells Are Not Affected by Silencing of PV or SOM Interneurons

Considering that grid cells also need information about direction and environmental geometry to accurately reflect the animal’s changing position, we next asked if PV and SOM interneurons affected firing patterns in head direction cells and border cells recorded simultaneously with grid cells and speed cells. In the PV-Cre group, we identified 53 head direction cells and 42 border cells, using similar statistical criteria as for grid and speed cell (STAR Methods). Head direction cells were largely confined to MEC layer III (50 cells in layer III, 3 cells at layer II-III border). Border cells were recorded in both layers II and III (12 cells in layer II, 10 in layer III, 19 at border). The functional identity of the border cells was confirmed by showing that a new border field formed after insertion of a free-standing wall in the box (Figure S6; Solstad et al., 2008).

Figure S6.

Introducing a Standalone Wall Causes Appearance of a New Border Field in MEC Border Cells, Related to Figure 5

Addition of firing fields in MEC border cells after insertion of stand-alone wall in experiment with mice expressing hM4D-mCitrine in PV interneurons (top 4 panels) or SOM interneurons (bottom 2 panels). The wall was inserted before CNO administration. Top to bottom in each panel: rate maps, trajectory maps, and autocorrelation maps. Wall is indicated by white bar. Symbols otherwise as in Figure 1B.

CNO had no detectable effect on the directional tuning of head direction cells in the PV group (mean vector length: before CNO, 0.42 ± 0.027; 30 min after CNO, 0.43 ± 0.026; paired-sample t test, t (52) = 0.25, p = 0.80; Figures 5A and 5B; Figure S4E) or on the border scores of the border cells (0.55 ± 0.010 Hz versus 0.53 ± 0.011; t (41) = 0.22, p = 0.83; Figures 5C and 5D; Figure S4G). CNO increased the mean firing rates of the head direction cells (before CNO, 1.81 ± 0.30 Hz; 30 min after CNO, 2.12 ± 0.31; t (52) = 2.50, p = 0.02; 12 hr after, 1.65 ± 0.28; paired-sample t test, t (52) = 1.46, p = 0.15; Figure 5B; Figure S4E), suggesting that the decrease in PV-cell inhibition was effective. The impact on mean firing rate in the border cells was not significant (before CNO, 1.57 ± 0.26 bits per spike; 30 min after CNO, 2.21 ± 0.34 bits per spike; t (41) = 0.97, p = 0.34; Figure 5D; Figure S4G).

Figure 5.

Inactivation of PV or SOM Interneurons Has No Detectable Effect on Tuning Profiles of Head Direction Cells and Border Cells

(A) Representative head direction cells from animal with hM4D-mCitrine in PV interneurons. Data were collected before CNO, 30 min after, and 12 hr after. (Top and middle) Rate and trajectory maps. Polar plots showing firing rate as a function of head direction (bottom). Peak firing rate is shown at the top of the rate map, mean vector length is indicated above the polar plot.

(B) Cumulative frequency diagrams showing no change in mean length of head direction vectors after inactivation of PV interneurons (top). The mean firing rate of the head direction cells shows a slight increase (bottom).

(C) Representative firing fields of MEC border cell from animal with hM4D-mCitrine in PV interneurons. Symbols for rate maps, trajectory maps, and autocorrelograms (top to bottom) as in Figure 1B. Peak rates are shown at the top of the rate maps, border scores at the top of the autocorrelograms.

(D) Cumulative frequency diagrams showing no CNO-induced change in border score (top) or mean firing rate (bottom) in the PV group.

(E) Representative MEC head direction cells from animal with hM4D-mCitrine in SOM interneurons. Symbols as in Figure 1B.

(F) Cumulative frequency diagrams showing no CNO-induced change in mean vector length or mean firing rate of head direction cells in the SOM group.

(G) Representative MEC border cell from animal with hM4D-mCitrine in SOM interneurons.

(H) Cumulative frequency diagrams indicating no change in border scores or mean firing rates of border cells after CNO in the SOM group.

The distribution of absolute scores in (B), (F), (D), and (H) is shown in Figure S4.

See also Figures S1, S2, S4, and S6.

A similar lack of effect was seen after inactivation of SOM interneurons. In the SOM-Cre mice, we identified 30 head direction cells and 33 border cells. Head direction cells were recorded mostly in layer III of MEC (24 cells in layer III, 6 cells at layer II-III border), whereas border cells originated from both layers (10 in layer II, 15 in layer III, and 8 at the border). CNO had no detectable effect on tuning of head direction cells (mean vector length before CNO, 0.30 ± 0.032; 30 min after CNO, 0.25 ± 0.026; t (29) = 1.67, p = 0.11; Figures 5E and 5F; Figure S4F) or on firing along borders in the border cells (border score before CNO, 0.47 ± 0.014; 30 min after CNO, 0.48 ± 0.012; t (32) = 0.21, p = 0.84; Figures 5G and 5H; Figure S4H). There was a significant increase in the mean firing rate of the head direction cells after CNO (from 1.10 ± 0.29 to 1.40 ± 0.30 Hz; t (29) = 2.13, p = 0.04; 12 hr after CNO, 1.24 ± 0.31 Hz; t (29) = 1.32, p = 0.20; Figure 5F; Figure S4F). Border cells did not change firing rates significantly (from 1.91 ± 0.33 Hz to 1.98 ± 0.28 Hz; t (32) = 0.50, p = 0.62; Figure 5H; Figure S4H).

Aperiodic Spatial Cells Are Impaired by Inactivation of SOM Interneurons, but Not PV Interneurons

MEC contains a substantial fraction of spatially tuned cells with aperiodic firing fields (Zhang et al., 2013, Buetfering et al., 2014, Diehl et al., 2017). While some of these cells may be grid cells with grid periods too large to be detected in regularly sized recording environments, other cells have circumscribed but asymmetric and irregularly spaced firing fields not compatible with a grid pattern. The firing fields of many of these cells also do not line up with local borders, suggesting that they are not border cells. Cells with such properties were abundant in the present data. Thus, we asked whether PV and SOM inactivation affected the firing properties of these cells in a different manner than of simultaneously recorded grid cells and border cells. Spatial tuning was estimated by the same measures of spatial information and spatial correlation used to examine grid cells and border cells. Aperiodic spatially tuned cells were defined as cells that (1) had spatial information values above the 99^th percentile value of a shuffled distribution (PV group: spatial info > 0.43 bits per spike; SOM group: spatial info > 0.48 bits per spike) and (2) did not pass criteria for grid cells or border cells. A total of 214 cells satisfied these criteria, 160 in PV mice (152 in MEC and 8 in parasubiculum) and 54 in SOM mice (52 in MEC and 2 in parasubiculum).

While inactivation of PV interneurons disrupted the spatial information content of grid cells, there was no detectable effect in the PV group on cells with discrete aperiodic firing fields (spatial information before CNO, 0.68 ± 0.015 bits per spike; 30 min after, 0.66 ± 0.031 bits per spike; paired-sample t test, t (159) = 0.73, p = 0.46, Figures 6A and 6B; Figure S4I). Similarly, in these cells, the spatial correlation between the rate maps on the baseline and CNO trials was indistinguishable from the correlation between baseline trial and 12 hr post CNO trials (r = 0.46 ± 0.029 and r = 0.44 ± 0.028, respectively; t (159) = 1.16, p = 0.25; Figure 6B).

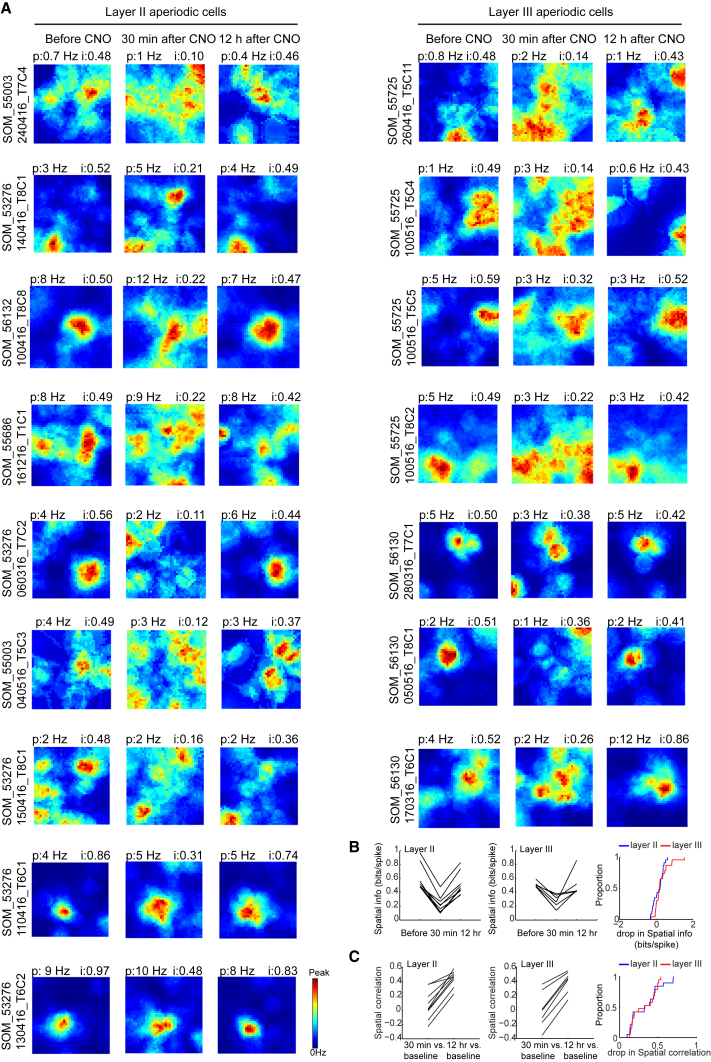
Figure 6.

Inactivation of SOM, but Not PV, Interneurons Impairs Spatial Selectivity in Aperiodic Spatial Cells with Firing Fields Not Aligned with Any of the Walls

Aperiodic cells have (1) spatial information values higher than the 99^th percentile value of shuffled data and (2) grid and border scores below the criterion for grid and border cells.

(A) Representative aperiodic spatial cell from MEC of animal with hM4D-mCitrine in PV interneurons. Data were collected before CNO, 30 min after, and 12 hr after (left to right). (Top to bottom) Rate maps, trajectory maps, and autocorrelation maps.

(B) Cumulative frequency diagrams showing that mean firing rate, spatial information, and spatial correlation did not change after inactivation of PV interneurons.

(C) Representative aperiodic spatial cell from MEC of animal with hM4D-mCitrine in SOM interneurons, plotted as in (A).

(D) Cumulative frequency diagrams showing that inactivation of SOM interneurons reduced spatial information and spatial correlation in aperiodic spatial cells. Mean firing rate was not changed.

The distribution of absolute scores in (B) and (D) is shown in Figure S4.

See also Figures S1, S2, and S4.

In contrast, spatial tuning in aperiodic cells was compromised after silencing of SOM interneurons (Figures 6C and 6D; Figure S4J; Figure 7; Figure S7). Spatial information in the SOM group was significantly decreased by CNO (before, 0.80 ± 0.042 bits per spike; 30 min after, 0.59 ± 0.039 bits per spike; paired-sample t test, t (53) = 4.36, p = 6.18 × 10⁻⁵). The decrease was reversed 12 hr after CNO (0.78 ± 0.058 bits per spike; t (53) = 0.41, p = 0.68). The impairment did not reflect general drift or instability in the recorded data; spatial information was reduced after CNO in all 16 of the 16 cells with the most stable firing fields between baseline and the 12 hr post CNO trial (Figures 7A and 7B). CNO also reduced spatial correlation with the rate map from the baseline trial (baseline versus 30 min after CNO, r = 0.13 ± 0.035; baseline versus 12 hr after CNO, 0.46 ± 0.015; t (53) = 15.1, p = 2.90 × 10⁻²⁰; Figures 6D, 7A, and 7C). Spatial information was similarly reduced among all ten of the ten cells with the highest spatial information scores in the CNO-free baseline state (Figure S7).

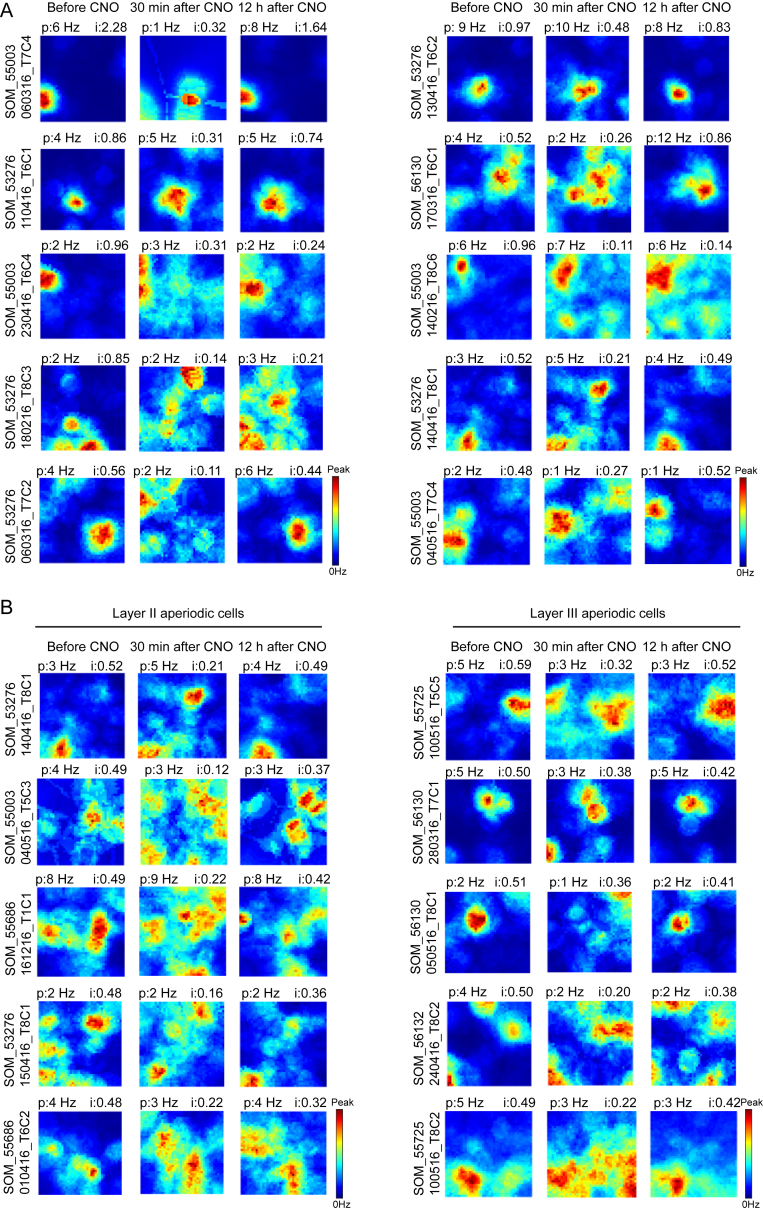
Figure 7.

Examples of Aperiodic Spatial Cells after Inactivation of SOM Interneurons

(A) Triads of rate maps show firing rate distribution before, 30 min after, and 12 hr after CNO for the nine cells in layer II (left) and the seven cells in layer III (right) that had the most similar spatial information values on the baseline trial and the trial conducted 12 hr after CNO. Rate maps are ranked from top to bottom based on the difference between baseline and 12 hr trials. Peak rates (p) and spatial information scores (i) are indicated.

(B and C) Spatial information (B) and spatial correlation (C) for the sixteen cells in (A). (Left and middle) Values for individual cells (one line per cell). Layer II and III cells are shown separately. Note that for all 16 cells, information values and spatial correlations were reduced at 30 min post CNO. (Right) Cumulative frequency diagram comparing distribution of drops in spatial information values and spatial correlation (baseline-30 min versus baseline-12 hr). Note lack of difference between layers.

See also Figures S1, S2, and S7.

Figure S7.

Further Examples of Aperiodic Spatial Cells after Inactivation of SOM Interneurons, Related to Figure 7

(A) Aperiodic spatial cells after inactivation of SOM interneurons. Triads of rate maps show firing rate distribution before, 30 min after, and 12 hr after CNO for the 10 cells that had the highest average spatial information values on the baseline trial. Rate maps are ranked from top left to bottom right according to the mean information value of the baseline and 12 hr trials. Maximum average information value at top right.

(B) Similar triads of rate maps for 5 representative pairs of layer II and III cells with matched spatial information values on the baseline trial. Peak rates (p) and spatial information scores (i) are indicated above each rate map; animal and cell numbers are shown to the left.

The impact on the spatial information values of aperiodic cells in the SOM-Cre group was not detectably different between layer II and III cells (25 cells in layer II, 23 cells in layer III, and six cells not considered because they were at layer border; Figure 7; Figure S7). In layer II, the information values dropped from 0.76 ± 0.047 bits per spike during baseline to 0.63 ± 0.06 bits per spike on the first test after CNO. In layer III, the values dropped from 0.76 ± 0.049 to 0.48 ± 0.050. The layer difference in the change of information was not significant (independent-samples t test: t (46) = 1.71, p = 0.09; Figure 7B). The drop in spatial correlation with the rate map from the baseline trial was also not different between layers (Figure 7C). In layer II, the correlation between baseline and the 30 min CNO trial (r = 0.12 ± 0.047) was significantly lower than the correlation between baseline and the 12 hr post CNO trial (r = 0.47 ± 0.017; paired-sample t test, t (24) = 8.12, p = 1.35 × 10⁻⁷). In layer III, the correlations were 0.14 ± 0.047 and 0.46 ± 0.021, respectively (t (22) = 9.06, p = 3.99 × 10⁻⁸). The spatial correlation between baseline and 30 min rate maps did not differ between layers (independent-samples t test, t (46) = 0.27, p = 0.79). Neither treatment (PV or SOM silencing) changed significantly the mean firing rates of the aperiodic spatial cells (PV: before CNO, 0.98 ± 0.075 Hz; 30 min after CNO, 1.03 ± 0.081 Hz; paired-sample t test, t (159) = 0.56, p = 0.58; Figure 6B; Figure S4I; SOM: before CNO, 1.88 ± 0.24 Hz; 30 min after CNO, 1.66 ± 0.29 Hz; paired-sample t test, t (53) = 1.89, p = 0.07; Figure 6D; Figure S4J).

The effect of SOM inactivation was not caused by inclusion of grid cells or speed cells with scores below the 99^th percentile selection threshold. Average grid scores of the aperiodic spatial cell population were 0.010 ± 0.02 in the PV group and −0.112 ± 0.027 in the SOM group (means ± SEM); average border scores were 0.032 ± 0.031 and −0.130 ± 0.11, respectively. The cells were not directionally tuned (mean vector lengths: 0.089 ± 0.022 and 0.082 ± 0.014) and showed minimal response to running speed (speed scores: 0.016 ± 0.005 and 0.015 ± 0.007). Among the aperiodic spatial cells of the SOM group, there was no significant correlation between the CNO-induced change in spatial information and the baseline grid scores or speed scores of the same cells (grid score: r = 0.0058, p = 0.97; speed score: r = 0.015, p = 0.92).

Taken together, these findings suggest that unlike grid cells and border cells, the entorhinal population of simultaneously recorded spatially tuned cells with discrete asymmetric or aperiodic firing fields was uniquely controlled by SOM interneurons.

Discussion

The MEC comprises multiple non-overlapping classes of GABAergic interneurons. Two of these classes are characterized by immunoreactivity to either PV or SOM. We show here that PV and SOM interneurons interact in different ways with discrete spatially modulated cell classes of the MEC. Using an experimental approach that allows silencing of either PV or SOM interneurons, we find that PV interneurons are required specifically for tuning of grid cells and speed cells, with no detectable impact on border cells or cells with other forms of aperiodic spatial firing fields. In contrast, SOM interneurons exert a unique influence on the spatial selectivity of cells with aperiodic firing fields, while grid cells, speed cells, and border cells remain unaffected. This double dissociation in simultaneously recorded neurons suggests that PV and SOM interneurons form parts of MEC networks with distinguishable roles in spatial representation.

The impairment of the grid pattern following silencing of PV cells is consistent with functions proposed for this interneuron population in computational attractor network models of grid cells (Couey et al., 2013, Bonnevie et al., 2013). In such models, the hexagonal structure of the grid pattern is thought to emerge as an equilibrium state following competitive interactions mediated via strong recurrent connections between cells with similar spatial phase preferences. In the first generation of models, hexagonally patterned firing was obtained by combining short-range recurrent excitation between similarly tuned cells with long-range inhibition between more differently tuned cells (Fuhs and Touretzky, 2006, McNaughton et al., 2006). Later models showed that in the presence of tonic excitation, inhibitory circuitry may be sufficient to generate grid patterns without direct excitatory recurrent connections (Burak and Fiete, 2009, Couey et al., 2013, Pastoll et al., 2013). The latter theoretical work is particularly relevant for grid cells in MEC layer II, where stellate cells are connected exclusively via GABAergic interneurons, many of which are PV immunoreactive (Dhillon and Jones, 2000, Beed et al., 2013, Couey et al., 2013, Pastoll et al., 2013, Fuchs et al., 2016). Although the exact wiring pattern enabling grid formation in inhibition-dominated networks remains to be determined (Buetfering et al., 2014, Roudi and Moser, 2014), our study confirms the prediction that PV interneurons are necessary for the maintenance of invariable periodic spatial tuning in layer II grid cells. In layer III, grid formation may to a larger extent occur without PV cells because principal cells in this layer are also linked via excitatory connections (Dhillon and Jones, 2000).

The loss of grid structure was accompanied by impaired speed coding in speed cells. This raises the possibility that the increased noise in the grid pattern reflects inaccuracy in the translation of the animal’s movement in space to changes in the subset of active grid cells in the MEC network. Speed-modulated cells have been proposed to contribute to this translation mechanism (McNaughton et al., 2006, Sargolini et al., 2006, Kropff et al., 2015). Loss of speed information in the input to the grid cells might result in dispersed and more variable firing locations, as observed after PV-cell inactivation in the present work.

It is worth noting that the inactivation of the PV interneurons did not completely abolish the structure of the grid pattern. While the hexagonal firing pattern was blurred by enhanced firing between the grid fields, the average locations of the firing vertices were mostly retained, resulting in low, but non-zero, grid scores. Such residual hexagonality might be expected, for example, if the tuning of the speed cells is only partly abolished, as in the present data. Grid patterns might also be maintained by recurrent pathways in other subcircuits of the MEC, involving connections via other subtypes of interneurons, or direct excitatory connections between pyramidal cells, in layer II or III (Dunn et al., 2015, Tocker et al., 2015). Finally, it is possible that drift was compensated by periodic resetting of the path integrator based on speed-independent stationary sensory inputs, such as visual cues (Hardcastle et al., 2015).

Our findings point to a functional differentiation between PV and SOM interneurons in the MEC. While inactivation of PV interneurons reduced speed coding and grid structure, SOM-expressing neurons were required to maintain the spatial specificity of cells with aperiodic firing fields. Silencing SOM interneurons did not visibly impair tuning patterns in grid cells or speed cells. This double dissociation of functions identifies aperiodic spatial cells as a distinct cell population, modulated or generated by different mechanisms than those responsible for grid patterns. The parameters controlling the properties of this cell class are not known, and there may be considerable functional heterogeneity within the population. Aperiodic spatial cells were distinct, however, from border cells, which were not affected by either treatment, suggesting that border cells form a different class with its own properties.

The exact role of SOM interneurons in maintaining aperiodic spatial firing fields remains to be determined, but the organization of connections between SOM interneurons and medial entorhinal principal cells provides some initial hints. SOM interneurons have axonal bundles that ramify between clusters of stellate cells and distribute widely among principal-cell dendrites in layer I (Fuchs et al., 2016). Like SOM interneurons in other cortical regions (Freund and Buzsáki, 1996, Rudy et al., 2011, Urban-Ciecko and Barth, 2016), SOM cells may primarily target the dendrites, and not the soma, of principal cells in the MEC. This puts them in a position to selectively gate subdomains of the input to the target neurons, distinguishing them from the PV cells, which—with their perisomatic projection patterns—mostly control firing in an all-or-none manner. Furthermore, by targeting selected dendritic inputs, SOM cells may play a more prominent role in experience-dependent plasticity in the MEC circuit. The strong facilitation exhibited by SOM interneurons in other systems (Ali and Thomson, 1998, Reyes et al., 1998, Losonczy et al., 2002) points to a possible contribution to frequency-dependent synaptic modification. It will remain for future studies to determine which parameters of experience are encoded by the aperiodic cells, whether these cells consist of subclasses with distinct functions, whether some or all of them are modulated by SOM interneurons, and finally how the SOM-cell network interacts with the PV-cell-controlled grid-cell system to enable dynamic spatial representation and navigation.

STAR★Methods

Key Resources Table

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Antibodies
Rabbit monoclonal anti-NeuN	Abcam	Cat# ab177487; RRID: AB_2532109
Chicken polyclonal anti-GFP	Abcam	Cat# ab13970; RRID: AB_300798
Rabbit polyclonal anti-Parvalbumin	Abcam	Cat# ab11427; RRID: AB_298032
Goat polyclonal anti-Somatostatin	Santa Cruz	Cat# SC-7819; RRID: AB_2302603
Donkey Anti-Rabbit IgG H&L (Alexa Fluor® 555)	Abcam	Cat# ab150074; RRID: AB_2636997
Goat Anti-Chicken IgY H&L (Alexa Fluor® 488)	Abcam	Cat# ab150169; RRID: AB_2636803
Donkey Anti-Goat IgG H&L (Alexa Fluor® 555)	Abcam	Cat# ab150134
Donkey Anti-Goat IgG H&L (Alexa Fluor® 488)	Abcam	Cat# ab150129; RRID: AB_2687506
Bacterial and Virus Strains
AAV8-hSyn-DIO-hM4D-mCitrine	University of North Carolina at Chapel Hill (UNC)’s gene therapy center	NaN
AAV8-hSyn-DIO-mCitrine	University of North Carolina at Chapel Hill (UNC)’s gene therapy center	NaN
Chemicals, Peptides, and Recombinant Proteins
Paraformaldehyde	Sigma	158127-500G
Cresyl Violet acetate	Sigma	C5042
Goat serum	DAKO	X090710-8
4′,6′-diamidino-2-phenylindole (DAPI)-containing Vectashield mounting medium	Vector Laboratories	H-1200
Clozapine N-oxide	Enzolifesciences	BML-NS105-0025
Experimental Models: Organisms/Strains
Mouse: B6;129P2-Pvalbtm1(cre)Arbr/J	The Jackson Laboratory	JAX: 008069
Mouse: B6N.Cg-Ssttm2.1(cre)Zjh/J	The Jackson Laboratory	JAX: 013044
Mouse: C57BL/6	Charles River	NaN

Contact for Reagent and Resource Sharing

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Edvard I. Moser (edvard.moser@ntnu.no).

Experimental Model and Subject Details

Twenty of the 22 subjects of this study were male B6;129P2-Pvalbtm1(cre)Arbr/J (PV-cre mice) and male B6N.Cg-Ssttm2.1(cre)Zjh/J (SOM-cre mice) mice (Jackson Laboratory, Bar Harbor, ME). The remaining two subjects were C57BL/6 wild-type mice. All mice weighed 22-35 g at implantation (age: 3-4 months). They were housed individually in transparent Plexiglass cages (35 cm × 30 cm × 30 cm) in a humidity- and temperature-controlled environment. All animals were kept at 90% of free-feeding body weight and maintained on a 12-h light/ 12-h dark schedule. Testing occurred in the dark phase.

Ten PV-Cre and 6 SOM-Cre mice received injections of AAV8-hSyn-DIO-hM4D-mCitrine virus. Four randomly selected PV-Cre and SOM-Cre mice (two in each group) received control injections of AAV8-hSyn-DIO-mCitrine. The two wild-type mice were used to examine co-expression of PV and SOM. Experimenters were not blind to the group identify of the mice. Sample sizes were chosen based on previous experience with similar experiments.

Experiments were performed according to the Norwegian Animal Welfare Act and the European Convention for the Protection of Vertebrate Animals used for Experimental and Other Scientific Purposes. The experiments were approved by the National Animal Research Authorities of Norway. The animals were not involved in previous procedures. The microbiological health of the animals was defined as free of pathogenic organisms according to recommendations by FELASA, with the exception of the presence of Entamoeba spp in intestinal contents.

Method Details

Virus used

AAV8-hSyn-DIO-hM4D-mCitrine and AAV8-hSyn-DIO-mCitrine were obtained from the University of North Carolina at Chapel Hill (UNC)’s gene therapy center. The plasmid used to generate AAV8-hSyn-DIO-hM4D-mCitrine and AAV8-hSyn-DIO-mCitrine was obtained from Bryan Roth’s lab, University of North Carolina at Chapel Hill (UNC). The titer of the virus was 10¹² viral genomic particles/ ml.

Surgery, virus injection and electrode preparation

All 20 virus-injected mice received tetrode implants. Before surgery, the animals were anesthetized with isoflurane (air flow: 0.8-1.0 L/min, 0.5%–3% isoflurane, adjusted according to physiological condition). Isoflurane was gradually reduced from 3% to 1%. Depth of anesthesia was examined by testing tail and pinch reflexes as well as breathing. Subcutaneous injections of bupivacaine (Marcaine) and buprenorphine (Temgesic) were given at the start of the surgery.

Upon induction of anesthesia, the animal was fixed in a Kopf stereotaxic frame for injection of virus and implantation of tetrodes. Holes were drilled in the skull above the right MEC. During the first part of the surgery, before the tetrodes were inserted, a 10 μL NanoFil syringe (World Precision Instruments, Sarasota, Florida, USA) and a 33-gauge beveled metal needle were used to inject virus i in MEC (0.4-0.35 mm anterior of the transverse sinus, 3.2-3.5 mm from midline, 1.2 mm below dura for dorsal injections). Injection volume (0.5 to 1 μL at each location) and flow rate (0.1 μl/min) were controlled with a Micro4 Microsyringe Pump Controller (World Precision Instruments). After injection, the needle was left in place for 10 min before it was withdrawn slowly.

During the second part of the surgery, each mouse was implanted with a Neuralynx VersaDrive-4 microdrive, connected to 4 tetrodes. The tetrodes were made of 17 μm polyimide-coated platinum-iridium (90% - 10%) wire. The electrode tips were plated with platinum to reduce electrode impedances to around 100-250 kΩ at 1 Hz. The tetrodes were inserted 0.35-0.40 mm anterior of the transverse sinus, 3.2-3.5 mm lateral to the midline in the right hemisphere, and 0.8-1.2 mm below dura, at a 5 degree angle in the sagittal plane, with electrode tips pointing in the posterior direction. The microdrives were secured to the skull with jewellers’ screws and dental cement. Two front screws were connected to ground.

Electrode turning and recording procedures

Turning of tetrodes started 2 to 3 days after the surgery. Data collection began within 3 weeks. Testing of control animals was interleaved with testing of experimental animals.

Before each recording trial, the mouse rested on a towel in a large flower pot on a pedestal. The mouse was connected to the recording equipment via AC-coupled unity-gain operational amplifiers close to the head and a counterbalanced cable that allowed the animal to move freely. Over the course of 20 to 60 days, the tetrodes were lowered in steps of 50 μm or less, until well-separated single neurons could be recorded. When the signal amplitudes exceeded four times the noise level (20 to 30 μV), and single units were stable for more than 1 hr, data were collected.

Recorded signals were amplified 8000 to 25,000 times and band-pass filtered between 0.8 and 6.7 kHz. Triggered spikes were stored to disk at 48 kHz (50 samples per waveform, 8 bits/sample) with a 32-bit time stamp (clock rate at 96 kHz). Electroencephalograms (EEG) were recorded single-ended from one of the electrodes. The local field potential was amplified 3000 to 10,000 times, low pass–filtered at 500 Hz, sampled at 4800 Hz, and stored with the unit data. Through a video camera, the recording system obtained the position of two light-emitting diodes (LEDs) on the headstage of the mouse. The LEDs were tracked individually at a rate of 50 Hz. The two LEDs were separated by 4 cm and aligned with the body axis of the mice.

Over the course of 3 to 6 weeks following surgery, the mice were first trained to run in a 1 m square black aluminum enclosure polarized by a white cue card. In mice with putative border cells, these trials were occasionally succeeded by a test in the same box with a 50 cm long and 50 cm high wall insert in the center of the box (Figure S6). In hM4d-expressing mice, the recordings were followed by i.p. injection of 2 mg/kg of clozapine-N-oxide (CNO, Sigma). One SOM-Cre mouse received a higher dose of 4 mg/kg on multiple occasions with different cell samples. Thirty minutes after injection, the mice ran another trial in the open box. A final box trial was conducted 12 hr after the injection. Trials were 15 min each. Running was motivated by scattering crumbs of chocolate at random locations in the box at 10-to-15 s intervals.

Histological procedures and electrode positions

The mice received an overdose of pentobarbital and were subsequently perfused intracardially with saline followed by either 4% formaldehyde or 4% freshly depolymerized paraformaldehyde in phosphate buffer (PFA). The brains were extracted and stored in the same fixative, and frozen sagittal sections (10 μm) were cut on a cryostat. Every 10^th section was stained with cresyl violet. In the infected and implanted part of MEC, all sections were collected. Tetrodes were identified and the tip of each electrode was found by comparison with adjacent sections.

For cell counting, the MEC was divided into 12 100-μm wide blocks from medial to lateral. In each block, we selected one section (usually the first). PV or SOM-immunopositive infected cells were counted from this section and the total number for the block was extrapolated. The remaining sections of the block were not counted in order to avoid double-counting of cells. Cells in MEC were classified as layer II or III cells based on the location of the end of the tetrode trace. If the end of the tetrode was in layer III, all MEC cells from the mouse were classified as layer III cells, given that tetrodes did not pass through the deep layers as they entered MEC (Figure S2). If the tetrode passed into or through layer II, cells at the end of the recording were classified as originating from layer I or II, depending on where the trace ended (mostly layer II). For preceding recordings in these mice, layer locations were determined based on the tetrode turning protocol. Cells were classified as layer II or III cells only if the location was unequivocal. Cells near the border of layers II and III (50 μm on either side) were assigned to a separate category not used for layer comparisons.

For immunostaining, sections were rinsed 3 times for 10 min in 1 × phosphate buffer (PBS; pH 7.6) at room temperature, and pre-incubated for 2 hr in 10% normal goat serum in PBST (1 × PBS with 0.5% Triton X-100). Between incubation steps, sections were rinsed in PBST. Sections were incubated either with antibodies against NeuN, raised in rabbit (Abcam, 1:1000), against GFP, raised in chicken (Abcam, 1:2000), against PV (Santa Cruz, 1:1000) raised in rabbit (Abcam, 1:2000), or against SOM (Santa Cruz, 1:1000), raised in goat (Abcam, 1:2000). The sections were incubated in antibody-blocking buffer at 4°C for 72 hr. After three times of 15 min washing in PBST at room temperature, the sections were incubated either in a Donkey Anti-Rabbit antibody or a Goat Anti-Chicken antibody or Donkey-anti goat antibody conjugated with either Alexa Fluor® 555or Alexa Fluor® 488 (Abcam,1:2000) for 2 hr at room temperature. After rinsing in PBS, the sections were mounted onto glass slides with 4′,6′-diamidino-2-phenylindole (DAPI)-containing Vectashield mounting medium (Vector Laboratories, Burlingame, California, USA), and a coverslip was applied. Expression of hM4D was estimated with anti-GFP, since mCitrine was fused with hM4D in the viral construct and GFP antibody also specifically binds with mCitrine. NeuN was used for staining neurons.

Quantification and Statistical Analysis

Analyses were performed with cells as units (n). Units of analysis are reported for each analysis in the Results. Parametric statistics was used for all analyses, though normality of the distributions was not explicitly checked for individual analyses.

Rate maps, firing fields and spatial information

Position estimates were based on tracking of LEDs on the head stage connected to the microdrive. Tracked positions were smoothed with a 15 point mean filter offline. To characterize firing fields, the position data were sorted into bins of 3 × 3 cm² and the firing rate was determined for each bin. A spatial smoothing algorithm was used (Fyhn et al., 2004). The average rate in any bin x was estimated as:

$$\lambda \left(x\right)=\sum _{i=1}^{n}g\left(\frac{s_i-x}{h}\right)/\underset{0}{\overset{T}{\int }}g\left(\frac{y\left(t\right)-x}{h}\right)dt$$

where g is a smoothing kernel, h is a smoothing factor, n is the number of spikes, s_i the location of the i-th spike, y(t) the location of the mice at time t, and [0, T] the period of the recording. A Gaussian kernel was used with g and h = 3. In order to avoid error from extrapolation, we considered positions more than 3 cm away from the tracked path as unvisited.

The cell’s peak rate was estimated as the highest firing rate observed in any bin of the smoothed rate map. For each cell, the spatial information content in bits per spike (Skaggs et al., 1993) was calculated as

$$\text{information content}={\sum }_i{p}_i\frac{{\lambda }_i}{\lambda }{\log }_2\frac{{\lambda }_i}{\lambda }$$

where ${\lambda }_i$ is the mean firing rate of a unit in the i-th bin, $\lambda$ is the overall mean firing rate, and p_i is the probability of the animal being in the i-th bin (occupancy in the i-th bin / total recording time).

To compare firing rates inside and outside of grid fields, we first identified firing fields by a local-maximum detection procedure. Local maxima were identified in the baseline trial as bins with firing rates exceeding those of all surrounding 8 bins. For each maximum, we next identified all bins surrounding the local maximum in which firing rates were higher than 20% of this maximum. If a minimum of 9 contiguous bins around the local maximum passed the 20% criterion, and if the rate at the local maximum exceeded a threshold of 1 Hz, the bins were collectively defined as a firing field (or grid field, if the cell also passed the shuffling criterion for grid cells). Firing rates were finally determined for areas inside and outside the grid field boundaries. For the CNO and post CNO trials, we applied the same field boundaries as in the baseline trial.

Cells with a high mean firing rate (> 5Hz) were identified as putative interneurons (Frank et al., 2001, Buetfering et al., 2014).

Analysis of grid cells

Methods for analysis of grid cells have been adapted from those described in previous studies (Fyhn et al., 2007, Langston et al., 2010). For all cells with more than 100 spikes, we calculated the spatial autocorrelation for each smoothed rate map. Autocorrelograms were based on Pearson’s product moment correlation coefficient with corrections for edge effects and unvisited locations. With λ (x, y) denoting the average rate of a cell at location (x, y), the autocorrelation between the fields with spatial lags of τ_x and τ_y was estimated as:

$$r\left({\tau }_x,{\tau }_y\right)=\frac{n\sum \lambda \left(x,y\right)\lambda \left(x-{\tau }_x,y-{\tau }_y\right)-\sum \lambda \left(x,y\right)\sum \lambda \left(x-{\tau }_x,y-{\tau }_y\right)}{\sqrt{n\sum \lambda {\left(x,y\right)}^2-{\left(\sum \lambda \left(x,y\right)\right)}^2}\sqrt{n\sum \lambda {\left(x-{\tau }_x,y-{\tau }_y\right)}^2-{\left(\sum \lambda \left(x-{\tau }_x,y-{\tau }_y\right)\right)}^2}}$$

where the summation is over all n pixels in λ (x, y) for which rate was estimated for both λ (x, y) and λ (x - τ_x, y - τ_y). Autocorrelations were not estimated for lags of τ_x, τ_y where n < 20.

The degree of spatial periodicity (‘grid score’) was determined for each recorded cell by taking a circular sample of the autocorrelogram, centered on the central peak but with the central peak excluded, and comparing rotated versions of this sample. The Pearson correlation of this circle with its rotation in α degrees was obtained for angles of 60° and 120° on one side and 30°, 90° and 150° on the other. The cell’s grid score was defined as the minimum difference between any of the elements in the first group and any of the elements in the second. Grid cells were defined as cells in which rotational symmetry-based grid scores exceeded the 99^th percentile of a distribution of grid scores for shuffled recordings from the entire population of MEC cells. Shuffling was performed by time-shifting, for each permutation trial, the entire sequence of spikes fired by the cell along the animal’s path by a random interval between 20 s and 20 s less than the length of the trial (usually 600-20 = 580 s), with the end of the trial wrapped to the beginning. The shuffling procedure was repeated 400 times for each trial of data. For each permutation, a firing rate map and an autocorrelation map were constructed, and a grid score was calculated. The 99th percentile was then read out from the overall distribution of grid scores.

Analysis of head-direction cells

Methods for analysis of head direction cells have been reported in previous studies (Giocomo et al., 2014, Langston et al., 2010). The rat’s head direction was calculated for each tracker sample from the projection of the relative position of the two LEDs onto the horizontal plane. The directional-tuning function for each cell was obtained by plotting firing rate as a function of the rat’s directional heading, divided into bins of 3° and smoothed with a 30° mean window filter (five bins on each side). The preferred firing direction was defined by the mean vector of the directional-tuning function.

Head direction-modulated cells were defined as cells with mean vector lengths significantly exceeding the degree of directional tuning that would be expected by chance. Chance values were determined by a shuffling procedure performed in the same way as for grid cells and using a similar number of permutations per cell. Cells were defined as directionally modulated if the mean vector from the recorded data was longer than the 99^th percentile of mean vector lengths in the distribution generated from the shuffled data.

Analysis of Border cells

Methods for analysis of border cells have been reported previously (Bjerknes et al., 2014, Solstad et al., 2008). Border cells were identified by computing, for each cell with an average rate above 0.2 Hz, the difference between the maximal length of a wall touching on any single firing field of the cell and the average distance of the field from the nearest wall, divided by the sum of those values. Border scores thus ranged from −1 for cells with infinitely small central fields to +1 for cells with infinitely narrow fields that lined up perfectly along the entire wall.

Border cells were defined as cells with border scores significantly exceeding chance levels determined by a shuffling procedure performed in the same way as for grid cells, using a similar number of permutations per cell, but with the addition of a spatial information criterion (Bjerknes et al., 2014). Cells were defined as border cells if (i) the cell’s border score from the recorded data was higher than the 99^th percentile for border scores in the shuffled data, and (ii) the spatial information content in the recorded data was higher than the 99^th percentile value for spatial information in the shuffled data.

Analysis of Speed cells

Methods for analysis of speed cells are similar to those reported in a previous study (Kropff et al., 2015). Instantaneous firing rate was obtained by dividing the whole trial into 20-ms bins, coinciding with the frames of the tracking camera. A temporal histogram of spiking was then smoothed with a 250-ms-wide Gaussian filter. The speed score for each cell was defined as the Pearson product-moment correlation between the cell’s instantaneous firing rate and the rat’s instantaneous running speed, on a scale from −1 to 1. A cell was defined as a speed cell if its speed score exceeded the 99^th percentile of speed scores in the distribution of shuffled data. Shuffling was performed in the same way as for grid cells and head direction cells.

Image analysis

Boundaries of MEC with neighboring regions such as postrhinal cortex, parasubiculum, presubiculum, lateral entorhinal cortex, and subiculum, were defined as described in detail before (Miao et al., 2015). Unfolded maps of MEC were prepared by mapping, for each sagittal brain section, the dorsal border of MEC onto a straight line. For each section, the surface length of MEC was measured with Image-Pro Plus software and subsequently mapped onto a straight line perpendicular to the line that represents the dorsal border. All borders were established using cytoarchitectonic criteria that can reliably be established irrespective of the plane of sectioning, as described in detail for the rat brain (Boccara et al., 2015). These borders, as defined in the rat, can be reliably applied to the mouse brain (Witter, 2011, Miao et al., 2015).

Images of entorhinal cortex were scanned with an automated scanner (MIRAX MIDI, Carl Zeiss). Using Image-Pro Plus software, we considered areas with mCitrine expression as infected when the 488 nm-signal of mCitrine inside the area was significantly higher than 2 SD of the mean value of the corresponding background signal at the appropriate wavelength. The number of infected cells with mCitrine expression was also calculated with Image-Pro Plus® software. A neuron was considered as infected when the signal of mCitrine was significantly higher than 2 SD of the mean value of the background signal. Cells were identified as double-labeled for mCitrine and either PV or SOM (at 555 nm) when the signals for mCitrine and anti-PV or anti-SOM were both significantly higher than 2 SD of the background signal.

Data and Software Availability

Data and code are available upon request to the Lead Contact.

Author Contributions

C.M., Q.C., M.-B.M., and E.I.M. designed research. C.M. and Q.C. collected and analyzed data. M.-B.M. and E.I.M. supervised the project. C.M. and E.I.M. wrote the paper with input from all authors.

Published: September 28, 2017