Abstract
Aims
Early‐onset emphysema attributed to α‐1 antitrypsin deficiency (AATD) is frequently overlooked and undertreated. RAPID‐RCT/RAPID‐OLE, the largest clinical trials of purified human α‐1 proteinase inhibitor (A1‐PI; 60 mg kg–1 week–1) therapy completed to date, demonstrated for the first time that A1‐PI is clinically effective in slowing lung tissue loss in AATD. A posthoc pharmacometric analysis was undertaken to further explore dose, exposure and response.
Methods
A disease progression model was constructed, utilizing observed A1‐PI exposure and lung density decline rates (measured by computed tomography) from RAPID‐RCT/RAPID‐OLE, to predict effects of population variability and higher doses on A1‐PI exposure and clinical response. Dose–exposure and exposure–response relationships were characterized using nonlinear and linear mixed effects models, respectively. The dose–exposure model predicts summary exposures and not individual concentration kinetics; covariates included baseline serum A1‐PI, forced expiratory volume in 1 s and body weight. The exposure–response model relates A1‐PI exposure to lung density decline rate at varying exposure levels.
Results
A dose of 60 mg kg–1 week–1 achieved trough serum levels >11 μmol l–1 (putative ‘protective threshold’) in ≥98% patients. Dose–exposure–response simulations revealed increasing separation between A1‐PI and placebo in the proportions of patients achieving higher reductions in lung density decline rate; improvements in decline rates ≥0.5 g l–1 year–1 occurred more often in patients receiving A1‐PI: 63 vs. 12%.
Conclusion
Weight‐based A1‐PI dosing reliably raises serum levels above the 11 μmol l–1 threshold. However, our exposure–response simulations question whether this is the maximal, clinically effective threshold for A1‐PI therapy in AATD. The model suggested higher doses of A1‐PI would yield greater clinical effects.
Keywords: chronic obstructive pulmonary disease, imaging, modelling and simulation
What is Already Known about this Subject
Genetic deficiency in α‐1 proteinase inhibitor (A1‐PI) predisposes to early onset emphysema.
Purified human A1‐PI is well documented as biochemically effective.
RAPID‐RCT and RAPID‐OLE were the first trials to indicate clinical efficacy by significantly reducing the rate of lung density decline, measured by computed tomography scans.
What this Study Adds
Our analysis provides additional confirmation of the clinical efficacy A1‐PI and the stability of weight‐based dosing in raising serum A1‐PI levels.
Additionally, we present evidence of a linear relationship between A1‐PI dose and clinical response. The effect of higher doses remains to be tested in future clinical studies.
Introduction
Alpha‐1 antitrypsin deficiency (AATD) is a rare genetic disorder characterized by reduced levels of α‐1 antitrypsin, also known as α‐1 proteinase inhibitor (A1‐PI) 1. A1‐PI has a central role in maintaining lung tissue integrity by preventing the degradation of lung tissue that occurs following exposure to elevated levels of uninhibited neutrophil elastase. The resultant lung density decline eventually progresses to clinically evident emphysema 2.
Currently, the only treatment available that targets the underlying cause of AATD is infusion with purified human A1‐PI. The use of A1‐PI therapy has been accompanied by the assumption that increasing serum levels of A1‐PI would increase neutrophil elastase inhibition and help to arrest lung tissue deterioration 2. Serum concentrations of A1‐PI >11 μmol l–1 have been suggested as a protective threshold against lung damage/emphysema 2. This level is equivalent to the 10th percentile of the A1‐PI range of individuals with the moderately deficient PI*SZ genotype – who express a minimal increased risk of developing lung disease as compared with normal humans (PI*MM) – and is considered to be sufficient to prevent lung tissue damage 3. However, this putative protective threshold is controversial; it was based on historical epidemiological data and the estimation made use of nonvalidated standards 4. Despite the limitations of this threshold, it remains an important clinical criterion in the decision to prescribe A1‐PI therapy 4, 5.
In the Randomized, placebo‐controlled trial of augmentation therapy in Alpha‐1 Proteinase Inhibitor Deficiency (RAPID‐RCT) study, A1‐PI treatment (60 mg kg–1 week–1) significantly reduced lung density decline rate vs. placebo: –1.45 g l–1 year –1 vs. –2.19 g l–1 year–1; difference 0.74 g l–1 year–1 [95% CI 0.06–1.42], P = 0.03 6. Data from the 2‐year open‐label RAPID‐OLE trial indicated that patients who switched from placebo to A1‐PI subsequently benefitted from a statistically significant reduction (difference 0.52 g l–1 year–1 [95% CI 0.22–0.83], P = 0.001) in the rate of lung density decline. However, these patients never caught up with those who had started active treatment in RAPID‐RCT, owing to irreversible destruction of the lung tissue 7.
To further evaluate the treatment effect of A1‐PI therapy in the RAPID programme, and characterize potential sources of variability, we report post hoc pharmacometric modelling of the combined RAPID‐RCT and RAPID‐OLE data. Two analyses were conducted using a sequential modelling approach. The objective of the initial dose–exposure analysis was to characterize the relationship between A1‐PI dose and post‐baseline A1‐PI serum levels (exposure). In addition, we also sought to characterize potential sources of variability in A1‐PI concentrations, both in placebo‐treated and A1‐PI‐treated patients. The second analysis was an exposure–response analysis; using lung density at total lung capacity (TLC) as the measure of clinical response, we sought to evaluate the extent to which A1‐PI exposure relates to clinical response. In addition, the clinical efficacy of the 60 mg kg–1 week–1 dosing strategy, and potential sources of variability in lung density decline rate, were evaluated.
Methods
This study was conducted in accordance with the International Conference on Harmonization Good Clinical Practice guidelines, the Declaration of Helsinki (version of 1996), the US Code of Federal Regulations, and local legal requirements. CSL Behring and the investigators informed each other in writing that all ethical and legal requirements were met before the first subject was enrolled in the study.
The RAPID programme
The analysis included data on A1‐PI concentrations, computed tomography (CT) lung density measurements and baseline weight, age, body‐mass index (BMI) and forced expiratory volume in 1 s (FEV1) collected from the RAPID programme: RAPID‐RCT (NCT00261833) and RAPID‐OLE (NCT00670007). The multicentre, double‐blind, randomized RAPID‐RCT trial involved doses of 60 mg kg–1 week–1 A1‐PI (Zemaira®) or placebo over 2 years in 180 adult patients (93 active; 87 placebo) with evidence of clinical emphysema and A1‐PI levels ≤11 μmol l–1. The RAPID‐OLE trial was a 2‐year open‐label continuation of RAPID‐RCT in 140 patients in sites outside of the USA as A1‐PI was unavailable in non‐USA countries. Patients who previously received A1‐PI in RAPID‐RCT continued their weekly infusions in the RAPID‐OLE trial and formed the Early‐Start group (A1‐PI–A1‐PI; n = 76); those patients who received placebo in RAPID‐RCT were switched to A1‐PI in RAPID‐OLE and are referred to as the Delayed‐Start group (Placebo–A1‐PI; n = 64). Samples for serum A1‐PI measurement were collected every 3 months at trough (defined as 7 days after last infusion) throughout the full 4‐year RAPID programme; CT lung scans were performed at baseline and 3, 12, 21, 24, 36 and 48 months post‐randomization. Baseline demographics at the beginning of the RAPID‐RCT study are shown in Table 1. Demographics were similar between A1‐PI and placebo groups and between RAPID‐RCT and RAPID‐OLE 6, 7. Additionally, withdrawal rates were comparable between study cohorts; primary results from the RAPID programme have previously been published 6, 7.
Table 1.
Baseline demographics in RAPID‐RCT (ITT population) 6
| Parameter | A 1 ‐PI (n = 93) | Placebo (n = 87) |
|---|---|---|
| Age, years | 53.8 (6.9) | 52.4 (7.8) |
| Weight, kg | 75.9 (16.2) | 79.5 (13.9) |
| Body mass index, kg m–2 | 25.5 (4.8) | 26.6 (4.1)a |
| FEV1, l | 1.6 (0.5) | 1.6 (0.5) |
| CT lung density (TLC), g l–1 | 45.5 (15.8) | 48.9 (15.5) |
| Antigenic A 1 ‐PI serum concentration, μmol l–1 | 6.38 (4.62) | 5.94 (2.42) |
A1‐PI, α‐1 proteinase inhibitor; FEV1, forced expiratory volume in 1 s; ITT, intention to treat; TLC, total lung capacity
All values presented as mean (standard deviation)
n = 86 (one subject with missing data)
Data sets
The dose–exposure analysis contained all randomized patients with at least one postbaseline A1‐PI measurement. From the RAPID‐RCT cohort, baseline A1‐PI data were available from 170 patients (89 active; 81 placebo); from RAPID‐OLE, data were available from 138 patients (74 Early‐Start; 64 Delayed‐Start). The exposure–response analysis included all subjects in the dose–exposure model who had at least one postbaseline CT lung density measurement; data were available from 61 placebo and 73 active patients. For each subject, an average dose rate, expressed in mg day–1 (i.e., not standardized with respect to weight) and a median nominal trough exposure, expressed as μmol l–1, were computed for each of the trials (RAPID‐RCT and open‐label RAPID‐OLE). In some cases, nominal trough values may not have reflected true troughs, e.g., due to errant values derived from serum samples collected outside ± 1 day of the sampling time points stipulated in the study protocol. To protect against the influence of nontrough samples, exposure profiles over time (within each trial) were summarized using median rather than mean values.
Software
All data assembly and data analyses (including exploratory data analysis, modelling and simulation) were carried out using version 3.2.3 of R 8. All models were fit using the nlme function in the nlme package for R, version 3.1‐125.
Modelling strategy
Two analyses were conducted using a sequential modelling approach: (i) dose–exposure analysis, and (ii) exposure–response analysis. The modelling strategy is described as dose–exposure rather than a pharmacokinetic analysis as only summary exposure measures were modelled. Covariates tested in the models were included due to mechanistic plausibility and clinical interest (see Supporting Information). All models were based on a single dose strength of A1‐PI, i.e., 60 mg kg–1 week–1, as used in the RAPID‐RCT and RAPID‐OLE trials.
Dose‐exposure model
Exposure data for placebo‐treated patients were available from RAPID‐RCT only. In order to compare A1‐PI and placebo for the combined duration of the RAPID‐RCT and RAPID‐OLE trials, RAPID‐RCT was used as a starting point and extended with a random effect, accounting for the repeated measures structure of the data. The average dose rate (D) and the median exposure levels (C) for patient i, in the two phases of the RAPID programme (i.e., RAPID‐RCT and RAPID‐OLE) are denoted D i1 & D i2 and C i1 & C i2 , respectively. The base model is represented by equation (1), with j denoting study phase:
| (1) |
If this regression model were to be used in the context of a nonbiological agent with linear pharmacokinetics, the slope of steady‐state concentration with respect to dose rate would be interpretable as the reciprocal of clearance. Such a parameter interpretation is only approximately correct for an endogenous compound with non‐negligible baseline levels, and the model must therefore be understood as a linear empirical characterization of the relationship. With regard to distributional assumptions, both the random effects η1 , i and the residual errors ϵij are assumed to be normally (independently and identically) distributed for all i.
The base model was extended to incorporate covariates. Observed (pre‐treatment) baseline A1‐PI exposure was naturally assumed to be predictive of on‐treatment A1‐PI levels and so was included in the model as a pre‐set covariate, multiplying the intercept by the expression
where is the observed baseline A1‐PI and the denominator, 5.5, equates approximately to the median pre‐treatment A1‐PI concentration among those who were randomized to placebo in the RAPID‐RCT study. Covariates on slope were selected using a stepwise algorithm based on Akaike's Information Criterion (AIC), as described in the Supporting Information. Covariate effects on slope were incorporated into the base equation as multiplicative terms on θ2 as .
Exposure‐response model
The exposure–response model was developed to relate A1‐PI exposure during RAPID‐RCT/RAPID‐OLE to a physiological endpoint, i.e., lung density determined by CT at TLC. In the combined duration of RAPID‐RCT and RAPID‐OLE, each patient had seven scheduled lung density assessments – five within the first 2 years, with annual scans over the last 2 years.
Based on graphical exploration of individual longitudinal profiles for TLC lung density vs. study day (see randomly selected individual profiles in Figure S1), a base model that was piecewise linear in time was selected:
| (2) |
Here, Y denotes lung density at TLC; the subscript i again indexes patients, subscript j indexes study phase (j = 1 or 2 to indicate RAPID‐RCT or RAPID‐OLE, respectively), and now subscript k indexes assessment times. Time tijk is expressed in days since randomization of patient i in the RAPID‐RCT study. The expressions minimum(720, tijk) and maximum(0, tijk – 720) allow for a slope transition from DPi1 to DPi2 at tijk = 720 days, when the Extension study begins (this is the piecewise linearity assumption). The term ϵijk reflects residual error, assumed to be normally distributed. The base model incorporates submodels used for the intercepts and disease‐progression rates as follows:
| (3) |
| (4) |
| (5) |
All four η terms indicate patient‐specific random effects, all of which were assumed to be multivariate normal (with zero mean vector). For example, the expression θ1 + η1 , i represents patient‐specific baseline disease severity for patient i. The asterisks in the terms and indicate that exposure levels were centred at the median placebo levels observed in RAPID‐RCT. This facilitates the interpretation of model parameters, such that θ2 + η2 , i represents the patient‐specific progression rate for patient i during RAPID‐RCT that would have been observed in the absence of treatment, i.e., the natural rate of lung density decline for this patient. Note that since the progression rates DPi1 and DPi2 share the common expression , the intertrial difference in progression rate for patient i is formalized by the expression (θ4 + η4,i). (Such intertrial differences may reflect blinded vs. open‐label study conduct and/or changes in the rate of disease progression that may occur naturally over sufficiently long time scales.) Interpatient variation represented by η4 was not of any direct interest, but inclusion of this random effect allows for the possibility that changes in slope may not be fully accounted for by changes in exposure.
It was not clear whether the base model with four random effects could be fit reliably to the data, particularly when using a full block covariance matrix (i.e., requiring only that this matrix be positive definite, with no further restrictions). Consequently, random effect covariance matrices with some structural zeroes on the off‐diagonal were used. Specifically, the parameters associated with η4,i were considered to be ancillary, and it was judged to be acceptable to assume that this random effect was uncorrelated with the other three (the other three were, however, allowed to be correlated with each other).
In addition to the linear functions of concentration shown in equations (4) and (5), models with disease progression rates expressed as nonlinear (Emax and exponential) functions of concentration were also evaluated.
The base model was extended to incorporate covariate effects as described for the dose–exposure model (see Supporting Information). Covariate effects were formalized as linear adjustments to θ2 (corresponding to the covariate associations with the natural progression) and/ or θ3 (corresponding to associations with the effect of exposure).
Model evaluation/simulation and resampling
The adequacy of the final dose–exposure and exposure–response models was investigated with simple predictive checks and bootstrap predictive check methods. Bootstrap replication and population simulations based on fitted models were used to evaluate the likely effect of higher dose levels as well the effect on enrolling particular baseline characteristics. In total four simulations were performed as follows: (i) bootstrapping of predicted decline rate for a reference individual; (ii) bootstrapping of predicted covariate effects in the exposure–response relationship to evaluate model‐predicted differences as functions of covariate settings; (iii) bootstrapping of model‐predicted differences in clinical response as a function of covariate settings in the combined dose–exposure–response relationship; and (iv) bootstrapping to predict the likely range of clinical responses if a similar patient population were dosed at 90 or 120 mg kg–1 week–1. Further details of each simulation are provided in the Supporting Information.
Nomenclature of targets and ligands
Key protein targets and ligands in this article are hyperlinked to corresponding entries in http://www.guidetopharmacology.org, the common portal for data from the IUPHAR/BPS Guide to PHARMACOLOGY 9, and are permanently archived in the Concise Guide to PHARMACOLOGY 2015/16 10.
Results
Dose‐exposure model
The dose–exposure model was fit to the dose–exposure analysis data set. The final covariates selected were: (i) baseline weight (kg) and (ii) baseline A1‐PI. The final dose–exposure model, incorporating these covariate effects, is described below:
| (6) |
Parameter estimates for the final model are provided in Table 2. Of particular interest is the baseline weight effect on slope (θ3 = –0.85), which is consistent with allometric scaling of clearance according to Kleiber's law. The exponent is also sufficiently close to –1 to justify weight‐based dosing.
Table 2.
Final dose–exposure model
| Parameter | Description | Estimate | Std. Error | 95% LB | 95% UB |
|---|---|---|---|---|---|
| θ 1 | Log A1‐PI exposure for placebo (μmol l–1) | 5.42 | 5.23 | 5.62 | |
| θ 2 | A1‐PI slope w.r.t. dose rate [(μmol l–1/(mg day–1)] | 0.02 | 0.00 | 0.01 | 0.02 |
| θ 3 | Baseline weight effect on slope | –0.85 | 0.09 | –1.02 | –0.68 |
| θ 4 | Endogenous A1‐PI effect on slope | –0.12 | 0.08 | –0.27 | 0.04 |
| θ 5 | Endogenous A1‐PI effect (independent of dose) | 0.73 | 0.06 | 0.62 | 0.84 |
| ω 1 | Interindividual SD for log A1‐PI exposure for placebo | 0.07 | 0.02 | 0.28 | |
| σ | Residual SD | 0.15 | 0.13 | 0.17 |
A1‐PI, α‐1 proteinase inhibitor; LB, lower bound of the 95% confidence interval; SD, standard deviation; Std., standard; UB, upper bound of the 95% confidence interval; w.r.t., with respect to.
The variance terms ω 1 and σ are approximately interpretable as coefficients of variation, and may be converted to proper coefficients of variation using the expressions sqrt(exp(ω 1 2)‐1) and sqrt(exp(σ 2)‐1).
The dose–exposure model was used to predict A1‐PI concentrations as a function of covariate settings. Bootstrap estimates of covariate effects (baseline weight and A1‐PI) on the dose–exposure model are displayed in Figure 1 and companion Table S1. Covariate settings were computed to the 10th and 90th population percentiles, evaluated as isolated adjustments to a reference individual with a weight of 77.0 kg and an A1‐PI serum concentration of 5.3 μmol l–1 – the typical (median) postbaseline A1‐PI serum level in the absence of treatment. Baseline weight was found to have a greater effect on exposure than baseline A1‐PI; however, the effects were predicted to be small for both covariates.
Figure 1.
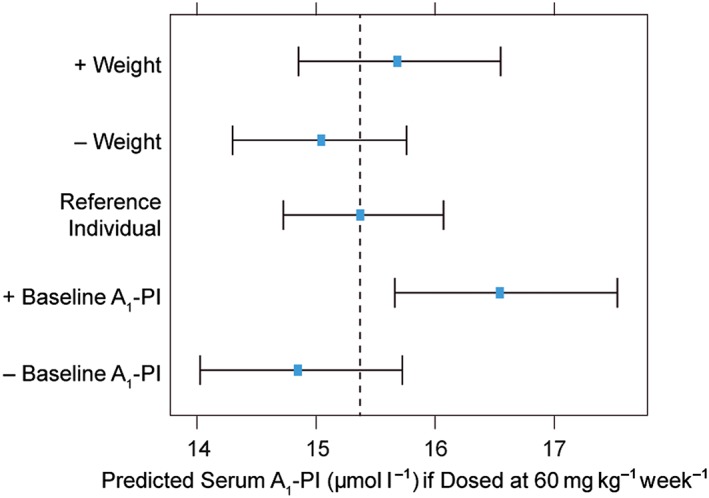
Bootstrap derived 95% confidence intervals and point estimates (bootstrap means) for predicted A1‐PI concentrations (μmol l–1) as a function of covariate settings, based on the final dose–exposure model. The vertical dashed line represents the model‐predicted post‐treatment A1‐PI exposure level for a reference individual (with baseline A1‐PI and baseline weight equal to study median values) when dosed at 60 mg kg–1 week–1. –/+ covariate indicates the model‐predicted A1‐PI serum level in which the covariate has been set to the 10th/90th percentile value, respectively, of a reference individual. A1‐PI, α‐1 proteinase inhibitor
Weight‐based dosing at 60 mg kg–1 week–1 is predicted to maintain steady‐state concentrations above the theoretical protective threshold of 11 μmol l–1 for approximately 98% of treated patients (Figure 2A). Two control patients had postbaseline exposure levels above the protective threshold; these patients were found to be heterozygous for the severe deficiency (Z) allele.
Figure 2.
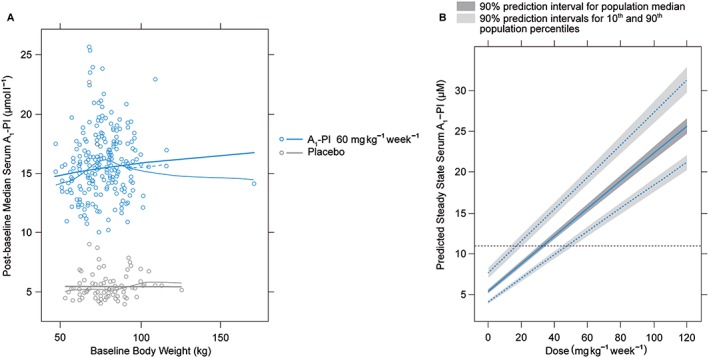
(A) Predicted A1‐PI exposure levels as a function of body weight, assuming proportional weight‐based dosing. Thick solid lines represent model predictions, thin solid lines represent a loess smooth and thin dashed lines represent a loess smooth with outlying (kg > 150) individual removed. (B) Predicted distribution of exposure levels as a function of dose, based on bootstrap population simulations. Solid blue line represents predicted population median exposure at different dose levels, dashed blue lines represent predicted 90th (top) and 10th (bottom) population percentiles for A1‐PI exposure at different dose levels, and horizontal dashed black line represents 11 μmol l–1 target threshold for A1‐PI exposure. A1‐PI, α‐1 proteinase inhibitor
Bootstrap population simulations were used to predict the expected range of trough exposure levels at doses of up to 120 mg kg–1 week–1 (Figure 2B and companion Table S2). Of particular note is that the 10th population percentile at 60 mg kg–1 week–1 is estimated at 12.8 μmol l–1, which is in line with the observed data shown in Figure 2A.
Exposure‐response model
Graphical exploration of individual response trajectories supported the model's piecewise linearity assumption with respect to time (see trajectories for 16 randomly selected individuals in Figure S1). Linearity of progression rate with respect to A1‐PI exposure was also supported over the available range of exposures, in the sense that slopes from separately fitted individual piecewise linear regressions had relationships with exposure that were essentially indistinguishable from linearity (compare the model‐based prediction with the loess fit in Figure 3A). Similarly, the alternative base models with disease progression rates expressed as nonlinear (Emax and exponential) functions of concentration resulted in predictions that were practically indistinguishable from the linear model fit over the range of the observed data (results not shown). Since the nonlinear model fits suffered from very large standard errors for the nonlinearity parameters, while providing no predictive advantage, these models were not pursued further.
Figure 3.
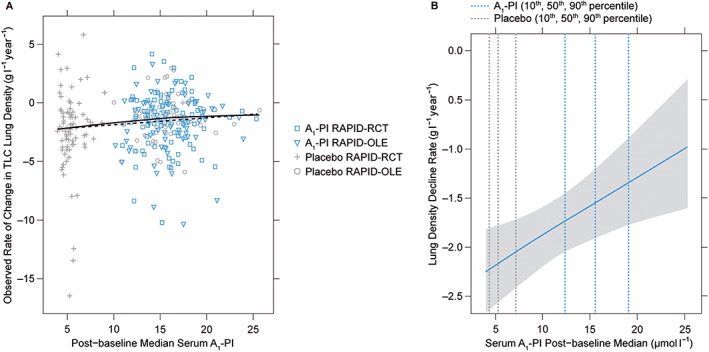
(A) Exploratory visualization to assess parametric form of exposure–response model. Individual data points are based on individual piecewise linear fits. These estimates are nonparametric in the sense that no parametric random effect distribution is assumed and no single model is used to jointly model all data. As such, these slope estimates provide a relatively assumption‐free assessment of model‐fit. Slope estimates and the solid line represents a loess fit to those slope estimates. The dashed line represents model predictions from the final exposure–response model for a hypothetical individual with typical covariate values. (B) Predicted decline rate as a function of exposure. A1‐PI, α‐1 proteinase inhibitor; TLC, total lung capacity
The final covariates selected were: (i) baseline lung density and (ii) baseline FEV1. The base model was expanded with covariate effect resulting in a final model with FEV1 as a covariate on the rate of natural progression in lung density decline. Thus, the final model may be expressed as:
| (7) |
| (8) |
| (9) |
| (10) |
Parameter estimates for the fitted final exposure–response model can be seen in Table 3. With the exception of the ω 4 parameter, standard errors and confidence intervals were suggestive of identifiable and well‐estimated parameters. Notwithstanding the poor estimation of ω 4, the η4 random effects were retained in the model in order to err on the side of more conservative predictive inferences. (Specifically, a model without the η4 random effects would predict progression rate changes with a nominal degree of precision that would be unwarranted given that there is at least some unexplained interpatient variability in the observed changes.) Diagnostic plots for the final model are available in the Supporting Information (Figures S2 and S3).
Table 3.
Final exposure–response model fit
| Par. | Description | Estimate | Std. Error | 95% LB | 95% UB |
|---|---|---|---|---|---|
| θ 1 | Pre‐treatment lung density (g l−1) | 46.89 | 1.21 | 44.53 | 49.25 |
| θ 2 | Lung density decline rate for placebo (g l–1 year–1) | –2.18 | 0.22 | –2.61 | –1.74 |
| θ 3 | A1‐PI effect on decline rate [(g l–1 year–1)/(μmol l–1)] | 0.06 | 0.02 | 0.01 | 0.11 |
| θ 4 | Change in decline rate in RAPID‐OLE phase (g l–1 year–1) | 0.20 | 0.26 | –0.30 | 0.70 |
| θ 5 | Baseline FEV1 effect on decline rate [(g l–1 year–1) l–1] | 0.56 | 0.22 | 0.12 | 1.00 |
| ω 1 | IIV SD for pre‐treatment lung density | 15.28 | 13.69 | 17.05 | |
| ω 2 | IIV SD for lung density decline rate | 1.32 | 0.90 | 1.93 | |
| ω 3 | IIV SD for concentration effect on decline rate | 0.09 | 0.03 | 0.30 | |
| ω 12 | IIV correlation: pre‐treatment vs. decline | –0.270 | –0.56 | 0.08 | |
| ω 13 | IIV correlation: pre‐treatment vs. concentration effect on slope | 0.26 | –0.33 | 0.71 | |
| ω 23 | IIV correlation: decline vs. concentration effect | –0.75 | –0.93 | –0.32 | |
| ω 4 | IIV SD for study phase effect on decline rate | 0.23 | 0.00 | 6644.52 | |
| σ | Residual SD | 2.60 | 2.45 | 2.75 |
A1‐PI, α‐1 proteinase inhibitor; FEV1, forced expiratory volume in 1 s; IIV, inter‐individual variability; LB, lower bound of the 95% confidence interval; SD, standard deviation; Std., standard; UB, upper bound of the 95% confidence interval
The observed slope differences for A1‐PI vs. placebo revealed a trend toward increasing improvement in lung density decline rate with higher postbaseline A1‐PI exposure (Figure 3A). The model‐predicted decline rates as a function of postbaseline exposure (Figure 3B) show a similar pattern to the observed data; note the differences between the 10th, 50th and 90th percentiles for A1‐PI vs. placebo (also shown in Table S3), demonstrating treatment‐effect with A1‐PI. A similar pattern was also seen when observed slope differences were computed in relation to changes in postbaseline A1‐PI concentration (Figure 4A). Again, the model predicted an analogous relationship to the observed data (Figure 4B).
Figure 4.
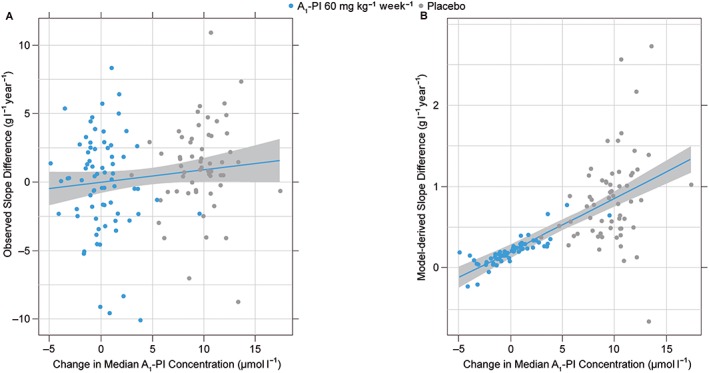
(A) Changes in rate of observed lung density decline as a function of exposure. (B) Changes in rate of model‐derived lung density decline as a function of exposure. Blue lines represent simple linear regression through the plotted points (not formal theoretical prediction from the model) and are added only as visual aids. Grey regions indicate point‐wise 95% confidence intervals associated with this regression
Effect of covariates on exposure‐response model
The exposure–response model was used to predict lung density decline rates as a function of covariate settings. The final exposure–response model does not include any covariates that modify the effect of exposure. The effect of FEV1, the only covariate retained in the exposure–response model, does not directly influence exposure.
Predicted slopes, as a function of covariates used in both the dose–exposure model and the exposure–response models, are presented in Figure 5 and companion Table S4. Overall, baseline FEV1 was predicted to have the greatest impact on decline rate; baseline A1‐PI and weight had negligible effects on slope change.
Figure 5.
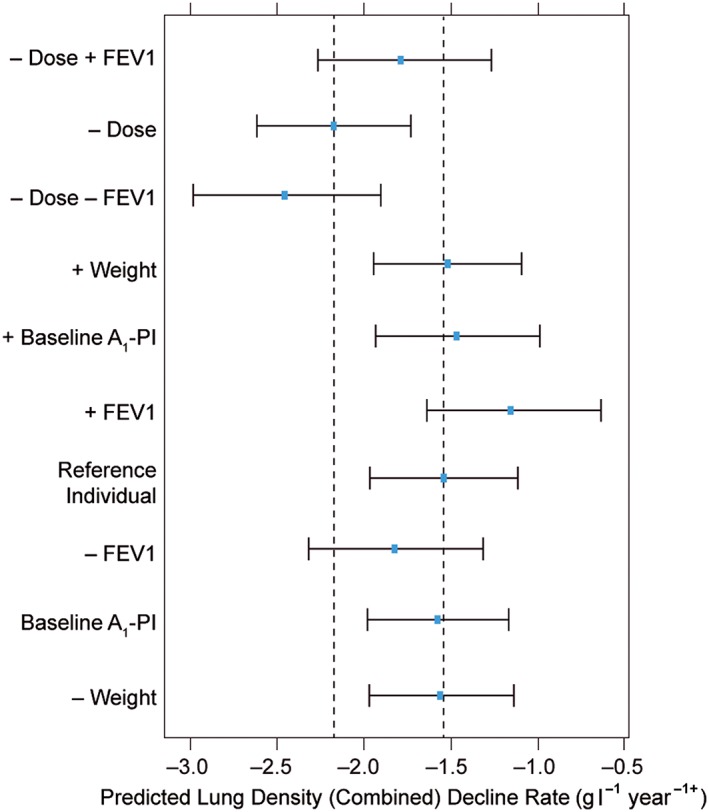
Predicted decline rate as a function of covariate settings. Study phase effects are not included, i.e., rates reflect conditions seen in the initial RAPID‐RCT phase of the RAPID programme. Point estimates are bootstrap means, and intervals are 95% bootstrap confidence intervals. Dashed vertical lines indicate point estimates (bootstrap means) under reference conditions for placebo (leftmost line) and A1‐PI 60 mg kg–1 week–1 (rightmost line). –/+ covariate indicates the model‐predicted rate of lung density decline in which the covariate has been set to the 10th/90th percentile value, respectively, of a reference individual. A1‐PI, α‐1 proteinase inhibitor; FEV1, forced expiratory volume in 1 s
Exposure‐response – clinical outcomes
The exposure–response model predicted the median decline rate as –1.56 g l–1 year–1 in A1‐PI treated patients, compared to –2.17 g l–1 year–1 in placebo. To determine the clinical efficacy of A1‐PI treatment, the proportion of patients showing improvements in lung density decline rates was determined by simulating from the exposure–response model over a range of thresholds (Figure 6). Over 4 years, an estimated 63% of A1‐PI‐treated patients demonstrated a reduction in annual lung density decline rate (in a positive direction) of 0.50 g l–1 year–1, compared to 12% of placebo‐treated patients. Moreover, Figure 6 demonstrates an increasing separation between A1‐PI‐treated patients and placebo‐treated patients with higher threshold improvements in lung density decline rate, which further supports treatment effect with A1‐PI vs. placebo.
Figure 6.
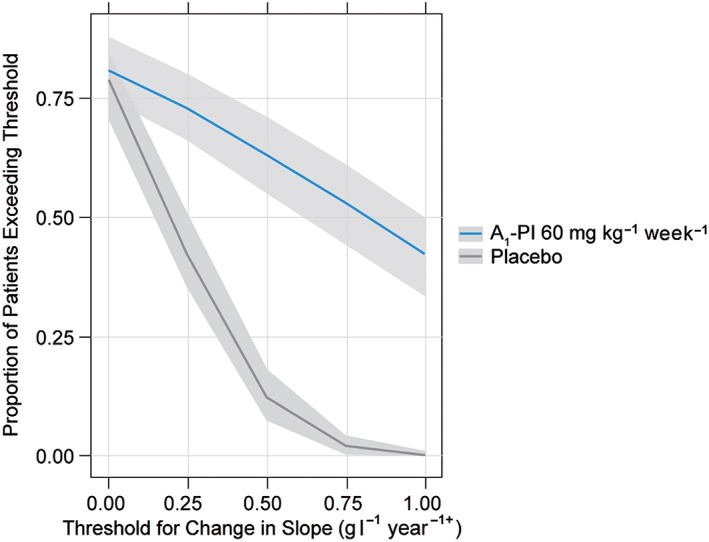
Proportion of patients exceeding (in the beneficial direction) a threshold abatement in rate of decline, over a range of threshold values. As shown in Table S5, these estimated proportions do not appreciably depend on covariate settings, and so are shown here under reference (baseline median) covariate settings only. The grey areas indicate the 90% confidence intervals for the true proportion of patients exceeding the threshold (these intervals reflect parameter uncertainty but not interpatient variability, as they refer only to a reference patient)
The stability of the previously described threshold improvements in lung density decline rate (Figure 6), were also tested in relation to the covariates examined in both the dose–exposure and exposure–response models. Baseline weight, A1‐PI and FEV1 had negligible effects on the proportion of patients improving by at least 0.50 g l–1 year–1 compared to the previously described reference individual (Table S5).
Discussion
The present pharmacometric analysis was undertaken to fully explore data from the largest clinical trials of A1‐PI therapy completed to date, specifically to model the relationships between A1‐PI dose and exposure, and between A1‐PI exposure and clinical response. Data from this study confirm weight‐based dosing as the most appropriate strategy. Data from the dose–exposure model shows that weight based dosing is able to raise serum A1‐PI levels above the putative protective threshold in the majority of patients. Additionally, this study is the first to relate A1‐PI exposure to a clinical endpoint in a pharmacometric analysis. Data from the exposure–response model support previous findings that treatment with A1‐PI effectively reduces annual lung density decline in patients with AATD.
Evaluating A1‐PI dosing strategy
The findings of the dose–exposure analysis strongly support weight‐based dosing with A1‐PI therapy. Our analysis has shown that the current dosing strategy of 60 mg kg–1 week–1 elevates serum levels above the protective threshold in the majority of patients. The close relationship between A1‐PI and weight is visible in the final parameters for the dose–exposure model, with the parameter θ 3 (baseline weight effect on slope) found to be –0.84, which is approximate to –1. A value of exactly –1 would imply an entirely flat relationship between concentration and weight when subjects are dosed proportionally to their weight, as per Kleiber's Law, which observes that metabolic rate scales three‐quarters of body mass.
These findings are consistent with previous studies that demonstrated the pharmacokinetic efficacy of various A1‐PI preparations 11, 12, 13, 14. Moreover, our findings are consistent with a previous population pharmacokinetic analysis of patients in RAPID‐RCT, which found average trough levels of 16.2 μmol l–1 with 60 mg kg–1 week–1 A1‐PI treatment – well above the extrapolated 11 μmol l–1 threshold 13. The dose–exposure model further confirms these findings as ≥98% of A1‐PI‐treated patients attained steady‐state serum levels of ≥11 μmol l–1 and the model clearly shows a significant increase in A1‐PI levels above the historic threshold with active A1‐PI treatment compared to placebo.
Furthermore, the dose–exposure analysis provides limited rationale for dosing strategies that would depend on other covariates. To evaluate possible population variability, covariate influences on the dose–exposure model were examined. Due to the small effect that variability in weight was predicted to have on levels, proportional weight‐based dosing with A1‐PI was determined to be the most appropriate dosing strategy. The model‐predicted exposure levels associated with the 10th and 90th percentiles for weight in the study population were 15.3 and 16.2 μmol l–1, respectively. The relatively small difference in these predictions indicates that exposure targets will be met relatively consistently across a range of weights. After weight, the only other covariate in the final dose–exposure model is baseline A1‐PI exposure. The predictions provided for high and low baseline A1‐PI values suggest that any effect due to this variable is modest in magnitude. Therefore, weight alone was found to have a significant effect on post‐baseline A1‐PI levels. However, this conclusion is accompanied by a degree of caution since some potential covariate relationships were excluded on the basis of AIC (see Supporting Information).
The dose–exposure model also allowed the extrapolation of exposure levels at higher doses. The model suggests a linear relationship between A1‐PI dose and exposure, with no clear evidence of a plateau at any serum concentration, including 11 μmol l–1. Double (120 mg kg–1) weekly doses of A1‐PI have previously been shown to be well tolerated and can increase serum levels further than the standard 60 mg kg–1 dose 11. Furthermore, in RAPID‐RCT, 333 doses of 120 mg kg–1 A1‐PI were administered to cover 2‐week periods, with no relevant increase in treatment‐related adverse events observed 15. However, the long‐term safety and efficacy of A1‐PI therapy at 120 mg kg–1 and above has yet to be proven; data are awaited from studies incorporating 120 mg kg–1 dosing 16, 17.
Clinical efficacy of A1‐PI therapy
In contrast to previous pharmacokinetic studies in AATD, the availability of lung density data from the RAPID programme enabled the modelling of A1‐PI exposure in relation to a valid, clinically‐relevant endpoint. The exposure–response model strongly supports the clinical efficacy of 60 mg kg–1 week–1 A1‐PI therapy established in RAPID‐RCT 6. Furthermore, predictions for the median decline rate in A1‐PI vs. placebo patients presented in this analysis are consistent with the observed decline rates reported from RAPID‐RCT 6. However, since a high proportion of the variability in observed decline rates is unexplained by the model, substantial regression to the mean occurs, resulting in notable differences between the observed and predicted decline rates. Overall, reductions in lung density decline rates were maintained over the 4‐year combined duration of the trials in the Early‐Start group, and were comparable between the Early‐Start and Delayed‐Start groups in RAPID‐OLE, where both groups were administered active treatment with weight‐based dosing of A1‐PI. These data support the observed findings from the RAPID programme and the increasing body of evidence that supports the efficacy of A1‐PI therapy to slow disease progression in patients with AATD 18, 19, 20. The observed data also suggest a relationship between decreasing lung density decline rates with increasing A1‐PI exposure and is supported by the analogous model‐predicted exposure–response relationship. Specifically, for an increment of 18.5 μmol l–1 in A1‐PI exposure above A1‐PI levels associated with placebo, the predicted rate of decline is approximately half of the rate of decline for placebo: 1.11 vs. 2.22 g l–1 year–1, respectively (calculated from data in Table S5). Furthermore, by examining individual yearly threshold reductions in lung density decline rate, it is apparent that there is increasing separation between A1‐PI‐treated patients and placebo‐treated patients in the proportions of patients achieving more stringent thresholds of clinical improvement (the rate of lung density decline; Figure 6). In context, improvements of approximately a quarter of the natural decline rate in the study cohort (0.50 g l–1 year–1), occurred regularly in A1‐PI‐treated patients but rarely in placebo‐treated patients. The benefit of treatment vs. nontreatment becomes apparent when it is considered that AATD causes irreversible destruction of lung tissue, as demonstrated by the disease‐modifying effect of treatment indicated by RAPID‐OLE 7. Evidence is also beginning to show an association between CT lung density and survival, which supports the potential clinical significance of reductions in decline rate such as 0.50 g l–1 year–1 21.
Whilst a differential response is not expected as a function of FEV1, patients with lower FEV1 were predicted to have higher lung density decline rates (independent of exposure). This finding is supported by the fact that lung density decline rate, as measured by CT, has previously been correlated with FEV1 7, 19, 21, 22. Because lung function once lost is not regained, earlier intervention could potentially be targeted at slowing disease progression and preserving both lung tissue and function.
Model validity and limitations
Overall, there was good correlation between the observed and the predicted data, as indicated by the standard graphical diagnostics we have presented. A number of factors are supportive of the robustness of the models. The models contain only one exceptionally large standard error, namely that for ω 4. Additionally, refitting the models across bootstrap estimates proved to be successful and when the models were refitted excluding certain data, model‐predicted estimates proved to be relatively insensitive. Therefore, these factors suggest that the model parameters are identifiable, stably estimated and are not overly influenced by any outlying points in the data.
The linearity of the dose–exposure relationship is not directly evaluable from the present data as only one dose strength (60 mg kg–1 week–1) was administered in the RAPID programme. However, the linearity was previously established in a pharmacokinetic study (RPR 118635–101), which evaluated post‐baseline A1‐PI concentrations at several dose levels 23. Therefore, a linear relationship between dose and exposure (with no clear evidence of a plateau at any serum concentration) is expected. The safety of higher doses, however, is not evaluable from the present analysis and, as previously discussed, the long‐term evidence for the safety of higher A1‐PI doses, although supportive, remains limited 12, 15, 18, 24, 25.
The exposure–response model was also fitted in a linear fashion – implying increasing response with increasing exposure. The assumed linearity in the exposure–response relationship is supported over the range of the observed data in the sense that both the nonlinear models and nonparametric fit provided essentially linear predictions over this range. However, it is unlikely that linear extrapolation is valid for extremely high dose levels as this would imply increasing lung densities over time. This would not be possible as the progressive loss of lung tissue is considered to be an irreversible process. Therefore, with the available data, we are not able to estimate at what point the linearity of the relationship between exposure and response ceases to be valid, which limits the utility of the model in predicting response at higher exposure levels. If one were to attempt to identify the plateau in clinical efficacy as A1‐PI exposure increases, data from a dose‐ranging trial – studying higher doses than previously tested – would be required. The inclusion of only a single dose of A1‐PI in the RAPID programme limited our modelling analysis, and our conclusions must therefore be treated with a degree of caution. However, based on the available data, it remains a valid assumption that higher exposure levels would plausibly yield greater reductions in lung density decline rates. Although biomarker data might have informed construction of a mechanistic pharmacokinetic/pharmacodynamic model, no validated biomarker currently exists to assess disease progression in A1‐PI deficiency. Therefore, the model presented is empirical in nature.
Moreover, there are also limitations surrounding the finding that the final dose‐exposure–response model shows extremely uniform outcomes across the covariate settings tested. This is a tentative finding, as potential covariate relationships were excluded on the basis of AIC (see Supporting Information). Nonetheless, the assumption that efficacy as reflected by slope change does not depend on the measured covariates remains a valid working assumption based on the available data.
Conclusions
Our analysis is highly supportive of weight‐based dosing as a stable, predictable method of A1‐PI administration. Moreover, the current 60 mg kg–1 week–1 dosing strategy achieves adequate A1‐PI levels above the 11 μmol l–1 protective threshold in >98% of patients studied. We found no clear evidence of a plateau in clinical efficacy as A1‐PI exposure increased, calling into question whether 11 μmol l–1 is the maximal, clinically effective threshold for A1‐PI therapy in AATD. The exposure–response model supports the conclusion from the primary RAPID‐RCT analysis that A1‐PI therapy is clinically effective in slowing the rate of lung density decline in patients with AATD. Improvements in decline rate of at least 0.50 g l–1 year–1 (approximately a quarter or the natural decline rate) occurred more frequently in A1‐PI‐treated patients vs. placebo. Final dose–exposure–response simulations indicated the limited effect that covariates had on slope change with A1‐PI. Low FEV1 was determined to be a predictor of lower lung density, providing a rationale to potentially treat those patients earlier in an effort to slow disease progression and delay the eventual loss of lung tissue and function.
Competing Interests
There are no competing interests to declare.
The RAPID programme and preparation of this manuscript were funded by CSL Behring . Editorial assistance was provided by Meridian HealthComms Ltd, funded by CSL Behring. Parts of this research was presented as posters at the ERS International Congress, 26th–30th September 2015, Amsterdam, the Netherlands, and the ASCPT annual meeting, 8th–12th March 2016, San Diego, CA, USA.
Contributors
M.A.T., J.A.R., O.V., M.B. and J.M.E. conceived the study. J.A.R. and M.A.T. performed and reviewed the analyses. J.A.R. wrote the statistical analysis report. J.A.R., M.A.T. and O.V. assisted in the preparation of the manuscript. K.R.C., J.B., R.A.S., J.S. and N.G.M. were investigators on CSL Behring's RAPID‐RCT trial. K.R.C., P.J.T., N.G.M. and J.C.W. were investigators on CSL Behring's RAPID‐OLE trial. All authors reviewed the manuscript and provided their approval for submission.
Supporting information
Table S1 Summary of predicted A1‐PI concentrations (μmol l–1) as a function of covariate settings, based on the final dose–exposure model
Table S2 Bootstrap median estimates of predicted exposure levels as a function of dose
Table S3 Predicted rate of decline as a function of exposure. Exposure percentiles refer to observed values
Table S4 Predicted rate of decline as a function of covariate settings. Point estimates are bootstrap means, and intervals are 95% bootstrap confidence intervals
Table S5 Proportion of patients improving by at least 0.5 g l–1 year–1, by covariate settings. Success proportions under alternative definitions of clinical success (i.e., slope change thresholds other than 0.5 g l–1 year–1) are shown in Figure 6
Figure S1 Example (randomly selected) longitudinal profiles for combined lung density. Solid lines are individually fit (not based on our final developed model) linear splines with fixed knot at day 720. Note that these individual fits are for exploratory purposes only: the actual model‐based analyses are not based on these individual fits, and properly account for the amount of longitudinal information obtained for each patient
Figure S2 (A) Exposure–response dependent variable (DV) vs. IPRED; B) Exposure–response residuals vs. PRED; C) Exposure–response residuals vs. time; D) Exposure–response residuals vs. exposure; E) Exposure–response residual Q‐Q plot; F) Exposure–response random effects: histogram
Figure S3 Changes in rate of lung density decline for A1‐PI and placebo: predicted vs. observed
Tortorici, M. A. , Rogers, J. A. , Vit, O. , Bexon, M. , Sandhaus, R. A. , Burdon, J. , Chorostowska‐Wynimko, J. , Thompson, P. , Stocks, J. , McElvaney, N. G. , Chapman, K. R. , and Edelman, J. M. (2017) Quantitative disease progression model of α‐1 proteinase inhibitor therapy on computed tomography lung density in patients with α‐1 antitrypsin deficiency. Br J Clin Pharmacol, 83: 2386–2397. doi: 10.1111/bcp.13358.
References
- 1. Stoller JK, Aboussouan LS. A review of alpha1‐antitrypsin deficiency. Am J Respir Crit Care Med 2012; 185: 246–259. [DOI] [PubMed] [Google Scholar]
- 2. American Thoracic Society/European Respiratory Society statement: standards for the diagnosis and management of individuals with alpha‐1 antitrypsin deficiency. Am J Respir Crit Care Med 2003; 168: 818–900. [DOI] [PubMed] [Google Scholar]
- 3. Ferrarotti I, Thun GA, Zorzetto M, Ottaviani S, Imboden M, Schindler C, et al. Serum levels and genotype distribution of alpha1‐antitrypsin in the general population. Thorax 2012; 67: 669–674. [DOI] [PubMed] [Google Scholar]
- 4. Tonelli AR, Brantly ML. Augmentation therapy in alpha‐1 antitrypsin deficiency: advances and controversies. Ther Adv Respir Dis 2010; 4: 289–312. [DOI] [PubMed] [Google Scholar]
- 5. Brantly ML, Wittes JT, Vogelmeier CF, Hubbard RC, Fells GA, Crystal RG. Use of a highly purified alpha 1‐antitrypsin standard to establish ranges for the common normal and deficient alpha 1‐antitrypsin phenotypes. Chest 1991; 100: 703–708. [DOI] [PubMed] [Google Scholar]
- 6. Chapman KR, Burdon JG, Piitulainen E, Sandhaus RA, Seersholm N, Stocks JM, et al. Intravenous augmentation treatment and lung density in severe alpha1 antitrypsin deficiency (RAPID): a randomised, double‐blind, placebo‐controlled trial. Lancet 2015; 386: 360–368. [DOI] [PubMed] [Google Scholar]
- 7. McElvaney NG, Burdon JG, Holmes M, Glanville A, Wark PAB, Thompson PJ, et al. Long‐term efficacy and safety of alpha1‐proteinase inhibitor treatment for emphysema caused by severe alpha1 antitrypsin deficiency: the RAPID open‐label extension trial. Lancet Respir Med 2017; 5: 51–60. [DOI] [PubMed] [Google Scholar]
- 8. R Core Team . R: a language and environment for statistical computing. R foundation for statistical computing. Vienna, Austria, 2015. Available at https://www.R‐project.org/ (Accessed May 2017)
- 9. Southan C, Sharman JL, Benson HE, Faccenda E, Pawson AJ, Alexander SPH, et al. The IUPHAR/BPS guide to pharmacology in 2016: towards curated quantitative interactions between 1300 protein targets and 6000 ligands. Nucleic Acids Res 2016; 44: D1054–1068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Alexander SPH, Fabbro D, Kelly E, Marrion N, Peters JA, Benson HE, et al. The Concise Guide to PHARMACOLOGY 2015/16: Enzymes. Br J Pharmacol 2015; 172: 6024–6109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Campos MA, Kueppers F, Stocks JM, Strange C, Chen J, Griffin R, et al. Safety and pharmacokinetics of 120 mg/kg vs. 60 mg/kg weekly intravenous infusions of alpha‐1 proteinase inhibitor in alpha‐1 antitrypsin deficiency: a multicenter, randomized, double‐blind, crossover study (SPARK). COPD 2013; 10: 687–695. [DOI] [PubMed] [Google Scholar]
- 12. Soy D, de la Roza C, Lara B, Esquinas C, Torres A, Miravitlles M. Alpha‐1‐antitrypsin deficiency: optimal therapeutic regimen based on population pharmacokinetics. Thorax 2006; 61: 1059–1064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Tortorici MA, Vit O, Bexon M, Sandhaus R, Burdon J, Piitulainen E, et al. Population pharmacokinetics of A1‐PI in patients with alpha‐1 antitrypsin deficiency. Eur Respir J 2015; 46 (suppl 59): PA1486. [Google Scholar]
- 14. Stocks JM, Brantly M, Pollock D, Barker A, Kueppers F, Strange C, et al. Multi‐center study: the biochemical efficacy, safety and tolerability of a new alpha1‐proteinase inhibitor, Zemaira. COPD 2006; 3: 17–23. [DOI] [PubMed] [Google Scholar]
- 15. Seersholm N, Sandhaus R, Chapman KR, Burdon J, Piitulainen E, Stocks J, et al. Safety of bi‐weekly infusion of A1‐PI augmentation therapy in RAPID. Eur Respir J 2015; 46 (suppl 59): PA999. [Google Scholar]
- 16. Clinicaltrials.gov . Efficacy and safety of alpha1‐proteinase inhibitor (human), modified process (alpha‐1 MP) in subjects with pulmonary emphysema due to alpha1 antitrypsin deficiency (AATD) (SPARTA). Available at https://clinicaltrials.gov/ct2/show/NCT01983241 (last accessed 07 March 2017).
- 17. Clinicaltrials.gov . Effect of double dose of alpha 1‐antitrypsin augmentation therapy on lung inflammation. Available at https://clinicaltrials.gov/ct2/show/NCT01669421?term=NCT01669421&rank=1 (last accessed 07 March 2017).
- 18. Dirksen A, Dijkman JH, Madsen F, Stoel B, Hutchison DC, Ulrik CS, et al. A randomized clinical trial of alpha(1)‐antitrypsin augmentation therapy. Am J Respir Crit Care Med 1999; 160: 1468–1472. [DOI] [PubMed] [Google Scholar]
- 19. Dirksen A, Piitulainen E, Parr DG, Deng C, Wencker M, Shaker SB, et al. Exploring the role of CT densitometry: a randomised study of augmentation therapy in alpha1‐antitrypsin deficiency. Eur Respir J 2009; 33: 1345–1353. [DOI] [PubMed] [Google Scholar]
- 20. Chapman KR, Stockley RA, Dawkins C, Wilkes MM, Navickis RJ. Augmentation therapy for alpha1 antitrypsin deficiency: a meta‐analysis. COPD 2009; 6: 177–184. [DOI] [PubMed] [Google Scholar]
- 21. Green CE, Parr DG, Edgar RG, Stockley RA, Turner AM. Lung density associates with survival in alpha 1 antitrypsin deficient patients. Respir Med 2016; 112: 81–87. [DOI] [PubMed] [Google Scholar]
- 22. Parr DG, Stoel BC, Stolk J, Stockley RA. Validation of computed tomographic lung densitometry for monitoring emphysema in α1‐antitrypsin deficiency. Thorax 2006; 61: 485–490. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23. U.S. Food and Drug Administration . Zemaira™ summary basis for approval. 2003. Available at http://www.fda.gov/ucm/groups/fdagov‐public/@fdagov‐bio‐gen/documents/document/ucm244464.pdf (last accessed 07 March 2017).
- 24. Hubbard RC, Sellers S, Czerski D, Stephens L, Crystal RG. Biochemical efficacy and safety of monthly augmentation therapy for alpha 1‐antitrypsin deficiency. JAMA 1988; 260: 1259–1264. [PubMed] [Google Scholar]
- 25. Barker AF, Iwata‐Morgan I, Oveson L, Roussel R. Pharmacokinetic study of alpha1‐antitrypsin infusion in alpha1‐antitrypsin deficiency. Chest 1997; 112: 607–613. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Table S1 Summary of predicted A1‐PI concentrations (μmol l–1) as a function of covariate settings, based on the final dose–exposure model
Table S2 Bootstrap median estimates of predicted exposure levels as a function of dose
Table S3 Predicted rate of decline as a function of exposure. Exposure percentiles refer to observed values
Table S4 Predicted rate of decline as a function of covariate settings. Point estimates are bootstrap means, and intervals are 95% bootstrap confidence intervals
Table S5 Proportion of patients improving by at least 0.5 g l–1 year–1, by covariate settings. Success proportions under alternative definitions of clinical success (i.e., slope change thresholds other than 0.5 g l–1 year–1) are shown in Figure 6
Figure S1 Example (randomly selected) longitudinal profiles for combined lung density. Solid lines are individually fit (not based on our final developed model) linear splines with fixed knot at day 720. Note that these individual fits are for exploratory purposes only: the actual model‐based analyses are not based on these individual fits, and properly account for the amount of longitudinal information obtained for each patient
Figure S2 (A) Exposure–response dependent variable (DV) vs. IPRED; B) Exposure–response residuals vs. PRED; C) Exposure–response residuals vs. time; D) Exposure–response residuals vs. exposure; E) Exposure–response residual Q‐Q plot; F) Exposure–response random effects: histogram
Figure S3 Changes in rate of lung density decline for A1‐PI and placebo: predicted vs. observed


