Abstract
Surface traps are ubiquitous to nanoscopic semiconductor materials. Understanding their atomistic origin and manipulating them chemically have capital importance to design defect-free colloidal quantum dots and make a leap forward in the development of efficient optoelectronic devices. Recent advances in computing power established computational chemistry as a powerful tool to describe accurately complex chemical species and nowadays it became conceivable to model colloidal quantum dots with realistic sizes and shapes. In this Perspective, we combine the knowledge gathered in recent experimental findings with the computation of quantum dot electronic structures. We analyze three different systems: namely, CdSe, PbS, and CsPbI3 as benchmark semiconductor nanocrystals showing how different types of trap states can form at their surface. In addition, we suggest experimental healing of such traps according to their chemical origin and nanocrystal composition.
Colloidal semiconductor nanocrystals (also known as quantum dots, QDs) show size-dependent optoelectronic properties governed by quantum confinement effects, which are a key feature for QD-based applications, especially in (electro-)luminescent devices.1−3 Colloidal QDs usually span a 2–10 nm diameter, thus displaying a large number of atoms at the surface, as opposed to bulk semiconductors in which the surface is only a tiny fraction of the whole solid.
The QD surface is a highly dynamic region, coordinated by chemical species (ligands) and exposed to the surroundings (solvents and other species in solution, matrices, etc.) that can have drastic effects on the QD properties. These effects are typically ascribed to the lower coordination of surface atoms compared to bulk atoms, which may lead to localized electronic states or highly reactive sites, which are prone to chemical and redox processes. In these conditions, the formation of shallow, or deep, midgap states as surface traps that provide pathways for nonradiative exciton recombination is highly likely, which is detrimental for QD-based optoelectronic applications. The most exploited approach to eliminate surface traps relies on the growth of a (thick) shell of a wider band gap material around the (photo)active core, thus moving surface defects to the outer region of the inorganic shell.4 In this configuration, the exciton is localized in the core, thus leading to almost unitary photoluminescence quantum yields (PLQY), as signature of the low probability of trapping photogenerated charge carriers in the outermost surface sites.5,6 Core/shell heterostructures have drawbacks, however: charge carrier localization in the core hinders transport in core/shell QD solids and lattice mismatch between the core and the shell materials may induce strain, ultimately deteriorating the overall optoelectronic properties.
The actual elimination of trap states in core-only QDs has therefore paramount importance toward application and to this aim it is mandatory to deeply understand their atomistic origin. In this framework, the main questions we address are the following:
-
(1)
What are surface traps?
-
(2)
How do they originate?
-
(3)
How can we eliminate them?
To answer these questions, we believe that it is very important to combine the knowledge of the QD surface chemistry attained in recent experiments7−10 with modern computational chemistry tools, which are now at the stage of accurately simulating realistic QD systems, thus providing a radical advancement of description toward control of the optoelectronic properties of colloidal QDs.
The goal of this Perspective is to provide the basis for understanding the surface chemistry of QDs by merging the most recent discoveries in both experiments and theory. To this aim, we will discuss three benchmark QD systems with different structural and electronic features (CdSe, PbS, and CsPbI3) and identify the processes leading to surface trap states, suggesting feasible postsynthesis treatments for their elimination.
QD Classification and Notation. Careful analytical studies have recently disclosed structure and composition of colloidal QDs, demonstrating (size-dependent) metal-rich stoichiometries of II–VI8,11 and IV–VI metal chalcogenides,12−14 whereas metal halide perovskites seem not to show relevant off-stoichiometry probably due to their relatively large size, with diameters usually above 10 nm.15−17
Chemical species at the QD surface have been extensively characterized by determining ligand type, surface coverage, and their eventual lability.8,14,16 In addition, such surface ligands guarantee overall QD charge neutrality, which is mandatory in low polarity solvents commonly used to disperse as-synthesized colloidal QDs. Usually, charge neutral QDs can be regarded as intrinsic, or doped, whether they satisfy, or not, the charge balance condition, which can be conveniently expressed according to the charge-orbital balance model (CBM), first introduced for computational purposes by Voznyy et al.18 Such model counts the number of excess/deficient valence electrons of a neutral QD by assuming that each core atom and surface ligand is in its thermodynamically most favorable oxidation state (as an example, + 2 for Pb and −2 for S in PbS) and charge contribution (e.g., −1 for iodide, but valid also for carboxylates or thiolates; 0 for amines or phosphines, not considered here), respectively. It is thus possible to derive a simple formula that provides a quantitative expression for charge balance in neutral QDs:
where Ndop is the number of excess/deficient electrons in the QD and Ni is the number of core atoms/surface ligands of type i with oxidation state/charge contribution qi. When the chosen QD model satisfies the condition of Ndop = 0, it means that the QD is intrinsic and exhibits a closed-shell configuration, i.e., an effectively charge-balanced QD. Usually, this is a necessary, but not sufficient condition for a clean band gap material. Suitable QD models thus may satisfy the condition Ndop = 0, upon assuming that the core atoms and the ligands are in their thermodynamically most stable oxidation state and charge contribution, respectively.
When the QD is charge unbalanced (Ndop ≠ 0), then the QD can be regarded as doped. For Ndop < 0, excess electrons fill the conduction band (CB), raising the energy levels compared to vacuum and n-doping the QD; conversely, for Ndop > 0 electrons are removed from the valence band (VB), lowering the energy levels and p-doping the QD. As an example, upon removing two iodide ligands at the PbS QD surface to form molecular iodine would lead to Ndop = −2, with excess electrons filling the CB and forming reduced, n-doped PbS QDs.
This information has led to an inferred atomic-level description of the QDs and sets the standards for building reliable QD models, which are nowadays computable with any available quantum chemistry (QM) package and go beyond the widely used models such as [CdSe]33. A review that covers the most successful outcomes of these cluster models was recently published and will not be covered here.19
In order to describe the chemical bonding at the QD surface, the covalent bond classification (CBC) scheme mutuated from organometallic chemistry is commonly adopted.20 Within this framework, both the metal chalcogenide core, hereafter referred to as [MmEn], and the surface ligands are considered as neutral species, with the latter named after the number of electrons that they donate to the surface atoms of the inorganic core: L-type for 2-electron donors, X-type for 1-electron donors and Z-type for 0-electron donors.8 A nonstoichiometric [MmEn] core, with m > n commonly attained experimentally, provides a source of (m – n)·v unpaired electrons (with v as the number of valence electrons of each neutral M atom). Here, charge-balance is obtained when such unpaired electrons are saturated with one-electron donor species (X-type ligands), ultimately leading to a general molecular formula for the QD (including also L-type ligands), as [MmEn]X(m–n)·vLp. Such QD chemical formula can alternatively be written as [ME]n(MXv)m−nLp, thus highlighting the M stoichiometric excess and the presence of Z-type ligands (the electron-withdrawing (MXv) moiety that also includes X-type ligands), which have been demonstrated to be active elements at the QD surface.
Important Note. At this point, we must draw attention to the possible confusion that may arise by the use of both CBM and CBC models, as the former deals with ionic species and the latter with neutral species. This contradiction is evident in [ME]n(MXv)m–nLp QDs when discussing the role of X surface species that can be regarded either as anions, which balance charges of excess M cations in an ionic representation of the QD (CBM), and as radicals that saturate valences of excess M atoms in a covalent representation of chemical bonding at the QD surface (CBC). On the other hand, CBM and CBC models can be considered as analogous for the (MXv) and L motifs (Z-type and L-type ligands in the CBC), because they are charged neutral in both representations.
As a result, we hereafter refer to either CBM or CBC when discussing QD doping or surface chemistry, respectively: CBM is indeed more intuitive for evaluating charge balance in those QDs regarded as mostly ionic, while CBC is more comprehensive to analyze the chemical bonding at the QD surface.8
QD Model. On this basis, we constructed our QD models as follows. For II–VI QDs, we adopted the zinc-blende structure and charge-balanced chemical formula as [ME]m(MX2)n. We omitted additional Z- and L-type ligands at the chalcogenide- and metal-terminated [111] facets, because bare under-coordinated surface atoms in those facets do not lead to localized states and affect only little the electronic structure.22
In terms of size, the [CdSe]55(CdX2)13 model (∼2.0 nm) represents a good starting point for many simulations based on density functional theory (DFT), because it already exhibits a dense set of states around the band edges and is still small enough to be computationally affordable. Similarly, for IV–VI QDs we adopted models with rock salt crystal structure and analogous charge-balanced chemical formula [ME]m(MX2)n, with M as Pb divalent cation. Reliable models for metal halide perovskites ABX3 (A = Cs, methylammonium, formamidinium; B = Sn, Pb; X = halide) include distorted cubic/orthorhombic crystal structures and chemical formula as [ABX3]m(AX)n to satisfy charge balance. We note that perovskite QDs of experimental sizes (above ∼10 nm) exhibits n ≪ m, thus they assume an overall A:B:X stoichiometry close to 1:1:3; in smaller QDs, n and m values are of the same order of magnitude, and their proportion depends on surface termination.17 Several theoretical works that employ charge-balanced II–VI, IV–VI, and perovskite QDs with off-stoichiometric inorganic cores have already appeared in the literature.18,23−30
In Figure 1 we illustrate the structures of II–VI, IV–VI, and metal halide perovskite QDs used for the discussion. Our CdSe, PbS, and CsPbI3 models show similar sizes (about 2.6 nm) and iodide anions as surface ligands, which are convenient both to mimic atomic ligands for optoelectronic applications and to limit computational effort. All calculations have been carried out at the DFT31 level with a PBE exchange-correlation functional.32 Core electrons were described using effective core-potentials and outer electrons with a double-ζ basis-set augmented with polarization functions (DZVP).33 Calculations were run using the CP2k 3.0 code.34
Figure 1.
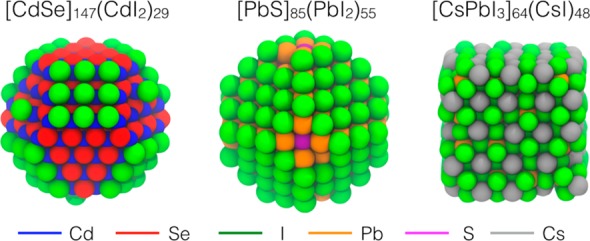
Relaxed structures of three types of QDs (∼2.6 nm) optimized at the DFT/PBE level of theory: (left) a zinc-blende CdSe QD passivated with iodide atoms; (center) a rock-salt PbS QD passivated with iodide atoms; (right) a slightly distorted cubic/orthorhombic CsPbI3 QD.
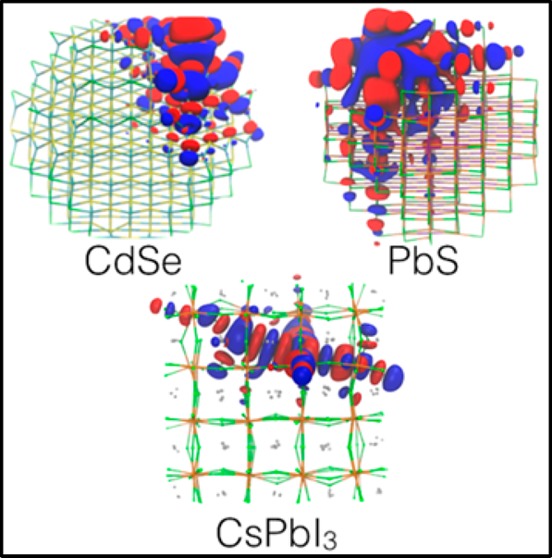
In Figure 2 we present the electronic structure of such benchmark QD systems, which are intrinsic and exhibit electronic structures with clean band gap without midgap states, although with different band energies. The orbitals at the band edges of each system are also plotted to illustrate the delocalization over most of the atoms composing the QDs.
Figure 2.
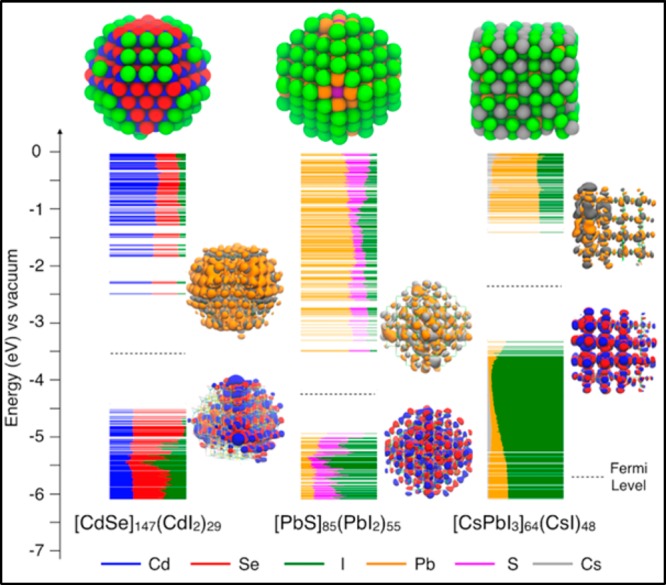
Electronic structures of three types of QDs (∼2.6 nm) optimized at the DFT/PBE level of theory: (left) the CdSe QD; (center) the PbS QD; (right) the CsPbI3 QD. The energy levels are aligned according to their computed vertical ionization potential, which corresponds to the correct position of the valence band edge. The LUMO energy levels of CdSe QD have been rigidly shifted to higher energies to match the experimental gap of CdSe QDs of similar size; it is well-known that the DFT/PBE approach severely underestimates the band gap of CdSe QDs.35 For PbS and CsPbI3 QDs the band gap is already well reproduced at the same level of theory. The energy levels are aligned according to their computed vertical ionization potential, which corresponds to the correct position of valence band edge.
Surface Trap States in Charge-Balanced, Intrinsic QDs. We anticipated earlier that when Ndop = 0, the QD is charge-balanced, providing a necessary condition for a clean band gap. This is especially true for the DFT models shown in Figure 2, which indeed exhibit trap-free electronic structures.
As-synthesized CdSe QDs exhibit rather low PLQYs (below 10%),8,36 thus suggesting that traps are already present upon synthesis/purification, whose origin is yet to be straightforwardly demonstrated. In 2013, Anderson et al. experimentally identified a source of trap states by adding Lewis bases, as L-type ligands, to CdSe QDs that induced Z-type ligand displacement, as L–MX2 moieties, leading to a significant PL quenching.8 In a recent work based on DFT calculation, Houtepen et al. systematically studied the effect of displacing Z-type ligands from the surface of CdSe QDs and noticed that after each displacement, the surface would reconstruct, but in some cases the surface generates stable dicoordinated Se atoms.22 These atoms would provide a source of traps localized on nonbonding 4p orbitals that would fall inside the band gap, and can be regarded as dangling bonds.
For completeness, we performed DFT calculations on a (larger) CdSe QD model (as shown in Figure 3) upon the displacement of one Z-type ligand as CdI2: here, the formation of the trap is clearly noticeable, whose electronic density is mostly localized on the dicoordinated Se atom and only partially delocalized to nearby atoms.
Figure 3.
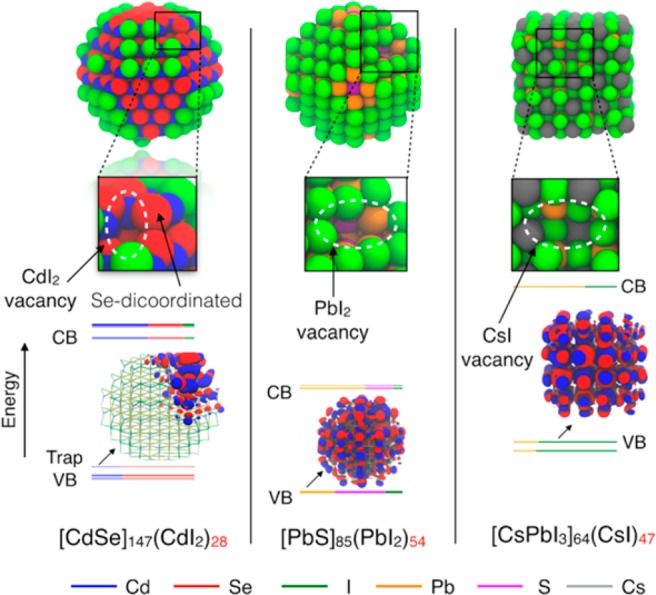
Relaxed structures of three types of QDs (∼2.6 nm) optimized at the DFT/PBE level of theory and with one Z-type ligand displaced: (left) a zinc-blende CdSe QD passivated with iodide ions; (center) a rock-salt PbS passivated with iodide ions; (right) a slightly distorted cubic/orthorhombic CsPbI3 perovskite QD.
We additionally made a preliminary extension of the work of Houtepen et al.22 to see the effect of Z-type displacement on PbS and CsPbI3 QDs. Interestingly, in both cases, upon displacement of several Z-type ligands, we did not notice any effect on their electronic structures, which preserve a clean band gap. We further investigated the origin of this discrepancy with CdSe QDs and noticed that this can be mainly related to the coordination number of surface atoms upon Z-type displacement. In PbS and CsPbI3, the removal of PbI2 or CsI leaves behind atoms with a high coordination number (as a result of their rock-salt and cubic/orthorhombic crystal structure, respectively), whose frontier atomic orbitals are still delocalized. Upon removal of several Z-type ligands, dicoordinated atoms would form at the surface in a very high energetic state and would immediately reconstruct to form new bonds and heal dangling bonds. The zinc-blende crystalline structure of CdSe QDs could instead favor the formation of stable dicoordinated atoms at the surface, thus leading to states that intrude the band gap albeit being in closed-shell electronic configuration. As III–V QDs also show zinc-blende crystal structure,38,39 we could expect under-coordinated surface atoms leading to trap states in these QD systems.
As this type of trap has specific structural (dicoordinated atoms) and electronic (lone-pairs on np chalcogenide orbitals) features, it is possible to suggest a way to heal it: indeed, Lewis acids (such as Z-type ligands) could be employed to re-establish the higher coordination of Se atoms and thereby eliminate the traps. An example of this strategy can be found in the literature, as in the work by Anderson et al.,8 and more recently by Gao et al.40 that used Cd-formate (a Z-type ligand) to eliminate the traps and attain a PLQY close to 100% for core-only CdSe QDs; the latter study may imply that dicoordinated Se at the QD surface are the most relevant source of traps for CdSe and may result from the eventual intrinsic lability of Z-type ligands already after the synthetic stage or during purification.
We are also currently performing further analysis on PbS and CsPbI3 QDs to verify the possibility of finding a correlation between the number of Z-type ligands displaced and the occurrence of surface traps, which could provide a hint on the defect tolerance of these materials and its relationship with the intrinsically larger PLQYs of as-synthesized PbS and CsPbI3 QDs compared to CdSe QDs.
Surface Trap States in Charge-Unbalanced, Doped QDs. Doping the QDs (Ndop ≠ 0) is probably the most common source of midgap states for any type of semiconductor material achievable via air-oxidation and impurities in the reaction flasks; it is also the most studied theoretically by DFT and tight-binding methods.27,41−45 Doping of QDs can be related to the band energy position of intrinsic QDs, eventually close to reducing and oxidizing agents. This is immediately evident in Figure 2, in which, for example, the CB of the calculated PbS QD model is much lower in energy than in CdSe and CsPbI3 QDs. As-synthesized PbS QDs commonly show one oleate ligand per excess Pb atom, which is expected in the 2+ oxidation state;12,14 albeit the presence of hydroxide species at the QD surface has been qualitatively demonstrated,14,46 charge neutrality may result also from reduced Pb atoms (i.e., in the 1+ or, the more likely, 0 oxidation state) with concomitant n-doping of the QDs; this scenario, however, seems improbable for as-synthesized PbS QDs, as demonstrated by their rather high PLQYs (the higher the smaller the QDs, up to about 60%).47 Upon solid-phase ligand exchange with iodide, PbS QDs were found to be Pb-rich, beyond the expected 1:2 ratio for Pbexcess:I,28 suggesting n-doping in iodide-capped PbS QDs. Our calculations show the high electron affinity of PbS QDs, thus they are amenable to undergo reduction processes. However, n-doping of PbS does not directly imply the formation of trap (localized) states as also pointed out by Voznyy et al.,23 which suggested that the formation of traps in n-doped QDs depends on the magnitude of doping, with three to four electrons needed to form under-coordinated Pb atoms undergoing dimerization at the QD surface.
In Figure 4, we sketched this process highlighting the formation of a high energy state, filled with two electrons, after removing two iodine atoms (Ndop = −2). This state lies near the CB, shifting significantly the position of the Fermi level. Despite this, the state is still significantly delocalized and not a trap yet. Only when two more iodine ligands are displaced do under-coordinated Pb surface atoms dimerize (i.e., form Pb–Pb bonds), generating a localized state, as evidenced in the orbital diagram shown in Figure 4. This may be regarded as a possible reason for the size-dependent PLQY of PbS QDs, in which larger [111] facets of larger QDs are more prone to Pb–Pb dimerization than in smaller QDs. The open circuit voltage deficit in PbS QD-based photovoltaics48 may also be partly related to the formation of Pb–Pb dimers during solid-state ligand exchange with iodide and thiolate ligands, promoted by their (photoinduced) oxidation to molecular iodine and disulfides, respectively.
Figure 4.
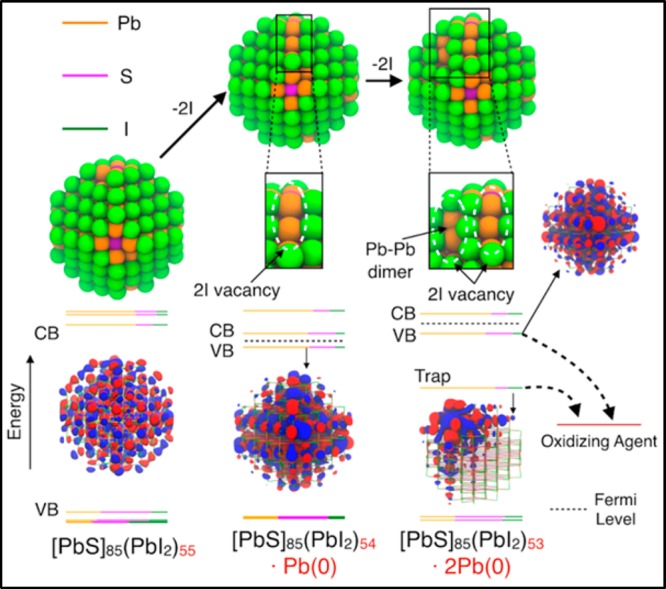
Relaxed structures of a PbS QD (∼2.6 nm) optimized at the DFT/PBE level of theory upon displacement of two (center) and four (right) iodine atoms.
The outcomes shown above provide some hints on how these trap states can be eliminated: oxidizing agents, such O2 and I2 or viologen and quinones, could favor the re-establishment of intrinsic PbS QDs, as shown schematically in Figure 4. The treatment of PbS QD solids with benzoquinone has been already shown to be successful by Hwang et al.28 In addition, a recent work by Lan et al.,49 shows the use of gaseous iodine to increase the power conversion efficiencies of PbS QD-based solar cells. The authors attribute the improvement to the following redox reaction: PbS + I2 → PbI2 + S; however, we suggest another mechanism taking place at the QD surface, in which I2 oxidizes the QD surface traps, leading to two I– species as ligands, thus breaking Pb–Pb dimers and re-establishing an intrinsically charge-balanced QD system. Air-annealing of lead chalcogenide QD solids has been also used to improve QD-based device performances, but usually leads to uncontrollable oxidation processes also involving the chalcogenide atoms.50−52
The CB levels of CdSe and CsPbI3 QDs are much higher in energy than in PbS QDs, implying less favored reduction (Figure 2). On the other hand, the rather high VB energy compared to vacuum of CsPbI3 QDs suggests that they may actually be prone to oxidation. We thus studied the effect of removing reduced Pb atoms from the QD surface, which could be favored, for example, by the oleylamine present in the reaction flask53 (unreacted precursor removal in CsPbX3 QD synthesis indeed seems to be not quantitative). Analogously to PbS QDs, oxidation of metal halide perovskites does not directly imply the formation of traps as supported by the high PLQYs of QDs (the lower the PLQYs, the more electronegative the halide atom in the QDs, up to about 90%).15,54,55 Indeed, oxidized QDs upon displacement of one metallic Pb atom (Ndop = 2) would present a shift of the Fermi level, although near the VB edge and still delocalized (Figure 5), whereas further oxidation (Ndop = 4) leads to localized states near the Fermi level (Figure 5), related to the formation of I–I dimers. The halide-dependent PLQY of AMX3 nanocrystals may thus be partly related to the different electronegativity of halide atoms and their propensity to form X–X dimers. A way of healing traps in perovskite QDs could consequently rely on the use of reducing agents like (decamethyl-)ferrocene and cobaltocene or tetrathiafulvalene.
Figure 5.
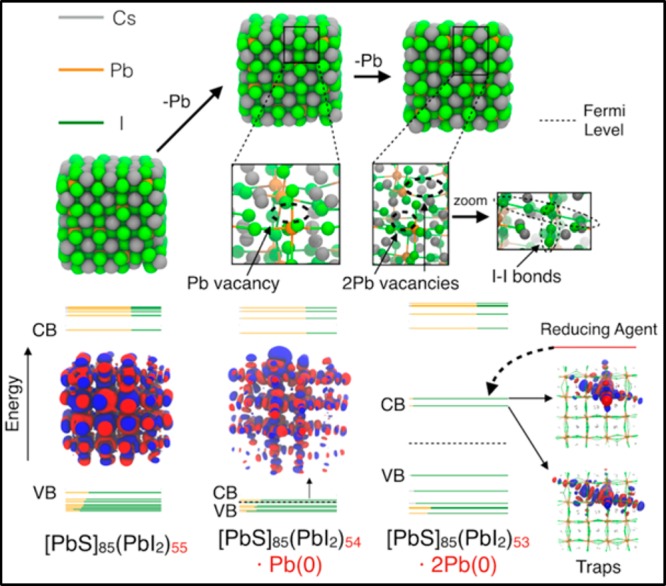
Relaxed structures of a CsPbI3 QD (∼2.6 nm) optimized at the DFT/PBE level of theory upon displacement of one (center) and two (right) Pb atoms.
Discussion. Based on the outcomes of the previous sections, we demonstrated that experiments suggest reliable theoretical models, and theory provides descriptions and explanations that can be experimentally verified, reinforcing each other and contributing to the development of this promising research field toward effective QD-based optoelectronic devices.
Below we summarize some of the most relevant conclusions on the origin of traps on different types of colloidal QDs.
For II–VI semiconductors with zinc-blende crystal structure, the main source of traps is likely related to dicoordinated chalcogenide atoms at the QD surface, which is promoted by the displacement of metal complexes (as Z-type ligands). The energetic positions of the CB and VB edges in these systems disfavor doping. This means that for these systems, elimination of traps can in principle be attained by quantitatively coordinating the QD surface with Lewis acids.
IV–VI semiconductors are more defect-tolerant and partial displacement of Z-type ligands does not markedly affect the electronic structure mainly because surface atoms in a rock-salt configuration have enough high coordination to be always delocalized inside the CB and VB. On the other hand, these materials are prone to n-type doping due to their high electron affinity. To eliminate the traps, IV–VI QDs could be exposed to oxidizing agent, like molecular halogens, benzoquinone, and similar.
Metal halide perovskite nanocrystals of the ABX3 type seem to have the most favorable conditions to avoid traps from the outset as inferred by their high PLQYs. The cubic/orthorhombic structure seems to indicate that partial Z-type displacement does not lead to the formation of dangling bonds. However, the rather low ionization potential makes, in principle, perovskite CsPbI3 QDs prone to oxidation, which could be controlled by exogenous reducing agents, such as ferrocene and similar. This cannot, however, explain the rather low PLQY of CsPbCl3 QDs, which could be expected to instead show rather high electron affinity due to the presence of electronegative chloride atoms.
For III–V semiconductors, not directly discussed here, we expect that both type of traps could affect these systems. The zinc-blende crystalline structure favors the formation of dangling bonds at the QD surface, whereas energy levels closer to vacuum might suggest that these materials could be easily oxidized. Elimination of traps would thus require addition of both a Lewis acid and a reducing agent.
Acknowledgments
I.I. would like to thank The Netherlands Organization of Scientific Research (NWO) for providing financial support within the Innovational Research Incentive (Vidi) Scheme (Grant No. 723.013.002). This work was carried out on the Dutch national e-infrastructure with the support of SURF Cooperative. C.G. thanks the “Future In Research” program by Regione Puglia (‘Sol-Urbis’, code: ZCZP7C3). We acknowledge Simon Böhme for carefully reading the manuscript.
Biographies
Carlo Giansante, born and raised in Pescara (IT), studied chemistry at the Università di Bologna (IT) where, in 2008, he earned his doctoral degree dealing with discrete supramolecular systems and their photophysical and electrochemical properties in the group coordinated by Prof. Vincenzo Balzani. During this period, he spent six months at the University of California at Santa Barbara (US) working on nonlinear optical properties of conjugated polymers. He then stepped up the ladder of matter complexity at the Université de Bordeaux (FR) studying self-assembled organic nanostructures and their photophysics down to the single molecule level. He’s now a researcher at the Istituto di Nanotecnologia NANOTEC–CNR in Lecce (IT), where he has established his own research line on nanoscopic surfaces and interfaces using colloidal semiconductor nanocystals as soluble frameworks, with regard to optoelectronic and photonic applications.
Ivan Infante studied chemistry at the Universitá della Basilicata (IT). He then moved to the Vrije Universiteit in Amsterdam (NL) where he earned his Ph.D. in October 2006 under the supervision of Lucas Visscher and Evert Jan Baerends, with a thesis aimed at the spectroscopic characterization of actinide molecules using highly precise ab initio computational methodologies. After a two-year postdoc experience under the supervision of Laura Gagliardi at the University of Geneva (CH), he was bestowed a Juan de la Cierva grant and moved to the University of the Basque Country (ES) where he could pursue his independent research career. In May 2014, he was awarded a prestigious Vidi grant from The Netherlands organization for scientific research. This grant has enabled him to establish his own research group as an Assistant Professor at the Vrije Universiteit in Amsterdam (NL). His current research is in the field of colloidal semiconductor nanocrystals, with a special emphasis in characterizing trap states combining theoretical calculations and experiments through his many collaborations.
The authors declare no competing financial interest.
References
- Shirasaki Y.; Supran G. J.; Bawendi M. G.; Bulović V. Emergence of Colloidal Quantum-Dot Light-Emitting Technologies. Nat. Photonics 2012, 7, 13–23. 10.1038/nphoton.2012.328. [DOI] [Google Scholar]
- Kovalenko M. V.; Manna L.; Cabot A.; Hens Z.; Talapin D. V.; Kagan C. R.; Klimov V. I.; Rogach A. L.; Reiss P.; Milliron D. J.; et al. Prospects of Nanoscience with Nanocrystals. ACS Nano 2015, 9, 1012–1057. 10.1021/nn506223h. [DOI] [PubMed] [Google Scholar]
- Talapin D. V.; Lee J.-S.; Kovalenko M. V.; Shevchenko E. V. Prospects of Colloidal Nanocrystals for Electronic and Optoelectronic Applications. Chem. Rev. 2010, 110, 389–458. 10.1021/cr900137k. [DOI] [PubMed] [Google Scholar]
- Reiss P.; Protière M.; Li L. Core/Shell Semiconductor Nanocrystals. Small 2009, 5, 154–168. 10.1002/smll.200800841. [DOI] [PubMed] [Google Scholar]
- Chen O.; Zhao J.; Chauhan V. P.; Cui J.; Wong C.; Harris D. K.; Wei H.; Han H.-S.; Fukumura D.; Jain R. K.; et al. Compact High-Quality CdSe–CdS Core–shell Nanocrystals with Narrow Emission Linewidths and Suppressed Blinking. Nat. Mater. 2013, 12, 445–451. 10.1038/nmat3539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nasilowski M.; Spinicelli P.; Patriarche G.; Dubertret B. Gradient CdSe/CdS Quantum Dots with Room Temperature Biexciton Unity Quantum Yield. Nano Lett. 2015, 15, 3953–3958. 10.1021/acs.nanolett.5b00838. [DOI] [PubMed] [Google Scholar]
- Owen J. The Coordination Chemistry of Nanocrystal Surfaces. Science (Washington, DC, U. S.) 2015, 347, 615–616. 10.1126/science.1259924. [DOI] [PubMed] [Google Scholar]
- Anderson N. C.; Hendricks M. P.; Choi J. J.; Owen J. S. Ligand Exchange and the Stoichiometry of Metal Chalcogenide Nanocrystals: Spectroscopic Observation of Facile Metal-Carboxylate Displacement and Binding. J. Am. Chem. Soc. 2013, 135, 18536–18548. 10.1021/ja4086758. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Roo J.; De Keukeleere K.; Hens Z.; Van Driessche I. From Ligands to Binding Motifs and Beyond; the Enhanced Versatility of Nanocrystal Surfaces. Dalt. Trans. 2016, 45, 13277–13283. 10.1039/C6DT02410F. [DOI] [PubMed] [Google Scholar]
- Boles M. A.; Ling D.; Hyeon T.; Talapin D. V. The Surface Science of Nanocrystals. Nat. Mater. 2016, 15, 141–153. 10.1038/nmat4526. [DOI] [PubMed] [Google Scholar]
- Jasieniak J.; Mulvaney P. From Cd-Rich to Se-Rich – The Manipulation of CdSe Nanocrystal Surface Stoichiometry. J. Am. Chem. Soc. 2007, 129, 2841–2848. 10.1021/ja066205a. [DOI] [PubMed] [Google Scholar]
- Moreels I.; Fritzinger B.; Martins J. C.; Hens Z. Surface Chemistry of Colloidal PbSe Nanocrystals. J. Am. Chem. Soc. 2008, 130, 15081–15086. 10.1021/ja803994m. [DOI] [PubMed] [Google Scholar]
- Choi H.; Ko J.-H.; Kim Y.-H.; Jeong S. Steric-Hindrance-Driven Shape Transition in PbS Quantum Dots: Understanding Size-Dependent Stability. J. Am. Chem. Soc. 2013, 135, 5278–5281. 10.1021/ja400948t. [DOI] [PubMed] [Google Scholar]
- Grisorio R.; Debellis D.; Suranna G. P.; Gigli G.; Giansante C. The Dynamic Organic/Inorganic Interface of Colloidal PbS Quantum Dots. Angew. Chem., Int. Ed. 2016, 55, 6628–6633. 10.1002/anie.201511174. [DOI] [PubMed] [Google Scholar]
- Protesescu L.; Yakunin S.; Bodnarchuk M. I.; Krieg F.; Caputo R.; Hendon C. H.; Yang R. X.; Walsh A.; Kovalenko M. V. Nanocrystals of Cesium Lead Halide Perovskites (CsPbX 3, X = Cl, Br, and I): Novel Optoelectronic Materials Showing Bright Emission with Wide Color Gamut. Nano Lett. 2015, 15, 3692–3696. 10.1021/nl5048779. [DOI] [PMC free article] [PubMed] [Google Scholar]
- De Roo J.; Ibáñez M.; Geiregat P.; Nedelcu G.; Walravens W.; Maes J.; Martins J. C.; Van Driessche I.; Kovalenko M. V.; Hens Z. Highly Dynamic Ligand Binding and Light Absorption Coefficient of Cesium Lead Bromide Perovskite Nanocrystals. ACS Nano 2016, 10, 2071–2081. 10.1021/acsnano.5b06295. [DOI] [PubMed] [Google Scholar]
- ten Brinck S.; Infante I. Surface Termination, Morphology, and Bright Photoluminescence of Cesium Lead Halide Perovskite Nanocrystals. ACS Energy Lett. 2016, 1, 1266–1272. 10.1021/acsenergylett.6b00595. [DOI] [Google Scholar]
- Voznyy O.; Zhitomirsky D.; Stadler P.; Ning Z.; Hoogland S.; Sargent E. H. A Charge-Orbital Balance Picture of Doping in Colloidal Quantum Dot Solids. ACS Nano 2012, 6, 8448–8455. 10.1021/nn303364d. [DOI] [PubMed] [Google Scholar]
- Kilina S. V.; Tamukong P. K.; Kilin D. S. Surface Chemistry of Semiconducting Quantum Dots: Theoretical Perspectives. Acc. Chem. Res. 2016, 49, 2127–2135. 10.1021/acs.accounts.6b00196. [DOI] [PubMed] [Google Scholar]
- Green M. L. H. A New Approach to the Formal Classification of Covalent Compounds of the Elements. J. Organomet. Chem. 1995, 500, 127–148. 10.1016/0022-328X(95)00508-N. [DOI] [Google Scholar]
- Houtepen A. J.; Hens Z.; Owen J. S.; Infante I. On the Origin of Surface Traps in Colloidal II–VI Semiconductor Nanocrystals. Chem. Mater. 2017, 29, 752–761. 10.1021/acs.chemmater.6b04648. [DOI] [Google Scholar]
- Voznyy O.; Thon S. M.; Ip A. H.; Sargent E. H. Dynamic Trap Formation and Elimination in Colloidal Quantum Dots. J. Phys. Chem. Lett. 2013, 4, 987–992. 10.1021/jz400125r. [DOI] [PubMed] [Google Scholar]
- Boehme S. C.; Azpiroz J. M.; Aulin Y. V.; Grozema F. C.; Vanmaekelbergh D.; Siebbeles L. D. A.; Infante I.; Houtepen A. J. Density of Trap States and Auger-Mediated Electron Trapping in CdTe Quantum-Dot Solids. Nano Lett. 2015, 15, 3056–3066. 10.1021/acs.nanolett.5b00050. [DOI] [PubMed] [Google Scholar]
- Giansante C.; Infante I.; Fabiano E.; Grisorio R.; Suranna G. P.; Gigli G. Darker-than-Black” PbS Quantum Dots: Enhancing Optical Absorption of Colloidal Semiconductor Nanocrystals via Short Conjugated Ligands. J. Am. Chem. Soc. 2015, 137, 1875–1886. 10.1021/ja510739q. [DOI] [PubMed] [Google Scholar]
- Debellis D.; Gigli G.; ten Brinck S.; Infante I.; Giansante C. Quantum-Confined and Enhanced Optical Absorption of Colloidal PbS Quantum Dots at Wavelengths with Expected Bulk Behavior. Nano Lett. 2017, 17, 1248–1254. 10.1021/acs.nanolett.6b05087. [DOI] [PubMed] [Google Scholar]
- Voznyy O.; Sargent E. H. Atomistic Model of Fluorescence Intermittency of Colloidal Quantum Dots. Phys. Rev. Lett. 2014, 112, 157401. 10.1103/PhysRevLett.112.157401. [DOI] [PubMed] [Google Scholar]
- Hwang G. W.; Kim D.; Cordero J. M.; Wilson M. W. B.; Chuang C.-H. M.; Grossman J. C.; Bawendi M. G. Identifying and Eliminating Emissive Sub-Bandgap States in Thin Films of PbS Nanocrystals. Adv. Mater. 2015, 27, 4481–4486. 10.1002/adma.201501156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walravens W.; De Roo J.; Drijvers E.; ten Brinck S.; Solano E.; Dendooven J.; Detavernier C.; Infante I.; Hens Z. Chemically Triggered Formation of Two-Dimensional Epitaxial Quantum Dot Superlattices. ACS Nano 2016, 10, 6861–6870. 10.1021/acsnano.6b02562. [DOI] [PubMed] [Google Scholar]
- De Nolf K.; Cosseddu S. M.; Jasieniak J. J.; Drijvers E.; Martins J. C.; Infante I.; Hens Z. Binding and Packing in Two-Component Colloidal Quantum Dot Ligand Shells: Linear versus Branched Carboxylates. J. Am. Chem. Soc. 2017, 139, 3456–3464. 10.1021/jacs.6b11328. [DOI] [PubMed] [Google Scholar]
- Parr R. G.; Yang W.. Density-Functional Theory of Atoms and Molecules; Oxford University Press: Oxford, 1989. [Google Scholar]
- Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- VandeVondele J.; Hutter J. Gaussian Basis Sets for Accurate Calculations on Molecular Systems in Gas and Condensed Phases. J. Chem. Phys. 2007, 127, 114105. 10.1063/1.2770708. [DOI] [PubMed] [Google Scholar]
- Hutter J.; Iannuzzi M.; Schiffmann F.; Vandevondele J. Cp2k: Atomistic Simulations of Condensed Matter Systems. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2014, 4, 15–25. 10.1002/wcms.1159. [DOI] [Google Scholar]
- Azpiroz J. M.; Ugalde J. M.; Infante I. Benchmark Assessment of Density Functional Methods on Group II–VI MX (M = Zn, Cd; X = S, Se, Te) Quantum Dots. J. Chem. Theory Comput. 2014, 10, 76–89. 10.1021/ct400513s. [DOI] [PubMed] [Google Scholar]
- Huang Z.; Li X.; Yip B. D.; Rubalcava J. M.; Bardeen C. J.; Tang M. L. Nanocrystal Size and Quantum Yield in the Upconversion of Green to Violet Light with CdSe and Anthracene Derivatives. Chem. Mater. 2015, 27, 7503–7507. 10.1021/acs.chemmater.5b03731. [DOI] [Google Scholar]
- Tamang S.; Lincheneau C.; Hermans Y.; Jeong S.; Reiss P. Chemistry of InP Nanocrystal Syntheses. Chem. Mater. 2016, 28, 2491–2506. 10.1021/acs.chemmater.5b05044. [DOI] [Google Scholar]
- Cossairt B. M. Shining Light on Indium Phosphide Quantum Dots: Understanding the Interplay among Precursor Conversion, Nucleation, and Growth. Chem. Mater. 2016, 28, 7181–7189. 10.1021/acs.chemmater.6b03408. [DOI] [Google Scholar]
- Gao Y.; Peng X. Photogenerated Excitons in Plain Core CdSe Nanocrystals with Unity Radiative Decay in Single Channel: The Effects of Surface and Ligands. J. Am. Chem. Soc. 2015, 137, 4230–4235. 10.1021/jacs.5b01314. [DOI] [PubMed] [Google Scholar]
- Zherebetskyy D.; Zhang Y.; Salmeron M.; Wang L.-W. Tolerance of Intrinsic Defects in PbS Quantum Dots. J. Phys. Chem. Lett. 2015, 6, 4711–4716. 10.1021/acs.jpclett.5b02202. [DOI] [PubMed] [Google Scholar]
- Califano M.; Gómez-Campos F. M. Universal Trapping Mechanism in Semiconductor Nanocrystals. Nano Lett. 2013, 13, 2047–2052. 10.1021/nl4003014. [DOI] [PubMed] [Google Scholar]
- Wei H. H.-Y.; Evans C. M.; Swartz B. D.; Neukirch A. J.; Young J.; Prezhdo O. V.; Krauss T. D. Colloidal Semiconductor Quantum Dots with Tunable Surface Composition. Nano Lett. 2012, 12, 4465–4471. 10.1021/nl3012962. [DOI] [PubMed] [Google Scholar]
- Wang L.-W.; Califano M.; Zunger A.; Franceschetti A. Pseudopotential Theory of Auger Processes in CdSe Quantum Dots. Phys. Rev. Lett. 2003, 91, 56404. 10.1103/PhysRevLett.91.056404. [DOI] [PubMed] [Google Scholar]
- Kim D.; Kim D.-H.; Lee J.-H.; Grossman J. C. Impact of Stoichiometry on the Electronic Structure of PbS Quantum Dots. Phys. Rev. Lett. 2013, 110, 196802. 10.1103/PhysRevLett.110.196802. [DOI] [PubMed] [Google Scholar]
- Zherebetskyy D.; Scheele M.; Zhang Y.; Bronstein N.; Thompson C.; Britt D.; Salmeron M.; Alivisatos P.; Wang L.-W. Hydroxylation of the Surface of PbS Nanocrystals Passivated with Oleic Acid. Science 2014, 344, 1380–1384. 10.1126/science.1252727. [DOI] [PubMed] [Google Scholar]
- Semonin O. E.; Johnson J. C.; Luther J. M.; Midgett A. G.; Nozik A. J.; Beard M. C. Absolute Photoluminescence Quantum Yields of IR-26 Dye, PbS, and PbSe Quantum Dots. J. Phys. Chem. Lett. 2010, 1, 2445–2450. 10.1021/jz100830r. [DOI] [Google Scholar]
- Chuang C. H. M.; Maurano A.; Brandt R. E.; Hwang G. W.; Jean J.; Buonassisi T.; Bulovic V.; Bawendi M. G. Open-Circuit Voltage Deficit, Radiative Sub-Bandgap States, and Prospects in Quantum Dot Solar Cells. Nano Lett. 2015, 15, 3286–3294. 10.1021/acs.nanolett.5b00513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lan X.; Voznyy O.; Kiani A.; García de Arquer F. P.; Abbas A. S.; Kim G.-H.; Liu M.; Yang Z.; Walters G.; Xu J.; et al. Passivation Using Molecular Halides Increases Quantum Dot Solar Cell Performance. Adv. Mater. 2016, 28, 299–304. 10.1002/adma.201503657. [DOI] [PubMed] [Google Scholar]
- Luther J. M.; Law M.; Song Q.; Perkins C. L.; Beard M. C.; Nozik A. J. Structural, Optical, and Electrical Properties of Self-Assembled Films of PbSe Nanocrystals Treated with 1,2-Ethanedithiol. ACS Nano 2008, 2, 271–280. 10.1021/nn7003348. [DOI] [PubMed] [Google Scholar]
- Choi M.-J.; Oh J.; Yoo J.-K.; Choi J.; Sim D. M.; Jung Y. S. Tailoring of the PbS/metal Interface in Colloidal Quantum Dot Solar Cells for Improvements of Performance and Air Stability. Energy Environ. Sci. 2014, 7, 3052. 10.1039/C4EE00502C. [DOI] [Google Scholar]
- Stadelmann K.; Elizabeth A.; Martín Sabanés N.; Domke K. F. The SERS Signature of PbS Quantum Dot Oxidation. Vib. Spectrosc. 2017, 91, 157–162. 10.1016/j.vibspec.2016.08.008. [DOI] [Google Scholar]
- Mourdikoudis S.; Liz-Marzán L. M. Oleylamine in Nanoparticle Synthesis. Chem. Mater. 2013, 25, 1465–1476. 10.1021/cm4000476. [DOI] [Google Scholar]
- Koscher B. A.; Swabeck J. K.; Bronstein N. D.; Alivisatos A. P. Essentially Trap-Free CsPbBr 3 Colloidal Nanocrystals by Postsynthetic Thiocyanate Surface Treatment. J. Am. Chem. Soc. 2017, 139, 6566–6569. 10.1021/jacs.7b02817. [DOI] [PubMed] [Google Scholar]
- Tong Y.; Bladt E.; Aygüler M. F.; Manzi A.; Milowska K. Z.; Hintermayr V. A.; Docampo P.; Bals S.; Urban A. S.; Polavarapu L.; et al. Highly Luminescent Cesium Lead Halide Perovskite Nanocrystals with Tunable Composition and Thickness by Ultrasonication. Angew. Chem., Int. Ed. 2016, 55, 13887–13892. 10.1002/anie.201605909. [DOI] [PubMed] [Google Scholar]


