Significance
Lithium superionic conductors with Li+ conductivity that is comparable with that of the organic liquid electrolytes are critical for the development of practically useful all-solid-state batteries. Here, we show that cluster-based lithium superionic conductors can have very high conductivities of 10−2 to over 10−1 S/cm at room temperature, low activation energy under 0.210 eV, a giant band gap of 8.5 eV, and desired mechanical properties that entail great flexibility and can inhibit the dendric growth of Li metal. The high Li+ conductivity of the materials results from the thermal excitation of quasirigid unit modes of the cluster ions and the exceptionally large channel size created by mixing large cluster ions together with the elementary ions.
Keywords: lithium superionic conductor, antiperovskite, cluster, quasirigid unit modes, all-solid-state battery
Abstract
Enjoying great safety, high power, and high energy densities, all-solid-state batteries play a key role in the next generation energy storage devices. However, their development is limited by the lack of solid electrolyte materials that can reach the practically useful conductivities of 10−2 S/cm at room temperature (RT). Here, by exploring a set of lithium-rich antiperovskites composed of cluster ions, we report a lithium superionic conductor, Li3SBF4, that has an estimated 3D RT conductivity of 10−2 S/cm, a low activation energy of 0.210 eV, a giant band gap of 8.5 eV, a small formation energy, a high melting point, and desired mechanical properties. A mixed phase of the material, Li3S(BF4)0.5Cl0.5, with the same simple crystal structure exhibits an RT conductivity as high as 10−1 S/cm and a low activation energy of 0.176 eV. The high ionic conductivity of the crystals is enabled by the thermal-excited vibrational modes of the cluster ions and the large channel size created by mixing the large cluster ion with the small elementary ion.
From cell phone to artificial heart and from electric vehicle to satellites, batteries have become an indispensable technology in our modern society. Compared with the current batteries with liquid electrolytes, batteries with solid electrolytes hold the promise of greater safety, higher power, and higher energy densities. However, development of the all-solid-state batteries is limited by the relatively low conductivity of the solid electrolyte materials. Most families of the superionic conductors have an activation energy in the range of 0.3–0.6 eV and exhibit ionic conductivities of the order of 10−4–10−3 S/cm at room temperature (RT) (1–8). However, a typical organic liquid electrolyte (9) or a gel electrolyte (10) in practical batteries has an RT conductivity around 10−2 S/cm. Attaining an Li+ conductivity over 10−3 S/cm in the solid state is particularly challenging (1), and it is highly desirable to develop superionic conductors that exhibit 3D RT Li+ conductivities over 10−2 S/cm and activation energies smaller than 0.25 eV. Very few lithium solid electrolytes can reach an RT conductivity of 10−2 S/cm. These include Li7P3S11 (1.7 × 10−2 S/cm), with an activation energy of 0.18 eV (11, 12), and the LGPS materials [i.e., Li3.25Ge0.25P0.75S4 (2.2 × 10−3 S/cm) (13) and Li10GeP2S12 (1.2 × 10−2 S/cm) (14)], with activation energies of 0.22–0.25 eV (14, 15). In addition, Li7P3S11 has issues of chemical stability (16), while the LGPS materials only show a 1D conduction pathway (along the c-axis) and contain expensive Germanium, making these materials not ideal for practical applications (17, 18). In 2016, a chlorine-doped system, Li9.54Si1.74P1.44S11.7Cl0.3, with the LGPS crystal structure was discovered, which has an activation energy similar to that of LGPS and sets the record of RT Li+ conductivity to 2.5 × 10−2 S/cm for a crystalline system (18).
Most recently, Braga et al. (19–22) have synthesized A3−2 × 0.005Ba0.005OCl (A = Li or Na) glass based on the antiperovskite Li3OCl and showed that it is an advanced superionic conductor with RT conductivity >10−2 S/cm and activation energy as low as 0.06 eV. The mechanism for the glass to have such a low activation energy is quite different from the conduction mechanism of crystalline systems. The extremely low activation energy is accompanied by large dielectric constant of the material (22). Because of the amorphous state of the glass, there exist some dipole-rich clusters [e.g., AO− and A2O (A = Li or Na)] that can rotate and coalesce (22). These clusters may even condense to form negative chain segments, which would significantly reduce the bonding and the activation energy of A+ inside the material (22). We studied a Ba-doped crystalline model of antiperovskite Li3OCl and found that Ba doping will reduce the melting point of the crystal and introduce strain inside the material. This, in turn, would significantly reduce the Li+ activation energy (23), resulting in an estimated RT conductivity >10−2 S/cm according to the Arrhenius model (SI Methods). More details of this study are given in SI Methods and Fig. S1.
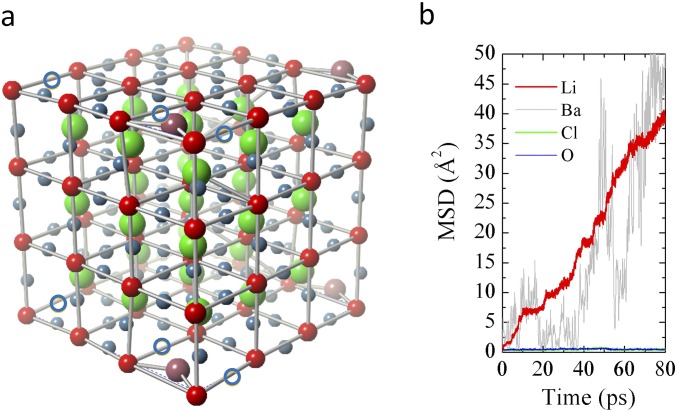
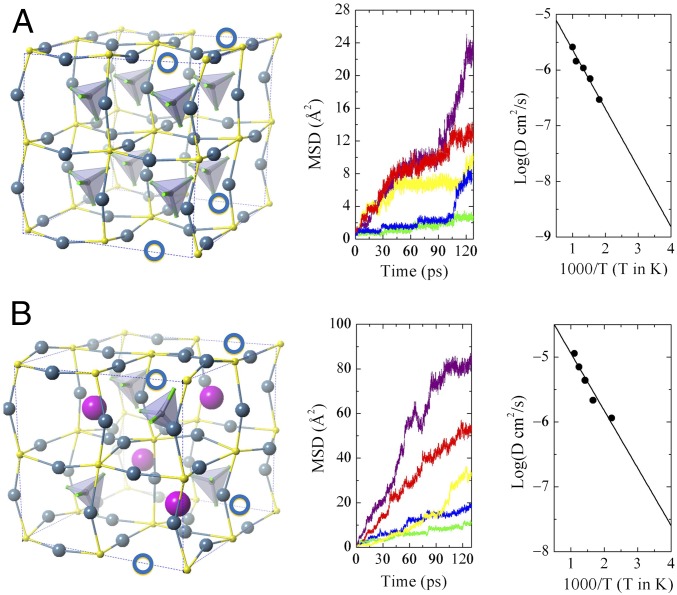
Fig. S1.
(A) Optimized 3 × 3 × 3 supercell of Li3OCl with one intrinsic Li+ defect and one Li substituted by one Ba. The two Li vacancies are indicated by blue open circles. Li is in blue, O is in red, Cl is in green, and Ba is in purple. (B) MSDs of various atoms calculated from the AIMD simulation (SI Methods) at 1,900 K.
Here, by exploring a set of lithium-rich antiperovskites (LRAPs) composed of cluster ions (Li3O+/Li3S+ and BH4−/AlH4−/BF4−), we report crystalline materials that have estimated RT conductivity of 10−2 S/cm and activation energies around 0.2 eV. We coin the term “super-LRAP” for these materials, because they are composed of the cluster cations and cluster anions, which are known as superalkalis and superhalogens, respectively. The superalkalis have ionization potentials (IPs) smaller than those of alkali elements, and the superhalogens have vertical detachment energy (VDE) larger than that of halogen elements. We show that a lithium superionic conductor Li3SBF4 with a simple crystal structure has an estimated RT conductivity of 10−2 S/cm and an activation energy of 0.210 eV. The material also exhibits a giant band gap around 8.5 eV, a high melting point over 600 K, a small formation energy less than 40 meV per atom, and favorable mechanical properties. By partially replacing the superhalogen ion BF4− with chlorine, the mixed phase material, Li3S(BF4)0.5Cl0.5, shows a stellar conductivity over 10−1 S/cm at RT and an activation energy as low as 0.176 eV.
The discovery of the super-LRAP is guided by the recently synthesized LRAP Li3OA (A = halogen). As solid electrolytes, these conductors exhibit improved properties from A = I to Cl, with Li3OCl showing the highest Li+ conductivity at RT (0.85 × 10−3 S/cm), the lowest activation energy of 0.303 eV, and the largest band gap of about 5 eV among the series (24–27). In the halogen group, Cl provides the optimal radius ratio against oxygen and lithium. Consequently, the stabilized antiperovskite structure of Li3OCl possesses the largest channel size, defined as the available space for Li+ to migrate, among the group elements. These results are shown in Table 1. The valence band maximum (VBM) of Li3OA (A = halogen) corresponds to the valence orbital of the halogen. Among all of the halogen elements, chlorine has the highest VDE—defined as the energy needed to remove an electron from Cl−. This suggests that the valence orbital of chlorine and hence, the VBM of Li3OCl are at the lowest energy in the group, causing Li3OCl to have the largest band gap. Based on these arguments, if some “super” halogens having higher VDE than that of chlorine could exist beyond the limitation of periodic table, the antiperovskites stabilized by these super halogens should have larger band gaps than that of Li3OCl. Since the band gap provides an upper limit of the electrochemical stability window (ESW) (17), larger band gap is preferred for a solid electrolyte. Moreover, by finding a super halogen with the right ionic radius, larger channel size and higher ionic conductivity compared with Li3OCl may also be achieved.
Table 1.
Key information about the cluster ions in the super-LRAP family
| Cluster | VDE (BI), eV | BL (cluster), Å | BL (crystal), Å | R, Å | CS, Å3 per unit cell | LP, Å | t |
| AlH4− | 4.46 (0.73) | 1.64 | 1.67 | 2.66 | 56.27 | 4.73 | 1.03 |
| BH4− | 4.44 (0.56) | 1.24 | 1.22 | 2.03 | 42.74 | 4.00 | 1.04 |
| BF4− | 7.42 (3.69) | 1.44 | 1.42 | 2.43 | 62.48 | 4.72 | 1.10 |
| Cl− | 3.71 (−0.17) | — | — | 1.67 | 31.89 | 3.91* | 1.19 |
| Br− | 3.58 (−0.30) | — | — | 1.82 | 31.33 | 4.02* | 1.12 |
In each case, the channel size (CS) is calculated using the volume of the unit cell minus the volumes of all of the ions inside. The used ionic radii (R) of Li, O, S, B, Al, H, and F are 0.90, 1.26, 1.70, 0.41, 0.68, 0.81, and 1.01 Å, respectively. The volume of a superhalogen ion is defined as the volume of the cube enclosing the superhalogen tetrahedron. The value in the parentheses is the calculated bonding ionicity (BI) measured by the value of the VDE of the superhalogen ions AlH4−/BH4−/BF4− minus the IP of the superalkali ions Li3O+/Li3S+ (3.88/3.72 eV) in (Li3S)(AlH4), (Li3O)(BH4), (Li3S)(BF4), (Li3O)Cl, and (Li3O)Br. (Li3S)(BF4) has the largest bonding ionicity of all; t is the calculated Goldschmidt's tolerance factor. BL is the bond length inside the superhalogens. LP is the calculated lattice parameter of the corresponding crystal.
Experimental values from ref. 25.
In fact, cluster ions that show higher VDE than chlorine are called superhalogens and have already been known (28). It was suggested by Gutsev and Boldyrev (29) nearly 35 years ago that one could create a cluster of atoms by varying its composition and size, such that its VDE is higher than that of any halogen atom. The authors also showed that clusters called superalkalis could be similarly created with IPs that are lower than those of alkali atoms (30). Later, Khanna and Jena (31) showed that, in general, it is possible to design clusters to mimic the chemistry of elements in the periodic table, and they coined the term “superatoms” for these clusters. Thus, superhalogens and superalkalis belong to a subgroup of superatoms. The superhalogen ion BH4− with four hydrogen atoms tetrahedrally bonded to one boron is a good example. We note that, experimentally, BH4− has been used to synthesize new metal salts, Na3BH4B12H12 and (Li0.7Na0.3)3BH4B12H12, which exhibit superionic conductivities of the order of 10−4 S/cm at RT (32). BH4− has also been used in recent experiments to create more than 30 new hydride-based perovskites by replacing halogens (33). In addition, new organic–inorganic hybrid perovskites for solar cell and photoluminescent applications have been designed by replacing halogens with BH4− (34–36). Most recently, we have initiated the study of using BH4− to make new LRAPs (37). Given that BH4− has a very similar ionic radius as Br− (34), the superhalogen can indeed stabilize the antiperovskite structure to make Li3OBH4, which turns out to be a lithium superionic conductor with an RT conductivity similar to that of Li3OCl (37). The higher VDE of BH4− indeed produces a larger band gap of 7.0 eV in Li3OBH4 compared with that in Li3OCl.
Other superhalogen ions, like BH4−, include AlH4− and BF4−, which have different sizes and VDEs. One can define the ionic radius of a superhalogen ion as the sum of the bond length of M-Y (M = Al, B; Y = H, F) and the ionic radius of Y (Y = H, F). The bond lengths and the calculated ionic radii of the superhalogens are given in Table 1. Note that the ionic radii of both AlH4− and BF4− are significantly larger than that of BH4−. According to a simple geometric consideration, the Goldschmidt tolerance factor for the antiperovskite Li3OX is given as
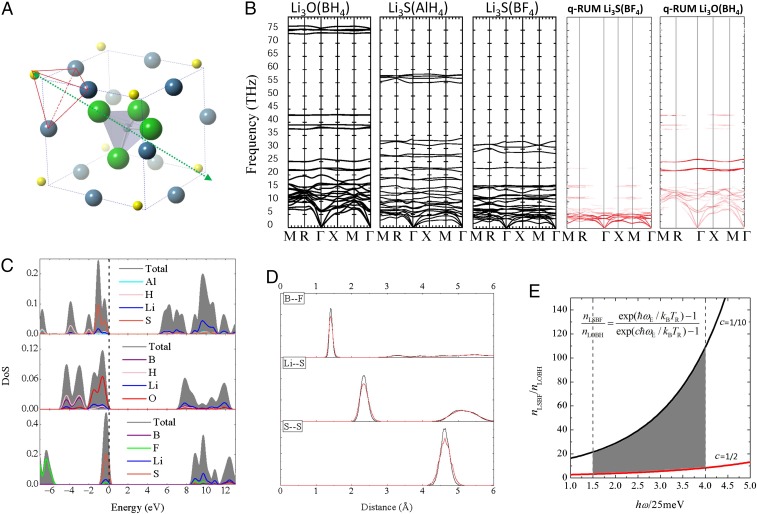
| [1] |
where rA is the ionic radius of oxygen, rB is the radius of X, and rC is the radius of lithium ion. To stabilize the antiperovskite structure with large superhalogen ions, such as X = AlH4− and BF4−, the oxygen atom should be replaced by a larger group element, such as sulfur. The resulting materials are Li3SAlH4 and Li3SBF4. As shown in Table 1, Li3SAlH4, Li3OBH4, and Li3SBF4 all have a tolerance factor around 1.0, with BF4− generating a tolerance factor closer to those of Li3OA (A = halogen). This suggests the high ability of BF4− to stabilize the structure. Indeed, studies of the phonon spectra (Fig. 1B) confirm that all of these materials are lattice-dynamically stable in the antiperovskite structure. The calculated formation energy of Li3SBF4 antiperovskite for the reaction LiBF4 + Li2S → Li3SBF4 is 39.4 meV per atom, which is significantly lower than 58.8 meV per atom of the antiperovskite Li3OBH4 (LiBH4 + Li2O → Li3OBH4) and is close to those of Li3OA (LiA + Li2O → Li3OA) of 13.9 and 25.8 meV per atom for A = Cl and Br, respectively (25).
Fig. 1.
(A) Optimized unit cell of Li3SBF4, with Li in blue, S in yellow, B in gray, and F in green. The green arrow indicates the C3v orientational symmetry adopted by the BF4− tetrahedral unit in the cubic cell. The red outline highlights the pyramidal configuration of Li3S+. (B) Calculated phonon spectra of the studied super-LRAP. The red-colored spectra of Li3SBF4 and Li3OBH4 show the positions of the q-RUMs in these materials. The modes with large distortion of superhalogen ions are colored in white. (C) HSE06 calculated (partial) DoS of the studied super-LRAP. The Fermi level is set to zero in each case. (D) Calculated radial distribution functions of Li3SBF4 using MD trajectory data over 100 ps at 400 and 600 K under ambient pressure. (E) Estimated range of ratio between the ionic conductivity of Li3SBF4 and that of Li3OBH4 at RT by using the energy of the q-RUMs of these materials in a simple Einstein model. nLSBF and nLOBH are the mean phonon occupation numbers at RT TR of Li3SBF4 and Li3OBH4, respectively.
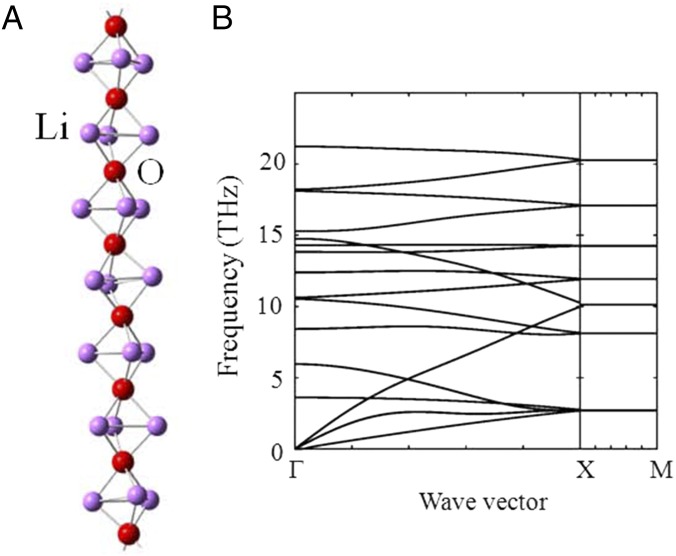
Interestingly, the cluster Li3S, like Li3O, is a superalkali, as its IP is lower than that of lithium (34). Isolated Li3S+/Li3O+ has a planar configuration (as shown in Fig. S2). However, when they interact with each other, they flip like an umbrella, adopting a pyramidal configuration, as shown by the molecular dynamics (MD) simulation in Fig. S3. The pyramidal configuration is like the one in the antiperovskite crystal, highlighted by the red edges in Fig. 1A. This is caused by the attraction (repulsion) between the three positive lithium atoms (the lone pair on oxygen/sulfur) of one Li3S+/Li3O+ and the lone pair on oxygen/sulfur of its neighboring Li3S+/Li3O+. To show further the strong interaction between lithium and oxygen in these clusters, we considered a 1D chain of Li3O. As shown in Fig. S4, the periodic nanowire is lattice-dynamically stable. The eigenvector of the highest mode (∼22 THz) at Γ point corresponds to spring-like compression and elongation of the nanowire, as shown by the cartoon movie in Movie S1 (Gamma22THz). The attraction (repulsion) of the neighboring oxygen–lithium (oxygen) is clearly visible from this vibrational mode. The tendency of lithium and oxygen to form clusters and chains inside the antiperovskite can also be seen in the melting state of the material. As shown in Fig. S5, lithium and oxygen atoms in the amorphous state will form chain segments composed by LiO−, Li2O, and Li3O+ clusters. The result is consistent with the finding by Goodenough and coworkers (22) that, in A3−2 × 0.005Ba0.005OCl (A = Li or Na) glass, dipole-rich clusters and chain segments are formed by Na (or Li) and oxygen, which introduce a large dielectric constant of the amorphous material. Thus, one may also view the antiperovskites (Li3S/O)+X− (X = AlH4, BH4, BF4) as ionic crystals of alkali halides (e.g., CsCl). This analogy suggests that the larger the VDE of the superhalogen X, the larger the band gap of (Li3S/O)+X−. Recall that the band gap of alkali halides is determined by the bonding ionicity, which can be measured by the value of the VDE of (super)halogen minus the IP of (super)alkali (34).
Fig. S2.
The planar configurations of the superalkalis Li3O+ and Li3S+ in the gas phase. Lithium is in violet, oxygen is in red, and sulfur is in yellow.
Fig. S3.
MD simulation at 300 K for the superalkalis inside a perovskite framework of AGeI3 (A = the superalkali). The planar configuration of the superalkali will become a pyramidal configuration because of the interaction between the neighbors.
Fig. S4.
(A) Periodic nanowire formed by Li3O clusters. (B) Calculated phonon spectrum of the Li3O nanowire.
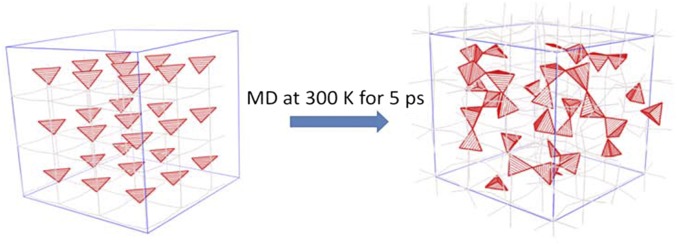
Fig. S5.

Melting state of the Ba-doped Li3OCl system at a simulation temperature of 2,000 K. The red polyhedra are clusters formed by Li and O. Ba and Cl atoms are removed for clarity.
As shown in Table 1, since BF4− has the largest VDE and hence, the largest bonding ionicity with Li3S+, (Li3S)(BF4) crystal is expected to have the largest band gap among the studied materials. Indeed, the electronic density of states (DoS) of Li3SBF4 in Fig. 1C, calculated using the HSE06 functional shows the largest band gap of 8.5 eV compared with the 5.0 eV of Li3SAlH4, 7.0 eV of Li3OBH4, and those of Li3OA (A = halogen). No known crystalline electrolyte with high Li+ conductivity exhibits such a large band gap. For example, the calculated band gap of Li10GeP2S12 is only 3.6 eV, and its observed ESW of 5 V is likely caused by some passivation phenomenon (17). The valence band of Li3SBF4 is contributed by sulfur and BF4−, and the conduction band has contributions from lithium and BF4−. This makes a good analogy to those of Li3OA, where the valence band is contributed by oxygen and halogen A = Cl/Br and the conduction band is contributed by lithium and Cl/Br (25).
Thermal stability of the super-LRAP, including Li3SAlH4, Li3OBH4, and Li3SBF4, is tested by MD simulations at constant temperature and pressure. The radial distribution functions are calculated using the MD trajectory data collected over 100 ps. As shown in Fig. 1D for Li3SBF4, no melting is observed up to 600 K. The calculated linear thermal expansion coefficient of Li3SBF4 from the MD data is 1.6 × 10−5/K, which is smaller than 3.0 × 10−5/K of Li3OBH4. The value is also smaller than 2.1 × 10−5/K and 1.8 × 10−5/K of Li3OA for A = Cl and Br, respectively. This should be considered as another advantage of Li3SBF4—smaller thermal expansion means higher compatibility with other parts inside a composite device, subject to large temperature fluctuations (38).
The magnitude of Li+ conductivity of the (super)-LRAP may be indicated by the channel size (i.e., the space available for Li+ to migrate inside the material). By considering the volume of the unit cell and the volume of the ions inside, we calculated the channel size for each material as shown in Table 1. Li3OCl has a larger channel size than Li3OBr, which is consistent with the experimentally observed higher Li+ conductivity of the former compared with the latter. Li3SBF4 provides a much larger channel size compared with the rest, which may be caused by the highly negative charge distributed on each F (−1.9e) of BF4− compared with the charge on each H (−0.8e) of AlH4− and on each H (−0.6e) of BH4−, making more room between sulfur and BF4− in the crystal to reduce the repulsion. In addition, the interaction between sulfur and Li+ is known to be significantly lower than that between oxygen and Li+ (17). All of these results suggest that Li3SBF4 should exhibit a much higher Li+ ion conductivity than the other materials.
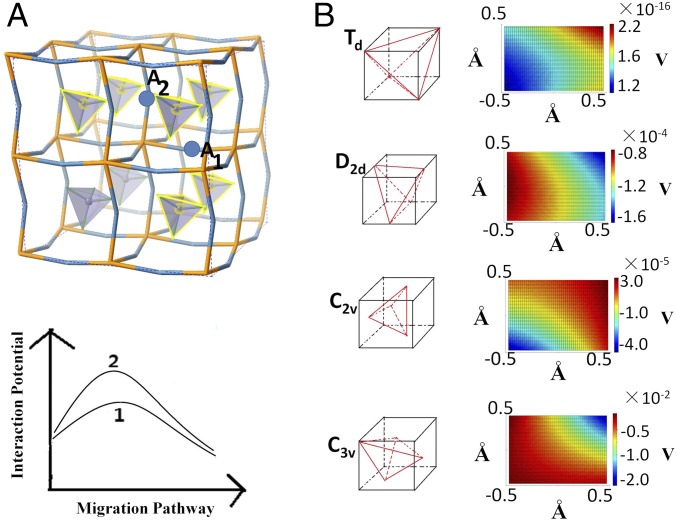
From the studies of Li3OA (A = halogen) (25) and Li3OBH4 (37), we understand that the Li+ conductivity in the super-LRAP is triggered by the Li+ vacancy defect and is correlated to the translational and rotational modes of the superhalogen ions. On thermal excitation, these modes can constantly change the orientations of the superhalogen tetrahedra from their C3v ground-state symmetry, as shown in Fig. 1A. This, in turn, generates a shifting and varying potential surface throughout the crystal, which can then facilitate fast ion migration of Li+ between different sites. For Li3SBF4, these are shown in a modeled system in Fig. 2A. Each Li+ ion is coordinated by four BF4− tetrahedral units. When the Li+ ion migrates from site A1 to A2, rotation of the BF4− units can generate a preferred potential profile along the pathway, as shown in Fig. 2A by comparing the potential curves 1 and 2. To quantify the relation between the motions of the four BF4− units and the potential surface created by them at the Li+ site, we calculated the dipole plus quadrupole terms of the potential according to different orientational symmetries of BF4− (SI Methods). As shown in Fig. 2B, the orientation with C3v symmetry generates the lowest potential of −10−2 V, while the other high-symmetry orientations generate practically zero dipole plus quadrupole terms. In each case, the varying magnitude of the potential surface in an area of 1.0 × 1.0 Å around the Li+ site shows the effect of the translational motions of the BF4− units.
Fig. 2.
(A) The model used to study the relation between the rotation of the BF4− units and the interaction potential felt by the Li+ ion as it migrates from A1 site to A2 site. The four coordinating BF4− units at each site are highlighted in yellow. Curve 1 and curve 2 show two possible potential profiles along the migration pathway created by the rotation of the BF4− units. (B) Calculated potential surfaces in an area of 1.0 × 1.0 Å around the Li+ site for different orientational symmetries of the BF4− tetrahedra. The C3v symmetry generates the lowest potential of the order of −10−2 V. Effect of the translational motions of the BF4− units on the potential surface is shown by the changing color.
The vibrational modes involving the translations and rotations of the superhalogen ion as a “rigid” body are more important, since any large distortion of the superhalogen itself will make the modes high in energy, making them less relevant to the conductive property at RT and medium temperatures. One way to pinpoint the important modes originating from motions of the superhalogen ion with zero or small distortion is to find out the so-called quasirigid unit modes (q-RUMs) by mapping the lattice-dynamic eigenvectors of a model system with the superhalogens as rigid bodies onto the real phonon eigenvectors of the material (39) (SI Methods). The vibrational modes are colored according to how much they look like a rigid unit mode. For example, a red color indicates that the superhalogen ions vibrate as completely rigid units, while a white color indicates large distortion inside the superhalogens. These are shown in the colored phonon spectra of Li3SBF4 and Li3OBH4 in Fig. 1B. It is found that all of the q-RUMs are in the range of 2.5–10 THz for Li3SBF4 and 5.0–25 THz for Li3OBH4. According to the conduction mechanism of super-LRAP discussed before, at certain temperature, as more of the q-RUMs (translational and rotational modes of the superhalogen units) are thermally excited, higher numbers of favorable potential profiles for Li+ to migrate will be present, and more Li+ will pass through per unit area per unit time. This will result in a higher diffusion coefficient given a certain gradient of the Li+ concentration. In other words, the Li+ conductivity at certain temperatures should be proportional to the diffusion coefficient and therefore, proportional to the number of excited q-RUMs at that temperature. In a simple Einstein model, the mean phonon occupation number at temperature T is
| [2] |
where is the Einstein frequency, which should serve as a characteristic frequency of the q-RUMs here. Thus, we can compute the ratio between the mean phonon occupation number of Li3SBF4 (LSBF) and that of Li3OBH4 (LOBH) at temperature T as
| [3] |
where the coefficient c is the ratio between the Einstein frequency of Li3SBF4 and that of Li3OBH4. Here, we do not know the exact value of the Einstein frequency . However, with knowledge of the energy range of the q-RUMs of Li3SBF4 (2.5–10 THz) vs. that of Li3OBH4 (10–25 THz), we can estimate a range of ratio r according to Eq. 3 by assuming a lower limit of the coefficient c = 2.5/25 = 1/10 and an upper limit of c = 2.5/5.0 = 1/2. The resulting range of r at RT (300 K ∼ 25 meV) for = 37–100 meV ( ∼ 9–25 THz) is shown by the shaded area in Fig. 1E. According to the previous discussions, r should measure the ratio between the Li+ conductivity of Li3SBF4 and that of Li3OBH4 at RT. Thus, as indicated by Fig. 1E, it is predicted that Li3SBF4 will exhibit a much higher RT conductivity—from several (∼3) up to over 100 times higher than those of Li3OBH4 and Li3OCl [since Li3OBH4 shows a similar ionic conductivity with Li3OCl (37)].
Both the calculated channel size and the study of q-RUMs of the materials suggest that Li3SBF4 should have a much higher ionic conductivity compared with the others. To provide a quantitative estimate of the conductivity of Li3SBF4, we carry out MD simulations at 550, 650, 750, 900, and 1,000 K over 130 ps using a supercell with one Li+ vacancy shown in Fig. 3A (SI Methods). The mean square displacement (MSD) of Li+ ions is calculated from the MD trajectory data. The Li+ diffusion coefficient (D) at each temperature is obtained by a linear fit to the MSD. The Arrhenius model is then used to fit to the values of D at different temperatures to obtain the conductivity at RT and the activation energy. These are shown in Fig. 3A. Compared with the calculated activation energy of 0.303 eV and the RT conductivity 0.12 × 10−3 S/cm of Li3OCl with the same theoretical method, the calculated activation energy of Li3SBF4 is 0.210 eV, and its RT conductivity is 0.14 × 10−2 S/cm—about 12 times higher, which falls well within our predicted range in Fig. 1E. It is known that the absolute value of the calculated conductivity will be significantly underestimated by the theoretical method here because of the fixed volume in the MD simulations (25). However, such method can reproduce the correct activation energy and the right ratio between the conductivities of materials (25). Given that the experimentally observed RT conductivity of Li3OCl is 0.85 × 10−3 S/cm (24, 25), it is expected that Li3SBF4 can reach an RT conductivity of 1.0 × 10−2 S/cm (12 times of 0.85 × 10−3 S/cm)—a value the same as that of the organic liquid electrolyte used in practical batteries (9). This 3D superionic conductivity is shown in Movie S2, a movie made from the MD data (at 550 K). The low activation energy (0.210 eV) of Li3SBF4 enables very high ionic conductivities at low temperatures, which is considered to be an advantage of solid electrolytes over the liquid ones (14, 18). At −30 °C (∼243 K), for example, the conductivity of Li3SBF4 is still about 1.7 times the RT conductivity of Li3OCl, suggesting a value over 10−3 S/cm. This allows batteries to still operate at very low temperatures (14). At high temperatures, below the melting point (for instance, 500 K), the ionic conductivity of Li3SBF4 is expected to be well above 10−1 S/cm.
Fig. 3.
(A) The MD simulations to study the Li+ ion superionic conductivity of Li3SBF4. A 2 × 2 × 2 supercell with one Li+ vacancy is used, where Li is in blue, S in yellow, B in gray, and F in green. The MSD and the diffusion coefficients are calculated at 550 (green), 650 (blue), 750 (yellow), 900 (red), and 1,000 K (purple) (SI Methods). (B) The MD simulations to study the Li+ ion superionic conductivity of Li3S(BF4)0.5Cl0.5. A 2 × 2 × 2 supercell with one Li+ vacancy is used, where Li is in blue, S in yellow, B in gray, F in green, and Cl in magenta. The MSD and the diffusion coefficients are calculated at 450 (green), 600 (blue), 700 (yellow), 800 (red) and 900 K (purple).
It is expected that, by partially replacing BF4− with Cl− inside Li3SBF4 to make Li3S(BF4)1−xClx (0 < x < 1), the Li+ superionic conductivity may be further increased. The reason is that, by putting the elementary halogen and the large superhalogen together in the same structure, the lattice will maintain a large size to accommodate the superhalogen (BF4−), resulting in large redundant space around the halogen (Cl−) site. This will provide Li+ with unusually large space to migrate in the halogen-containing cells, while keeping the original conductivity for the cells containing the superhalogens.
Indeed, in our study of Li3S(BF4)0.5Cl0.5, as shown in Fig. 3B, the optimized volume of the mixed phase is only 5% smaller than that of the pure Li3SBF4 system. The calculated channel size of the former is 69.07 Å3 per unit cell, which is significantly higher than that of Li3SBF4 (62.48 Å3 per unit cell) and much larger than that of Li3OCl (31.89 Å3 per unit cell). We further calculated the Li+ conductivity of Li3S(BF4)0.5Cl0.5 using MD simulations at 450, 600, 700, 800, and 900 K. The results are shown in Fig. 3B. The calculated RT conductivity is 1.9 × 10−2 S/cm, which is already higher than the conductivity of the organic liquid electrolytes (10). Considering that the value is about 14 times higher than the calculated value of Li3SBF4, it is expected that the real RT conductivity of Li3S(BF4)0.5Cl0.5 could be well above 10−1 S/cm—a value that is more than 10 times higher than that of the organic liquid electrolytes. The material also has an extremely low activation energy of 0.176 eV, which leads to a calculated conductivity of 0.38 × 10−2 S/cm at −30 °C—about 19 times higher than that of Li3SBF4 (0.20 × 10−3 S/cm). This suggests that the real conductivity of the material should be well above 10−2 S/cm at such a low temperature.
Mechanical properties of a superionic conductor are important in making flexible all-solid-state batteries. One can extract the elastic tensors of Li3SBF4 from the acoustic branches of its phonon spectrum in Fig. 1B (SI Methods). Other elastic constants of the material can be further computed using the elastic tensors (SI Methods). These values are given in Table 2. There is a threshold for the shear modulus, above which the dendric growth of an Li metal anode can be inhibited by a solid electrolyte. This threshold is four times the shear modulus of the Li metal (40), which is about 35 GPa. The shear modulus of Li3SBF4 is 46 GPa, which is well above the threshold. Typical flexible materials often have both small Young’s modulus and Poisson’s ratio. The Young’s modulus of Li3SBF4 is 142 GPa—between the values of copper (125 GPa) and mild steel (210 GPa). The Poisson’s ratio of the material υ = 0.1 is between those of carbon fiber (0.045) and aluminum (0.34). All of these results suggest that the superionic conductor Li3SBF4 has the desired mechanical properties for flexible electronics.
Table 2.
Calculated elastic tensors and constants (in gigapascals) as well as Poisson’s ratio of Li3SBF4 from the acoustic branches (SI Methods)
| Elastic tensor | Tensor value | Elastic constant | Constant value |
| c11 | 138 | Poisson’s ratio (υ) | 0.1 |
| c12 | 17 | Young’s modulus (E) | 142 |
| c44 | 46 | Shear modulus (μ) | 46 |
In summary, by exploring a set of LRAPs composed of cluster ions (i.e., superalkalis and superhalogens) called super-LRAPs, we find that lithium superionic conductors Li3SBF4 and Li3S(BF4)0.5Cl0.5 have the potential for ideal solid electrolytes. Li3SBF4 exhibits a band gap of 8.5 eV, an RT conductivity of 10−2 S/cm, an activation energy of 0.210 eV, a relatively small formation energy, and desired mechanical properties. Its mixed phase with halogen, Li3S(BF4)0.5Cl0.5, exhibits an RT conductivity over 10−1 S/cm and an activation energy of 0.176 eV. The high melting point over 600 K and the low activation energy allow these materials to operate over a wide range of temperatures from below −30 °C with conductivity above 10−3 S/cm to over 300 °C with conductivity well above 10−1 S/cm. The superior properties of the materials are achieved because of the following reasons. (i) Cluster ions, called superhalogens, having higher VDE than that of chlorine can produce larger band gaps of the super-LRAP than Li3OCl. (ii) With proper ionic radius and proper internal charge distribution, a cluster ion can stabilize the antiperovskite structure with large channel size, which provides more space for Li+ to migrate. (iii) A large channel size also produces a set of low-energy phonon modes called q-RUMs, which correspond to the translational and rotational motions of the superhalogens acting more like rigid bodies. These motions generate a constantly shifting and varying potential surface throughout the material, which then facilitates the fast ion migration of Li+ ions from one site to another. (iv) Partial replacement of the large superhalogen with halogen inside the antiperovskite structure creates large redundant space around the halogen sites. This enables an unusually large channel size of the material and further improves the ionic conductivity of a super-LRAP.
SI Methods
Cluster Calculations of VDE and IP.
The calculations are carried out using the GAUSSIAN 03 package (41). The hybrid density functional theory (DFT) with Becke three-parameter Lee–Yang–Parr (42, 43) prescription for the exchange–correlation energy and 6–31+G(d,p) basis sets are used. The optimized ground states correspond to the structures with the minimum energy and without any imaginary frequency.
Geometry Optimization.
DFT calculations are carried out to optimize the unit cell of the super-LRAP using Perdew–Burke–Ernzerh generalized gradient approximation for exchange–correlation functional (44) implemented in the VASP package (45). The projector augmented wave (46) pseudopotential method and an 8 × 8 × 8 Monkhorst-Pack k-point mesh are used in the calculation. The cutoff energy is 550 eV. The energy convergence is set to 10−6 eV, and the force convergence is set to 0.005 eV/Å. The van der Waals interaction [as implemented in the DFT + D2 method (47, 48)] is considered during the optimization calculations.
Internal Charge Distribution of the Clusters.
Bader charge analysis is used to obtain charge distribution of the clusters in the studied crystals.
Lattice Dynamics.
The phonon dispersion relations of the super-LRAP are calculated using the density functional perturbation theory with the van der Waals interaction. Geometry of the unit cell is optimized with an energy convergence of 10−8 eV and force convergence of 10−4 eV/Å. Phonon frequencies are first calculated on a q grid of 5 × 5 × 5. Frequencies for other q points are then interpolated from the calculated points.
q-RUMs of the Super-LRAP.
The q-RUMs of the studied materials are found by mapping the phonon eigenvectors of a model system containing rigid superhalogen ions to the eigenvectors of the studied system. The model system is created and calculated using an improved version of CRUSH code (49–51).
Potential Terms Created by BF4−.
The interaction potential created by each of the BF4− units on the Li+ ion can be expressed by a multipole expansion:
| [S1] |
where q = −e is the total charge of the BF4− superhalogen ion, and is the vector from boron at the center of one BF4− unit to the Li+ ion; is the dipole moment generated by the charge distribution inside one BF4− unit:
| [S2] |
where = −0.25e is the charge on each F atom in the model (Fig. 2A), represents the coordinates of each F atom, and is the relative coordinate of each F atom from the boron center. is the quadrupole term:
| [S3] |
where is the charge on each F atom, and is the ith coordinate of the kth F atom. In Eq. S1, both the dipole and the quadrupole terms are determined by the orientational symmetry of the BF4− unit inside the cubic cell.
Thermodynamics and Superionic Conductivity.
Ab initio molecular dynamics (AIMD) simulations are conducted using a 3 × 3 × 3 supercell and 1.0-fs time step in a constant pressure and constant temperature (NpT) ensemble to study the thermodynamics of the material at 400 and 600 K. To study the Li+ transport, AIMD simulations with 2.0-ps time step and constant volume and constant temperature (NVT) ensemble are carried out at 550, 650, 750, 900, and 1,000 K using a 2 × 2 × 2 supercell with one Li+ vacancy to speed up the ion hopping process (17, 25). At each temperature, the AIMD lasts over 130 ps after a 40-ps preequilibrium run to make the linear fitting to the averaged MSD of Li+ converge. The diffusion coefficient (D) at each temperature is calculated by fitting to the MSD according to
| [S4] |
with as the displacement of Li+ at time t. The conductivity () is then calculated from the Nernst–Einstein relation
| [S5] |
with N being the number of ion pairs per 1 cm3. Other symbols have their customary meaning. The activation energy Ea is obtained by using the Arrhenius model:
| [S6] |
where A is the fitting parameter.
Elastic Constants.
Instead of using the strain–stress method (48) and the equation of state (52, 53) to calculate the elastic tensors and the modulus, we take advantage of the cubic symmetry of Li3SBF4 and calculate the elastic tensors of the material by using the following relations (54). The subscripts of ω denote the directions of motion of the atoms.
| Direction 1 | Direction 2 | Direction 3 |
The Young’s modulus (E), shear modulus (μ), and the Poisson’s ratio (υ) are then calculated as
| [S7] |
| [S8] |
| [S9] |
Model Study of a Barium-Doped Li3OCl Crystal.
Using AIMD simulations combined with experimental measurements, Goodenough and coworkers (22) reported that the advanced superionic conductivity (with RT σ > 10−2 S/cm and activation energy Ea = 0.06 eV) of the A3−2 × 0.005Ba0.005OCl (A = Li or Na) glass is accompanied by large dielectric constant of the material. The mechanism that they proposed is that, because of the amorphous state of the glass, there exist some dipole-rich clusters, such as AO− and A2O, which can rotate and coalesce because of dipole–dipole interactions. These dipole-rich clusters may even condense to form negative chain segments when they are aligned. These will significantly reduce the bonding of A+, leading to the activation energy of 0.06 eV. Thus, the amorphous glass system is different from the crystalline systems of Li3OCl and Li3SBF4 studied here. Although the AIMD approach that we used in this work to obtain the activation energy and the ion transport mechanism have been proved to be suitable for the crystalline systems as evidenced in the literature (17, 25, 55, 56), such a method will not be applicable to the A3−2 × 0.005Ba0.005OCl (A = Li or Na) glass system. To obtain the activation energy and extrapolate the RT conductivity, the Arrhenius model has to be valid for the entire temperature range. With AIMD, one can only obtain apparent ion diffusion within affordable simulating timescale at relatively high simulation temperatures, and the Arrhenius model must hold at these high temperatures. For the Li3−2 × 0.005Ba0.005OCl glass, however, the glass transition temperature is only about 75 °C (375 K) (20), and the behavior becomes non-Arrhenius beyond this temperature, because the glass becomes liquid or rubber alike. Attaining a reliable activation energy by fitting the Arrhenius model to the diffusion coefficients from AIMD around RT will be prohibitively expensive and beyond our computational power. Therefore, to study the superionic conductivity of the glass by using the Arrhenius model, we adopt the following strategy. We use a 3 × 3 × 3 supercell of Li3OCl with one intrinsic Li+ defect and one Li substituted by one Ba. Because of the “2+” valence state of Ba, an additional Li vacancy is created in the supercell. We carry out AIMD on the supercell at one high simulation temperature (1,900 K) without melting the system. The 3 × 3 × 3 supercell is the largest that we can use in such a simulation according to our computational power. The doping concentration of Ba in such a supercell is still much higher than that of Li3−2 × 0.005Ba0.005OCl (<0.2% Ba vs. Li). Therefore, such a model system will emphasize the effects of Ba doping and Li vacancy on the ion conductivity. Fig. S1 shows the MSD of various atoms from the simulation. One can see that the system is not melting, since Cl and O have almost zero MSD. The apparent Li+ diffusion is accompanied by large Ba2+ movements (as indicated by the large MSD of the atom).
It has been reported that tensile strain can greatly increase the ion conductivity of Li3OCl because of linear reduction of the migration barrier with the strain (23). According to the Arrhenius model, the conductivity ratio between the strained (σs) Li3OCl and the unstrained (σ0) one is
| [S10] |
where ΔEa ∼ 3.3 × ε (electronvolts) is the reduction of the activation energy of Li+ caused by the tensile strain ε (percentage) in the lattice (23). We found that the doped Ba will introduce strain in the Li3OCl lattice, especially when Ba moves through the lattice as shown by MSD in Fig. S1B. We found that the average strain in the lattice parameter caused by Ba is about 2.5% (0.025), which corresponds to a reduction of the activation energy by ΔEa ∼ 3.3 × 0.025 ∼ 0.08 eV. Given that the original activation energy of Li3OCl is about 0.3 eV (25), the activation energy of the Ba doped system will be (0.3 − 0.08) = 0.22 eV. With the diffusion coefficient extracted from the MSD in Fig. S1B, the Li+ RT conductivity of the Ba-doped system can be calculated by the Arrhenius model to be about 1.7 × 10−3 S/cm. This value is about 14 time higher than the calculated RT conductivity (0.12 × 10−3 S/cm) of Li3OCl (25). Given that the real RT conductivity of Li3OCl is about 0.85 × 10−3 S/cm, the real estimated RT conductivity of the Ba-doped system should be >10−2 S/cm (14 × 0.85 × 10−3 = 1.9 × 10−2 S/cm). We want to emphasize that, to use the Arrhenius model, the current Ba-doped model system does not include the effect of amorphization of atoms, where freely rotating clusters and chain segments are present (22). This is probably why the estimated activation energy 0.22 eV is still larger than the experimental 0.06 eV of the glass and the estimated RT conductivity is still smaller than the experimental 2.5 × 10−2 S/cm. There is also an overestimation of the strain caused by Ba in our modeled system, because the doping concentration of Ba in our supercell is larger than that of the real glass system. However, the presence of tensile strain in the glass is reasonable—other than the strain caused by the doped Ba, strain is likely to be produced when the glassy state is formed from liquid by cooling. The tensile strain would create more room in the glass, allowing the dipole-rich clusters to rotate and coalesce freely as well as align into chain segments according to external fields, which is consistent with the result of Goodenough and coworkers (22). We found that, with Ba doping, the model system is more likely to melt and become amorphous. Fig. S5 shows the melting state of the Ba-doped Li3OCl at a simulation temperature of 2,000 K when the pure Li3OCl will not start melting. We observe clusters, such as LiO− and Li2O, as well as chain segments in such state, which agrees with what was reported by Goodenough and coworkers (22) for the case of Na+.
Supplementary Material
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1704086114/-/DCSupplemental.
References
- 1.Wang Y, et al. Design principles for solid-state lithium superionic conductors. Nat Mater. 2015;14:1026–1031. doi: 10.1038/nmat4369. [DOI] [PubMed] [Google Scholar]
- 2.Bruce PG. The A-C conductivity of polycrystalline LISICON, Li2+2xZn1-nGeO4, and a model for intergranular constriction resistances. J Electrochem Soc. 1983;130:662–669. [Google Scholar]
- 3.Aono H. Ionic conductivity of solid electrolytes based on lithium titanium phosphate. J Electrochem Soc. 1990;137:1023–1027. [Google Scholar]
- 4.Inaguma Y, et al. High ionic conductivity in lithium lanthanum titanate. Solid State Commun. 1993;86:689–693. [Google Scholar]
- 5.Murugan R, Thangadurai V, Weppner W. Fast lithium ion conduction in garnet-type Li(7)La(3)Zr(2)O(12) Angew Chem Int Ed Engl. 2007;46:7778–7781. doi: 10.1002/anie.200701144. [DOI] [PubMed] [Google Scholar]
- 6.Yu X, Bates JB, Jellison GE, Hart FX. A stable thin-film lithium electrolyte: Lithium phosphorus oxynitride. J Electrochem Soc. 1997;144:524–532. [Google Scholar]
- 7.Goodenough JB, Hong HYP, Kafalas JA. Fast Na+-ion transport in skeleton structures. Mater Res Bull. 1976;11:203–220. [Google Scholar]
- 8.Mizuno F, Hayashi A, Tadanaga K, Tatsumisago M. New, highly ion-conductive crystals precipitated from Li2S-P2S5 glasses. Adv Mater. 2005;17:918–921. [Google Scholar]
- 9.Stallworth PE, et al. NMR, DSC and high pressure lectrical conductivity studies of liquid and hybrid electrolytes. J Power Sources. 1999;81:739–747. [Google Scholar]
- 10.Song JY, Wang YY, Wan CC. Conductivity study of porous plasticized polymer electrolytes based on poly(vinylidene fluoride)–A comparison with polypropylenen separators. J Electrochem Soc. 2000;147:3219–3225. [Google Scholar]
- 11.Yamane H, et al. Crystal structure of a superionic conductor, Li7P3S11. Solid State Ion. 2007;178:1163–1167. [Google Scholar]
- 12.Seino Y, Ota T, Takada K, Hayashi A, Tatsumisago M. A sulphide lithium super ion conductor is superior to liquid ion conductors for use in rechargeable batteries. Energy Environ Sci. 2014;7:627–631. [Google Scholar]
- 13.Kanno R, Murayama M. Lithium ionic conductor thio-LISICON: The Li2S-GeS2-P2S5 system. J Electrochem Soc. 2001;148:A742–A746. [Google Scholar]
- 14.Kamaya N, et al. A lithium superionic conductor. Nat Mater. 2011;10:682–686. doi: 10.1038/nmat3066. [DOI] [PubMed] [Google Scholar]
- 15.Kuhn A, Duppel V, Lotsch BV. Tetragonal Li10GeP2S12 and Li7GePS8 -exploring the Li ion dynamics in LGPS Li electrolytes. Energy Environ Sci. 2013;6:3548–3552. [Google Scholar]
- 16.Ohtomo T, et al. All-solid-state lithium secondary batteries using the 75Li2S•25P2S5 glass and the 70Li2S•30P2S5 glass-ceramic as solid electrolytes. J Power Sources. 2013;233:231–235. [Google Scholar]
- 17.Ong SP, et al. Phase stability, electrochemical stability and ionic conductivity of the Li10±1MP2X12 (M = Ge, Si, Sn, Al or P, and X = O, S or Se) family of superionic conductors. Energy Environ Sci. 2012;6:148–156. [Google Scholar]
- 18.Kato Y, et al. High-power all-solid-state batteries using sulfide superionic conductors. Nat Energy. 2016;1:16030. [Google Scholar]
- 19.Braga MH, Grundish NS, Murchison AJ, Goodenough JB. Alternative strategy for a safe rechargeable battery. Energy Environ Sci. 2017;10:331–336. [Google Scholar]
- 20.Braga MH, Ferreira JA, Stockhausen V, Oliveira JE, El-Azab A. Novel Li3ClO based glasses with superionic properties for lithium batteries. J Mater Chem A Mater Energy Sustain. 2014;2:5470–5480. [Google Scholar]
- 21.Braga MH, Murchison AJ, Ferreira JA, Singh P, Goodenough JB. Glass-amorphous alkali-ion solid electrolytes and their performance in symmetrical cells. Energy Environ Sci. 2016;9:948–954. [Google Scholar]
- 22.Braga MH, Ferreira JA, Murchison AJ, Goodenough JB. Electric dipole and ionic conductivity in a Na+ glass electrolyte. J Electrochem Soc. 2017;164:A207–A213. [Google Scholar]
- 23.Mouta R, Paschoal CWA. 2016. Boosting room-temperature Li+ conductivity via strain in solid electrolytes for lithium-ion batteries. arXiv:1603.04830v2[cond-mat.mtrl-sci]
- 24.Zhao Y, Daemen LL. Superionic conductivity in lithium-rich anti-perovskites. J Am Chem Soc. 2012;134:15042–15047. doi: 10.1021/ja305709z. [DOI] [PubMed] [Google Scholar]
- 25.Zhang Y, Zhao Y, Chen C. Ab initio study of the stabilities of and mechanism of superionic transport in lithium-rich antiperovskites. Phys Rev B. 2013;87:134303. [Google Scholar]
- 26.Emly A, Kioupakis E, Van der Ven A. Phase stability and transport mechanisms in antiperovskite Li3OCl and Li3OBr superionic conductors. Chem Mater. 2013;25:4663–4670. [Google Scholar]
- 27.Lü X, et al. Li-rich anti-perovskite Li3OCl films with enhanced ionic conductivity. Chem Commun (Camb) 2014;50:11520–11522. doi: 10.1039/c4cc05372a. [DOI] [PubMed] [Google Scholar]
- 28.Jena P. Beyond the periodic table of elements: The role of superatoms. J Phys Chem Lett. 2013;4:1432–1442. doi: 10.1021/jz400156t. [DOI] [PubMed] [Google Scholar]
- 29.Gutsev GL, Boldyrev AI. DVM-Xα calculations on the ionization potentials of MXk+1− complex anions and the electron affinities of MXk+1 “Superhalogens.”. Chem Phys Lett. 1981;56:277–283. [Google Scholar]
- 30.Gutsev GL, Boldyrev AI. DVM-Xa calculations on the electronic structure of “Superalkali” cations. Chem Phys Lett. 1982;92:262–266. [Google Scholar]
- 31.Khanna SN, Jena P. Atomic clusters: Building blocks for a class of solids. Phys Rev B Condens Matter. 1995;51:13705–13716. doi: 10.1103/physrevb.51.13705. [DOI] [PubMed] [Google Scholar]
- 32.Sadikin Y, Brighi M, Schouwink P, Cerny R. Superionic conduction of sodium and lithium in anion-mixed hydroborates Na3BH4B12H12 and (Li0.7Na0.3)3BH4B12H12. Adv Energy Mater. 2015;5:1501016. [Google Scholar]
- 33.Schouwink P, et al. Structure and properties of complex hydride perovskite materials. Nat Commun. 2014;5:5706. doi: 10.1038/ncomms6706. [DOI] [PubMed] [Google Scholar]
- 34.Fang H, Jena P. Super-ion inspired colorful hybrid perovskite solar cells. J Mater Chem A Mater Energy Sustain. 2016;4:4728–4737. [Google Scholar]
- 35.Fang H, Jena P. Molecular origin of properties of organic-inorganic hybrid perovskites: The big picture from small clusters. J Phys Chem Lett. 2016;7:1596–1603. doi: 10.1021/acs.jpclett.6b00435. [DOI] [PubMed] [Google Scholar]
- 36.Yao Q, Fang H, Deng K, Kan E, Jena P. Superhalogens as building blocks of two-dimensional organic-inorganic hybrid perovskites for optoelectronics applications. Nanoscale. 2016;8:17836–17842. doi: 10.1039/c6nr05573g. [DOI] [PubMed] [Google Scholar]
- 37.Fang H, Wang S, Liu J, Sun Q, Jena P. Superhalogen-based Li-ion superionic conductors. J Mater Chem A Mater Energy Sustain. 2017;5:13373–13381. [Google Scholar]
- 38.Dove MT, Fang H. Negative thermal expansion and associated anomalous physical properties: Review of the lattice dynamics theoretical foundation. Rep Prog Phys. 2016;79:066503. doi: 10.1088/0034-4885/79/6/066503. [DOI] [PubMed] [Google Scholar]
- 39.Fang H, Dove MT, Rimmer L, Misquitta A. Simulation study of pressure and temperature dependence of the negative thermal expansion in Zn(CN)2. Phys Rev B. 2013;88:104306. [Google Scholar]
- 40.Monroe C, Newman J. The impact of elastic deformation on deposition kinetics at lithium/polymer interfaces. J Electrochem Soc. 2005;152:A396–A404. [Google Scholar]
- 41.Frisch MJ. 2003. Gaussian03 (Gaussian, Inc., Wallingford, CT), Revision B. 03.
- 42.Becke A. Density-functional thermochemistry. III. The role of exact exchange. J Chem Phys. 1993;98:5648–5652. [Google Scholar]
- 43.Lee C, Yang W, Parr RG. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys Rev B Condens Matter. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 44.Perdew JP, Burke K, Ernzerhof M. Generalized gradient approximation made simple. Phys Rev Lett. 1996;77:3865–3868. doi: 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
- 45.Kresse G, Furthmueller J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. J Comput Mater Sci. 1996;6:15–50. doi: 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
- 46.Kresse G, Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B Condens Matter. 1996;54:11169–11186. doi: 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
- 47.Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J Comput Chem. 2006;27:1787–1799. doi: 10.1002/jcc.20495. [DOI] [PubMed] [Google Scholar]
- 48.Fang H, Dove MT, Refson K. Ag-Ag dispersive interaction and physical properties of Ag3Co(CN)6. Phys Rev B. 2014;90:054302. [Google Scholar]
- 49.Giddy AP, Dove MT, Pawley GS, Heine V. The determination of rigid unit modes as potential soft modes for displacive phase transitions in framework crystal structures. Acta Crystallogr A. 1993;49:697–703. [Google Scholar]
- 50.Hammonds KD, Dove MT, Giddy AP, Heine V. CRUSH: A FORTRAN program for the analysis of the rigid unit mode spectrum of a framework structure. Am Mineral. 1994;79:1207–1209. [Google Scholar]
- 51.Fang H, Dove MT. A phenomenological expression to describe the temperature dependence of pressure-induced softening in negative thermal expansion materials. J Phys Condens Matter. 2014;26:115402. doi: 10.1088/0953-8984/26/11/115402. [DOI] [PubMed] [Google Scholar]
- 52.Fang H, et al. High-pressure lattice dynamic and thermodynamic properties of Ir by first principle calculation. Physica B. 2010;405:732–737. [Google Scholar]
- 53.Fang H, et al. Plane-wave pseudopotential study for the structural stability of Hf: The role of spin-orbit interaction. Physica B. 2011;406:1744–1748. [Google Scholar]
- 54.Dove MT. Introduction to Lattice Dynamics. Cambridge Univ Press; Cambridge, UK: 1993. [Google Scholar]
- 55.Yang J, Tse JS. Li ion diffusion mechanisms in LiFePO4: An ab initio molecular dynamics study. J Phys Chem A. 2011;115:13045–13049. doi: 10.1021/jp205057d. [DOI] [PubMed] [Google Scholar]
- 56.Mo Y, Ong SP, Ceder G. First principles study of the Li10GeP2S12 lithium super ionic conductor material. Chem Mater. 2012;24:15–17. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.