Chemical substitutions in the selectivity filter of potassium channels do not rule out constricted-like conformations for C-type inactivation

Significance

After opening in response to a specific stimulus, some potassium channels undergo C-type inactivation. Crystal structures of KcsA have revealed that the selectivity filter constricts under conditions associated with C-type inactivation. Functional studies based on semisynthetic KcsA channels with either D-ala77 or amide-to-ester backbone substitutions provide important observations arguing against the constricted conformation of the selectivity filter as the molecular basis of C-type inactivation. In this study, molecular dynamics simulations based on atomic models of the KcsA channel are performed to clarify the impact of these chemical modifications on the conformation of the selectivity filter. The results support the notion that the constricted conformation of the selectivity filter, indeed, corresponds to the functional C-type inactivated state of the KcsA channel.

Abstract

In many K⁺ channels, prolonged activating stimuli lead to a time-dependent reduction in ion conduction, a phenomenon known as C-type inactivation. X-ray structures of the KcsA channel suggest that this inactivated state corresponds to a “constricted” conformation of the selectivity filter. However, the functional significance of the constricted conformation has become a matter of debate. Functional and structural studies based on chemically modified semisynthetic KcsA channels along the selectivity filter led to the conclusion that the constricted conformation does not correspond to the C-type inactivated state. The main results supporting this view include the observation that C-type inactivation is not suppressed by a substitution of D-alanine at Gly77, even though this modification is believed to lock the selectivity filter into its conductive conformation, whereas it is suppressed following amide-to-ester backbone substitutions at Gly77 and Tyr78, even though these structure-conserving modifications are not believed to prevent the selectivity filter from adopting the constricted conformation. However, several untested assumptions about the structural and functional impact of these chemical modifications underlie these arguments. To make progress, molecular dynamics simulations based on atomic models of the KcsA channel were performed. The computational results support the notion that the constricted conformation of the selectivity filter corresponds to the functional C-type inactivated state of the KcsA. Importantly, MD simulations reveal that the semisynthetic KcsA^D-ala77 channel can adopt an asymmetrical constricted-like nonconductive conformation and that the amide-to-ester backbone substitutions at Gly77 and Tyr78 perturb the hydrogen bonding involving the buried water molecules stabilizing the constricted conformation.

Introduction

Potassium channels regulate the selective flux of K⁺ ions across the cell membrane. Structures from X-ray crystallography of the bacterial K⁺ channel KcsA from Streptomyces lividians provided the first glimpse of their overall molecular architecture (1, 2). Four identical subunits with two transmembrane $\alpha$-helices (TM1 and TM2) separated by a long pore (p) loop come together around a common axis to form a tetrameric structure. On the extracellular side of the channel is the narrow selectivity filter constituted by the pore loop, which allows the permeation of K⁺ in single file while excluding other ion species such as Na⁺. On the intracellular side is the activation gate sensing external stimulus, formed by the TM2 inner helices of the pore domain. Allosterically coupled to the channel’s intracellular activation gate (3, 4), the filter remains in a conductive state for a period after activation, after which it transitions to a nonconductive state through a process called C-type inactivation (5, 6). A wide range of evidence attribute C-type inactivation to subtle conformational changes at the selectivity filter (3, 7–9).

Identifying the structural features associated with C-type inactivation in K⁺ channels is a very important goal, and in this regard, the bacterial KcsA channel has played a critical role. Although C-type inactivation has traditionally been associated with a functional behavior of voltage-gated channels such as Shaker (5, 6), all of the known functional markers of C-type inactivation are experimentally recapitulated by KcsA, providing a coherent view of the molecular determinants that affect inactivation (3, 8, 9). In addition, because the TTVGYGD canonical selectivity filter sequence is highly conserved, it is expected that the accessible conformational states of the selectivity filter—that is, conductive and inactivated—ought to be fairly similar throughout most of the K⁺ channel family. Multiple X-ray structures of the KcsA with the inner gate in the open state suggest that the inactivated state might correspond to a “constricted” conformation of the selectivity filter (3). This constricted filter is conformationally indistinguishable from the KcsA structure previously captured with a closed inner gate at low concentration of K⁺ ions (low-K⁺) (2).

Regardless of whether it is induced by low-K⁺ conditions or via a coupling with the activation gate, the KcsA selectivity filter adopts a constricted conformation characterized by a narrowing at the central glycine residue at position 77 along the selectivity filter. The cross-subunit distance between the C_α atoms of Gly77 is $8.1$ Å for the conductive conformation, which reduces to $5.5$ Å for the constricted conformation.

Because the pore is considerably narrower in the constricted conformation, it is reasonable to assume that this is a nonconductive state. More recently, it was shown that a small number of water molecules bound behind the filter of the KcsA channel are indispensable to stabilize the constricted conformation (10, 11).

Nevertheless, due to the scarcity of structural information, the conformation of the selectivity filter associated with C-type inactivation remains uncertain. Even in the KcsA channel, for which multiple crystallographic structures are available, the functional significance of the constricted conformation of the selectivity filter has recently become a matter of debate. One of the major evidences against the constricted conformation is the observation that C-type inactivation is not suppressed in a semisynthetic KcsA channel in which the filter’s central glycine residues at position 77 have been replaced by a D-alanine (12). Based on the assumption that the D-alanine side chain prohibits the constricted conformation and essentially locks the selectivity filter in a conductive state, it was concluded that “the constricted conformation of the selectivity filter is not the C-type inactivated state” (12). Additional evidence is that C-type inactivation is suppressed following amide-to-ester substitutions in the backbone of the selectivity filter at Gly77 and Tyr78 (13, 14). Based on the observation that the substitutions decrease ion binding at the site S2, a site that must be unoccupied in the constricted conformation, it was concluded that C-type inactivation must involve structural rearrangements elsewhere along the selectivity filter other than the 1K4D-like constriction near Gly77 (13, 14).

While these results represent an important contribution to the body of knowledge about the conformational plasticity and structural polymorphism of the selectivity filter of K⁺ channels, three key issues weaken the conclusion derived from them. First, the presence of a D-ala side chain at position 77 in KcsA is assumed to preclude any conformational transitions toward a nonconductive constricted-like state (12, 15). Second, the impact of backbone amide-to-ester substitutions on the protein–water hydrogen bonding, critical for the stability of constricted conformation (10, 11), is ignored (13, 14). Third, the allosteric coupling between the intracellular activation gate and the selectivity filter conformation is not taken into consideration, as the X-ray structures of semisynthetic KcsA channels were determined with a closed gate (13–16). In the absence of additional structural information from experiments, computational approaches offer a powerful avenue to test whether the assumptions regarding the conformations accessible to the semisynthetic KcsA channels are plausible. The goal of the present study is to use MD simulations to clarify the structural implications of the D-ala77 and backbone amide-to-ester substitutions and how they might impact the accessibility of constricted-like conformations associated with C-type inactivation in the KcsA channel.

Results

Substitution of Glycine 77 by a D-Alanine Does Not Lock the Filter in a Conductive Conformation.

A molecular dynamics (MD) simulation of the KcsA^D-ala77 channel with a constricted filter and open inner gate was carried out based on a model constructed by combining the information from the crystal structures 3F7V and 1K4D (trajectory 3 in SI Appendix, Table S1). The results are displayed in Fig. 1 and SI Appendix, Fig. S1. Over the course of the 1.2-$\mu$s trajectory, the selectivity filter relaxed to a partially constricted asymmetrical conformation, with the D-ala side chains occluding the permeation pathway (Fig. 1A). The filter gradually transitions away from the starting symmetrical conformation toward an asymmetrical conformation, where one pair of opposing filter subunits is spread apart to the width of a conductive filter (Fig. 1B), while the other pair is constricted (Fig. 1C). A top view of the asymmetrical conformation of the filter is illustrated in Fig. 1D. Water molecules remain bound to their three specific sites behind the pair of constricted filter units throughout the entire simulation, which may contribute to stabilize the asymmetrical conformation. Further analysis indicates that the asymmetrical conformation should be nonconductive. No permeation events are observed during the simulation, despite that only two opposing filter units are truly constricted in accord with 1K4D (SI Appendix, Fig. S1). Furthermore, the pore of this asymmetrical conformation is clearly too narrow to allow ion permeation (Fig. 1D). Only a particle with a diameter ≤ 0.9 Å can pass through the pore between the central D-ala residues. The presence of the D-ala narrows the pore because the side chain partially occludes the permeation pathway. The 2D potential of mean force (PMF) as a function of the two cross-subunit glycine C_α–C_α distances provides a way to quantitatively characterize the thermodynamic stability of the different conformations of the selectivity filter of the KcsA^D-ala77 channel with an open inner gate. The 2D-PMF is shown in Fig. 1E. The local minimum along the diagonal with cross-subunit distances around 8 Å corresponds to the symmetrical 1K4C-like conductive conformation of the selectivity filter, while the two off-diagonal minima with one cross-subunit distances around 5 and 7.5 Å correspond to the asymmetrical conformations (Fig. 1E). According to the 2D-PMF calculated with an inner gate in the open state, the nonconductive asymmetrical conformation of the selectivity filter is slightly more stable than the conductive conformation for the KcsA^D-ala77 channel. This is consistent with the trajectory of the KcsA^D-ala77 displayed in Fig. 1A, where the nonconductive asymmetrical constricted conformation of the filter first appears at about 300 ns and then persists for about 1 $\mu$s. Interestingly, the asymmetrical conformations of the filter observed with the KcsA^D-ala77 channel are also observed as local free energy minima in the 2D-PMF of the wild-type KcsA channel (SI Appendix, Fig. S2).

Fig. 1.

KcsA^D-ala77 adapted an asymmetrically constricted conformation in MD simulation (trajectory 3 in SI Appendix, Table S1). (A) Time series of the cross-subunit distance between the C_α atoms of Gly77 of diagonally opposed monomers A and C (Left) and B and D (Right). (B and C) Conformations of the selectivity filter with buried water molecules at the end of the simulation shown for each pair of subunits. The pair of subunits A and C is not constricted, as shown in B, whereas the other pair of subunits B and D is constricted (C). (D) Top view of a typical snapshot for the backbone of selectivity filter residues—that is, Val76, D-ala77, and Tyr78—and the side chains of D-ala77. The surface of D-ala77 is shown as wireframe. (E) 2D-PMF of the KcsA^D-ala77 channel reveals two local free-energy basins corresponding to asymmetrically constricted conformations. The horizontal and vertical reaction coordinates, respectively, represent the cross-subunit distance between the C_α atoms of Gly77 of diagonally opposed monomers A and C, and B and D.

Hydrogen Bonds with Buried Water Stabilize the Constricted Selectivity Filter.

MD simulations of the modified KcsA channels with backbone amide-to-ester backbone substitutions at Val76, Gly77, and Tyr78 were carried out. All of the MD simulations were started from channels with an open inner gate and the selectivity filter in a constricted conformation (trajectories 6 to 8 in SI Appendix, Table S1). Fig. 2 shows the variations in the average number of water molecules behind the filter and their mean turnover time for all of the modified KcsA channels with amide-to-ester backbone substitution at Val76, Gly77, and Tyr78 (times series are shown in SI Appendix, Fig. S3). Results from MD simulations of the wild-type KcsA channel are also included to provide a comparison (trajectory 5 in SI Appendix, Table S1). There is a clear correlation between the average number of water molecules and the mean turnover time from these simulations, with the depth of C-type inactivation ($I_f/I_o$) observed in functional experiments (14). Furthermore, the trend observed in Fig. 2 is consistent with the hydrogen bonding properties of the inactivating water molecule observed in the wild-type KcsA channel (Table 1). Accordingly, a high probability of hydrogen bonding for the constricted conformation relative to that of the conductive conformation in the wild-type KcsA correlates with the impact of amide-to-ester substitutions on C-type inactivation. For example, the position that is the most strongly affected by the amide-to-ester substitution is Gly77. In the wild-type channel, this position displays a high probability of hydrogen bonds with the buried water molecules for the constricted conformation (60%), whereas there are no hydrogen bonds for the conductive conformation. In this case, losing the ability to form the hydrogen bonds with water in G77ester strongly destabilizes the constricted conformation. This residue has the most water–backbone hydrogen bonding to lose by an amide-to-ester substitution. The computational results are consistent with the observation in functional assays that C-type inactivation is essentially suppressed for G77ester (13, 14). MD simulations of the G77ester channel display the smallest average number of water behind the filter and the shortest turnover time for these waters (Fig. 2). The amide-to-ester substitution has less impact at Gly79 because both the conductive and constricted conformation can form hydrogen bonds with the buried water molecules (Table 1). Finally, the substitution has essentially no impact at Val76 because neither the constricted nor the conductive conformation forms hydrogen bonds with the buried water molecules (Table 1).

Fig. 2.

Binding of inactivating water molecules behind the selectivity filter in wild-type and amide-to-ester substituted KcsA. (A) The linear correlation between I_f/I_o from the experiment and the average number of water molecules (Upper), and mean turnover time of each inactivating water binding (Lower) from simulations that started from the structure with a constricted filter (trajectories 5 to 8 in SI Appendix, Table. S1). I_f/I_o is the fraction of the current remaining at the end of the inactivation pulse divided by the peak current from the previous report (14). The number of inactivating water molecules is measured behind the selectivity filter within each subunit. Each subunit is treated as an individual sample for calculating the mean (SD) and weighted linear regression as shown in the plot. (B) Typical snapshot from each simulation for constricted wild-type and amide-to-ester substituted KcsA to show H bonds formed between buried water and backbone of the selectivity filter.

Table 1.

Ester substitutions and hydrogen bonding

		MD simulations based on wild-type KcsAb
Residue	Experiments based on semisynthetic KcsA-estera If/Io	$P_{\text{conductive}}$	$P_{\text{constricted}}$
Gly79	0.19 ± 0.07	45.3 ± 3.5	89.1 ± 1.4
Tyr78	0.64 ± 0.09	0.1 ± 0.1	4.7 ± 0.8
Gly77	0.80 ± 0.15	0	60.2 ± 0.6
Vla76	0.26 ± 0.12	0	0

^aI_f/I_o is the fraction of the current remaining at the end of the inactivation pulse divided by the peak current determined from the experiments (14). KcsA constructs also contain the S69A, V70C, and Y82C substitutions required for semisynthesis and are to be compared with the corresponding control value of 0.17 ± 0.10 obtained for wild-type KcsA (also containing the same substitutions).

^bP_conductive and P_constricted are the fraction of time a hydrogen bond between water and a specific backbone amide group is observed when the selectivity filter is in the conductive or constricted conformation, respectively. The uncertainty was evaluated by comparing the average from each of the four subunits of the channel. Data are taken from trajectories 1 to 2 in SI Appendix, Table S1.

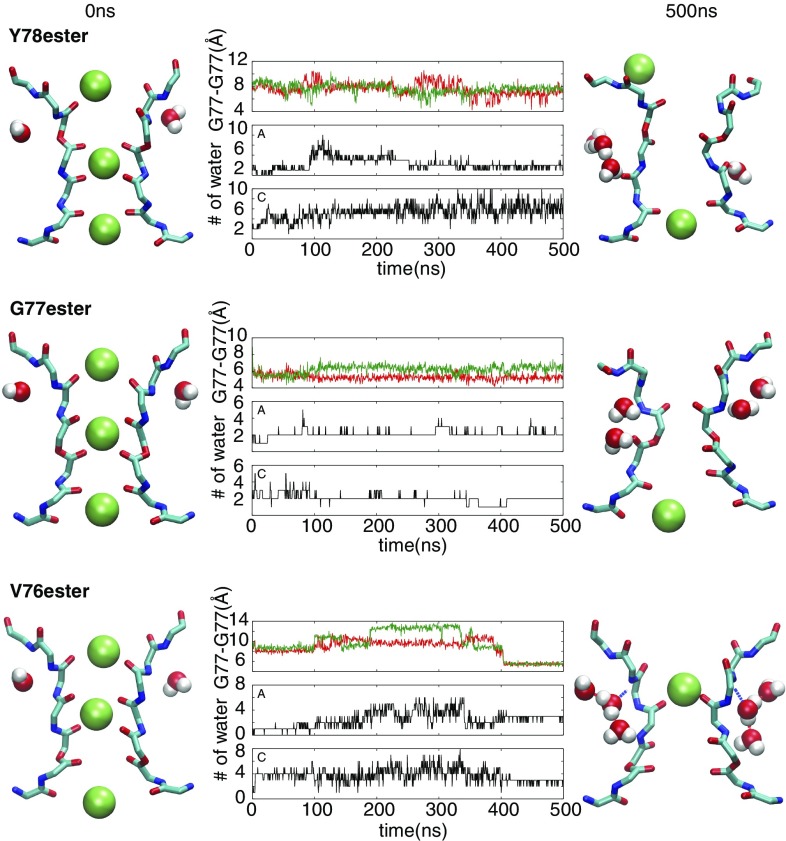
To provide a more complete perspective, the modified KcsA channels were also simulated starting with an open inner gate and the selectivity filter in a conductive conformation (trajectories 10 to 12 in SI Appendix, Table S1). The results from these MD simulations are shown in Fig. 3. The main observation is that the selectivity filter of the V76ester channel undergoes a spontaneous transition (around 400 ns) from the conductive to the constricted conformation. This conformation is stabilized by the binding of three water molecules per subunit, as previously observed with the wild-type channel (10, 11). In contrast, the G77ester and Y78ester channels do not undergo a spontaneous transition toward a stable constricted conformation, although they display considerable flexibility and the cross-subunit distance between the C_α atoms of Gly77 fluctuates markedly. During the trajectories, water molecules frequently access the cavity behind the selectivity filter but never form a stable water wire as observed with the V76ester channel (Fig. 3). As a comparison, a simulation of the wild-type KcsA channel started with an open inner gate and the selectivity filter in a conductive conformation spontaneously transits toward the constricted conformation (SI Appendix, Fig. S4), a behavior that is similar to that of the V76ester channel.

Fig. 3.

Conformational dynamics of three amide-to-ester mutants, Y78ester, G77ester, and V76ester, started from the conductive filter (trajectories 10 to 12 in SI Appendix, Table. S1). (Left and Right) Conformations of the selectivity filter with buried water molecules at the beginning (Left) and the end (Right) of simulations shown for a pair of subunits. (Middle) Time series of the cross-subunit distance between the C_α atoms of Gly77 of diagonally opposed monomers (upper panel) and number of water molecules buried behind the selectivity filter of each subunit (Middle and Lower).

Discussion

D-Alanine Substitution.

The semisynthetic KcsA^D-ala77 channel incorporated in lipid bilayers can be activated into a conductive state by a pH stimulus until the channel ultimately undergoes C-type inactivation and becomes nonconductive (12). A critical assumption underlying the conclusion of Valiyaveetil and coworkers is that the selectivity filter must be essentially “locked” in the 1K4C-like conductive conformation and that any conformational transition toward a 1K4D-like constricted filter conformation is abolished by the D-ala77 substitution (12, 15). However, during MD simulations of $\sim$1.2 $\mu$s, the KcsA^D-ala77 channel started from a constricted filter, and an open inner gate spontaneously led to an asymmetrical conformation where the filter completely constricts on two subunits (Fig. 1 A and B). Because the simulation was started with a constricted filter in a symmetrical conformation, this result suggests that the asymmetrical conformation is more stable for the KcsA^D-ala77. This stability of the asymmetrical conformation of the filter suggested by the unbiased MD is consistent with the 2D-PMF shown in Fig. 1E. Interestingly, the asymmetrical conformation occurring with the KcsA^D-ala77 channel is also observed in the 2D-PMF of the wild-type KcsA channel (SI Appendix, Fig. S2), providing further support that this is a genuine state of the selectivity filter. The 2D-PMF of the wild-type KcsA channel with an open inner gate has its deepest minimum at the 1K4D-like symmetrical constricted conformation, whereas this state is essentially forbidden for the KcsA^D-ala77 channel. The pore of KcsA^D-ala77 is actually even narrower with this asymmetrical conformation than with the symmetrical constricted conformation 1K4D adopted by the wild-type KcsA at low K⁺. This is because the D-ala side chain ends up protruding into the permeation pathway, where it compensates for the two filter units that are not pinched (Fig. 1D). These computational results show that the D-ala substitution at position 77 does not rigidly “lock” the selectivity filter in a conductive conformation and does not preclude the occurrence of an asymmetrical constricted nonconductive conformation.

Amide-to-Ester Substitutions.

Following amide-to-ester backbone substitutions at Gly77 and Tyr78, C-type inactivation is suppressed in functional measurement, whereas it is not suppressed following amide-to-ester backbone substitutions at Gly79 and Val76 (13, 14). In contrast to the D-ala77 substitution, amide-to-ester backbone substitutions are structure-conserving modifications that, in principle, are not expected to prevent the selectivity filter from adopting the constricted conformation. However, X-ray structures of the modified KcsA channel with amide-to-ester backbone substitutions at Gly79, Tyr78, Gly77, and Val76 showed a selectivity filter that is in the conductive conformation. Observing that the binding of K⁺ in specific sites along the selectivity filter was altered, Valiyaveetil and coworkers proposed that this was the critical factor affecting C-type inactivation (13, 14).

Two important structural aspects are ignored in this analysis. First, by virtue of the allosteric coupling between the selectivity filter and the intracellular activation gate, one expects to primarily observe a conductive filter when the inner gate is closed and a constricted filter primarily when the inner gate is open (lowering the K⁺ concentration also promotes the constricted filter with a closed inner gate, but the effect is not as clear as with the open gate). However, all of the X-ray structures of the modified KcsA channel were obtained with the inner gate closed, which would naturally promote the conductive conformation of the selectivity filter (13–16). This is consistent with our observation in the MD simulations that the selectivity filter maintained conductive conformation for all of the KcsA mutants with a closed inner gate (SI Appendix, Fig. S5). It is also noteworthy that the X-ray structure of the modified channel T75G was found in the constricted state, although this result was dismissed as insignificant (14). Second, the hydrogen bonding ability of the amide group as a donor is eliminated by backbone-ester substitutions. Loss of hydrogen bonding as a result of these ester substitutions was ruled out because they do not cause any appreciable changes in the structure of the surrounding residues. However, disruption of hydrogen bonds between water molecules and the backbone of the selectivity filter may have a complex impact on the relative stability of the conductive or constricted conformations of the channel. We previously showed that three water molecules buried behind the selectivity filter of each subunit played a critical role in the stability of the constricted conformation of the KcsA channel (10, 11). The results from MD simulations of the KcsA channel with the different amide-to-ester backbone substitutions shown in Fig. 2 are highly consistent with the functional study showing that only amide-to-ester substitutions at Gly77 and Tyr78 reduce inactivation, while the same substitutions at Gly79 and Val76 have much less impacts on inactivation. Simulations show that water molecules accessing the region behind selectivity filter cannot stabilize the constricted conformation of the four subunits in two cases: G77ester and Y78ester. The general trends with respect to hydrogen bonding with the buried inactivating water molecules in the wild-type KcsA channel (Table 1) are in qualitative agreement with the results from the simulations of the semisynthetic ester channels (Fig. 2). Furthermore, simulations of the modified KcsA channels that started with the selectivity filter in the conductive conformation highlight the enhanced flexibility caused by the amide-to-ester substitution (Fig. 3) and reveal a spontaneous transition of the KcsA–V76ester channel toward a constricted conformation.

The results from the MD simulations provide an alternative interpretation of the functional effects of amide-to-ester substitutions. Based on the present results, it is clear that the amide-to-ester backbone substitutions perturb the binding of the buried water molecules behind the selectivity filter. It was shown previously that the binding of water molecules behind the selectivity filter stabilize the 1K4D constricted conformation (10, 11), Consequently, it is not surprising that the amide-to-ester substitutions affect the stability of the constricted conformation. Rather than ruling out the constricted conformation as a C-type inactivated state, the functional studies of amide-to-ester substitutions further highlight the importance of hydrogen bonding of buried water molecules with the backbone of the selectivity filter. Nonetheless, it is important to keep in mind that factors affecting ion occupancy might also play a role. The amide-to-ester substitutions modify the local charge distribution of the backbone, and ion occupancy is expected to be exquisitely sensitive to any variations in the backbone electrostatics. Indeed, QM calculations indicate that the atomic partial charges of the carbonyl group are altered by the chemical changes (SI Appendix, Force Field Parameters). Thus, ion occupancy may also have an indirect effect on the relative stability of the conductive and constricted conformations of the filter.

Conclusion

There is abundant and unambiguous evidence from functional data (8, 9), X-ray crystallography (2, 3, 17), NMR spectroscopy (11), and computations (4, 10, 11) that the C-type inactivated state of the KcsA channel is associated with the constricted conformation of the selectivity filter. The present computational study demonstrates that the experimental results obtained with the KcsA^D-ala77 and and V76ester, G77ester, and Y78ester channels can be rationally explained while remaining broadly consistent with this view. Undoubtedly, much remains to be understood about the selectivity filter of K⁺ channels—a flexible and dynamic element able to display considerable structural polymorphism. In that sense, the X-ray structures of the KcsA channel displaying a constricted filter are particularly important because they provide atomic-resolution information about the C-type inactivated state of this channel (2, 3, 17). Nevertheless, our knowledge at the present time regarding the accessible conformations of the selectivity filter of K⁺ channels remains limited. In contrast with families of well-characterized soluble proteins where analysis has revealed the existence of multiple conformational states of functional importance (18, 19), we do not yet have access to a large ensemble of structures for any given member of the K⁺ channel family, even for KcsA, to draw general conclusions. Essentially, we know the conductive conformation [1BL8 (1) and 1K4C (2)], the constricted conformation [1K4D (2) and 3F7V (3)], and the flipped conformation observed with the noninactivating E71A mutant of KcsA [2ATK (8) and 3OGC (20)]. While the constricted and flipped conformations have only been observed with the KcsA channel, the conductive conformation has also been observed with a number of K⁺ channels (21–25), even though the crystals were obtained under conditions that might have favored the C-type inactivated state in some cases. This is sometimes perceived as evidence suggesting that the constricted conformation observed with KcsA is perhaps an outlier, unrepresentative of a true C-type inactivated state. Due to the scarcity of data, it is important to remind ourselves that the absence of X-ray structures does not prove anything about unobserved conformations.

Materials and Methods

Two crystallographic structures, 1K4C and 1K4D, of wild-type KcsA with a closed inner gate (2) exemplify the conformations of the selectivity filter referred to as conductive and constricted: 1K4C representing a putatively conductive filter was obtained at high K⁺ concentration, while 1K4D with a constricted filter was obtained at a low K⁺ concentration [structures taken from the Protein Data Bank (26) are referenced by their four-character access codes]. The width of the constricted filter in 1K4D, defined here as the cross-subunit distance between the C_α atoms of Gly77 of the diagonally opposed monomer, is 5.5 Å. In comparison, the width of the conductive filter in 1K4C is 8.1 Å. Atomic models of the wild-type KcsA were constructed based on crystal structures—that is, 1K4C (2), 1K4D (2), and 3F7V (3)—that respectively represent closed-conductive, closed-constricted, and open-constricted structural states. To produce an open-conductive model from the 3F7V structure, the 2.0 Å resolution X-ray structure 1K4C was used as a template. The filter was aligned to the channel using the backbone atoms of residues 65 to 74 and 80 to 84 such that the backbone atoms of the filter residues 71 to 80 could be used as target coordinates for harmonic positional restraints (force constant 100 kcal mol⁻¹). Once the filter coordinates matched that of 1K4C, K⁺ ions were swapped into the filter at positions S1 and S3 with water in between. The restraints on the filter were then linearly scaled to zero over a period of 10 ns during the final stages of equilibration. The transmembrane $\alpha$-helices TM1 and TM2, incomplete in 3F7V, were extended to obtain a construct comprising residues 22 to 124. The semisynthetic ^D-ala77 KcsA channel was constructed based on the open-constrict model. To build the KcsA^D-ala77, Gly77 was substituted by a D-ala based on default bond, angle, and dihedral parameters using the PSFGEN package in VMD (27). While the filter in the 3F7V structure is also in a constricted conformation, the coordinates of the selectivity filter from the higher resolution structure 1K4D were used to restrain the initial model. To allow the protein to adapt to the presence of the D-ala side chain, the simulation was initiated with restraints holding the filter in the constricted conformation as in 1K4D. Water molecules buried behind the filter were also initially restrained, as the conformation would be unstable without them. After 25 ns, the restraints were switched off to allow the complete equilibration of the system without any artificial biases. The semisynthetic amide-to-ester KcsA channels were built based on the open-conductive model. For amide-to-ester substitutions, patches were added to change the two neighboring residues to one segment and replace the amide group linking them to a ester group. Three amide-to-ester substitution patches for the two-residues segments T75-V76ester, V76-G77ester, and G77-Y78ester were created, and the needed force field parameters were determined using quantum mechanical (QM) calculations (see below). The amide-to-ester residue patches and force field parameters are given in SI Appendix.

For all MD simulations, the channel was embedded in a bilayer of 3POPC:1POPG lipids and solvated in 150 mM or 200 mM KCl using the web service CHARMM-GUI (28, 29). Most residues were assigned their standard protonation state at pH 7. E71 is protonated to form a key hydrogen bond with D80 for the normal function of selectivity filter (30, 31). In addition, H25, E118, and H124 were protonated to keep the activation gate open. The total number of atoms in the MD systems is $\sim$41,000. The CHARMM force field PARAM36 for protein (32–34), lipids (35), and ions (36) was used. Explicit water was described with TIP3P model (37). The phi–psi dihedral energy surface of D-ala was generated by inverting the CMAP spline table of L-ala (33). For simulating the backbone mutations in selectivity filter, amide-to-ester unnatural amino acids were parameterized as a two-residue patch. The unnatural amino acid mutants V76ester, G77ester, and Y78ester were parameterized separately by generating two short oligopeptides consisting of an alanine with its N terminus acetylated and having its C terminus bonded through an ester bond to the modified amino acid, Glycine or Tyrosine. The latest was capped at its C terminus by M-Methylamide, simulating an amide bond to the next amino acid. All parameters not implying the ether oxygen of the ester were initially taken from the CHARMM36 protein parameters (32–34). The Lennard–Jones, bond, and angle parameters for the ester bond were taken from CGenFF (38). We used the General Automated Atomic Model Parameterization (GAAMP) program (39) to reparametrize a subset of charges and dihedral. To do so, all of the charges were kept fixed to their CHARMM36 values, except for one of both oxygens and carbon of the ester bond as well as the C beta of the modified amino acid and its hydrogen atoms. A constraint was added to maintain the total charge of this subgroup and of the full system, to 0.0. All of the flexible dihedrals implied in the ester bond were reparametrized against QM data. As an alanine was used, the dihedral implied in between the ester bond and atoms of the first residue side chain behind the first one were taken directly from CHARMM. Two QM methods were used for the GAAMP parameterization, Hartree–Fock (HF)/6-31G* and MP2/SVP (second order MollerPlesset perturbation with split valence plus polarization). In all cases, HF was used to determine the charges of the ester bond subgroup, as it is the convention for CHARMM force field parameterization. For the dihedral, no significant difference could be found when using MP2, except for the Glycine residue’s $\psi$ dihedral angle. However, it was determined that the HF calculation was not sufficiently accurate to represent properly the torsion of the ester bond, and the MP2/SVP calculation was used instead (SI Appendix, Fig. S6). The glycine charges were kept to their HF values, but the dihedral angles were updated.

The models of KcsA were refined using energy minimization for at least 5,000 steps, and the ions and nonfilter backbone atoms were kept fixed throughout the minimization procedure. All of the simulations were performed under constant NPT conditions at 310K and 1 atmosphere, and periodic boundary conditions with electrostatic interactions were treated by the particle-mesh Ewald (PME) method (40) and a real-space cutoff of 12 Å. The simulations use a time step of 2 fs, with bond distances involving hydrogen atoms fixed using the SHAKE algorithm (41). After minimization and equilibration with harmonic positional restraints on all of the C_α atoms, the equilibrated systems were simulated either using NAMD version 2.11 (42) or on the special purpose computer Anton (Pittsburgh Supercomputer Center) (43). In all cases, data collection for the figures begins only after all restraints are removed. All of the MD simulations considered for the present study are summarized in SI Appendix, Table S1.

The water-binding cavity within each subunit is defined as the space with a distance less than 7 Å from both the nitrogen (or substituted ester oxygen) atom from Gly77 and the C_α from E71 in the same monomer. The number of water molecules within each subunit was determined as the average water number within this pocket during specific trajectory. The mean turnover time of water molecules within each subunit is defined as $T_{\text{MD}}⟨N⟩/n_{\text{d}}$, where $T_{\text{MD}}$ is the length of the trajectory, $⟨N⟩$ is the average number of water molecules in one cavity, and $n_{\text{d}}$ is the number of distinct water molecules that visited the cavity at least once during the simulation. Each of the four subunits was treated as an individual sample to estimate the average and SD. Weighted linear regressions were performed using (1/${\sigma }^2$) as the weight to plot in Fig. 2.

The 2D PMFs (Fig. 1E) with respect to the two coordinates were calculated using NAMD 2.11 (42). One reaction coordinate $r$ describes the width of the selectivity filter and is defined as the average cross-subunit distance between the C_α atoms of Gly77, whereas the other reaction coordinate $z$ indicates the position of the external K⁺ ion along z axis relative to the center of the selectivity filter. The region of interest in the ($r$, $z$) space was covered by a grid of equally spaced umbrella sampling (US) windows. To improve the statistical sampling, the US calculations were carried out using Hamiltonian replica-exchange simulations (US/$\mathcal{H}$-REMD) (44, 45). For the 2D-PMF calculation of the wild-type KcsA channels, some initial coordinates for the US windows were taken from the unbiased trajectories. Initial coordinates for the missing windows were obtained by driven MD simulations along the reaction coordinates to the space of the missing windows. For the 2D-PMF calculation of KcsA^D-ala77, the initial seeds were generated by mutating corresponding wild-type conformations. Different from a previous study (10), there is no restraint on water molecules to access or leave the inactivating water binding site behind the selectivity filter. All 85 windows were extended to 80 ns for WT and 150 ns for KcsA^D-ala77. Only the last 50 ns were used to construct the 2D PMF, as the equilibration is much longer for the mutant. The total aggregate simulation time used to produce the US/H-REMD calculations is about 20 $\mu$s. Exchange attempts were made every 500 steps (or 1 ps of simulation of time), and neighboring windows were swapped if the Metropolis Monte Carlo exchange probability was satisfied. The US data were processed and unbiased using the Weighted Histogram Analysis Method (WHAM) (46, 47). Finally, the 2D-PMF was constructed for the two coordinates representing the cross-subunit distance between the C_α atoms of Gly77 of diagonally opposed monomers A & C and B & D were symmetrized by swapping between two neighboring monomers—that is, A and B, or C and D.