Improved Confidence Interval for Average Annual Percent Change in Trend Analysis

Abstract

This paper considers an improved confidence interval for the average annual percent change in trend analysis, which is based on a weighted average of the regression slopes in the segmented line regression model with unknown change-points. The performance of the improved confidence interval proposed by Muggeo is examined for various distribution settings, and two new methods are proposed for further improvement. The first method is practically equivalent to the one proposed by Muggeo, but its construction is simpler and it is modified to use the t-distribution instead of the standard normal distribution. The second method is based on the empirical distribution of the residuals and the resampling using a uniform random sample, and its satisfactory performance is indicated by a simulation study.

1 Introduction

In cancer trend analysis, the annual percent change (APC) has been used to estimate the rate of change in a given time period and it is estimated by fitting a simple linear regression model for the logarithm of the age-adjusted rates. The APC value of c% means that the cancer rates change at c% of the rate per year, and it is a measure that is comparable across scales, for both rare and common cancers. When the trend changes over a time period, a segmented line regression model was proposed to describe such changes in cancer incidence and mortality trends (Kim et al. [1]), and the average annual percent change (AAPC) provides a summary measure of the APCs over a period of time where the trend is not constant. Clegg et al. [2] proposed the AAPC as a measure to summarize “rates of change that are not constant over a given time period,” discussed how to calculate a confidence interval for the AAPC, and applied it to US cancer incidence and mortality data. The AAPC has proven to be a very useful measure when summarizing recent trends across a large number of data series (e.g. cancer sites) in a single table. Investigators have found an AAPC over a fixed segment is more easily compared across data series than the final segment APCs and starting years. For example, in Tables 3 and 4 in The Annual Report to the Nation on the Status of Cancer (Kohler et al. [3]) (a high profile paper representing a collaboration by the Centers for Disease Control and Prevention, the American Cancer Society, the National Cancer Institute, and the North American Association of Central Cancer Registries), 5 and 10 year AAPCs are presented for incidence and mortality rates respectively for the top 15 cancer sites by sex, race, and ethnicity.

In Clegg et al. [2], the confidence interval (CI) for the AAPC is obtained by using the asymptotic normality of the estimated slopes, conditional on the estimated locations of the change-points where the trends change. Muggeo [4] proposed to incorporate the joint distribution of the estimated slope parameters and change-point estimators, and showed via simulations that the conditional confidence intervals (CCI) used in Clegg et al. [2] are usually conservative, while Muggeo’s confidence interval is more accurate.

In this paper, we follow up on the suggestion made by Muggeo [4], investigate how to further improve the accuracy of the AAPC confidence interval, and compare various confidence interval estimates for the AAPC. In Section 2, we formally describe the segmented line regression model, review the confidence intervals proposed in Clegg et al. [2] and Muggeo [4], and discuss some issues in the construction of the AAPC confidence interval. In Section 3, we propose two new methods to construct the confidence interval of the AAPC: the first-last method that reformulates the parametric method and the empirical cumulative distribution function resampling method. Simulation results are presented in Section 4, and Section 5 includes examples. Further discussion is included in Section 6.

2 Confidence Intervals for the AAPC

Suppose that for i = 1, …, n, r_i denotes an age-adjusted cancer incidence/mortality rate at time x_i and y_i = log(r_i). The segmented line regression model with the continuity constraint assumes the following:

$$y_i=\text{log}(r_i)={\beta }_0+{\beta }_1{x}_i+{\delta }_1{(x_i-{\tau }_1)}^{+}+\cdots +{\delta }_k{(x_i-{\tau }_k)}^{+}+{\epsilon }_i,$$ (1)

where the τ’s are unknown change-points, also called break-points, joinpoints, etc. in literature, the ε_i are independent errors, and t⁺ = max(0, t). This model can also be expressed as

$$E(y_i|x_i)=\{\begin{array}{c}{\alpha }_1+{\beta }_1{x}_i,\\ {\alpha }_2+{\beta }_2{x}_i,\\ ⋮\\ {\alpha }_{k+1}+{\beta }_{k+1}{x}_i,\end{array}\begin{array}{l}\text{if }{\tau }_0\le x_i\le {\tau }_1,\hfill \\ \text{if }{\tau }_1\le x_i\le {\tau }_2,\hfill \\ ⋮\hfill \\ \text{if }{\tau }_k\le x_i\le {\tau }_{k+1},\hfill \end{array}$$ (2)

where τ₀ = min{x_i}, τ_k+1 = max{x_i}, and α_j + β_jτ_j = α_j+1 + β_j+1τ_j for j = 1, …, k.

The segmented line regression model described above has been studied by many authors and called a piecewise, broken-line, or multi-phase regression model in literature. Hinkley [5, 6] studied inference problems in a broken-line regression model with one change-point and Feder [7] studied asymptotic properties of the estimators in a general segmented regression model. Since then, many authors investigated various models and fitting algorithms, and we include a short list of references on multi-phase regression with the continuity constraint [8–16]. For an extensive list of references on multi-phase regression covering models with abrupt changes, Bayesian approaches, and testing procedures can be found in [17]. More recently, Muggeo [18] proposed a method to fit piecewise regression models with unknown break-points and the algorithm is available as an R package [19]. Kim et al. [1] applied the model (1) to describe changes in cancer trends where the unknown change-points were called joinpoints and the model was referred as the joinpoint regression model. They [1] used the least squares method to estimate the model parameters in the joinpoint regression model with k joinpoints and proposed the permutation test procedure to determine the number of joinpoints by sequentially conducting the tests. For a model with k joinpoints, Kim et al. [20] discussed how to construct confidence intervals for the model parameters and studied their small sample properties via simulations. Their algorithms to determine the number of joinpoints, fit the joinpoint regression model, estimate confidence intervals for the model parameters, and obtain the p-values to assess the significance of the regression slopes are implemented in JOINPOINT software available at http://surveillance.cancer.gov/joinpoint. Our focus in this paper is on the model with a fixed number of joinpoints, and further discussion related to selecting the number of joinpoints is included in the discussion section.

For the joinpoint regression model (2) with k joinpoints, the APC for a segment with the slope of β_j is defined as

$$\text{APC}=\{\text{exp}({\beta }_j)-1\}\times 100,$$

and the AAPC over the entire study period [a, b] is defined as

$$\text{AAPC}=\left\{\text{exp}\left({\displaystyle \sum _{j=1}^{k+1}{w}_j{\beta }_j}\right)-1\right\}\times 100,$$ (3)

where w_j = (τ_j − τ_j−1)/(b − a) for j = 1, …, k + 1 with τ₀ = a and τ_k+1 = b. Note that the original definition of the AAPC in Clegg et al. [2] uses “a⁻” in place of “a” in w_j of (3), where a⁻ = a − Δx with Δx → 0 when x is continuous and Δx = 1 when x is discrete. However, in order to avoid ambiguity in defining the APC for the period of (a⁻, a) = (a − 1, a) with annually observed data, JOINPOINT software adopted the new definition of w_j using “a” as in (3), and (3) will be used throughout this paper. For a subinterval [c, d], where a ≤ c < d ≤ b, the AAPC is defined similarly with w_j = max{min(d, τ_j) − max(c, τ_{j − 1}), 0}/(d − c).

Let $\mu ={\displaystyle {\sum }_{j=1}^{k+1}{w}_j{\beta }_j}$ and denote its estimator as $\widehat{\mu }={\displaystyle {\sum }_{j=1}^{k+1}{\widehat{w}}_j{\widehat{\beta }}_j}$ where ${\widehat{\beta }}_j$ and ${\widehat{\tau }}_j$ are the least squares estimators of β_j and τ_j (j = 1,…, k + 1) and the ŵ_j are accordingly estimated. Clegg et al. [2] estimated the standard error of $\widehat{\mu }$ as ${\widehat{\sigma }}_{\widehat{\mu }}=\sqrt{{\displaystyle {\sum }_{i=1}^{k+1}{w}_j^2{\widehat{\sigma }}_j^2}}$, where ${\widehat{\sigma }}_j^2$ is the estimated variance of ${\widehat{\beta }}_j$ and w_j is computed conditional on the estimated values of the τ_j’s, and calculated the 100(1 − α)% confidence limits for the AAPC as

$$\begin{array}{l}{\text{AAPC}}_{L(\alpha )}=\left\{\text{exp}\left[\widehat{\mu }-z_{1-\alpha /2}{\widehat{\sigma }}_{\widehat{\mu }}\right]-1\right\}\times 100,\\ {\text{AAPC}}_{U(\alpha )}=\left\{\text{exp}\left[\widehat{\mu }+z_{1-\alpha /2}{\widehat{\sigma }}_{\widehat{\mu }}\right]-1\right\}\times 100,\end{array}$$ (4)

based on the asymptotic normality of the least squares estimators ${\widehat{\beta }}_j’\mathrm{s}$, where z_p is the p-th percentile of the standard normal distribution. Noting that “ignoring uncertainly in ŵ may overestimate the true variance of $\widehat{\mu }$,” Muggeo [4] proposed to incorporate the joint distribution between ŵ = (ŵ₁, …, ŵ_k+1)′ and $\widehat{\beta }={({\widehat{\beta }}_1,\dots ,{\widehat{\beta }}_{k+1})}^{\prime }$ by using the first order Taylor series expansion:

$$\text{Var}(\widehat{\mu })\approx \text{Var}({\widehat{w}}^{\prime }\beta +w^{\prime }\widehat{\beta }).$$ (5)

Note that Muggeo [4] considered the AAPC over the entire study period, [a, b], for the model with k joinpoints, and Muggeo’s approach can be applied to a general subinterval [c, d], which is motivated by that we often consider the last 5 or 10 year AAPC in cancer trend analysis.

Now, we consider the AAPC over a general subinterval [c, d] and express a general form of $\text{Var}(\widehat{\mu })$ using the arguments of Muggeo [4]. For [c, d] on which the AAPC is estimated, let I and J denote the indices such that τ_I−1 < c ≤ τ_I < ⋯ < τ_J ≤ d < τ_J+1 where 1 ≤ I < J ≤ k, and define a (k + 2) × 1 vector

$${\eta }_{[c,d]}={(\underset{I}{\underbrace{c,\dots ,c,}}\underset{J-I+1}{\underbrace{{\tau }_I,\dots ,{\tau }_J,}}\underset{k+1-J}{\underbrace{d,\dots ,d}})}^{\prime }.$$ (6)

Then,

$${\mathbf{w}}_{[c,d]}=\frac{1}{d-c}\left(\begin{array}{cccccc}-1& 1& 0& \cdots & 0& 0\\ 0& -1& 1& \cdots & 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& 0& \cdots & -1& 1\end{array}\right){\mathbf{\eta }}_{[c,d]}=B{\mathbf{\eta }}_{[c,d]},$$

where B is a (k + 1) × (k + 2) matrix.

For notational simplicity, we will use η for η_[c,d] and w for w_[c,d] from now on, and note that β = Aθ, where

$$\begin{array}{l}\beta ={({\beta }_1,\dots ,{\beta }_{k+1})}^{\prime },\\ \theta =\left(\begin{array}{c}{\alpha }_1\\ {\beta }_1\\ {\alpha }_2\\ {\beta }_2\\ ⋮\\ {\alpha }_{k+1}\\ {\beta }_{k+1}\end{array}\right)=\left(\begin{array}{c}{\beta }_0\\ {\beta }_1\\ {\beta }_0-{\delta }_1{\tau }_1\\ {\beta }_1+{\delta }_1\\ ⋮\\ {\beta }_0-{\displaystyle {\sum }_{j=1}^k{\delta }_j{\tau }_j}\\ {\beta }_1+{\displaystyle {\sum }_{j=1}^k{\delta }_j}\end{array}\right),\\ A=A_{(k+1)\times 2(k+1)}=\left(\begin{array}{ccccccc}0& 1& 0& 0& \cdots & 0& 0\\ 0& 0& 0& 1& \cdots & 0& 0\\ ⋮& ⋮& ⋮& ⋮& \ddots & ⋮& ⋮\\ 0& 0& 0& 0& \cdots & 0& 1\end{array}\right).\end{array}$$

We also let $\xi =\left(\begin{array}{c}\eta \\ \theta \end{array}\right)$ and h′ = (β′B, w′A) with A and B defined above. Then, as in Muggeo [4], we note that

$$\begin{array}{l}\text{Var}(\widehat{\mu })\approx \text{Var}({\beta }^{\prime }\widehat{w}+w^{\prime }\widehat{\beta })\\ =\text{Var}({\beta }^{\prime }B\widehat{\eta }+w^{\prime }A\widehat{\theta })\\ =\text{Var}\left[({\beta }^{\prime }B,w^{\prime }A)\left(\begin{array}{c}\widehat{\eta }\\ \widehat{\theta }\end{array}\right)\right]=h^{\prime }\text{Cov}(\widehat{\xi })h,\end{array}$$

where $\widehat{\mathbf{\eta }}$ and $\widehat{\mathbf{\theta }}$ are the least squares estimators of η and θ.

Now let ${\mathrm{\Lambda }}_{I,J}=\text{Cov}({\widehat{\mathbf{\tau }}}_{IJ})$ with ${\widehat{\mathbf{\tau }}}_{IJ}={({\widehat{\tau }}_I,\dots ,{\widehat{\tau }}_J)}^{\prime }$, ${\mathrm{\Gamma }}_{I,J}=\text{Cov}({\widehat{\mathbf{\tau }}}_{IJ},\widehat{\mathbf{\theta }})$, and $\mathrm{\sum }=\text{Cov}(\widehat{\mathbf{\theta }})$, where Λ_I,J, Γ_I,J, and Σ are (J − I + 1) × (J − I + 1), (J − I + 1) × 2(k + 1), and 2(k + 1) × 2(k + 1) matrices, respectively. Then the (3k + 4) × (3k + 4) covariance matrix of $\widehat{\mathbf{\xi }}$ is

$$\text{Cov}(\widehat{\mathbf{\xi }})=\left(\begin{array}{cccc}0& 0& 0& 0\\ 0& {\mathrm{\Lambda }}_{I,J}& 0& {\mathrm{\Gamma }}_{I,J}\\ 0& 0& 0& 0\\ 0& {\mathrm{\Gamma }}_{I,J}^{\prime }& 0& \mathrm{\sum }\end{array}\right),$$

and with the estimated covariance matrix $\widehat{\text{Cov}}(\widehat{\mathbf{\xi }})$, we estimate $\text{Var}(\widehat{\mu })$ as

$$\widehat{\text{Var}}(\widehat{\mu })\approx ({\widehat{\beta }}^{\prime }B,{\widehat{w}}^{\prime }A)\widehat{\text{Cov}}(\widehat{\xi }){({\widehat{\beta }}^{\prime }B,{\widehat{w}}^{\prime }A)}^{\prime }.$$

To estimate $\mathrm{\Lambda }=\text{Cov}(\widehat{\tau })$ for $\widehat{\tau }={({\widehat{\tau }}_1,\dots ,{\widehat{\tau }}_k)}^{\prime }$, we first note that ${\widehat{\tau }}_j=\frac{{\widehat{\alpha }}_j-{\widehat{\alpha }}_{j+1}}{{\widehat{\beta }}_{j+1}-{\widehat{\beta }}_j}$ and use the delta method to obtain

$$\widehat{\tau }-\tau =M(\widehat{\theta }-\theta )(1+o_p(1)),$$

where

$$M=\left(\begin{array}{ccccccccccc}\frac{1}{{\beta }_2-{\beta }_1}& \frac{{\tau }_1}{{\beta }_2-{\beta }_1}& -\frac{1}{{\beta }_2-{\beta }_1}& -\frac{{\tau }_1}{{\beta }_2-{\beta }_1}& 0& 0& \cdots & 0& 0& 0& 0\\ 0& 0& \frac{1}{{\beta }_3-{\beta }_2}& \frac{{\tau }_2}{{\beta }_3-{\beta }_2}& -\frac{1}{{\beta }_3-{\beta }_2}& -\frac{{\tau }_2}{{\beta }_3-{\beta }_2}& \cdots & 0& 0& 0& 0\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& ⋮& & \\ 0& 0& 0& 0& 0& 0& \cdots & \frac{1}{{\beta }_{k+1}-{\beta }_k}& \frac{{\tau }_k}{{\beta }_{k+1}-{\beta }_k}& -\frac{1}{{\beta }_{k+1}-{\beta }_k}& -\frac{{\tau }_k}{{\beta }_{k+1}-{\beta }_k}\end{array}\right).$$

Then, we get $\mathrm{\Lambda }=\text{Cov}(\widehat{\mathbf{\tau }})\approx M\mathrm{\sum }{M}^{\prime }$ and $\mathrm{\Gamma }=\text{Cov}(\widehat{\mathbf{\tau }},\widehat{\mathbf{\theta }})\approx M\mathrm{\sum }$with $\mathrm{\sum }=\text{Cov}(\widehat{\mathbf{\theta }})$. The covariance matrix of the estimated regression coefficients or equivalently $\mathrm{\sum }=\text{Cov}(\widehat{\mathrm{\theta }})$ can be estimated by using the unconstrained information matrix discussed in Hinkley [6], and it is produced by JOINPOINT software. Also, M is estimated using the values obtained by the consistent estimators of the model parameters. This method based on Muggeo [4] provides a more accurate standard error estimate of $\widehat{\mu }$, and we call the confidence interval constructed using this improved standard error estimate in (4) as MCI.

Muggeo [4] conducted simulations to compare the accuracies of the confidence interval estimates, and we reproduced Muggeo’s simulation in Table 1. In this simulation study, we generated data that follow the model in Muggeo [4]:

$$y_i=3.5+0.2x_i+0.2{(x_i-n/2)}^{+}-0.6{(x_i-3n/4)}^{+}+{\epsilon }_i,$$

where ε_i ~ N(0, σ = 0.06), x_i = i, for i = 1, 2, ⋯, n, and n = 30, 50, 100. Table 1 includes the empirical standard error estimate of $\widehat{\mu }$, $\text{sd}(\widehat{\mu })$, obtained with 1,000 replications of $\widehat{\mu }$, where $\mu ={\displaystyle {\sum }_{j=1}^3{w}_j{\beta }_j}$, and the average of the standard error estimates, Ave(SE), approximated by each of the CCI and MCI methods. Note that the numbers do not exactly match even after taking 100 multiplied in Muggeo’s Table 1 into consideration, and the observed discrepancy could be explained by (i) the use of “c” instead of “c⁻” in the definition of the AAPC over [c, d], (ii) possible differences in the fitting constraints, and (iii) possibly different methods used to estimate the variances of the estimated slopes and estimated joinpoints as well as the covariance between the estimated slopes and joinpoints. Regarding (ii), we used the grid search option of JOINPOINT with the minimum number of observations between two joinpoints set as four, the minimum number of observations from a joinpoint to either end of the data set as three, and the number of grid points between the two consecutive x-values as three (quarterly grid), while Muggeo [4] used an iterative algorithm to make a continuous fit. For (iii), our standard error estimates of the slope parameters are obtained deleting offending data points that coincide with the estimated joinpoints and using an unconstrained estimate of the covariance matrix that is obtained without the continuity constraint. The use of the unconstrained estimate is justified in Hinkley [6] and simulation studies to compare the unconstrained model standard error estimates to the constrained model standard error estimates were conducted in [20]. The deletion of the offending observations is proposed in Lerman [21] to avoid ambiguity at the estimated joinpoints that coincide with observed x-values in getting unconstrained standard error estimates, and further details can be found in [20].

Table 1. Table 1 in Muggeo [4].

Average Standard Error Estimates of $\widehat{\mu }$ by Two Methods: CCI and MCI

n	[c, d]	From Muggeo’s table*			From our simulation results
		$\text{sd}(\widehat{\mu })$	Ave(SE)			Ave(SE)
			Method 1 (CCI)	Method 2 (MCI)	$\text{sd}(\widehat{\mu })$	Method 1 (CCI)	Method 2 (MCI)
30	[1,30]	0.00194	0.00385	0.00166	0.00174	0.00414	0.00168
50	[1,50]	0.00089	0.00183	0.00079	0.00082	0.00190	0.00080
100	[1,100]	0.00031	0.00065	0.00029	0.00028	0.00068	0.00029

^*: The numbers in Muggeo [4] represent the actual estimates multiplied by 100.

Table 1 indicates that the CCI overestimates the standard error of $\widehat{\mu }$, and the standard error estimate computed by (5) for the MCI is more accurate although there is a slight tendency of underestimating.

Muggeo [4] only used σ = 0.06 in the simulation study, and we considered the cases with σ = 0.1, 0.6, and 1.2 as well in order to examine how the accuracy of the confidence interval depends on σ, whose results are summarized in Table 2. We also considered various subintervals [c, d] over which the AAPCs are estimated. In Table 2, CP and AW denote the coverage probability, the proportion of the simulation runs whose 95% confidence interval contains the true value of μ, and the average width, the average width of the 1,000 confidence intervals, respectively. Note that for n = 30, 50, and 100, the first cases with σ = 0.06 and [c, d] = [1, n] correspond to the cases considered in Table 1. When [c, d] belongs to one segment of the fitted mean function, a modified CCI (mCCI) was constructed using t_1−α/2,df instead of z_1−α/2 in (4), where t_p,d is the p-th percentile of the t-distribution with d degrees of freedom and the degrees of freedom df is obtained considering the number of data points deleted as offending data points. That is, df = n − k − (2k + 2) = n − 3k − 2 for the model with k joinpoints in the annual grid search case. This modification was proposed in order to produce the AAPC confidence interval consistent with the APC confidence interval when [c, d] belongs to one segment, and the t-interval for APC has been implemented since JOINPOINT V 3.5.

Table 2.

Comparison of mCCI and MCI for μ

n	σ	[c, d]	μ	$\widehat{\mu }$	$\text{sd}(\widehat{\mu })$	mCC			MCI
						Ave(SE)	CP	AW	Ave(SE)	CP	AW
30	0.06	[1, n]	0.1483	0.1481	0.0017	0.0041	1.000	0.0162	0.0017	0.920	0.0066
		[n/4, 3n/4]	0.3000	0.2992	0.0030	0.0058	0.999	0.0226	0.0030	0.920	0.0118
		[n/2, 3n/4]	0.4000	0.3963	0.0078	0.0107	0.966	0.0436	0.0075	0.911	0.0292
		[5n/8, 7n/8	0.1000	0.1000	0.0042	0.0072	0.996	0.0281	0.0041	0.927	0.0162
	0.1	[1, n]	0.1483	0.1479	0.0029	0.0069	1.000	0.0272	0.0028	0.924	0.0110
		[n/4, 3n/4]	0.3000	0.2981	0.0047	0.0096	1.000	0.0376	0.0050	0.933	0.0198
		[n/2, 3n/4]	0.4000	0.3923	0.0124	0.0177	0.962	0.0713	0.0125	0.911	0.0491
		[5n/8, 7n/8	0.1000	0.1001	0.0069	0.0120	0.998	0.0471	0.0069	0.943	0.0271
	0.6	[1, n]	0.1483	0.1441	0.0219	0.0535	1.000	0.2099	0.0171	0.873	0.0670
		[n/4, 3n/4]	0.3000	0.2899	0.0273	0.0690	0.928	0.2712	0.0259	0.843	0.1017
		[n/2, 3n/4]	0.4000	0.3565	0.0671	0.1235	0.787	0.4880	0.0546	0.748	0.2142
		[5n/8, 7n/8	0.1000	0.1074	0.0632	0.1077	0.935	0.4224	0.0502	0.870	0.1966
	1.2	[1, n]	0.1483	0.1406	0.0508	0.1207	0.999	0.4732	0.0356	0.840	0.1395
		[n/4, 3n/4]	0.3000	0.2861	0.0536	0.1299	0.906	0.5116	0.0455	0.837	0.1783
		[n/2, 3n/4]	0.4000	0.3415	0.1241	0.2116	0.619	0.8346	0.0872	0.633	0.3419
		[5n/8, 7n/8	0.1000	0.1068	0.1296	0.1997	0.828	0.7862	0.1007	0.796	0.3949
n	σ	[c, d]	μ	$\widehat{\mu }$	$\text{sd}(\widehat{\mu })$	mCC			MCI
						Ave(SE)	CP	AW	Ave(SE)	CP	AW
50	0.06	[1, n]	0.1490	0.1490	0.0008	0.0019	1.000	0.0075	0.0008	0.939	0.0031
		[n/4, 3n/4]	0.3000	0.2997	0.0015	0.0026	0.998	0.0103	0.0014	0.916	0.0055
		[n/2, 3n/4]	0.4000	0.3983	0.0038	0.0049	0.967	0.0197	0.0035	0.917	0.0136
		[5n/8, 7n/8	0.1000	0.1001	0.0020	0.0033	0.996	0.0131	0.0019	0.932	0.0075
	0.1	[1, n]	0.1490	0.1490	0.0014	0.0032	1.000	0.0125	0.0013	0.940	0.0052
		[n/4, 3n/4]	0.3000	0.2991	0.0023	0.0044	0.998	0.0171	0.0024	0.935	0.0092
		[n/2, 3n/4]	0.4000	0.3962	0.0061	0.0082	0.963	0.0325	0.0059	0.909	0.0231
		[5n/8, 7n/8	0.1000	0.1001	0.0033	0.0056	0.998	0.0218	0.0032	0.940	0.0125
	0.6	[1, n]	0.1490	0.1484	0.0086	0.0209	1.000	0.0821	0.0080	0.925	0.0313
		[n/4, 3n/4]	0.3000	0.2936	0.0125	0.0296	0.995	0.1160	0.0132	0.908	0.0518
		[n/2, 3n/4]	0.4000	0.3738	0.0332	0.0538	0.908	0.2122	0.0314	0.827	0.1230
		[5n/8, 7n/8	0.1000	0.1052	0.0253	0.0418	0.986	0.1637	0.0212	0.902	0.0830
	1.2	[1, n]	0.1490	0.1463	0.0225	0.0589	1.000	0.2307	0.0168	0.893	0.0657
		[n/4, 3n/4]	0.3000	0.2893	0.0266	0.0787	0.917	0.3090	0.0236	0.829	0.0927
		[n/2, 3n/4]	0.4000	0.3546	0.0637	0.1452	0.776	0.5708	0.0494	0.725	0.1938
		[5n/8, 7n/8	0.1000	0.1129	0.0640	0.1297	0.912	0.5086	0.0511	0.862	0.2002
n	σ	[c, d]	μ	$\widehat{\mu }$	$\text{sd}(\widehat{\mu })$	mCC			MCI
						Ave(SE)	CP	AW	Ave(SE)	CP	AW
100	0.06	[1, n]	0.1495	0.1495	0.0003	0.0007	1.000	0.0027	0.0003	0.953	0.0011
		[n/4, 3n/4]	0.3000	0.2999	0.0004	0.0009	0.997	0.0037	0.0005	0.964	0.0021
		[n/2, 3n/4]	0.4000	0.3995	0.0013	0.0018	0.983	0.0070	0.0012	0.946	0.0049
		[5n/8, 7n/8	0.1000	0.1001	0.0007	0.0012	0.999	0.0048	0.0007	0.952	0.0027
	0.1	[1, n]	0.1495	0.1495	0.0005	0.0011	1.000	0.0045	0.0005	0.944	0.0019
		[n/4, 3n/4]	0.3000	0.2997	0.0008	0.0016	0.997	0.0061	0.0009	0.936	0.0034
		[n/2, 3n/4]	0.4000	0.3987	0.0022	0.0029	0.968	0.0116	0.0021	0.915	0.0084
		[5n/8, 7n/8	0.1000	0.1001	0.0012	0.0020	0.999	0.0079	0.0011	0.934	0.0045
	0.6	[1, n]	0.1495	0.1495	0.0029	0.0068	1.000	0.0268	0.0029	0.945	0.0114
		[n/4, 3n/4]	0.3000	0.2973	0.0042	0.0093	1.000	0.0365	0.0051	0.940	0.0199
		[n/2, 3n/4]	0.4000	0.3900	0.0116	0.0172	0.955	0.0678	0.0129	0.909	0.0505
		[5n/8, 7n/8	0.1000	0.1006	0.0072	0.0122	0.999	0.0479	0.0069	0.939	0.0271
	1.2	[1, n]	0.1495	0.1492	0.0058	0.0138	1.000	0.0542	0.0058	0.946	0.0227
		[n/4, 3n/4]	0.3000	0.2949	0.0083	0.0189	1.000	0.0741	0.0098	0.933	0.0383
		[n/2, 3n/4]	0.4000	0.3802	0.0228	0.0343	0.920	0.1349	0.0240	0.861	0.0939
		[5n/8, 7n/8	0.1000	0.1024	0.0160	0.0256	1.000	0.1004	0.0142	0.924	0.0556

• mCCI: modified conditional confidence interval; MCI: confidence interval based on Muggeo [4]

• $\text{sd}(\widehat{\mu })$: standard deviation of the simulated values of $\widehat{\mu }$

• AVE(SE): average of standard error estimates obtained by each method

• CP: coverage probability

• AW: average width of 95% confidence intervals

The results show that the standard error estimates of $\widehat{\mu }$ used in the mCCI are always overestimating, which usually lead to conservative mCCIs. As noted in Muggeo [4], treating the weight ŵ as fixed lead to an over-estimated standard error of $\widehat{\mu }$, which seems to be because changes in $\widehat{\mu }$ based on different values of ŵ are not incorporated and thus it is likely that $\widehat{\mu }$ conditional on the observed value of ŵ deviates further from the true value of μ more often. However, even with over-estimated standard error values, coverage probabilities of the mCCI are sometimes quite below the nominal level of 0.95, more so for a narrower interval [c, d], larger σ, and smaller n. The method based on Muggeo [4] accurately estimates the standard error of $\widehat{\mu }$ except when σ is large and n is small/medium, but the MCIs are usually liberal with their CP values below 0.95, more so as σ increases and [c, d] gets narrower, and this improves as n increases. We also note that these parametric confidence intervals lose accuracy more when c and/or d coincide with τ_i, and mCCI even becomes liberal in some cases where σ is not very small. Such inaccuracy would be because the estimated joinpoints, ${\widehat{\tau }}_1$ and ${\widehat{\tau }}_2$ could be either inside or outside of [c, d] and this may lead to an accumulation of errors in parametric confidence interval estimation where the standard error estimates are based on the partition of the x values. A more accurate fit that can be achieved for small σ seems to mitigate such inaccuracy. When n is 30 or 50, however, the CP values of the MCI are mostly below 0.95 even with accurate standard error estimates, and this indicates that the asymptotic normality of the pivotal quantity used to construct the MCI may not be satisfactory for small/medium sample size cases. In summary, the results in Table 2 indicate that the MCI works reasonably well if n is large, for example 100 in our simulations, except when the joinpoint location is close to c or d or [c, d] is short with large σ. However, in cancer trend analysis, we usually work with the rates over 10-40 years, and this motivated us to study how to further improve the confidence interval for AAPC.

3 Reformulated and New Methods

In this section, we propose two methods to construct the confidence interval of the AAPC. The first method is practically equivalent to the MCI, in terms of the standard error calculation, but it is based on a simpler expression using the parameters only in the first and last segments as shown below and we also propose to use the t-distribution for the pivotal quantity instead of the standard normal distribution. In the parameterizations (1) and (2) given above, we note that for j = 2, …, k + 1,

$${\alpha }_j={\alpha }_{j-1}-{\delta }_{j-1}{\tau }_{j-1}\text{and}{\beta }_j={\beta }_{j-1}+{\delta }_{j-1},$$

and it follows that

$$E(y|{\tau }_j)-E(y|{\tau }_{j-1})={\beta }_j({\tau }_j-{\tau }_{j-1})$$

and

$$\mu ={\displaystyle \sum _{j=1}^{k+1}{w}_j{\beta }_j={\displaystyle \sum _{j=1}^{k+1}\frac{({\tau }_j-{\tau }_{j-1}){\beta }_j}{b-a}}={\displaystyle \sum _{j=1}^{k+1}\frac{E(y|{\tau }_j)-E(y|{\tau }_{j-1})}{b-a}}=\frac{E(y|{\tau }_{k+1})-E(y|{\tau }_0)}{b-a}},$$

with w_j = (τ_j − τ_j−1)/(b − a). Then it can be shown that

$$\begin{array}{l}\mathit{\text{AAPC}}=\left\{\text{exp}\left({\displaystyle \sum _{j=1}^{k+1}{w}_j{\beta }_j}\right)-1\right\}\times 100\\ =\left\{\text{exp}\left(\frac{E(y|{\tau }_k)-E(y|{\tau }_0)}{b-a}\right)-1\right\}\times 100\\ =\left\{\text{exp}\left(\frac{{\alpha }_{k+1}+{\beta }_{k+1}b-{\alpha }_1-{\beta }_{1}a}{b-a}\right)-1\right\}\times 100.\end{array}$$

That is, the AAPC that is originally defined as a function of the weighted average of the slope parameters can be expressed in terms of the regression mean values at x = a of the first segment and x = b of the last segment, and it motivated us to call this method the First-Last method. Based on this presentation of the AAPC, we estimate μ and its standard error using

$$\begin{array}{l}\widehat{\mu }=\frac{{\widehat{\alpha }}_{k+1}+{\widehat{\beta }}_{k+1}b-{\widehat{\alpha }}_1-{\widehat{\beta }}_{1}a}{b-a},\\ \text{Var}(\widehat{\mu })=\frac{1}{{(b-a)}^2}\text{Var}({\widehat{\alpha }}_{k+1}+{\widehat{\beta }}_{k+1}b-{\widehat{\alpha }}_1-{\widehat{\beta }}_{1}a)\\ =\frac{l^{\prime }{\displaystyle {\sum }_{1}l}}{{(b-a)}^2},\end{array}$$

where ${\displaystyle {\sum }_1=\text{Cov}({\widehat{\alpha }}_1,{\widehat{\beta }}_1,{\widehat{\alpha }}_{k+1},{\widehat{\beta }}_{k+1})}$ and l = (−1, −a, 1, b)′. For a general subinterval [c, d], we can estimate μ and its standard error using the similar argument.

Note that the standard error calculation in the First-Last method does not require to estimate $\mathrm{\Lambda }=\text{Cov}(\widehat{\mathbf{\tau }})$ and $\mathrm{\Gamma }=\text{Cov}(\widehat{\mathbf{\tau }},\widehat{\mathbf{\theta }})$, which were used in the construction of the MCI. It can be shown that $\text{Var}(\widehat{\mu })$ estimated by the First-Last method is analytically equivalent to the improved variance estimate by Muggeo [4] in a simple case of k = 2, and Σ₁ is a block diagonal matrix when we use the unconstrained estimate of the covariance matrix of $\widehat{\mathbf{\theta }}$. In our preliminary simulations, we observed that the use of the t-distribution instead of the standard normal distribution to approximate the distribution of the pivotal quantity improves the coverage level, so we used the t-interval as follows. With the standard error of $\widehat{\mu }$ estimated as ${\widehat{\sigma }}_{\widehat{\mu }}={\left\{\frac{l^{\prime }{\widehat{\mathrm{\sum }}}_{1}l}{{(b-a)}^2}\right\}}^{1/2}$, the confidence limits of the AAPC are calculated as

$$\begin{array}{l}{\text{AAPC}}_{L(\alpha )}=\left\{\text{exp}\left[\widehat{\mu }-t_{1-\alpha /2,df}{\widehat{\sigma }}_{\widehat{\mu }}\right]-1\right\}\times 100,\\ {\text{AAPC}}_{U(\alpha )}=\left\{\text{exp}\left[\widehat{\mu }+t_{1-\alpha /2,df}{\widehat{\sigma }}_{\widehat{\mu }}\right]-1\right\}\times 100,\end{array}$$

where the degrees of freedom df of the t-distribution is obtained deleting offending data points as described earlier. This interval is called the First-Last t-interval (FLT). Although it is not reported here, we observed in our simulations that the First-Last z-interval with the z-scores as in (4) and MCI produced the same coverage probabilities, which empirically supports the analytic equivalence discussed above.

As to be indicated in Tables 3(a) and 3(b), however, MCI and FLT sometimes underestimate the nominal level of 0.95 too much, which motivated us to consider a resampling method. We investigated both permutation and a few basic bootstrap confidence intervals, but their performances were not satisfactory even with large n, which might be due to non-zero correlation among the residuals that converge to zero too slowly and/or the sampling distribution of the residuals that is not quite symmetric. Based on such observations in our preliminary simulations and noting that the empirical distribution of the observed residuals may not be close enough to the uniform distribution, we propose a new method to use the uniform random sample and the empirical distribution of the residuals, and we call it the empirical cumulative distribution function (CDF) quantile interval (EmpQ). It can be considered as a variation of the ordinary Bootstrap confidence interval and works as follows:

• Step 1: Generate n independent samples from the uniform distribution on (0, 1), U(0, 1). That is, for each b = 1, …, B, generate ${\mathit{U}}^{(b)}={(u_1^{(b)},\dots ,u_n^{(b)})}^{\prime }$, where the $u_i^{(b)}’\mathrm{s}$ form a random sample from U(0, 1).

• Step 2: For b = 1, …, B, generate ${\epsilon }^{(b)}={\widehat{F}}_n^{-1}({\mathbf{U}}^{(b)})$, where ${\widehat{F}}_n$ denotes the empirical distribution function of the residuals, $\widehat{\epsilon }={({\widehat{\epsilon }}_1,\dots ,{\widehat{\epsilon }}_n)}^{\prime }$ with ${\widehat{\epsilon }}_i=y_i-{\widehat{y}}_i$.

• Step 3: Let y^(b) = ŷ + ε^(b), where ŷ is the least squares fit of the original data.

• Step 4: Fit the model (1) for y^(b) and estimate ${\widehat{\mu }}^{(b)}$ for the b-th resample data y^(b).

Table 3(a).

Coverage Probability of 95% Confidence Interval for AAPC over [c, d]: One joinpoint model case

n	τ1	σ	[c, d]	mCCI	MCI	FLT	EmpQ	n	τ1	σ	[c, d]	mCCI	MCI	FLT	EmpQ
10	7	0.01	[1, 10]	0.984	0.869	0.929	0.917
			[6, 10]	0.966	0.895	0.931	0.916
		0.05	[1, 10]	0.986	0.866	0.932	0.949
			[6, 10]	0.937	0.801	0.894	0.906
		0.1	[1, 10]	0.983	0.872	0.932	0.950
			[6, 10]	0.937	0.798	0.897	0.900
	6	0.01	[1, 10]	0.981	0.871	0.926	0.918
			[6, 10]	0.933	0.868	0.922	0.910
		0.05	[1, 10]	0.983	0.869	0.937	0.953
			[6, 10]	0.925	0.819	0.892	0.918
		0.1	[1, 10]	0.986	0.872	0.935	0.950
			[6, 10]	0.931	0.810	0.891	0.903
	3	0.01	[1, 10]	0.985	0.881	0.939	0.935
			[6, 10]	0.951	0.896	0.951	0.917
		0.05	[1, 10]	0.980	0.874	0.920	0.952
			[6, 10]	0.933	0.814	0.894	0.890
		0.1	[1, 10]	0.982	0.867	0.925	0.947
			[6, 10]	0.935	0.800	0.896	0.894
20	17	0.01	[1, 20]	0.999	0.922	0.939	0.969	40	37	0.01	[1, 40]	0.999	0.928	0.946	0.963
			[11, 20]	1.000	0.923	0.944	0.968				[31, 40]	1.000	0.938	0.947	0.959
			[16, 20]	0.987	0.919	0.942	0.968				[36, 40]	0.992	0.931	0.945	0.966
		0.05	[1, 20]	0.998	0.875	0.901	0.991			0.05	[1, 40]	0.991	0.817	0.833	0.986
			[11, 20]	0.871	0.781	0.816	0.968				[31, 40]	0.716	0.669	0.675	0.960
			[16, 20]	0.717	0.652	0.673	0.973				[36, 40]	0.650	0.612	0.620	0.947
		0.1	[1, 20]	0.998	0.881	0.910	0.997			0.1	[1, 40]	0.998	0.857	0.870	0.995
			[11, 20]	0.911	0.787	0.834	0.965				[31, 40]	0.612	0.522	0.539	0.968
			[16, 20]	0.690	0.598	0.633	0.966				[36, 40]	0.496	0.435	0.454	0.950
	13	0.01	[1, 20]	0.997	0.937	0.955	0.969		33	0.01	[1, 40]	0.999	0.935	0.943	0.969
			[11, 20]	0.988	0.933	0.953	0.965				[31, 40]	0.999	0.946	0.956	0.976
			[16, 20]	0.955	0.939	0.955	0.969				[36, 40]	0.966	0.956	0.966	0.984
		0.05	[1, 20]	0.998	0.880	0.902	0.980			0.05	[1, 40]	0.999	0.904	0.915	0.968
			[11, 20]	0.938	0.884	0.901	0.971				[31, 40]	0.901	0.901	0.914	0.976
			[16, 20]	0.879	0.829	0.847	0.978				[36, 40]	0.993	0.868	0.873	0.981
		0.1	[1, 20]	0.997	0.880	0.921	0.991			0.1	[1, 40]	0.994	0.861	0.872	0.985
			[11, 20]	0.906	0.812	0.844	0.969				[31, 40]	0.813	0.762	0.768	0.973
			[16, 20]	0.835	0.751	0.781	0.976				[36, 40]	0.768	0.709	0.716	0.988
	11	0.01	[1, 20]	0.997	0.937	0.953	0.973		31	0.01	[1, 40]	0.997	0.932	0.939	0.966
			[11, 20]	0.960	0.923	0.944	0.949				[31, 40]	0.976	0.930	0.943	0.962
			[16, 20]	0.946	0.925	0.946	0.969				[36, 40]	0.950	0.939	0.950	0.983
		0.05	[1, 20]	0.995	0.887	0.910	0.979			0.05	[1, 40]	0.995	0.908	0.922	0.965
			[11, 20]	0.910	0.872	0.891	0.969				[31, 40]	0.926	0.885	0.901	0.972
			[16, 20]	0.893	0.851	0.874	0.976				[36, 40]	0.912	0.893	0.907	0.979
		0.1	[1, 20]	0.996	0.880	0.902	0.991			0.1	[1, 40]	0.995	0.880	0.889	0.980
			[11, 20]	0.897	0.820	0.844	0.965				[31, 40]	0.859	0.824	0.833	0.977
			[16, 20]	0.887	0.810	0.838	0.972				[36, 40]	0.854	0.813	0.819	0.984
	5	0.01	[1, 20]	0.999	0.924	0.946	0.971		20	0.01	[1, 40]	0.999	0.936	0.939	0.962
			[11, 20]	0.946	0.929	0.946	0.964				[31, 40]	0.936	0.926	0.936	0.966
			[16, 20]	0.946	0.929	0.946	0.964				[36, 40]	0.936	0.926	0.936	0.966
		0.05	[1, 20]	0.994	0.873	0.904	0.982			0.05	[1, 40]	0.995	0.926	0.932	0.968
			[11, 20]	0.949	0.886	0.914	0.960				[31, 40]	0.929	0.921	0.929	0.967
			[16, 20]	0.947	0.896	0.919	0.958				[36, 40]	0.929	0.921	0.929	0.967
		0.1	[1, 20]	0.996	0.876	0.902	0.993			0.1	[1, 40]	0.998	0.908	0.919	0.979
			[11, 20]	0.956	0.851	0.890	0.968				[31, 40]	0.917	0.900	0.908	0.978
			[16, 20]	0.954	0.869	0.906	0.968				[36, 40]	0.916	0.903	0.911	0.978

• Model: y_i = β₀ + β₁x_i + δ₁(x_i − τ₁) + ε_i, (i = 1, …, n), where a⁺ = max(0, a) and ε_i ∼ N(0, σ²).

• $({\text{APC}}_1,{\text{APC}}_2)=((e^{{\beta }_2}-1)\times 100,(e^{{\beta }_2}-1)\times 100)=(0.5,-2)$

Table 3(b).

Coverage Probability of 95% Confidence Interval for AAPC over [c, d]: Two joinpoint model case

n	τ1, τ2	σ	[c, d]	mCCI	MCI	FLT	EmpQ	n	τ1, τ2	σ	[c, d]	mCCI	MCI	FLT	EmpQ
20	13,17	0.01	[1, 20]	0.999	0.886	0.918	0.964	40	33, 37	0.01	[1, 40]	0.999	0.870	0.881	0.972
			[11, 20]	0.994	0.874	0.899	0.942				[31, 40]	0.993	0.884	0.898	0.966
			[16, 20]	0.898	0.840	0.860	0.918				[36, 40]	0.897	0.861	0.870	0.946
		0.05	[1, 20]	1.000	0.845	0.886	0.983			0.05	[1, 40]	1.000	0.876	0.889	0.986
			[11, 20]	0.948	0.849	0.872	0.950				[31, 40]	0.966	0.883	0.895	0.972
			[16, 20]	0.848	0.754	0.802	0.954				[36, 40]	0.854	0.799	0.812	0.965
		0.1	[1, 20]	1.000	0.802	0.850	0.971			0.1	[1, 40]	1.000	0.859	0.869	0.981
			[11, 20]	0.926	0.826	0.867	0.966				[31, 40]	0.829	0.764	0.777	0.961
			[16, 20]	0.790	0.699	0.742	0.961				[36, 40]	0.740	0.683	0.690	0.965
	11, 17	0.01	[1, 20]	0.999	0.892	0.920	0.958		31, 37	0.01	[1, 40]	0.996	0.887	0.901	0.963
			[11, 20]	0.977	0.867	0.896	0.927				[31, 40]	0.975	0.871	0.886	0.942
			[16, 20]	0.916	0.852	0.880	0.916				[36, 40]	0.902	0.865	0.871	0.924
		0.05	[1, 20]	0.999	0.847	0.887	0.979			0.05	[1, 40]	1.000	0.867	0.884	0.989
			[11, 20]	0.920	0.826	0.857	0.939				[31, 40]	0.946	0.868	0.881	0.963
			[16, 20]	0.817	0.702	0.763	0.955				[36, 40]	0.830	0.774	0.786	0.970
		0.1	[1, 20]	1.000	0.810	0.855	0.975			0.1	[1, 40]	1.000	0.863	0.871	0.987
			[11, 20]	0.909	0.824	0.860	0.961				[31, 40]	0.847	0.790	0.802	0.942
			[16, 20]	0.818	0.713	0.772	0.966				[36, 40]	0.781	0.715	0.733	0.973
	5, 17	0.01	[1, 20]	1.000	0.906	0.940	0.961		20, 37	0.01	[1, 40]	0.997	0.923	0.932	0.960
			[11, 20]	0.992	0.898	0.926	0.943				[31, 40]	0.990	0.935	0.939	0.956
			[16, 20]	0.950	0.884	0.906	0.928				[36, 40]	0.961	0.910	0.917	0.961
		0.05	[1, 20]	0.998	0.819	0.863	0.961			0.05	[1, 40]	1.000	0.818	0.838	0.984
			[11, 20]	0.901	0.790	0.838	0.939				[31, 40]	0.723	0.634	0.662	0.969
			[16, 20]	0.670	0.572	0.618	0.934				[36, 40]	0.450	0.394	0.399	0.932
		0.1	[1, 20]	0.999	0.778	0.836	0.955			0.1	[1, 40]	1.000	0.851	0.865	0.991
			[11, 20]	0.931	0.804	0.859	0.948				[31, 40]	0.795	0.710	0.724	0.974
			[16, 20]	0.812	0.686	0.758	0.951				[36, 40]	0.534	0.464	0.482	0.936
	5, 13	0.01	[1, 20]	1.000	0.912	0.944	0.944		20, 33	0.01	[1, 40]	1.000	0.934	0.944	0.963
			[11, 20]	0.985	0.929	0.951	0.951				[31, 40]	0.998	0.954	0.963	0.973
			[16, 20]	0.941	0.912	0.938	0.938				[36, 40]	0.941	0.932	0.941	0.974
		0.05	[1, 20]	0.999	0.858	0.897	0.971			0.05	[1, 40]	1.000	0.864	0.873	0.985
			[11, 20]	0.930	0.831	0.870	0.949				[31, 40]	0.790	0.731	0.739	0.957
			[16, 20]	0.840	0.742	0.780	0.957				[36, 40]	0.721	0.665	0.673	0.965
		0.1	[1, 20]	0.999	0.806	0.859	0.960			0.1	[1, 40]	1.000	0.863	0.877	0.995
			[11, 20]	0.934	0.827	0.872	0.957				[31, 40]	0.750	0.672	0.693	0.971
			[16, 20]	0.874	0.761	0.820	0.963				[36, 40]	0.649	0.571	0.593	0.965
	5, 11	0.01	[1, 20]	1.000	0.921	0.955	0.969		20, 31	0.01	[1, 40]	1.000	0.931	0.944	0.961
			[11, 20]	0.952	0.913	0.928	0.924				[31, 40]	0.959	0.933	0.940	0.950
			[16, 20]	0.939	0.916	0.934	0.962				[36, 40]	0.940	0.933	0.940	0.967
		0.05	[1, 20]	0.999	0.864	0.912	0.974			0.05	[1, 40]	1.000	0.875	0.884	0.988
			[11, 20]	0.916	0.820	0.862	0.952				[31, 40]	0.806	0.765	0.776	0.950
			[16, 20]	0.896	0.790	0.834	0.959				[36, 40]	0.798	0.742	0.751	0.974
		0.1	[1, 20]	0.999	0.812	0.866	0.962			0.1	[1, 40]	1.000	0.862	0.877	0.994
			[11, 20]	0.930	0.833	0.867	0.954				[31, 40]	0.762	0.682	0.702	0.962
			[16, 20]	0.910	0.804	0.852	0.963				[36, 40]	0.756	0.672	0.698	0.969
	4, 8	0.01	[1, 20]	0.999	0.897	0.927	0.966		10, 20	0.01	[1, 40]	1.000	0.941	0.956	0.964
			[11, 20]	0.936	0.899	0.923	0.957				[31, 40]	0.941	0.936	0.941	0.963
			[16, 20]	0.934	0.888	0.918	0.959				[36, 40]	0.941	0.936	0.941	0.963
		0.05	[1, 20]	0.998	0.852	0.890	0.964			0.05	[1, 40]	1.000	0.901	0.910	0.991
			[11, 20]	0.948	0.842	0.887	0.948				[31, 40]	0.895	0.825	0.843	0.982
			[16, 20]	0.930	0.822	0.869	0.958				[36, 40]	0.895	0.833	0.855	0.982
		0.1	[1, 20]	0.999	0.808	0.859	0.955			0.1	[1, 40]	1.000	0.882	0.898	0.991
			[11, 20]	0.944	0.827	0.879	0.949				[31, 40]	0.854	0.753	0.777	0.990
			[16, 20]	0.921	0.812	0.862	0.961				[36, 40]	0.852	0.773	0.793	0.989

• Model: y_i = β₀ + β₁x_i + δ₁(x_i − τ₁)⁺ + δ₂(x − τ₂)⁺ + ε_i, (i = 1,…, n), where a⁺ = max(0; a) and ε_i ~ N(0; σ₂).

• $(AP{C}_1,AP{C}_2,AP{C}_3)=\left((e^{{\beta }_1}-1)\times 100,(e^{{\beta }_2}-1)\times 100,(e^{{\beta }_3}-1)\times 100\right)=(1.5,-1,-2.5)$

In Step 2, we used the following definition of a truncated ${\widehat{F}}_n$ and ${\widehat{F}}_n^{-1}$. For the ordered residuals, ${\widehat{\epsilon }}_{(1)}\le \cdots \le {\widehat{\epsilon }}_{(n)}$, define the end points of the intervals where ${\widehat{F}}_n$ is constant as z₍₀₎, z₍₁₎, …, z_(n+1) where $z_{(0)}={\widehat{\epsilon }}_{(n)}-D$, $z_{(i)}={\widehat{\epsilon }}_{(i)}$ for i = 1, …, n, and $z_{(n+1)}={\widehat{\epsilon }}_{(n)}+D$ with $D=\text{log}(3.0+\text{log}n)\ast (\text{third quartile of }\widehat{\epsilon }-\text{first quartile of }\widehat{\epsilon })$. Note that the choice of D is made to ensure the range large enough to cover almost all possible values of the residuals and to allow it to slowly increase as n increases, and the interquartile range was used as a robust measure of the dispersion of the residuals. Then, define ${\widehat{F}}_n$ and ${\widehat{F}}_n^{-1}$ as follows:

$$\begin{array}{l}{\widehat{F}}_n(t)={(n+1)}^{-1}{\displaystyle \sum _{i=1}^{n+1}I(z_{(i)}\le t)},\\ {\widehat{F}}_n^{-1}(u)=\{\begin{array}{l}{z}_{(i)}+\left(z_{(i+1)}-z_{(i)}\right)\ast u^{\prime },\hfill \\ z_{(i+1)},\hfill \end{array}\begin{array}{l}\text{if }u\in \left[\frac{i}{n+1},\frac{i+1}{n+1}\right)\text{for }i\in \{0,\dots ,n\}\hfill \\ \text{if }u=1,\hfill \end{array}\end{array}$$

where u and u′ are independent random numbers from the uniform distribution on (0, 1). We also considered the use of $u^{\prime }=\left(u-\frac{i}{n+1}\right)\ast (n+1)$ and observed that the two methods perform comparably. Once we estimate ${\widehat{\mu }}^{(b)}$ for b = 1, …, B, a confidence interval can be constructed using the 100α-th and 100(1 − α)-th percentiles of the resampled $\widehat{\mu }$ :

$$\left({\widehat{\mu }}_{(\alpha B)}^{(b)},{\widehat{\mu }}_{((1-\alpha )B)}^{(b)}\right),$$

where ${\widehat{\mu }}_{(p)}^{(b)}$ denotes the p-th percentile of $\{{\widehat{\mu }}^{(1)},\dots ,{\widehat{\mu }}^{(B)}\}$. We call this the EmpQ confidence interval. Our motivation of resampling as above is to obtain resamples from a distribution closer to an ideal sampling distribution such that the empirical distribution of the resampled residuals is close to the uniform distribution, and its accuracy is empirically justified in our simulation study.

4 Simulations

We conducted further simulations to investigate the accuracy of the various AAPC confidence intervals discussed in the previous sections. The values for the parameters are chosen based on actual cancer incidence and mortality data, and β₀ is set as 1 in all of these simulations. For a given choice of the regression slope parameters, simulations are conducted with various choices of the number of data points (n), the standard deviation of the error term (σ), and the joinpoint locations (τ), and the number of simulations was 1,000. For the interval [c, d] over which the AAPC is calculated, we considered three cases of the entire data range, the last 5 years, and the last 10 years, which are often of our interest in cancer trend analysis. The model fitting was done using JOINPOINT with the fitting parameters set as described in Section 2, including the quarterly grid search. In our simulation study, we also considered the basic grid search where the x-values of the observations serve as the grid points, for which similar results are obtained, and the results with the quarterly grid search are presented in Tables 3(a) and 3(b).

Tables 3(a) and 3(b) compare the accuracy of the four types of the confidence intervals, the modified confidence interval based on the CCI of Clegg et al. [2] (mCCI), the improved confidence interval based on the Muggeo’s method (MCI), the First-Last t-interval (FLT), and the empirical CDF quantile interval (EmpQ) with 1,000 replications. For each simulation setting, the values reported are the coverage probabilities, the proportion of simulation runs where the 95% confidence interval contains the true value of μ. Tables 3(a) and 3(b) report the coverage probabilities for the cases with k = 1 and 2, respectively.

The mCCI is usually conservative with its coverage probability larger than the nominal level of 0.95 when [c, d] = [1, n], but the mCCI underestimated the coverage probability in many cases with [c, d] = [d − 4, d] and for some cases with [c, d] = [d − 9, d]. The observed under-coverage is possibly due to skewness in the distribution of the AAPC estimates, and such under-coverage gets worse as σ increases. This under-coverage tendency was observed even with many of the t-intervals used instead of the z-intervals when [c, d] belongs to one segment: e.g. n = 10, τ = 3, [c, d] = [6, 10] and n = 40, τ = 20, [c, d] = [31, 40]. The under-coverage tends to be worse when the location of joinpoint is close to c, especially when σ is not very small.

The MCI that incorporates the joint distribution between the estimated regression slope coefficients and estimated joinpoints is usually liberal, and its coverage probabilities are sometimes much below 0.95. When the subinterval is considered, additional uncertainty involved in estimating I and J in (6) might have contributed to poor performance of the MCI, and it is especially so when σ is large. The MCI also tends to underestimate the coverage probability more for cases with larger σ, but the coverage probabilities are at least 0.92 when σ = 0.01 and n ≥ 20 for k = 1 and in some cases with σ = 0.01 and n = 40 for k = 2. When k = 2, the performance of the MCI seems better when τ₁ is much below c for [c, d]. In general, it was observed in Tables 3(a) and 3(b) that the MCI works better as n increases with small σ, which matches with our finding in Table 2 that the MCI performs reasonably well when n = 100 except for a few cases. The FLT that is practically equivalent to the MCI but constructed with the t-percentiles improves the MCI, and the coverage probability of the FLT are close to 0.95, although still under 0.95, when σ is small as 0.01 for all of n = 10, 20 and 40 when k = 1 in Table 3(a) and when σ is small as 0.01 and both joinpoints are not in [n − 9, n] when k = 2 in Table 3(b). But, it still underestimates the coverage probability, especially for large σ.

In most of cases we tried, the EmpQ method works best keeping its coverage probability close to 0.95. The EmpQ method improves severe under-coverage observed by other parametric methods, and when both the EmpQ CI and mCCI are conservative, the EmpQ CI is less conservative than the mCCI. For a situation with small n such as 10, the method that produced the average coverage probability closest to 0.95 is the mCCI, but as shown in Table 2, the mCCI usually overestimates the standard error of $\widehat{\mu }$ and its coverage probability is often close to 1 if [c, d] = [1, n]. Thus, our general recommendation is to use the EmpQ confidence interval, and one may consider the FLT or mCCI when the sample size is as small as 10, σ is small, and [c, d] is short, which is the case where EmpQ performs somewhat liberal.

5 Examples

In this section, we apply the confidence intervals discussed in the previous sections to several cancer sites. We consider incidence rates of several cancer sites for various cohorts observed during the period of [1975, 2010], and the data are obtained from the Surveillance, Epidemiology, and End Results Program (SEER) of the National Cancer Institute. JOINPOINT V 4.0.5 was used to fit the joinpoint regression model with the annual grid search and the default setting described in Section 2, and the fits are shown in Figures 1, 2, 3, 4, and 5. For each data set, JOINPOINT selects the model, i.e. the number of joinpoints, by using the permutation procedure at the overall significance level of 0.05 and with the maximum number of joinpoints set at 5, and the AAPCs under the selected model are presented in Table 4. Table 4 summarizes the AAPC estimates during the last five [2006–2010] and/or ten year [2001–2010] periods, and includes the confidence intervals obtained by the mCCI, FLT, and EmpQ methods.

Figure 1.

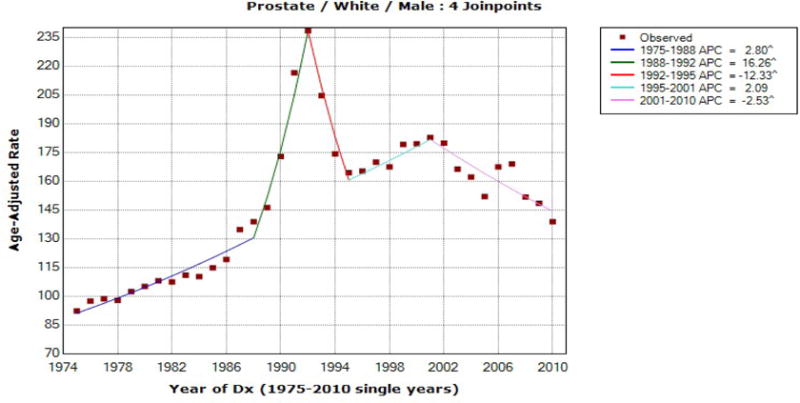
Prostate Cancer Incidence for White Males

Figure 2.

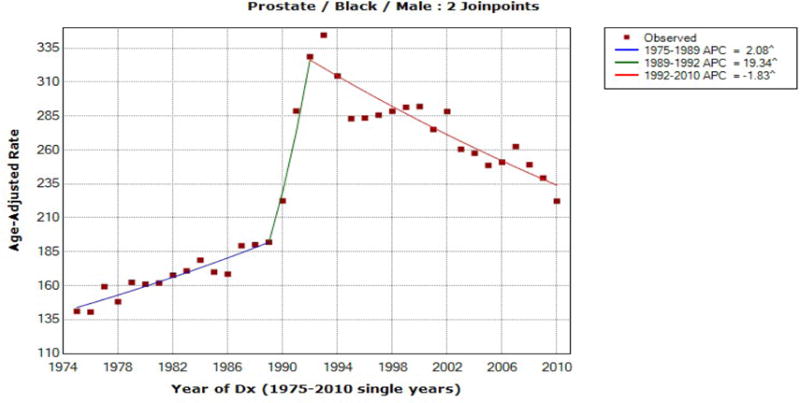
Prostate Cancer Incidence for Black Males

Figure 3.

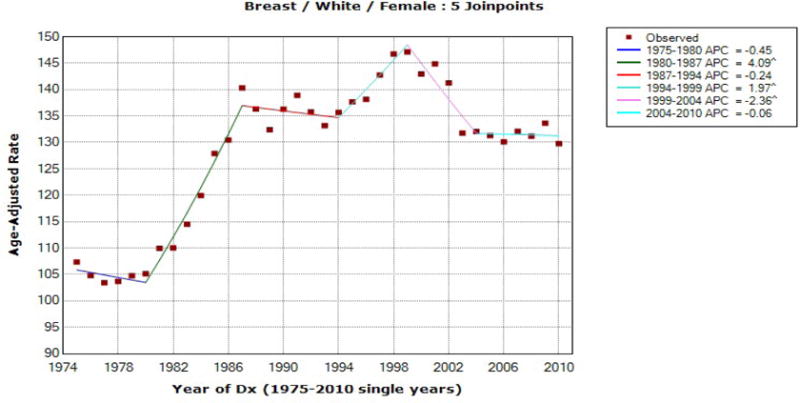
Breast Cancer Incidence for White Females

Figure 4.

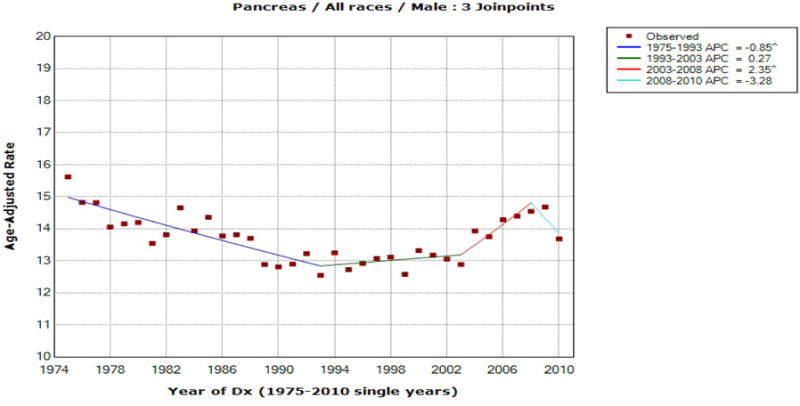
Pancreas Cancer Incidence for Males (All Races)

Figure 5.

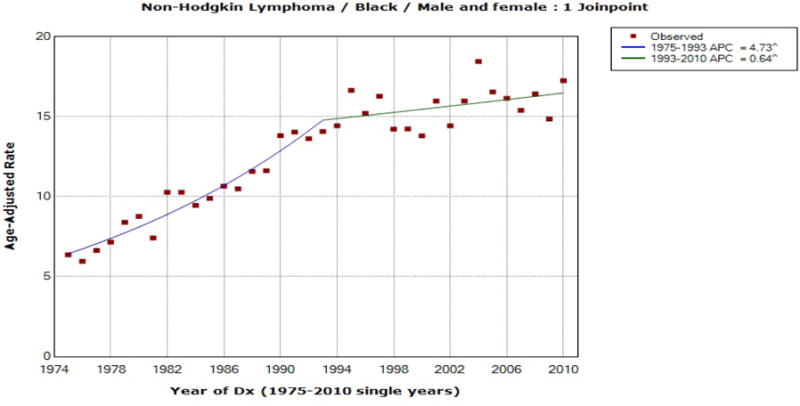
Non-Hodgkin Lymphoma Incidence for Blacks (Both Sexes)

Table 4.

Confidence Intervals for AAPC over [c, d]

	Joinpoint estimates	[c, d]	AAPC	95% CI for AAPC
				mCCI	FLT	EmpQ
Prostate Incidence (White male)	88, 92, 95, 01	[2006, 2010] [2001, 2010]	−2.535 −2.535	(−3.428, −1.633)* (−3.428, −1.633)*	(−3.428, −1.633)* (−3.476, −1.585)*	(−4.282, −1.709)* (−3.161, −1.676)*
Prostate Incidence (Black male)	89, 92	[2006, 2010] [2001, 2010]	−1.830 −1.830	(−2.160, −1.499)* (−2.160, −1.499)*	(−2.160, −1.499)* (−2.160, −1.499)*	(−2.160, −1.526)* (−2.160, −1.526)*
Breast Incidence (White female)	80, 87, 94, 99, 04	[2006, 2010] [2001, 2010]	−0.056 −0.831	(−0.858, 0.752) (−1.512, −0.146)*	(−0.858, 0.752) (−1.165, −0.497)*	(−0.631, 0.854) (−1.142, −0.518)*
Pancreas Incidence (Male: All races)	93, 03, 08	[2001, 2010]	0.610	(−1.011, 2.257)	(0.069, 1.154)*	(0.111, 1.311)*
Non-Hodgkin Lymphoma (Blacks: Both sexes)	93	[2001, 2010]	0.640	(0.010, 1.275)*	(0.010, 1.275)*	(−0.577, 1.339)

• ^*: significant at 0.05 level of significance

• mCCI: modified conditional confidence interval; FLT: First-Last t-confidence interval; EmpQ: Empitical qantile method confidence itnerval

For white male prostate cancer incidence rates, JOINPOINT selected the model with four joinpoints, and the estimated joinpoints are 1988, 1992, 1995, and 2001. The estimated AAPCs during the 2006–2010 and 2001–2010 periods are the same as −2.535, and the same AAPC estimate during these two time intervals is expected because there was no joinpoint estimated after 2001. The mCCIs for these two time periods are the same as well. When the FLT method was used for white male prostate cancer incidence, there is a difference between the FLT confidence limits during these two time periods, [2006, 2010] and [2001, 2010], although the AAPC estimates remain unchanged. This is due to the fact that the year of 2001 was the last joinpoint estimated and the FLT CI over [2001, 2010] incorporated the distribution of the estimators in the fourth segment as well as in the fifth segment. Note that for [c, d] = [2006, 2010], the FLT CI and mCCI estimates are identical, which is expected by the use of the t-interval for the slope of the fifth segment in both approaches. The EmpQ confidence limits are included in the last column and the difference between the EmpQ CIs for the AAPC during two time periods is considerably larger than the difference between the FLT CIs for these two time periods. This can be explained by that resampled data may or may not have the last joinpoint in [2001, 2010] and thus larger variability in the resampled AAPC values, compared to the standard error estimates in the parametric methods, is anticipated. This example illustrates that the mCCI and FLT CI are identical if the period [c, d] is composed with one segment and does not touch the estimated joinpoint at either end, but the FLT confidence limits change and thus the mCCI and FLT limits are different if a joinpoint is estimated at c or d.

For black male prostate incidence data, the joinpoints are estimated at 1989 and 1992 and we observe the exact matches between mCCI and FLT confidence limits for both time periods, [2006, 2010] and [2001, 2010], and the EmpQ confidence intervals for these two time periods are also identical. Differently from the last ten year AAPC for white male prostate incidence, the estimated last joinpoint of 1992 for black male prostate incidence indicates that the AAPC during the last ten year of [2001, 2010] for the resampled data is likely to be based on one segment only and thus the identical EmpQ CIs for the last five and ten year AAPCs seem reasonable. For white female breast cancer incidence data, the joinpoints are estimated as 1980, 1987, 1994, 1999, and 2004, and thus the AAPC confidence interval estimates are expected to be different between the two periods and also among the methods used. The estimated AAPCs are −0.056 and −0.831 for the last five and ten years, respectively, and the confidence intervals are presented in Table 4. The mCCI and FLT confidence intervals for the last five year AAPC match, but the mCCI and FLT confidence limits for the last ten year AAPC are different, which is due to the joinpoint estimated at 2004.

In summary, if [c, d] is composed with several segments, then mCCI, FLT CI, and EmpQ CI will be all different in general (for example, white female breast cancer incidence for [2001, 2010]). When [c, d] is composed with one segment but a joinpoint is estimated at c or d, these three methods are also expected to produce different confidence intervals (for example, white male prostate cancer incidence for [2001, 2010]). If [c, d] is composed with one segment and doesn’t touch the estimated joinpoint at either end, the confidence limits obtained by the mCCI and FLT methods will match, but these will be different from the confidence limits of the EmpQ method in general. For example, see the case of black male prostate incidence for [2001, 2010].

For the first six rows of Table 4, the significance of AAPC does not change depending on the method of the confidence interval used, but the two cases reported at the bottom of Table 4 illustrate a situation where the significance of AAPC varies depending on the method used to construct the confidence interval. For male (all races) pancreas incidence rates, the final model selected by JOINPOINT was the one with three joinpoints at 1993, 2003 and 2008, and the 95% confidence interval for the AAPC during the last ten year period is obtained as (−1.011, 2.257) by the mCCI method, (0.069, 1.154) by the FLT method, and (0.111, 1.311) by the empirical quantile method. Thus, if one’s interest is on the significance of the last 10 year AAPC, the EmpQ CI and the FLT CI indicate its significance, while it is not significant based on the mCCI method. In the Non-Hodgkin lymphoma case, however, the last 10 year AAPC is not significant based on the EmpQ confidence interval, while it is significant based on the mCCI and FLT methods. Incidence rates for the Non-Hodgkin lymphoma has a larger variability than those of pancreas incidence, and [2001, 2010] includes estimated joinpoints for the pancreas incidence data, while there is no estimated joinpoint in [2001, 2010] for the Non-Hodgkin lymphoma data. This matches with the findings for n = 40 and [c, d] = [31, 40] in Table 3(b): for small σ of 0.01 and (τ₁, τ₂) = (31, 37), the mCCI CI tends to be more conservative than the EmpQ CI and the coverage probability of the FLT CI is considerably below 0.95, while for large σ of 0.1 and (τ₁, τ₂) = (10, 20), the mCCI and FLT CI tend to be liberal and the EmpQ CI is conservative. Based on our simulation study summarized in Tables 3(a) and 3(b), a change from a significant mCCI, which is the method currently being used in JOINPOINT, to a non-significant EmpQ CI is possible if [c, d] is short and σ is large, and/or the estimated joinpoint is near the end of the interval, [c, d]. On the other hand, one could observe a change from a non-significant mCCI to a significant EmpQ CI if [c, d] is long or σ is small. The examples of pancreas and Non-Hodgkin lymphoma incidence data illustrate such situations.

6 Discussion

This paper considers how to obtain an improved confidence interval for the AAPC in trend analysis, which is a function of a weighted average of the regression slope coefficients in segmented line regression with unknown change-points. As indicated in Muggeo [4] and further investigated in this paper, it was found that the coverage probability of the conditional confidence interval proposed by Clegg et al. [2] is often larger than the nominal level, especially when the time period in consideration is long, and incorporating the joint distribution between the estimated regression coefficients and change-points was considered as a way to improve the CCI. However, our simulations indicated that the improved confidence interval originally proposed by Muggeo [4] and further improved in this paper by using a t-distribution is not still satisfactory, especially when the interval over which the AAPC is calculated is short, data vary a lot around the mean function, or the number of observations is not large enough. This is possibly due to skewness of the sampling distribution or an inaccurate small sample estimate of the standard error of the estimated change-points as well as an inaccurate small sample estimate of the covariance between the estimated regression coefficients and change-points. Also, as indicated in Hinkley [6], the convergence of the distribution of the estimated change-point to a normal distribution is rather slow and this may influence the convergence of the distribution of the AAPC estimators. With improved estimates of these standard errors and covariance values, an improved confidence interval could be achieved, but we expect that such slower convergence of the estimated change-point distribution may still require a very large number of observations in order to achieve a reasonable accuracy.

The empirical CDF quantile (EmpQ) confidence interval proposed in this paper performs quite accurately for cases with n such as 20 or 40, regardless of the length of the interval over which the AAPC is calculated, and it outperforms other parametric methods except for cases with a small number of observations such as 10, σ is small, and a short interval over which the AAPC is calculated.

As illustrated in the examples, JOINPOINT program selects the model, i.e. the number of joinpoints, using some selection methods such as the permutation procedure or Bayes Information Criteria, and it should be noted that the results presented in this paper are valid under the model with the true number of joinpoints. Under certain conditions, the consistency of the estimated number of joinpoints can be achieved (Kim et al. [22] and Kim and Kim [23]), and then the EmpQ CI is expected to maintain the confidence level to the level observed in this paper. It is our plan to conduct further simulation studies to investigate the accuracy of the various CIs incorporating the model selection procedure, and it will be pursued in our future research.