User Intent Prediction with a Scaled Conjugate Gradient Trained Artificial Neural Network for Lower Limb Amputees Using a Powered Prosthesis

Abstract

Powered lower limb prostheses have the ability to provide greater mobility for amputee patients. Such prostheses often have pre-programmed modes which can allow activities such as climbing stairs and descending ramps, something which many amputees struggle with when using non-powered limbs. Previous literature has shown how pattern classification can allow seamless transitions between modes with a high accuracy and without any user interaction. Although accurate, training and testing each subject with their own dependent data is time consuming. By using subject independent datasets, whereby a unique subject is tested against a pooled dataset of other subjects, we believe subject training time can be reduced while still achieving an accurate classification. We present here an intent recognition system using an artificial neural network (ANN) with a scaled conjugate gradient learning algorithm to classify gait intention with user-dependent and independent datasets for six unilateral lower limb amputees. We compare these results against a linear discriminant analysis (LDA) classifier. The ANN was found to have significantly lower classification error (P<0.05) than LDA with all user-dependent step-types, as well as transitional steps for user-independent datasets. Both types of classifiers are capable of making fast decisions; 1.29 and 2.83 ms for the LDA and ANN respectively. These results suggest that ANNs can provide suitable and accurate offline classification in prosthesis gait prediction.

I. INTRODUCTION

By 2020 it is estimated that there will be over 2.2 million people living with limb loss in the United States, 879,000 of which will have a major (excluding toes) lower limb amputation [1]. Powered knee and ankle prostheses are assistive devices that have shown great promise in treating above knee amputation. These devices use motors to provide positive mechanical work at both joints, and often contain pre-programmed locomotive modes to assist in navigating environmental obstacles such as stairs and inclines. These programmed modes can alleviate some of the difficulties encountered with passive or microprocessor controlled prostheses [2]. However, switching between modes requires manual intervention such as compensatory movement, physical prosthesis interaction, or use of a smartphone interface [3], all of which are slow, cumbersome, and create a cognitive burden for the user. An optimal system would recognise and change the locomotive mode based on the upcoming obstacle, without any user input.

In previous studies, our group has applied machine learning techniques to powered prostheses in order to automatically predict the required locomotive mode for level walking and stairs/ramp ascent/descent. Using feature information from mechanical sensors on-board the prosthesis, and linear discriminant analysis (LDA) classification methods, results have shown promising offline and real-time application [4]–[6].

Although suitable results have been demonstrated with these techniques, they require lengthy data collection sessions in which the user navigates a controlled environment. Their data is then used in training the learning algorithm. An alternative method, where the learning algorithm is trained on a pooled dataset of multiple other users and is tested against a unique user, has been previously applied with promising initial results [7]. This ‘user-independent’ training methodology can reduce individual user training times substantially. However, pooling data across multiple users has resulted in lower classification accuracies.

It is possible that user-independent classification involves learning a more complicated and perhaps non-linear feature space. If so, then a non-linear artificial neural network (ANN) classifier would be better suited for this application. The objective of this study was to evaluate the performance of an ANN intent recognition system to classify four locomotive modes; level walking, stairs ascent, stairs descent, and ramp descent. The performance was compared to a previously used LDA classifier for both user-dependent and user-independent classification. Furthermore, both the feed-forward operations of the ANN and LDA were timed while classifying on our embedded system to determine their computational efficiency and suitability in future real-time applications.

II. METHODOLOGY

A. Experimental Protocol

Six unilateral lower limb amputees (five male and one female, five transfemoral and one knee disarticulation, four with left and two with right leg amputation, aged between 23 and 65, height between 1.6 and 1.93 m, and weight between 52 and 96 kg) participated in this study, with approval from the Northwestern University Institutional Review Board. Written and verbal consent was obtained from each subject involved.

All subjects were fitted with a powered knee and ankle prosthesis, developed by Vanderbilt University [8]. Each subject was trained to use the leg and their impedance parameters were hand-tuned using a previously described method prior to the data collection [9]. During a single collection session, the subjects were asked to perform a number of repeated activities including level walking and ascending/descending stairs/ramps. The protocol of this procedure has been described in detail in a previous study [10]. Briefly, an experimenter used a key-fob to automatically transition the leg between activities and label the activity that the user was performing. Data from mechanical sensors were also collected and included: relative knee and ankle positions, velocities, and commanded joint torques. Other sensors included a six degree of freedom load cell and a six degree of freedom IMU, both mounted midway through the shank. A complimentary filter was used to compute the angle of the thigh and the angle of the shank relative to the vertical.

B. Signal Processing

All data were collected and stored on-board an embedded system on the prosthesis, and signal processing was performed offline using MATLAB. The data were normalised between subjects to account for the side of amputation. Subjects with a right leg amputation had the appropriate mechanical channels transformed (reversed sign) prior to processing.

The axial load through the prosthesis was used to segment gait phases into a stance and swing phase. The time points where the device transitioned from stance to swing was labelled as toe-off and the time point where the device transitioned from swing to stance was labelled as heel-contact. The device was allowed to transition between different activities at only these discrete events. The mechanical sensor data were segmented into a 300 ms window prior to a transition point, and six features were extracted from the window including mean, standard deviation, min, max, initial, and final value of each sensor channel, producing a one by 120 feature vector per window [10], [11].

Each feature vector had a corresponding ground-truth locomotion mode (level walking (LW), stairs ascent (SA), stairs descent (SD), or ramp descent (RD)) and the step-type, which provides information on whether the step changed from one mode to another (transitional (T)) or remained in the same mode (steady-state (SS)). The prosthesis uses the same impedance parameters for ramp ascent as level walking, and therefore all ramp ascent triggers were reassigned as LW. Each subject’s features were split into heel-contact or toe-off, based on when each of the triggers were fired.

C. Classifiers

The ANN had one hidden layer and 20 hidden neurons and was trained using a scaled conjugate gradient learning algorithm [12] and a hyperbolic tangent activation function. Each classifier was trained over 1000 epochs with a break clause once the training error improvement plateaued at a precision of 0.001. Weights were initialised randomly between a range of:

$$\left(\frac{-1}{\sqrt{fv}},\frac{1}{\sqrt{fv}}\right)$$ (1)

Where fv represents the number of inputs, which in this case is 120, resulting in initial weights between ±0.091. The LDA has no initialisation of weights and no iterative process, and therefore has a simpler topology. Training consists of a single iteration with no error feedback or learning process.

D. Performance Evaluation

Validation was performed using a randomised 75/25% training and test dataset split, respectively. In order to reduce discrepancies seen in the results produced by the randomised validation sets and weights, the classifiers were run ten times for each subject/classifier group, and the mean error (%) was taken and processed.

This study investigated two classification methods:

1. Dependent Classification: Each subject was trained and tested using their own data in order to obtain a dependent accuracy in learning.

2. Independent Classification: The feature/output datasets were pooled between subjects. Using a leave-one-out method, six groups were produced using the data from five subjects. The sixth subject had their data tested against the grouped classifier data of the remaining five subjects in order to obtain an independent accuracy in learning.

The average intent recognition error, across all subjects and classifier groups, was used as our primary performance metric for both the dependent and independent tests. Error rates are presented in a combined form (both SS and T together), as well as individual SS and T. ANN and LDA results are presented side by side, with a paired t-test analysis to determine significant differences between classification methods. Confusion matrices are also presented, displaying individual locomotive mode accuracies for ANN and LDA results, in both dependent and independent test sets.

Finally, to determine the ANN’s future suitability for real-time classification, its computational processing time was recorded while classifying on-board our embedded system; a Texas Instruments DM3730 processor running at 600 MHz. To determine classifier times this evaluation was run without any classifier to calculate a baseline, and then again individually with the ANN and LDA classifiers to determine added time required for classification. An average time was calculated by running this test on five independent subject datasets, three times each, for the baseline, ANN, and LDA classifiers.

II. RESULTS

Classification error percentages using subject dependent and independent data can be seen represented in Fig. 1 and Table I, as well as corresponding standard error of the mean (SEM) values.

Figure 1.

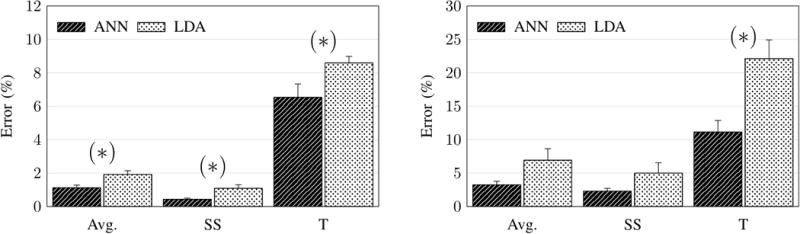
Classification results for ANN and LDA classifiers for subject dependent (left) and independent (right) datasets (error bars represent SEM, asterisk indicates significant difference (P<0.05)). Avg. represents the combined weighted average across SS and T

Table 1.

ERROR RATES FOR ANN AND LDA CLASSIFIERS FOR SUBJECT DEPENDENT (LEFT) AND INDEPENDENT (RIGHT) DATASETS (% [SEM]). AVG. REPRESENTS THE COMBINED WEIGHTED AVERAGE ACROSS SS AND T.

	Avg.	SS	T		Avg.	SS	T
ANN	1.12 [0.16]	0.43 [0.07]	6.53 [0.80]	ANN	3.25 [0.52]	2.29 [0.41]	11.13 [1.73]
LDA	1.92 [0.22]	1.09 [0.21]	8.59 [0.39]	LDA	6.92 [1.72]	4.99 [1.55]	22.12 [2.79]

Table II shows the confusion matrices of the dependent and independent tests, where a value in row i and column j represents the prediction known to be in mode i but predicted to be in mode j. Values displayed in bold indicate the accuracy of a correct prediction.

Table 2.

CONFUSION MATRICES FOR ANN AND LDA CLASSIFICATION OF THE FOUR GAIT MODES FOR SUBJECT DEPENDENT (LEFT) AND INDEPENDENT (RIGHT) DATASETS.

		LW	SA	SD	RD			LW	SA	SD	RD
ANN	LW	99.37	0.08	0.08	0.47	ANN	LW	98.41	0.36	0.14	1.08
	SA	5.70	94.30	0.00	0.00		SA	8.14	91.71	0.00	0.15
	SD	1.09	0.00	98.91	0.00		SD	2.29	0.00	97.34	0.37
	RD	2.79	0.00	0.00	97.21		RD	17.65	0.00	0.10	82.25
LDA	LW	98.15	0.35	0.28	1.22	LDA	LW	92.75	1.57	1.05	4.63
	SA	5.03	94.97	0.00	0.00		SA	6.91	93.09	0.00	0.00
	SD	1.09	0.00	98.91	0.00		SD	0.46	0.27	98.53	0.73
	RD	1.60	0.00	0.00	98.40		RD	7.99	0.00	0.00	92.01

Differences between ANN and LDA results were found to be significant (P<0.05) in all dependent sets, however, only significant in the transitional independent set.

Online computational times for the entire control system process (feature extraction, state-machine progression, and construction of motor command outputs) were found to be 12.42 [1.06], 13.70 [0.45], and 15.25 [0.56] ms [standard deviation] for the baseline, LDA, and ANN classifiers respectively. LDA and ANN times were subtracted from the baseline to obtain individual classifier processing times of 1.29 and 2.83 ms, respectively.

III. DISCUSSION

These results indicate that the ANN yields lower classification errors than that produced by the LDA, in both dependent and independent data sets. Error rates are expectedly higher in transitional classification than steady-state, due to the added complexities in classifying a change in locomotive mode, as opposed to classification of no change in mode seen in the SS results. However, transitional steps make up only 11% of the total steps across all subjects and therefore this has a smaller impact on the average error rate. Furthermore in prior work we have found that even steady-state errors are capable of causing moderate or substantial perturbations to the user [13]. Consequently it is important to reduce both error types as much as possible. Likewise, error rates are higher in the independent dataset analysis when compared against the dependent results as the variability seen in each subject’s gait technique is expected to affect classification.

Other than the dependent transitional results, the LDA classifier had larger SEM values than the ANN (Fig. 1, Table I). This is particularly interesting for the independent subject datasets, as this would indicate better classification adaption for each individual subject when using an ANN.

Correct locomotive mode classification, as seen in the diagonal columns of Table II show that the LDA has better classification than the ANN in all locomotive modes other than LW, for both dependent and independent datasets. However, as LW makes up 79% of the total gait activity (SA, 5%; SD, 8%; RD 8%) the ANN achieves a higher weighted accuracy overall.

Real-time classification times show that the LDA performs faster than the ANN. However, it is worth noting that while the LDA classifies in a single iteration, the ANN has to propagate the data/weights through each layer, resulting in a three-stage classification process. In previous work resulting in real-time ambulation, we allowed for a control system processing time of up to 30 ms which was not noted by the user [13], [14]. Both the ANN (15.25 ms) and LDA (13.70 ms) comfortably allow for operation within this time window.

This preliminary evaluation has some limitations. Firstly, we evaluated only six subjects. With more subjects it may be possible to match the user-independent subjects with a subset of overall subjects based on weight, height, side of amputation, and residual limb length. This would likely allow for better user-independent classification performance. Secondly, this was an offline study meaning that a member of the research team transitioned the prosthesis for the subject using a key-fob.

However, in previous work we have found a strong correlation between offline classification error and real-time performance [13] suggesting that our results will extend to online testing.

IV. CONCLUSION

The results presented here demonstrate that an ANN with a scaled conjugate gradient learning algorithm can produce suitable results in offline prosthetic classification when compared against an LDA classifier. In future work, we will investigate adapting the ANN in real-time to determine if it is possible to automatically converge from user-independent error-rates to user-dependent error-rates using an online learning algorithm.