A comparative Raman study between PrMnO₃, NdMnO₃, TbMnO₃ and DyMnO₃

Abstract

In this paper, we present a detailed Raman study of the non-multiferroic compounds PrMnO ₃ and NdMnO ₃ and the multiferroic compounds TbMnO ₃ and DyMnO ₃ as a function of temperature and magnetic field. All studied systems show anomalous phonon shifts close to the Néel transition T _N. In PrMnO ₃ and NdMnO ₃, the frequency softenings are partly attributed to an orbital-spin-phonon coupling whereas in TbMnO ₃ and DyMnO ₃, the relatively weak frequency shifts are rather attributed to an expansion of the Mn−O bond lengths. On the other hand, the frequencies of TbMnO ₃ phonons are shifted as a function of magnetic field, while those of PrMnO ₃ remain unaffected. These frequency shifts are interpreted in terms of local oxygen rearrangements under magnetic field that could play an important role in the multiferroicity of TbMnO ₃ and DyMnO ₃.

Introduction

In the last decade, the study of the perovskite manganites RMnO ₃ (R = lanthanides, Y and Bi) have attracted a considerable interest because of their fascinating properties such as colossal magnetoelectric and magnetocaloric effects^1,2. Their physical properties are determined by a delicate interplay of charge, spin, orbital, and lattice degrees of freedom^3–5. The study of the coupling between the lattice and the magnetic properties of these compounds represents an interesting starting point to understand the microscopic parameters controlling their magnetoelectric effects at low temperature. The RMnO ₃ with larger ionic radius (R = La, Pr, Nd,… and Dy) compounds crystallise in the orthorhombic structure with a space group Pbnm, whereas the compounds with smaller ionic radius (R = Dy, Ho, Er and Y) can be obtained either in the orthorhombic or the hexagonal structure with a space group P6₃ cm ^6,7. In the orthorhombic compounds the Mn ion has the $t_{2g}^3{e}_g^1$ electronic configuration. The $e_g^1$ orbital degeneracy is lifted by the Jahn-Teller distortion^5,8. These compounds exhibit an orbital ordering at high temperature $T_{OO}\sim 780-1500K$ ^9–11. Below T _OO, the orbital degree of freedom is spontaneously frozen by the real-space C–type ordering of the e _g orbitals accompanied by the development of a static Jahn-Teller lattice distortion of the MnO ₆ octahedra^3,4. Many previous works have suggested a strong coupling between the spin and the orbital degrees of freedom in the RMnO ₃ systems^3,8,12–14. Murakami et al.⁸ have reported an experimental evidence of the orbital ordering in LaMnO ₃ by measuring the (3,0,0) reflection intensity of resonant x-ray scattering⁸. They have found that its integrated intensity, which is related to the order parameter of the orbital ordering, becomes constant below the magnetic ordering temperature T _N ≈ 140 K and decreases above it, which suggests that the spin and the orbital orders are intercoupled. The orbital ordering temperature in RMnO ₃ is significantly enhanced by increasing the GdFeO ₃-type lattice distortion with decreasing the ionic radius of R (r _R)^3,11. These lattice distortions increase the orbital ordering frustration and provoke a change of the lattice parameters as shown by x-ray and neutron diffraction measurements^15,16 with a sharp fall in the ordering temperature of the Mn spins³. For example, PrMnO ₃ (NdMnO ₃) exhibits an A-type antiferromagnetic magnetic structure at T _N ≈ 100 K (T _N ≈ 80 K) in which the spins are aligned ferromagnetically in the basal plane (xz) and antiferromagnetically along the perpendicular direction (y)^17,18. In more distorted compounds (R = Dy, Tb and Gd) the spin structure becomes sinusoidally modulated in the ab–plane below 39–43 K and spirally modulated below 18-17 K ¹⁹. This last transition coincides with the appearance of a spontaneous electric polarization P _S parallel to the c–axis^1,20. In these spin-spiral systems the magnetic field is able to flip their electric polarization from c to a–axis.

Raman scattering spectroscopy is a powerful tool to investigate the driving force of the interplay of charge, spin, orbital and lattice degrees of freedom^21–25. The Raman spectra of RMnO ₃ orthorhombic compounds have been previous studied^21,22,26. In particular, they have explained the frequency softening of the 490 cm ⁻¹ and 600 cm ⁻¹ modes below T _N in terms of spin-phonon coupling caused by the phonon modulation of the superexchange integral^21,22,26. Recently, Xu et al.²⁷ have attributed the softening behavior of the two excitations at 490 cm ⁻¹ and 610 cm ⁻¹ of LaMnO ₃ to an orbital-spin-phonon (OSP) coupling rather than limited to a spin-phonon coupling only. The verification of the suggested theoretical models requires more studies of the effects of magnetic and orbital orderings on the phonon frequencies in the RMnO ₃ compounds.

In this paper, we investigate the Raman-active phonons in PrMnO ₃, NdMnO ₃, TbMnO ₃ and DyMnO ₃ compounds as a function of temperature and magnetic field. The objectives are (i) to study and compare the Raman response of the non-multiferroic systems PrMnO ₃ and NdMnO ₃ to those of the multiferroic compounds TbMnO ₃ and DyMnO ₃, (ii) to study the effect of a magnetic field on the Raman-active phonons in the representative compounds PrMnO ₃ and TbMnO ₃ at low temperature.

Results and Discussion

Based on group-theory, the orthorhombic RMnO ₃ (space group Pbnm) has twenty-four Raman-active modes (7A _g + 7B _1g + 5B _2g + 5B _3g)²⁸. The RMnO ₃ unit cell contains two MnO ₆ octahedra along the y–direction with two apical O2 and four equatorial O1 oxygen ions at the summits. The Mn − O2 bond is along the y–axis while the Mn − O1 bonds are in the xz plane (ab–plane).

Figure 1 shows the polarized Raman spectra of RMnO ₃ (R = Pr, Nd, Tb and Dy) in the xx (aa) and xz (ab) configurations at 5 K. The typical phonons associated with the orthorhombic RMnO ₃ manganites are observed^21,22. For both configurations, six A _g and six B _1g Raman-active phonons are detected. The selection rules are well respected and the phonon linewidths are close to 3–7 cm ⁻¹ attesting the high crystalline quality of the samples. With decreasing temperature, no additional modes appear indicating a structural phase stability of the RMnO ₃ compounds. The frequencies of the A _g and B _1g Raman active phonons of PrMnO ₃, NdMnO ₃, TbMnO ₃ and DyMnO ₃ are reported in Table 1. Their vibrational characters are assigned in agreement with previous Raman measurements²⁹. With decreasing the ionic radius of R (r _Pr > r _Nd > r _Tb > r _Dy) most phonon frequencies shift towards higher values. Simultaneously, there is a transfer of intensity between the two high-frequency A _g phonons close to 500 cm ⁻¹ due to lattice distortions induced by the ionic radius size that mixes the symmetry characters of some phonon excitations²¹. Here we focus on the microscopic mechanisms and the theoretical models required to explain the phonon frequency shifts and how they differ in the multiferroic TbMnO ₃ and DyMnO ₃ compounds as compared to the non-multiferroic compounds PrMnO ₃ and NdMnO ₃.

Figure 1.

The polarized Raman spectra of PrMnO ₃, NdMnO ₃, TbMnO ₃ and DyMnO ₃ in the xx (a) and xz (b) configurations at T = 5 K. (★) indicates plasma lines.

Table 1.

Frequencies (cm ⁻¹) of the Raman-active modes in PrMnO ₃, NdMnO ₃, TbMnO ₃ and DyMnO ₃ at 5 K.

Modes	Atomic displacements21,22,28	PrMnO 3	NdMnO 3	TbMnO 3	DyMnO 3
A g	Ag
(6)	R and O2 displacements	147	146	146	143
(2)	in-phase MnO 6 y rotation	228	245	283	288
(7)	O1(x)	282	289	317	325
(4)	out of phase MnO 6 x rotations	325	334	385	392
(1)	O2 antistretching	463	467	495	494
(3)	MnO6 bending	490	494	513	516
B 1g	B1g
(6)	R, O2 and O1 displacements	160	161	164	169
(4)	R and O2 displacements	208	210	310	312
(7)	O1(z)	309	313	338	338
(3)	out-of-phase MnO6 bending	448	450	480	481
(2)	in-phase O2 scissorslike	496	502	534	536
(1)	in plane O2 stretching	600	602	615	612

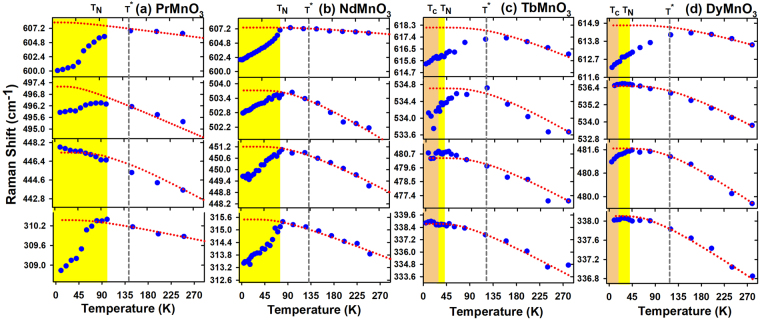
Figures 2 and 3 respectively show the temperature dependences of the A _g and B _1g phonon frequencies for PrMnO ₃ (a), NdMnO ₃ (b) TbMnO ₃ (c) and DyMnO ₃ (d). Between 300 K and T ^★, the temperature evolutions of the different RMnO ₃ phonon frequencies are very similar: they harden with decreasing temperature. This frequency hardening is due to the anharmonic effect (dashed line) which can be simulated by the following formula: $\omega (T)={\omega }_0-C\left(1+\frac{2}{e^x-1}\right)$, where $x=\frac{\hslash {\omega }_0}{2K_{B}T}$, ω ₀ and C are adjustable parameters. For PrMnO ₃ (NdMnO ₃), the frequencies of the most detected modes soften significantly below $T_N\sim 100K$ ($T_N\sim 80K$). Remarkably, the frequencies of A _g(2) at 228 cm ⁻¹ (245 cm ⁻¹), A _g(3) at 490 cm ⁻¹ (494 cm ⁻¹) and B _1g(1) at 600 cm ⁻¹ (602 cm ⁻¹) phonons soften by 1.3, 0.5, and 1.0 % (0.7, 0.4 and 0.8 %) respectively below T ^N. For TbMnO ₃, the frequencies of the phonons A _g(3) at 513 cm ⁻¹, B _1g(2) at 534 cm ⁻¹ and B _1g(1) at 615 cm ⁻¹ deviate from the regular anharmonic behavior and soften unexpectedly below 130 K. These frequency softenings are slightly pronounced below T _N and much weaker as compared to their corresponding in PrMnO ₃ and NdMnO ₃. For example, the frequency softening of the B _1g(1) mode is 2 cm ⁻¹ for TbMnO ₃ while it is 6 cm ⁻¹ for PrMnO ₃. Also, frequencies of the A _g(4) mode and A _g(7) mode show a weak energy softening about 0.6 cm ⁻¹ below $T_N\sim 40K$, whereas those of A _g(1), A _g(2), B _1g(3) and B _1g(7) reproduce an anharmonic behavior. For DyMnO ₃, the temperature behaviors of the phonon frequencies are similar to those of TbMnO ₃. Interestingly, the unexpected frequency softenings of the Jahn-Teller phonons (A _g(3) et B _1g(1)) start well above T _N and are slightly enhanced below T _N.

Figure 2.

Temperature dependence of the A _g phonon frequencies of PrMnO ₃, NdMnO ₃, TbMnO ₃ and DyMnO ₃. Dotted lines correspond to the anharmonic behaviour.

Figure 3.

Temperature dependence of the B _1g phonon frequencies of PrMnO ₃, NdMnO ₃, TbMnO ₃ and DyMnO ₃. Dotted lines correspond to the anharmonic behaviour.

Analysis of temperature effects

The frequency softening of Raman phonons below T _N in the A–type RMnO ₃ compounds was previously associated to a spin-phonon coupling^22,26. Considering the nearest neighbours of the Mn ³⁺ ions, Granado et al. have shown that the Raman frequency shift is proportional to the square of the Mn ³⁺ ferromagnetic sublattice magnetization, [M(T)]² as defined in eq. (1).

$${(\mathrm{\Delta }{\omega }_{\alpha })}_{s-ph}\approx -\frac{2}{{\mu }_{\alpha }{\omega }_0}\left(\frac{{\partial }^2{J}_{xz}}{\partial u_{O1}^2}-\frac{1}{2}\frac{{\partial }^2{J}_y}{\partial u_{O2}^2}\right){\left[\frac{M(T)}{4{\mu }_B}\right]}^2$$ 1

where J _xz and J _y are the exchange constants in the equatorial plane and along the apical axis respectively and u _k is the displacement vector from the equilibrium positions of the k ^th O ²⁻ ion. Xu et al.²⁷ have revised the spin-phonon coupling model and have developed a theoretical model that takes into account the contribution of the orbital ordering. The total frequency shift Δω _OSP(T) is written as a function of the effective force constant of the spin-phonon coupling (first term) and the effective force constant of orbital-spin-phonon (second term).

$$\mathrm{\Delta }{\omega }_{OSP}(T)\approx -\frac{1}{2{\mu }_{\alpha }{\omega }_0}\sum _{i,j}\left(\frac{{\partial }^2{J}_1}{\partial u^2}{S}_i{S}_j+4\frac{{\partial }^2{J}_3}{\partial u^2}{S}_i{S}_j{\tau }_i{\tau }_j\right)$$ 2

where τ _i τ _j are the orbital correlation operators and S _i S _j are the spin correlation functions for the i and j Mn³⁺ ions. Using the multivariable Taylor expansion ∑_i,j(S _i S _j τ _i τ _j) ≈ ∑_i,j(〈S _i S _j〉〈τ _i τ _j〉 + 〈S _i S _j〉δτ + 〈τ _i τ _j〉δS), where $\delta \tau \equiv {\tau }_i{\tau }_j-\langle {\tau }_i{\tau }_j\rangle {|}_{S_i{S}_j=\langle S_i{S}_j\rangle }$ and $\delta S\equiv S_i{S}_j-\langle S_i{S}_j\rangle {|}_{{\tau }_i{\tau }_j=\langle {\tau }_i{\tau }_j\rangle }$, one can establish the expression of the frequency softening of some Raman active modes²⁷. The frequency shift Δω(T) of the in-phase stretching mode at $\sim 600c{m}^{-1}$ becomes

$$\begin{array}{l}\mathrm{\Delta }{\omega }_N^{B_{1g}\mathrm{(1)}}(T)(-{\omega }_0)\left(\frac{m}{2}\right)\approx \left[\frac{{\partial }^2{J}_1^{xz}}{\partial u_{O1}^2}+4\frac{{\partial }^2{J}_3^{xz}}{\partial u_{O1}^2}\left({\langle {\tau }_i{\tau }_j\rangle }_{xz}+\delta S_{xz}\right)\right]{\left(\frac{M(T)}{4{\mu }_B}\right)}^2\\ +4\frac{{\partial }^2{J}_3^{xz}}{\partial u_{O1}^2}{\langle {\tau }_i{\tau }_j\rangle }_{xz}\delta S_{xz}\end{array}$$ 3

and the Δω(T) of the out-of-phase bending mode at $\sim 490c{m}^{-1}$:

$$\begin{array}{l}\mathrm{\Delta }{\omega }_N^{A_g\mathrm{(3)}}(T)(-{\omega }_0)\left(\frac{m}{2}\right)\approx \gamma \left[\frac{{\partial }^2{J}_1^{xz}}{\partial u_{O1}^2}-\frac{1}{2}\frac{{\partial }^2{J}_1^y}{\partial u_{O2}^2}+4\left(\frac{{\partial }^2{J}_3^{xz}}{\partial u_{O1}^2}+\frac{1}{2}\frac{{\partial }^2{J}_3^y}{\partial u_{O2}^2}\right)\left({\langle {\tau }_i{\tau }_j\rangle }_{xz}+\delta S_{xz}\right)\right]\\ {\left(\frac{M(T)}{4{\mu }_B}\right)}^2+4\gamma \left(\frac{{\partial }^2{J}_3^{xz}}{\partial u_{O1}^2}+\frac{1}{2}\frac{{\partial }^2{J}_3^y}{\partial u_{O2}^2}\right){\langle {\tau }_i{\tau }_j\rangle }_{xz}\delta S_{xz}\end{array}$$ 4

The common form of these last equations is a linear function Y = SX + B where S is the slope and X is the square of the sublattice magnetization. The intercept B, which is related to the effective force constant of orbital-spin-phonon coupling k _OSP, is nonzero only if the interaction exists. This model is successfully used to explain the frequency softening of LaMnO ₃ phonons²⁷. However, detailed studies and more concrete experimental evidences are needed to confirm that the OSP coupling clearly exists, below T _N in the A–type RMnO ₃ compounds. To assess the validity of the OSP coupling in the case of PrMnO ₃ (and NdMnO ₃), we have examined the frequency softening behavior, not only of the high frequency modes at 490 cm ⁻¹ (494 cm ⁻¹) and 600 cm ⁻¹ (602 cm ⁻¹), but also of the low frequency mode at 228 cm ⁻¹ (245 cm ⁻¹) since it corresponds to a rotational Raman-active mode sensitive to the orbital ordering fluctuations as observed in KCuF ₃ ³⁰. The Δω(T) of this in-phase MnO ₆ y rotation mode can be written as:

$$\begin{array}{l}\mathrm{\Delta }{\omega }_N^{A_g\mathrm{(2)}}(T)(-{\omega }_0)\left(\frac{m}{2}\right)\approx \left[\frac{{\partial }^2{J}_1^{xz}}{\partial u_{RotO1}^2}+4\frac{{\partial }^2{J}_3^{xz}}{\partial u_{RotO1}^2}\left({\langle {\tau }_i{\tau }_j\rangle }_{xz}+\delta S_{xz}\right)\right]{\left(\frac{M(T)}{4{\mu }_B}\right)}^2\\ +4\frac{{\partial }^2{J}_3^{xz}}{\partial u_{RotO1}^2}{\langle {\tau }_i{\tau }_j\rangle }_{xz}\delta S_{xz}\end{array}$$ 5

where u _Rotk is the displacement vector of the k ^th O ²⁻ ion relative to the rotational mode. According to Granado model (eq. 1), the variation of log(ω(T _N) − ω(T)) versus $\log \left(\frac{M_{Sub}(T)}{3.8{\mu }_B}\right)$ should yield a linear line with a slope of +2 if the spin-phonon coupling is solely responsible for the frequency softening below T _N. Figure 4(a) (Fig. 4(c)) shows a logarithmic plot of the frequency softening {ω(T _N) − ω(T)} in PrMnO ₃ (NdMnO ₃) for the 600 cm ⁻¹ (602 cm ⁻¹), 490 cm ⁻¹ (494 cm ⁻¹) and 228 cm ⁻¹ (245 cm ⁻¹) modes with respect to the sublattice magnetization $\log \left(\frac{M_{Sub}(T)}{3.8{\mu }_B}\right)$ at temperatures between 5 K and $T_N\sim 100K$ ($T_N\sim 80K$). The estimated slope S is significantly different from the prediction value of +2. The slope S for a linear fit (dashed line) is around 2.22 (2.16), 2.28 (2.20) and 2.20 (2.13) for the 228 cm ⁻¹ (245 cm ⁻¹), 490 cm ⁻¹ (494 cm ⁻¹) and 600 cm ⁻¹ (602 cm ⁻¹) modes respectively. This suggests that the spin-phonon coupling alone does not adequately explain the observed frequency softening below T _N in PrMnO ₃ and NdMnO ₃.

Figure 4.

(a) A logarithmic plot of the mode frequency softening {ω(T _N) − ω(T)} with respect to the sublattice magnetization for temperatures between 5 K and 100 K in PrMnO ₃. (b) Δ(ω) as a function of ${\left(\frac{M_{sub}(T)}{3.8{\mu }_B}\right)}^2$ of the 228 cm ⁻¹, 490 cm ⁻¹ and 600 cm ⁻¹ modes in PrMnO ₃. (c) and (d) represent their corresponding variations in NdMnO ₃. The variation of ${\left(\frac{M_{sub}(T)}{3.8{\mu }_B}\right)}^2$ is taken from Refs^15,22,31.

Figure 4(b) shows a good linear correlation between Δω(T) and $X={\left(\frac{M_{Sub}(T)}{3.8{\mu }_B}\right)}^2$ which is in agreement with the linear function of equations 3, 4 and 5. The extrapolation of the linear function at X = 0 gives the intercept B: 1.65, 0.94 and 0.71 for the 228 cm ⁻¹, 490 cm ⁻¹ and 600 cm ⁻¹ modes respectively. These behaviors are also observed in NdMnO ₃ with B values: 0.58, 0.73 and 0.29 for the 245 cm ⁻¹, 494 cm ⁻¹ and 602 cm ⁻¹ modes respectively (Fig. 4(d). These finite positive values indicate that the spin and the orbital orders are also coupled in PrMnO ₃ and NdMnO ₃. In addition, the nonzero value of B at T _N implies that this coupling does not vanish completely above T _N but remains nonzero for a finite temperature range due to the magnetic correlations in the paramagnetic phase. The term B is interpreted as the effective force constant of the OSP coupling k _OSP. The effective force constants k _SP (of spin-phonon coupling) and k _OSP (of orbital-spin-phonon coupling) are reported in Table 2. For the three modes, the k _SP and the k _OSP decrease with the ionic radius of the rare-earth. For all compounds, the k _OSP of the A _g(3) ($\sim 490c{m}^{-1}$) mode is slightly stronger than those of the A _g(2) and B _1g(1) modes. This indicates that the A _g(3) mode, intimately related to the Jahn-Teller distortions, is more sensitive to the spin-orbital coupling. The k _OSP of the A _g(3) decreases with r _R (of La, Pr and Nd) while the ratio k _OSP/k _SP is almost constant. These facts underline the important role of the ionic-radius size and the apical O2 vibration in the phonon modulation of the spin-orbital interaction in the RMnO ₃ A–type compounds.

Table 2.

The effective force constants k _SP (spin-phonon coupling) and k _OSP (orbital-spin-phonon coupling) of the A _g(2), A _g(3) and B _1g(1) Raman-active modes in LaMnO ₃ ²⁷, PrMnO ₃ and NdMnO ₃.

Compounds/modes	kSP (dynes/cm)			kOSP (dynes/cm)			kOSP/kSP (%)
Modes	Ag(2)	Ag(3)	B1g(1)	Ag(2)	Ag(3)	B1g(1)	Ag(2)	Ag(3)	B1g(1)
LaMnO 3 27	—	1000	—	—	70	—	—	7.0	—
PrMnO 3	651	865	2622	54	66	61	8.2	7.6	2.3
NdMnO 3	193	655	2413	20	51	25	10.3	7.7	1.0

As mentioned above, the frequency softenings of phonons in TbMnO ₃ and DyMnO ₃ are much weaker than those in PrMnO ₃ and NdMnO ₃. The origin of their frequency softening remains unclear: it has been qualitatively assigned to a spin-phonon coupling³² or to an expansion in the Mn − O bond lengths²². However, there are no concrete experimental proofs to determine their true origin. The phonon frequency shifts induced by the change of the ionic binding energies due to the lattice expansion/contraction, is usually approximated by the Grüneisen law Δω _α(T)/ω ₀ = −γ _α(ΔV/V ₀) where γ _α is the Grüneisen parameter for the normal mode α. This later approximation is applicable for isotopically expanded lattices. One should also consider the possibility of phonon frequency shifts due to lattice anomalies, even in the absence of a lattice unit cell volume change. Indeed, for some phonons the displacement of the involved atoms is either unidimensional or restricted in a plane. Blasco et al.¹⁶ have observed an expansion in TbMnO ₃ a–lattice parameter below 130 K and no significant changes are observed for the b and c parameters.

Figure 5 shows the temperature dependence of the frequency of B _1g(1) mode (red squares) in TbMnO ₃ (a) and NdMnO ₃ (b). The black dots indicate the variation of −γω ₀ΔA/A ₀ as a function of temperature where A = a × b and γ is the Grüneisen parameter. The frequency softenings of the B _1g(1) mode are in agreement with the thermal expansion in the ab–plane with a Grüneisen parameter of $\sim 0.0416$ in the case of TbMnO ₃ whereas it is clearly not the case of NdMnO ₃ below $T\sim 80K$. This confirms that in the case of TbMnO ₃ the frequency shift of the B _1g(1) mode is mainly due to an expansion in the Mn − O distances related to discrete orbital rearrangements close to the magnetic order transition, a phenomenon not discussed before, in this much-distorted compounds RMnO ₃ (R = Tb and Dy). Indeed, the negative thermal expansion, recently observed in some magnetic materials (Ca ₂ Ru _1−x M _x O ₄ where M = Mn and Fe) at low temperatures, is attributed to a strong coupling between orbital and magnetic orders^33,34. In addition, the frustrated magnetic order in TbMnO ₃ is usually attributed to its frustrated orbital ordering as compared to TbMnO ₃ ³.

Figure 5.

(a) The filled red squares show the temperature dependence of the 615 cm ⁻¹ mode in TbMnO ₃. The filled black circles show the variation of −γω ₀ΔA/A ₀ as a function of temperature where A = a × b ¹⁶. In (b) their corresponding variations in NdMnO ₃.

Analysis of magnetic-field effects

In order to further investigate the spin-lattice coupling in a frustrated multiferroic system TbMnO ₃ againt a non-multiferroic compound PrMnO ₃, we also study the evolutions of Raman active phonon frequencies of both compounds under an applied magnetic field at 4.2 K, below $T_N^{R=Pr,Tb}$.

Figure 6 shows the magnetic field dependence of the unpolarized macro-Raman spectra of PrMnO ₃ (a) and TbMnO ₃ (b) up to 7 Tesla. The applied magnetic field is quasi-parallel to the c–axis. While some of TbMnO ₃ phonon frequencies are shifted as a function of magnetic field, those of PrMnO ₃ remain unaffected. Similarly to TbMn ₂ O ₅ ³⁵, these magnetic-field induced frequency shifts reflect the frustration of the spin configuration in TbMnO ₃ and its sensitivity to the presence of a magnetic field. The most affected phonons in TbMnO ₃, by the magnetic field, are the Jahn-Teller modes at 615 cm ⁻¹ (B _1g(1)) and 513 cm ⁻¹ (A _g(3)). Their frequencies soften by $\sim 1c{m}^{-1}$ and $\sim 2c{m}^{-1}$ at 7 Tesla respectively. These phonons involve mainly the O1 oxygen vibrations in the xz–plane and the Mn − O distances suggesting a magnetic-field modulation of the Mn − O − Mn bond lengths. These findings are in agreement with previous results indicating that a magnetic field induces a magnetoelastic coupling in TbMnO ₃ ^36,37. Also, in our study of the Tb ³⁺ crystal-field excitations in TbMnO ₃ single crystals, we have found that some excitations are significantly shifted under an applied magnetic field along the c–axis at 4.2 K ³⁸. This observation is in favor of oxygen displacements under magnetic-field in agreement with a prominent role of the oxygen ions in the multiferroicity of TbMnO ₃ and DyMnO ₃ as recently reported by Huang et al.³⁹. Hence the ferroelectricity is related to local oxygen arrangements following the increase of the Mn − O1 bond length as induced by Dzyaloshinskii-Moriya interaction rather than a pure electronic mechanism as suggested by Kastura et al.^40,41.

Figure 6.

Unpolarised Raman spectra of PrMnO ₃ (a) and TbMnO ₃ (b) as a function of magnetic field (up to 7 T) applied along the c–axis.

Conclusion

In this comparative Raman study of the PrMnO ₃, NdMnO ₃, TbMnO ₃ and DyMnO ₃ single crystals, the phonon frequency shifts in PrMnO ₃ and NdMnO ₃ observed below T _N, are explained by an orbital-spin-phonon coupling whereas those in TbMnO ₃ and DyMnO ₃, observed below 130 K, are attributed to an expansion of the Mn − O distances. In our PrMnO ₃ and TbMnO ₃ magneto-Raman measurements, it is shown that some TbMnO ₃ phonons are shifted as a function of magnetic field, while those of PrMnO ₃ remain unaffected. The magnetic-field dependence of the TbMnO ₃ phonon frequencies is associated to a magnetic modulation of the O1 oxygen displacements and suggests that Mn − O1 bond polarization may play a significant role in the magnetoelectric properties of TbMnO ₃.

Methods

RMnO ₃ (R = Pr, Nd, Dy and Tb) single-crystals were grown by the floating zone method as described in reference⁴². The Raman spectra were recorded at temperatures between 300 K and 5 K and were obtained in the backscattering configuration using a He − Ne laser (632.8 nm) and a Labram-800 micro-Raman spectrometer equipped with a X − 50 objective microscope (focus diameter around $\sim 3\mu m$), an appropriate notch filter and a nitrogen-cooled CCD detector. The studied single crystals were mounted in a continuous flow temperature regulated liquid helium Janis cryostat. We have also measured the Raman active excitations under applied magnetic field up to 7 Tesla. The Raman measurements under magnetic field were obtained with an Ar ⁺ incident laser (514.5 nm) and with a magnetic field parallel to the c–axis.

Data Availability

Most data generated or analysed during this study are included in this published article. The Raman spectra of RMnO ₃ (R = Pr, Nd, Dy and Tb) compounds at different temperatures are available from the corresponding author on reasonable request.

Author Contributions

S.M. and S.J. conceived the study. A.M., V.Y.I., and A.B. prepared the samples. S.M. performed the measurements. S.M. and S.J. analyzed the results. S.M. wrote the manuscript. All authors commented on the manuscript.

Competing Interests

The authors declare that they have no competing interests.