Abstract
The intricate properties of articular cartilage and the complexity of the loading environment are some of the key challenges in developing models for biomechanical analysis of the knee joint. Fibril-reinforced poroelastic (FRPE) material models have been reported to accurately capture characteristic responses of cartilage during dynamic and static loadings. However, high computational and time costs associated with such advanced models limit applicability of FRPE models when multiple subjects need to be analyzed. If choosing simpler material models, it is important to show that they can still produce truthful predictions. Therefore, the aim of this study was to compare depth-dependent maximum principal stresses and strains within articular cartilage in the 3D knee joint between FRPE material models and simpler isotropic elastic (IE), isotropic poroelastic (IPE) and transversely isotropic poroelastic (TIPE) material models during simulated gait cycle.
When cartilage-cartilage contact pressures were matched between the models (15% allowed difference), maximum principal stresses in the IE, IPE and TIPE models were substantially lower than those in the FRPE model (by more than 50%, TIPE model being closest to the FRPE model), and stresses occurred only in compression in the IE model.
Additional simulations were performed to find material parameters for the TIPE model (due to its anisotropic nature) that would yield maximum principal stresses similar to the FRPE model. The modified homogeneous TIPE model was in a better agreement with the homogeneous FRPE model, and the average and maximum differences in maximum principal stresses throughout the depth of cartilage were 7% and 9%, respectively, in the lateral compartment and 9% and 11% in the medial compartment. This study revealed that it is possible to match simultaneously maximum principal stresses and strains of cartilage between non-fibril-reinforced and fibril-reinforced knee joint models during gait. Depending on the research question (such as analysis of fibril strain necessitates the use of fibril-reinforced material models) or clinical demand (fast simulations with simpler material models), the choice of the material model should be done carefully.
Keywords: Articular cartilage, knee joint, finite element analysis, material parameters, gait cycle, magnetic resonance imaging
INTRODUCTION
Articular cartilage is a multiphasic, inhomogeneous and anisotropic soft tissue that exhibits strong creep and stress-relaxation behavior, and is often subjected to dynamic loading (Mow et al., 1989). In order to understand joint mechanics, these unique material properties of cartilage together with realistic loading conditions need to be considered.
Finite element (FE) modeling could help identify changes in tissue-level mechanical stresses and strains and describe how these parameters might relate to potential joint and cartilage pathologies (Kazemi et al., 2013). The accuracy of the FE model can be validated by how precisely it can simulate the reality and it can depend on multiple variables such as the geometry of the articulating surfaces, material models and properties, joint loads, and boundary conditions (Besier et al., 2005). For example, Shirazi-Adl (Shirazi-Adl, 1989) already demonstrated with an axisymmetric FE model that normal stresses of annulus fibrosus are highly sensitive to different material models even if strains and displacements match. However, the effect of material model on articular cartilage stresses and strains has not been shown in 3D knee joint model during gait.
Various material models have been developed to describe the mechanical behavior of articular cartilage (Donahue et al., 2002; Mononen et al., 2011; Peña et al., 2007; Yang et al., 2010a). Due to computational costs and time-consuming nature associated with 3D FE modeling, cartilage is often considered as homogenous, isotropic and linearly elastic material, and interstitial fluid flow is sometimes neglected (Peña et al., 2007). Such models can be applied to characterize the equilibrium or instantaneous response of cartilage, but they fail to incorporate time- and direction-dependent behavior of cartilage and compression-tension nonlinearity (Cohen et al., 1998; DiSilvestro et al., 2001; Korhonen and Jurvelin, 2010). Isotropic biphasic/poroelastic (Donahue et al., 2002), isotropic hyperelastic (Anderson et al., 2008) and transversely isotropic biphasic/poroelastic (Vaziri et al., 2008; Wilson et al., 2003) material models of cartilage have also been used for knee joint FE modeling. It has been reported that fibril-reinforced models are able to represent the characteristic dynamic, static and time-dependent responses of articular cartilage, as experimentally validated using in vitro stress-relaxation and creep tests in different measurement geometries (Julkunen et al., 2008; Korhonen et al., 2003; Li et al., 2000; Li et al., 2001; Wilson et al., 2006). Such material models are able to take into account the mechanical effects of the nonfibrillar and fibrillar matrices of cartilage. In recent studies, fibril-reinforced material models of articular cartilage in the knee joint have been used for analyzing knee internal forces (Adouni and Shirazi-Adl, 2013; Adouni and Shirazi-Adl, 2014) and cartilage stresses during gait (Halonen et al., 2013; Korhonen et al., 2015; Li et al., 2000; Li et al., 2001; Marouane et al., 2015).
Even though fibril-reinforced poroelastic material models are able to take into account the mechanical roles of collagen, proteoglycans and fluid, there are high computational costs associated with more advanced knee joint models. For instance, a single run of a knee joint model with the fibril reinforced cartilage material may take days or even weeks (Kazemi et al., 2013). This limits the applicability of the fibril reinforced models when biomechanics of many subjects need to be studied. Simpler material models are easier and faster to generate and the simulation becomes much quicker. It is however important to know whether simpler models can still produce truthful predictions. Therefore, the aim of this study was to compare maximum principal stresses (total non-fibrillar/fibrillar solid and fluid) and maximum/minimum principal logarithmic strains of cartilage with different material models in a healthy knee joint during simplified gait cycle. Implemented material models were isotropic elastic, isotropic poroelastic, transversely isotropic poroelastic and fibril-reinforced poroelastic. Furthermore, we aimed to find material parameters of cartilage so that depth-wise stresses and strains would be similar in the transversely isotropic poroelastic and fibril-reinforced poroelastic models.
2. MATERIALS AND METHODS
Magnetic Resonance Imaging (MRI) data from the healthy right knee joint of a female subject, obtained from the Osteoarthritis Initiative (OAI) database (http://www.oai.ucsf.edu/), were used in this study. For more detailed information on the generation of the model geometry and FE mesh, see Supplementary material.
2.1. Material models for cartilage
Material models
As the aim was to investigate the influence of the material model on articular cartilage mechanics during gait, we constructed and simulated the knee joint function using six different material models of cartilage: 1) homogeneous isotropic elastic (IE), 2) homogeneous isotropic poroelastic (IPE), 3) homogeneous transversely isotropic poroelastic (TIPE), 4) homogenous fibril-reinforced poroelastic (FRPE), 5) depth-dependent TIPE, and 6) depth-dependent FRPE model. In all models, menisci were considered as a transversely isotropic elastic material (Table 1) and material properties were obtained from previous experimental studies (Danso et al., 2015; Elliott et al., 2002; Goertzen et al., 1997; Mow and Ratcliffe, 1997). Additional information about the material models can be found in Supplementary material.
Table 1.
Material parameters for different material models, i.e., isotropic elastic, isotropic poroelastic, transversely isotropic poroelastic and fibril-reinforced poroelastic models of cartilage and transversely isotropic elastic meniscus (Danso et al., 2015; Goertzen et al., 1997; Mow et al., 2005; Vaziri et al., 2008).
| Material model | Parameter | Cartilage | Meniscus | |
|---|---|---|---|---|
|
| ||||
| Simulation 1 | Simulation 2.1 | Literature | ||
|
| ||||
| Isotropic elastic | E (MPa) | 20.00 | - | - |
| (Mow et al., 2005) | ν (−) | 0.49 | - | - |
|
| ||||
| Isotropic poroelastic | E (MPa) | 10.00 | - | - |
| Mow et al., 2005 Wilson et al., 2004) | ν (−) | 0.15 | - | - |
| k (10−15 m4/Ns) | 1.00 | - | - | |
| e0 (−) | 4.00 | - | - | |
|
| ||||
| Transversely isotropic poroelastic | Ep (MPa) | 5.80 | 16.00 | 159.60 |
| Et (MPa) | 0.46 | 0.46 | 20.00 | |
| (Danso et al., 2014; Elliott et al., 2002; Mow et al., 2005; Vaziri et al., 2008; Wilson et al., 2004) | νp (−) | 0.87 | 0.42 | 0.30 |
| νtp (−) | 0.03 | 0.09 | 0.01 | |
| Gt (MPa) | 2.50 | 8.00 | 50.00 | |
| k (10−15 m4/Ns) | 1.00 | 1.00 | - | |
| e0 (−) | 4.00 | 4.00 | - | |
|
| ||||
| Fibril-reinforced poroelastic | Ef (MPa) | 5.80 | - | - |
| Em (MPa) | 0.46 | - | - | |
| (Danso et al., 2014; Halonen et al., 2014; Mow et al., 2005; Wilson et al., 2003; Wilson et al., 2004) | νm (−) | 0.42 | - | - |
| k (10−15 m4/Ns) | 1.00 | - | - | |
| e0 (−) | 4.00 | - | - | |
Simulation 1, for the isotropic elastic and isotropic poroelastic models, Young’s moduli were adjusted to match the average contact pressures with the fibril reinforced model. Parameters in Simulation 1 for the transversely isotropic model are based on the literature. Parameters for isotropic elastic model: E- Young’s modulus and ν- Poisson’s ratio; isotropic poroelastic:E- Young’s modulus and ν- Poisson’s ratio, k- permeability and e0- void ratio; transversely isotropic poroelasticEp- in-plane Young’s modulus, Et- out-of-plane Young’s modulus, νp- in-plane Poisson’s ratio, νtp- out-of-plane Poisson’s ratio, Gt- out-of-plane shear modulus, k- permeability and e0- void ratio; and fibril-reinforced poroelasticEf- fibril network modulus, Em- non-fibrillar matrix modulus, νm- Poisson’s ratio of the non-fibrillar matrix, k-permeability and e0-void ratio. For the transversely isotropic poroelastic cartilage in Simulation 2.1, νtp was adjusted so that the material stability conditions were fulfilled (ABAQUS Documentation, 2013).
Depth-dependencies
In order to study the effect of tissue inhomogeneity on stresses and strains, depth-dependent TIPE and FRPE models of cartilage were also constructed. Since collagen fibrils (together with fluid) control primarily cartilage response during short-term loading (Mononen et al., 2012) such as walking (as was simulated here), we only concentrated on the inhomogeneity caused by the collagen fibril network. Zonal thicknesses of the superficial, middle and deep zones were set to 12%, 32% and 56% of the total thickness for the tibial cartilage (Changoor et al., 2011; Kurkijärvi et al., 2008; Nissi et al., 2006), respectively, while femoral cartilage was always homogenous (in order to allow better comparison of stresses and strains in the tibial plateau cartilage with corresponding homogeneous models). In the depth-dependent FRPE model, the well-organized primary fibrils formed an arcade-like architecture in the tibial cartilage (Benninghoff, 1925), consisting of the superficial zone with fibrils oriented parallel to the cartilage surface, bending fibrils in the middle zone, and fibrils oriented perpendicular with the tissue surface in the deep zone. This structural inhomogeneity causes also mechanical inhomogeneity, thus, the tensile stiffness parallel to the cartilage surface is the highest in the superficial zone (Korhonen and Herzog, 2008). In the depth-dependent TIPE model, the material depth-dependency was taken into account by changing the material stiffness as a function of the actual collagen fibril orientation (Mow et al., 2005), i.e., by decreasing the in-plane Young’s modulus parallel to the cartilage surface (Akizuki et al., 1986) in the middle and deep zones (Table 2) because the tensile stiffness is the lowest perpendicular to the collagen fibril alignment.
Table 2.
Material parameters and their values for the inhomogeneous models of cartilage, i.e., depth-dependent transversely isotropic poroelastic and fibril-reinforced poroelastic models.
| Model | Parameters | Superficial zone | Middle zone | Deep zone | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
| ||||||||||
| Sim. 1 | Sim 2.1 | Sim. 2.2 | Sim. 1 | Sim 2.1 | Sim 2.2 | Sim. 1 | Sim. 2.1 | Sim. 2.2 | ||
|
| ||||||||||
| Depth-dependent transversel y isotropic poroelastic | Ep (MPa) | 5.80 | 20.00 | 24.00 | 4.00 | 14.14 | 16.97 | 2.00 | 7.07 | 8.49 |
| Et (MPa) | 0.46 | 0.46 | 0.46 | 0.46 | 0.46 | 0.46 | 0.46 | 0.46 | 0.46 | |
| νp (−) | 0.87 | 0.42 | 0.42 | 0.87 | 0.42 | 0.42 | 0.87 | 0.42 | 0.42 | |
| νtp (−) | 0.030 | 0.07 | 0.06 | 0.05 | 0.08 | 0.08 | 0.20 | 0.12 | 0.12 | |
| Gt (MPa) | 2.50 | 10.00 | 12.00 | 2.00 | 7.07 | 8.45 | 1.00 | 3.53 | 4.24 | |
| (Danso et al., 2014; Elliott et al., 2002; Mow et al., 2005; Vaziri et al., 2008; Wilson et al., 2004) | k (10−15 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 |
| m4/Ns) | 4.00 | 4.00 | 4.00 | 4.00 | 4.00 | 4.00 | 4.00 | 4.00 | 4.00 | |
| e0 (−) | ||||||||||
|
| ||||||||||
| Depth-dependent fibril-reinforced poroelastic | Ef (MPa) | 5.80 | - | - | 5.80 | - | - | 5.80 | - | - |
| Em (MPa) | 0.46 | - | - | 0.46 | - | - | 0.46 | - | - | |
| νm (−) | 0.42 | - | - | 0.42 | - | - | 0.42 | - | - | |
| k (10−15 | 1.00 | - | - | 1.00 | - | - | 1.00 | - | - | |
| m4/Ns) | 4.00 | - | - | 4.00 | - | - | 4.00 | - | - | |
| (Danso et al., 2014; Halonen et al., 2014; Mow et al., 2005; Wilson et al., 2003; Wilson et al., 2004) | e0 (−) | |||||||||
Parameters in Simulation (Sim.) 1 for the transversely isotropic poroelastic model are based on the literature. Parameters for depth-dependent transversely isotropic poroelastic model: Ep- the in-plane Young’s modulus, Et- out-of-plane Young’s modulus, νp- in-plane Poisson’s ratio, νtp- the Poisson’s ratio determining strain resulting from the stress which is normal to the plane of isotropy, Gt - out-of-plane shear modulus, k- permeability and e0- void ratio; and fibril-reinforced poroelasticEf - the fibril network modulus, Em- non-fibrillar matrix modulus, νm- Poission’s ratio of the non-fibrillar matrix, k- permeability and e0- void ratio. For the transversely isotropic poroelastic cartilage Simulation (Sim.) 2.1 and Simulation (Sim.) 2.2, the longitudinal Poisson’s ratio (νtp) was adjusted so that the material stability conditions were fulfilled (ABAQUS Documentation, 2013).
2.2. Boundary conditions, contact and implementation of gait cycle
Bottom nodes of the tibial cartilage were fixed in all directions. The femoral cartilage-bone interface was fixed into the reference point, located at a middle point between lateral and medial epicondyles of the femur (Mononen et al., 2015), using the coupling constraint method in Abaqus. Fluid flow through the cartilage surfaces and the cartilage-bone interface was not allowed as fluid flow through the surfaces during short term dynamic loading was assumed negligible. The meniscal horns were fixed to bone using linear spring elements (type SPRINGA) with a total spring constant of 350 N/mm per horn (Villegas et al., 2007). All contacts were discretized by using surface-to-surface “hard” contact formulation with finite-sliding tracking and they were enforced by using default penalty method in Abaqus. For the simplified gait cycle, axial forces and extension–flexion rotations (Bergmann et al., 2014; Kutzner et al., 2010) were applied into the reference point (Mononen et al., 2015) as time-dependent boundary conditions and varus-valgus alignment was allowed to be free (see more from Supplementary material).
2.3. Simulations
Simulation 1
First, the material parameters (Young’s moduli) of the IE and IPE models were manually optimized so that the average contact pressures were close to those of the depth-dependent FRPE model, while the material parameters for the TIPE and FRPE cartilages were taken from earlier studies (Danso et al., 2015; Halonen et al., 2014; Mow et al., 2005; Vaziri et al., 2008; Wilson et al., 2003; Wilson et al., 2004). For the TIPE models, the material parameters were chosen as follows: in-plane Young’s modulus (Ep) corresponded the fibril network modulus (Ef) and out-of-plane Young’s modulus (Et) corresponded the non-fibrillar matrix modulus (Em) of the FRPE model (Simulation 1 in Table 1 and Table 2). For the depth-dependent TIPE model, Ep was reduced in the middle and deep zones of cartilage as presented above (see chapter 2.1). Finally, average maximum principal stresses (total non-fibrillar/fibrillar solid and fluid) and maximum/minimum principal logarithmic strains over the contact areas were compared between the models (see more from Supplementary material).
Simulation 2
Following Simulation 1, an additional parametric analysis was conducted to investigate whether it is possible to match depth-wise maximum principal stresses and strains between the TIPE and FRPE models. For this purpose, material parameters of the homogenous TIPE model were first parametrically modified (Simulation 2.1 in Table 1) and stresses and strains were compared with the homogenous FRPE model. Then, this parametric investigation was further expanded to the depth-dependent TIPE and depth-dependent FRPE models (Simulation 2.1 and Simulation 2.2 in Table 2).
3. RESULTS
3.1. Comparison of different material models
Joint contact forces
Cartilage-cartilage contact forces in the medial and lateral compartment were similar (maximum difference was 16%) between the material models. On average, in the lateral compartment they were 510 N and 518 N for the 1st and 2nd peak force, respectively, while those in the medial compartment were 392 N and 590 N. Reaction forces through the entire surfaces of the lateral compartment cartilage were almost identical between the models (Figure 2 in the Supplementary material) and were 646 N and 727 N for the 1st and 2nd peak force, respectively, while those in the medial side were 575 N and 690 N (0.88 – 1.12 BW, maximum of 2.2 BW through the joint). Forces transferred through the lateral meniscus were 135 N and 209 N for the 1st and 2nd peak force, respectively, while those through the medial side were 183 N and 100 N, and were similar between the material models (maximum difference was 16%).
Figure 2.
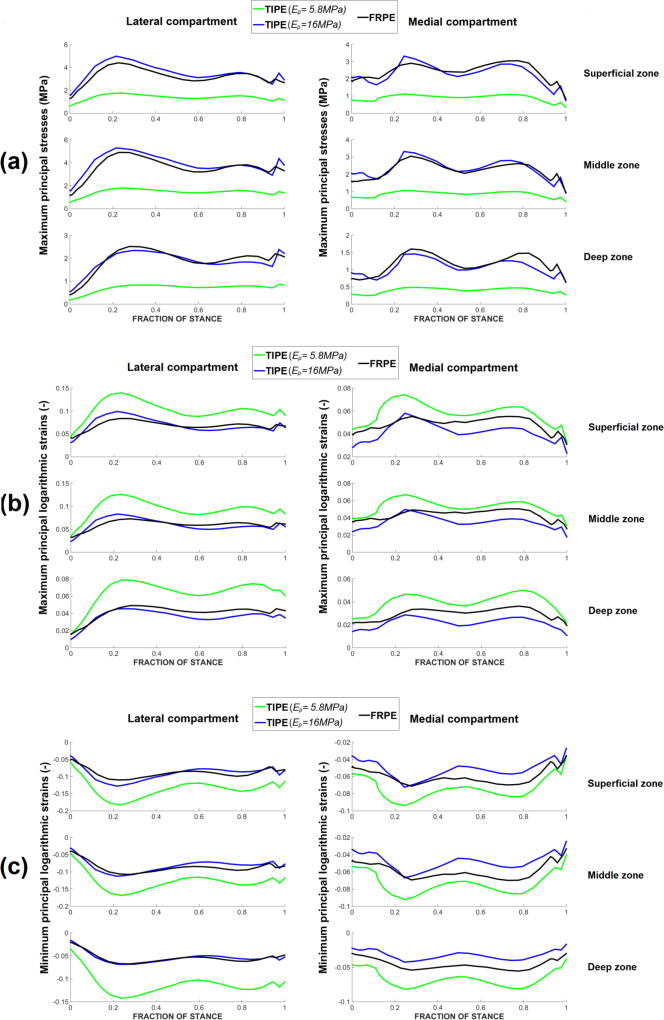
Average maximum principal stresses (a), maximum principal logarithmic strains (b) and minimum principal logarithmic strains (c) during the stance phase of gait in the transversely isotropic poroelastic model (TIPE) with two different transverse (in-plane) Young’s moduli (Ep = 5.8 MPa - literature based, Ep = 16MPa - from parametric analysis) and fibril-reinforced poroelastic (FRPE) model. Material parameters for the models can be found in Table 1.
Maximum principal stresses
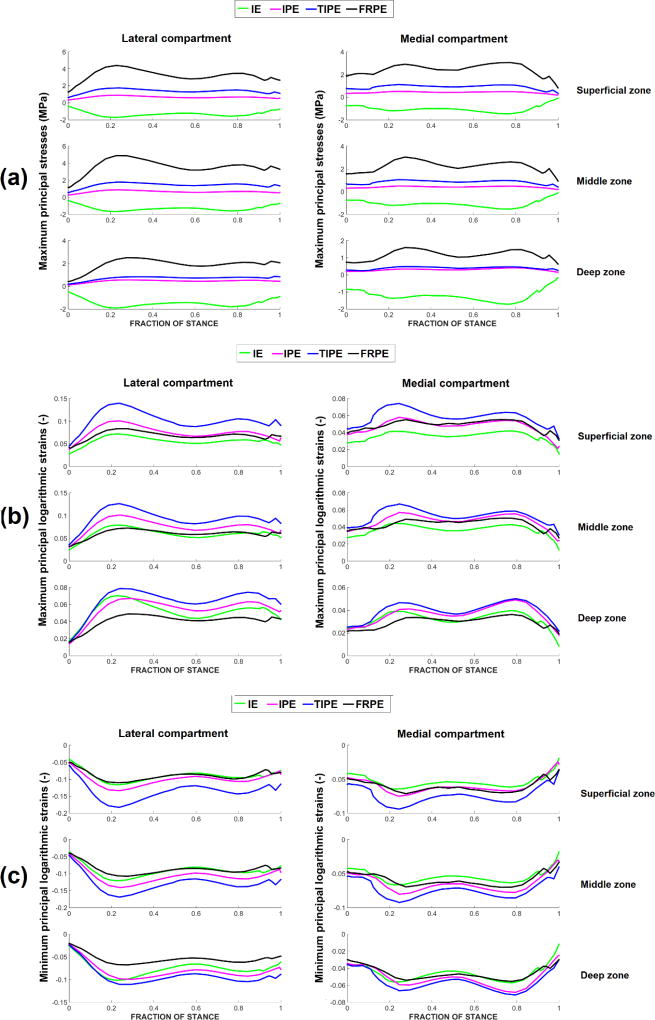
In contrast with the other models, the IE model showed constantly negative maximum principal stresses (Figure 1-a). Compared with the FRPE model, the IPE and TIPE models showed lower maximum principal stresses throughout the depth of cartilage.
Figure 1.
Average (over the contact area) maximum principal stresses (a), maximum principal logarithmic strains (b) and minimum principal logarithmic strains (c) during the stance phase of gait in the isotropic elastic (IE), isotropic poroelastic (IPE), transversely isotropic poroelastic (TIPE) and fibril-reinforced poroelastic (FRPE) models. Values are obtained using the contact area of the fibril-reinforced model. Material parameters can be found in Table 1.
Maximum principal logarithmic strains
Lateral compartment cartilage: compared with the FRPE model, the IE model had similar maximum principal logarithmic strains in the superficial and middle zones but higher in the deep zone (Figure 1-b). The IPE model showed similar maximum principal strains in the superficial zone of cartilage but higher in the middle and deep zones. Compared with the other models, the TIPE models had higher maximum principal logarithmic strains throughout the depth of cartilage.
Medial compartment cartilage: compared with the FRPE model, the IE model had lower strains in the superficial zone and similar strains in the middle and deep zones (Figure 1-b). The IPE model showed similar maximum principal strains in the superficial and middle zones but higher in the deep zone. Compared with the other models, the TIPE models had higher maximum principal logarithmic strains throughout the depth of cartilage.
Minimum principal logarithmic strains
Lateral compartment cartilage: compared with the FRPE model, the IE model showed similar minimum principal strains in the superficial and middle zones but higher in the deep zone (Figure 1-c). The IPE model showed similar minimum principal strains with the FRPE model in the superficial zone and higher in the middle and deep zones. Compared with the other models, the TIPE model showed higher minimum principal logarithmic strains throughout the depth of cartilage.
Medial compartment cartilage: compared with the FRPE model, the IE model had similar minimum principal strains through the tissue depth. The IPE model showed similar minimum principal strains with the FRPE model in the superficial and middle zones but higher in the deep zone. Compared with the other models, the TIPE showed higher minimum principal logarithmic strains throughout the depth of tibial cartilage.
3.2. Parametric analysis for transversely isotropic poroelastic models
3.2.1. Homogeneous model
The TIPE model with Ep = 16 MPa showed similar maximum principal stresses with the FRPE model throughout the depth of cartilage (Figure 2-a). It also showed similar maximum and minimum principal logarithmic strains with the FRPE model throughout the depth of the lateral compartment cartilage (Figure 2), while those in the medial compartment cartilage were slightly lower in the TIPE model (Figure 2-b,c).
3.2.2. Inhomogeneous model
Maximum principal stresses
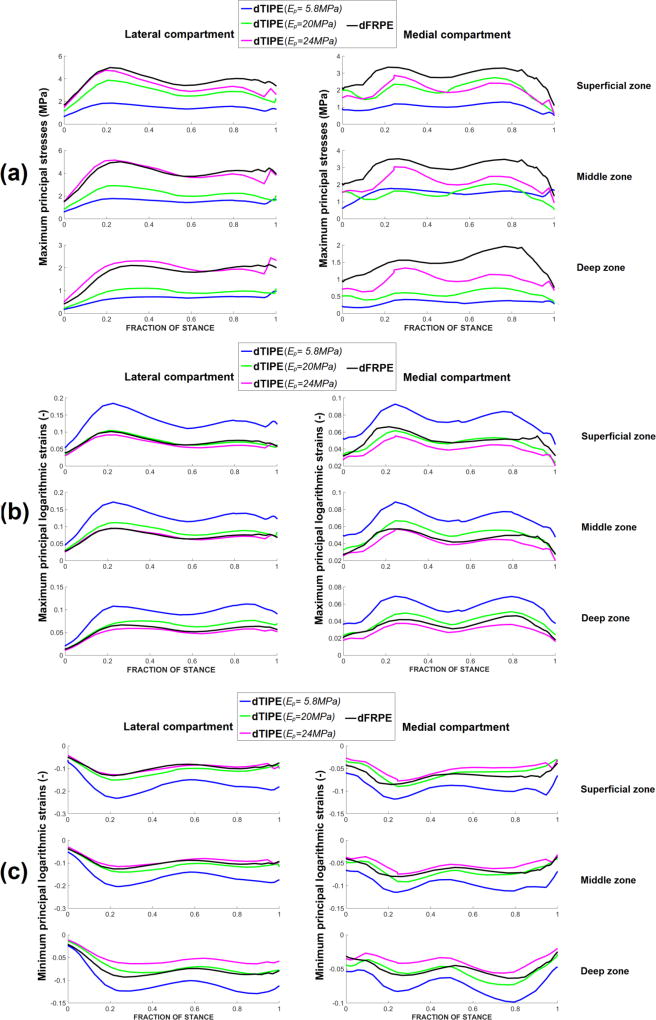
Lateral compartment cartilage: compared with the depth-dependent FRPE model, the depth-dependent TIPE model with Ep = 20 MPa in the superficial zone (Simulation 2.1 in Table 2) had lower stresses throughout the depth of cartilage (Figure 3-a). The depth-dependent TIPE model with Ep = 24 MPa in the superficial zone (Simulation 2.2 in Table 2) showed similar maximum principal stresses with the depth-dependent FRPE model throughout the depth of cartilage.
Figure 3.
Average maximum principal stresses (a), maximum principal logarithmic strains (b) and minimum principal logarithmic strains (c) during the stance phase of gait in the depth-dependent transversely isotropic poroelastic model (dTIPE) with three different transverse (in-plane) Young’s moduli (superficial zone Ep = 5.8 MPa-literature based, middle zone Ep = 4 MPa, deep zone Ep = 2 MPa; superficial zone Ep = 20 MPa, middle zone Ep = 14.14 MPa, deep zone Ep = 7.07 MPa and superficial zone Ep = 24 MPa, middle zone Ep = 16.97 MPa, deep zone Ep = 8.48 MPa -from parametric analysis) and depth-dependent fibril-reinforced poroelastic (dFRPE) model. Material parameters for each model can be found in Table 2.
Medial compartment cartilage: compared with the depth-dependent FRPE model, the depth-dependent TIPE model with Ep = 20 MPa in the superficial zone (Simulation 2.1 in Table 2) had lower stresses throughout the depth of cartilage (Figure 3-a). Stresses approached to those of the depth-dependent FRPE model when the in-plane modulus of the depth-dependent TIPE model was increased to Ep = 24 MPa in the superficial zone (Simulation 2.2 in Table 2).
Maximum and minimum principal logarithmic strains
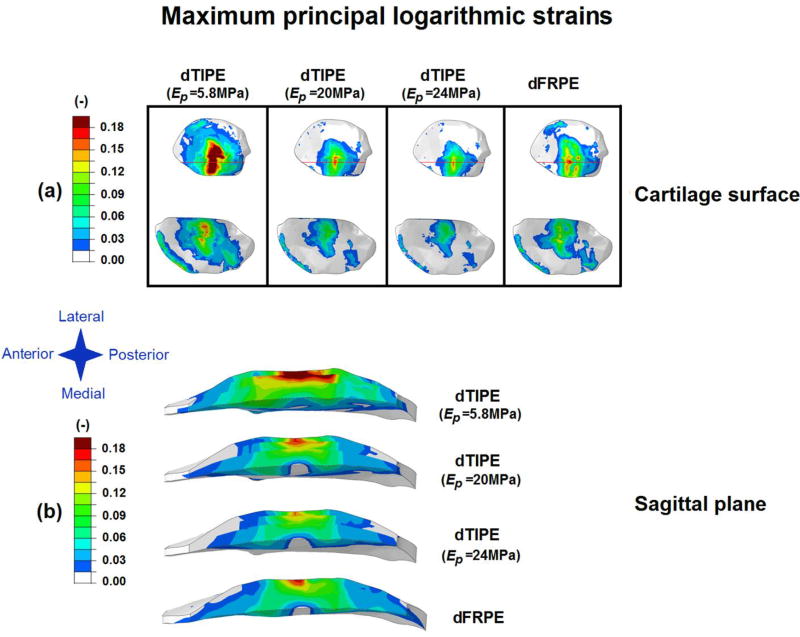
Compared with the depth-dependent FRPE model, the depth-dependent TIPE model with Ep= 20 MPa and 24 MPa in the superficial zone showed similar maximum principal logarithmic strains throughout the depth of cartilage (Figure 3-b, Figure 4) and similar minimum principal logarithmic strains in the superficial and middle zones of cartilage (Figure 3-c). Slightly lower compressive strains were observed in the deep zone of cartilage in the model with Ep = 24 MPa in the superficial zone.
Figure 4.
Maximum principal logarithmic strains (a) on the cartilage surface (the red line indicates the location of the sagittal plane image of the tibial cartilage) and (b) in the sagittal plane (depth-wise distribution) for the 1st peak force of the gait cycle in the depth-dependent transversely isotropic poroelastic model (dTIPE) with three different transverse (in-plane) Young’s moduli (superficial zone Ep = 5.8 MPa-literature based, middle zone Ep = 4 MPa, deep zone Ep = 2 MPa; superficial zone Ep = 20 MPa, middle zone Ep = 14.14 MPa, deep zone Ep = 7.07 MPa and superficial zone Ep = 24 MPa, middle zone Ep = 16.97 MPa, deep zone Ep = 8.48 MPa -from parametric analysis) and depth-dependent fibril-reinforced poroelastic (dFRPE) model. Material parameters for each model can be found in Table 2.
4. DISCUSSION
In this study, differences in stresses and strains between different material models of articular cartilage in the 3D knee joint FE model were analyzed during a stance phase of gait. The IE, IPE and TIPE (homogeneous and depth-dependent) material models of cartilage were compared with the FRPE model (with and without depth-wise collagen architecture). It was found that matching average cartilage-cartilage contact pressures and maximum principal cartilage stresses and strains is not simultaneously possible between the presented non-fibril-reinforced and fibril-reinforced material models. However, certain analyzed parameters (such as stress or strain) can be the same between different material models during the gait cycle.
This study clearly demonstrated that simpler material models could not capture maximum principal stresses in the knee joint cartilage during gait similarly with the FRPE models (when contact pressures were matched). This was consistent with a previous study by Shirazi-Adl (Shirazi-Adl, 1989), where normal stresses between the orthotropic model (with transverse isotropy) and the fibril-reinforced model of disc annulus were substantially different even though strains were similar. Furthermore, the IE material model (elastic) showed maximum principal stresses in compression while they were in tension in the other models. This was due to the lack of fluid pressure in the IE material model. Normal joint loading causes fluid to flow horizontally, increasing tensile stresses in a flow direction. Previous studies have suggested that the fluid load support in cartilage can be even 5–15 MPa (supporting ~90% of the load) during walking (Ateshian et al., 1998; Korhonen et al., 2015; Tanska et al., 2015; Venäläinen et al., 2016).
Average normal stresses (over the cartilage-cartilage contact area) in the IE model varied between 0.7MPa and 2.4MPa in the lateral compartment and between 0.3MPa and 1.8MPa in the medial compartment and were in a similar range as those reported by Yang et al. 2010 (Yang et al., 2010a; Yang et al., 2010b) for the knee model, where cartilage was also considered as isotropic elastic and meniscus as transversely isotropic elastic. However, in all our models maximum principal stresses and joint reaction forces were distributed quite evenly between the lateral and medial compartments while in Yang’s model they were concentrated more in the medial compartment. This difference can be explained by the differences in the geometry and alignment of the subject’s knee joint and gait loading. Particularly, the model by Yang et al. (Yang et al., 2010b) emphasizes the inclusion of varus-valgus moment for the knee joint motion and distribution of joint forces while we used earlier adopted boundary condition and allowed varus-valgus angle to be free. However, quite even distribution of forces between lateral and medial compartments has also been reported before (Kumar et al., 2013). See more discussion from Supplementary material.
In the depth-dependent TIPE model, the transverse Young’s moduli were estimated based on the FRPE model, fibril orientation defining the tensile modulus (the highest value in the superficial zone and lowest in the deep zone). This way contact pressures of the TIPE model were only ~15% lower compared to those of the FRPE model, but maximum principal stresses were substantially lower and strains higher. This can be explained with one fundamental difference between these models. In the FRPE model, the density ratio between the primary and secondary fibrils (C=3.74, obtained from the literature, see Supplementary material) increases the stress of the fibrillar network (Wilson et al., 2004) and the modulus values may not be comparable. In the TIPE model this indicates higher Young’s modulus in the horizontal direction. By multiplying the original Young’s moduli (Table 2, Simulation 1) with C, the following moduli are obtained for the superficial, middle and deep zones: 21.7 MPa, 15.0 MPa and 7.5 MPa, respectively. As seen from Table 2 and Figure 6, the FRPE and TIPE models give similar maximum principal stresses and strains when using moduli close to these values.
Since the OAI database does not have gait analysis data for the subjects, and varus-valgus angles vary between subjects (Kadaba et al., 1990; Kozanek et al., 2009; Scanlan et al., 2010), the simplified gait cycle simulation was based on axial force and flexion-extension angle (Bergmann et al., 2014; Kutzner et al., 2010) applied into the knee joint’s center of rotation, while varus-valgus rotation was free, similarly as done earlier (Mononen et al., 2015; Mononen et al., 2016). However, varus–valgus rotation in our models (Figure 3-b in the Supplementary material) showed similar behavior to those measured in the earlier experimental study (Kadaba et al., 1990). Though, we acknowledge the fact that changes in the location where the compressive force is applied into our knee models could affect medial/lateral loads and varus-valgus rotations. We conducted also additional simulations for the depth-dependent TIPE and FRPE models with different gait input from healthy subjects (Kozanek et al., 2009). Based on the results, the difference between the material models remained similar (see more from Figure 4 in Supplementary material).
Since the aim of this study was to compare different material models of cartilage with the same geometry and loading conditions, we did not include other soft tissues into the models and applied simplified loading. This is a limitation of our study. We tested the simplified gait cycle loading for the FRPE model with ligaments and found that ligaments have a small effect on the total joint reactions forces and varus/valgus rotation in our model with the simplified gait (Figure 3 in Supplementary material). However, it should be noted that our models were driven by flexion-extension angles and axial forces with free varus-valgus rotations, not by forces and moments. In models driven mainly by forces and moments, the effects of other tissues and structures would be more important (Halonen et al., 2016; Tanska et al., 2015).
Due to low permeability of articular cartilage, negligible fluid flow occurs through cartilage surfaces under short-term loading (Ateshian et al., 1998); we assumed this boundary condition for fluid flow in the models (also default option in Abaqus). Similar assumption has also been done in earlier studies (Kazemi et al., 2012; Li and Gu, 2011; Mononen et al., 2015; Tanska et al., 2015). In reality, free fluid flow through the cartilage surface may occur at the regions that are not in contact. Nonetheless, pore pressures at contacting surfaces of articular cartilage were within 10% between all material models (additional information can be found in Supplementary material). We also did additional analyses with eight times finer tibial mesh for the IPE model, and predicted peak values and average pore pressures were within 1% and 6%, respectively.
In order to allow fair comparison between different material models of cartilage, we incorporated the same transversely isotropic material properties of the meniscus in each model, as obtained from the previous studies (Danso et al., 2015; Elliott et al., 2002; Goertzen et al., 1997; Mow and Ratcliffe, 1997). While in reality meniscus is a fibril reinforced poroelastic material and it has been modeled as such earlier (Kazemi et al., 2012; Shirazi et al., 2008), our chosen material model for the meniscus should describe adequately forces going through the meniscus during short term loading (negligible or limited volume change and fluid flow through surfaces). The same material model of meniscus was used in our earlier models (Mononen et al., 2015; Mononen et al., 2016). However, we included poroelasticity to cartilage models because fluid pressure is an important parameter for the cartilage tissue response (carries ~80–90% of the load).
The only depth-dependency in the FRPE model was the collagen architecture and varying in-plane Young’s modulus in the TIPE model, while the other depth-dependent material properties (void-ratio dependent permeability, non-fibrillar matrix modulus) were excluded from the model. The main feature in the fibril-reinforced and transversely isotropic models is compression-tension nonlinearity, i.e., different properties in axial and transverse direction. This anisotropy and its depth-dependency are very important for cartilage behavior during gait (Halonen et al., 2014). The other parameters certainly also affect the depth-dependent cartilage behavior, but are not as fundamental in nature in the knee model during gait (Halonen et al., 2014) and do not affect compression-tension nonlinearity (which collagen is causing). If more depth-dependent properties would be included, the depth-wise results would slightly change but they should not change any of the conclusions with regard to comparison between different material models.
This study suggests that it is possible to match maximum principal stresses and strains between non-fibril-reinforced and fibril-reinforced material models in the knee during gait. Depending on the research question (such as analysis of fibril strain necessitates the use of fibril-reinforced material models) or clinical demand (fast simulations with simpler material models), the choice of the material model should be done carefully. As the fibril-reinforced models usually have longer computation time compared with, e.g., transversely isotropic elastic models, it can be more desirable to select the material model depending on the problem at hand and/or what parameters are scientifically or clinically relevant.
Supplementary Material
Acknowledgments
The research leading to results in the manuscript has received funding from the University of Oulu (strategic funding), European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013)/ERC Grant Agreement no. 281180, Academy of Finland (grants 286526 and 268378), Sigrid Juselius Foundation, and Finnish Cultural Foundation (North Savo regional fund, grant no. 65142194). CSC—IT Center for Science, Finland, is acknowledged for providing the modeling software. The OAI is a public-private partnership comprised of five contracts (N01-AR-2-2258; N01-AR-2-2259; N01-AR-2-2260; N01-AR-2-2261; N01-AR-2-2262) funded by the National Institutes of Health, a branch of the Department of Health and Human Services, and conducted by the OAI Study Investigators. Private funding partners include Merck Research Laboratories; Novartis Pharmaceuticals Corporation, GlaxoSmithKline; and Pfizer, Inc. Private sector funding for the OAI is managed by the Foundation for the National Institutes of Health. This manuscript was prepared using an OAI public use data set and does not necessarily reflect the opinions or views of the OAI investigators, the NIH, or the private funding partners.
Footnotes
Conflict of interest statement
Authors have no conflicts of interest.
References
- ABAQUS Documentation. Dassault Systèmes. Providence, RI, USA: 2013. [Google Scholar]
- Adouni M, Shirazi-Adl A. Partitioning of knee joint internal forces in gait is dictated by the knee adduction angle and not by the knee adduction moment. Journal of Biomechanics. 2014;47:1696–1703. doi: 10.1016/j.jbiomech.2014.02.028. [DOI] [PubMed] [Google Scholar]
- Adouni M, Shirazi-Adl A. Consideration of equilibrium equations at the hip joint alongside those at the knee and ankle joints has mixed effects on knee joint response during gait. Journal of Biomechanics. 2013;46:619–624. doi: 10.1016/j.jbiomech.2012.09.035. [DOI] [PubMed] [Google Scholar]
- Akizuki S, Mow VC, Müller F, Pita JC, Howell DS, Manicourt DH. Tensile properties of human knee joint cartilage: I. Influence of ionic conditions, weight bearing, and fibrillation on the tensile modulus. Journal of Orthopaedic Research. 1986;4:379–392. doi: 10.1002/jor.1100040401. [DOI] [PubMed] [Google Scholar]
- Anderson AE, Ellis BJ, Maas SA, Peters CL, Weiss JA. Validation of finite element predictions of cartilage contact pressure in the human hip joint. Journal of Biomechanical Engineering. 2008;130:051008. doi: 10.1115/1.2953472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ateshian G, Wang H, Lai W. The role of interstitial fluid pressurization and surface porosities on the boundary friction of articular cartilage. Journal of Tribology. 1998;120:241–248. [Google Scholar]
- Benninghoff A. Form und Bau der Gelenkknorpel in ihren Beziehungen zur Funktion. Cell and Tissue Research. 1925;2:783–862. [Google Scholar]
- Bergmann G, Bender A, Graichen F, Dymke J, Rohlmann A, Trepczynski A, Heller MO, Kutzner I. Standardized loads acting in knee implants. PloS One. 2014;9:e86035. doi: 10.1371/journal.pone.0086035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Besier TF, Gold GE, Beaupré GS, Delp SL. A modeling framework to estimate patellofemoral joint cartilage stress in vivo. Medicine and Science in Sports and Exercise. 2005;37:1924. doi: 10.1249/01.mss.0000176686.18683.64. [DOI] [PubMed] [Google Scholar]
- Changoor A, Nelea M, Méthot S, Tran-Khanh N, Chevrier A, Restrepo A, Shive M, Hoemann C, Buschmann M. Structural characteristics of the collagen network in human normal, degraded and repair articular cartilages observed in polarized light and scanning electron microscopies. Osteoarthritis and Cartilage. 2011;19:1458–1468. doi: 10.1016/j.joca.2011.09.007. [DOI] [PubMed] [Google Scholar]
- Cohen B, Lai W, Mow V. A transversely isotropic biphasic model for unconfined compression of growth plate and chondroepiphysis. Journal of Biomechanical Engineering. 1998;120:491–496. doi: 10.1115/1.2798019. [DOI] [PubMed] [Google Scholar]
- Danso E, Honkanen J, Saarakkala S, Korhonen R. Comparison of nonlinear mechanical properties of bovine articular cartilage and meniscus. Journal of Biomechanics. 2014;47:200–206. doi: 10.1016/j.jbiomech.2013.09.015. [DOI] [PubMed] [Google Scholar]
- Danso E, Mäkelä J, Tanska P, Mononen M, Honkanen J, Jurvelin J, Töyräs J, Julkunen P, Korhonen R. Characterization of site-specific biomechanical properties of human meniscus—Importance of collagen and fluid on mechanical nonlinearities. Journal of Biomechanics. 2015 doi: 10.1016/j.jbiomech.2015.01.048. [DOI] [PubMed] [Google Scholar]
- DiSilvestro MR, Zhu Q, Suh JF. Biphasic poroviscoelastic simulation of the unconfined compression of articular cartilage: II—Effect of variable strain rates. Journal of Biomechanical Engineering. 2001;123:198–200. doi: 10.1115/1.1351887. [DOI] [PubMed] [Google Scholar]
- Donahue TLH, Hull M, Rashid MM, Jacobs CR. A finite element model of the human knee joint for the study of tibio-femoral contact. Journal of Biomechanical Engineering. 2002;124:273–280. doi: 10.1115/1.1470171. [DOI] [PubMed] [Google Scholar]
- Elliott DM, Narmoneva DA, Setton LA. Direct measurement of the Poisson’s ratio of human patella cartilage in tension. Journal of Biomechanical Engineering. 2002;124:223–228. doi: 10.1115/1.1449905. [DOI] [PubMed] [Google Scholar]
- Goertzen D, Budney D, Cinats J. Methodology and apparatus to determine material properties of the knee joint meniscus. Medical Engineering & Physics. 1997;19:412–419. doi: 10.1016/s1350-4533(97)00011-8. [DOI] [PubMed] [Google Scholar]
- Halonen K, Mononen M, Jurvelin J, Töyräs J, Korhonen R. Importance of depth-wise distribution of collagen and proteoglycans in articular cartilage—A 3D finite element study of stresses and strains in human knee joint. Journal of Biomechanics. 2013;46:1184–1192. doi: 10.1016/j.jbiomech.2012.12.025. [DOI] [PubMed] [Google Scholar]
- Halonen K, Mononen M, Jurvelin J, Töyräs J, Salo J, Korhonen R. Deformation of articular cartilage during static loading of a knee joint-experimental and finite element analysis. Journal of Biomechanics. 2014;47:2467–2474. doi: 10.1016/j.jbiomech.2014.04.013. [DOI] [PubMed] [Google Scholar]
- Halonen K, Mononen ME, Jurvelin JS, Töyräs J, Kłodowski A, Kulmala J, Korhonen RK. Importance of Patella, Quadriceps Forces, and Depthwise Cartilage Structure on Knee Joint Motion and Cartilage Response During Gait. Journal of Biomechanical Engineering. 2016;138:071002. doi: 10.1115/1.4033516. [DOI] [PubMed] [Google Scholar]
- Julkunen P, Wilson W, Jurvelin JS, Rieppo J, Qu C, Lammi MJ, Korhonen RK. Stress-relaxation of human patellar articular cartilage in unconfined compression: prediction of mechanical response by tissue composition and structure. Journal of Biomechanics. 2008;41:1978–1986. doi: 10.1016/j.jbiomech.2008.03.026. [DOI] [PubMed] [Google Scholar]
- Kadaba M, Ramakrishnan H, Wootten M. Measurement of lower extremity kinematics during level walking. Journal of Orthopaedic Research. 1990;8:383–392. doi: 10.1002/jor.1100080310. [DOI] [PubMed] [Google Scholar]
- Kazemi M, Li L, Buschmann M, Savard P. Partial meniscectomy changes fluid pressurization in articular cartilage in human knees. Journal of Biomechanical Engineering. 2012;134:021001. doi: 10.1115/1.4005764. [DOI] [PubMed] [Google Scholar]
- Kazemi M, Dabiri Y, Li LP. Recent advances in computational mechanics of the human knee joint. Computational and Mathematical Methods in Medicine 2013. 2013 doi: 10.1155/2013/718423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Korhonen RK, Herzog W. Depth-dependent analysis of the role of collagen fibrils, fixed charges and fluid in the pericellular matrix of articular cartilage on chondrocyte mechanics. Journal of Biomechanics. 2008;41:480–485. doi: 10.1016/j.jbiomech.2007.09.002. [DOI] [PubMed] [Google Scholar]
- Korhonen RK, Jurvelin JS. Compressive and tensile properties of articular cartilage in axial loading are modulated differently by osmotic environment. Medical Engineering & Physics. 2010;32:155–160. doi: 10.1016/j.medengphy.2009.11.004. [DOI] [PubMed] [Google Scholar]
- Korhonen RK, Laasanen MS, Töyräs J, Lappalainen R, Helminen HJ, Jurvelin JS. Fibril reinforced poroelastic model predicts specifically mechanical behavior of normal, proteoglycan depleted and collagen degraded articular cartilage. Journal of Biomechanics. 2003;36:1373–1379. doi: 10.1016/s0021-9290(03)00069-1. [DOI] [PubMed] [Google Scholar]
- Korhonen RK, Tanska P, Kaartinen SM, Fick JM, Mononen ME. New Concept to Restore Normal Cell Responses in Osteoarthritic Knee Joint Cartilage. Exercise and Sport Sciences Reviews. 2015;43:143–152. doi: 10.1249/JES.0000000000000051. [DOI] [PubMed] [Google Scholar]
- Kozanek M, Hosseini A, Liu F, Van de Velde Samuel K, Gill TJ, Rubash HE, Li G. Tibiofemoral kinematics and condylar motion during the stance phase of gait. Journal of Biomechanics. 2009;42:1877–1884. doi: 10.1016/j.jbiomech.2009.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kumar D, Manal KT, Rudolph KS. Knee joint loading during gait in healthy controls and individuals with knee osteoarthritis. Osteoarthritis and Cartilage. 2013;21:298–305. doi: 10.1016/j.joca.2012.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurkijärvi JE, Nissi MJ, Rieppo J, Töyräs J, Kiviranta I, Nieminen MT, Jurvelin JS. The zonal architecture of human articular cartilage described by T 2 relaxation time in the presence of Gd-DTPA 2−. Magnetic Resonance Imaging. 2008;26:602–607. doi: 10.1016/j.mri.2007.10.013. [DOI] [PubMed] [Google Scholar]
- Kutzner I, Heinlein B, Graichen F, Bender A, Rohlmann A, Halder A, Beier A, Bergmann G. Loading of the knee joint during activities of daily living measured in vivo in five subjects. Journal of Biomechanics. 2010;43:2164–2173. doi: 10.1016/j.jbiomech.2010.03.046. [DOI] [PubMed] [Google Scholar]
- Li L, Buschmann M, Shirazi-Adl A. The asymmetry of transient response in compression versus release for cartilage in unconfined compression. Journal of Biomechanical Engineering. 2001;123:519–522. doi: 10.1115/1.1388295. [DOI] [PubMed] [Google Scholar]
- Li L, Buschmann M, Shirazi-Adl A. A fibril reinforced nonhomogeneous poroelastic model for articular cartilage: inhomogeneous response in unconfined compression. Journal of Biomechanics. 2000;33:1533–1541. doi: 10.1016/s0021-9290(00)00153-6. [DOI] [PubMed] [Google Scholar]
- Li L, Gu K. Reconsideration on the use of elastic models to predict the instantaneous load response of the knee joint. Proceedings of the Institution of Mechanical Engineers, Part H: Journal of Engineering in Medicine. 2011:0954411911412464. doi: 10.1177/0954411911412464. [DOI] [PubMed] [Google Scholar]
- Marouane H, Shirazi-Adl A, Hashemi J. Quantification of the role of tibial posterior slope in knee joint mechanics and ACL force in simulated gait. Journal of Biomechanics. 2015 doi: 10.1016/j.jbiomech.2015.04.017. [DOI] [PubMed] [Google Scholar]
- Mononen M, Julkunen P, Töyräs J, Jurvelin J, Kiviranta I, Korhonen R. Alterations in structure and properties of collagen network of osteoarthritic and repaired cartilage modify knee joint stresses. Biomechanics and Modeling in Mechanobiology. 2011;10:357–369. doi: 10.1007/s10237-010-0239-1. [DOI] [PubMed] [Google Scholar]
- Mononen M, Mikkola M, Julkunen P, Ojala R, Nieminen M, Jurvelin J, Korhonen R. Effect of superficial collagen patterns and fibrillation of femoral articular cartilage on knee joint mechanics—A 3D finite element analysis. Journal of Biomechanics. 2012;45:579–587. doi: 10.1016/j.jbiomech.2011.11.003. [DOI] [PubMed] [Google Scholar]
- Mononen ME, Jurvelin JS, Korhonen RK. Implementation of a gait cycle loading into healthy and meniscectomised knee joint models with fibril-reinforced articular cartilage. Computer Methods in Biomechanics and Biomedical Engineering. 2015;18:141–152. doi: 10.1080/10255842.2013.783575. [DOI] [PubMed] [Google Scholar]
- Mononen ME, Tanska P, Isaksson H, Korhonen RK. A Novel Method to Simulate the Progression of Collagen Degeneration of Cartilage in the Knee: Data from the Osteoarthritis Initiative. Scientific Reports. 2016;6:21415. doi: 10.1038/srep21415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mow VC, Gu WY, Chen FH. Structure and function of articular cartilage and meniscus. Lippincott Williams & Wilkins; 2005. pp. 181–258. [Google Scholar]
- Mow VC, Ratcliffe A. Structure and function of articular cartilage and meniscus. Basic Orthopaedic Biomechanics. 1997;2:113–177. [Google Scholar]
- Mow V, Gibbs M, Lai W, Zhu W, Athanasiou K. Biphasic indentation of articular cartilage—II. A numerical algorithm and an experimental study. Journal of Biomechanics. 1989;22:853–861. doi: 10.1016/0021-9290(89)90069-9. [DOI] [PubMed] [Google Scholar]
- Nissi M, Rieppo J, Töyräs J, Laasanen M, Kiviranta I, Jurvelin J, Nieminen M. T 2 relaxation time mapping reveals age-and species-related diversity of collagen network architecture in articular cartilage. Osteoarthritis and Cartilage. 2006;14:1265–1271. doi: 10.1016/j.joca.2006.06.002. [DOI] [PubMed] [Google Scholar]
- Peña E, Del Palomar AP, Calvo B, Martínez M, Doblaré M. Computational modelling of diarthrodial joints. Physiological, pathological and pos-surgery simulations. Archives of Computational Methods in Engineering. 2007;14:47–91. [Google Scholar]
- Scanlan SF, Chaudhari AM, Dyrby CO, Andriacchi TP. Differences in tibial rotation during walking in ACL reconstructed and healthy contralateral knees. Journal of Biomechanics. 2010;43:1817–1822. doi: 10.1016/j.jbiomech.2010.02.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shirazi R, Shirazi-Adl A, Hurtig M. Role of cartilage collagen fibrils networks in knee joint biomechanics under compression. Journal of Biomechanics. 2008;41:3340–3348. doi: 10.1016/j.jbiomech.2008.09.033. [DOI] [PubMed] [Google Scholar]
- Shirazi-Adl A. On the fibre composite material models of disc annulus—comparison of predicted stresses. Journal of Biomechanics. 1989;22:357–365. doi: 10.1016/0021-9290(89)90050-x. [DOI] [PubMed] [Google Scholar]
- Tanska P, Mononen ME, Korhonen RK. A multi-scale finite element model for investigation of chondrocyte mechanics in normal and medial meniscectomy human knee joint during walking. Journal of Biomechanics. 2015;48:1397–1406. doi: 10.1016/j.jbiomech.2015.02.043. [DOI] [PubMed] [Google Scholar]
- Vaziri A, Nayeb-Hashemi H, Singh A, Tafti BA. Influence of meniscectomy and meniscus replacement on the stress distribution in human knee joint. Annals of Biomedical Engineering. 2008;36:1335–1344. doi: 10.1007/s10439-008-9515-y. [DOI] [PubMed] [Google Scholar]
- Venäläinen M, Mononen M, Väänänen S, Jurvelin J, Töyräs J, Virén T, Korhonen R. Effect of bone inhomogeneity on tibiofemoral contact mechanics during physiological loading. Journal of Biomechanics. 2016 doi: 10.1016/j.jbiomech.2016.02.033. [DOI] [PubMed] [Google Scholar]
- Villegas DF, Maes JA, Magee SD, Donahue TLH. Failure properties and strain distribution analysis of meniscal attachments. Journal of Biomechanics. 2007;40:2655–2662. doi: 10.1016/j.jbiomech.2007.01.015. [DOI] [PubMed] [Google Scholar]
- Wilson W, Huyghe J, Van Donkelaar C. A composition-based cartilage model for the assessment of compositional changes during cartilage damage and adaptation. Osteoarthritis and Cartilage. 2006;14:554–560. doi: 10.1016/j.joca.2005.12.006. [DOI] [PubMed] [Google Scholar]
- Wilson W, Van Donkelaar C, Van Rietbergen B, Ito K, Huiskes R. Stresses in the local collagen network of articular cartilage: a poroviscoelastic fibril-reinforced finite element study. Journal of Biomechanics. 2004;37:357–366. doi: 10.1016/s0021-9290(03)00267-7. [DOI] [PubMed] [Google Scholar]
- Wilson W, Van Rietbergen B, Van Donkelaar C, Huiskes R. Pathways of load-induced cartilage damage causing cartilage degeneration in the knee after meniscectomy. Journal of Biomechanics. 2003;36:845–851. doi: 10.1016/s0021-9290(03)00004-6. [DOI] [PubMed] [Google Scholar]
- Yang N, Canavan P, Nayeb-Hashemi H, Najafi B, Vaziri A. Protocol for constructing subject-specific biomechanical models of knee joint. Computer Methods in Biomechanics and Biomedical Engineering. 2010a;13:589–603. doi: 10.1080/10255840903389989. [DOI] [PubMed] [Google Scholar]
- Yang NH, Nayeb–Hashemi H, Canavan PK, Vaziri A. Effect of frontal plane tibiofemoral angle on the stress and strain at the knee cartilage during the stance phase of gait. Journal of Orthopaedic Research. 2010b;28:1539–1547. doi: 10.1002/jor.21174. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.