Online Estimation of Elbow Joint Angle Using Upper Arm Acceleration: A Movement Partitioning Approach

Abstract

Estimating the elbow angle using shoulder data is very important and valuable in Functional Electrical Stimulation (FES) systems which can be useful in assisting C5/C6 SCI patients. Much research has been conducted based on the elbow-shoulder synergies.

The aim of this study was the online estimation of elbow flexion/extension angle from the upper arm acceleration signals during ADLs. For this, a three-level hierarchical structure was proposed based on a new approach, i.e. ‘the movement phases’. These levels include Clustering, Recognition using HMMs and Angle estimation using neural networks. ADLs were partitioned to the movement phases in order to obtain a structured and efficient method. It was an online structure that was very useful in the FES control systems. Different initial locations for the objects were considered in recording the data to increase the richness of the database and to improve the neural networks generalization.

The cross correlation coefficient (K) and Normalized Root Mean Squared Error (NRMSE) between the estimated and actual angles, were obtained at 90.25% and 13.64%, respectively. A post-processing method was proposed to modify the discontinuity intervals of the estimated angles. Using the post-processing, K and NRMSE were obtained at 91.19% and 12.83%, respectively.

Introduction

Activities of Daily Living (ADLs) recognition is one of the key factors in evaluating the life quality and human health. The diagnosis of abnormal conditions can indicate serious health problems. Many researches have been focused on recognizing and monitoring the activities of elderly-sick people [1]. Online recognition of ADLs can make it possible for real-time learning and acquiring knowledge from the environment for the subjects. So, using feedbacks, they can modify their movements. There are several classifiers used to recognize ADLs such as Support Vector Machine (SVM) [2], Fuzzy Basis Function (FBF) classifier [3], decision tree [4], Hidden Markov Model (HMM) [5-8], etc. HMMs are the most common classifiers used for online recognition of the sequences.

In ADL recognition, many researchers proposed a two-level hierarchical structure: at the first level, state recognition was done where a state is classified as the static and dynamic then at the second level, the activities under each state were recognized separately [8-12]. In FES systems, the elbow angle estimation from the shoulder data is an important problem and can be useful in helping C5/C6 SCI patients [13-16]. In this field, many researches have been done based on the elbow-shoulder synergies. There is a nonlinear relationship between these two joints, so the Artificial Neural Networks (ANNs) are the most widely used tools that can learn to map the input space (shoulder data) to the output space (elbow position) [13,14,17-20]. Popovic et al. (2001) used inductive learning to determine the synergies between the movements of joints while reaching 2D spaces. This learning generated a decision tree to estimate the elbow flexion/extension angular velocity from the shoulder flexion/extension angular velocity [21]. In 2002, they continued their research to identify the coordinated synergies and their relations with task phases [22]. Some researchers proposed an online practical hierarchical structure where at low level, a classifier recognizes the classes then at high level, an estimator such as ANN was trained for each class to estimate the elbow angle from shoulder data [14,23]. According to the previous researches, if the movements are clustered to some groups and an estimator is trained for each cluster, the estimation performance will be improved [24]. One ADL consists of several movement phases. For example, in answering the phone, the subject moves his/her hand from the initial position to the phone place and then picks up the phone and brings it to his/her ear. After holding it for a while, he/she returns it back to its first place. An ANN is not able to learn all the movement phases properly. In this article, the elbow flexion/extension angle was estimated during ADLs, using the upper arm acceleration data based on a new approach, i.e. ‘the movement phases’. We proposed a three-level hierarchical structure. These levels were comprised of clustering the movement phase, classification using HMMs and the angle estimation using ANNs. The proposed structure was online that was very useful in FES control systems. It must be noted that individual and environmental conditions are not constant all the time. For example, in answering the phone, the hand initial position or the phone place may be in different locations. This issue can have an adverse effect on ANNs performance. Considering this problem, in this research, different initial locations for different objects were considered in recording the data to increase the richness of the database and to improve the neural network generalization. This paper has been organized as follows: The next section describes the experimental workspace, data acquisition, pre-processing and different levels of the proposed structure. Afterwards, the results and discussion are described. Finally, the conclusion is given in the conclusion section.

Material and Methods

Experiments

We focused on five common ADLs comprising of drinking, answering the phone, eating, replacing the object and pouring a glass of water. In these ADLs, we asked the subject to move his/her hand from the initial position (rest position) and after doing movements return it back to the first place. For example, in drinking, the subject moved his/her hand from the rest position to the glass place then picked up the glass and brought it to his/her mouth. After drinking some water, he/she returned the glass back to its first place and moved back his/her hand to the rest position. An experimental workspace was designed as shown in Figure 1.

Figure1.

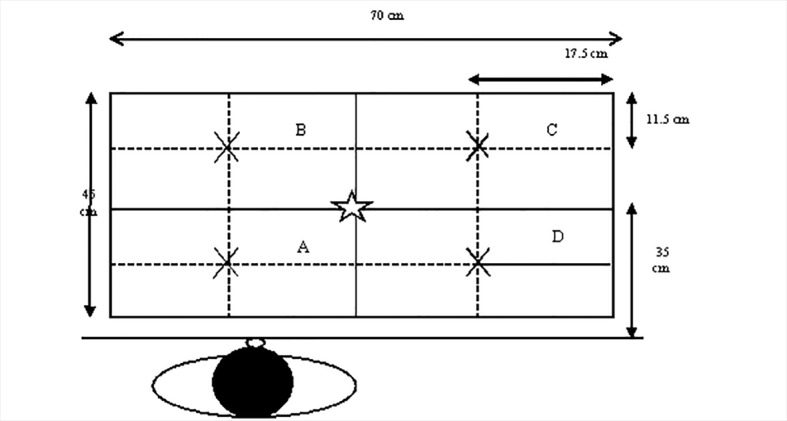
Experimental workspace. The hand rest position was constant in all ADLs as shown in ‘☆’. The target points in the horizontal plane were labeled ‘A’, ‘B’, ‘C’ and ‘D’.

According to the sweeping region of the subject’s hand in the horizontal plane, a rectangle (46cm×70cm) was drawn (Figure 1). It was divided into four rectangles with the same dimensions. Their centers were considered as the target points labelled ‘A’, ‘B’, ‘C’ and ‘D’. The hand rest position was constant in all ADLs as shown in ‘☆’. For three ADLs: eating/dinking/answering the phone, there was one target point in the horizontal plane which was the dish/glass/phone location. So, there were four conditions for each of these three ADLs. In replacing the object/pouring a glass of water, the first and the second locations of the object/the jar and the glass locations were the target points, respectively. Thus, there were two target points and twelve conditions for each of these two ADLs.

Data Acquisition and Pre-processing

We have recorded acceleration signals of the upper arm movement and the elbow flexion/extension angle during ADLs. We used a wireless, tri-axial acceleration sensor based on the micro-electromechanical systems (MEMS) [25] and an electro-goniometer SG110. The accelerometer was attached to the upper arm in 35% distances from the infraglenoid tubercle of scapula to the olecranon process interval. The x-axis of the sensor was aligned to the humerus. Also, when the subject kept his/her arm in the vertical position next to the body, x-y plane of the sensor would be parallel to the subject’s sagittal plane. The electro-goniometer was attached to the elbow joint to record the flexion/extension angle. The subject was a 17-year-old woman. Signals were filtered with a 4th order Butterworth low-pass filter using a cut-off frequency of 2.5 Hertz.

Proposed Structure for Online Estimation of Elbow Angle

Each ADL consists of several movement phases. An ANN is not able to learn all the movement phases properly due to the variety. In this research, we focused on ADLs phases. We partitioned the upper arm acceleration signals in correspondence to the maximum and minimum locations of the elbow angle. In order to estimate the elbow angle from the upper arm acceleration data, we proposed a three-level hierarchical structure. These levels included Clustering, Recognition and Angle estimation that would be introduced thoroughly. Figure 2 shows the block diagram of the proposed method.

Figure2.

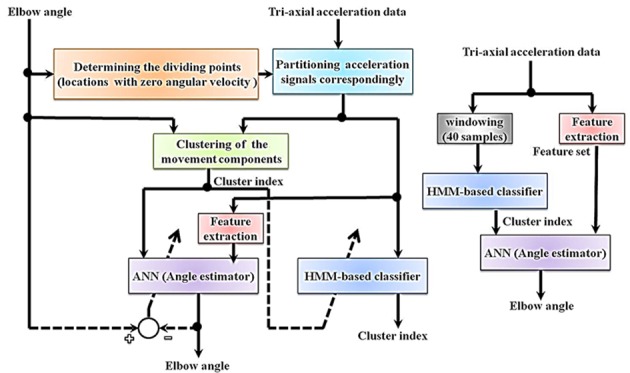
The block diagram of the proposed method. In the left and right panels, the offline training stages and the online estimation of the elbow angle are shown, respectively. The different colors are for the correspondence between the right and left panels.

The levels of the proposed structure are described as follows:

The first level

Movement phases of the data train were clustered at the first level. The upper arm acceleration signals were partitioned in correspondence to the maximum and minimum locations of the elbow angle. In this manner, 160 movement phases were achieved. The movement phases were clustered by K-means algorithm, using the following features:

φ(t), a_x(t), φ(t) - φ(t-1), a_x(t) - a_x(t-1). Where φ, a_x and t are the elbow angle, x-axis acceleration and time, respectively. The number of clusters was selectable in the program. It is necessary to emphasize that the data train was used only at this level.

The second level

At this level, the cluster (class) recognition of the samples was done. Using the data train, a five-state left-to-right HMM [26] was trained for each cluster. Figure 3 shows the state transition diagram of these HMMs.

Figure3.

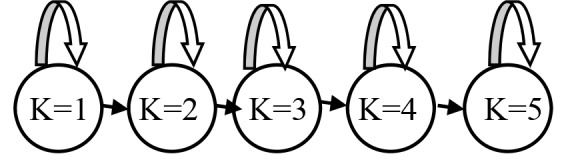
The state transition diagram of the HMMs.

HMMs were trained with the following features:

a_x (t),a_y (t),a_z (t),a_x (t)-a_x (t-1),a_y (t)-a_y (t-1),a_z (t)-a_z (t-1), $\mathrm{atan}\left(\frac{a_x\left(t\right)}{a_y\left(t\right)}\right)$

Where a_x, a_y, a_z and t are x, y, z-axis acceleration data and time, respectively. After training HMMs, online recognition of the data test was done from the sliding windows with 40 samples. For each sample of the data test, its corresponding window was comprised of the current sample and its 39 previous samples. This window was used as HMMs input. After calculating log-likelihood of the HMMs, the sample was assigned to the class with the biggest log-likelihood value. This online process was done for each sample of the data test.

The third level

At this level, the online estimation of flexion/extension elbow angle was done using the upper arm data. A feed-forward, one-layer ANN was trained for each cluster. 25 neurons have been considered in the hidden layer. The “tansig transfer function” and the “linear transfer function” were used for the hidden and output layer, respectively. The scaled conjugate gradient algorithm was utilized as the training function. The following features have been used to train the ANNs:

a_x(t), a_y(t), a_z(t), a_x(t) - a_x(t-1), a_y(t) - a_y(t-1), a_z(t) - a_z(t-1), a_x(t-5), a_y(t-5), a_z(t-5)

Experimental Results and Discussion

The data set was randomly divided into two parts: 80% as the training set and 20% as the testing set. To choose the appropriate number of clusters, the train and test processes were done for a different number of clusters as listed in Table 1, then the cross correlation coefficient (K) and the Normalized Root Mean Squared Error (NRMSE) were calculated between the estimated and desired (actual) elbow angles of the data test.

Table 1.

The results for a different number of clusters

Number of clusters	K (%)	NRMSE (%)
15	74.84	24.02
25	82.25	17.20
40	86.02	16.38
55	87.19	15.41
70	90.25	13.64
85	86.83	15.39
85	86.83	15.39

According to Table 1, selecting 70 clusters was appropriate due to the least value of NRMSE and the biggest value of K. As the clusters increased from 15 to 70, K and NRMSE would become higher and lower respectively, i.e. the estimation results would improve. But with a further increase, the estimation results weakened. As a reason, increasing clusters caused their within-class variances would become lower, so HMMs would better train for online recognition using the clusters data. But excessive increase of clusters has an adverse effect on the results, because the structure generalization weakened, and also the data of the clusters used for training HMMs would decrease, accordingly, HMMs parameters would not have proper values due to inadequate data train. In this research, 70 was chosen as the proper number of clusters. To represent the detailed results of 70 clusters, K and NRMSE are shown for each ADL and each target point in the horizontal plane (Table 2).

Table 2.

The results of 70 clusters, for each ADL and each of the target points in the horizontal plane.

Number of clusters	Target points	K (%)	NRMSE (%)
Drinking	A	92.18	13.33
	B	75.11	23.68
	C	79.28	24.71
	D	55.46	25.38
Answering the phone	A	97.58	7.28
	B	98.43	7.14
	C	95.17	8.79
	D	87.67	13.35
Eating	A	90.87	13.65
	B	94.11	10.13
	C	98.41	5.98
	D	94.87	12.54
Replacing the object	A-B	97.62	8.14
	A-C	97.27	9.18
	A-D	81.28	19.45
	B-A	97.74	7.09
	B-C	96.69	8.50
	B-D	97.69	7.56
	C-A	85.24	16.11
	C-B	77.27	23.77
	C-D	98.65	5.94
	D-A	96.90	8.68
	D-B	86.48	16.99
	D-C	98.28	7.56
Pouring glass of water	A-B	93.80	15.03
	A-C	94.40	11.04
	A-D	91.52	13.72
	B-A	98.53	6.31
	B-C	83.07	16.92
	B-D	99.06	5.66
	C-A	97.50	8.42
	C-B	87.71	15.40
	C-D	97.56	7.03
	D-A	82.38	22.78
	D-B	80.81	31.33
	D-C	89.77	17.03

To improve the estimation results, a post-processing method has been proposed. It was based on the second maximum of log-likelihoods of HMMs.

For example, if a sample is placed near the decision boundary between two classes, it will be probable to recognize its class incorrectly because the boundary decision is rigid and the decision regions have not been formed ideally. The regions belonging to the two classes with the first and the second maximum of log-likelihoods are close to each other.

In this research, if a discontinuity interval was created in the estimated elbow angle, it would be modified by checking some conditions, then angle estimation would continue in the usual manner. The post-processing method is comprised of the following sections:

• 1. For each cluster, the Difference Absolute of Elbow Angle time series (DAEA) was calculated as follows:

  |φ(t) - φ(t-1)|

  Where φ and t are the elbow angles of data train and time, respectively, then the Maximum value of DAED (MDAEA) was determined for each cluster. It must be emphasized that the data train was used only in this step.

• 2. In online estimation, the difference absolute of the estimated angle was calculated based on the current and the previous sample:

  |φ1(t) - φ1(t-1)|

  Where φ1 and t are the elbow angles of the data test and time (sample number), respectively.

  If this value was ‘n’ times greater than MDAEA of two clusters assigned to the current and previous samples, the next step would be done.

  As ‘n’ parameter’s value increases, the sensitivity becomes larger but may sometimes have undesirable performance. Considering a trade-off between these two cases, this value was set to 1.2.

• 3. One cause of the discontinuity may be the improper class recognition of the sample. For detecting this case, if two recognized clusters of the current and previous samples were different, these two clusters would be saved in the discontinuity location.

• 4. The mentioned steps would continue until another discontinuity was detected.

• 5. In this step, for the continuity interval, the samples were labelled to the classes with the second maximum of log-likelihoods and then the elbow angles were estimated again.

• 6. At the beginning and end of corresponding interval, if the jumps decreased and using these new estimated angles did not create any discontinuities and the current continuity interval was not bigger than the previous continuity interval, these modifying (new) estimated angles would be replaced with the earlier estimated angles.

Figure 4 illustrates two examples of the results with/without post-processing. In the top panels, the recognized clusters of the samples with/without post-processing are shown in red and blue, respectively. In the middle panels, the actual and the estimated angles (without post-processing) are shown in green and blue, respectively, and in the bottom panels, the actual and the estimated angles (with post-processing) are shown in green and red, respectively

Figure4.

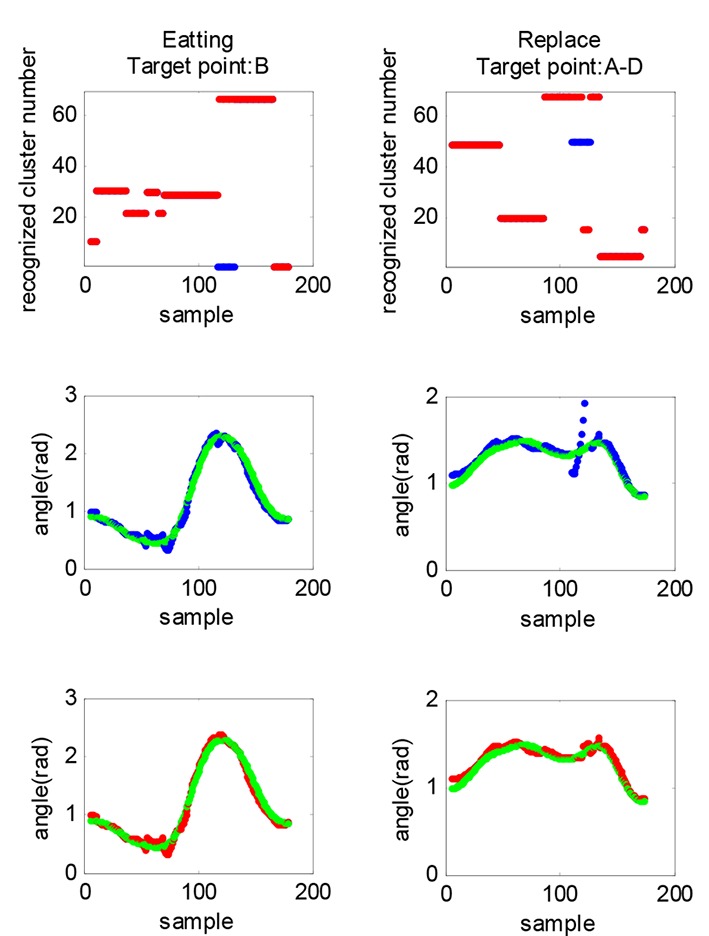
Two examples of the results with/without post-processing. In the top panels, recognized clusters of the samples with/without post-processing are shown in red and blue, respectively. In the middle panels, the actual and the estimated angles (without post-processing) are shown in green and blue, respectively and in the bottom panels, the actual and the estimated angles (with post-processing) are shown in green and red, respectively.

It is seen qualitatively that the discontinuity intervals are modified by the post-processing method.

Using post-processing, K and NRMSE between the estimated and real angles of the data test were obtained at 91.19% and 12.83%, respectively, where 0.94% and 0.81% improvement was achieved.

Conclusion

In this research, we estimated the elbow flexion/extension angle using the shoulder kinematic information. For this aim, we suggested a hierarchical structure comprising of three levels: clustering, recognition and the elbow angle estimation. Before clustering, the data train was partitioned to the movement phases according to the locations with zero elbow angular velocity. Then, at the first level, the obtained phases were clustered using K means algorithm. At the second level, for each cluster (class), a HMM was trained for online class recognition of the samples. At the third level, an ANN was trained for each cluster to estimate the elbow flexion/extension angle. The advantages of the proposed structure could be mentioned as follows:

• 1. An ANN cannot learn all the movement phases properly because of their variety. So, partitioning ADLs to the phases facilitated the ANNs functions.

• 2. There were some advantages due to hierarchical structure. At the first level, the movement phases of data train were clustered. According to previous studies [24], clustering improves the estimation results because the ANNs will have specialized performance. At the second level, online cluster (class) recognition was done by HMMs which was an important issue.

• 3. The proposed structure was online, being very suitable in the real-time FES control systems.

• 4. Different initial locations for the objects were considered in recording the data set to increase the richness of the database and to improve the neural networks generalization.

The number of clusters changed at the first level to achieve the optimal number, then, K and NRMSE between the estimated and actual elbow angle of the data test (108 data test) were calculated (Table 1). As clusters increased from 15 to 70, K and NRMSE would become higher and lower, respectively, i.e. the estimation results would improve. But with a further increase, the estimation results became weak. In this study, 70 was taken as the appropriate number of clusters. The reason could be mentioned as follows:

As clusters increased, their within-class variances would become lower; so HMMs would better train for online recognition using cluster data. But excessive increase of clusters has negative effects on the results because the structure generalization would reduce, and also the clusters data used for training HMMs would decrease, as a result, HMM parameters would not have the proper values due to inadequate data train.

K and NRMSE between the estimated and real angles of the data test were obtained at 90.25% and 13.64%, respectively which were acceptable values with regard to the variety of movements studied in this research. In order to improve the results, a post-processing method was proposed. This method modified the discontinuity intervals of the estimated angles in the presence of some conditions. Regarding the small lengths of the discontinuity intervals, it would not cause serious problems for being an online method. Comparing the middle and the bottom panels of , its positive effects on the discontinuity intervals would be clear. In this manner, K and NRMSE between the estimated and real angles of the data test were obtained at 91.19% and 12.83%, respectively which were 0.94% and 0.81% better than previous results.