Climate-driven endemic cholera is modulated by human mobility in a megacity

Abstract

Although a differential sensitivity of cholera dynamics to climate variability has been reported in the spatially heterogeneous megacity of Dhaka, Bangladesh, the specific patterns of spread of the resulting risk within the city remain unclear. We build on an established probabilistic spatial model to investigate the importance and role of human mobility in modulating spatial cholera transmission. Mobility fluxes were inferred using a straightforward and generalizable methodology that relies on mapping population density based on a high resolution urban footprint product, and a parameter-free human mobility model. In accordance with previous findings, we highlight the higher sensitivity to the El Niño Southern Oscillation (ENSO) in the highly populated urban center than in the more rural periphery. More significantly, our results show that cholera risk is largely transmitted from the climate-sensitive core to the periphery of the city, with implications for the planning of control efforts. In addition, including human mobility improves the outbreak prediction performance of the model with an 11 month lead. The interplay between climatic and human mobility factors in cholera transmission is discussed from the perspective of the rapid growth of megacities across the developing world.

1. Introduction

Seasonal outbreaks of endemic cholera are responsible of an estimated 3 million cases of acute watery diarrhea and 90’000 deaths each year [1]. The disease is associated with poor sanitary conditions given that fecal-oral transmission occurs either via the environment-to-human or human-to-human routes, bringing into play climatic, environmental and socio-economic factors [2, 3]. Megacities of the developing world are exposed to cholera (and other water-borne infections) due to their high population density and all too often inadequate water and sanitation infrastructure prompting exposure to the pathogens through various mechanisms [4, 5].

Dhaka, the capital of Bangladesh with an estimated 17 million people, is located in a floodplain and experiences two cholera incidence peaks per year [2, 6]. Rapid urbanization in recent decades has been accompanied by an increase in the prevalence of severe cholera cases during flooding events [7]. When studied at the regional scale, cholera is known to be influenced by the El Niño Southern Oscillation (ENSO) [8, 9], but the spatio-temporal patterns of incidence within large cities are not necessarily synchronized (contrary to what one would expect from the Moran effect [10]). This lack of synchrony points to the non-trivial relationship between global climatic drivers and local transmission dynamics [11], in particular in urban contexts [12]. The strong degree of spatial heterogeneity in population density and sanitary infrastructure in Dhaka has been hypothesized to underlie a differential sensitivity to climatic forcing between the densely populated city core and the more rural periphery (Fig. 1) [13]. Indeed, informal settlements, which often constitute hotspots of cholera transmission [14], are widespread in the city [15], and vulnerable to the intense yearly monsoon flooding which gains particular intensity in high-ENSO years [16, 17]. Although these conditions would explain the high cholera attack rates in the core, the pathways by which cholera spreads across the megacity remain unclear.

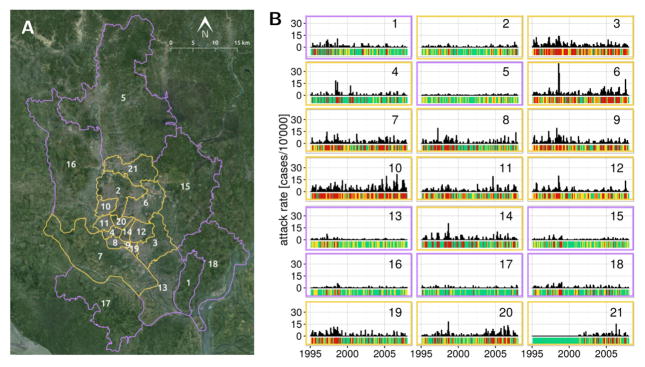
Figure 1.

Dhaka situation map and cholera incidence. (A) The 21 thanas of Dhaka are grouped in an inner core (yellow outline) and the periphery (purple outline). (B) Monthly cholera incidence in the thanas of Dhaka from 1995 to 2008, the bars beneath each timeseries indicates the discrete disease state in which the month is categorized, either no cholera (green), low cholera (yellow) or high cholera (red). The color of the frame indicates if the thana is in the core (yellow) or the periphery (purple) of the city.

Hydrological transport and human mobility are the two main mechanisms for the spatial spread of Vibrio cholera, although food networks can also play an important role in bacterial dissemination [for eg. see 18]. Both of the former have been considered in modeling studies at the national scale for epidemic cholera either together [19, 20], or separately for human mobility [21, 22] and hydrology [23]. Potential pathways of hydrological pathogen transport in Dhaka, through both the urban drainage system and the surface during flooding, have recently been explored using a high-resolution 2D advection-dispersion model [24]. This study suggested small-scale heterogeneities in pathogen exposure due to the mixing of wastewater with flood water, but the highlighted effects were mainly local and were subject to unresolved sources of uncertainty [24]. Although hydrology may indeed be an important explanatory factor of cholera attack rates at the neighborhood-scale, it remains to be shown that it also acts as a city-scale control of disease spread. Another mechanism underling spread would be human mobility which has recently been shown to be a crucial driver at the national level [22], but that to our knowledge has neither been quantified nor included in spatial models for cholera dynamics at the urban scale. This gap has also recently been stressed for the transmission of all climatically-forced infectious diseases [12]. Models of human mobility that depend only on the spatial distribution of population have been used in waterborne disease models in the absence of mobility data such as mobile phone records, but not within cities [25, 26]. The recent development of a high resolution (12m) Global Urban Footprint (GUF) extracted from remote sensing data opens the door to the application of mobility models at the megacity scale [27, 28]. We present here an approach to rely on such mobility models to improve on default near neighbor assumptions of connectivity in transmission models, when direct data on movement is not available.

Addressing the interplay between climate forcing and spreading mechanisms could prove useful in designing vaccination campaigns that take spatial structure into account, especially given the recent evidence showing the feasibility and protective effect of this kind of intervention in Dhaka [29, 30]. Indeed cholera models that account for spatial connectivity have been proposed to guide reactive vaccination interventions during urban cholera epidemics [31].

Here, we build on the existing framework of a multi-dimensional inhomogeneous Markov Chain model (MDIMC) for cholera transmission [13, 32]. We specifically incorporate inferred human mobility fluxes based on population distribution to investigate the spatio-temporal dynamics of cholera within the city. We then discuss the relevance of taking human mobility into account in water-borne disease transmission within megacities.

2. Data and Methods

2.1. Dhaka and cholera

Dhaka covers around 2’300 km² of a complex patchwork of land and water located North of the intersection between the Padma and the Meghna rivers. The city experiences regular flooding of particular intensity during high-ENSO years, of which 1998 and 2003 are the most memorable examples [17]. The part of the city we consider in this study is composed of 21 administrative units called thanas, which can be categorized into a densely populated city core and a more rural periphery (Fig 1 and [13, 33]).

Cholera, which has been reported for this region since the British colonial presence in the late 1800’s [34], continues to represent a public health issue for the city of Dhaka. Outbreaks are still common today, showing different temporal patterns in different parts of the city (Fig. 1). The epidemiological data, its collection protocol and the processing required by the MDIMC framework have been described elsewhere [13]. Briefly, cholera case data consisted of monthly cholera hospitalization counts at the International Center for Diarrhoeal Diseases Research, Bangladesh from 1995 to 2008. As mentioned in [13], the data correspond to El Tor infections confirmed by systematic laboratory analysis of a 4% sample of incoming patients with cholera symptoms from in 1995, and a 2% sample from 1996 onward. The attack rate data used in this study are the same as the ones used in [13], which were corrected for the difference in sampling effort. For modeling purposes and following [13], the monthly attack rate data was categorized into 3 discrete cholera states 0,1 and 2 corresponding to no (0 cases/10’000 people/month), medium ( less than 1.85 cases/10’000 people/month) and high (more than 1.11 cases/10’000 people/month) cholera incidence respectively (see Fig. 1). The average incidence in the medium and high cholera states were 1.11 cases/10’000 people/month and 4.58 cases/10’000 people/month respectively.

2.2. The model

A large palette of modeling techniques have been applied to study cholera (for an overview see [32]). Here we choose the MDIMC framework proposed by Reiner et al. [13] in which the observed monthly cholera attack rates are categorized into discrete states of cholera intensity, and the space-time dynamics of transmission modeled by a inhomogeneous Markov Chain [13, 32]. The transition from cholera in state i at time t to state j at time t + 1 (X_k,t = i) → (X_k,t+1 = j) occurs with baseline probability p_i,j. The baseline transition probability matrix is given by:

$$P=\left(\begin{array}{lll}{p}_{1,1}\hfill & (1-p_{1,1}-p_{1,3})\hfill & p_{1,3}\hfill \\ p_{2,1}\hfill & (1-p_{2,1}-p_{2,3})\hfill & p_{2,3}\hfill \\ p_{3,1}\hfill & (1-p_{3,1}-p_{3,3})\hfill & p_{3,3}\hfill \end{array}\right).$$

The effect of covariates can be accounted for through the modification of matrix P. In the case of Dhaka, the consideration of two groups of thanas with differential baseline probabilities was significant to explain the spatio-temporal attack rate patterns [13]. Furthermore, the seasonal variation of cholera risk and the effect the ENSO were shown to play important roles depending on the group to which each thana belongs (core or periphery, which we refer to interchangeably as inner and outer groups). We take both of these factors into account, in addition to the effect of human mobility which we specifically develop. More formally, the transition probability from state i to j with i < j or i = 3, of thana k in group g (inner or outer) is assumed to be modulated as:

$$p_{i,j,k,t}^{\prime }=p_{i,j}{(1+f_{g,t}^{\mathit{seas}})}^{{\beta }_{i,\mathit{sgn},g}}{(1+f_{k,t}^{\mathit{mob}})}^{{\nu }_g}(1+f_{g,t}^{\mathit{ENSO}}),\beta ,\nu >0$$ (1)

where $f_{g,t}^{\mathit{seas}},f_{k,t}^{\mathit{mob}}$ and $f_{g,t}^{\mathit{ENSO}}$ correspond to the time varying seasonal, human mobility and ENSO forcings respectively, the β parameters depend on the starting cholera state i and the sign (increase or decrease) of f^seas, and all exponents depend on the group g of the thana. The forcing functions are defined as:

$$\begin{array}{lll}\hfill f_{g,t}^{\mathit{seas}}& ={\alpha }_{m,g},\hfill & \hfill \alpha >-1,\\ \hfill f_{k,t}^{\mathit{mob}}& ={\gamma }_{in,g}\sum _{l\ne k}{\mathcal{Q}}_{lk}{X}_{l,t}+{\gamma }_{\mathit{out},g}\sum _{l\ne k}{\mathcal{Q}}_{kl}{X}_{l,t}\hfill & \hfill \gamma >0,\\ \hfill f_{g,t}^{\mathit{ENSO}}& =A_{g}tan\left(\frac{k_g}{2}\frac{\mathit{ENSO}(t-\tau )}{M_g}\right)tan{\left(\frac{k_g}{2}\right)}^{-1},\hfill & \hfill A,M>0;k\in (0,\pi )\end{array}$$

where the subscript m indicates the month, 𝒬_kl is the human mobility matrix describing the probability for a person to move from the origin thana, k, to destination, l, and to come back during a finite time interval, the parameters γ_in(γ_out) modulate multiplicatively the effects of the incoming (outgoing) mobility fluxes, and ENSO(t − τ) is the sea surface temperature (SST) anomaly corresponding to the El Nino 3.4 index at τ lags (in months) ([13]). The methodology to obtain 𝒬_kl relies on the spatial distribution of population density as explained below. In the original formulation, the effect of spatial connectivity was incorporated through a simple effect of the state of neighboring thanas. Here, we replace this assumption by estimating human mobility fluxes.

The functional form for f^ENSO is a flexible parametrization of the influence of the ENSO on cholera risk with k_g → 0 indicating a linear effect, whereas k_g → π a nonlinear one (see [13] for an illustration of functional shapes). Here we set τ = 10 months based on the results by [13] which identify this value as the most significant lag between ENSO and cholera outbreaks, consistent with previous studies [8, 35, 9]. This results in an 11-month lead prediction capacity. For any of the forcing functions, a negative (positive) value indicates a decrease (increase) in the probability of transitioning to a higher cholera state. The modified probabilities are normalized so that they sum to 1:

$$\begin{array}{ll}{p}_{i,1,k,t}^{\prime }=1-p_{i,2,k,t}^{\prime }-p_{i,3,k,t}^{\prime }\hfill & \hfill \text{if}i=1;\\ p_{i,1,k,t}^{\prime }=(1-p_{i,3,k,t}^{\prime })\frac{p_1}{p_1+p_2}\hfill & \hfill \text{if}i>1\\ p_{i,2,k,t}^{\prime }=(1-p_{i,3,k,t}^{\prime })\frac{p_2}{p_1+p_2}.\hfill & \hfill \end{array}$$

2.3. Population density and human mobility

Human mobility models have been extensively employed to infer mobility matrices (here Q) in the framework of spatially-explicit models for the spread of waterborne diseases [19, 25, 20, 36]. Indeed, we are here interested in the spatial repartition of mobility, rather than mobility fluxes themselves (people per unit time). A common choice is to use the gravity model and its different parametrizations, which state that the probability of moving from one location to another is proportional to their respective populations and inversely linked to a function of the distance which separates them [37]. Recently, the radiation model was introduced as a generalization of the gravity model and has been validated based on commuting data [38]. The radiation model draws from physical sciences in assuming that the movement of people follows radiation emission and absorption processes, where both the absorption threshold of trips emitted from a given location and the absorbance of the surroundings are a function of population density. Though tied to an underlying assumption of relatively uniform spatial distribution of mobile population, it presents the advantage of being ”parameter free” when inferring mobility patterns, and to directly depend on the spatial distribution of population density. The radiation model predicts that the fraction of journeys originating from a given origin u that reach destination v is given by:

$$Q_{uv}=\frac{H_u{H}_v}{(H_u+s_{uv})(H_u+H_v+s_{uv})},$$ (2)

where H_u(H_v) denotes the origin(destination) population and s_uv is the sum of the population within a circle centered at the location of the origin, of radius equal to the distance between u and v, d_uv, excluding the origin and destination populations. Given the large size and population differences between thanas (Fig. 1) the radiation model was not applied to the administrative units directly, but instead to a pixel-to-pixel basis using a gridded population density raster map.

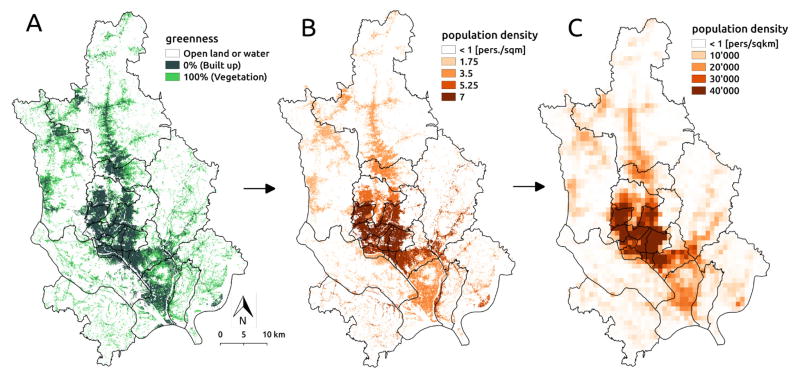
The population density map was produced by dasymetric mapping (sensu [39]) of census population counts available at the thana-level to the distribution of built up areas in the city. The methodology consisted of four steps: 1) computing the thana-specific population density of built-up areas, 2) aggregating population counts at a 1km² resolution, 3) computing pixel-to-pixel mobility fluxes, and 4) extracting thana-to-thana fluxes. The two first steps are illustrated in Fig. 2. The starting point of the methodology is a raster map of the built-up area produced and made available by the German Aerospace Center (DLR). The product results from the analysis of the Synthetic Aperture Radar (SAR) data from the TanDEM-X (TDM) mission merged with multispectral Landsat data (for methodological details and applications see [16, 40, 28, 41]). It consist of a raster with a 12m resolution in which values correspond to the percentage of each pixel’s area covered by constructions in 2013 (mapped in terms of ”greenness”, i.e. the fraction of the pixel covered by vegetation, in Fig. 2 A). Based on the built-up raster, the population density map was computed by multiplying the built-up surface of each pixel by the thana-specific population density in built-up areas, which was obtained by dividing the thana’s population by the total amount of built-up surface in the thana (Fig. 2 B). Since the population census data was not available for 2013, an exponential projection of the most recent census was used (see [13]). The population raster was then aggregated to a 1km resolution for the computation of mobility patterns (Fig. 2 C). The pixel-to-pixel mobility matrix, denoted by Q_pq hereafter, was computed using the radiation model in eq. 2 applied to the aggregated population density map. The final thana-to-thana mobility matrix 𝒬_kl was computed as:

$${\mathcal{Q}}_{kl}=\frac{1}{H_k}\sum _{p\in k}\sum _{q\in l}{Q}_{pq}\times H_p$$ (3)

where H_k = Σ_p∈k H_p is the sum of the pixel population densities H_p of thana k. The diagonal of 𝒬_kl indicates the probability of intra-thana movement, and the sum over each row equals to 1. The whole procedure can be easily applied to other urban settings since it only depends on (1) total population counts by administrative area (which could also be the overall population in the city) and (2) the built-up area map which can be provided on request for arbitrary areas of interest via DLR.

Figure 2.

Population aggregation methodology. (A) Built-up area map shown in terms of the percentage of each pixel covered by vegetation (”greenness” index). (B) Dasymetric mapping of thana-specific population density at 12m resolution. (C) Aggregated population density at 1km resolution used to compute mobility fluxes. Black lines represent thana administrative boundaries.

2.4. Model fitting

One of the advantages of the MDIMC formulation of the model is the simplicity of evaluating the agreement of a set of parameters to the data through a likelihood-based approach. Here we use the subplex algorithm [42], an extension of the straightforward Nelder-Mead (NM) algorithm used in previous MDIMC studies [43, 13, 32]. The subplex algorithm consists of iteratively applying the simplex algorithm on subspaces of the investigated parameter space, thus reducing computation time and improving convergence properties [42]. To impose parameter constraints (including positivity and probabilities summing to 1), we used the barrier method as done in previous studies [13, 32]. The optimal parameter set was obtained by running the subplex algorithm 100 times from different starting points using the subplex package in R [44, 45]. The subplex algorithm does not enable the direct computation of uncertainty bounds on the optimal parameter sets due to its heuristic nature. To give a quantification of uncertainty, the likelihood surface was further explored by profiling the parameters of interest. Profiling was performed on the parameters p_.,3 of the transition matrix for each thana group which capture the intrinsic difference in cholera risk between the different parts of the city. Methodological details and results on parameter profiling are given in the Supplementary Material (SM). The computations were run in parallel with the foreach package [46] on the CASTOR cluster of the Scientific IT and Application Support Center of the Ecole Polytechnique Fédérale de Lausanne.

2.5. Cross-validation and predictive capacity

To further assess model predictive capacity, we performed a 14-fold cross-validation following the methodology used by [13]. Briefly, the procedure consisted of sequentially removing one year of data (out of a total of 14 years), refitting the model to the remaining years with the subplex algorithm, and simulating cholera dynamics for the given year using the new best parameter set. Simulating cholera dynamics in the MDIMC framework is straightforward: since the model is stochastic, random numbers between 0 and 1 are drawn to update cholera states based on the probabilities of the state transition matrix (see [13] for details). A total of 10’000 simulations were performed for each data point of the time series for which an 11-month lead was feasible (corresponding to the ENSO forcing lag). To quantify outbreak prediction performance, the observed and simulated outbreaks were compared in a contingency matrix where an outbreak was defined as city-average cholera incidence higher than the 75th percentile of the observed aggregated monthly incidence a the city scale (2.06 cases/10’000 people). For the purpose of outbreak prediction, the simulated outbreak probability (i.e. the percentage of simulations that give an attack rate larger than the above-mentioned threshold) was used as a classification score. Following the methodology in [13], the optimal outbreak probability threshold retained for prediction was found using the Kolmogorov-Smirnov test. The threshold corresponds to the point of maximum distance between the Cumulative Mass Functions of the predicted outbreak probability in months where an outbreak did and did not occur [47]. Given the identified optimal threshold, the confusion matrix of observed and predicted outbreak was used a basis for the computation of predictive performance, including accuracy and false positive and negative rates.

To establish a baseline for comparison for the predictive ability of the MDIMC, we also fitted a seasonal autoregressive integrative moving average model (SARIMA) to the mean city-wide incidence time series. Details on model fitting and prediction results are given in the Supplementary Material.

3. Results

3.1. Predicted thana-to-thana mobility in Dhaka

The thana-to-thana mobility fluxes produced using the radiation model present strong heterogeneties in terms of both directionality and spatial connectivity. Indeed movement is predicted to occur with higher probability between the thanas of the core of the city, and to a lesser extent between the core and the periphery, except for some exceptions (for instance between Narayanganj Sadar (thana 12) and Keraniganj (thana 7), Fig. 3). In addition, outer-outer movement is less frequent probably because of the spatial configurations of the thanas that impose crossing the city core to reach each other. Outer-to-inner movement was predicted to occur with a similar probability to the inner-to-outer one (an average across thanas of around 0.4% of trips).

Figure 3.

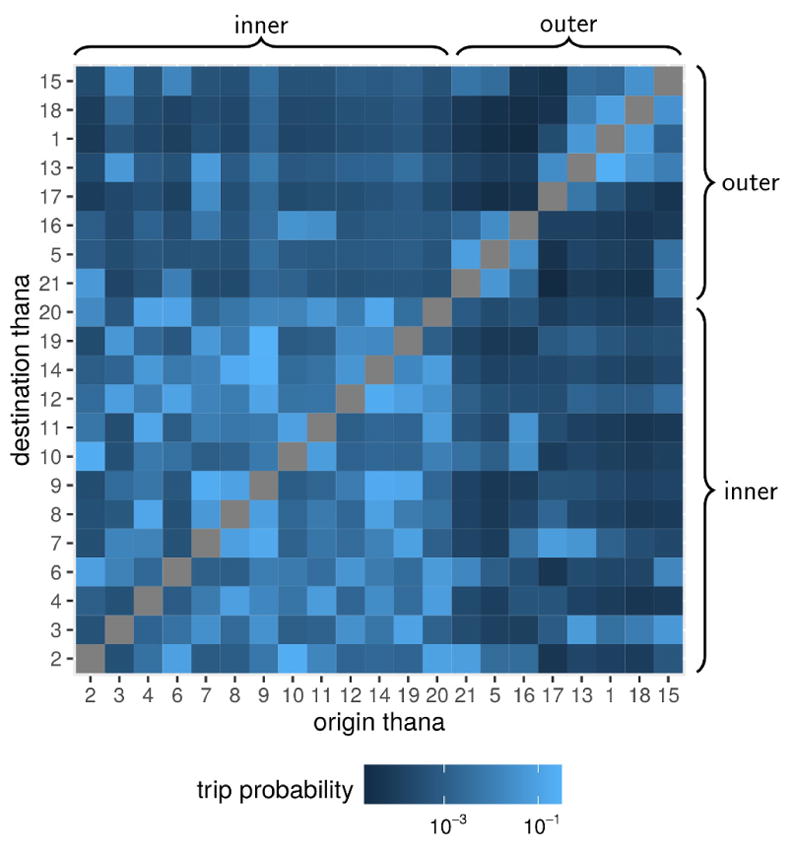
Mobility fluxes between thanas in Dhaka. The mobility patterns in the city are represented as the percentage of outgoing trips that are predicted to occur between the origin(row) to the destination(column) thana in the log10-color scale of each pixel in the grid. Thana groups (inner core and outer periphery) are indicated by braces.

3.2. Cholera, ENSO and the effect of human mobility

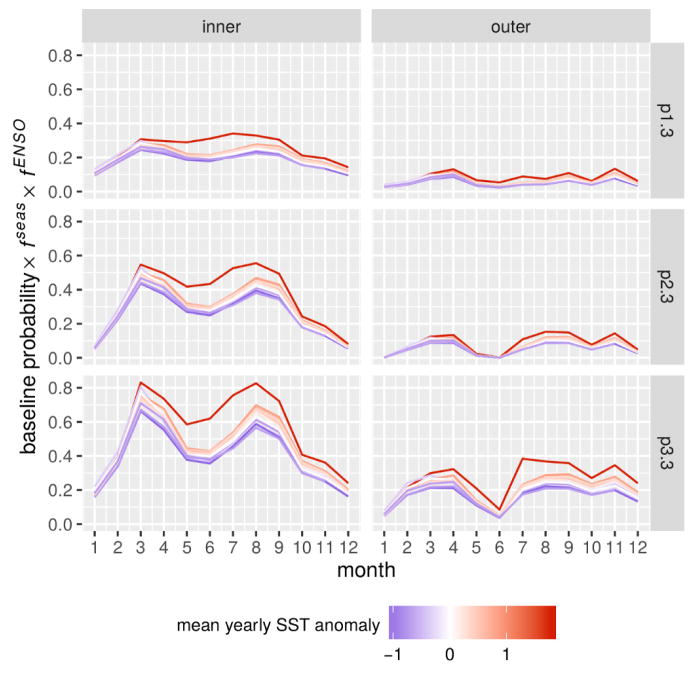
Model performance was quantified in terms of log-likelihood, the Akaike Information Criterion (AIC) [48], and the significance of the covariates evaluated using likelihood ratio tests applied to the nested models (for details see [13]). The model with all forcing effects (full model with 60 parameters) presented the best AIC score, and the inclusion of all effects was significant compared to all nested models (Table 1). The climatic forcing by ENSO was found to be the most significant effect after seasonality. Interestingly, the best-fitting parameter set of the full model suggests a very similar functional form for the ENSO effect in the two regions of the city (k_inner ≈ k_outer ≈ 2.5, corresponding to a nonlinear functional form more sensible to extremes, Table 2). In accordance with previous findings [13], cholera dynamics in thanas of the core of the city presented a stronger absolute sensitivity to the ENSO than the periphery (Fig. 4). Indeed, the final selected model suggests a stronger interannual variability of the probabilities to transition to high cholera in the inner thanas than in the outer ones. This is the result of the higher base probability of transitioning to high cholera, p_i,3, in the inner group and similar f^ENSO values (the forcing functions have a multiplicative effect on baseline probabilities). The inner vs. outer difference in cholera risk was further highlighted by the profiling results which indicate lower values of p_i,3 in the outer group (see SM Fig S1).

Table 1.

Model fit comparison. The presence(absence) of covariate effects is indicated by the symbol +(−). Nested models are compared against the full model (first line) by sequentially removing 1 covariate (grey rows), and then testing the removal of the other two covariates (white rows). Models are ranked by the AIC score using the number of parameters in each model (df) and the maximal log-likelihood (ℒ). The differences in AIC scores (ΔAIC) were computed against the overall best-performing model. Covariate significance (p-value) was computed using the likelihood ratio test on the Δℒs assuming a χ² distribution.

fseas	fENSO	fmob	df	ℒ	AIC	ΔAIC	p-value
+	+	+	60	−3110.36	6340.72	0.00	-
+	+	−	54	−3122.64	6353.27	12.56	1.75e-04
+	−	−	48	−3142.83	6381.66	40.94	1.74e-07
−	+	−	18	−3297.40	6630.80	290.08	2.35e-53
+	−	+	54	−3130.22	6368.45	27.73	2.33e-07
+	−	−	48	−3142.83	6381.66	40.94	1.33e-04
−	−	+	18	−3298.65	6633.29	292.57	7.11e-51
−	+	+	24	−3230.93	6509.86	169.14	1.47e-32
−	+	−	18	−3297.40	6630.80	290.08	1.50e-26
−	−	+	18	−3298.65	6633.29	292.57	4.46e-27

Table 2.

Optimal parameter set of the full model. Parameters are given by thana group (inner city core and outer periphery) for the baseline probability transition matrix P, the mobility effect f^mob and the ENSO effect f^ENSO. Parameters γ_in(γ_out) modulate the effect of incoming(outgoing) human mobility fluxes on the increased risk of cholera, ν regulates the overall effect of f^mob, and M, k and A correspond to the scale, phase and amplitude parameters of the ENSO functional form. The parameters of the seasonality forcing f^seas are not shown.

	Base probability			Mobility			ENSO
	P.0	P.1	P.2	γin	γout	ν	M	k	A
Inner	P0. 0.582	0.17	0.201
	P1. 0.370	0.341	0.289	330.7	13.9	0.032	2.568	2.581	0.534
	P2. 0.305	0.292	0.403
Outer	P0. 0.761	0.188	0.0505
	P1. 0.498	0.398	0.104	6.46	6.39	0.227	2.432	2.507	0.678
	P2. 0.475	0.275	0.251

Figure 4.

Climate effect on the interannual variability of cholera risk. The probability of transitioning to a high cholera state from no (p_1,3), low (p_2,3) and high cholera (p_3,3) is shown accounting for the effect of seasonality (f^seas) and the ENSO (f^ENSO) by month, year, and thana group. The intensity of the ENSO is indicated by the mean value of the SST anomaly in each year from low (blue) to high (red).

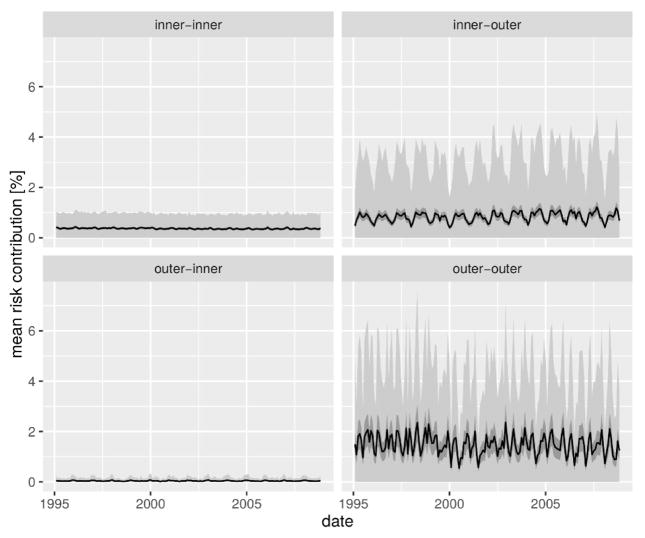
Human mobility was identified as a significant effect when compared to all nested models (Table 1). Furthermore, our MIDCM model of cholera dynamics presented an overall better fit than the best-performing model reported in [13], which accounted for connectivity with the simpler near-neighbor assumption, thus highlighting the relevance of a more realistic representations of human mobility. The significant role of this spreading mechanism provides an opportunity to elucidate the spatial directionality of climate-cholera transmission in Dhaka. To this end, we computed the risk contribution of each thana through human mobility to all other thanas. To account for the stochastic variation in cholera states we performed 1-month ahead predictions via simulations with the best parameter set, sequentially setting the state of each thana to 0 and recomputing the value of the mobility forcing ${\stackrel{\sim }{f}}_{t,-k}^{\mathit{mob}}$. The vector difference between the simulated mobility forcing, ${\stackrel{\sim }{f}}_t^{\mathit{mob}}$, and the simulated forcing without the contribution of the thana represents the increase in cholera risk due to mobility of thana k to each other thana. The simulations were run 1000 times and confidence intervals computed from the resulting difference vectors [ ${\stackrel{\sim }{f}}_t^{\mathit{mob}}-{\stackrel{\sim }{f}}_{t,-k}^{\mathit{mob}}$]. The grouping of risk contribution by origin and destination group (inner vs. outer) reveals that cholera risk spreads mainly from the inner to the outer thanas, and among the latter (Fig. 5). Although risk contribution varies between thanas in the inner-outer and outer-outer directions (see Supplementary Video 1 and SM Fig. S4–S5), their values are consistently larger than the outer-inner risk contribution which is close to 0 throughout the study period. It is interesting to note that the directionality of cholera risk propagation appears clearly in the modeling results, although the predicted inter-group mobility fluxes are very similar. Interestingly the mean risk contribution between thanas (averaged across simulations and the study-period) was found be linearly linked to the intensity of mobility between thanas, although the slope of the relation varied significantly between groups (p-value< 0.01, see SM Table 2 and SM Fig. S6), thus confirming the fundamental differences between the role that human mobility plays depending on the region of the city. This probably stems from the larger probability of experiencing high attack rates in the core than in the periphery.

Figure 5.

Cholera risk spread in the city due to human mobility. The thana-to-thana contribution in cholera risk is illustrated in terms of the overall mean percentage increase in the baseline transition probability between the two regions of the city (black line) along with the 95% confidence intervals of the value of the mean (dark gray ribbon) over 1000 simulations of the state transitions. The variability of the difference over realizations is given in terms of the mean ± standard deviation (light gray difference).

3.3. Model predictive capacity

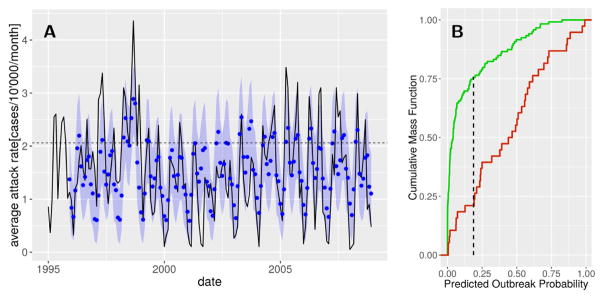
Cross-validation confirmed the forecasting capacity of the full model both in terms of inter- and intra-annual variation of cholera incidence and large outbreaks (Fig. 6 A). The cross-validation parameter sets tend to over-estimate cholera attack rates during the period 2002–2003, years in which the lagged ENSO anomaly was high but not accompanied by increased incidence. The optimal threshold for outbreak prediction was found to be an outbreak probability of 18.7% (Fig. 6 B), yielding false negative (21.1%) and positive (24.4%) rates that slightly outperform previously obtained results of ~ 25% by [13]. The overall accuracy of outbreak prediction is of 76.4%.

Figure 6.

Cholera outbreak prediction performance. (A) Eleven-month predictions of cholera incidence. The means (blue dots) and 95% confidence intervals (blue shadings) of the simulations are given together with the observed average city-wide cholera state (solid line). The outbreak threshold is indicated by the horizontal dashed line. (B) Kolmogorov-Smirnov test comparing the cumulative mass function of the predicted outbreak probability in months in which an outbreak did (green) and did not (red) occur. The point corresponding to the maximal distance between the two curves (vertical dashed line) is used as a threshold for outbreak prediction.

Furthermore, the MDIMC framework clearly outperformed the best-fitted SARIMA model, thus justifying the additional parametrization required for the MDIMC framework. Indeed, the SARIMA model reached an overall accuracy of 68.9% and much higher false negative rate (37.5%) which is of particular interest for operational reasons (see the SM and SM Fig. S2–S3).

4. Discussion

Dhaka with its heterogeneous landscape in population density and socioeconomic conditions presents a complex yet emblematic setting for waterborne disease transmission in urban centers across megacities of the developing world. Through our MDIMC modeling framework, we have disentangled the roles of climatic forcing and human mobility in shaping disease seasonality, inter-annual variability and spread.

The human mobility fluxes in Dhaka, as predicted by the radiation model, were found to be characterized by a strong intra-group connectivity, especially in the core of the city for which the majority of fluxes were predicted to occur among these densely populated thanas. The inter-group fluxes were predicted to be fairly symmetric. Fluxes were inferred using a simple and generalizable methodology based solely on the spatial distribution of population density. This approach could thus be implemented in other urban settings to study the effect of human mobility on the spread of cholera and other infectious diseases [49, 31, 33], provided urban settings are large enough to allow for the assumptions of the radiation model to apply. We here chose to use the radiation model by [38], although other parameter-free options exist [50], and refined models with calibrated parameters have been suggested to outperform the original formulation [51]. An assumption of our method is that mobility fluxes were computed based on the 2013 distribution of urban population in the city although the cholera data refers to the period 1995–2008. We therefore assume that mobility fluxes between thanas had the same structure throughout the study period, although Dhakas land cover has evolved significantly in the past 30–40 years with built-up areas rapidly extending into the rural peripheries of the city [16]. A full extension of our methodology would therefore require the availability of a time-series for the GUF product, which is not available. We nevertheless posit that the main result of the work, i.e. the directionality of the cholera spread from the inner thanas to the outer ones, would hold. In fact, progressive urbanization occurred mainly in the peripheral thanas [52], and thus the simplification made here would appear reasonable for the purpose of modeling cholera transmission, as it implies that weaker outer-to-outer fluxes with respect to prior urban settings. Furthermore, a sensitivity analysis (see the SM for details) showed that a variation of ±20% in the outer-to-inner mobility fluxes had only a marginal effect on the prediction outcomes at the city scale (difference in the attack rates < 0.1%, SM Fig S7), thus suggesting that our results are robust to the constant mobility matrix simplification made in this work. Despite these issues, our methodology could be easily modified to incorporate other model formulations, although the lack of access of mobility data such as mobile phone records hinders the applicability of models with free parameters. On the other hand, the use of mobile phone data has been shown to be relevant at the urban scale [53, 54], thus the increasing availability of mobile phone records in cholera-stricken countries could soon overcome the need for human mobility models altogether [21, 22, 55]. In an intermediate phase, and to inform efforts in locations where phone data are not readily available, comparisons of the fluxes based on methods such as the present one against phone data, where available, would be of interest. Indeed the built-up area raster dataset on which we based our current approach can be provided on request for arbitrary areas of interest via DLR. In summary, we have presented the application of an approach to examine whether a model of human movement provides a basis for modeling the connectivity of a spatio-temporal transmission model. In the absence of movement data, one can test whether a model of movement improves the fit of a transmission model to disease data. When this is the case, one has indirect evidence for the model of movement itself, and for the importance of further pursuing data on movement.

Transmission dynamics in the core and the periphery of the city appear to be fundamentally different, in particular with respect to the intrinsically higher probability of the inner thanas to transition to high cholera states. Poor water and sanitation infrastructure conditions, particularly in informal settlements and possibly exacerbated by rapid urbanization in the megacity, have already been pointed out as underlying factors of high cholera risk in the most densely populated areas of Dhaka and other cities [14, 7, 13]. Indeed, the thanas of the inner group presented higher average population densities and poorer sanitation conditions [13]. Our results support previous findings on the key role of global climatic forcing on cholera dynamics in Bangladesh [8, 35, 9], and its differential effect in the city of Dhaka [13]. Indeed, the inner thanas were found to be more sensitive to ENSO and presented a larger inter-annual variation of the probability of transition to high cholera states. These results are conditions on the choices both of the discretization of cholera attack rates into levels, and on the definition of the spatial grouping (here inner vs. outer). A future research direction would be to develop a more systematic way of determining the levels and groupings themselves (for instance through nonparamteric bayesian methods [56]), which would be extremely relevant to the application of the MDIMC framework to other settings and diseases.

The main finding of our work is that the inclusion of human mobility in the model reveals a clear directionality in the spread of cholera risk from the inner to the outer thanas, which had previously been proposed but not quantified. These results echo recent studies on epidemic cholera in urban settings that have revealed transmission hotspots, with implications for vaccination strategies [31]. Interestingly, these findings would suggest that even in the endemic context of Dhaka, secondary (i.e. human-mediated) transmission to (rather than from) the areas with suitable habitats for free-living V. cholerae is a main driver of disease outbreaks. Support for this transmission route could re-frame the emphasis placed on the physical and chemical characteristics of the environment that are suggested to produce outbreaks in endemic regions such as Bangladesh [57, 58, 59]. Although it is undeniable that local environmental indicators are a key piece in understanding cholera outbreaks in urban settings, the results of this study are illustrative of the significance of human-related factors in the dynamics of the disease in a megacity like Dhaka.

Finally, including human mobility not only enabled a better understanding of disease transmission within the city, but also improved to some extent the prediction capacity of the model. Indeed we preserved the 11-month lead prediction horizon, but improved upon predictability, with a 21.1% false negative rate using cross-validation. The MDIMC framework also clearly outperformed the baseline SARIMA model, in particular in terms of false negative rate which is crucial for operational decision-making, thus suggesting that the added complexity in the model is worthwhile. This result is encouraging for the usefulness of MDIMC models for the prediction of cholera, which has already been shown in other countries [32], and for their applicability to other climatic-driven diseases.

5. Conclusion

The transmission of waterborne diseases in urban settings is inextricably linked to the interactions between environmental, socio-economic and climatic factors. Given the rate at which megacities in the developing world are emerging and growing, it is crucial to better understand these linkages to better support disease management in the highly complex and heterogeneous landscapes that characterize them.

Seasonal outbreaks of endemic cholera in Dhaka serve as a striking example of these interactions when accounting for human mobility. The heterogeneous physical landscape of the city, implicitly captured here via population density, could not only be an explanation of the different sensitivity to ENSO between the core and the periphery as suggested by [13], but also yields predictions of mobility fluxes that act to spread the disease. By providing insight into the spatial nature of transmission, the increased understanding these processes may help in the design of large-scale vaccination campaigns supported by promising field studies [29, 30].

Highlights.

• A model of cholera transmission in Dhaka which includes human mobility is proposed

• Human mobility was inferred based on gridded estimates of on population density

• Climatic forcing drives transmission inter-annual variability at the megacity scale

• Cholera was found to spread from the densely populated city core to the rural periphery