Post-transfusion increase of hematocrit per se does not improve circulatory oxygen delivery due to increased blood viscosity

Abstract

BACKGROUND

Blood transfusion is used to treat acute anemia with the goal of increasing blood oxygen carrying capacity as determined by hematocrit (Hct), and oxygen delivery (DO₂). However, increasing Hct also increases blood viscosity, which may thus lower DO₂ if the arterial circulation is a rigid hydraulic system as the resistance to blood flow will increase. The net effect of transfusion on oxygen delivery in this system can be analyzed by using the relationship between Hct and systemic blood viscosity of circulating blood at the post transfusion Hct to calculate DO₂ and comparing this value to pre-transfusion DO₂. We hypothesized that increasing Hct would increase DO₂, and tested our hypothesis by mathematically modelling DO₂ in the circulation.

METHODS

Calculations were made assuming a normal cardiac output (CO) (5 l/min), with degrees of anemia ranging from 5% to 80% Hct deficit. We analyzed the effects of transfusing 0.5 or more units of 300 cc of packed red blood cells (PRBCs) at a Hct of 65% and calculated microcirculatory DO₂ after accounting for increased blood viscosity and assuming no change in blood pressure. Our model accounts for O₂ diffusion out of the circulation prior to blood arriving to the nutritional circulation, and for changes in blood flow velocity. The immediate post transfusion DO₂ was also compared to DO₂ after the transient increase in volume due to transfusion had subsided.

RESULTS

Blood transfusion of up to 3 units of pRBCs increased DO₂ when Hct (or hemoglobin) was 60% lower than normal, but did not increase DO₂ when administered prior to this threshold.

CONCLUSIONS

After accounting for the effect of increasing blood viscosity on blood flow due to increasing Hct, we found in a mathematical simulation of DO₂ that transfusion of up to 3 units of pRBCs does not increase DO₂, unless anemia is due to a Hct deficit greater than 60%. Observations that transfusions occasionally result in clinical improvement suggest that other mechanisms possibly related to increased blood viscosity may compensate for the absence of increase in DO₂.

INTRODUCTION

Anemia, defined as a hemoglobin concentration below normal, results in a decreased blood oxygen (O₂) carrying capacity (CaO₂) due to a lower hemoglobin (Hb) concentration. Blood transfusion is often used to treat acute anemia with the goal of increasing blood CaO₂ and oxygen delivery (DO₂). However, blood transfusion also introduces hydraulic changes that may limit its physiological effects. Blood transfusion is assumed to increase DO₂ by increasing Hb and thus DO₂. However, this increase is mitigated in a circulatory system where the blood pressure (mean arterial pressure, MAP) and the arterial blood vessel diameter component of peripheral vascular resistance (total peripheral resistance, TPR) remain constant, i.e., a “rigid linear hydraulic system”¹ because the increase of Hct increases blood viscosity (μ), which then decreases blood flow and reduces DO₂.

Other factors also complicate a simple relationship between Hct and DO₂. Blood transfusion increases blood volume, but this volume expansion seldom leads to hypervolemia, since clinically most transfusions are given to hypovolemic patients. Transfusion thus transiently improves the filling of the heart (increased end-diastolic volume; pre-load) and thus CO. However, anemia itself increases CO². By correcting anemia, packed RBC (pRBC) transfusion reverses this compensatory mechanism. The net result is that pRBC transfusion in many studies increases DO₂ only slightly, and in many instances O₂ consumption (VO₂) stays the same^2,3.

A consequence of the relationship between Hct and blood viscosity is that increasing the Hct in anemia may not correspondingly increase DO₂. This apparently paradoxical finding is because increasing Hct will increase blood viscosity, which in turn will impede blood flow and reduce DO₂. To test this possibility, we developed a mathematical model to determine how changes in Hct caused by a blood transfusion might affect CaO₂ and blood viscosity, and consequently DO₂ in an anemic organism.

METHODS

Model design

We assumed a model circulatory system where under normal conditions 5 liters of blood at a Hct = 45% (Hb = 14.5 g/dl) are circulated at the rate of 5 liters/minute, where blood exits the heart at a pressure P that remains constant for all conditions, and that blood is 100% O₂ saturated also for all conditions. Anemia is modeled as a % decrease in Hct, while all other circulatory parameters remain constant, except for blood viscosity. DO₂ is calculated as the product of CO times Hct. The O₂ saturation of blood arriving to the nutritional microcirculation is corrected for diffusional O₂ loss due to the transit of blood through the circulation, which is assumed to be blood flow velocity dependent. Furthermore we assume that blood is a Newtonian fluid which is mostly valid for Hct deficits of 40% or greater⁴.

Blood transfusion to correct Hb level is typically administered as packed red blood cells (pRBCs) delivering up to 2–3 units of blood, using leuko-reduced blood centrifuged to an Hct of 60–70%. To model this process, we defined a unit of blood as 300 ml of pRBCs at 65% Hct. We then modeled how transfusion accomplished the objective of increasing DO₂ by using pRBC transfusion.

To make our scenario clinically relevant, we simulated 0.5 to 3 unit transfusions. Hospitals reporting statistics on the number of units used per transfusion intervention⁵ support this assertion. In Western Australia 14% and 44% of the total blood supply is used in 1 and 2 units transfusions⁶ while the percentage of units used per event in 18 Austrian hospitals was 13% for 1 unit and 56% for 2 units transfusions⁷.

In this analysis, we calculate the effect of transfusing 0.5 units (150 cc), 1 unit (300 cc), 2 units (600 cc) and 3 units (900 cc) of pRBCs.

The effect of anemia on blood viscosity (μ)

Blood viscosity (μ) is a non-linear function of Hct and shear rate, which varies throughout the circulation. In our model we assumed a shear rate ~200 sec⁻¹ to be representative for the circulation. Arterial and venous Hcts (~3% higher than arterial) are the highest in the circulation and in terminal arterioles and capillaries Hct is about half the central value⁷. Although Hct varies between the arterial, microvascular and venous compartments, we assumed that the arterial Hct and any changes due to the addition of pRBCs was the effective Hct in determining blood viscosity. This assumption was supported in part because the arterial circulation accounts for 70% of TPR. The microcirculation where Hct is lower accounts for ~20% of TPR and the venous system contributes the remaining 10%.

Our model assumes that the circulation is rigid linear hydraulic system, that accommodates blood volume changes in the venous circulation. However since the venous systems accounts for only 10% of the total TPR we assume that venous diameter changes are negligible and therefore TPR depends only on blood viscosity which is a function of Hct.

The effect of Hct on μ was modeled by curve-fitting a quadratic equation to the data in the literature. This relationship was in part determined by the viscosity of plasma, which ranges from 1.10 to 1.35 cP (37^○C)⁹. As a reference, the viscosity of water is 0.695 cP at 37^○C. Few studies focus on the rheology of blood in anemia and no precise way exists to establish the asymptotic value of plasma viscosity at zero Hct because plasma proteins are not restricted to the vascular compartment. The variability of plasma viscosity is small and we assumed that plasma viscosity is the average of the reported range or 1.22 cP¹⁰.

Data on the relationship between μ and Hct for men and women in the normal population is reported by Kameneva et al.¹¹ as shown in Figure 1 which includes data of studies reporting measurements in anemic patients. In most instances the cause of anemia was not discussed. Data for anemic patients was reported by Stein and Sabah¹² obtained from patients primarily afflicted with chronic renal failure due to malignant neoplasm. We also included data reported by Vázquez et al.¹³ for healthy individuals with Hct lower than 35%. Stone et al. reported data on human μ diluted with plasma¹⁴. Cokelet et al¹⁵ reported theoretical values derived from the rigorous application of the Quemada equation for blood viscosity as a function of shear rate and Hct¹⁶. These data were fitted by equation [1] as follows:

$$\mu =1.22+0.00675\times \text{Hct}\times {10}^2+0.00208\times {\text{Hct}}^2\times {10}^4;{\mathrm{r}}^2=0.93$$ [1]

Figure 1.

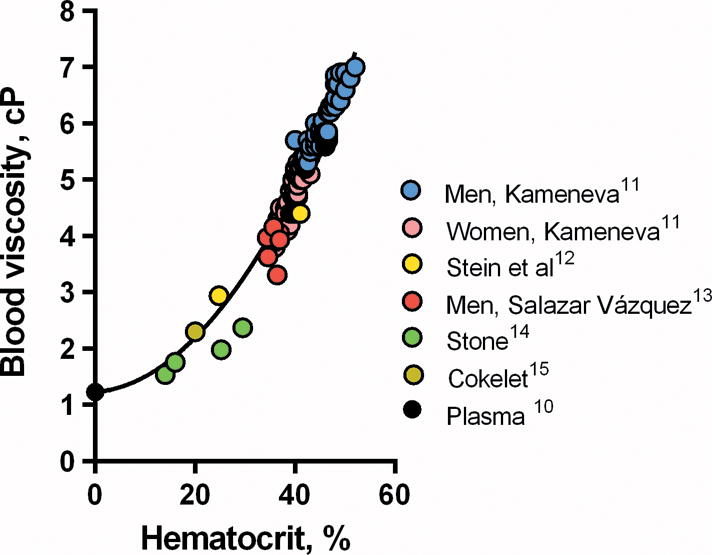
Blood viscosity as a function of hematocrit of normal and anemic individuals. Plasma viscosity 1.22 cP is the average of the available data in the literature.

The effect of transfusion on Hct, blood viscosity and DO₂

The increase in volume due to RBC transfusion on Hct is due to changes of plasma volume caused by changes of capillary pressure, which induce fluid filtration or absorption according to the Starling-Landis mechanism of fluid balance¹⁷.

The trajectory of fluid overload induced by transfusion is not well established. We assumed that blood volume returns to normovolemia after an unknown period following transfusion.

To evaluate how transfusion changes Hct we assumed a stoichiometric effect and calculated the resulting Hct as the ratio of total RBC volume resulting from the transfusion and the total circulating volume due to transfusion. In our model a unit of pRBCs has a volume of 300 ml and 65% Hct thus transfusing n units of pRBCs changes Hct according to the following equation:

$$Hc{t}_{\mathit{post}\mathit{transfusion}}=\frac{\mathit{Hct}\times bv+\text{RBC Vol added}}{bv+\text{Blood Vol added}}=\frac{\mathit{Hct}\times bv+n\times 0.65\times 0.3}{bv+n\times 0.3}$$ [2]

where Hct is that of the anemic patient and bv is the patient’s initial blood volume, or 5 liters.

The rate of oxygen delivery DO₂ is thus determined by the product:

$${\text{DO}}_2=\text{CO}\times {\text{CaO}}_2\left(\text{or Hct}\right)$$ [3]

where CO is determined by the pressure imparted to blood by the heart ΔP over the resistance to flow R according to Poiseuille’s equation:

$$\text{CO}=\frac{\mathrm{\Delta }P}{R}=\frac{\pi \times r^4}{8\times \mu \left(\mathit{Hct}\right)\times l}\mathrm{\Delta }P$$ [4]

Combining equations [3] and [4] for the “rigid linear hydraulic system” at constant pressure, CO becomes a function of blood viscosity and a constant k since the vessel radius r and length l are constant. CaO₂ is therefore directly proportional to Hct and DO₂ from equation [3] becomes:

$${\text{DO}}_2=\frac{k}{\mu (\mathit{Hct})}\mathit{Hct}$$ [5]

The change in post transfusion DO_2,T relative to DO_2,a in anemic conditions defines the ratio R_T,a, which eliminates the constant k according to:

$$R_{T,a}=\frac{{\text{DO}}_{2,\text{post trans }(\mathrm{T})}}{{\text{DO}}_{2,\text{anemic state }(\mathrm{a})}}=\frac{Hc{t}_T}{Hc{t}_a}\times \frac{{\mu }_a}{{\mu }_T}$$ [6]

Because the parameters in (6) are all known or can be measured, the ratio R_T,a gives a direct measure of how anemia affects DO₂ as Hct changes due to transfusion.

O₂ diffusional exit and the effect of blood flow velocity on DO₂

Equation [5] describes how DO₂ responds to changing Hct assuming that blood O₂ saturation does not change during transit from the lungs to the microcirculation to satisfy the tissue metabolism. However because the vasculature is not a barrier to O₂ diffusion, O₂ will diffuse out of the vessels prior to blood arriving to the microcirculation. The specific vascular locale of oxygen delivery was assumed to be the capillary system although Duling and Berne¹⁸ reported that terminal arterioles also provide a significant amount of O₂ to the tissue. In previous work we confirmed this observation, finding that most O₂ is delivered by the arteriolar system and that capillary blood pO₂ in most mammals was in the range of 25 –30 mmHg due to the diffusional loss¹⁹.

Data on microvascular and central pO₂ is available from the awake window chamber hamster (a fossorial species) model²⁰. In this model central pO₂ averaged 61.9 mmHg, or 88% O₂ saturation. Assuming that the nutritional circulation begins at the level of A3 arterioles, whose pO₂ is ~41 mmHg, blood O₂ saturation at that stage is approximately 76%¹⁹. Consequently, we modeled that the saturation change in blood from central to peripheral was 12.0%. We then extrapolated to estimate the O₂ saturation loss between the lungs and the start of the nutritional microcirculation. For an arterial saturation of 100%, A3 O₂ saturation would be:

$${\text{pO}}_2\mathrm{A}3\text{arterioles}=100\%/88\%=X/76\%\text{or}X=86.4\%$$

and the absolute change in saturation between central blood (100%) and the A3 arterioles = 13.64 ~ 14%. We therefore assumed that at the beginning of the nutritional circulation blood O₂ content had decreased by 14% due to diffusion in normal conditions.

To model O₂ delivery due to diffusion, we used the following logic. Oxygen exits from the blood vessels by constant diffusion, and is driven by the O₂ concentration gradient between blood and tissue. Therefore the flux of O₂ arriving to the nutritional microcirculation is the difference between DO₂ and the flux of O₂ that exits the blood vessels by diffusion (FO_2,diff). The increase of viscosity lowers blood flow, increasing the time for diffusion to extract O₂ and further decreasing DO₂ in the microcirculation.

A model for describing DO₂ in anemia relative to normal DO₂ was formulated by writing the O₂ flux balance for the rate of O₂ delivery to the microcirculation DO_2,mic as:

$${\text{DO}}_{2,\text{mic}}={\text{DO}}_2-{\text{FO}}_{2,\text{diff}}$$ [7]

Where DO₂ was the product of blood flow (i.e., CO, 5 liters/min) times Hct of fully O₂ saturated RBCs as per equation [3].

The flux FO_2,diff is a function of the O₂ concentration gradient between the amount of O₂ in blood and the O₂ dissolved in the tissues. The calculation of how the diffusional exit of O₂ varies with changes in CO was not possible. We thus simplified the analysis by focusing on the relative rather than absolute magnitude of change. In this context, geometry for the rigid linear hydraulic system model is constant for all conditions, and the principal variables are DO₂, the longitudinal vascular O₂ concentration gradient due to O₂ exit, and the transmural O₂ gradient, i.e., the local difference between intravascular and tissue O₂ concentration. Several potential solutions address this problem but none deals with Hct changes simultaneously affecting μ and DO₂. Furthermore, this problem is usually solved for single cylindrical tubes, not networks.

A simplified problem is formulated by assuming that the gradient that causes O₂ exit, determined by intravascular Hct and the tissue O₂, is characterized by a single nominal value. This assumption is largely justified since the changes in O₂ transport due to transfusion of 1–3 units of blood are relatively small. Neglecting this effect permitted us to model that the diffusional O₂ exit is primarily determined by the residence time of blood in the pre-microcirculation blood vessel, which is inversely related to blood flow velocity and therefore directly related to μ.

The dependence of the diffusional loss on the content of O₂ of blood is less pronounced than the dependence on viscosity, because tissue pO₂ tends to track blood pO₂. Therefore we assume that O₂ delivery to the microcirculation DO_{2,mic (a,N)} was determined by changes due to effects on blood flow minus the diffusional loss determined by blood flow velocity (which is dependent on viscosity) according to the following relationship:

$${\text{DO}}_{2,\text{mic}\left(\mathrm{a},\mathrm{N}\right)}={\text{DO}}_2\left(45\%\right)\times R_{a,N}-0.14\times {\text{DO}}_2\left(45\%\right)\times {\mu }_a/{\mu }_N$$ [8]

where R_a,N is the ratio of DO₂ between anemic (a) and normal conditions (N), and μ_a and μ_N are the blood viscosities in the anemic and normal condition respectively.

This expression is consistent with the physiological relationship that higher μ, due to increased Hct, leads to a higher intravascular O₂ concentration, an increased rate of diffusional oxygen loss and eventually decreased DO₂ at the capillary bed. Setting DO₂ (45%) = 1 and transposing we obtained the DO₂ in anemia relative to normal:

$${\text{Rel DO}}_{2,\text{mic}\left(\mathrm{a},\mathrm{N}\right)}=R_{\mathit{a},\mathit{N}}-0.14\times {\mu }_a/{\mu }_N$$ [9]

In the anemia transfusion scenario characteristics of the normal state are not known, and therefore this analysis is difficult to make. However, it is also informative to obtain a relative measure of the resulting intervention, namely the change in O₂ delivery DO_2,mic relative to the anemic condition due to transfusing n units, which can be estimated by using the ratio R_T,a defined in [6] which describes the change in DO₂ induced by BT in an anemic individual, given by:

$${\text{Rel DO}}_{2,\text{mic}\left(\mathrm{T},\mathrm{a}\right)}={\mathit{R}}_{\mathit{T},\mathit{a}}\mathbf{-}0.14\times {\mu }_T/{\mu }_a$$ [10]

Physiology and physics of the O₂ diffusional loss

Our model includes an “O₂ diffusion loss” which identifies a fraction of DO₂ that does not contribute to supplying O₂ the tissue because it is consumed by the vessel walls and is shunted to venules running in parallel. Data on this phenomenon is available from pO₂ measurements in an awake hamster model with sufficient resolution to discern how pO₂ varies as blood transits from large to small arterioles, through the capillaries and then from small venules to large¹⁹. This data exists only for “window chamber” hamsters and shows that capillaries have the lowest pO₂ in the vascular network. The data is derived from measurements with a spatial resolution of ±2 μm in subcutaneous muscle, adipose and connective tissue. There are comparable data for the hamster cheek pouch, but this tissue is not in a window chamber, and has to be irrigated. As a consequence the lowest pO₂ is that of the irrigation solution, which tend to be contaminated by atmospheric pO₂²¹.

Overall “diffusional loss” thus comprises both O₂ shunting to the venular circulation and the local O₂ consumption in the vascular and microvascular vessel wall, which is a true O₂ “loss” occurring before O₂ enters the tissue in all blood vessels^21,22.

A fraction of the diffusional O₂ “loss” thus does not participate in tissue metabolism, but is shunted back into the venules, due to the parallel and juxtaposed configuration of arterioles and venules which shunt O₂ to the venous return²³.

The underlying mechanics of this “loss” and/or “shunting” is that oxygenated blood moves in pipes whose walls are as permeable to O₂ exit as the plasma in which O₂ diffuses. As a consequence, vessels walls offer little resistance to O₂ exit and the quantity of O₂ that arrives to the microcirculation is the difference between the rate at which O₂ carrying blood arrives to the microcirculation and the rate at which O₂ exists the pre-microcirculatory vessels. A model of this process is transporting water in a leaky container. The quantity of water arriving at destination is a function of the difference between the container velocity and the rate of the water leak.

RESULTS

Our principal results are shown in Figure 2 which describes the effect of transfusing n units of blood in conditions of normovolemic anemia ranging from a Hb deficit of 0 to 80% (or Hct). We found that transfusion of up to 3 units of blood had practically no effect on DO₂ unless Hb is less than approximately a 60% Hb deficit or 5.8 g/dl. Improvements in DO₂ ranged from 14% for transfusion of 0.5 units to 47% after transfusions of 3 units relative to DO₂ in the anemic condition. Equation [10] assumes that the resulting Hct is determined by the changes in RBC concentration and blood volume associated with each given number of units transfused, and implies that the blood volume will be permanently increased (Figure 2A). This assumption is unlikely considering that transfusion of 2 units expands blood volume by 12% according to our model. Although the post transfusion change of blood volume with time is not specifically known, normalization of blood volume will lead to further increases of Hct. The effect of such normalization of blood volume is shown in Figure 2B.

Figure 2.

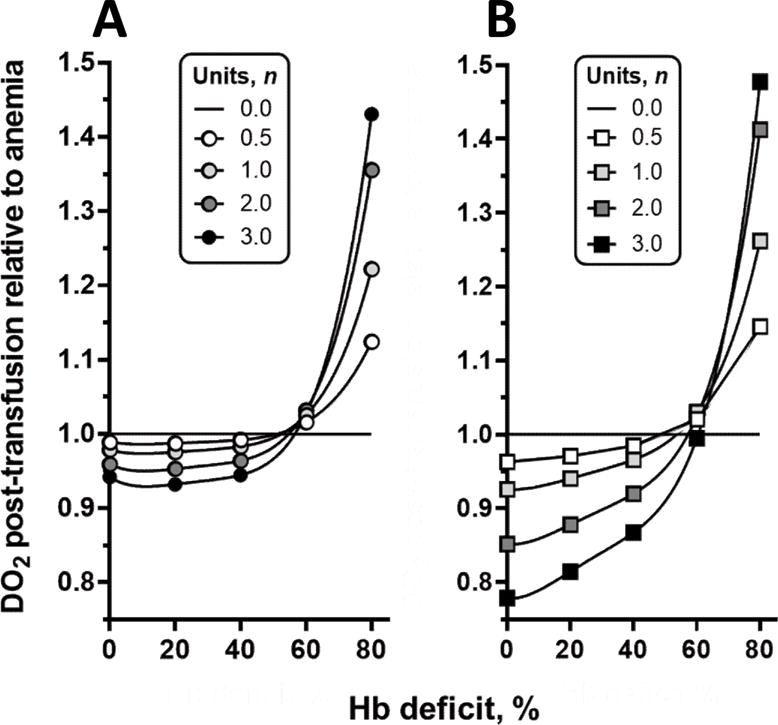
A: DO₂ after transfusion relative to anemic condition. Data points show the initial DO₂ after transfusion relative to DO₂ prior to transfusion for different levels of anemia expressed by Hb deficit. B: Change of DO₂ after transfusion, when hypervolemia induced by transfusion subsides and blood volume returns to baseline. This result differs from that in Figure 2 because Hct is higher, since return to normovolemia requires a decrease in plasma volume.

Figure 3 confirms that when blood volume normalizes after transfusion, transfusing 0.5 to 3.0 units of pRBCs will cause DO₂ to decrease for all Hb concentrations greater than 5.8 g/dl, an effect that reverses abruptly for anemic conditions with lower Hb levels.

Figure 3.

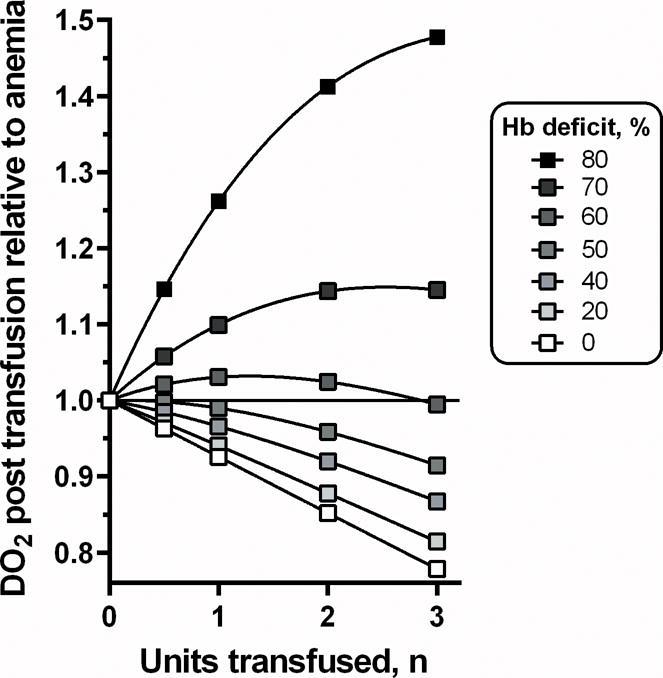
Effect of transfusing n units on DO₂ for different levels of Hb deficit after volume normalization. Transfusion of any number of units lowers oxygen delivery to the microcirculation when treating up to 60% Hb losses. Calculations were made using data from Figure 2.

DISCUSSION

In our mathematical simulation of the effects of transfusion on DO₂, we found that transfusion does not increase DO₂ unless the deficit in Hct (or Hb) is greater than 60 % of a normal baseline (blood Hb less than 5.8 g/dl) regardless of the number of units transfused. This surprising lack of increase in DO₂ is due to transfusion-associated increases in blood viscosity, which not only lowers blood flow to capillary beds but also increases the diffusional O₂ loss prior to blood arriving at the nutritional circulation.

The “diffusional O₂ loss” refers specifically to O₂ that is not delivered by the microcirculation. Oxygen exiting blood vessels should be consumed in the tissue, thus contributing to nutritional DO₂. However the configuration of arterioles and venules, running in parallel²⁴ indicates that this O₂ does not contribute to the tissue metabolic demand, since it returns via the venous circulation due to pre-microcirculatory arterio-venous O₂ shunting, whose magnitude is inversely related to blood flow velocity. As a consequence, lowering blood flow velocity increases the O₂ shunting. In our model the diffusional loss is 14% of DO₂ in the normal circulation which decreases to about 7% of DO₂ in the 50% anemia as shown in Figure 4.

Figure 4.

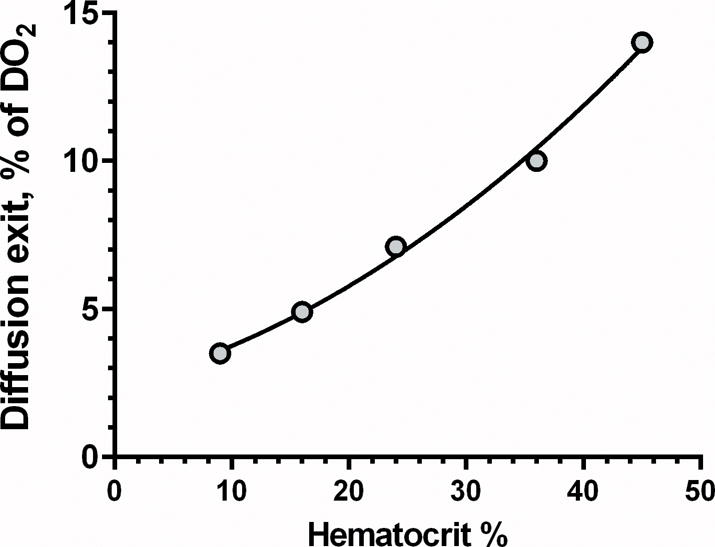
Effect of Hct on diffusional oxygen exit. ○: % O₂ diffusional exit at each level of anemia relative to DO₂ at Hct 45%. As an example, diffusional exit of DO2 is 14% at a Hct of 45% compared to 7.1% at Hct of 22.5%.

We reiterate that the effects shown by our model only deal with the physical aspects of the problem, and ignore the effects that transfusion per se may have on the circulation as a whole or on cardiac function. However, since changes in μ are likely relatively large, other effects of transfusion that increases O₂ delivery would need to be as large to have an impact.

Our model assumes an arterially rigid linear hydraulic system, where MAP is constant and TPR only changes in response to changes of Hct. A critical question is whether this assumption is applicable to the mammalian circulation. We are not aware of clinical data on how BT, i.e., increasing Hct in an anemic patient, affects MAP, CO and blood viscosity. Messmer et al. studied extensively the reverse effect due to hemodilution²⁵ reporting experimental findings in dogs. Comparison between human responses and experimental conditions are difficult, and additionally complicated by experimental model. We modeled an increasing Hct in our study, while Messmer et al. focused on decreasing Hct.

Another critical point is to assess the evidence supporting the effect of changing blood viscosity on TPR in the absence of other effects. The data of Messmer et al. allows testing of our model, since TPR was reported for different levels of hemodilution, and blood viscosity and at each level of Hct in a manner similar to our Figure 5. Thus if we assume that increasing and decreasing Hct are equivalent, we find that increasing Hct in the circulation of dogs behaves as our model, since MAP is approximately constant (122 ± 4 mmHg over the Hct range of 7.8 - 40.0%), and changes in CO are exclusively due to changes of μ.

Figure 5.

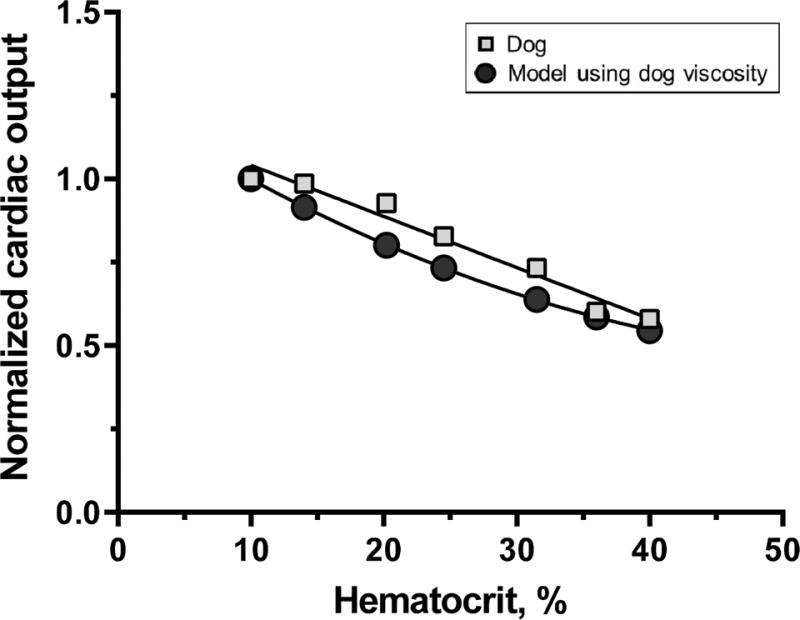
Comparison of cardiac output (CO) as a function of Hct in current model (circles) and results of Messmer et al.²⁴ (squares) on changes induced by hemodilution in dogs and using measured dog viscosity data in the model. This comparison simulates increasing Hct, and CO from an anemic condition due to 10% Hct. Model data is fitted by a quadratic relationship, while the experimental variability inherent to the measurement of CO and blood viscosity is best fitted by a linear relationship.

The experimental study of Messmer et al. was based on normovolemic anesthetized dogs, identical to our model. Anesthesia in general lowers CO, as well as macro and micro-circulatory regulation²⁶, therefore comparison of these two models is more realistic than comparing either model to the non-anesthetized condition, since Ickx et al. show that hemodilution and anesthesia decrease CO by comparison to hemodilution in the awake state indicating the presence of additional controls beyond merely physical reactions of the inert vasculature²⁷.

The effects on DO₂ due to normalization of blood volume after transfusion are also significant. Transfusion increases blood volume even if it were possible to transfuse only RBCs. The additional volume administered with pRBCs can expand blood volume by 10% and greater for transfusions greater than 2.0 units. The time course governing the eventual excretion of this additional volume is not specifically known, but it is unlikely to be permanent. Upon normalization of the initial volume to that prior to transfusion the Hct will increase even more, which in our model further worsens DO₂.

Our model is specific to treating normovolemic anemia, in non-bleeding conditions. To understand the effect of transfusion in anemic hypovolemia we computed the effects of transfusing a 50% anemic patient (Hct 22.5%) and an 80% anemic patient (Hct 9%), in patients with a 20% intravascular volume deficit (4 l blood volume). In the first case, transfusion of one unit of pRBCs caused Hct to increase from 22.5% to 25.5% for hypovolemia (instead of 24.9% for normovolemia), changing post transfusion viscosity from 2.68 cP to 2.74 cP, and decreasing DO₂ by about 1%. In the second case transfusing 3 units in extreme anemia (Hct 9%) increased DO₂ by 2.5% over that in the normovolemic patient. Thus the limited effect of transfusing hypovolemic patients is due to the same phenomenon that limits the effectiveness of blood transfusion in general, namely the effects of increased Hct and blood viscosity.

Our results show that transfusions of up to 3 units to correct for up to a 55% Hb deficit causes DO₂ to decrease relative to the anemic state (Figure 2A) and that the fall in DO₂ worsens as blood volume normalizes (Figures 2B and 3). Increases in DO₂ relative to anemia only occur in our model when treating Hb deficits greater than 60%. However, the actual improvement obtained is generally surprisingly small. A 3 unit transfusion in a patient with 80% Hct deficit (Hb = 2.9 g/dl), causes DO₂ to change from 0.22% to 0.33% of normal.

One unknown factor is that the organism could eventually adapt to the increased blood viscosity and establish a new operating set point for normalized Hct and CO due to the significant increase of blood viscosity . Incorporating that factor may have changed our findings.

Considering the assumptions made, and the many factors that could influence DO₂, including the variability between individuals and quantity of RBCs administered per transfusion, it is possible that in the real world transfusion may increase DO₂. However our simulation suggests that the change in DO₂ will be small relative to the anemia being treated and well within the variability of many factors that control and measure DO₂. We thus raise the question that transfusion may have limited benefit considering the available evidence on adverse effects of transfusion²⁸.

A limitation of our model is that we do not include other factors that adapt the circulation to anemia and mitigate the decrease of O₂ availability to the pre-nutritional circulatory compartment. In particular, a left shift of the O₂-Hb dissociation curve would decrease the percentage of diffusional O₂ exit that we assume to be 14% in our model thus increasing O₂ availability in anemia and DO₂. An often mentioned factor is the increased O₂ extraction that may occur during anemia due to increased capillary density, however studies in the microcirculation in extreme hemodilution tend to show a decrease in functional capillary density²⁰. A weakness of our model is the assumption that MAP does not change as a function of transfusion, i.e., changes in CaO₂, although the experimental study of Messmer et al., supports this assumption for anesthetized, isovolemic and anemic dogs. Furthermore we assume that blood is a Newtonian fluid which is mostly valid for Hct deficits of 40% or greater⁴.

Another critique is the simplistic treatment of the complex physics associated with the change of CaO₂ due to changes in Hct. We previously reported the effect of flow velocity on DO₂ for a single tube²⁹, and the effect of blood viscosity on O₂ delivery in a branching network³⁰. In this study we developed a hybrid approach for the solution of how DO₂ is managed in anemia upon transfusion of pRBCs by establishing a mass balance between O₂ convective supply and diffusional delivery referred to specific in vivo mammalian microvascular data. Clearly a more sophisticated approach based on exact solutions for branching circulatory systems characteristic of the different organs would make the analysis more accurate³¹.

In summary, we found in a mathematical model of the human circulation that for the majority of anemic and normovolemic conditions encountered clinically, increases in DO₂ were modest at best, or nonexistent. One limitation of this model is the assumption that cardiac function is independent of Hct. This critique is valid, since cardiac function is determined by DO₂. However, the experiments of Messmer et al. show the existence of conditions where cardiac function is only a function of blood viscosity.

Our model suggests that transfusion of 1–2 units of pRBCs is unlikely to increase DO₂ unless treating extreme normovolemic anemia where Hb < 5.8 g/dl (Hct deficit > 60%). As this finding is not consistent with clinical practice, we hypothesize the existence of mechanisms not addressed in our model that ultimately negate the effect of increasing viscosity on blood flow and facilitate DO₂. One possibility is the decrease of TPR through vasodilatation, which may be mediated by increased mechanotransduction and production of nitric oxide^{32, 33,34}. However, in these studies changes in Hct were induced without changes in volume.

The presence of additional phenomena not related to the physical effects described in our modelling is also suggested by Yuruk et al. who investigated the sublingual microcirculation in patients receiving up to 3 units of blood upon undergoing cardiopulmonary bypass assisted heart surgery³⁵ and in anemic patients³⁶. Both these studies, treated Hb deficits of 55%, and found increased functional capillary density, microvascular Hct and tissue pO₂, although no evidence of increased microvascular perfusion. In contrast a previous study by Creteur et al.,³⁷ did not find any change in tissue pO₂.

Conclusions

Using a physical model of transfusion, we found that increasing Hct in anemic patients increases blood viscosity, which severely limits the effect of increasing Hct on DO₂. In our model, transfusing up to 3 units of pRBCs to treat 5.8 g Hb/dl does not increase DO₂ and may reduce DO₂ when correcting a higher Hb level. We also show that the reduction of blood volume post transfusion further increases Hct and lowers DO₂.

Our analysis suggests that physical effects that underlay BT may preclude the possibility of transfusion increasing DO₂ unless other effects not related to baseline hydraulic/viscosity considerations are present. Since DO₂ is the product of CO and Hb and since increases in Hb are limited by the number of RBC units than can be transfused, the effectiveness of blood transfusion thus depends primarily on the increases of CO. We advance the possibility that positive effects due to transfusion may be due vasodilation in response increased blood viscosity More work is needed to better understand how the circulation and DO₂ respond to transfusion.