A new framework for prediction and variable selection for uncommon events in a large prospective cohort study

Abstract

When prediction is a goal, validation utilizing data outside of the prediction effort is desirable. Typically, data is split into two parts: one for a development and one for validation. But this approach becomes less attractive when predicting uncommon events, as it substantially reduces power. When predicting uncommon events within a large prospective cohort study, we propose the use of a nested case-control design, which is an alternative to the full cohort analysis. By including all cases but only a subset of the non-cases, this design is expected to produce a result similar to the full cohort analysis. In our framework, variable selection is conducted and a prediction model is fit on those selected variables in the case-control cohort. Then, the fraction of true negative predictions (specificity) of the fitted prediction model in the case-control cohort is compared to that in the rest of the cohort (non-cases) for validation. In addition, we propose an iterative variable selection using random forest for missing data imputation, as well as a strategy for a valid classification. Our framework is illustrated with an application featuring high-dimensional variable selection in a large prospective cohort study.

1. Introduction

In a large prospective cohort study, prediction and variable selection important to an outcome are frequently investigated. Variables are often selected because of their higher predictive power based on some measure of prediction performance. However, the predictive power needs to be assessed in data that was not used for the technical development. In epidemiological studies, prediction and variable selection are often criticized for lacking proper validation (1,2). To make an out-of-data validation available, one could split the full cohort data proportionally into two: a training data set to perform a prediction and variable selection development and a validation data set to validate the development. However, when the event of interest is uncommon, this approach is not attractive since it limits statistical power in both training and validation data sets.

In this paper, instead of splitting the cohort, we propose to use a nested case-control design that includes all the cases of interest but selects controls for a case among those subjects who were event free at the case’s event time in the full cohort (risk-set matched case-control design). This design is expected to produce a similar result that the full cohort analysis would have produced (7,8). We use the case-control cohort as the training data set without losing statistical power in the development and the rest of the cohort as the validation data set. Then, since all cases are included in the case-control cohort, only partial validation is available based on the fraction of true negative prediction (specificity). However, when predicting uncommon clinical events, limiting false positive prediction (1-specificity) is often more of interest than limiting false negative prediction. In the nested case-control cohort, we conduct variable selection and fit a prediction model on those selected variables. Then, we validate the selection by comparing the specificity of the fitted prediction model in the case-control subjects (internal) to that in the subjects who were not selected as controls within the cohort (external).

On the other hand, a prospective cohort study often gathers extensive data to investigate the nature of exposures and their relations to a clinical outcome. Variable selection is commonly used as a data driven search to find exposures relevant to an outcome. One may look for significant variables through exhaustive analyses of one variable at a time, but this inflates false positive findings and ignores correlations between variables. A standard approach analyzing multiple variables together is to do a stepwise selection by fitting a multiple regression model. However, when interactions between exposures are considered, the dimensionality increases exponentially, and such selection becomes unavailable or shows poor performance (3). High-dimensional data is common in genetic research and imaging studies, and machine learning methods have been extensively used for variable selection in those fields. They have also attracted increasing attention in epidemiologic studies, but interpretation has been difficult (4–6).

For high dimensional variable selection, utilizing a nested case-control design not only makes external validation available without losing statistical power but also provides ways to control confounders and interpret the selection through a fitted prediction model. Featuring high-dimensional variable selection, we propose a new variable selection strategy to address missing data issues/problems. By repeating the variable selection process in data imputed using a random forest technique, we select the variables consistently included in those repetitions. Through comparisons between the internal and external specificities, prediction and variable selection are directly assessed, and a cut-point for a valid classification is determined where internal and external specificities are equivalent at a desired specificity. Our framework is illustrated through an example from a large prospective cohort study.

2. Materials and methods

In this section, we review existing methods to conduct prediction and variable selection in a matched case-control design.

2.1. Design and analysis

A nested case-control design is a matched case-control design including all cases. When matching is used, statistical analysis should take into account the condition matched per case-control pair. In unmatched case-control studies, logistic regression analysis is well accepted because it provides consistent estimates and standard errors of all coefficients, except for the intercept term (9–11). However, in matched case-control studies, the standard logistic regression analysis can produce severely biased estimates from a mis-specified function of the matching factors that appears in the model (12). Thus, for matched case-control studies, conditional likelihood methods are the analyses of choice, as they cancel out the effect of the matching factors in estimating the parameters of interest (13). Although matched case-control designs are commonly used in epidemiologic studies, it is relatively recent that studies dealing with high dimensional data have started acknowledging that the analysis should reflect the design (14,15). There are only five published papers that considered the matched design in high dimensional variable selection (16–20). This is because variable selection is motivated to select factors with the best prediction of an outcome, but a matched case-control design is not developed for prediction.

2.2. Prediction model for a matched case-control design

Prediction is usually not a goal when a matched case-control design is used. But as indicated in (17), a prediction model can be fit when a matched case-control design is set up in a prospective cohort study.

When the odds is considered in a matched case-control design, it can be written as follows:

$$\frac{P(Y=1\mid X,Z,V=1)}{P(Y=0\mid X,Z,V=1)}=\frac{P(V=1\mid Y=1,X,Z)}{P(V=1\mid Y=0,X,Z)}\frac{P(Y=1\mid X,Z)}{P(Y=0\mid X,Z)}$$

where Y is an outcome (Y = 1 for cases and Y = 0 for controls), X is the vector of the selected variables, Z is the vector of matching variables, and V = 1 indicates that a subject is sampled into the matched case-control study and V = 0 indicates otherwise.

Here, $\frac{P(Y=1\mid X,Z)}{P(Y=0\mid X,Z)}$ is the odds if the full cohort is analyzed, which can be fit using unconditional logistic regression logitP(Y = 1|X,Z) = α + β^TX + γ^TZ. As for the term $\frac{P(V=1\mid Y=1,X,Z)}{P(V=1\mid Y=0,X,Z)}$, if we assume the sampling of cases and controls is independent of X, it can be written as $\frac{P(V=1\mid Y=1,Z)}{P(V=1\mid Y=0,Z)}$, which is the same as $\frac{P(Y=0\mid Z)}{P(Y=1\mid Z)}\frac{P(Y=1\mid V=1,Z)}{P(V=0\mid V=1,Z)}$. Then, depending on the size of design (say 1 to m matched design), $\frac{P(Y=1\mid V=1,Z)}{P(Y=0\mid V=1,Z)}=\frac{1}{m}$. Hence, logitP(Y = 1|X,Z,V = 1) = α + β^TX + γ^TZ + f(Z) where $f(Z)=\mathit{log}\frac{P(Y=0\mid Z)}{P(Y=1\mid Z)}-\mathit{logm}$. Generally, $\frac{P(Y=0\mid Z)}{P(Y=1\mid Z)}$ is unknown in matched case-control studies, but it is estimable if the matched case-control study was constructed from a prospective cohort study. Then, unconditional logistic regression model with f(Ẑ) as offset can be fit for prediction, where  denotes an estimate of A.

Prediction performances must be measured using new data that was not used for developing a prediction model (21). Based on the property of discrimination, the predictive power can be assessed by the fraction of true positive prediction (sensitivity) and the fraction of true negative prediction (specificity) at a given cut-point for classification. The area of under the Receiver Operating Characteristic curve (AUC) is commonly used, which plots sensitivity against 1-specificity for consecutive cut-points for the probability of an outcome. From the AUC, the Youden index determines the cut-point for classification where the sum of sensitivity and specificity -1 is the highest (22). The sensitivity and specificity at the cut-point determined by the Youden index is often reported with the AUC to assess the predictability. These performance measures are expected to be the best when they are obtained from the data that was used for the prediction model development.

2.3. Variable selection for a matched case-control design

sIn a matched case-control design, variable selection can be done using a conditional logistic regression model. When multiple variables are analyzed together, a stepwise selection can be used by fitting a multiple conditional logistic regression model. But this approach becomes unstable or infeasible with a large number of variables. For high-dimensional variable selection, the penalized likelihood method with the lasso penalty (LASSO) is frequently used, since this method produces a subset of variables with nonzero regression coefficients (23). Another common approach is random forest (RF) since it produces the so-called “variable importance (VIMP) score” for each input variable (24). Recently, two approaches for a matched case-control design have been published based on a penalized conditional likelihood. One is a penalized conditional logistic regression model proposed by (20). This approach uses a cyclic coordinate descent algorithm (25, 26) and allows the choice of the lasso, ridge, or elastic net penalty. The other is an algorithm proposed by (16) to obtain VIMP scores in a matched case-control design, using the ridge penalty for a penalized conditional logistic regression. Applying the RF technique, the average VIMP score is obtained for each variable over all bootstrap replicates in which the variable was selected as one of the selected variables.

3. Proposed framework

In our framework, in order to make the out-of-data validation available within a cohort, we set up a nested case-control design for developing a prediction model, and then the rest of the cohort is used for validating the model. In the case-control cohort, a set of variables are first selected using a method appropriate for a matched case-control design. For the selected variables, the parameter of interest β is estimated by fitting a multiple conditional logistic regression. This independent estimation of β makes the estimation robust to other parameter estimation. Then, we fit the prediction model using unconditional logistic regression with β̂^TX + f(Ẑ) as offset. Finally, the selection is evaluated by assessing the performance of the prediction model internally using the subjects included in the case-control study and externally using the subjects in the rest of the cohort.

Validation

In order to assess whether internal predictive power remains the same in external evaluation, we propose to use a graphical approach, overlapping the internal and external specificities at consecutive cut-points for the predicted probability of the event. Better overlap will indicate better overall validity of prediction and variable selection. Also, greater area under the curve will indicate better specificity of the prediction fitted on the selected variables. We obtain the area under the curve for specificity plot using the method by (27). For a valid classification, we propose to choose the cut-point for classification where the difference between internal and external specificities can be ignored at the maximum of desired specificity, through an exhaustive search.

Missing data

When conducting variable selection, subjects with a missing data are generally removed. The loss is greater with more input variables possibly including missing data. In a matched design, the loss is even greater because a subject with a missing variable leads to removing pairs including the subject. RF can be used for imputation of missing values and performs well in mixed types of variables where complex interactions and nonlinear relationships are suspected (28, 29). Here, RF is applied to data roughly imputed by the mean or frequency and produces a proximity matrix, which is a symmetric matrix whose (i,j) entry is the frequency that two subjects i and j occur within the same terminal node. Then the missing values are imputed by the proximity weighted average of the non-missing data. RF is again applied to the updated data, and the imputation is repeated to get a stable solution (RF imputed data). The imputed data can be used for further analysis.

Implementing RF imputation for missing data, we conduct a multiple imputation that repeats variable selection in imputed data sets and choose variables jointly selected from repeated variable selections. In each repetition, we use unsupervised RF to generate the RF imputed data, and then variables are selected by an available method. After a desired number of repetitions, among those variables selected contingent on imputation, we order the variables from the most frequently selected to the least. Our approach selects variables from the highest rank until the frequency drops at the maximum.

4. Application

To illustrate our proposed framework, an example was used from a prospective cohort study including 109 cases and 4,326 non-cases. Total 136 variables were used as input variables. After matching, we considered three study designs by varying the number of controls per case to be randomly selected from non-cases: 1 to 1 matched (3% of control selection); 1 to 3 matched (8%); and 1 to 10 matched (25%). Of the 109 cases, 98 had complete data for all 136 variables. The 1 to 1 matched design included 109 pairs, but the complete data for all 136 variables were available only in 91 pairs (83%) from 199 subjects (91%). That is, the proportion of missing was about 9% at the subject level but became 17% at the pair level. In this example, the data completeness in the input variables was similar between designs; 84% of pairs and 92% of subjects in the 1 to 3 design and 84% of pairs and 93% of subjects in the 1 to 10 design (Table 1).

Table 1.

Design and missing data

Design	Planned			Without a missing variables among 136 input variables
	% of controls in case-control cohort	Number of subjects	Number of cases/Number of pairs	Number of subjects	Number of cases/Number of pairs
1 to 1	3%	218	109/109	199	98/91
1 to 3	8%	436	109/327	401	98/276
1 to 10	25%	1199	109/1090	1110	98/915

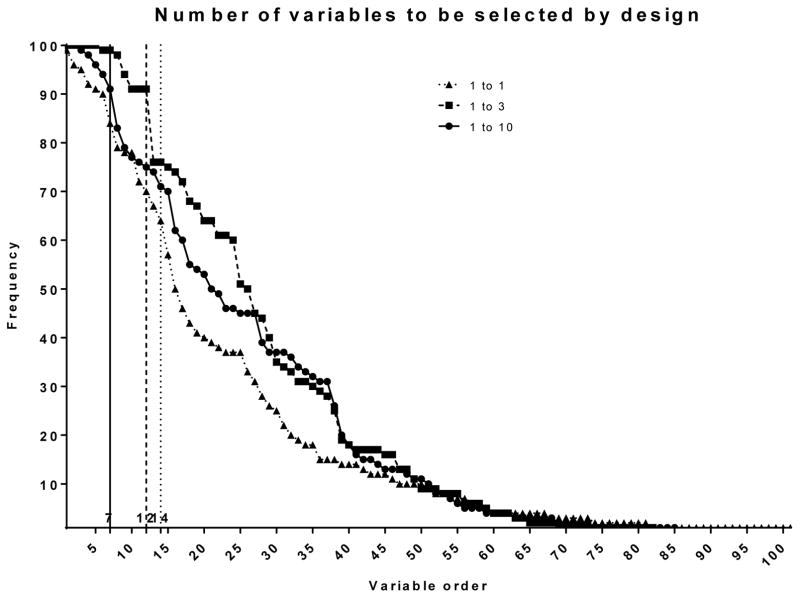
For variable selection, we used the approach for a matched case-control design proposed by (20): Conditional LASSO. Conditional LASSO selected 24 variables (18%) of the 136 input variables in the 1 to 1 design, 28 variables (21%) in the 1 to 3 design, and 19 variables (14%) in the 1 to 10 design by using the complete data only. Next, our proposed framework was applied to handle missing data. Conditional LASSO was repeated in 100 RF imputed data sets: RF imputed conditional LASSO. The 100 repetitions selected 101 variables at least once in the 1 to 1 design, 82 in the 1 to 3 design, and 85 in the 1 to 10 design. By ordering those variables from the most frequent selection to the least, the maximum separation occurred after the 14^th variable in the 1 to 1 design, the 12^th variable in the 1 to 3 design, and the 7^th variable in the 1 to 10 design (Fig. 1). Hence, the most frequently appearing 14 variables in the 1 to 1 design (10%), 12 variables (9%) in the 1 to 3 design, and 7 variables (5%) in the 1 to 10 design were selected by RF imputed conditional LASSO.

Figure 1.

Variable frequency in RF imputed conditional LASSO

As shown in Table 2, of the 136 input variables, 44 variables were selected at least once out of the 6 variable selections attempted. Irrespective of the design, a random selection appearing only once (green) happened more in Conditional LASSO, compared to RF imputed conditional LASSO (33% vs. 7% in the 1 to 1 design, 14% vs. 0% in the 1 to 3 design, and 21% vs. 0%). Three variables were selected in all of the 6 selections (light blue). Two variables appeared in 5 of the 6, 5 variables did in 4 of the 6, 6 variables did in 3 of the 6, and 10 variables did in 2 of the 6. The RF imputed LASSO selection showed a good overlap with the Conditional LASSO selection: 79% in the 1 to 1 design, 100% in the 1 to 3 design and 71% in the 1 to 10 design).

Table 2.

Variable selection: Green – once, Purple – twice, Blue – three times; Yellow – four times, Orange – five times, Light blue- six times; (p=number of selected variables, percentage of variable selection)

	1 to 1 design		1 to 3 design		1 to 10 design
Variable ID	Conditional LASSO (p=24, 18%)	RF imputed LASSO (p=14, 10%)	Conditional LASSO (p=28, 21%)	RF imputed LASSO (p=12, 9%)	Conditional LASSO (p=19, 14%)	RF imputed LASSO (p=7, 5%)
1	p
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

The proposed prediction model was built on those variables selected by each approach. Internal validation within the case-control cohort was conducted and compared to external validation in the cohort but not in the case-control study (Table 3). In the internal validation, the AUC was higher in Conditional LASSO than in RF imputed conditional LASSO in all designs, suggesting worse classification in RF imputed conditional LASSO. Although the AUC was generally higher with more variables, RF imputed conditional LASSO in the 1 to 3 design produced a higher AUC value with 12 variables (77%), compared to RF imputed conditional LASSO in the 1 to 1 design (76% with 14 variables) or Conditional LASSO in 1 to 10 design (75% with 19 variables). We obtained the sensitivity and specificity at the cut-point determined by the Youden index. The specificity was lower in RF imputed conditional LASSO than Conditional LASSO in all designs.

Table 3.

Prediction and validation

Design	Validation	Conditional LASSO		RF imputed conditional LASSO
		Internal	External	Internal	External
1 to 1	Number of variables	24		14
	AUC	0.774	n.a.	0.759	n.a.
	Sensitivity by the Youden index	0.684	n.a.	0.818	n.a.
	Specificity by the Youden index**	0.723	0.649	0.624	0.563
	Area under the specificity curve	0.686	0.610	0.641	0.617
1 to 3	Number of variables	28		12
	AUC	0.822	n.a.	0.770	n.a.
	Sensitivity by the Youden index	0.827	n.a.	0.776	n.a.
	Specificity by the Youden index	0.726	0.621*	0.686	0.614*
	Specificity by the proposed approach to find a valid classification **	0.574	0.517	0.637	0.581
	Area under the specificity curve	0.828	0.755	0.805	0.760
1 to 10	Number of variables	19		7
	AUC	0.752	n.a.	0.713	n.a.
	Sensitivity by the Youden index	0.857	n.a.	0.816	n.a.
	Specificity by the Youden index**	0.559	0.554	0.546	0.523
	Area under the specificity curve	0.916	0.907	0.914	0.909

Internal, from case-control cohort; External, from the rest of cohort; AUC, Area under the ROC curve; Sensitivity, fraction of true positive prediction; Specificity, fraction of true negative prediction;

^*Significant difference between internal and external;

^**Valid classification

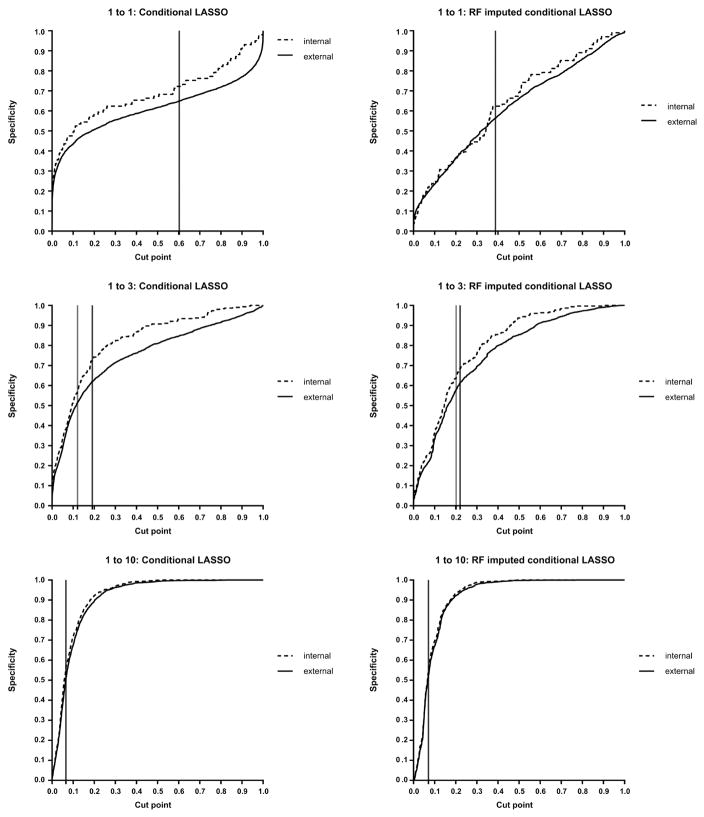
Except for the 1 to 3 design, the external specificity was not significantly different from the internal specificity, implying that the classification by the Youden index is valid. For overall validation, we plotted those internal and external specificities against consecutive cut-points. The internal and external specificities overlapped better in RF imputed conditional LASSO. In the 1 to 1 design, although the internal and external specificities were similar, the area under the specificity curve was 61 to 69%, requiring a higher cut-point to reach an acceptable specificity. The 1 to 10 design showed a desirable shape with higher area under the specificity curve (91 to 92%), but selecting 10 controls per case (25% of control selection) may not be necessary or feasible in most studies. The 1 to 3 design also showed a good shape with relatively high area under the specificity curve (76 to 83%), but the internal and external specificities by the Youden index were significantly different. Hence, our proposed approach was used to find the cut-point for a valid classification (reference line in grey in Fig. 2).

Fig. 2.

Internal and external specificities: Black reference line indicates the cut-point by the Youden index, and grey reference line indicates the proposed cut-point.

Finally, we applied each prediction model in the full cohort (Table 4). As expected, the AUC decreased in both approaches, but the change in RF imputed conditional LASSO was less in all designs. Since the sensitivity is the same between the case-control cohort and the full cohort, this AUC reduction is due to the specificity change. The trend of higher AUC with more variables remained. But when the lowest AUC was 70% with 7 variables by RF imputed conditional LASSO in the 1 to 10 design, the 1 to 1 design by Conditional LASSO produced 71% of the AUC with 24 variables. The sensitivity and specificity were obtained at the cut-point determined to be a valid classification in each design. The valid specificity was similar across designs in RF imputed conditional LASSO (57% in the 1 to 1 design, 59% in the 1 to 3 design and 53% in the 1 to 10 design). Additionally, the independent effect of the selected variables was examined using the standard unconditional logistic regression after adjusting for the matching factor in the full cohort. When those variables with p-value < 0.01 were counted, higher proportion was shown in RF imputed conditional LASSO in all designs.

Table 4.

Prediction and validation in the full cohort

		Variable selection
Design	Validation	Conditional LASSO	RF imputed conditional LASSO
1 to 1	AUC	0.705	0.728
	Valid sensitivity	0.684	0.818
	Valid specificity	0.651	0.566
	Number of variables whose univariate p-value<0.01	9 (38%)	8 (57%)
1 to 3	AUC	0.754	0.721
	Valid sensitivity	0.867	0.786
	Valid specificity	0.521	0.585
	Number of variables whose univariate p-value<0.01	11 (39%)	6 (50%)
1 to 10	AUC	0.733	0.701
	Valid sensitivity	0.857	0.816
	Valid specificity	0.525	0.529
	Number of variables whose univariate p-value<0.01	10 (53%)	5 (71%)

Internal validation suggested better performance in Conditional LASSO, but external validation suggested otherwise. In both variable selection approaches, the area under the specificity curve suggested that selecting 3 or more controls is reasonable for overall validity. Variable selection and prediction by RF imputed conditional LASSO were more consistent in external evaluation by including fewer variables with a higher proportion of a significant independent effect. Hence, in this example, the RF imputed conditional LASSO prediction and variable selection in the 1 to 3 design seem to be an efficient choice when a simpler prediction model or variable selection is desired. In our application, the prediction developed in the 1 to 3 design is expected to be 59% specific and 79% sensitive.

5. Discussion

Instead of the full cohort analysis, our framework constructs a nested case-control design to make an appropriate validation available. By including all cases, this design preserves statistical power for prediction and variable selection, but the validation is restricted to specificity only. When the outcome is common, our framework may not help much, compared to the typical approach of splitting data into a training set and a validation set. However, when the outcome is uncommon, the possibility of misclassifying negative subjects as positive is more of a concern since the error can affect more subjects. In this context, our framework can be preferred as it controls specificity in the development.

The impact of missing data can be greater in a matched case-control study, due to the exclusion of pairs. In high-dimensional data analysis, the algorithms use a cross-validation to determine the amount of regularization by repeating a sub-sampling approach. This process produces generally unstable selection contingent on the sub-sampling (30). Also, more limited sample size compared to the number of input variables tends to include more variables, leading to over-fitting the prediction model. By including variables repeatedly selected through iterations, our proposed approach selected fewer variables with a higher proportion of variables with independent effects, irrespective of the design. While this could be an indication of improving stability in variable selection and prediction, a simpler model not only helps interpretation, but also reduces the impact of missing data.

Prediction performance is expected to be worse when they were measured in data that was not used for the development, compared to the internal assessment. Our proposed framework also showed that the internal AUC in the nested case-control cohort was an over-estimate when it was validated in the full cohort. However, in RF imputed conditional LASSO, the AUC reduction was smaller (about 7% vs. 5%) and internal specificity was similar to external specificity, indicating better validity. The sensitivity and specificity were also similar across different designs when the proposed classification was applied for validity.

In this paper, our framework was illustrated in the use of high-dimensional data where the number of variables is close to or moderately higher than the number of subjects. But this approach also helps with low-dimensional data with appropriate variable selection. The LASSO selection was arbitrarily chosen, so any variable selection procedure can replace the LASSO selection. In a matched case-control design, the methods for high dimensional variable selection are currently limited. Since our framework separates variable selection from fitting the prediction model for the matched design, variable selection ignoring the matched design may not have a severe impact on the prediction model performance. A further investigation can be pursued. On the other hand, a nested case-control design is mostly used in the need of costly data collection. In this context, data is only available in the case-control cohort, so our framework using external specificity is not directly available. However, one may use our framework for available data in the full cohort to guide in validating the findings from data only available in the case-control cohort. In future work, we will investigate the use of our framework when data are available only in the case-control cohort.