Abstract
Background
Despite over 35 years of study, the relationship between life events (LEs) and alcohol use disorder (AUD) treatment outcome lacks consistent empirical support, which may be due to a lack of theoretically driven designs and corresponding statistical analyses. The purpose of this study was to elucidate the LEs-AUD treatment outcome relationship by statistically modeling the dynamic relationship between negative LEs and alcohol use post-treatment, as it is conceptualized within the dynamic model of relapse.
Methods
Existing longitudinal data from 417 AUD treatment-seeking adults were randomly assigned to two demographically comparable samples. One sample (N = 208) was used to estimate a series of dynamic bivariate latent change score models that differentially relate latent indicators of distal and proximal negative LEs (i.e., events subjectively rated as negative) and percent heavy drinking days across 12 months. Cross-validation was conducted on the second sample (N = 209).
Results
Findings indicated that distal negative LEs were positively associated with a greater increase in negative LEs, but not heavy drinking, over the subsequent 12 months. Proximal negative LEs were significantly associated with subsequent increases in heavy drinking, though heavy drinking was not a determinant of change in negative LEs. These findings were cross-validated with the second sample.
Conclusions
This study provides initial justification for the further study of the LEs-alcohol use relationship as it is described in the dynamic model of relapse.
Keywords: Alcohol use disorder, negative life events, heavy drinking, bivariate latent change score analysis
1. Introduction
Life events (LEs), defined as occurrences likely to bring about readjustment-requiring changes in people’s lives (Holmes and Rahe, 1967), have been studied as factors that may influence the treatment outcome (i.e., alcohol use frequency and quantity) of an alcohol use disorder (AUD), as defined by the Diagnostic and Statistical Manual (DSM-5; American Psychiatric Association, 2013). However, the nature of the LEs-AUD treatment outcome relationship remains unclear due to inconsistent findings (Krenek and Maisto, 2013). Moreover, the dynamic relationship between LEs and alcohol use, as hypothesized within the dynamic model of relapse (Witkiewitz and Marlatt, 2004), has not been empirically evaluated.
Krenek and Maisto’s (2013) review identified 18 studies published from 1988 to 2010 that examined the association between LEs and AUD/substance use disorder (SUD) treatment outcomes. No additional relevant published studies were identified since this review. Among the studies reviewed, 12 found that more negative LEs were associated with poorer SUD treatment outcome, 7 reported no relationship between negative LEs and treatment outcome, and 2 found that more positive LEs were associated with better treatment outcome. These findings support previous research showing that negative, not positive, LEs are more likely to be associated with poor treatment outcome (Dohrenwend, 2006). Thus, the current study focuses on negative LEs only. These findings also suggested that the data are inconsistent regarding the association between negative LEs and post-treatment substance use, possibly due to minimal use of theorydriven hypotheses, study design, and analyses.
The dynamic model of relapse provides a conceptual framework of substance use behavior that is both clinically relevant and empirically testable, and could be applied to evaluating the LEs-AUD treatment outcome relationship. The model, which describes substance use as a nonlinear process differentially influenced by present and past factors, predicts that the occurrence of LEs (e.g., divorce) can operate as both a proximal and distal risk of substance use. An acute LE may act as a transient risk that precipitates substance use. Further, feedback loops in the model predict that, following use, the likelihood of a LE occurring increases, potentially resulting in an increase in substance use. Lastly, the occurrence of past LEs may serve as a distal risk that predisposes an individual to substance use by continuing to have a negative impact on the individual.
Research within the SUD treatment outcome literature has primarily focused on understanding the proximal, unidirectional influence of LEs on treatment outcome, producing an inconsistent pattern of findings (cf., Krenek and Maisto, 2013; O’Doherty and Davies, 1987). Consistent across the 18 studies in the 2013 review is the use of analytic techniques that do not assess the potential reciprocal relationship between LEs and substance use as described in the dynamic model and thus cannot detect any existing relation between substance use and subsequent LEs. Moreover, it has been suggested that the inclusion of a LE that is “a consequence or potential consequence” of a SUD (Paykel, 1997; p. 303) as a predictor of SUD symptomatology may confound the LEs-SUDs outcome relationship, because substance use consequences may also be SUD symptomatology (Hart and Fazaa, 2004). However, the exclusion of SUD-related LEs may result in an underestimation of an individual’s LE milieu, thereby potentially portraying the individual’s life experiences as less severe and biasing the prediction of substance use. Thus, the inclusion of SUD-related LEs may be warranted within the conceptualization that LEs and substance use are reciprocally related across time. Finally, no studies have used longitudinal statistical techniques that can test the dynamic bidirectional association between LEs and treatment outcomes at multiple time points over time, thereby ignoring how LEs that may be consequences of substance use and may affect subsequent use.
The use of statistical techniques for longitudinal data applied to AUD clinical course data may provide the methods required to appropriately examine the LEs-AUD treatment outcome relationship (Hedeker and Mermelstein, 1996). Witkiewitz (2011) used bivariate latent change score analysis (BLCS; McArdle, 2001) to address the complex relationships described in the dynamic model. BLCS analysis is a statistical approach to modeling dynamic relationships that is especially relevant for examining determinants of change and thus can be used to test the dynamic model. It has not been applied to the LEs-AUD treatment outcome relationship.
Lastly, within the dynamic model, distal risks represent factors that may predispose an individual to substance use, thereby increasing the individual’s sensitivity to proximal factors. The extent to which past LEs predispose individuals to subsequent use has received limited research attention within AUD/SUDs treatment literature. One study showed that, among U.S. military Veterans with SUD, presence of chronic stressors did not affect the relationship between acute LEs and substance use (Tate et al., 2006).
In summary, the literature on the relationship between LEs and substance use is inconsistent, which may be due to limited examination of LEs within a theoretical framework using appropriate statistical analyses. Specifically, the majority of the LEs-SUDs treatment outcome literature has focused on the unidirectional influence of LEs on subsequent use, has neglected the potential reciprocal relationship between these factors, and the extent to which prior LEs predispose an individual to subsequent use remains unclear.
1.1. Current Study
Given the gaps in the literature, the current study aimed to examine the bidirectional association between proximal negative LEs and AUD treatment outcome, as described in the dynamic model of relapse using appropriate analytic techniques to guide future research in this area. We tested a series of BLCS models that represent potential associations between negative LEs and alcohol use. We hypothesized that increases in proximal negative LEs are associated with increases in subsequent alcohol use over time, and increases in alcohol use predict increases in subsequent proximal negative LEs over time. Additionally, it was expected that higher levels of distal negative LEs predict greater dynamic risk between proximal negative LEs and alcohol use over time. Given the inconsistencies reported in the literature regarding the negative LEs-alcohol use relationship, cross-validation was conducted to determine stability of findings.
2. Method
2.1. Participants
Data were collected as part of the Relapse Replication and Extension Project (RREP; Lowman et al., 1996). RREP was designed to examine the course of alcohol involvement following treatment initiation. Adults with DSM-III-R alcohol abuse or dependence were recruited from inpatient and outpatient addictions treatment programs across three sites. Data from two sites were used in this study because the third site did not administer a key questionnaire.
Eligibility criteria included: ≥18 years of age (21 years at one site), presence of alcohol abuse or dependence within the past six months, absence of more severe concurrent drug diagnoses other than alcohol, no intravenous drug use in the past six months, absence of comorbid severe mental illness, at least eighth grade reading ability, completed detoxification, and signed informed consent. Across the two sites, 417 participants met eligibility criteria and consented to participate.
2.2. Procedures and Measures
Assessments occurred at baseline and bimonthly over 12 months. Baseline, 6-month, and 12-month interviews were conducted in-person, while 2-, 4-, 8-, and 10-month follow-ups were phone interviews. Only measures relevant to the current study are described.
2.2.1. Life Events
LEs were assessed at baseline for the previous 12 months and at 6- and 12-months for the previous 6 months using the Life Experiences Survey (LES; Sarason et al., 1978), which has demonstrated adequate reliability and validity. The LES is a self-report questionnaire that lists 46 positive, neutral, and negative events, with space to add four additional events. Participants identified events that occurred, indicated the date of each endorsed event, and rated the subjective desirability/undesirability of each endorsed event on a 7-point Likert-type scale from −3 (extremely negative) to 3 (extremely positive). Only negatively rated events (scores between −3 and −1) were included in the analyses.
A composite LEs variable was used in analyses and consisted of the number of endorsed negative LEs and the mean desirability rating of those events (Maisto et al., 2006). Endorsed negative events were recoded to values from 1 to 3, with higher values indicating greater undesirability. Non-endorsed events were assigned a value of 0 so that participants who did not experience any LE during a timeframe would be included in analyses. Ratings were summed across events for each timeframe.
For distal LEs, the composite variable included all negative LEs and associated desirability ratings endorsed during the baseline assessment. Composite variables for proximal LEs were computed for 2-month intervals for the duration of the 12-month study, resulting in scores at six timepoints. Baseline interview date and event dates were used to determine in which 2-month interval LEs occurred.
2.2.2. Alcohol Use
The Form-90: A Structured Assessment Interview for Drinking and Related Behaviors (Miller, 1996) was used to assess daily quantity of alcohol consumption. Participants were assessed for the 90 days prior at baseline and bimonthly for 12 months. Missing drinking data from missed assessments were collected at the subsequent interview.
Percent heavy drinking days (PHD) was used as the alcohol outcome variable because it is a clinical indicator of severity that accounts for both frequency and intensity of alcohol use. PHD was computed by dividing the number of heavy drinking days (≥5 drinks for men, ≥4 drinks for women) by total drinking days and multiplying by 100 for each 2-month period that corresponds to the proximal LEs’ timeframes.
2.2.3. Baseline Covariates
These variables included pre-treatment alcohol use, coping (Maisto et al., 2006; Miller et. al., 1996), and prior treatment history (Connors et al., 1996). Coping was assessed using the Coping Behaviors Inventory (CBI; Litman et. al., 1983), a self-report questionnaire with adequate validity and reliability that provides four scale scores: positive thinking, negative thinking, avoidance/distraction, and seeking social support. Treatment history was assessed using the Lifetime Treatment History Interview as part of the Form-90. Participants reported number of past inpatient and outpatient treatment episodes for AUD and SUDs in their lifetime.
2.3. Data Analyses
2.3.1. BLCS Analyses
Bivariate latent change score (BLCS; McArdle, 2001; McArdle and Grimm, 2010) analyses were used to test the associations among distal and proximal LEs and PHD. BLCS models are structural equation models that are extensions of autoregressive and latent growth models. Thus, BLCS models simultaneously estimate systematic growth components (i.e., latent slope and intercept) and cross-lagged associations (McArdle, 2009). These models are structured to allow for examining the extent to which variable X (e.g., LEs) predicts changes in variable Y (e.g., alcohol use) and vice versa, across multiple time points, in addition to other change parameters. Results from BLCS models provide information regarding determinants of change and more general parallel latent processes.
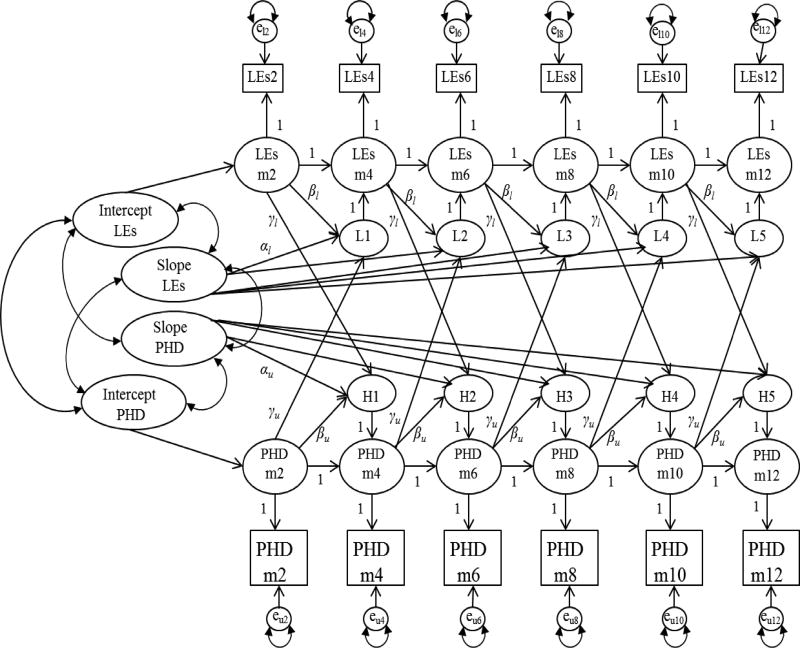
As shown in Figure 1, the trajectories for proximal LEs and PHD each include a latent intercept with a mean and variance, and a latent slope with a mean and loadings. These models estimate overall changes in LEs and PHD over time, unlike standard auto-regressive models. In the proposed models, the latent intercept directly predicts the initial latent score, and is therefore indirectly related to all subsequent scores. The latent slope affects the individual latent change scores through the constant change coefficient α, which measures the degree of change in the latent change scores across time. Further, β represents the proportional change across time. BLCS models assume a known, fixed, and constant time interval, which allows latent change scores to be interpreted as a rate of change (McArdle, 2001). Finally, the dynamic relationship between the two trajectories is represented by the γ coefficients, which describe the relationship between the latent change score of one variable regressed on the latent score of the other variable.
Figure 1.
Proposed bivariate latent change score model of proximal negative life events (LEs) and percent heavy drinking days (PHD). m = month; L1–L5 = latent change score for proximal LEs; H1–H5 = latent change score for PHD; αu=constant change coefficient for PHD; αl = constant change coefficient for proximal LEs; βu= proportion change coefficient for PHD; βl= proportion change coefficient for LEs; γl = bivariate change coefficient for LEs regressed on PHD; γu= bivariate change coefficient for PHD regressed on LEs. Distal negative LEs and other pre-treatment factors predicting the initial latent slopes for both proximal LEs and PHD are not depicted in this model.
2.3.2. Model Estimation
Models were first estimated using the calibration sample, and cross-validated with the validation sample using methods described later. Four models were estimated, representing the potential relationships between proximal LEs and PHD: (a) baseline model: no relationship, (b) PHD leading model: PHD predicts changes in LEs, (c) LEs leading model: LEs predict changes in PHD, (d) coupling model: PHD predicts changes in LEs and LEs predict changes in PHD (see Figure 1). Models a, b, and c were estimated by constraining the relevant parameters to zero (e.g., constraining the path from PHD to LEs to zero in model c).
For all models, a latent intercept and slope, each with a mean and variance, were estimated for PHD and LEs, along with correlations among them. The constant change parameter α for each factor was constrained to 1.0, reflecting a constant rate of change (McArdle, 2001). This allows the latent slope to be interpreted as the mean change in the variable over time. The proportional change coefficient β was constrained to be equal across time, allowing for the interpretation that the dynamics are constant across time (Grimm et. al., 2012). Although these parameters are held constant across time points, it does not mean that expectations of change are constant; rather, it means that change accumulates in a systematic way. Thus, BLCS models produce coefficients γ that are stable over time, though incorporate accumulated change over the 12-month period. Placing constraints on change coefficients follows the standard approach to modeling dynamic relationships using BLCS analysis and allows for interpretation of determinants of change.
Distal LEs were included in models as a predictor of the latent slope for LEs and alcohol use, thereby accounting for variance in changes in LEs and PHD across time (Witkiewitz, 2011). Distal LEs were also included as a predictor of the latent intercept for LEs, and baseline PHD was included as a predictor of the latent intercept for PHD. Baseline covariates were included in the models as predictors of the latent slope for PHD.
Analyses were conducted using Mplus version 6.12. Parameters were estimated using maximum likelihood estimation with robust standard errors and chi-square (MLR), which corrects for both missing at random and non-normally distributed data (Enders, 2001; Muthén and Asparouhov, 2002; Schafer and Graham, 2002). PHD and LEs variables were non-normally distributed. LEs composite scores were log transformed to help reduce the extent of non-normality.
Model fit was assessed using root-mean-square error of approximation (RMSEA), the fit index recommended for interpreting BLCS models (McArdle, 2001), and MLR chi-squared values. Models were considered to have good fit if RMSEA was below 0.08 (Hu and Bentler, 1999). Nested models were compared using a chi-squared difference test, where a significant difference in chi-square value between the baseline model and comparison model indicate better fit for the comparison model. The chi-square difference test was conducted using the recommended method for MLR estimation of computing the strictly positive robust chi-square (Satorra and Bentler, 2010).
2.3.3. Cross-Validation
Two random samples of the data (calibration sample: N = 208; validation sample: N = 209) were determined using the random sample generator in SPSS Version 18. Power calculations for covariance structure modeling were conducted using recommendations for power calculations described by MacCallum and colleagues (1996). The baseline model included 19 observed variables, 32 parameters, and df = 142. For a model with these specifications, 134 participants are needed to achieve a power of 0.80 at alpha = .05 for a test of close fit where RMSEA equals 0.05 (MacCallum et al., 1996; Preacher and Coffman, 2006). Thus, the sample size of the two samples was adequate.
Partial cross-validation (Bentler, 1980), which involves holding the linear coefficients as fixed in the cross-validation, and re-estimating the variances and covariances, was used (MacCallum et. al., 1994). The linear coefficients obtained for the best fitting model using the calibration sample were used to estimate the same model using the validation sample, thus forcing the validation data to fit within the model obtained using the calibration data. Model fit and stability were then assessed using RMSEA.
3. Results
3.1. Sample Characteristics
The calibration and validation samples did not differ from the full sample on any demographic variable (Table 1), nor did the calibration and the validation samples differ on demographics and baseline variables (Table 2).
Table 1.
Participant characteristics for the full sample (N = 417) and two random samples (Nc = 208, Nv = 209).
| Full Sample | Calibration | Validation | |
|---|---|---|---|
| M (SD) | M (SD) | M (SD) | |
| Age | 34.6 (8.76) | 34.4 (8.56) | 34.8 (8.97) |
| Years of Education | 11.1 (7.81) | 11.9 (2.45) | 12.0 (2.39) |
| N (%) | N (%) | N (%) | |
| Male | 235 (56.4) | 117 (56.3) | 118 (56.5) |
| Ethnicity/Race | |||
| Caucasian | 306 (73.4) | 160 (76.9) | 146 (69.9) |
| Black/AA | 74 (17.7) | 32 (15.4) | 42 (20.1) |
| Hispanic | 8 (1.9) | 4 (1.9) | 4 (1.9) |
| Other | 29 (5.5) | 12 (5.7) | 17 (8.1) |
| Employment | |||
| Full-time | 191 (45.9) | 88 (42.3) | 103 (49.3) |
| Part-time | 109 (26.2) | 62 (29.8) | 47 (22.5) |
| Unemployed | 75 (18.0) | 39 (18.8) | 36 (17.2) |
| Other/Retired | 41 (9.8) | 18 (8.7) | 23 (11.0) |
| Marital Status | |||
| Single | 169 (40.5) | 79 (38.0) | 90 (43.1) |
| Divorced | 73 (17.5) | 36 (17.3) | 37 (17.7) |
| Separated | 65 (15.6) | 30 (14.4) | 35 (16.7) |
| Married | 87 (20.9) | 50 (24.0) | 37 (17.7) |
| Recruitment Site | |||
| Brown | 290 (69.5) | 138 (66.3) | 152 (72.7) |
| RIA | 127 (30.5) | 70 (33.7) | 57 (27.3) |
Note. AA = African American; RIA = Research Institute on Addictions.
Table 2.
Means and Standard Deviations for Percent Heavy Drinking Days (PHD), Life Events (LEs), and Baseline Covariates for Calibration and Validation Samples.
| Calibration Sample |
PHD | LEs Score | # of LEs | LEs Desirabilitya | |||
|---|---|---|---|---|---|---|---|
| N | M(SD) | N | M(SD) | M(SD; Range) | N | M(SD) | |
| Baseline | 208 | 51.9 (29.3) | 208 | 9.2 (8.05) | 3.6 (2.99; 0–16) | 166 | −2.5 (0.45) |
| Months 1–2 | 208 | 4.7 (14.0) | 190 | 0.5 (1.50) | 0.2 (0.64; 0–4) | 31 | −2.2 (0.70) |
| Months 3–4 | 205 | 9.6 (20.7) | 190 | 1.0 (2.04) | 0.5 (1.02; 0–5) | 49 | −2.2 (0.74) |
| Months 5–6 | 201 | 13.1 (24.5) | 191 | 1.5 (2.65) | 0.6 (1.12; 0–6) | 69 | −2.2 (0.67) |
| Months 7–8 | 198 | 14.4 (26.4) | 192 | 1.1 (2.57) | 0.5 (0.99; 0–6) | 47 | −2.2 (0.78) |
| Months 9–10 | 196 | 13.0 (26.1) | 190 | 1.1 (2.31) | 0.5 (0.90; 0–6) | 58 | −2.2 (0.84) |
| Months 11–12 | 189 | 12.4 (24.2) | 189 | 1.7 (2.89) | 0.8 (1.26; 0–8) | 78 | −2.2 (0.74) |
| Covariates | N | M(SD) | |||||
| Prior Tx Episodes | 208 | 4.6 (8.5) | |||||
| Positive Coping | 208 | 1.5 (0.7) | |||||
| Negative Coping | 208 | 1.7 (0.7) | |||||
| Avoidance | 208 | 1.3 (0.6) | |||||
| Seeking Social | 208 | 1.3 (0.8) | |||||
| Validation Sample | PHD | LEs Score | # of LEs | LEs Desirabilitya | |||
| N | M(SD) | N | M(SD) | M(SD; Range) | N | M(SD) | |
| Baseline | 209 | 46.6 (30.0) | 209 | 10.0 (8.70) | 3.9 (3.23; 0–14) | 174 | −2.5 (0.50) |
| Months 1–2 | 209 | 8.8 (20.4)* | 183 | 0.8 (2.33) | 0.4 (1.00; 0–7) | 35 | −2.1 (0.74) |
| Months 3–4 | 207 | 11.9 (24.2) | 183 | 1.0 (2.23) | 0.5 (0.99; 0–6) | 51 | −2.1 (0.76) |
| Months 5–6 | 199 | 12.4 (23.4) | 184 | 1.4 (2.64) | 0.6 (1.11; 0–7) | 61 | −2.2 (0.74) |
| Months 7–8 | 196 | 11.2 (23.3) | 194 | 0.7 (1.78) | 0.3 (0.78; 0–5) | 41 | −2.3 (0.77) |
| Months 9–10 | 192 | 12.1 (25.1) | 187 | 1.2 (3.04) | 0.5 (1.14; 0–8) | 50 | −2.4 (0.67) |
| Months 11–12 | 187 | 11.7 (24.4) | 186 | 2.0 (3.99) | 0.8 (1.53; 0–8) | 70 | −2.2 (0.71) |
| Covariates | N | M(SD) | |||||
| Prior Tx Episodes | 209 | 4.5 (9.2) | |||||
| Positive Coping | 209 | 1.5 (0.7) | |||||
| Negative Coping | 209 | 1.7 (0.7) | |||||
| Avoidance | 209 | 1.3 (0.6) | |||||
| Seeking Social | 209 | 1.4 (0.7) | |||||
Note.
Desirability means include only endorsed events; Tx = Treatment;
Significant difference between samples, p = .02
3.2. BLCS Analyses
3.2.1. Calibration
PHD variables tended to correlate with each other, and a portion of PHD variables and LEs scores were significantly positively correlated (Supplemental Table 11). Table 3 displays the fit indices for the BLCS models. The Baseline model showed good fit (RMSEA = .065). Neither the PHD Leading model nor the LEs Leading model fit significantly better than the Baseline model. The Coupling model provided a significant improvement in fit over the Baseline model. The path from LEs to changes in PHD was significant (b = 115.97, p = .03). The path from PHD to changes in LEs was not significant (b = 0.00, p = .97). Given the significant improvement in model fit, the hypothesized Coupling model was retained as the optimal model.
Table 3.
Fit Indices for Bivariate Latent Change Score Models Predicting Percent Heavy Drinking Days.
| Calibration | Validation | ||||
|---|---|---|---|---|---|
| Baseline | PHD Leading | LEs Leading | Coupling | Coupling | |
| χ2 (df) | 267 (142) | 269 (140) | 258 (140) | 220 (139) | 317 (153) |
| §Δχ2 (Δdf) | -- | 0.49 (2) | 5.53 (2) | 42.53 (3)*** | -- |
| RMSEA (CI) | .065 (.053–.077) | .066 (.054–.078) | .064 (.051–.076) | .053 (.039–.066) | .072 (.060–.083) |
Note. PHD = percent heavy drinking days; χ2 = MLR chi-square;
Satorra-Bentler scaled chi-square difference value; RMSEA = root-mean-square error of approximation; CI = 90% confidence interval.
p < .001.
Table 4 provides the unstandardized parameter estimates for the Coupling model. Means and variances are provided for the intercept (initial level) and the rate of change (slopes) for LEs and PHD. There was significant individual variation around the initial LEs level (b = .01, p < .01). Slopes indicated that LEs significantly increased over the 12-month period (b = 0.05, p < .01), with significant individual variation around the slope. There was significant individual variation in the rate of change in PHD (b = 447.07, p = .05). On average, individuals who had higher initial PHD had greater increases in PHD over time (b = 140.89, p = .05). The proportional change coefficients for both proximal LEs and PHD were negative and significant (b = −0.65, p < .01; b = −1.50, p < .001), indicating that higher proximal LEs scores and higher PHD were associated with a decrease in LEs score and PHD at a subsequent time point, respectively. Correlations between growth factors indicated that higher initial level of PHD was associated with increases in LEs over time (b = 0.44, p = .02). Additionally, higher distal LEs scores were associated with an increase in proximal LEs over time (b = 0.10, p < .01), though distal LEs were not associated with changes in PHD. Higher distal LEs scores were associated with higher initial proximal LEs score (b = 0.10, p < .01).
Table 4.
Unstandardized Parameter Estimates (Standard Error) for Coupling PHD Bivariate Latent Change Score Model with Life Events and PHD.
| Parameter | Life Events b (SE) |
PHD b (SE) |
||
|---|---|---|---|---|
| Means: Level | 0.04(0.02) | 1.51(1.45) | ||
| Variances: Level | 0.01(0.01)** | −39.06(55.49) | ||
| Means: Slope | 0.05(0.12)** | −0.99(5.46) | ||
| Variances: Slope | 0.01(0.00)* | 477.07(219.47)* | ||
| Level w/slope | 0.01(0.00) | 140.89(71.67)* | ||
| Proportional change | −0.65(0.21)** | −1.50(0.26)*** | ||
| Constant change | =1 | =1 | ||
| Coupling coefficients | b (SE) | |||
| PHD → Δ LEs | 0.00(0.00) | |||
| LEs → Δ PHD | 115.97(51.85)* | |||
| Correlations | b (SE) | |||
| LevelLEs w/levelPHD | 0.31(0.40) | |||
| LevelLEs w/slopePHD | −1.16(0.93) | |||
| SlopeLEs w/levelPHD | 0.44(0.19)* | |||
| SlopeLEs w/slopePHD | 0.36(0.72) | |||
| Life Events | PHD | |||
| Covariates | Level | Slope | Level | Slope |
| Distal life events | 0.10(0.04)** | 0.10(0.04)** | -- | −11.41(8.74) |
| Baseline PHD | -- | -- | 0.05(0.03) | 0.11(0.06) |
| Prior tx | -- | -- | -- | 0.00(0.10) |
| Positive coping | -- | -- | -- | 4.92(4.31) |
| Negative coping | -- | -- | -- | 1.79(3.55) |
| Avoidance | -- | -- | -- | −3.06(2.85) |
| Seeking social | -- | -- | -- | −3.06(2.44) |
Note: Level = intercept; Slope = rate of change; LEs = life events; PHD = percent heavy drinking days; ‘--’= not estimated. Due to the transformation of the variables, parameter estimates cannot be interpreted as the raw data.
p<.05;
p<.01;
p≤.001.
3.2.2. Validation
There were fewer significant correlations between PHD and LEs scores in the validation sample (Supplemental Table 22). Cross-validation was conducted by fitting the optimal Coupling model obtained using the calibration sample to the data in the validation sample, resulting in good model fit (RMSEA = .072). This suggests that the findings obtained using the calibration sample were replicated with the validation sample.
4. Discussion
Findings revealed that the hypothesized model in which the bidirectional relationship between PHD and LEs was estimated was the optimal model and showed a good fit to the data. Nevertheless, the bidirectional associations between LEs and PHD were not statistically significant. Proximal LEs were a significant determinant of change in PHD, suggesting that the occurrence of LEs is associated with subsequent increases in drinking severity, though alcohol use severity did not predict changes in proximal LEs. The data also provided partial support for the hypothesis that distal LEs influence changes in both LEs and heavy alcohol use over time. Specifically, more distal LEs were associated with increases in the occurrence of negative LEs, not heavy alcohol use, suggesting that experiencing more negative LEs during a prior time may set the occasion for an individual’s experiencing more negative events during a later time. These findings were cross-validated.
An interpretation for the non-statistically significant bidirectional relationship between LEs and changes in alcohol use severity is that there may be other contributing factors that inform the dynamic relationship. The dynamic model of relapse (Witkiewitz and Marlatt, 2004) predicts that factors influencing alcohol use occur in conjunction with and in the context of other factors. It may be that the association between LEs and alcohol use is only relevant within the context of other concurrent post-treatment variables. For instance, ability to cope with LEs may alter the effect that they have on subsequent alcohol use. However, the decision to focus exclusively on the relationship between LEs and alcohol use in the context of baseline factors was based on the lack of empirical evidence that there is a reciprocal relationship between LEs and alcohol use. Thus, this study provides a first step to determining whether the experience of LEs fits within the heuristic provided by the dynamic model.
It also is possible that the specified models did not directly map on to the dynamic model of relapse, thereby contributing to the non-significant path from PHD to LEs in the optimal model. Most notably, lack of support for the hypotheses may have been influenced by the chosen time interval used in the models. In this study, proximal LEs were operationalized as those that occurred within a two-month timeframe preceding the predicted changes in alcohol use. This decision was based on previous research demonstrating that negative LEs can influence substance use outcomes for up to two months (Tate et. al., 2008) and to account for the relative infrequency of LEs. However, the influence of alcohol use on proximal LEs may follow a shorter time interval, though has not been previously empirically evaluated in a clinical sample. The two-month operationalization of proximal LEs may not be adequately sensitive in the context of these dynamic models and the theoretical conceptualization of proximal. There may also be considerable variability in the timing of the events, such that some could have occurred early in the two months while others occurred immediately preceding the subsequent two months. Calculating a LEs composite score from these differently timed events reduces the variability and would result in changing the potential impact that PHD may have had on LEs. Thus, given the nature of the data, a two-month interval provided the most substantive data and the highest sensitivity. Related to this, the absence of a significant association between distal LEs and heavy alcohol use may support prior research suggesting that negative LEs do not continue to exert their influence on alcohol use after several months.
The results of this study have both clinical and research implications. Based on the optimal model, this study provides initial justification for the further study of the LEs-alcohol use relationship as it is described in the dynamic model. In this initial investigation, negative LEs seem to be linked to alcohol use severity. This finding, along with the positive relationship observed between alcohol use severity and the rate of change in LEs, provide support for interventions that help to reduce heavy drinking episodes (e.g., harm reduction) and decrease negative reactions (i.e., substance use) to events (e.g., mindfulness based relapse prevention). Moreover, no previous study has examined the relationship among latent growth components of LEs and alcohol use. These findings provide justification for examining how these variables relate over time, as opposed to the more traditional approach of predicting a single future time point.
Lastly, this is the first study to directly examine the stability of findings related to the LEs-alcohol use relationship. Given the inconsistency of findings in previous research, the stability of results observed in this study provides additional justification for future research to continue to consider the LEs-alcohol use relationship within this conceptualization. BLCS models, in particular, can provide a flexible framework from which to test more complex and dynamic relationships.
A limitation that should be considered is that the original study for which the data were collected used a nested design, such that participants were nested in treatment programs and in different states. The present investigation did not incorporate the nested design in the analyses due to the level of complexity it would add to the BLCS models. Future studies using nested data could consider adding the hierarchal structure to the BLCS models, which would likely increase standard errors (Grimm, 2007).
In conclusion, this study’s use of dynamic modeling methods revealed new information on the relationship between negative LEs and heavy alcohol use over the course of one year post-alcohol treatment initiation. This study’s findings lay the groundwork for future research that can provide more complex, multi-factorial and sensitive tests of the dynamic model of relapse (Witkiewitz and Marlatt, 2004) that could serve as the empirical bases of more effective relapse prevention interventions.
Supplementary Material
Highlights.
Bivariate latent change score models tested the life event-alcohol use relationship
The optimal model reflected a bidirectional life event-alcohol use relationship
Negative life events were associated with increases in subsequent heavy drinking
However, heavy alcohol use was not associated with changes in negative life events
These findings were cross-validated using a comparable sample
Acknowledgments
Role of Funding Source
This work was performed in partial fulfillment of the requirements for the PhD degree of the first author under the supervision of the third author at Syracuse University. Preparation of this manuscript was supported in part by a grant from NIAAA (#2 K05 AA016928) awarded to Stephen A. Maisto, PhD.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Supplementary material can be found by accessing the online version of this paper at http://dx.doi.org and by entering doi:...
Contributors
Marketa Krenek, Ph.D. designed the study, conducted the analyses, and wrote the first draft of the manuscript. Mark A. Prince, Ph.D. and Stephen A Maisto, Ph.D. provided significant and valuable contributions to study design, conducting of analyses, and editing of the manuscript. All authors contributed to and approved the final manuscript.
Conflict of Interest
No conflict declared
References
- American Psychiatric Association. Diagnostic and statistical manual of mental disorders: DSM-5. American Psychiatric Association; Washington, D.C: 2013. [Google Scholar]
- Bentler PM. Multivariate analysis with latent variables: Causal modeling. Annu. Rev. Psychol. 1980;31:419–456. doi: 10.1146/annurev.ps.31.020180.002223. [DOI] [Google Scholar]
- Connors GJ, Maisto SA, Zywiak WH. Understanding relapse in the broader context of post-treatment functioning. Addiction. 1996;91:S173–S189. [PubMed] [Google Scholar]
- Dohrenwend BP. Inventorying stressful life events as risk factors for psychopathology: Toward resolution of the problem of intracategory variability. Psychol. Bull. 2006;132:477–495. doi: 10.1037/0033-2909.132.3.477. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enders CK. The impact of nonnormality on full information maximum-likelihood estimation for structural equation models with missing data. Psychol. Methods. 2001;6:352–370. doi: 10.1037/1082-989X.6.4.352. [DOI] [PubMed] [Google Scholar]
- Grant I, Sweetwood HL, Yager J, Gerst M. Quality of LEs in relation to psychiatric symptoms. Arch. Gen. Psychiatry. 1981;38:335–339. doi: 10.1001/archpsyc.1981.01780280103012. [DOI] [PubMed] [Google Scholar]
- Grimm K. A longitudinal dynamic analysis of the impacts of reading on mathematical ability in children and adolescents. Diss. Abstr. Int. 2007;67:5442. [Google Scholar]
- Grimm KJ, An Y, McArdle JJ, Zonderman AB, Resnick SM. Recent changes leading to subsequent changes: Extensions of multivariate latent difference score models. Struct. Equ. Modeling. 2012;19:268–292. doi: 10.1080/10705511.2012.659627. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hart KE, Fazaa N. Life stress events and alcohol misuse: Distinguishing contributing stress events from consequential stress events. Subst. Use Misuse. 2004;39:1319–1339. doi: 10.1081/JA-120039390. [DOI] [PubMed] [Google Scholar]
- Hedeker D, Mermelstein RJ. Methods for analyzing longitudinal data on relapse: Application of random-effects regression models in relapse research. Addiction. 1996;91:S211–S229. [PubMed] [Google Scholar]
- Holmes TH, Rahe RH. The Social Readjustment Rating Scale. J. Psychosom. Res. 1967;11:213–218. doi: 10.1016/0022-3999(67)90010-4. [DOI] [PubMed] [Google Scholar]
- Hu L, Bentler PM. Cutoff criteria for fit indexes in covariance structure analysis: Conventional criteria versus new alternatives. Struct. Equ. Modeling. 1999;6:1–55. doi: 10.1080/10705519909540118. [DOI] [Google Scholar]
- Krenek M, Maisto SA. Life events and treatment outcomes among individuals with substance use disorders: A narrative review. Clin. Psychol. Rev. 2013;33:470–483. doi: 10.1016/j.cpr.2013.01.012. [DOI] [PubMed] [Google Scholar]
- Litman GK, Stapleton J, Oppenheim AN, Peleg M. An instrument for measuring coping behaviors in hospitalized alcoholics: Implications for relapse prevention and treatment. Br. J. Addict. 1983;78:269–276. doi: 10.1111/j.1360-0443.1983.tb02511.x. [DOI] [PubMed] [Google Scholar]
- Lowman C, Allen J, Stout RL, The Relapse Research Group Replication and extension of Marlatt’s taxonomy of relapse precipitants: Overview of procedures and results. Addiction. 1996;91(Suppl. 1):51–71. [PubMed] [Google Scholar]
- MacCallum RC, Browne MW, Sugawara HM. Power analysis and determination of sample size for covariance structure modeling. Psychol. Methods. 1996;1:130–149. doi: 10.1037/1082-989X.1.2.130. [DOI] [Google Scholar]
- MacCallum RC, Roznowski M, Mar CM, Reith JV. Alternative strategies for cross-validation of covariance structure models. Multivariate Behav. Res. 1994;29:1–32. doi: 10.1207/s15327906mbr2901_1. [DOI] [PubMed] [Google Scholar]
- Maisto SA, Zywiak WH, Connors GA. Course of functioning 1 year following admission for treatment of alcohol use disorders. Addict. Behav. 2006;31:69–79. doi: 10.1016/j.addbeh.2005.04.008. [DOI] [PubMed] [Google Scholar]
- McArdle JJ. A latent difference score approach to longitudinal dynamic structural analysis. In: Cudeck R, Du Toit S, Sörbom D, editors. Structural equation modeling: Present and future. A Festschrift in honor of Karl Jöreskog. Scientific Software International; Lincolnwood, IL: 2001. pp. 341–380. [Google Scholar]
- McArdle JJ. Latent variable modeling of differences and changes with longitudinal data. Annu. Rev. Psychol. 2009;60:577–605. doi: 10.1146/annurev.psych.60.110707.163612. [DOI] [PubMed] [Google Scholar]
- McArdle JJ, Grimm KJ. Five steps in latent curve and latent change score modeling with longitudinal data. In: von Montfort K, editor. Longitudinal research with latent variables. Springer-Verlag; Berlin: 2010. pp. 245–273. [Google Scholar]
- Miller WR. Form 90: A Structured Assessment Interview for Drinking and Related Behaviors: Test manual (Vol. 5, Project MATCH monograph series) National Institute of Alcohol Abuse and Alcoholism; Bethesda, MD: 1996. [Google Scholar]
- Miller WR, Westerberg VS, Harris RJ, Tonigan J. Section IIB. extensions of relapse predictors beyond high-risk situations: What predicts relapse? Prospective testing of antecedent models. Addiction. 1996;91:S155–S171. [PubMed] [Google Scholar]
- Muthén B, Asparouhov T. Using Mplus Monte Carlo simulations in practice: A note on non-normal missing data in latent variable models. Version 2. 2002 Mar 22; 2002. [Google Scholar]
- O'Doherty F, Davies JB. Life events and addiction: A critical review. Br. J. Addict. 1987;82:127–137. doi: 10.1111/j.1360-0443.1987.tb01451.x. [DOI] [PubMed] [Google Scholar]
- Paykel ES. The interview for recent life events. Psychol. Med. 1997;27:301–310. doi: 10.1017/S0033291796004424. [DOI] [PubMed] [Google Scholar]
- Preacher KJ, Coffman DL. Computing power and minimum sample size for RMSEA [Computer software] 2006 May; Available from http://quantpsy.org/
- Sarason IG, Johnson JH, Siegel JM. Assessing the impact of life changes: Development of the life experiences survey. J. Consult. Clin. Psychol. 1978;46:932–946. doi: 10.1037/0022-006X.46.5.932. [DOI] [PubMed] [Google Scholar]
- Satorra A, Bentler PM. Ensuring positiveness of the scaled difference chi-square test statistic. Psychometrika. 2010;75:243–248. doi: 10.1007/s11336-009-9135-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schafer JL, Graham JW. Missing data: Our view of the state of the art. Psychol. Methods. 2002;7:147–177. doi: 10.1037/1082-989X.7.2.147. [DOI] [PubMed] [Google Scholar]
- Tate SR, Brown SA, Glasner SV, Unrod M, McQuaid JR. Chronic life stress, acute stress events, and substance availability in relapse. Addict. Res. Theory. 2006;14:303–322. doi: 10.1080/16066350500262817. [DOI] [Google Scholar]
- Tate SR, McQuaid JR, Brown SA. Characteristics of life stressors predictive of substance treatment outcomes. J. Subst. Abuse Treat. 2005;29:107–115. doi: 10.1016/j.jsat.2005.05.003. [DOI] [PubMed] [Google Scholar]
- Tate SR, Wu J, McQuaid JR, Cummins K, Shriver C, Krenek M, Brown SA. Comorbidity of substance dependence and depression: Role of life stress and self-efficacy in sustaining abstinence. Psychol. Addict. Behav. 2008;22:47–57. doi: 10.1037/0893-164X.22.1.47. [DOI] [PubMed] [Google Scholar]
- Witkiewitz K. Predictors of heavy drinking during and following treatment. Psychol. Addict. Behav. 2011;25:426–438. doi: 10.1037/a0022889. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Witkiewitz K, Marlatt GA. Relapse prevention for alcohol and drug problems: That was Zen, this is Tao. Am. Psychol. 2004;59:224–235. doi: 10.1037/0003-066X.59.4.224. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.