Connecting within and between-hosts dynamics in the influenza infection-staged epidemiological models with behavior change

Abstract

Influenza viruses are a major public health problem worldwide. Although influenza has been extensively researched, there are still many aspects that are not fully understood such as the effects of within and between-hosts dynamics and their impact on behavior change. Here, we develop mathematical models with multiple infection stages and estimate parameters based on within-host data to investigate the impact of behavior change on influenza dynamics. We divide the infected population into three and four groups based on the age of the infection, which corresponds to viral load shedding. We consider within-host data on viral shedding to estimate the length and force of infection of the different infectivity stages. Our results show that behavior changes, due to exogenous events (e.g., media coverage) and disease symptoms, are effective in delaying and lowering an epidemic peak. We show that the dynamics of viral shedding and symptoms, during the infection, are key features when considering epidemic prevention strategies. This study improves our understanding of the spread of influenza virus infection in the population and provides information about the impact of emergent behavior and its connection to the within and between-hosts dynamics.

1. INTRODUCTION

Even with the presence of vaccines and antiviral medication, seasonal and influenza pandemics lead to approximately 3 to 5 million cases of severe illness and 250,000 to 500,000 deaths worldwide.⁽¹⁾ There are various protective measures that can be used to reduce the spread of the influenza including treatment of infectives with antiviral drugs, vaccination, and social-distancing measures such as quarantine, school-closures, and isolation.^{(2, 3)} However, these methods, in particular, antiviral drugs and early diagnosis of infectives, are associated with a high cost^{(4, 5)} and vaccines may not be readily available.⁽⁶⁾

Other alternatives to reduce the likelihood of infection include limiting close contact with other individuals, staying home when sick, covering mouth and nose when coughing or sneezing, washing hands, and other protective measures.⁽⁷⁾ A review⁽⁸⁾ on hands hygiene in preventing transmission of severe acute respiratory syndrome (SARS) suggests that hand washing is an effective measure against disease transmission. During the 2003 SARS epidemic, residents of Hong Kong rapidly employed individual preventive strategies, which might have contributed to controlling the public health crisis.⁽⁹⁾ Several studies have analyzed the use of facemasks in preventing the spread of disease and have showed that they can be effective in reducing transmission.^{(10, 11)}

Furthermore, a survey conducted in the spring of 2009 about the novel influenza A (H1N1), demonstrated that 16–20% of Americans refrained from crowded places and 20% avoided contact with individuals not in their household⁽¹²⁾ (for additional information see Table I in Ref. [12]). Changes in human behavior are thought to be one of the major contributors to reducing the spread of disease, especially in the absence of pharmaceutical interventions.^(13–17)

There are many factors that can influence an individual to alter his/her behavior including demographic and psychological factors.⁽¹⁸⁾ Infected individuals may reduce the number of contacts with others due to onset of disease symptoms.⁽³⁾ Individuals who are not infected or are in asymptomatic stages of an infection may take protective measures due to media risk communication,⁽¹⁹⁾ for example, they may avoid crowded places and wash their hands more often, to lower the risk of becoming infected. Reasons affecting behavior change of individuals in asymptomatic and symptomatic infection stages differ, which might significantly impact the disease dynamics and this is the reason why we distinguish between them in our study.

Influenza infection is typically accompanied by severe symptoms such as fever, cough, sore throat, and muscle or body aches.⁽²⁰⁾ In addition, the infection stimulates the immune system leading to additional symptoms such as mucosal inflammation.^(21–23) In particular, in Ref. [23] it was shown that viral shedding correlates with the rise of local and systemic symptoms. Similarly, the levels in nasal lavage fluids were found to be directly associated with viral titers, temperature, mucus production, and symptoms scores in volunteers experimentally infected with influenza A/Texas/36/91 (H1N1).⁽²¹⁾ In another study, levels of cytokines and chemokines were characterized and were found to increase during influenza infection and correlate with symptoms.⁽²²⁾ In a review article on influenza infection, it was concluded that the total symptoms scores and viral shedding curves exhibited analogous dynamics (see Figure 5 in Ref. [24]). Moreover, the infectivity of an individual changes with the age of infection (i.e., the time since the individual was infected), as it is proportional to the degree of viral shedding.⁽²⁵⁾ Based on these studies, here we divided the infected population into groups according to the age of the infection, which is proportional to viral load shedding.

Changes in human behavior, due to disease symptoms, may impact the transmission rate, modeling assumptions for forecasting disease dynamics, and public health recommendations. Omitting spontaneous changes in human behavior when modeling the spread of infectious diseases might lead to an overestimation of the number of cases and the secondary rates of infection.⁽²⁶⁾ Here, we consider potential behavior changes possibly due to the impact of information in the media about the severity of the disease (e.g., a deadly epidemic might lead to drastic changes in human behavior, whereas a mild epidemic might lead to minimal changes in behavior) and due to the severity of symptoms.

Public health strategies during an influenza epidemic are influenced by the previous occurrences of epidemics. In addition to those experiences, mathematical models are needed to test prevention strategies based on changes in mobility and contact patterns, viral evolution, and technological and medical advances. Mathematical models are influential for preparing for disease outbreaks^{(2, 27–34)} and modeling of real-time epidemics.^(35–39) Moreover, a number of within-host mathematical models have given insight about the dynamics of influenza virus infection and immune responses.^(40–48) There are number of models considering the impact of changes in human behavior^{(15, 16, 49–51)} (also see review Ref. [52]). However, there are few models that link information obtained from within-host modeling to the epidemiological model parameters.^{(43, 53–56)} None of the models mentioned have investigated the impact of changes in behavior and infectivity based on within-host data.

In this study, we design mathematical models with multiple infection stages and estimated parameters based on within-host data to investigate the impact of the behavior change on influenza dynamics. We show that the viral shedding dynamics and symptoms during the infection are key features when considering the adoption of precautionary measures during an epidemic.

2. MATERIALS AND METHODS

2.1. Mathematical Model and Parameters

We develop a model to study the dynamics of influenza infection with parameters dependent on the within-host data profiles. The model consists of susceptible (S), infected (I), and recovered (R) individuals. We assume that the infected population is divided into n groups, i.e., $I_j^{N,B}$ where the subscript j = 1, …, n is based on time since infection, that is the age of the infection, which is directly related to viral load shedding. An infected individual progresses from $I_i^{N,B}$ to $I_{i+1}^{N,B}$ after 1/p_i days, i.e., the average rate of progression is p_i, where i = 1, …, n − 1. Individuals recover at the rate p_n and gain permanent immunity to that circulating strain of influenza. The infection rate for each stage is denoted by β_i, where i = 1, …, n.

In the model, susceptible individuals can change their behavior based on the perceived risk of infection, which might be due to amount of information available through several media sources on emerging influenza epidemics. The fraction of the population that changes its behavior immediately after becoming infected is represented by ρ. Also, infected individuals are likely to change their behavior due to the severity of the disease symptoms. The fraction of the population that alters its behavior at the end of the initial stage, at the onset of symptoms, and at the end of the most symptomatic stage are denoted by μ and ω, respectively. In our model, superscripts B and N represent the individuals that change their behavior and individuals that do not alter their behavior, respectively. Individuals that are taking preventive measures are assumed to have a reduced force of infection by a factor of η.

For simplicity and in agreement with the available within-host data, we consider models with three and four stages, i.e., n = 3 or 4 (further discussed below). The mathematical model for the three-stage infection (n = 3) with behavior changes is given by the following system of equations:

$$\mathit{\text{dS}}/\mathit{\text{dt}}=-S({\beta }_1{I}_1^N+{\beta }_2{I}_2^N+{\beta }_3{I}_3^N+(1-\eta )({\beta }_1{I}_1^B+{\beta }_2{I}_2^B+{\beta }_3{I}_3^B))$$

$${\mathit{\text{dI}}}_1^B/\mathit{\text{dt}}=\rho S({\beta }_1{I}_1^N+{\beta }_2{I}_2^N+{\beta }_3{I}_3^N+(1-\eta )({\beta }_1{I}_1^B+{\beta }_2{I}_2^B+{\beta }_3{I}_3^B))-p_1{I}_1^B$$

$${\mathit{\text{dI}}}_2^B/\mathit{\text{dt}}=p_1{I}_1^B+\mu p_1{I}_1^N-p_2{I}_2^B$$

$${\mathit{\text{dI}}}_3^B/\mathit{\text{dt}}=p_2{I}_2^B+\omega p_2{I}_2^N-p_3{I}_3^B$$ (1)

$${\mathit{\text{dI}}}_1^N/\mathit{\text{dt}}=(1-\rho )S({\beta }_1{I}_1^N+{\beta }_2{I}_2^N+{\beta }_3{I}_3^N+(1-\eta )({\beta }_1{I}_1^B+{\beta }_2{I}_2^B+{\beta }_3{I}_3^B))-p_1{I}_1^N$$

$${\mathit{\text{dI}}}_2^N/\mathit{\text{dt}}=(1-\mu )p_1{I}_1^N-p_2{I}_2^N$$

$${\mathit{\text{dI}}}_3^N/\mathit{\text{dt}}=(1-\omega )p_2{I}_2^N-p_3{I}_3^N$$

$$\mathit{\text{dR}}/\mathit{\text{dt}}=p_3{I}_3^B+p_3{I}_3^N$$

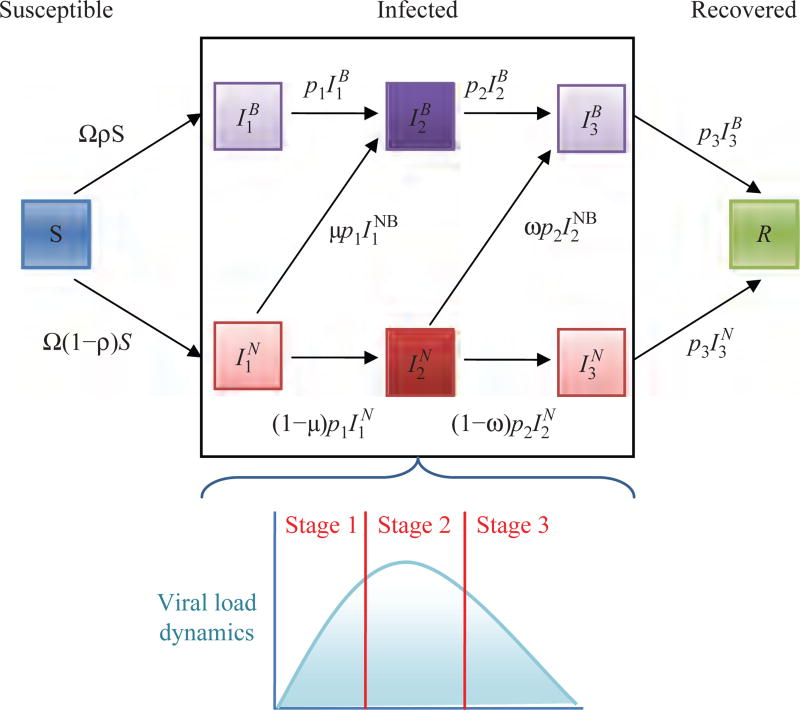
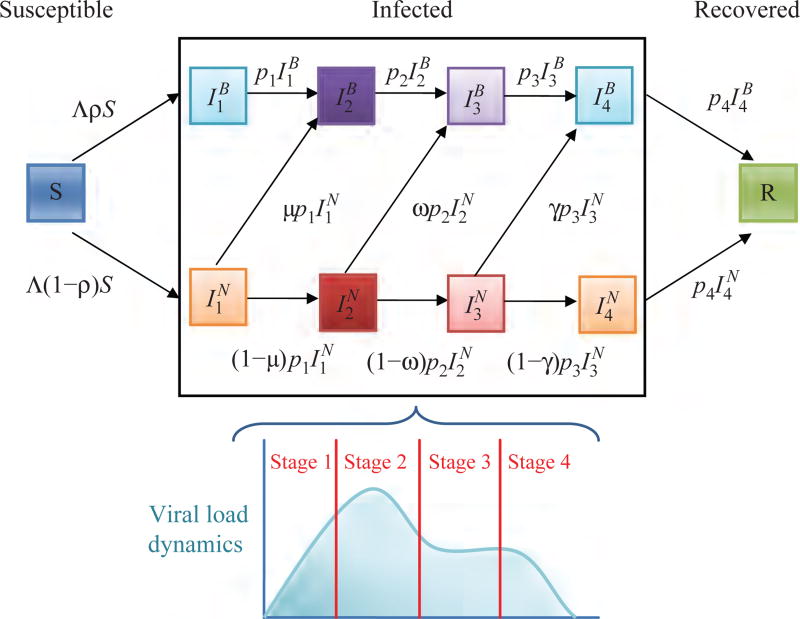
A mathematical model for the four-stage infection with behavior changes can be easily extended from the three-stage model given by Eq. (1), by adding additional groups of infectives, $I_4^{N,B}$ and the fraction of the population that alters its behavior when moving to the last stage of the disease, γ. Schematic diagrams of the three-stage and four-stage model are shown in Figures 1 and 2, respectively.

Fig. 1.

Schematic illustration of the three-stage model given by Eq. (1), where $\mathrm{\Omega }={\beta }_1{I}_1^N+{\beta }_2{I}_2^N+{\beta }_3{I}_3^N+(1-\eta )({\beta }_1{I}_1^B+{\beta }_2{I}_2^B+{\beta }_3{I}_3^B)$ and the superscripts B and N represent individuals that changed their behavior and individuals that did not change their behavior, respectively.

Fig. 2.

Schematic illustration of the four-stage model given by extending Eq. (1), where $\mathrm{\Lambda }={\beta }_1{I}_1^N+{\beta }_2{I}_2^N+{\beta }_3{I}_3^N+{\beta }_4{I}_4^N+(1-\eta )({\beta }_1{I}_1^B+{\beta }_2{I}_2^B+{\beta }_3{I}_3^B+{\beta }_4{I}_4^B)$ and the superscripts B and N represent individuals that changed their behavior and individuals that did not change their behavior, respectively.

Following Ref. [25], we assumed that the population is fully susceptible since we are interested in analyzing an outbreak; however, this assumption may be changed by lowering the initial susceptible population by a desired factor. We assume that the fraction of the population that adjusts its behavior (ρ, μ, ω, and γ) is between 0 and 1; where 0 means no one changed their behavior and 1 means that the whole population changed their behavior. Similarly, the reduction in infection rate, due to the behavior change (η), is assumed to be between 0 and 1; where 0 represents no reduction in the number of contacts and 1 stands for complete isolation. Variables and parameters of three-stage and four-stage models are summarized in Tables I and II.

Table I.

Variables of the three and four-stage models.

Variable	Definition
S	Number of susceptible individuals
$I_j^N$	Number of infected individuals not changing the behavior at the infection-stage j for j = 1, 2, and 3 for the three-stage model and j = 1, 2, 3, and 4 for the four-stage model
$I_j^B$	Number of infected individuals changing the behavior at the infection-stage j for j = 1, 2, and 3 for the three-stage model and j = 1, 2, 3, and 4 for the four-stage model
R	Number of recovered individuals

Table II.

Parameter definitions and values.

Symbol	Definition	Unit	Baseline	Range	Reference
N	Total population	People	1 million	0–300 million	[11]
1/N	Initially infected fraction of the population	1	0.00001	0–1	[11]
			initial value:
			$I_1^{NB}=10\text{ people}$
βj	Infection rate	People−1 Day−1	For three-stage:	0–1	[11, 58, 63, 64]
			β2 = 0.23 × 10−6		See text
			β1 = β3 = 0.4 × β2
			For four-stage:
			${\beta }_2^{\ast }=1.25\times {\beta }_2$
			${\beta }_1^{\ast }={\beta }_4^{\ast }=0.4\times {\beta }_2$
			${\beta }_3^{\ast }=0.75\times {\beta }_2$
1/pj	Duration of the stage j	Days	1/p1 = 1	0–7	See text
			For three-stage:
			1/p2 = 4, 1/p3 = 2
			For four-stage:
			1/p2 = 1/p3 = 1/p4 = 2
ρ, μ, ω, γ	Fraction of the population that changed the behavior immediately after the infection, or during stages 1, 2, or 3, respectively	1	0.2	0–1	See text
η	Reduction in infection rate due to the behavior change	1	0.2	0–1	See text

2.2. Estimation of Within-Host Parameters

In order to obtain a biologically realistic relation of viral load to symptoms and infectivity, we considered the data published in Ref. [41]. Further details about the data and the design of the experiment can be found in the original manuscript;⁽⁵⁷⁾ in short, the study consists of daily nasal washes of six volunteers injected with 10^4.2TCID₅₀ of cloned wild-type influenza A/Hong Kong/123/77 (H1N1). We assumed that the infectivity and symptoms vary with the age of infection, as they are proportional to the amount of viral shedding.

We consider a profile of the viral load based on Ref. [41] to estimate the length of the different infectivity stages. For the three-stage model, we divide the viral load profile into three stages with lengths 1, 4, and 2 days, respectively (Fig. 1). The first phase is the stage before the viral peak, the second stage contains the viral peak, and the third stage is the continuation of the viral load decline. To obtain the infectivity at each stage, we take the second phase of the three-stage model as a baseline infection rate (β = β₂) and express the infection rates in the remaining stages in terms of β, which results in the first and third phase to have the infection rate of β₁ = β₃ = 0.4 × β (see Fig. 1 and Table II). The resulting infectivity profiles are similar to the baseline values used in Ref. [25] taken from Ref. [58].

Following the bimodal behavior of viral load of the data, the mathematical model presented in Ref. [48], and studies of influenza virus infection,^{(59, 60)} we partitioned the profile of viral load into four stages with lengths 1, 2, 2, and 2 days, respectively for the four-stage model (Fig. 2). The first phase is the stage before the viral peak, the second stage contains the viral peak, the third stage is the viral plateau or a second minor peak, and the fourth is the viral load decline. Similar to the three-stage model, we estimate the infection rates as follows: β₂ = 1.25 × β, β₁ = β₄ = 0.4 × β, and β₃ = 0.75 × β (see Fig. 2 and Table II).

2.3. Basic Reproductive Ratio

The basic reproductive ratio (ℜ₀) is the average number of new infections caused by a single case in a fully susceptible population. Typically, if ℜ₀ > 1 then an epidemic will arise and if ℜ ₀ < 1 then an epidemic will not occur.

We used the Next Generation Method to find ℜ₀.⁽⁶¹⁾ We let F be the matrix of new infections and V the matrix of transfers between groups evaluated at the infection-free steady state (S₀ = N and $I_{1,2,3}^{B,N}=R=0$). ℜ₀ is given by the dominant eigenvalue of FV⁻¹ evaluated at the infection-free steady state.⁽⁶¹⁾

$$F=\left[\begin{array}{cccccc}\hfill \rho (1-\eta ){\beta }_{1}N\hfill & \hfill \rho (1-\eta ){\beta }_{2}N\hfill & \hfill \rho (1-\eta ){\beta }_{3}N\hfill & \hfill \rho {\beta }_{1}N\hfill & \hfill \rho {\beta }_{2}N\hfill & \hfill \rho {\beta }_{3}N\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill (1-\rho )(1-\eta ){\beta }_{1}N\hfill & \hfill (1-\rho )(1-\eta ){\beta }_{2}N\hfill & \hfill (1-\rho )(1-\eta ){\beta }_{3}N\hfill & \hfill (1-\rho ){\beta }_{1}N\hfill & \hfill (1-\rho ){\beta }_{2}N\hfill & \hfill (1-\rho ){\beta }_{3}N\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]\text{and }V=\left[\begin{array}{cccccc}{p}_1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ -p_1\hfill & \hfill p_2\hfill & \hfill 0\hfill & \hfill -\mu p_1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ 0\hfill & \hfill -p_2\hfill & \hfill p_3\hfill & \hfill 0\hfill & \hfill -\omega p_2\hfill & \hfill 0\hfill \\ 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill p_1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -(1-\mu )p_1\hfill & \hfill p_2\hfill & \hfill 0\hfill \\ 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill -(1-\omega )p_2\hfill & \hfill p_3\hfill \end{array}\right]$$

For the three-stage model, given by Eq. (1), the basic reproductive ratio (ℜ₀) is given by the expression:

$${\Re }_0=N[\frac{{\beta }_1}{p_1}(1-\eta \rho )+\frac{{\beta }_2}{p_2}[1-\eta (\mu +\rho (1-\mu ))]+\frac{{\beta }_3}{p_3}[1-\eta (\mu (1-\rho )+\omega (1-\mu )+\rho (1-\omega )+\rho \omega \mu )]]$$ (2)

The basic reproductive ratio for the four-stage model can be similarly calculated using the Next Generation Method⁽⁶¹⁾ and it is given by

$${\Re }_0^{\ast }={\Re }_0+N\frac{{\beta }_4}{p_4}[1-\eta [\omega (1-\rho )(1-\mu )+\gamma (1-\omega )(1-\rho )+\mu (1-\gamma )+\rho (1-\mu )+\gamma \mu (\omega +\rho (1-\omega ))]]$$ (3)

Notice that when there is no behavior change, the basic reproductive number for the three-staged model can be expressed as ${\Re }_0^{\ast \ast }=N[{\beta }_1/p_1+{\beta }_2/p_2+{\beta }_3/p_3]$.

In the Results section, we discuss the dependence of the basic reproductive ratio on the model parameters.

3. RESULTS

3.1. Impact of Behavior Change on Basic Reproductive Ratio

The basic reproductive ratios for three and four-stage models, ℜ₀ and ${\Re }_0^{\ast }$, given by Eqs. (2) and (3), respectively, depend on the fraction of the population that changed their behavior immediately after the infection, during stages 1, 2, and 3 (ρ, μ, ω, and γ, respectively); the reduction in infection rate due to the behavior change (η), and other parameters. It also follows that the basic reproductive ratio also depends on the infection rate, which changes based on the number of contacts and transmissibility of the influenza strain. In Table III we tested the impact of ρ, μ, ω, and γ on the basic reproductive ratios for three and four-stage models.

Table III.

Impact of the fraction of the population that changed their behavior immediately after the infection, or during stages 1 or 2, (ρ, μ, and ω), respectively, on the basic reproductive ratio of three and four-stage models, ℜ₀ and ${\Re }_0^{\ast }$, respectively.

Parameter variations	ℜ0 for the three-stage model		${\Re }_0^{\ast }$ for the four-stage model
η = 20%	Baseline*	Special case**	Baseline*	Special case**
ρ = μ = ω = γ =0%	1.196	1.426	1.196	1.426
ρ = μ = ω = γ =5%	1.172	1.397	1.167	1.391
ρ = μ = ω = γ =10%	1.149	1.370	1.141	1.358
ρ = μ = ω = γ =20%	1.108	1.322	1.094	1.302
ρ = μ = γ =0%, ω =20%	1.189	1.419	1.175	1.396
μ = ω = γ =0%, ω=20%	1.148	1.369	1.148	1.369
ρ = ω = γ =0%, ρ =20%	1.152	1.373	1.152	1.373
ρ = μ = ω =0%, γ =20%	–	–	1.189	1.419
η = 50%	Baseline*	Special case**	Baseline*	Special case**
ρ = μ = ω = γ =5%	1.136	1.355	1.124	1.228
ρ = μ = ω = γ =10%	1.079	1.287	1.058	1.257
ρ = μ = ω = γ =20%	0.976	1.165	0.945	1.119
ρ = μ = γ =0%, ω =20%	1.178	1.408	1.143	1.350
μ = ω = γ =0%, ρ=20%	1.076	1.283	1.076	1.283
ρ = ω = γ =0%, μ =20%	1.086	1.293	1.086	1.293
ρ = μ = ω =0%, γ =20%	–	–	1.178	1.408

Notes:

^*Parameters given in Table II.

^**In the special case: for the Three-Stage Model we take the following infection rates: 0.4 × β₂, 1.25 × β₂, 0.4 × β₂ for stages 1, 2, and 3, respectively, and for the Four-Stage Model we take: 0.4 × β₂, 1.25 × β₂, 1.25 × β₂, 0.4 × β₂ for stages 1, 2, 3, and 4, respectively. The rest of the parameters are baseline stated in Table II.

We compute the basic reproductive ratio for the baseline (parameter values listed in Table II) and for a special case (parameter values listed under Table III) for each of the models. In the baseline case, ℜ₀ and ${\Re }_0^{\ast }$ range between 1.0–1.2 (Table III) for various scenarios when 0–20% of individuals altered their behavior. In the special case, infection rates are higher, resulting in a greater basic reproductive number; ℜ₀ and ${\Re }_0^{\ast }$ range from 1.2 to 1.4. In both of these cases, the basic reproductive ratios for both models are within the ranges presented in Ref. [62].

We conclude that ${\Re }_0^{\ast }={\Re }_0$ has the highest value when there is no behavior change (Table III), which means that the transmission of the disease is the fastest. In contrast, as more people alter their behavior by reducing number of contacts and following CDC recommendations, the lower the basic reproductive ratio (Table III). For instance, if 20% of individuals in all stages change their behavior, this results in significantly reduced values of ℜ₀ and ${\Re }_0^{\ast }$. An important observation from Table III is that when 20% of individuals alter their behavior for the duration of the disease, immediately after the infection or at the end of the first stage of an infection, the results show a lower ℜ₀ and ${\Re }_0^{\ast }$, than when the same percentage of individuals adjust their daily routine at the later infection stages.

Moreover, the basic reproductive ratio for the three and four-stage models, ℜ₀ and ${\Re }_0^{\ast }$, are given by Eqs. (2) and (3), respectively, depend on p₂ (1/p₂ is the length of the most symptomatic and infectious phase). In the three-stage model, the most symptomatic phase is assumed to be four days and for the four-stage model it is taken to be two days. Hence, for the range of model parameters (Table II), we obtain ${\Re }_0^{\ast }\le {\Re }_0$ (Table III).

3.2. Sustained Behavior Change Due to Media and Upon the Onset of Symptoms Greatly Influences the Spread of Disease

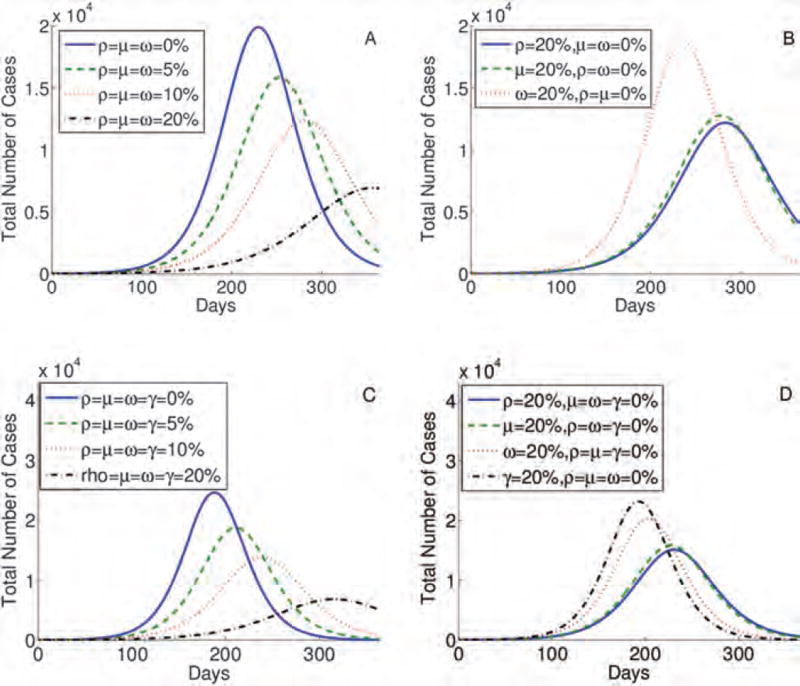
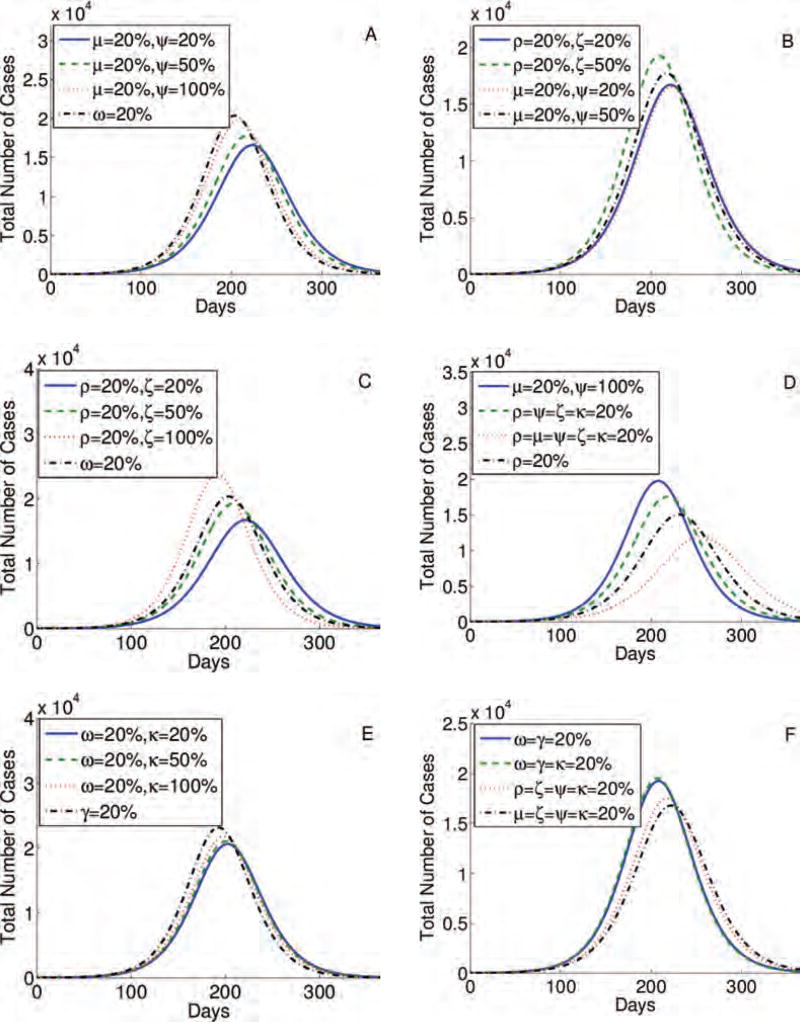
The highest epidemic peak (approximately 2 × 10⁴ cases) is obtained when individuals do not change their behavior (case ρ = μ = ω = 0% in Fig. 3(A)). When 20% of individuals alter their behavior in all stages (ρ = μ = ω = 20% in Fig. 3(A)), the peak is the lowest and the epidemic is delayed the longest, which can give time to develop a vaccine and other preventive strategies. Contour plots presented in Figures 4(A)–(F) show that the percentage of individuals altering their behavior immediately after the infection (ρ), at the end of the first stage, and at the onset of symptoms, (μ). The simulations show that these changes result in a lower epidemic peak than the one obtained by the same percentage of individuals changing their routines if they are implemented in the last stage of infection (ω). In particular, 20% of individuals altering their behavior immediately upon infection or at the onset of symptoms reduce the peak by approximately half (Fig. 3(B)). To conclude, in Figures 3 and 4, we observe that prolonged changes in behavior in these early stages of the infection are more effective than adjustments in daily routine during the last phase of an infection. Results are similar for the four-stage model (Figs. 3(C) and (D)).

Fig. 3.

Simulations for the three-stage (A) and (B) and four-stage (C) and (D) models, testing the impact of the sustained behavior change immediately after the infection, during stages 1, 2, and 3 (ρ, μ, ω, and γ) respectively. The higher the percentage of individuals following CDC recommendations the lower and more delayed epidemic peak (A) and (C). Also, the earlier the behavior is changed and sustained the lower and more delayed epidemic peak (B) and (D).

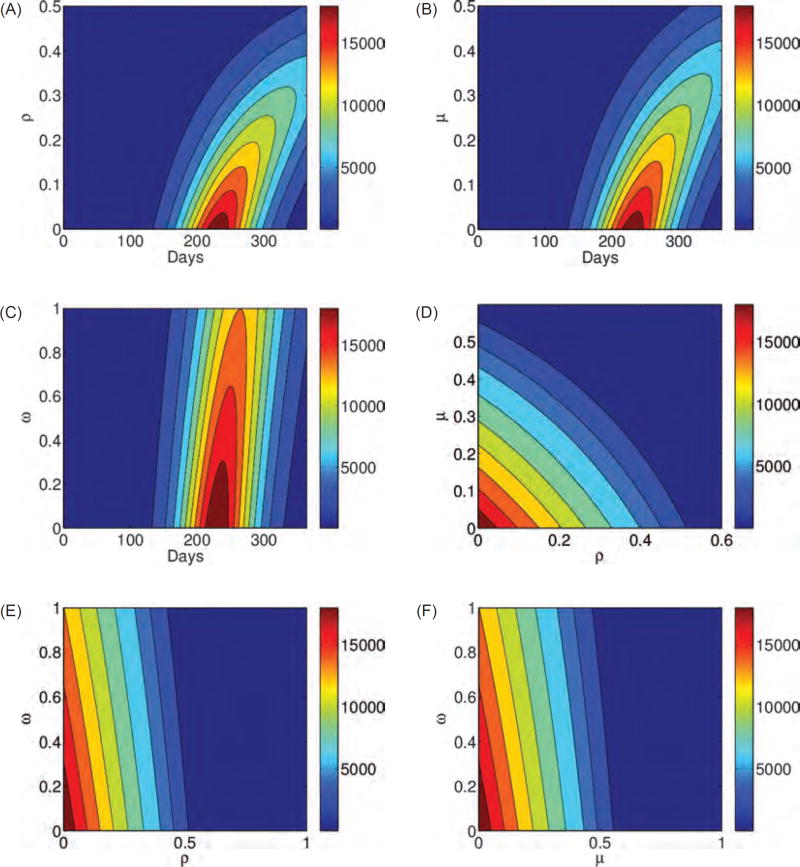
Fig. 4.

Contour plots A, B, and C of the three-stage model, given by Eq. (1), illustrate the total number of cases as a function of the fraction of the population that changed the behavior immediately after the infection, or during stages 1 or 2, (ρ, μ, and ω), respectively, and sustained these alteration in their daily routine. Contour plots D, E, and F show the peak of the total number of cases as a function of ρ and μ, ρ and ω, ω and μ, respectively. The higher the percentage of individuals following CDC recommendations and the earlier this preventive behavior is employed and sustained the lower and more delayed epidemic peak. Results are similar for the four-stage model.

3.3. Interrupted Behavior Change

We also varied the three and four-stage models by including a reverse change of behavior of infected individuals, who decide to no longer follow CDC recommendations on disease prevention methods (Figs. 5 and 6). The fraction of the population that goes back to the pre-infection daily routine while being in the first stage of the infection, at the onset of symptoms, is denoted by ξ. Similarly, individuals reversing their behavior at the end of the second and third stage of the infection (for the four-stage model) are given by ψ and κ, respectively. These scenarios are important because individuals either working or attending school are only able to take a few days off, which may be insufficiently long to fully recover from influenza infection and they may have to choose which days to miss.

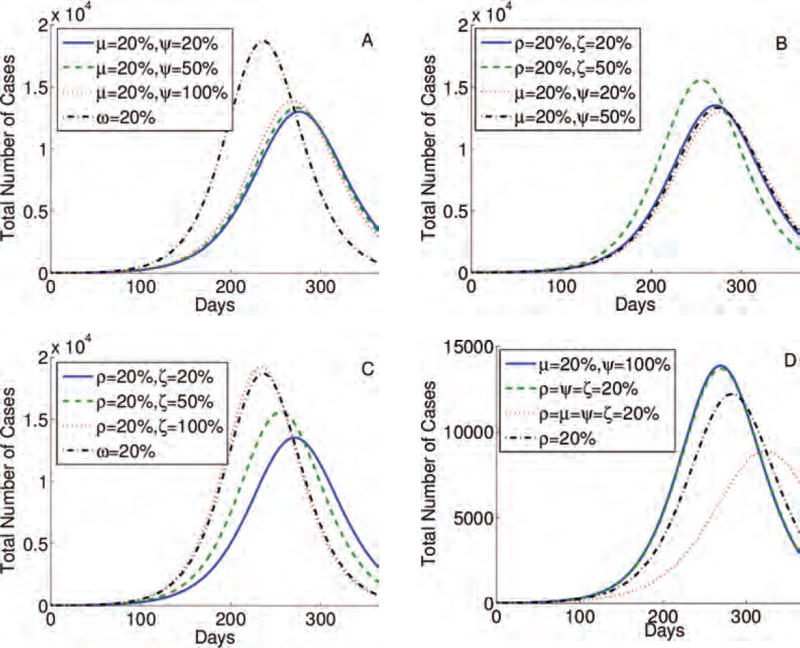
Fig. 5.

Simulations for the three-stage model, given by Eq. (1), testing the impact of the behavior change immediately after the infection, or during stages 1 or 2, (ρ, μ, and ω), respectively, which is interrupted during stages 1 or 2 (ξ and ψ), respectively. We compared variations of behavior changes in different infection stages and their reversions.

Fig. 6.

Simulations for the four-stage model, given by an extension of Eq. (1), testing the impact of the behavior change immediately after the infection, or during stages 1, or 2, or 3 (ρ, μ, ω, and γ), respectively, which is interrupted during stages 1, or 2, or 3 (ξ, ψ, and κ), respectively. We compared variations of behavior changes in different stages and their reversions.

The epidemic peak is lower and more delayed when the same percentage of individuals changes its behavior at the onset of symptoms, i.e., they are moving from stage I₁ to I₂, even if all of them stop following CDC recommendations at the end of the most asymptomatic stage (I₂). In addition, this result holds even when the same percentage of those changing their behavior during the last stages of the infection (I₃) (Figs. 5(A) and 6(A)). Moreover, the epidemic peak is similar even when 20% of individuals change their behavior immediately upon infection, most likely due to the media risk communication, and when the same percentage of population alter their schedules at the onset of symptoms, even if 20% of them will resume their daily routines when entering the infection stage that follows (Figs. 5(B) and 6(B)). Epidemic severity is lower when 20% of individuals begin following CDC recommendations immediately upon infection, even if 20% or 50% of them resume their daily schedules at the onset of symptoms (this case may be unlikely), than 20% of individuals changing their daily routines at the end of the most asymptomatic stage (Figs. 5(C) and 6(C)). In Figures 5(D) and 6(D)–(F), we show further combinations of behavior changes and their impact on the time and amplitude of an epidemic peak. We conclude that it is most effective when individuals change their behavior immediately upon infection and when the onset of symptoms begins than during the last stage (s) of an infection.

4. CONCLUSIONS AND DISCUSSION

We showed that behavioral changes greatly influence the dynamics of the spread of influenza. It was shown in Ref. [26] that the epidemic peak is achieved in four weeks when using an SIR model. However, when behavioral changes are introduced, the epidemic peak may be delayed and significantly lowered (see Fig. 3 in Ref. [26] and Figs. 3–6).

Predictions from both models, three and four-stage, show that that prolonged change of behavior in the early stages of the infection is more effective than adjustments in daily routine during the last phase of an infection (Figs. 3 and 4). We also found that the epidemic peak is lowered and further delayed when individuals change their behavior immediately upon infection or at the onset of symptoms, than during the last stage of an infection, even if a certain percentage of the population stops following disease preventive recommendations (Figs. 5 and 6).

Our results regarding basic reproductive numbers for both models suggests that the most optimal strategy is to follow CDC recommendations even before the disease symptoms begin or immediately at the onset of symptoms and sustain these protective activities for the duration of the disease (Table III). Hence, media risk communication plays an important role in warning individuals in asymptomatic stages of an infection to take preventive measures during an outbreak.

Considering spontaneous behavior change in a model is beneficial, especially if the model results are being used to guide public health policies. In addition, behavioral changes can influence disease control strategies and estimation of the epidemiological parameters, thus, epidemiological predictions may be inaccurate if behavior is not considered.

Our results suggest that it is crucial to educate the public about non-pharmaceutical interventions that can reduce their probability of becoming infected. More research is needed about effective communication strategies and compliance by various demographic characteristics.